Lens-Oppositional Wild Geese Optimization Based Clustering Scheme for Wireless Sensor Networks Assists Real Time Disaster Management

1  Introduction

Currently, wireless sensor network (WSN) is widespread all around the globe and it is utilized as an appealing field among research communities because of their significant developments in real-time disaster monitoring applications. The design of WSNs for disaster management is beneficial due to the following reasons: some of them are connected with minimal expense, adaptability, and versatility, and notwithstanding the whimsical catastrophic event over time, it confines and disperses the proper data to the related sensor nodes (SN) with the smallest latency [1]. Every anticipation is required to monitor disasters in the WSN environment. WSN is a wise and minimal expense arrangement that empowers the productivity and dependability improvement of numerous modern applications like wellbeing and security observation, home and building robotization, and smart grid. The WSNs for the most part comprise an enormous amount of SNs which are low power and little in size [2]. These SNs can function as independent gadgets and be conveyed in different kinds of conditions. In any case, there are many difficulties to bring the WSNs into real-time applications.

One of the fundamental worries while fostering WSNs is to broaden their lifespan [3]. In numerous applications, an SN is controlled by a limited energy source, for example, a battery or a supercapacitor that confines the WSNs’ lifetime. Sustainable power sources like solar or wind are examined and incorporated into the SNs as of late for longer activity [4]. The SNs in WSNs are ordinarily gathered into groups, and this clustering technique is utilized in WSNs to guarantee the adaptability of the organization [5]. It likewise ensures proficient resource exploitation and the board of restricted network assets, saving energy and monitoring the solidness of the organization [6]. Clustering models can be derived in the WSN to assuring effective resource utilization, reduced transmission overhead, minimum energy consumption, and low interference [7,8]. It involves the process of portioning the network into several groups of clusters. In addition, each cluster owns a cluster head (CH) which is accountable for several operations such as data aggregation and transmission [9]. The remaining nodes in the cluster are called cluster members (CMs). It helps in proficiency in balancing the load among all nodes in the network and thereby improves the network lifetime (NLT). The clustering process is considered a non-deterministic polynomial-time (NP) hard optimization problem and is addressed by bio-inspired optimization algorithms [10].

Due to the energy-constrained sensor nodes, real-time monitoring of disaster zones via WSN is a hard operation. As a result, the clustering process can be used to increase node energy efficiency and enhance the network’s overall performance [11]. The Scope of the proposed work is needed to propose improved energy efficiency and the lifetime of WSNs in real-time disaster management. The Objectives of the proposed work are to perform effective data collection and transmission processes in disaster regions and also improve the convergence rate, energy efficiency, and lifetime of WSNs in real-time disaster management scenarios. The remainder of the paper is organized as follows, Section 2 analysis the related works involved in the Real-time monitoring of disaster areas using WSN. Section 3 describes the Proposed LOWGO-EAC technique. Section 4 then analyses the experimental data and results, including a performance comparison with alternative methodologies. Finally, Section 5 concludes the key results of the proposed research.

2  Related Works

Sharad et al. [12] developed a multi-hop routing approach with an established improved invasive weed-based elephant herd optimization (IIWEHO) approach. During this technique, the WSN node is simulated originally, and it has been able to the clustering procedure. In the meantime, the CH was chosen with a low energy-based adaptive clustering model with the hierarchy (LEACH) technique. Then the CH selection (CHS), multi-path routing was executed by the established IIWEH method. Priyanka et al. [13] implemented a dynamic CHS in all subsectors is executed utilizing the Whale Optimization Algorithm (WOA). It is the estimated performance of the presented technique concerning renewable energy (RE) and network lifetime (NLT). It can be analyzed using the presented method and demonstrate that a nominally balanced energy depletion was attainable from the circular WSN with splitting.

Mohan et al. [14] found the optimal routes for underwater using improved metaheuristics-based clustering with multihop routing protocol for underwater wireless sensor networks (IMCMR-UWSN) technique. The IMCMR-UWSN technique’s main goal is to select cluster heads (CHs) and optimal routes to a destination. Bai et al. [15] developed a data collection approach for HWSNs dependent upon the clustering technique presented. The sink introduces an extreme learning machine convolutional neural network (ELM-CNN) technique. The common (CM) node chooses CHs dependent upon the RE of SNs, the number of neighbor nodes, and the distance to sink. An optimum CH node was chosen with the adaptive learning of the online sequence ELM technique.

Gorgich et al. created [16] a novel approach was presented that addresses the problem of optimum power utilization in WSN. Therefore, utilizing the fish swarm optimization (FSO) technique, it can be presented an energy-aware routing protocol for WSNs that optimizes power utilization. The presented protocol is inspired by OPNET 11.5 simulator and related to the ERA protocol. Yadav et al. [17] presented a novel energy-aware CHS for hierarchical routing in WSN by a novel hybrid optimized approach. Additionally, the selective drives with particular conditions like energy stabilization, minimized distance amongst nodes, and minimized delay under the data broadcast. Khan et al. [18] develop a new method for infrared small target detection (ISTD) using total variation and partial sum minimization. In this work, the proposed model replaces the infrared patch, nuclear norm minimization of singular values, and the total variance.

Guiloufi et al. [19] designed an unequal clustering algorithm in the name of energy degree distance unequal clustering algorithm. This work uses the ‘Sierpinski triangle’ technique to spilt the network into unequal clusters. The benefits of this work are effective energy consumption and better network lifetime. The work is not considered the Residual Energy and Packet Loss Rate. It is the drawback of this work. Sennan et al. [20] implement an energy-aware cluster-based routing protocol for WSN-based IoT. The pros of the work are increased the network’s lifetime and throughput. The cons of the work are the need to strengthen the data security when transferring data from cluster member to base station.

This study proposes a novel Lens-Oppositional Wild Goose Optimization based Energy Aware Clustering (LOWGO-EAC) scheme for WSN-assisted real-time disaster management. The LOWGO-EAC technique derives a novel LOWGO algorithm by the integration of the lens oppositional-based learning (LOBL) concept with the traditional WGO algorithm to improve the convergence rate. Moreover, the LOWGO-EAC technique derives a fitness function (FF) involving three input parameters such as residual energy (RE), distance to BS (DBS), and node degree (ND). The experimental validation of the LOWGO-EAC model is carried out and the results are examined under several aspects.

3  The Proposed Model

In this study, a new LOWGO-EAC technique has been developed for disaster monitoring in the WSN environment. The presented LOWGO-EAC model has accomplished effective data collection and transmission processes in disaster regions. Besides, the LOWGO-EAC technique derives a FF involving three input parameters such as RE, DBS, and ND.

3.1 Energy Model

In this study, the first-order radio energy model is exploited. The energy spent by the node comprises three elements, namely, the transceiver, the processor, and the sensing unit. Since the maximum amount of energy is spent on transmission and reception, the energy spent on processing and sensing is not considered into account [21–25]. The energy spent by the communication unit can be formulated as follows in Eq. (1).

Ec(u)=Eccomm(u) (1)

The expended energy by the transceiver comprises transmission energy ETx and reception energy ERx , formulated as follows in Eqs. (2)–(4).

Ec(u)=ETx(k,d)+ERx(k) (2)

ETx(k,d)=Eelec×k+ϵamp×k×dk (3)

ERx(k)=Eelec×k (4)

where Eelec implies electrical energy, k : packet length, ϵamp : transmit amplifier, and d : the distance between two nodes. Several studies reported that the energy spent is related to the length of the data packets k and the distance between two nodes d. Therefore, the energy dissipation can be reduced by decreasing these two parameters. Fig. 1 illustrates the overall process of the LOWGO-EAC technique.

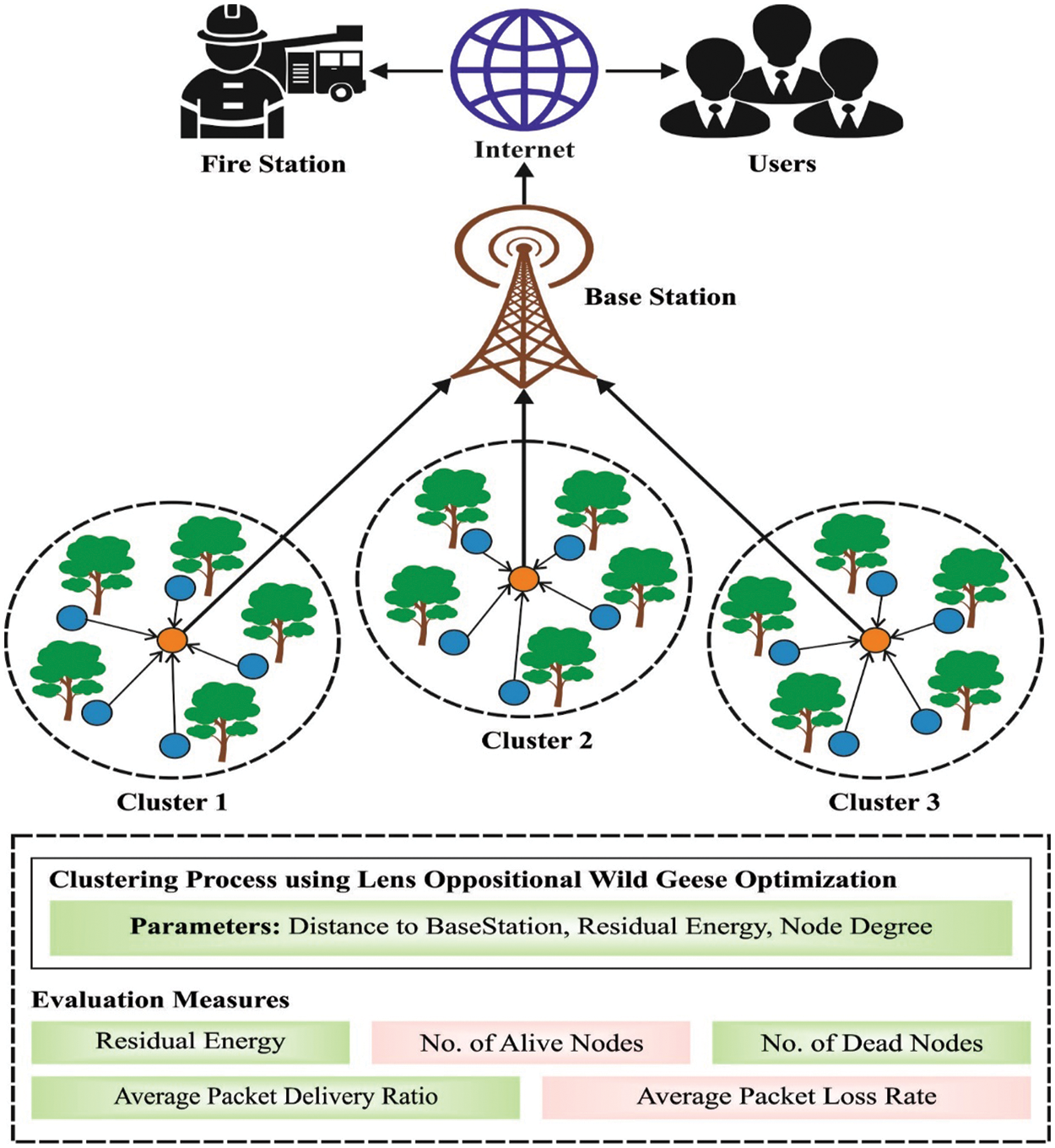
Figure 1: Overall process of LOWGO-EAC technique

3.2 Design of LOWGO Algorithm

The WGO algorithm is inspired by the behavior of wild geese in nature. It is used for modeling different aspects of their life like evolution, regular cooperative migration, and fatality. The mathematical modeling of the WGO algorithm is given in the following [26–29]:

The displacement and velocity equation considered the goose coordinate velocity as explained in the following in Eq. (5).

VjDItr+1=(R1,D×Vj,DItr+R2,D×(Vj+1,DItr−Vj−1,DItr))+R3,D×(Pj,DItr−Yj−1,DItr)+R4,D×(P+1j,DItr−Yj,DItr)+R5,D×(Pj+2,DItr−Yj+1,DItr)−R6,D×(Pj−1,DItr−Yj+2,DItr) (5)

The Dth dimensions of the existing place are YJ,D,PJ.′D and VJ,D . The arbitrary number R prefers the intervals of zero and one. Utilizing Eq. (5), the differences in all wild goose’s velocities and places are measured dependent upon the upfront and rear ember velocity. The place of a neighboring member is (Vj+1Itr,−VjItr−1) and Eq. (6) signifies the global optimum member.

Yj,D.V=PjItrD+R7,D×R8,D×((GDItr+Pj+1,DItr−2×Pj+1,DItr) +Vj,DItr+1)  (6)

The global optimum place amongst every member is GD. Fig. 2 showcases the steps involved in the WGO technique.

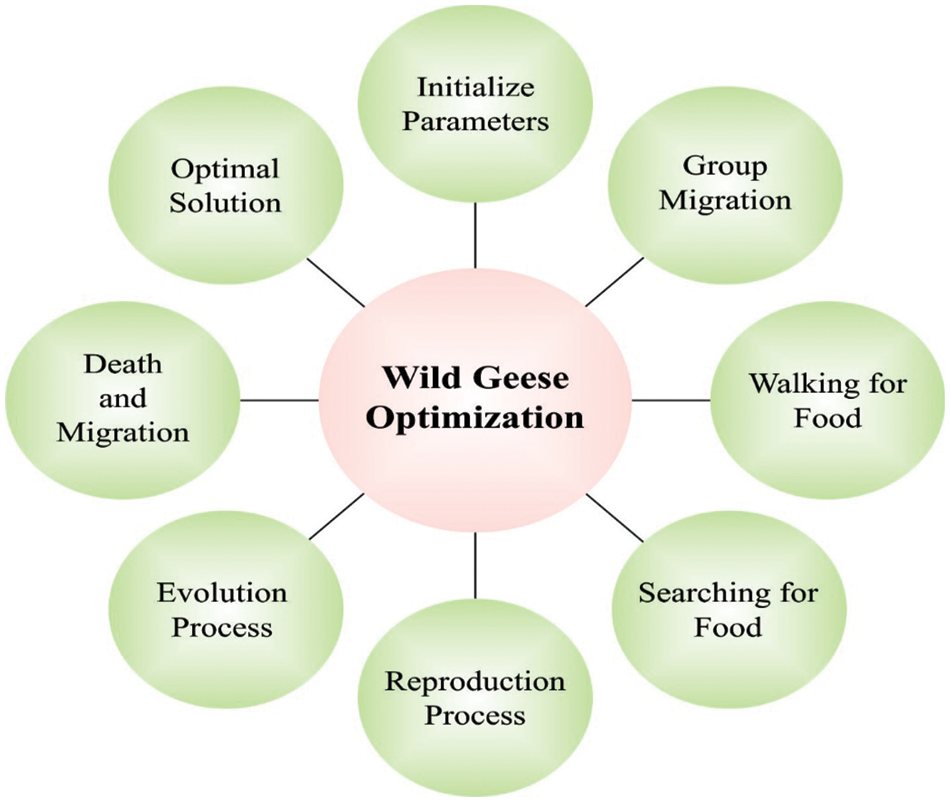
Figure 2: Steps involved in the WGO technique

The jth wild geese move forward the upfront member. The (j+1th) goose (q) attained by attempt jth geese. The below formula describes the search and walks of YjM wild geese to food in Eq. (7).

YjM=PjItr+R9,DD,D×R10,D×(Pj+1,D,Itr−PjItr) (7)

Reproduction and evolution are other phases of wild goose life. This procedure was modeled by combining the walk and searching for food (YjM) with migration (Yjy) . Wherever CR refers to the control parameter in Eq. (8).

Yj,DItr+1={Yj,DVifR11,D≤CRYj,DItr+1Otherwise (8)

For balancing performance, the compromised solution was recognized. During the technique iterations, this approach adjusts to a maximum amount of populations (MInitial) . During the last iteration, the population has linearly decreased to the last value (MFinal) in Eq. (9).

M=Round(MFinal−MInitial ∗ (FE/FEmaximum)) (9)

The amount of function estimation with their higher is FE and FEmaximum.

In this study, the LOWGO algorithm has been derived by the integration of the LOBL concept into the traditional WGO algorithm to improve the convergence rate. LOBL is employed to generate a solution closer to the global optima of the WGO algorithm with superior possibility. Therefore, during this case, the LOBL was employed for updating the candidate solution of the WGO algorithm under the exploration stage, enlarging the searching range, and supporting the technique for escaping from the local optimal. Taking the 1D searching space to illustrate, there is a convex lens with focal length f set at the base point O (the midpoint of the searching range [lb,ub]) . Furthermore, the object p with height h was located on the coordinate axis, and their projection is GX (candidate solution). The distance in the object to lens u is superior to twice f. With the lens imaging function, an inverted imaging p′ of height h∗ is obtained that is presented as GX∗ (reverse solution) on the x -axis. According to the rule of lens imaging and identical triangle, the geometrical connection attained is formulated as in Eq. (10).

(lb+ub)/2−GXGX∗−(lb+ub)/2=hh∗ (10)

At this point, assuming the scale factor n=h/h∗ , the reverse solution GX∗ was computed as transmitting in Eq. (11).

GX∗=lb+ub2 + lb+ub2n − GXn (11)

It can be apparent that if n=1 , is simplified as the common formulation of the OBL approach in Eq. (12).

GX∗=lb+ub−GX (12)

Therefore, it could regard the opposition-based learning (OBL) approach as a peculiar case of LOBL. Compared with OBL, the latter allows obtaining a dynamic reverse solution and a wider search range by tuning the scale factor n.

Usually, is extended as to D dimensional space in Eq. (13).

GXj∗=(lbj+ubj)/2+(lbj+ubj)/2n−GXj/n (13)

whereas lbj and ubj signify the lower and upper limits of jth dimensional correspondingly, j=1,2,⋯D,GXj∗ signifies the inverse solution of GXj from the jth dimensional.

If a novel inverse solution is created, there is no guarantee that it can be always superior to the existing candidate solution from the wild goose position. Thus, it can be essential for evaluating the fitness values of the inverse as well as candidate solutions, afterward the fitter one is chosen for continuing participation in the succeeding exploitation stage that is explained in Eq. (14).

GXnext={GX∗,ifF(GX∗)<F(GX)GX,otherwise (14)

whereas GX∗ stands for the reverse solution created by LOBL, GX represents the existing candidate solution, GXnext implies the chosen wild goose for continuing the succeeding place upgrade, and F refers to the FF of the problem. The pseudo-code of the LOBL technique is illustrated in Algorithm 1.

3.3 Algorithmic Process Involved in LOWGO-EAC Technique

For achieving the maximum lifetime in the disaster monitoring process, the LOWGO-EAC technique derives a FF for the clustering process involving three input parameters such as RE, DBS, and ND [30]. Once the nodes are arbitrarily deployed in the target region, the information collection process is carried out. The LOWGO algorithm derives a FF using three parameters as given in the following.

The ND of the target area can be defined as the ratio of the number of alive nodes present in the specific communication range to the total number of alive nodes in the network. It can be mathematically defined as follows in Eq. (15).

Density,d=CnTn (15)

The distance is defined by the product of node density and average distance as given below in Eq. (16).

Distance,  D=d∗∑dicndp  (16)

The energy (e) of every individual node can be computed using the difference between the energy spent by the CHs and the ratio of average energy. It can be mathematically represented using Eq. (17):

Energy, e=E(p)∑E(pi)cn−(D∗n) (17)

The FF (f) of the LOWGO algorithm is inversely proportional to the density of nodes that exist in the communication region, as given below in Eq. (18).

Fitness,f∝1d (18)

The aim of the LOWGO-EAC technique is the maximization of the fitness value and the node with maximum energy, minimum distance, and low degree can be considered as CHs, and thus the weight values were α1>α3>α2 . Therefore, the presented FF involving α1,α2 , and α3 , is represented using Eq. (19).

f=(α∗e)+(α∗D)+α3d (19)

where α1,α2 , and α3 hold non-negative values in the interval of [0, 1], such that α1+α2+α3=1 .

4  Experimental Validation

This section investigates the performance of the LOWGO-EAC model under different locations of the sink. Table 1 inspects the RER examination of the LOWGO-EAC model against existing models under distinct round and sinks positions. Fig. 3 showcases the simulation outcomes of the LOWGO-EAC model in terms of RER under the sink position of (0, 100). The experimental outcomes indicated that the LOWGO-EAC model has resulted in maximum RER over the other methods. For instance, with sink location (0, 100) and 5 rounds, the LOWGO-EAC model has accomplished an enhanced RER of 44.67 J, whereas the energy-efficient ensemble clustering methods-black widow optimization (EECM-BWO), energy-efficient cluster head selection, and routing (ECHSR), Two-tier particle swarm optimization-clustering and routing (TPSO-CR), and particle swarm optimization-hashing (PSO-HAS) models have obtained reduced RER of 48.90, 48.78, 48.40, and 47.40 J respectively. Moreover, with 40 rounds, the LOWGO-EAC model has gained a maximum RER of 12.80 J, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have obtained reduced RER of 10.41, 3.11, 0, and 0 J respectively.

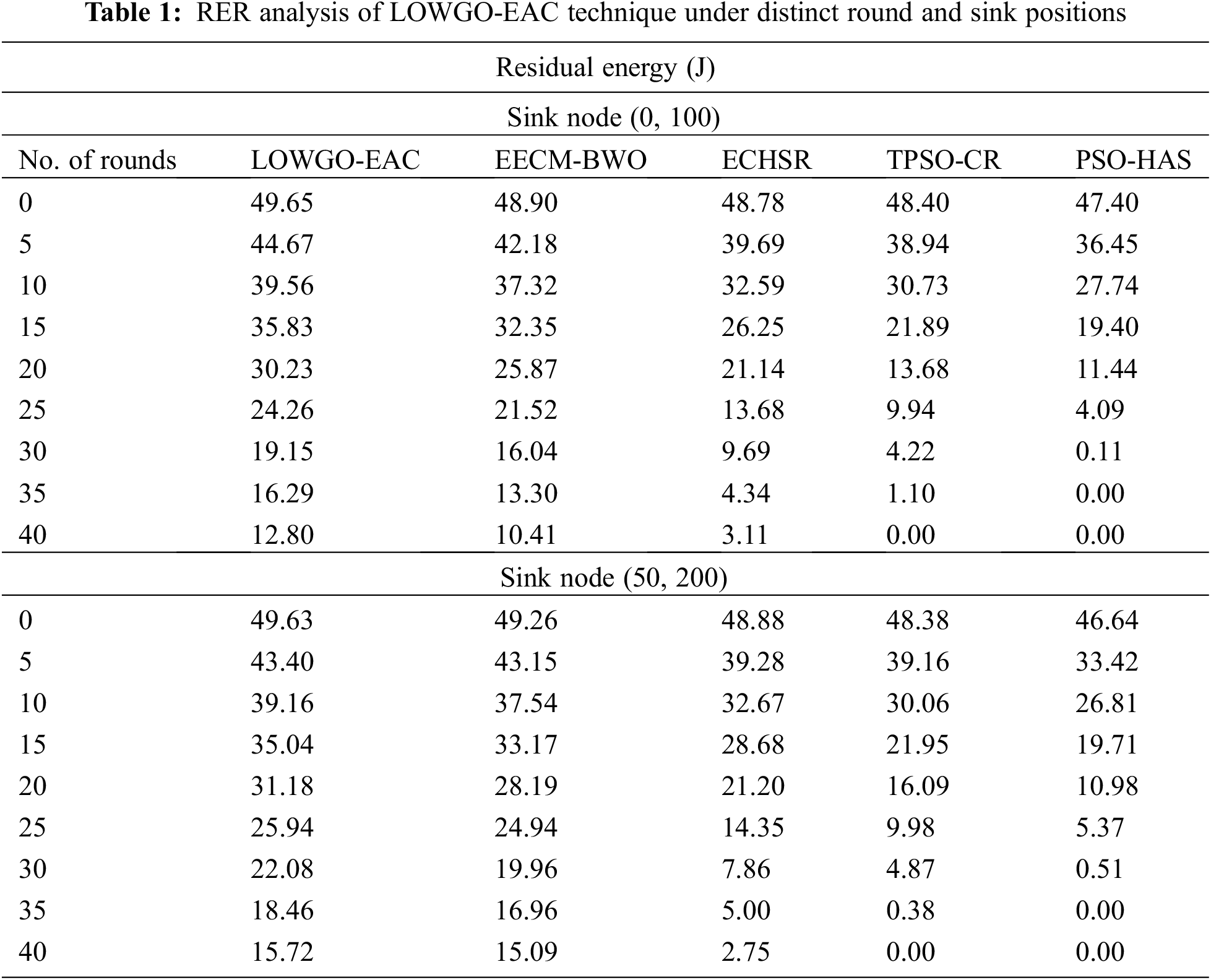
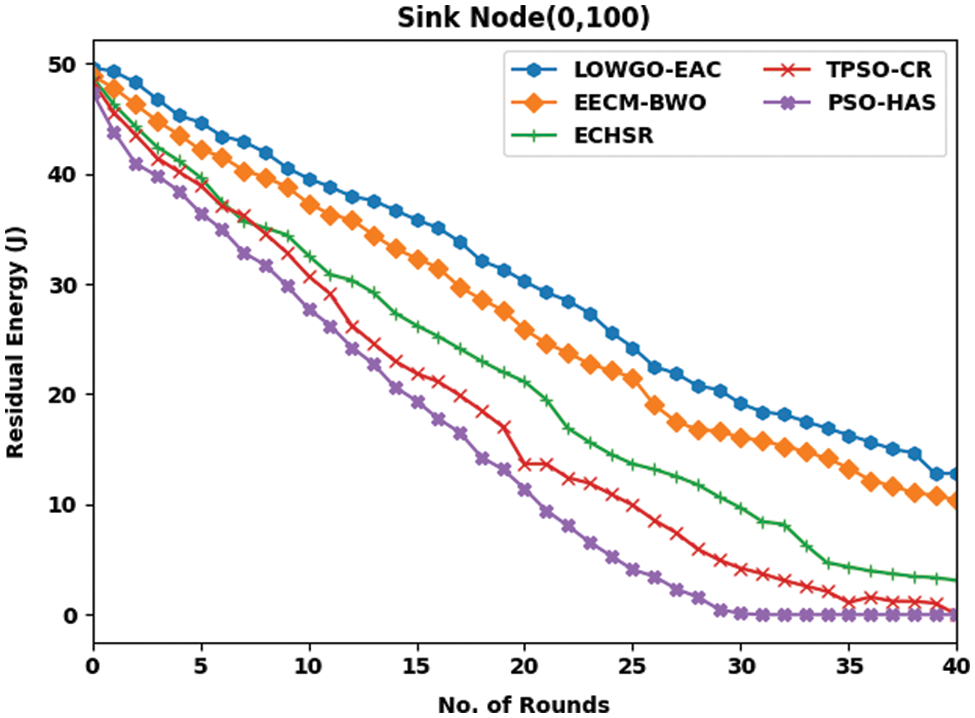
Figure 3: RER analysis of LOWGO-EAC technique under the sink position of (0, 100)

Fig. 4 offers a brief investigation of the LOWGO-EAC model in terms of RER under the sink position of (50, 200). The figure reveals that the LOWGO-EAC model has resulted in maximum RER over the other methods. For instance, with 5 rounds, the LOWGO-EAC model has resulted in an improved RER of 49.63 J, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have accomplished RER of 49.26, 48.88, 48.38, and 46.64 J respectively. Moreover, with 40 rounds, the LOWGO-EAC model has gained a maximum RER of 15.72 J, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have gained the least ARE of 15.09, 2.75, 0, and 0 J respectively.

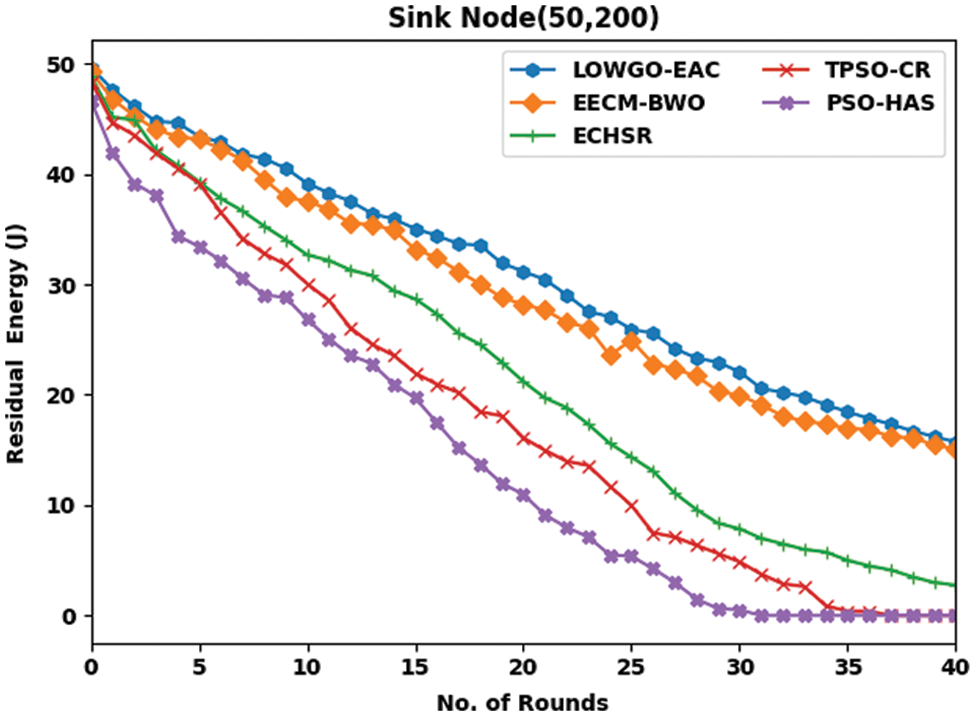
Figure 4: RER analysis of LOWGO-EAC technique under the sink position of (50, 200)

Table 2 reviews the number of alive node (NOAN) inspections of the LOWGO-EAC model with recent approaches under dissimilar round and sink positions. Fig. 5 portrays the experimental output of the LOWGO-EAC model in terms of NOAN under the sink position of (0, 100). The results highlighted that the LOWGO-EAC model has reached improved NOAN over the other methods. For instance, with sink location (0, 100) and 5 rounds, the LOWGO-EAC model has gained a higher NOAN of 100, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have accomplished lower NOAN of 99, 98, 93, 82 respectively. Furthermore, with 40 rounds, the LOWGO-EAC model has accomplished an increased NOAN of 65, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have resulted in decreased NOAN of 55, 48, 36, and 24 respectively.

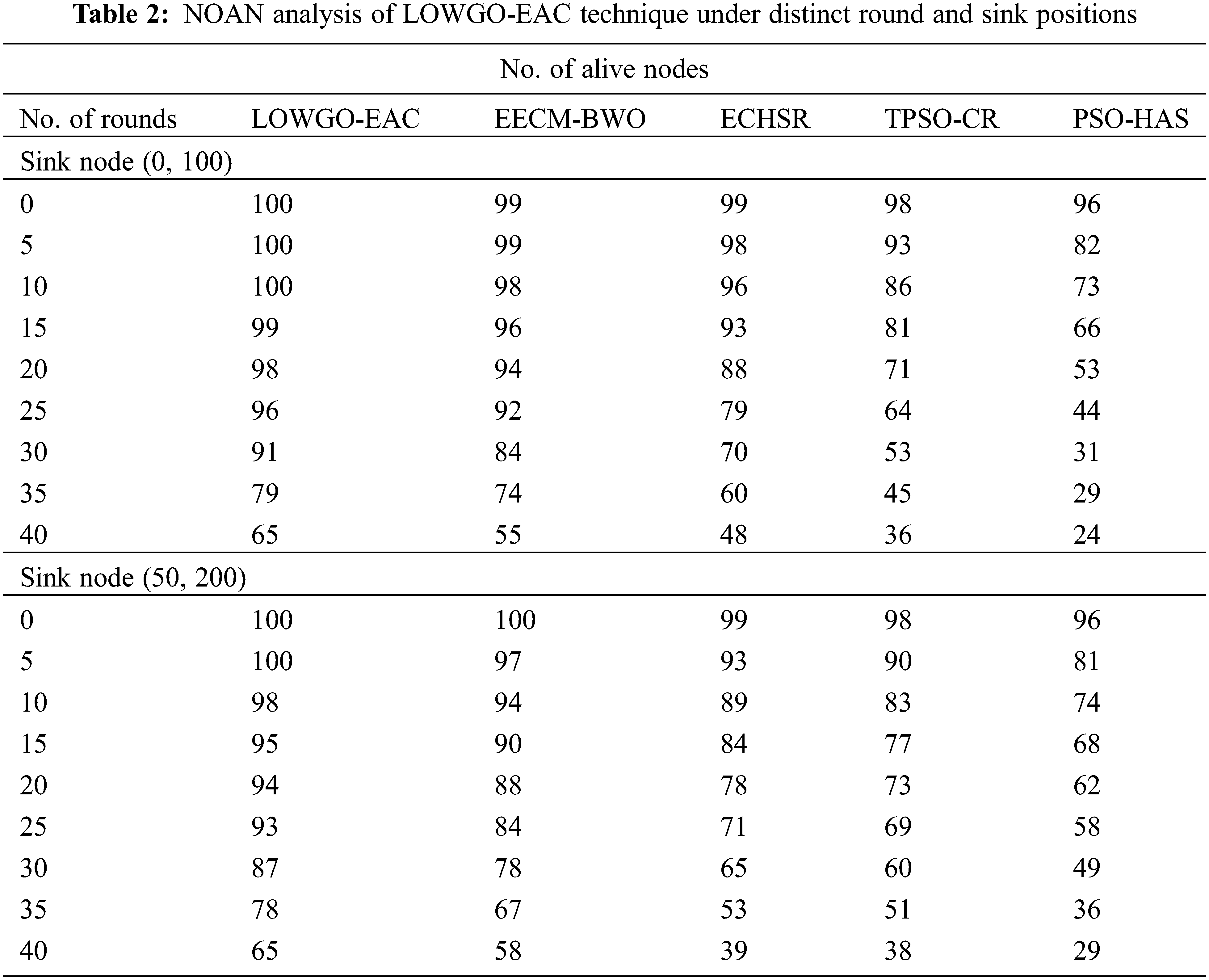
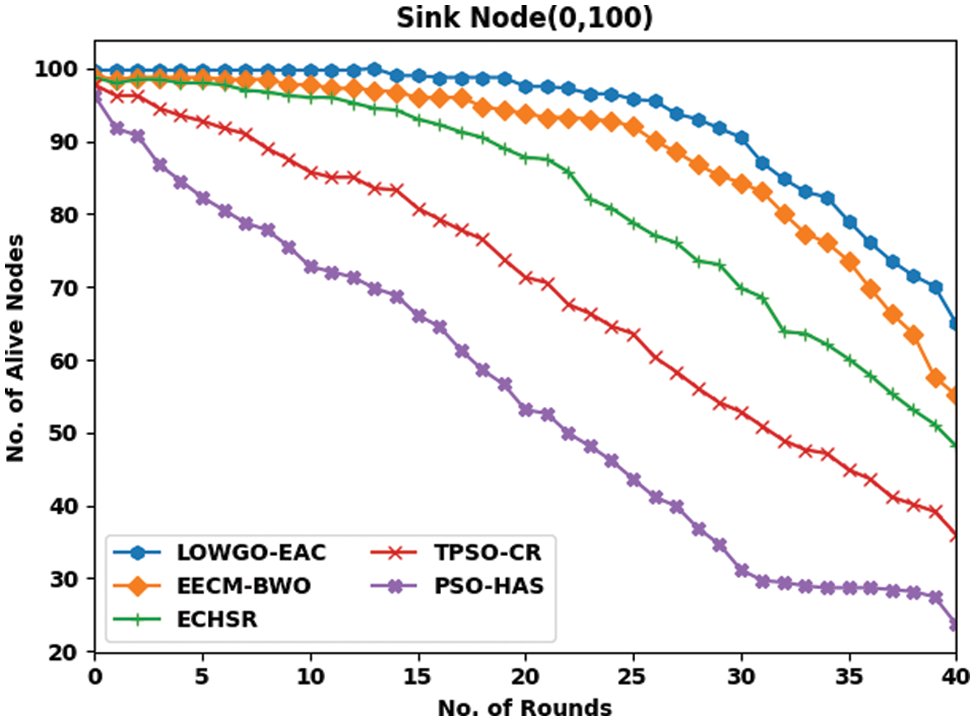
Figure 5: NOAN analysis of LOWGO-EAC technique under the sink position of (0, 100)

Fig. 6 reveals a detailed investigation of the LOWGO-EAC model in terms of NOAN under the sink position of (50, 200). The figure exposes that the LOWGO-EAC model has resulted in supreme NOAN over the other methods. For instance, with 5 rounds, the LOWGO-EAC model has reached a better NOAN of 100, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have resulted in NOAN of 97, 93, 90, and 81 respectively. Along with that, with 40 rounds, the LOWGO-EAC model has provided an increased NOAN of 65, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have reached decreased ARE of 158, 39, 38, and 29 respectively.

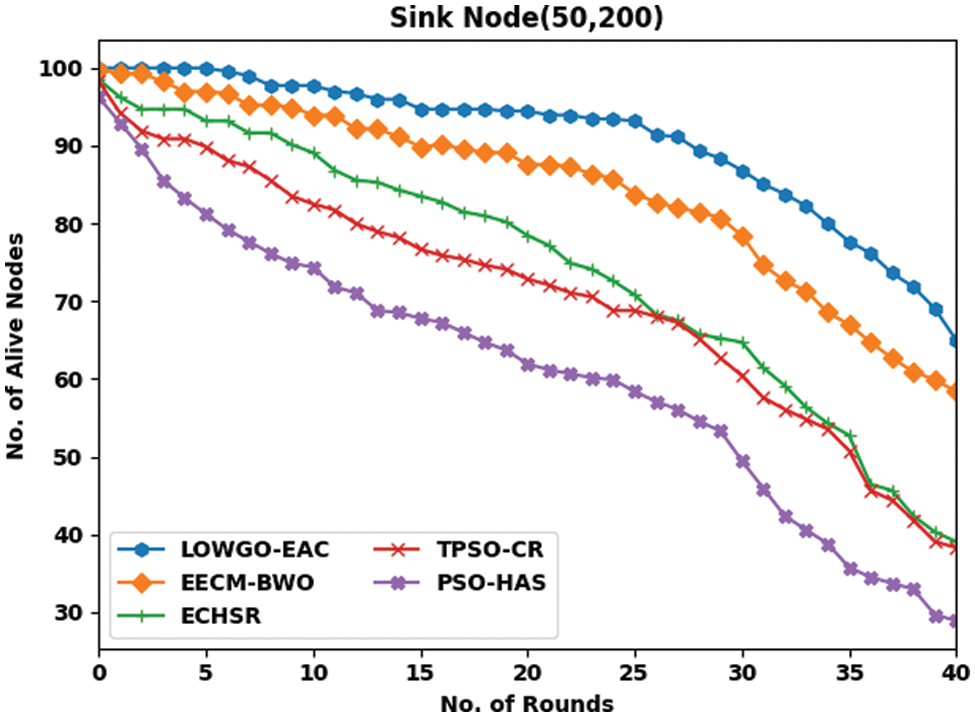
Figure 6: NOAN analysis of LOWGO-EAC technique under the sink position of (50, 200)

Table 3 studies the NODN analysis of the LOWGO-EAC model with the present model under diverse round and sink positions.

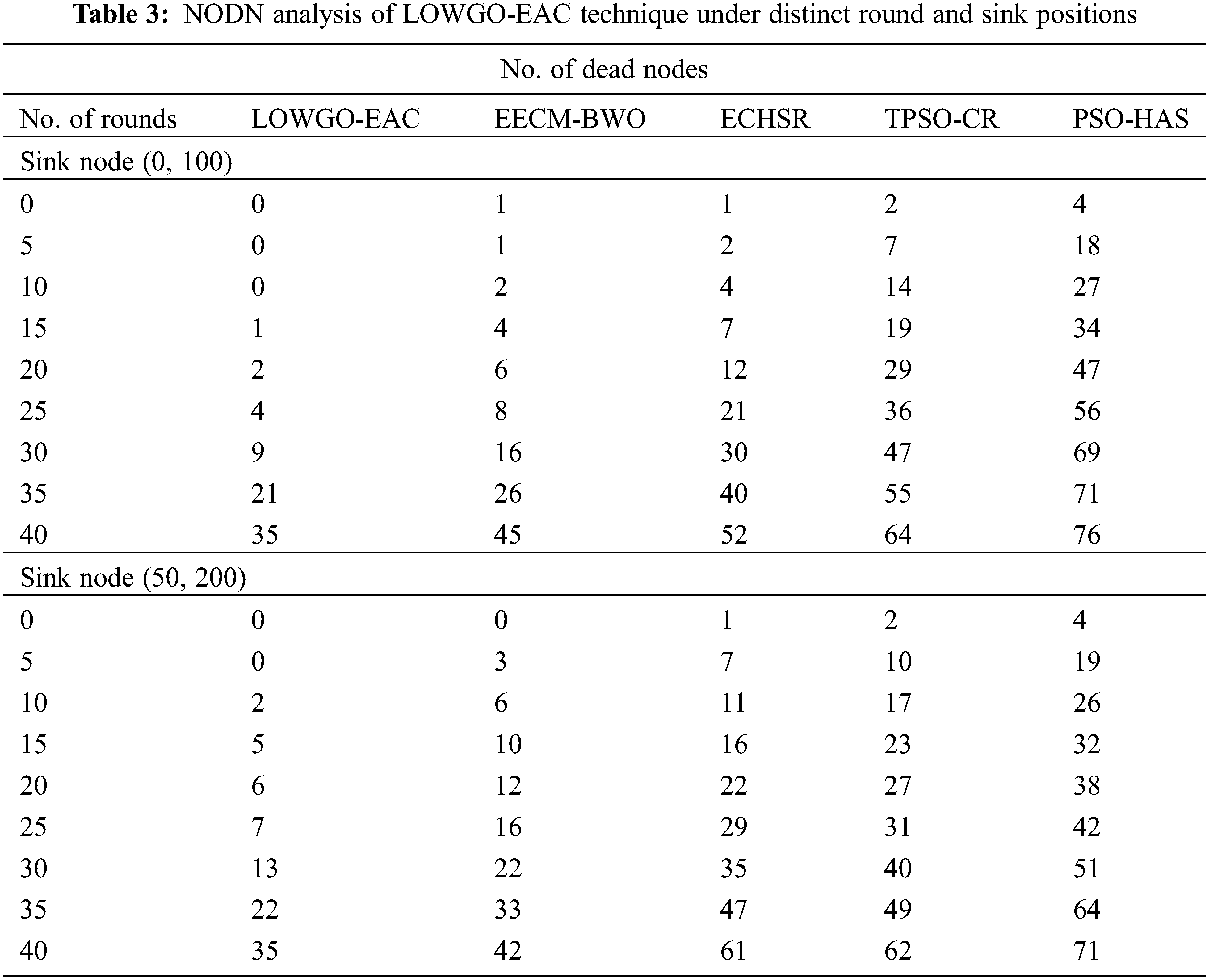
Fig. 7 exhibits the simulation outcomes of the LOWGO-EAC model in terms of NODN under the sink position of (0, 100). The obtained outcomes represented that the LOWGO-EAC model has exhibited minimal NODN over the other methods. For instance, with sink location (0, 100) and 5 rounds, the LOWGO-EAC model has resulted in a lower NODN of 0, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have provided higher NODN of 1, 2, 7, and 18 respectively. Moreover, with 40 rounds, the LOWGO-EAC model has accomplished an NODN of 35, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have demonstrated minimal NODN of 45, 52, 64, and 76 respectively.

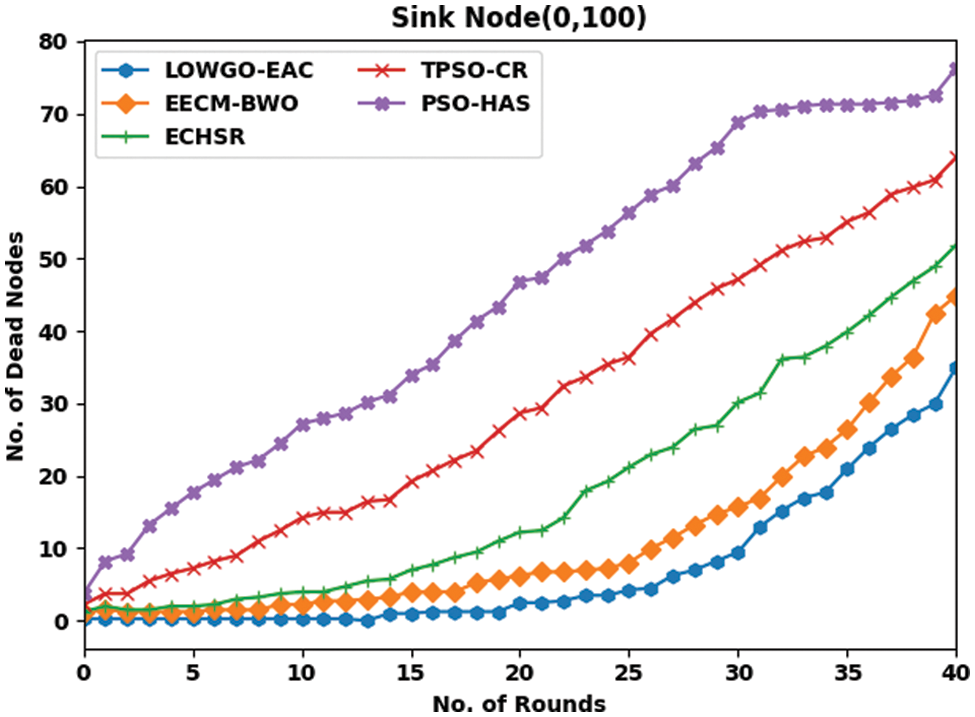
Figure 7: NODN analysis of LOWGO-EAC technique under the sink position of (0, 100)

Fig. 8 demonstrates a detailed inspection of the LOWGO-EAC model in terms of NODN under the sink position of (50, 200). The figure exposes that the LOWGO-EAC model has resulted in maximum NODN over the other methods. For instance, with 5 rounds, the LOWGO-EAC model has resulted in an inferior NODN of 0, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have accomplished superior NODN of 3, 7, 10, and 19 respectively. Moreover, with 40 rounds, the LOWGO-EAC model has gained an NODN of 35, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have reached the extreme ARE of 42, 61, 62, and 71 respectively.

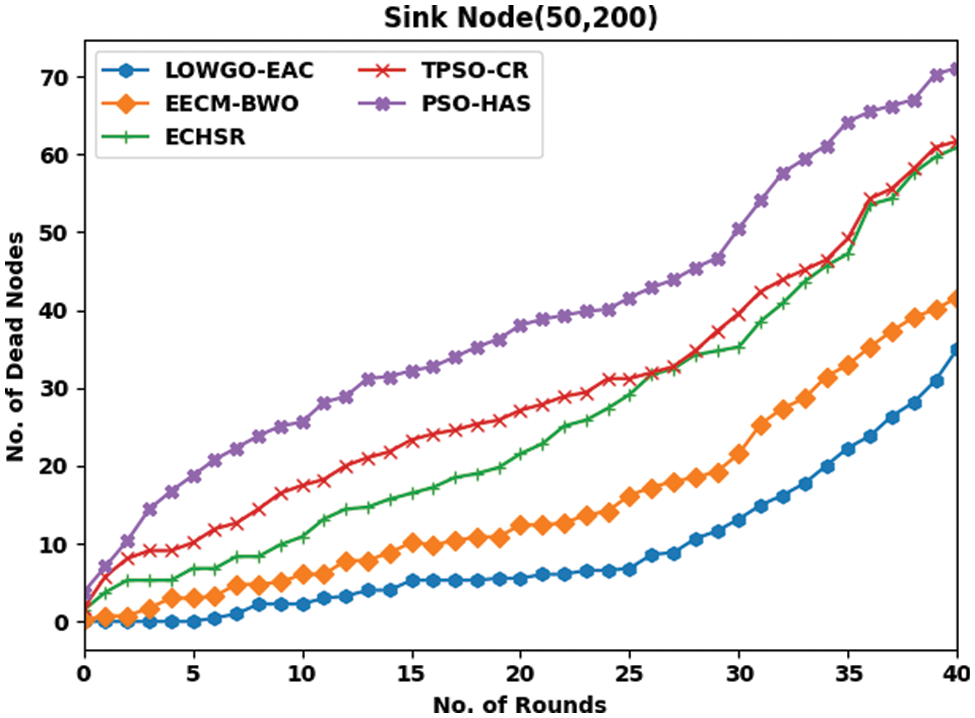
Figure 8: NODN analysis of LOWGO-EAC technique under the sink position of (50, 200)

Table 4 offers a detailed APDR and APLR examination of the LOWGO-EAC model with recent models under distinct sink locations [31]. Fig. 9 offers a brief EXAMINATION of the LOWGO-EAC model with other models. The results indicated that the LOWGO-EAC model has offered higher ARE under two sink locations. For instance, with sink location (0, 100), the LOWGO-EAC model has attained an increased ARE of 30.24 J, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have obtained reduced ARE of 27.24, 21.6, 18.35, and 15.42 J respectively. Followed by, sink location (50, 200), the LOWGO-EAC model has reached a maximum ARE of 30.98 J, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have gained minimal ARE of 29.31, 21.84, 18.26, and 14.82 J respectively.

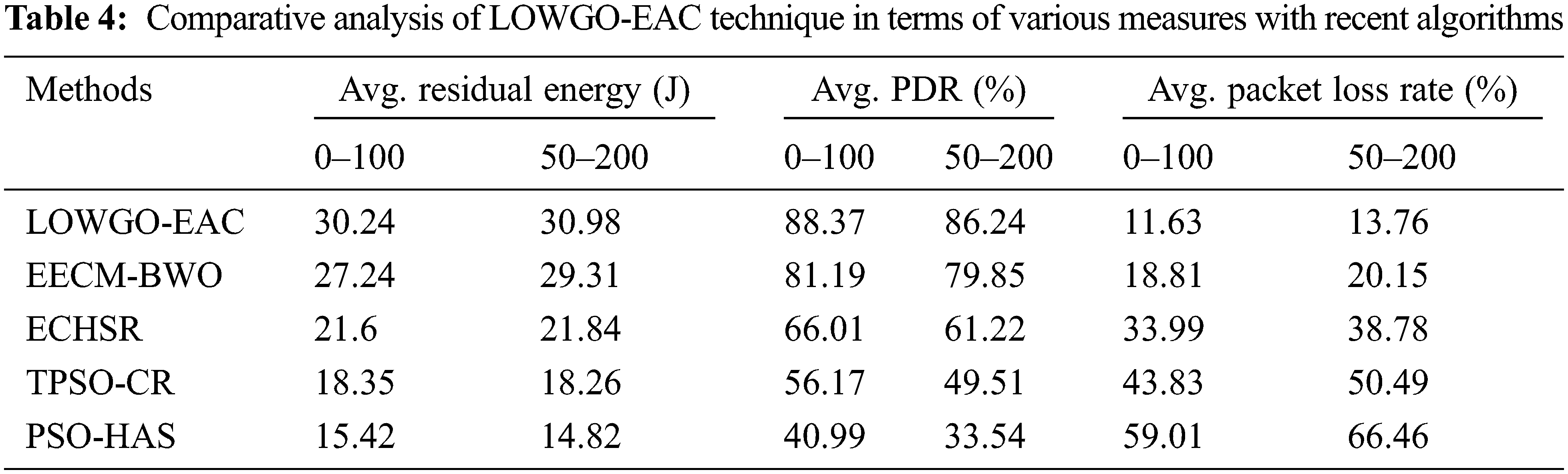
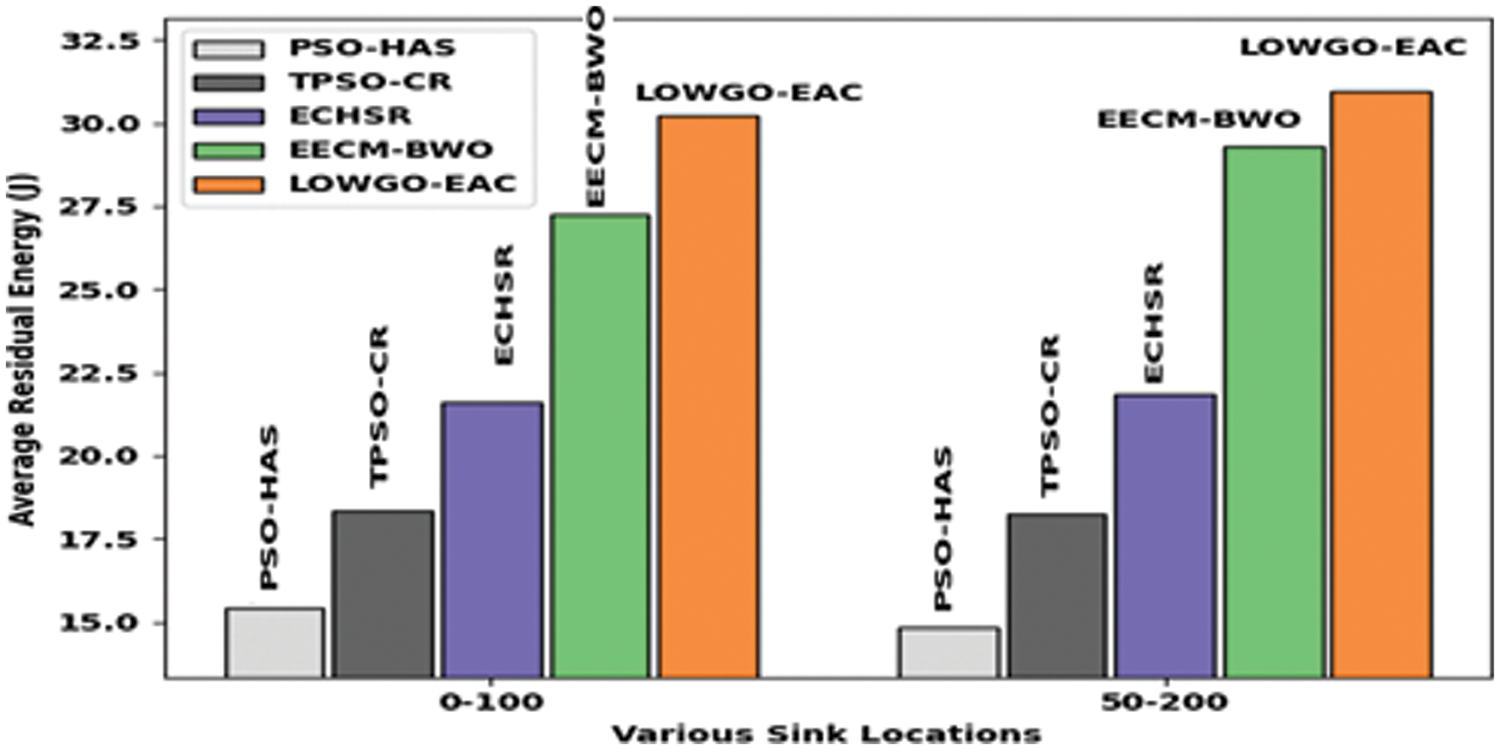
Figure 9: Analysis of LOWGO-EAC technique with recent algorithms

Next, a brief APDR inspection of the LOWGO-EAC model with existing approaches were performed in Fig. 10. The figure reports that the LOWGO-EAC model has accomplished increased APDR under two sink locations. For instance, with sink location (0, 100), the LOWGO-EAC model has reached an improved APDR of 88.37%, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have gained APDR of 81.19%, 66.01%, 56.17%, and 40.99% respectively. Besides, with sink location (50, 200), the LOWGO-EAC model has provided an enhanced APDR of 86.24%, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have offered decreased APDR of 79.85%, 61.22%, 49.51%, and 33.54% respectively.

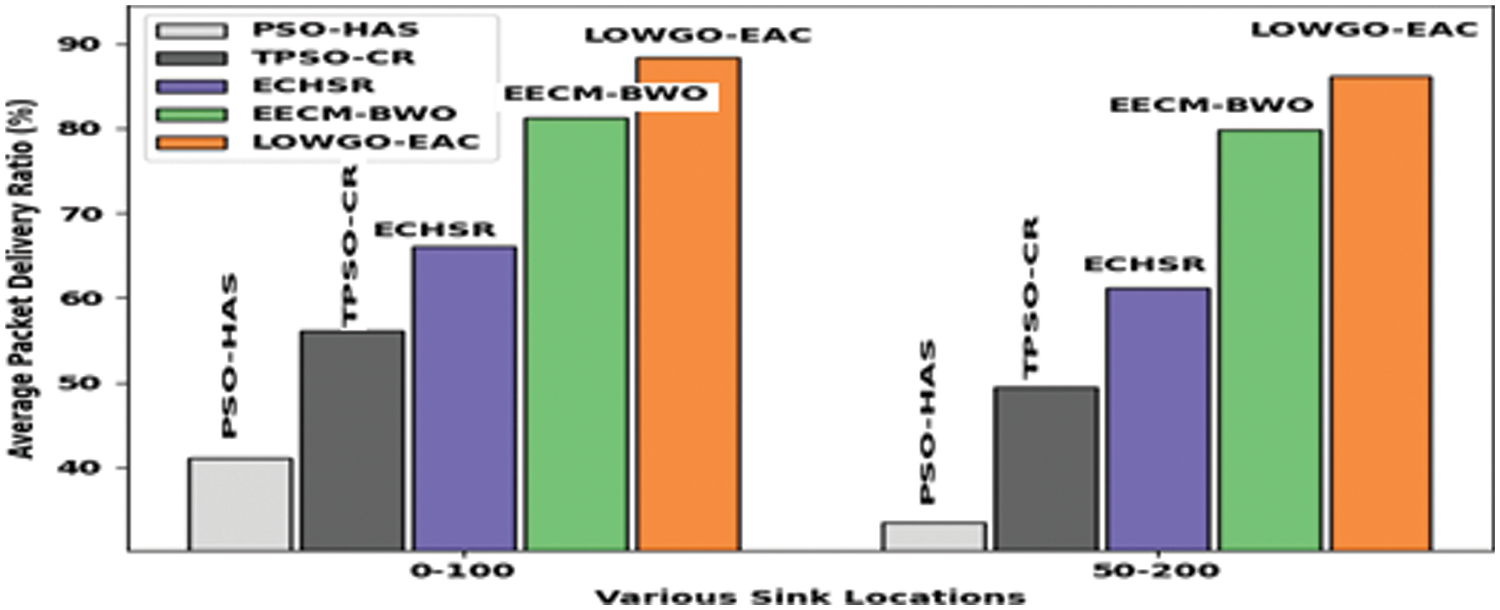
Figure 10: APDR analysis of LOWGO-EAC technique with recent algorithms

Finally, a detailed comparative study of the LOWGO-EAC model with other models of APLR has been performed in Fig. 11. The experimental outcome reported that the LOWGO-EAC model has resulted in APLR under two sink locations. For instance, with sink location (0, 100), the LOWGO-EAC model has attained a minimal APLR of 11.63%, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have offered a maximum APLR of 18.81%, 33.99%, 43.83%, and 33.54% respectively. In addition, with sink location (50, 200), the LOWGO-EAC model has reached a maximum APLR of 13.76%, whereas the EECM-BWO, ECHSR, TPSO-CR, and PSO-HAS models have gained minimal APLR of 20.15%, 38.87%, 50.49%, and 66.46% respectively.

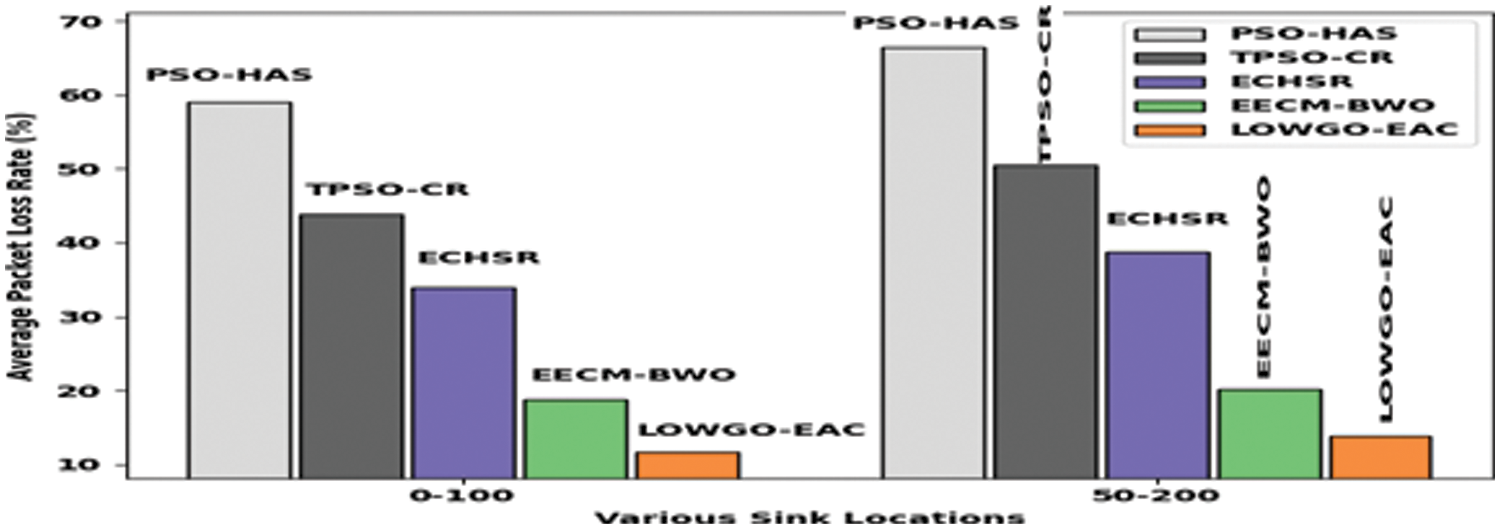
Figure 11: APLR analysis of LOWGO-EAC technique with recent algorithms

From the above-mentioned results and discussion, it can be confirmed that the LOWGO-EAC model has accomplished the maximum performance on WSN-assisted disaster management applications.

5  Conclusion

In this study, a new LOWGO-EAC technique has been developed for disaster monitoring in the WSN environment. The presented LOWGO-EAC model has accomplished effective data collection and transmission processes in disaster regions. Besides, the LOWGO-EAC technique derives a FF involving three input parameters such as RE, DBS, and ND. The proposed LOWGO-EAC technique can accomplish improved energy efficiency and lifetime of WSNs in real-time disaster management scenarios. The experimental validation of the LOWGO-EAC model is carried out and the results are examined under several aspects. Extensive comparative studies reported the enhanced performance of the LOWGO-EAC model over the recent approaches. In the future, data aggregation models can be designed to improve the lifetime of WSNs.

Acknowledgement: “The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4281755DSR01)”.

Funding Statement: This research is funded by the Deanship of Scientific Research at Umm Al-Qura University, Grant Code: 22UQU4281755DSR01.

Availability of Data and Materials: Available Based on Request. The datasets generated and/or analyzed during the current study are not publicly available due to the extension of the submitted research work and are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. J. Wilson and A. S. Radhamani, “Real time flood disaster monitoring based on energy efficient ensemble clustering mechanism in wireless sensor network,” Software: Practice and Experience, vol. 52, no. 1, pp. 254–276, 2022. [Google Scholar]

 2.  J. Uthayakumar, M. Elhoseny and K. Shankar, “Highly reliable and low-complexity image compression scheme using neighborhood correlation sequence algorithm in WSN,” IEEE Transactions on Reliability, vol. 69, no. 4, pp. 1398–1423, 2020. [Google Scholar]

 3.  S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

 4.  J. Uthayakumar, T. Vengattaraman and P. Dhavachelvan, “A new lossless neighborhood indexing sequence (NIS) algorithm for data compression in wireless sensor networks,” Ad Hoc Networks, vol. 83, no. 1, pp. 149–157, 2019. [Google Scholar]

 5.  M. P. Swapna and G. Satyavathy, “Energy-aware optimal clustering and secure routing protocol for heterogeneous wireless sensor network,” International Journal of Computer Networks and Applications, vol. 9, no. 1, pp. 12–21, 2022. [Google Scholar]

 6.  S. Arjunan and S. Pothula, “A survey on unequal clustering protocols in wireless sensor networks,” Journal of King Saud University-Computer and Information Sciences, vol. 31, no. 3, pp. 304–317, 2019. [Google Scholar]

 7.  S. Ali and R. Kumar, “Hybrid energy efficient network using firefly algorithm, PR-PEGASIS and ADC-ANN in WSN,” Sensors International, vol. 3, no. 1, pp. 100154, 2022. [Google Scholar]

 8.  R. Samadi and J. Seitz, “EEC-GA: Energy-efficient clustering approach using genetic algorithm for heterogeneous wireless sensor networks,” in Proc. 2022 Int. Conf. on Information Networking (ICOIN), IEEE, Bangkok, Thailand, pp. 280–286, 2022. [Google Scholar]

 9.  S. Arjunan, S. Pothula and D. Ponnurangam, “F5N-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. 1–14, 2018. [Google Scholar]

10. S. Famila, A. Jawahar, A. Sariga and K. Shankar, “Improved artificial bee colony optimization based clustering algorithm for SMART sensor environments,” Peer-to-Peer Networking and Applications, vol. 13, no. 4, pp. 1071–1079, 2020. [Google Scholar]

11. T. Tamilvizhi, R. Surendran, C. A. T. Romero and M. Sadish, “Privacy preserving reliable data transmission in cluster based vehicular adhoc networks,” Intelligent Automation & Soft Computing, vol. 34, no. 2, pp. 1265–1279, 2022. [Google Scholar]

12. H. V. Sharad, S. R. Desai and K. Y. Krishnrao, “Energy-aware multipath routing in WSN using improved invasive weed elephant herd optimization,” International Journal of Pervasive Computing and Communications, Online First, 2022. [Google Scholar]

13. B. N. Priyanka, R. Jayaparvathy and D. DivyaBharathi, “Efficient and dynamic cluster head selection for improving network lifetime in WSN using whale optimization algorithm,” Wireless Personal Communications, vol. 123, no. 1, pp. 1467–1481, 2022. [Google Scholar]

14. P. Mohan, N. Subramani, Y. Alotaibi, S. Alghamdi, O. I. Khalaf et al., “Improved metaheuristics-based clustering with multihop routing protocol for underwater wireless sensor networks,” Sensors, vol. 22, no. 4, pp. 1–16, 2022. [Google Scholar]

15. Y. Bai, L. Cao, S. Wang, H. Ding and Y. Yue, “Data collection strategy based on OSELM and gray wolf optimization algorithm for wireless sensor networks,” Computational Intelligence and Neuroscience, vol. 2022, no. 4489436, pp. 1–18, 2022. [Google Scholar]

16. S. Gorgich and S. Tabatabaei, “Proposing an energy-aware routing protocol by using fish swarm optimization algorithm in WSN (wireless sensor networks),” Wireless Personal Communications, vol. 119, no. 3, pp. 1935–1955, 2021. [Google Scholar]

17. R. K. Yadav and R. P. Mahapatra, “Energy aware optimized clustering for hierarchical routing in wireless sensor network,” Computer Science Review, vol. 41, no. 100417, pp. 1–10, 2021. [Google Scholar]

18. U. U. Khan, N. Dilshad, M. H. Rehmani and T. Umer, “Fairness in cognitive radio networks: Models, measurement methods, applications, and future research directions,” Journal of Network and Computer Applications, vol. 73, no. 1, pp. 12–26, 2016. [Google Scholar]

19. A. B. F. Guiloufi, N. Nasri and A. Kachouri, “An energy-efficient unequal clustering algorithm using ‘Sierpinski Triangle’ for WSNs,” Wireless Personal Communications, vol. 88, no. 3, pp. 449–465, 2016. [Google Scholar]

20. S. Sennan, K. Gopalan, Y. Alotaibi, D. Pandey and S. Alghamdi, “EACR-LEACH: Energy-aware cluster-based routing protocol for WSN based IoT,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2159–2174, 2022. [Google Scholar]

21. V. D. Vinayaki and R. Kalaiselvi, “Multithreshold image segmentation technique using remora optimization algorithm for diabetic retinopathy detection from fundus images,” Neural Processing Letters, vol. 54, pp. 2363–2384, 2022. [Google Scholar]

22. T. Tamilvizhi and P. Varthini, “Cessation of overloaded host by increase the inter-migration time in cloud data,” Journal of Theoretical and Applied Information Technology, vol. 95, no. 3, pp. 654–660, 2017. [Google Scholar]

23. K. S. Arikumar, V. Natarajan and S. C. Satapathy, “EELTM: An energy efficient lifetime maximization approach for WSN by PSO and fuzzy-based unequal clustering,” Arabian Journal for Science and Engineering, vol. 45, no. 12, pp. 10245–10260, 2020. [Google Scholar]

24. S. Sennan, D. Pandey, Y. Alotaibi and S. Alghamdi, “A novel convolutional neural networks based spinach classification and recognition system,” Computers, Materials & Continua, vol. 73, no. 1, pp. 343–361, 2022. [Google Scholar]

25. Manju, S. Singh, S. Kumar, A. Nayyar, F. Al-Turjman et al., “Proficient QoS-based target coverage problem in wireless sensor networks,” IEEE Access, vol. 8, no. 1, pp. 74315–74325, 2020. [Google Scholar]

26. T. Tamilvizhi, R. Surendran, K. Anbazhagan and K. Rajkumar, “Quantum behaved particle swarm optimization-based deep transfer learning model for sugarcane leaf disease detection and classification,” Mathematical Problems in Engineering, vol. 2022, no. 3452413, pp. 1–12, 2022. [Google Scholar]

27. M. Biabani, H. Fotouhi and N. Yazdani, “An energy-efficient evolutionary clustering technique for disaster management in IoT networks,” Sensors, vol. 20, no. 9, pp. 1–26, 2020. [Google Scholar]

28. Y. Alotaibi, “A new meta-heuristics data clustering algorithm based on tabu search and adaptive search memory,” Symmetry, vol. 14, no. 3, pp. 1–15, 2022. [Google Scholar]

29. P. Kollapudi, S. Alghamdi, N. Veeraiah, Y. Alotaibi, S. Thotakura et al., “A new method for scene classification from the remote sensing images,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1339–1355, 2022. [Google Scholar]

30. C. N. Vanitha, S. Malathy, R. K. Dhanaraj and A. Nayyar, “Optimized pollard route deviation and route selection using Bayesian machine learning techniques in wireless sensor networks,” Computer Networks: The International Journal of Computer and Telecommunications Networking, vol. 216, no. 109228, 2022. [Google Scholar]

31. A. M. Shatwan, “Visual pollution and the architecture of façade design: A case study in Jeddah,” Journal of Umm Al-Qura University for Engineering and Architecture, vol. 12, no. 2, pp. 26–29, 2021. [Google Scholar]