A Cross-Plane Color Image Encryption Algorithm Based on 1D-SLM

1  Introduction

Digital images can express information more intuitively, so the transmission of information through images has great applications [1–3]. The ensuing transmission process brings many security risks. Many image protection algorithms have been proposed nowadays [4–8]. Chaos and cryptography have many similarities and connections [9–11]. A chaotic system can generate a pseudo-random key stream with good performance, which is unpredictable and very suitable for cryptography [12–14].

In order to design efficient and secure cryptosystems, image encryption algorithms combined with chaos have gradually become a hot field [15,16]. Kang et al. used two identical 4D chaotic systems to couple into an 8D chaotic system. The system has eight initial values and eight control parameters. The key stream of the cryptosystem is generated by this 8D chaotic system, and combined with 2D-VMD, a new image encryption method is proposed [17]. Yu et al. proposed a 6D fractional-order chaotic system called 6D-FMHNN. They studied this system’s coexistence attractor characteristics and applied it to image encryption. The designed algorithm is secure and sensitive to secret keys [18]. Although high-dimensional chaotic systems have more control parameters and can provide a larger parameter space for cryptosystems, their keystream generation efficiency is not high [19–21]. The low-dimensional chaotic system has smaller control parameters, and its key stream generation is efficient. However, the low-dimensional chaotic system has fewer control parameters. The cryptosystem is challenging to resist brute force attacks. This paper designs a new one-dimensional chaotic system called 1D-SLM. This chaotic system has two control parameters, an improvement on the Logistic map. The parameters corresponding to the chaotic region of 1D-SLM are continuous, and the chaotic region is wide, which is very suitable for the design of cryptographic systems.

For color image encryption algorithms, only relying on chaotic mapping is not enough to ensure security [22]. Zhou et al. used a one-dimensional chaotic system to generate multiple different key streams, using different signals to encrypt the three channels of the color image separately. The proposed encryption algorithm is simple and efficient [23]. Wang et al. used the hyperchaotic Lorenz system to generate the key stream of the cryptographic system. In order to enhance the security of the algorithm, they introduced the matrix semi-tensor product diffusion strategy. The encryption algorithm showed promising results on grayscale images. They extended this algorithm to color image encryption [24]. These algorithms encrypt the three channels of the plaintext image simultaneously, ignoring the correlation between the three channels. The attacker can obtain all the plaintext information by deciphering the content of one channel [25,26]. This paper proposes an encryption algorithm for the cross-plane, which treats the three channels as a whole, and the three channels interact with each other during encryption. This design structure increases the algorithm’s security, can resist common attack methods, and ensures the security of color images during transmission.

2  Performance Analysis of the New Chaos System

2.1 Existing One-Dimensional Chaotic Systems

Table 1 gives some one-dimensional chaotic systems, including the analytic formulas and control parameters. In Table 1, f0 is the initial value, fn is the iterative value. p and q are the control parameters.

2.2 New Chaos System 1D-Sin-Logistic-Map

The Logistic map has only one control parameter, the mapping range of the chaotic state is narrow, and the parameters are discontinuous. Therefore, we designed a new chaotic system named 1D-Sin-Logistic-Map (1D-SLM). The 1D-SLM is defined as,

fn+1=sin⁡(q⋅(1−p⋅fn⋅(1−fn))×1002+1). (1)

In Eq. (1), f0 is the initial value, f0∈(0,1) . fn is the iterative value, fn∈(0,1) . p and q are control parameters, p∈(0,+∞) and q∈(0,+∞) .

2.3 Bifurcation Diagram of 1D-SLM

The bifurcation diagram reflects the trajectory of the nonlinear dynamic system from the periodic motion state to the chaotic motion state. The Bifurcation diagrams of 1D-SLM are shown in Fig. 1 under different parameter spaces. The Bifurcation diagrams of existing one-dimensional chaotic systems in Table 1 are shown in Fig. 2. Compared with the Logistic map, Cubic map, Sin Map, and 1D-SMCLM, the 1D-SLM has a larger chaotic interval and more complex chaotic behavior.

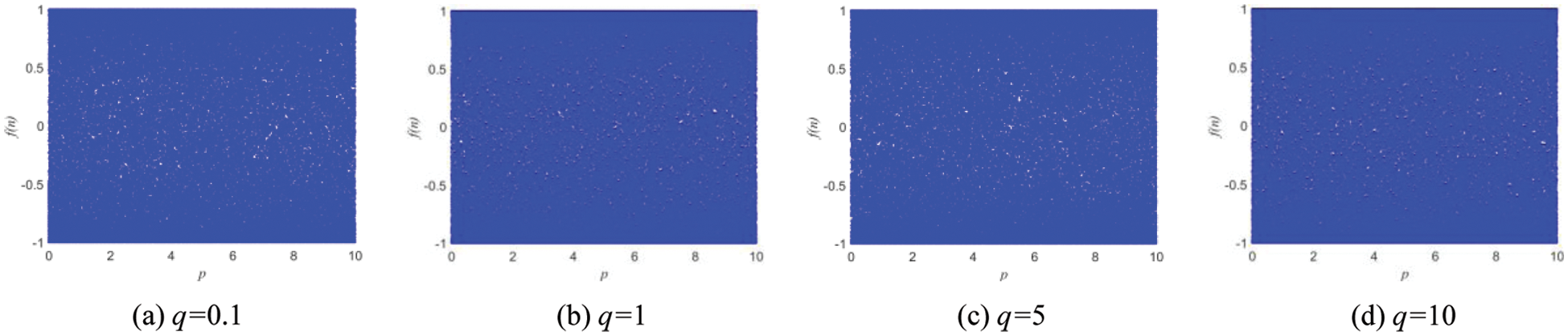
Figure 1: Bifurcation diagrams of 1D-SLM

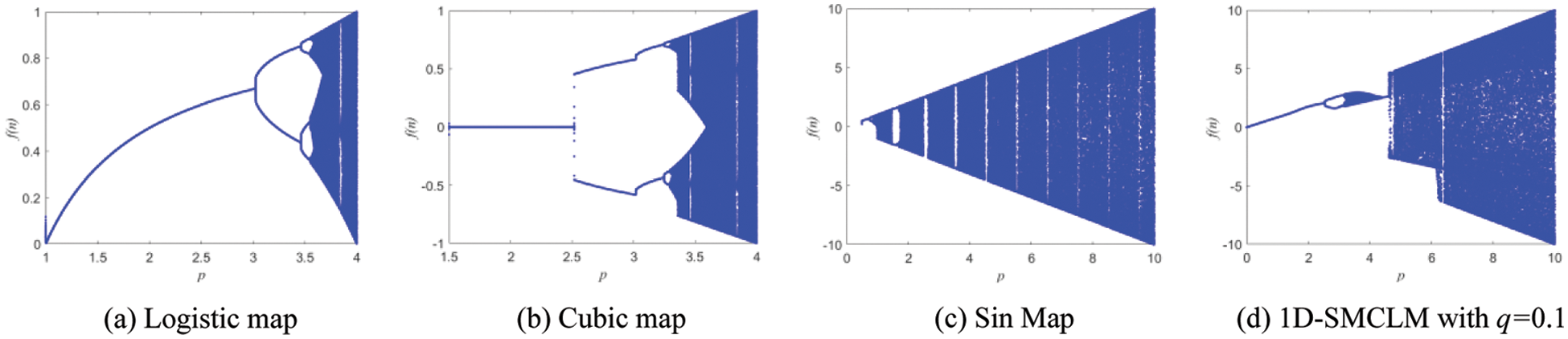
Figure 2: Bifurcation diagrams of existing one-dimensional chaotic systems

2.4 Lyapunov Exponents Analysis

Lyapunov exponents analysis is one of the most effective means of evaluating the dynamic behavior of nonlinear dynamical systems. The LE is defined as [31,32],

LE=limt→+∞1t∑i=1n−1ln⁡|f′(xi)|. (2)

When the Lyapunov exponent is greater than 0, it means that in this parameter space, the system is in a chaotic state. The Lyapunov exponents of 1D-SLM are shown in Fig. 3. The Lyapunov exponents of existing one-dimensional chaotic systems are shown in Fig. 4. It can be seen from Figs. 3 and 4 that the 1D-SLM shows the chaotic global state. Therefore, 1D-SLM can produce a keystream with excellent performance. Compared with other 1D chaotic systems, the 1D-SLM has a larger Lyapunov exponent, and the parameter space in the chaotic state is continuous.

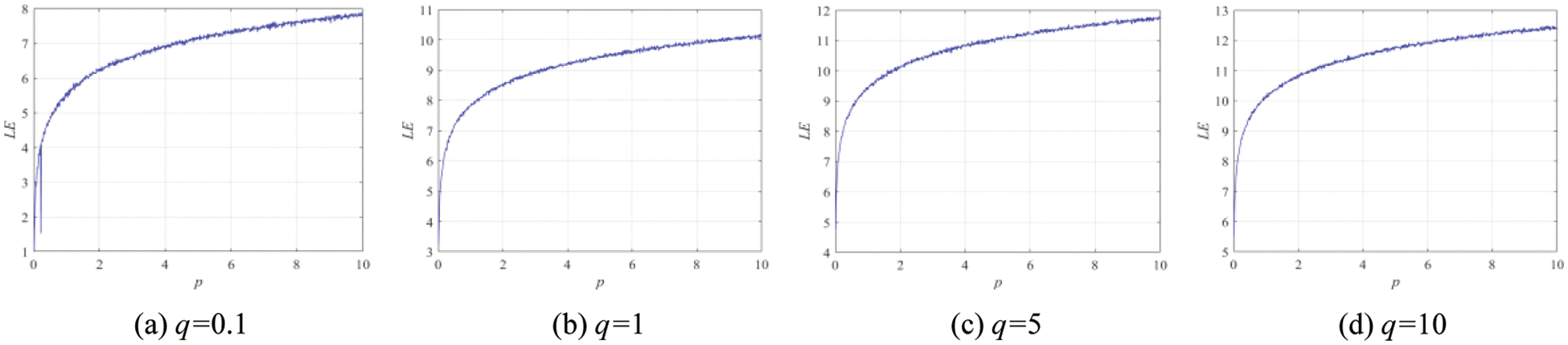
Figure 3: Lyapunov exponents analysis of 1D-SLM

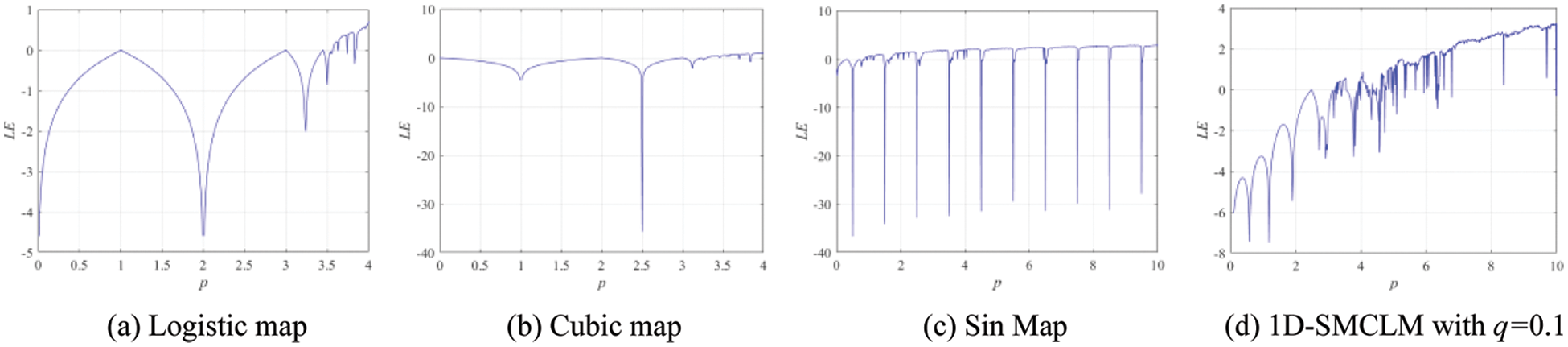
Figure 4: Lyapunov exponents analysis of existing one-dimensional chaotic systems

2.5 0–1 Test

The 0–1 test is a test algorithm that measures the presence of chaos in a time series. The 0–1 test of 1D-SLM is shown in Fig. 5. The 0–1 test of existing one-dimensional chaotic systems is shown in Fig. 6. Figs. 5 and 6 show the motion state of 1D-SLM is a Boolean motion state. The Logistic map, Cubic map, Sin map, and 1D-SMCLM exhibit regular motion states in the same parameters. It shows that 1D-SLM can provide sequences with more complex dynamical behavior.

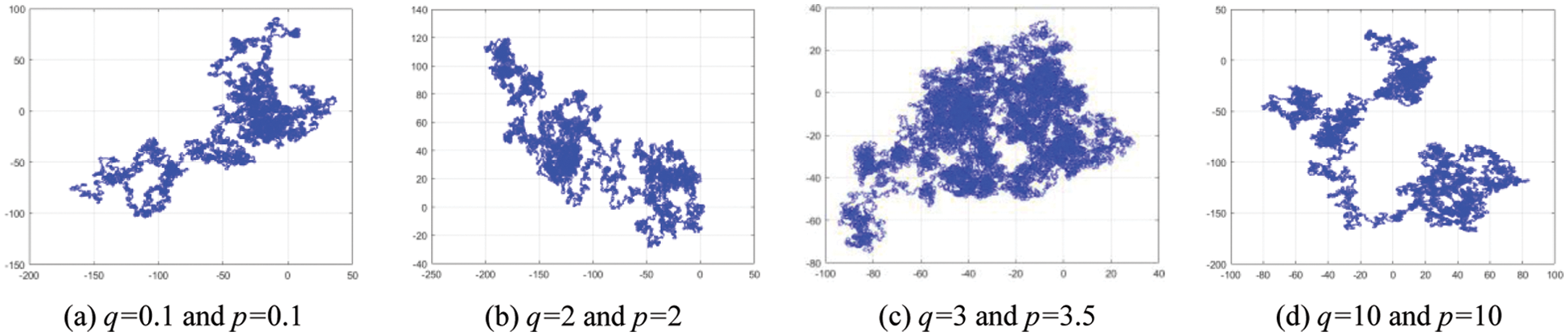
Figure 5: 0–1 test analysis of 1D-SLM

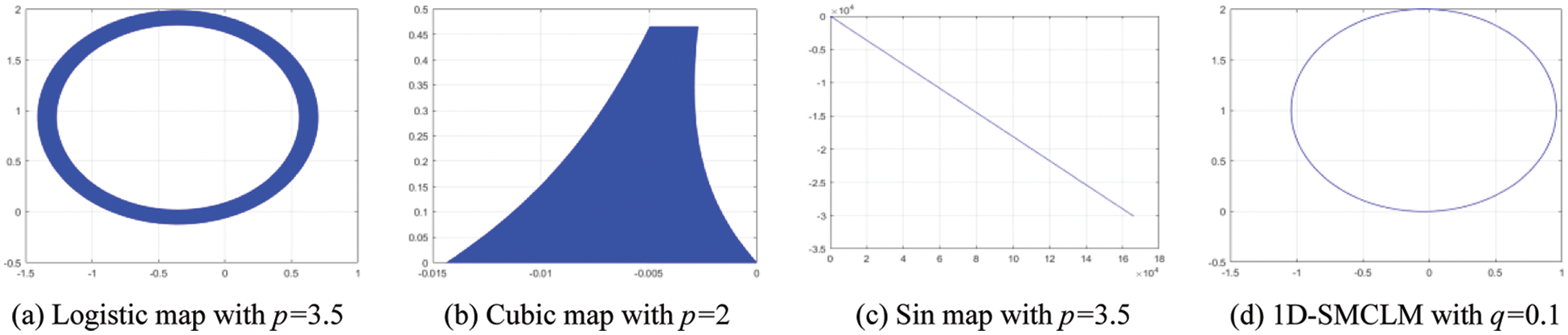
Figure 6: 0–1 test analysis of existing one-dimensional chaotic systems

2.6 Spectral Entropy Analysis

Spectral entropy reflects the energy of the signal. The greater the spectral entropy, the greater the signal’s energy and the more complex the dynamic behavior of the signal. The spectral entropy of 1D-SLM and the Logistic map, Cubic map, Sin map, and 1D-SMCLM are shown in Fig. 7. It can be seen from Fig. 7 that compared with the chaotic sequence generated by the Logistic map, Cubic map, Sin map, and 1D-SMCLM, the chaotic sequence generated by 1D-SLM has more potent energy, which indicates that the key stream generated by 1D-SLM has more complex dynamic behavior.

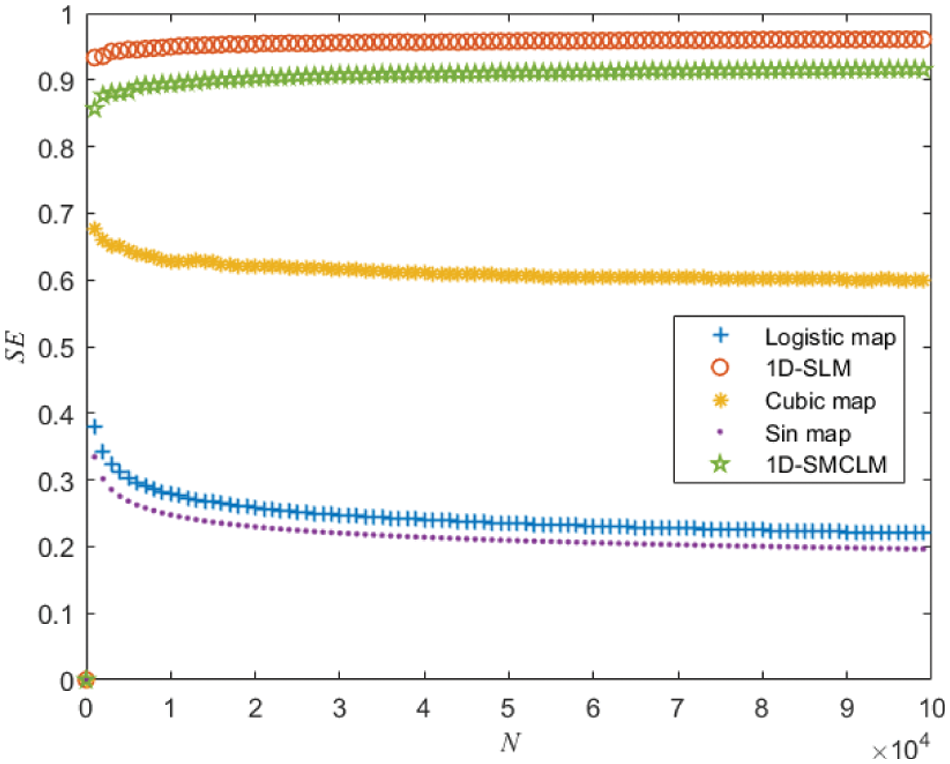
Figure 7: Spectral entropy of 1D-SLM and existing one-dimensional chaotic systems

3  Encryption Algorithm

3.1 Key Generation

The plaintext image is P ( L×W ), the R channel of the plaintext image is denoted as PR ( L×W ), the G channel is denoted as PG ( L×W ), and the B channel is denoted as PB ( L×W ). Calculate the sum of the plaintext pixel values of each channel by

{k1=sum(PR)k2=sum(PG)k3=sum(PB). (3)

The key of the cryptosystem is K1=k1/k2,K2=k2/k3,K3=k3/k1 .

3.2 Cross-Plane for Color Images

Given the original initial value v1 and parameter p1 , q1 of 1D-SLM. According to the secret key in Section 3.1, the new initial value and parameter are,

v1=v1+K1,p1=p1+K2,q1=q1+K3. (4)

The new initial value and parameters are brought into the 1D-SLM iteration to generate the key stream, discard the first 200 iterations of the initial value, denoted as X1 ( L×W ), definition

U=floor(|X1×1010|)mod6+1. (5)

The rule for cross-plane for color images is

{P(Rl,w,Gl,w,Bl,w)=P(Rl,w,Gl,w,Bl,w),Ul,w=1P(Rl,w,Gl,w,Bl,w)=P(Rl,w,Bl,w,Gl,w),Ul,w=2P(Rl,w,Gl,w,Bl,w)=P(Bl,w,Gl,w,Rl,w),Ul,w=3P(Rl,w,Gl,w,Bl,w)=P(Bl,w,Rl,w,Gl,w),Ul,w=4P(Rl,w,Gl,w,Bl,w)=P(Gl,w,Rl,w,Bl,w),Ul,w=5P(Rl,w,Gl,w,Bl,w)=P(Gl,w,Bl,w,Rl,w),Ul,w=6. (6)

3.3 Zigzag Scrambling

Concatenate the plaintext processed by cross-planes in Section 3.2 into a new plaintext P ( L×3W ), in the order of PR , PG , and PB . Perform zigzag scrambling on the new plaintext P to obtain the scrambled matrix S. The zigzag scrambling is shown in Fig. 8.

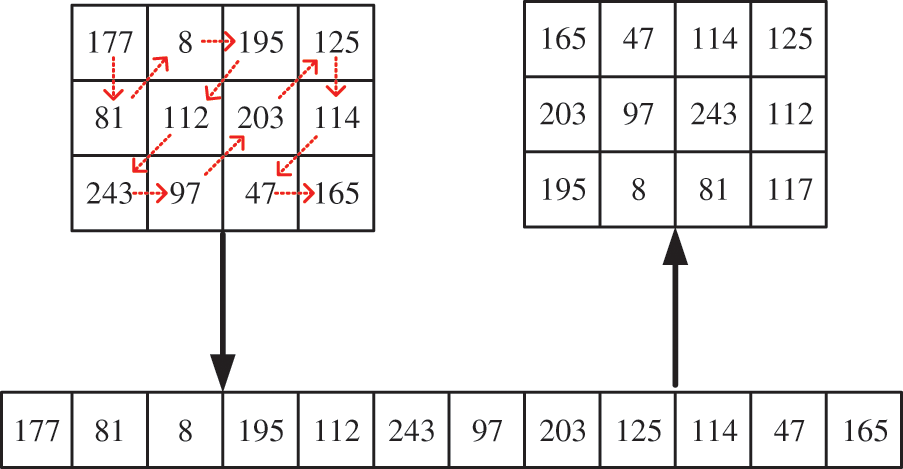
Figure 8: Zigzag scrambling of 3 × 4

3.4 Diffusion

Given the original initial value v2 and parameter p2 , q2 of 1D-SLM. According to the secret key in Section 3.1, the new initial value and parameter are,

v2=v2+K3,p2=p2+K1,q2=q2+K2. (7)

The new initial value and parameters are brought into the 1D-SLM iteration to generate the key stream, discard the first 200 iterations of the initial value, denoted as X2 ( L×3W ), definition

T=floor(|X2×1010|)mod256. (8)

The diffusion process is

{C[1,1]=T[1,1]⊕S[1,1],C[1,u]=T[1,u]⊕S[1,u]⊕C[1,u−1],u=2:3W,C[v,1]=T[v,1]⊕S[v,1]⊕C[v−1,1],v=2:L,C[v,u]=T[v,u]⊕C[v−1,u]⊕S[v,u]⊕C[v,u−1]. (9)

Output the ciphertext C, and synthesize the ciphertext color image.

3.5 Decryption Algorithm

The decryption algorithm is shown in Algorithm 1.

4  Performance Analysis

4.1 Simulation Experiments

The visual analysis of the proposed algorithm is shown in Figs. 9–11. Visual analysis shows that, visually, the proposed algorithm is safe.

Figure 9: Visual analysis of Lena with the size of 512 × 512

Figure 10: Visual analysis of Airplane with the size of 512 × 512

Figure 11: Visual analysis of Baboon with the size of 512 × 512

4.2 Histogram Analysis

The histogram analysis of the proposed algorithm is shown in Fig. 12 [33]. Histogram analysis shows that the distribution of pixel values obtained by the proposed algorithm is uniform, and the algorithm has excellent security.

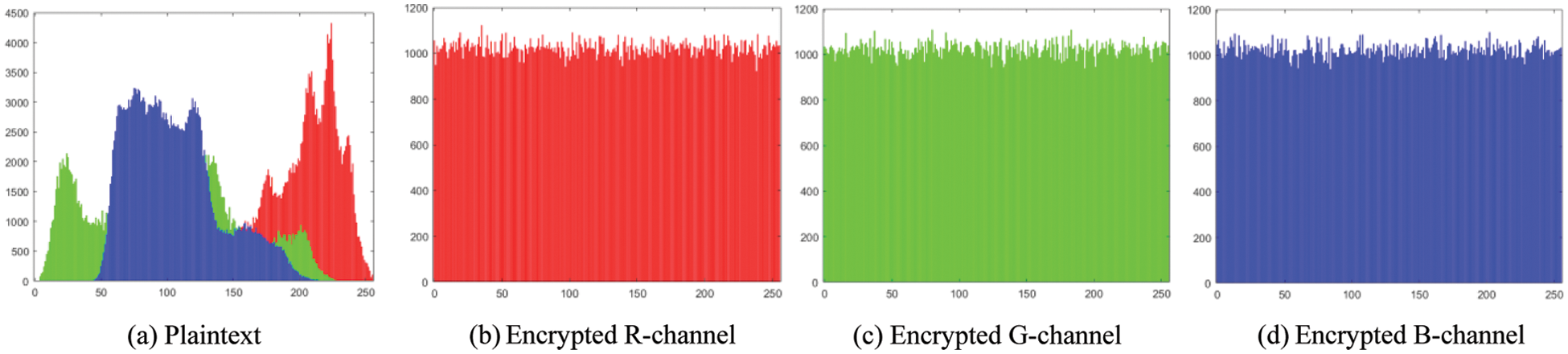
Figure 12: Histogram analysis

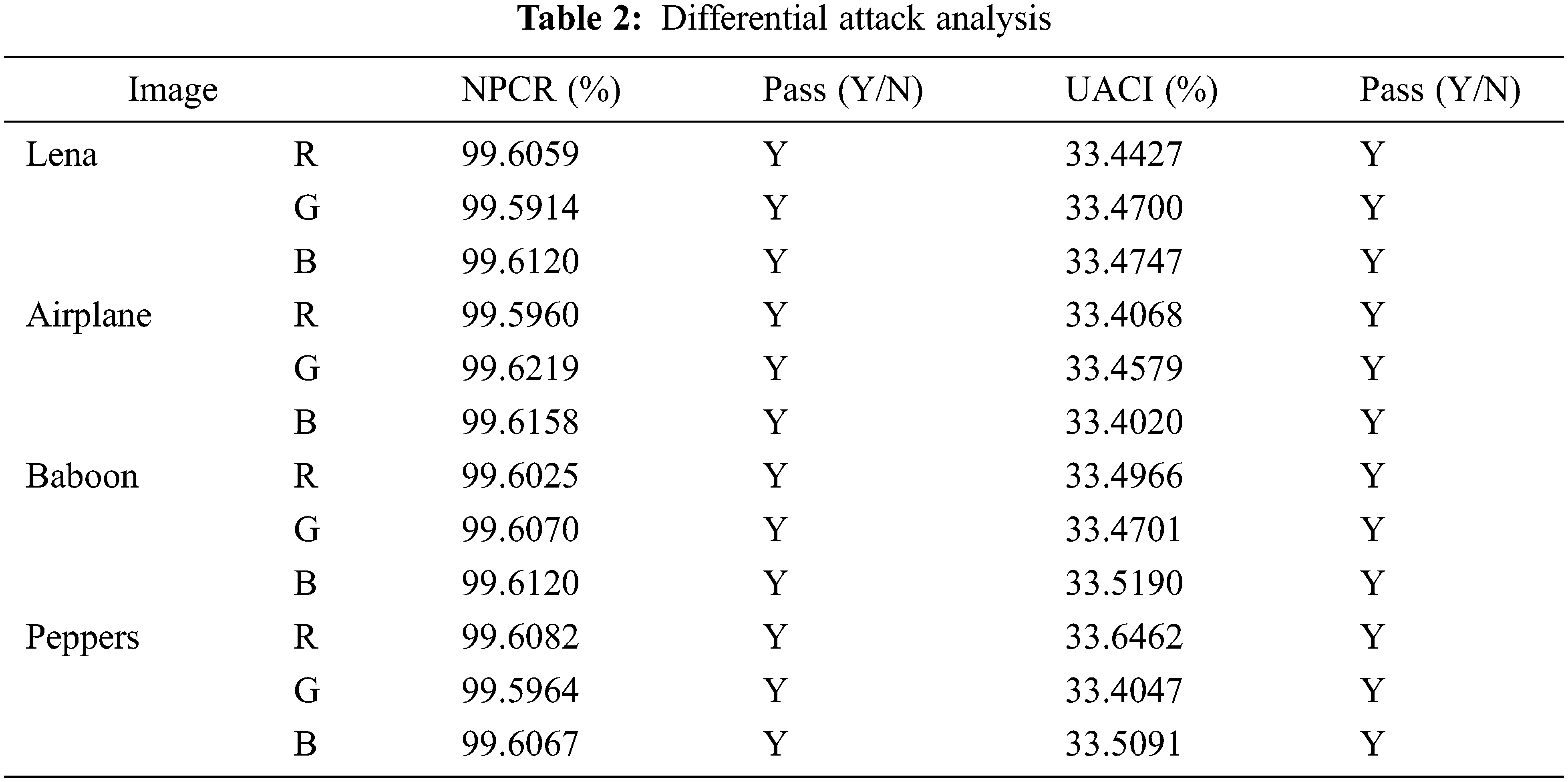
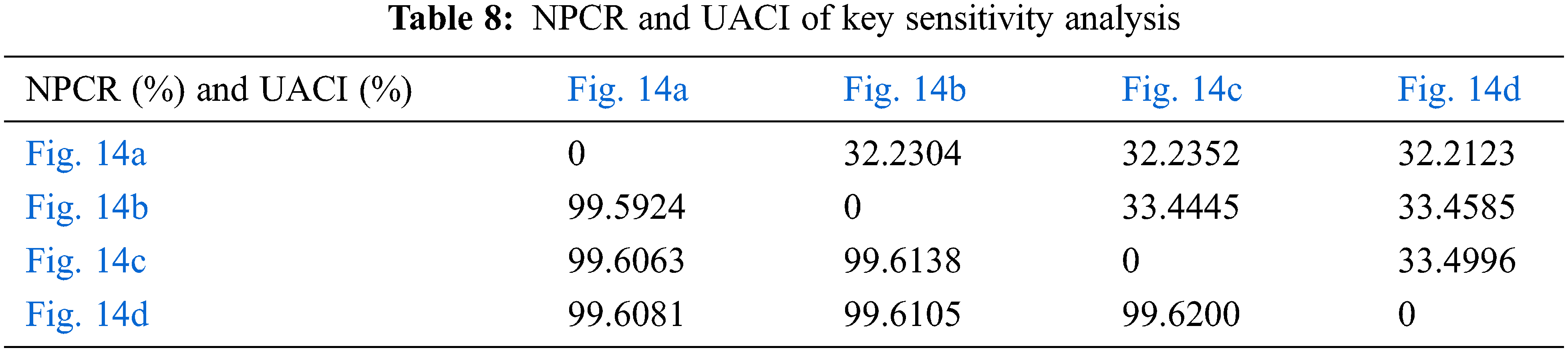
4.3 Differential Attack Analysis

A secure algorithm is sensitive to plaintext, and NPCR and UACI are two metrics for detecting plaintext sensitivity [34].

{ NPCR=∑i,j{ 1,c1(i, j)≠c2(i, j)0,c1(i, j)=c2(i, j)L×WUACI=1L×W∑i,j|c1(i, j)−c2(i, j)|255. (10)

For a image with the size of 512 × 512, when the value of NPCR is [99.5893%,100%] , and the value of UACI is [33.3730%,33.5541%] , at this point, it indicates that the algorithm is sensitive to plaintext. The test results of NPCR and UACI are shown in Table 2. The results of the differential attack show that the algorithm is sensitive to plaintext.

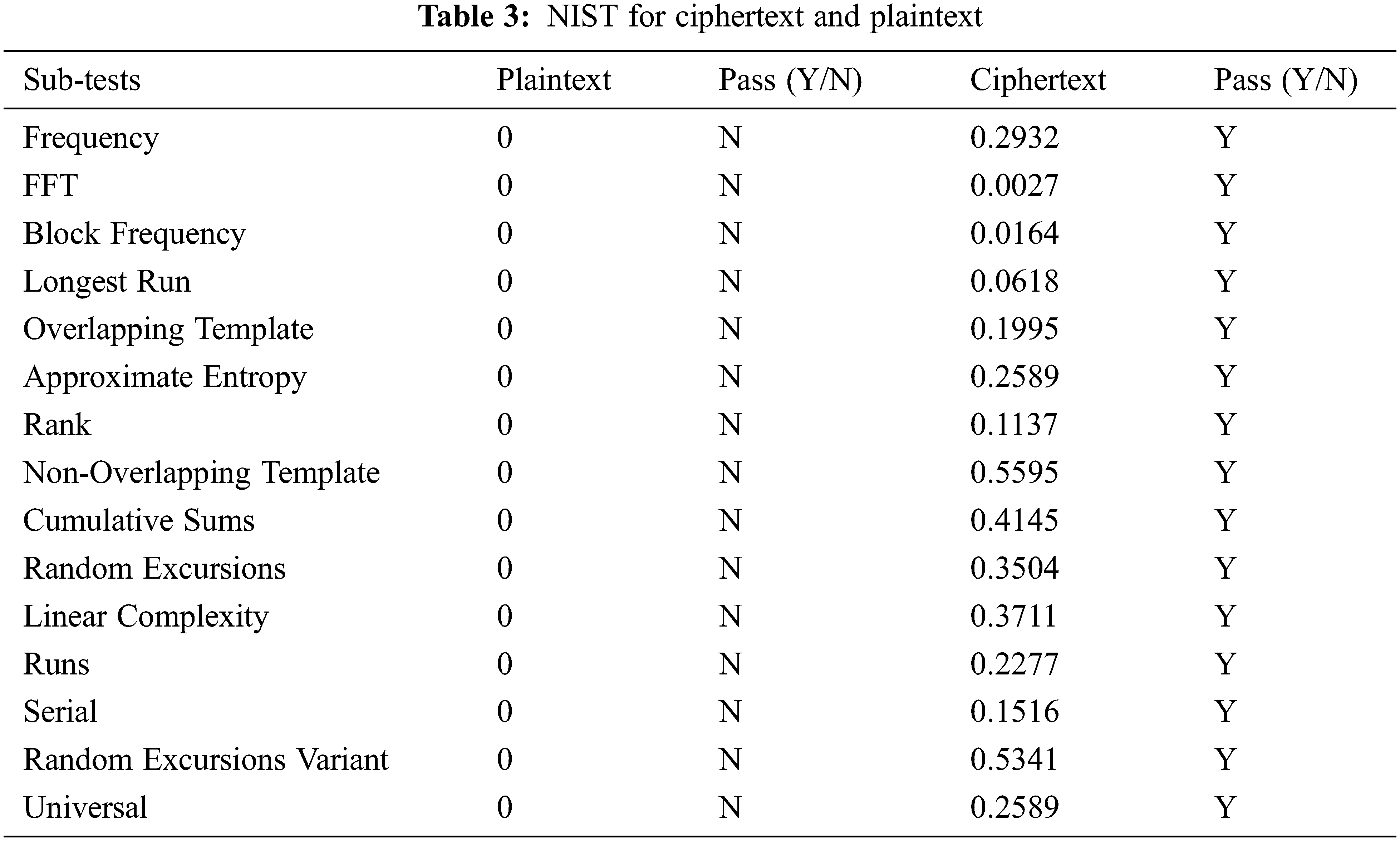
4.4 NIST for Ciphertext and Plaintext

The NIST effectively checks whether the data has randomness [35–37]. The NIST test results of ciphertext and plaintext are shown in Table 3. NIST test results show that the ciphertext has terrific randomness.

4.5 Adjacent Pixel Correlation Analysis

A secure encryption algorithm can reduce ciphertext’s horizontal, vertical, and diagonal adjacent pixel correlations. Otherwise, the algorithm can be easily cracked by statistical attacks. The adjacent pixel correlation analysis of the algorithm is shown in Fig. 13.

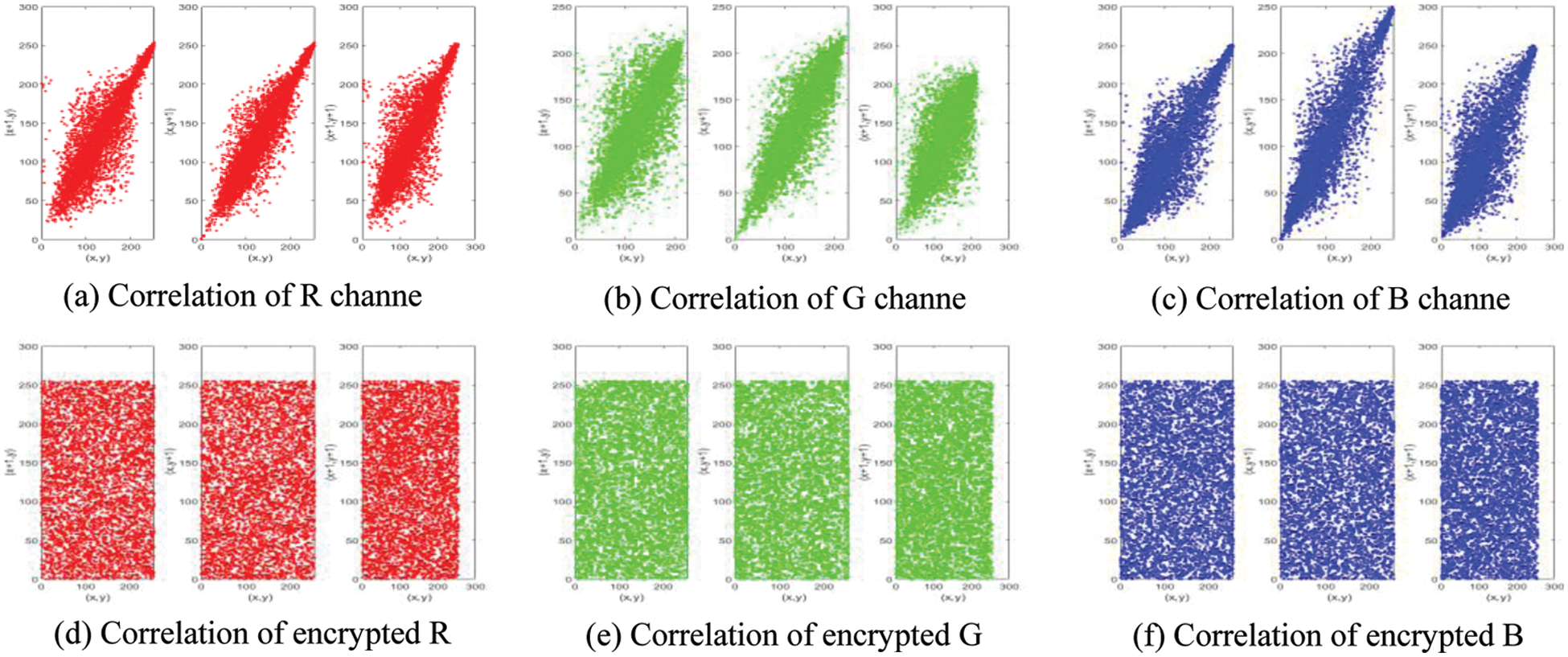
Figure 13: Correlation analysis of Baboon

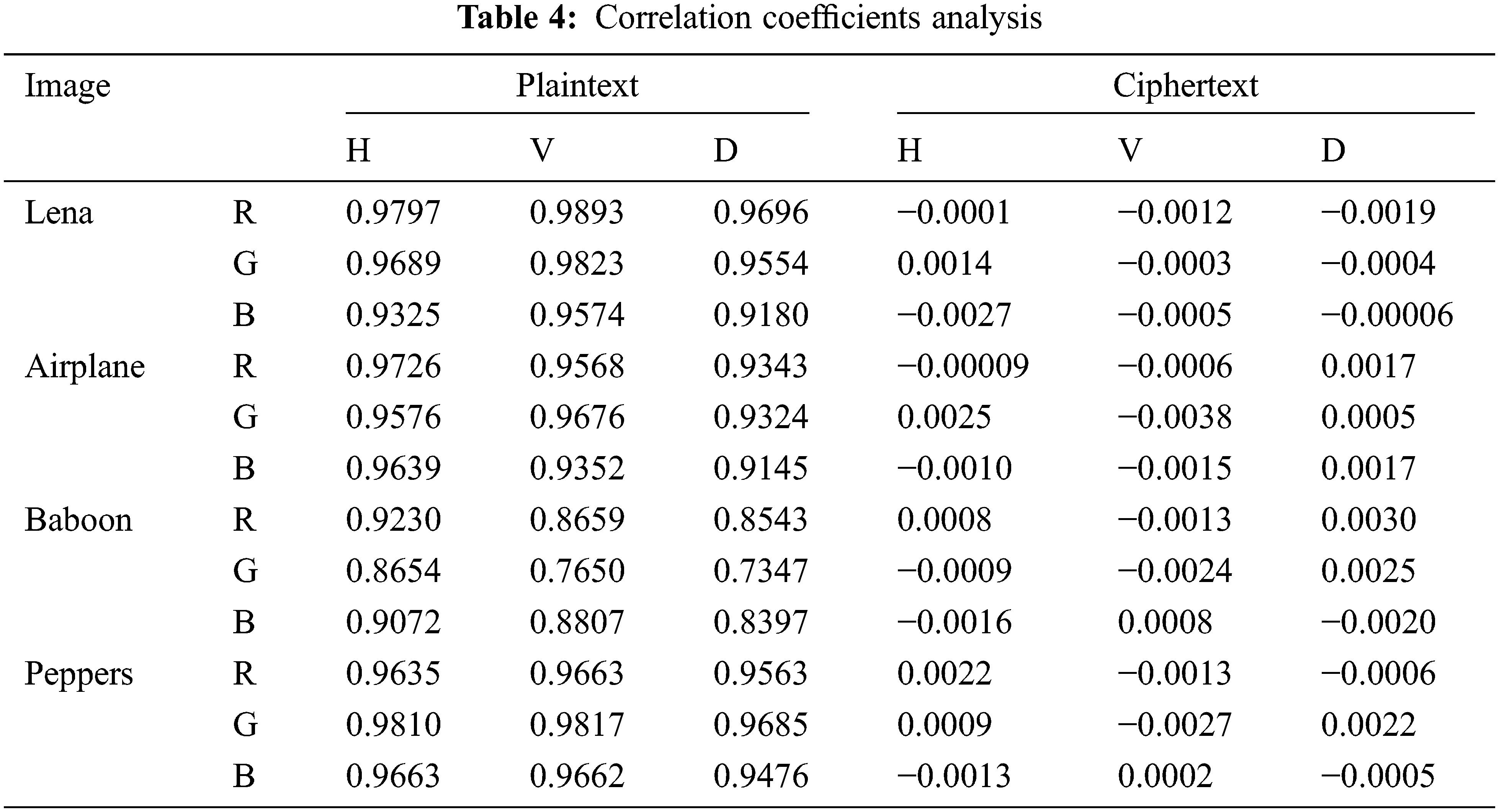
The quantitative results of the correlation analysis of the proposed algorithm are shown in Table 4. The correlation analysis shows that the correlation of the plaintext image in the three directions is very high. The correlation of the ciphertext image in the three directions is very high, close to 0 (theoretical value). Therefore, the proposed encryption algorithm has good security.

4.6 R, G, B Correlation Analysis

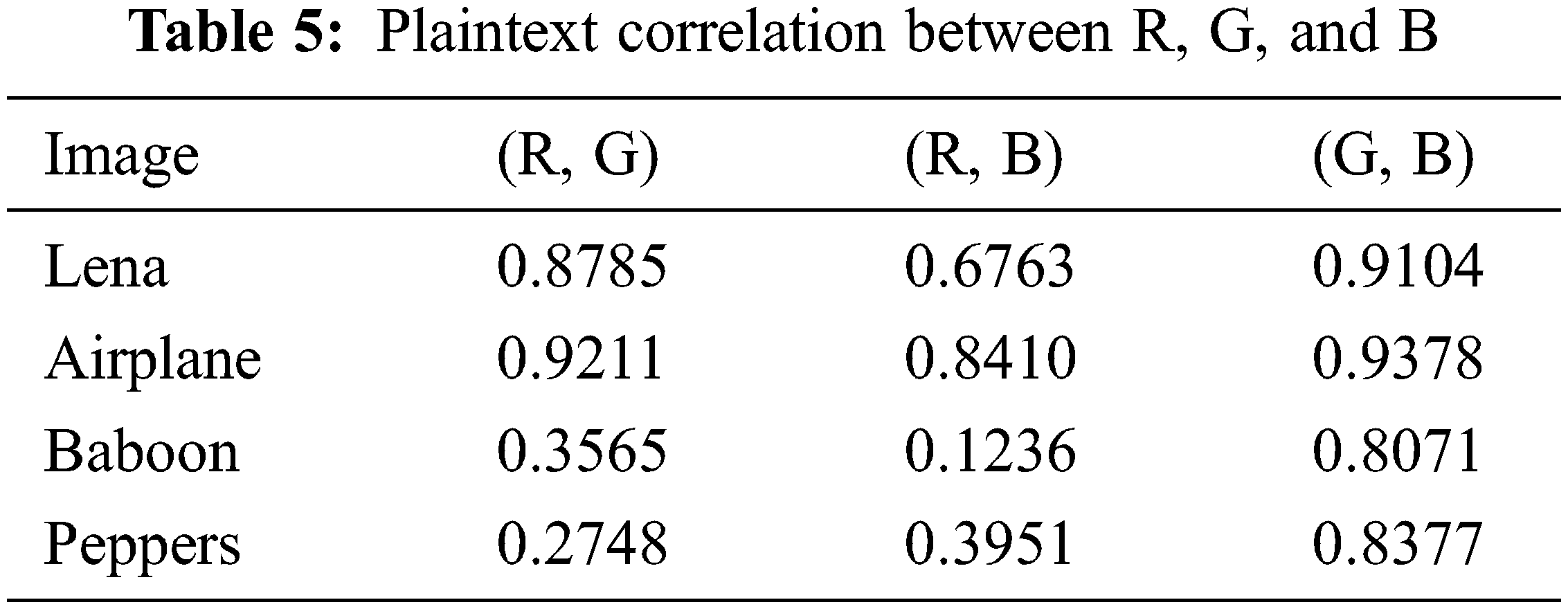
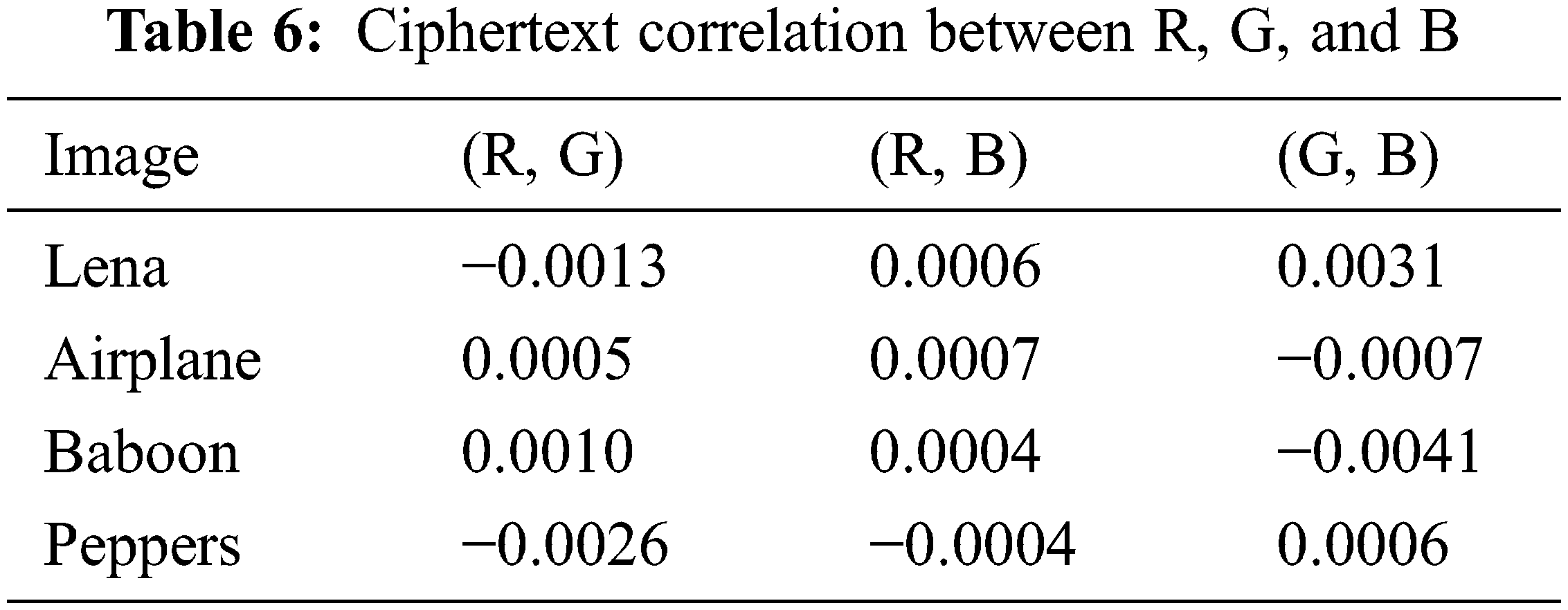
A safe algorithm requires a slight correlation between adjacent pixels and a small correlation between the three channels. The correlation analysis between the three channels of the proposed algorithm is shown in Tables 5 and 6. The results of correlation analysis show that the proposed algorithm can reduce not only the correlation of adjacent pixels but also the correlation between different channels, and the attacker cannot obtain the information of the remaining channels from one channel.

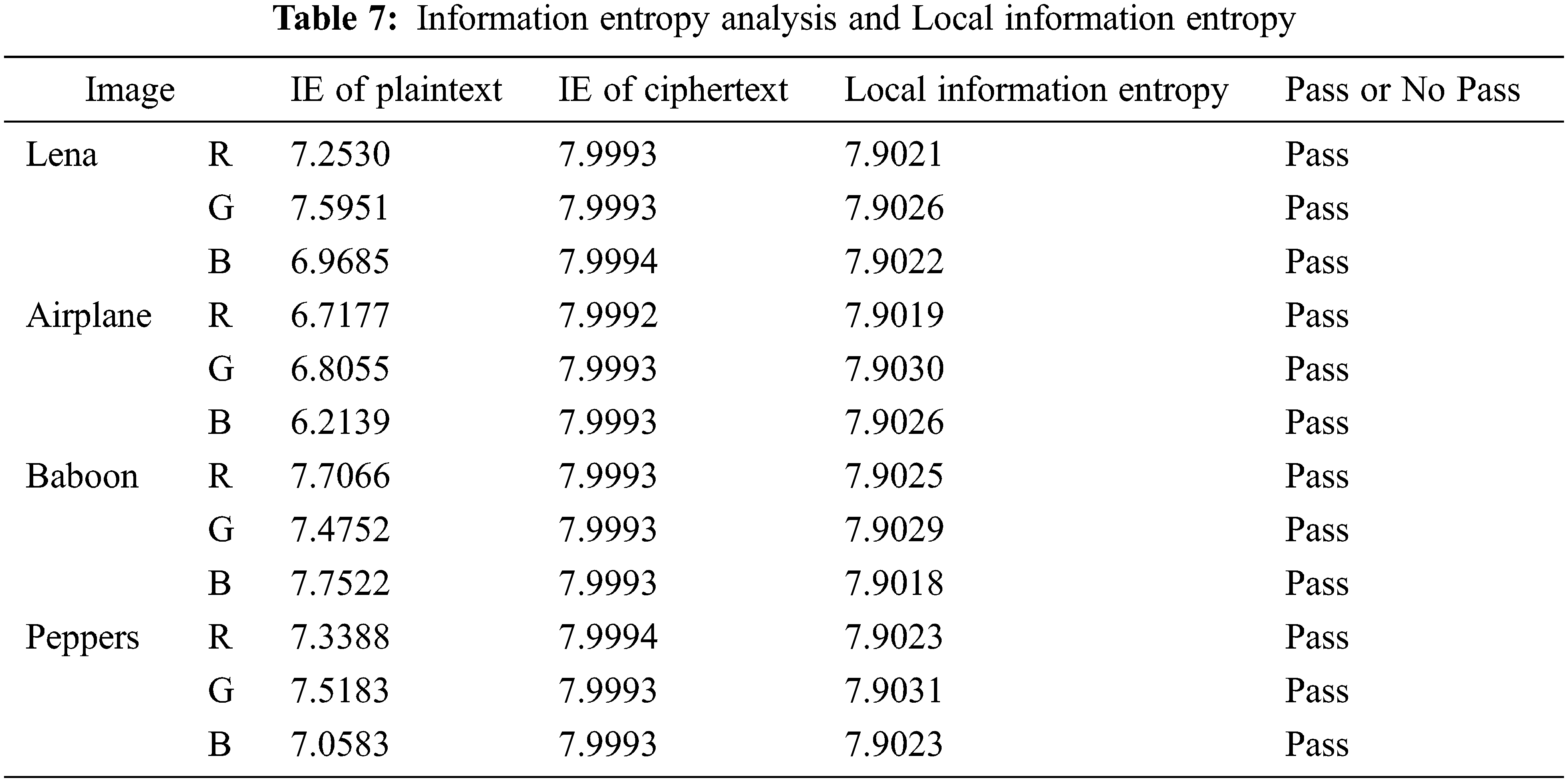
4.7 Information Entropy Analysis

The information entropy is defined as

H=∑i=0255p(gi)log21p(gi).

Information entropy is an index to analyze the randomness of image information distribution. The higher the information entropy, the more chaotic the information.

The information entropy analysis of the proposed algorithm is shown in Table 7. The local information entropy reflects the degree of local confusion of the image [38]. When the value of local information entropy is between 7.9015 and 7.9034, it indicates that the local information of the image has good randomness. The local information entropy is shown in Table 7. The information entropy analysis results show that the information entropy of the ciphertext is close to the theoretical value, indicating that the algorithm has a good encryption effect.

4.8 Key Analysis

The key space of a cryptographic system is at least greater than 2100 that to meet the conditions for resisting brute force attacks. The keys in this paper include v1 , p1 , q1 , v2 , p2 , q2 , K1 , K2 , K3 . If the computational precision of the computer is 1014 , the size of the key space of the proposed algorithm is,

K=1014×1028×1028×1014×1028×1028×1014×1014=10168≈2558.

The designed algorithm is strong enough to resist brute-force attacks.

A highly sensitive key is a necessary condition for an encryption algorithm. This section tests the key sensitivity of the proposed algorithm, with the initial key set to v2=0.985612 , p2=10.36985 , q2=11.23654 . The key sensitivity analysis is shown in Fig. 14. Key sensitivity analysis shows that the key of the proposed algorithm is sensitive. Calculate the difference between the images in Fig. 14 using NPCR and UACI shown in Table 8 [35,36].

Figure 14: Key sensitivity analysis

4.9 Robustness Analysis

The image will be interfered with by noise during transmission [39]. A safe algorithm should have good resistance to this attack. The robustness analysis of the algorithm is shown in Fig. 15. The PSNR is generally used to measure the restoring ability of images. The results of MSE are shown in Table 9. The results of PSNR are shown in Table 10.

Figure 15: Robustness analysis

4.10 Time Analysis

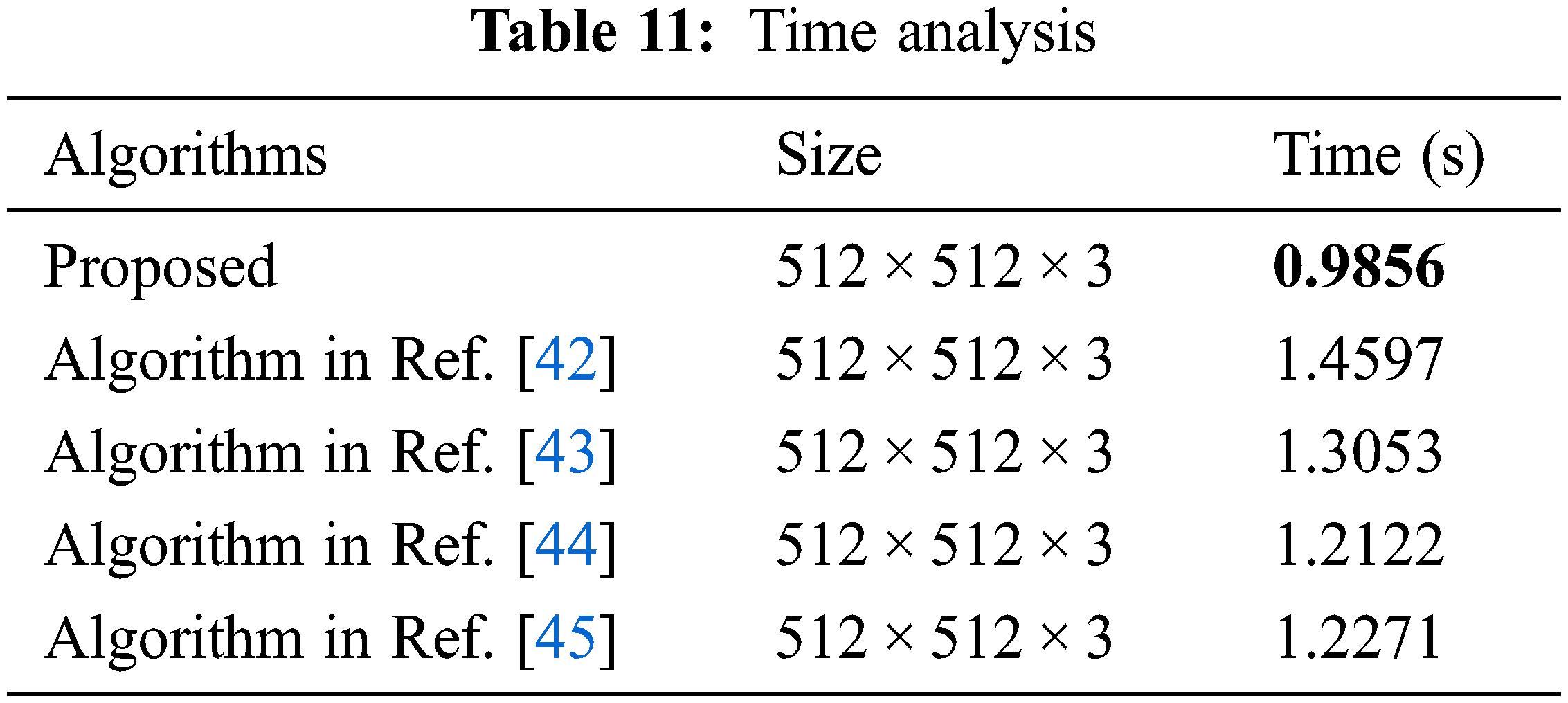
Efficiency analysis is an important index to evaluate the practicability of an algorithm [40,41]. The efficiency analysis of the proposed algorithm is shown in Table 11. Experimental environment, Matlab R2019a, Windows 11, Intel i3-10105. Efficiency analysis shows that the proposed algorithm has excellent performance and is more practical.

4.11 Comparative Analysis

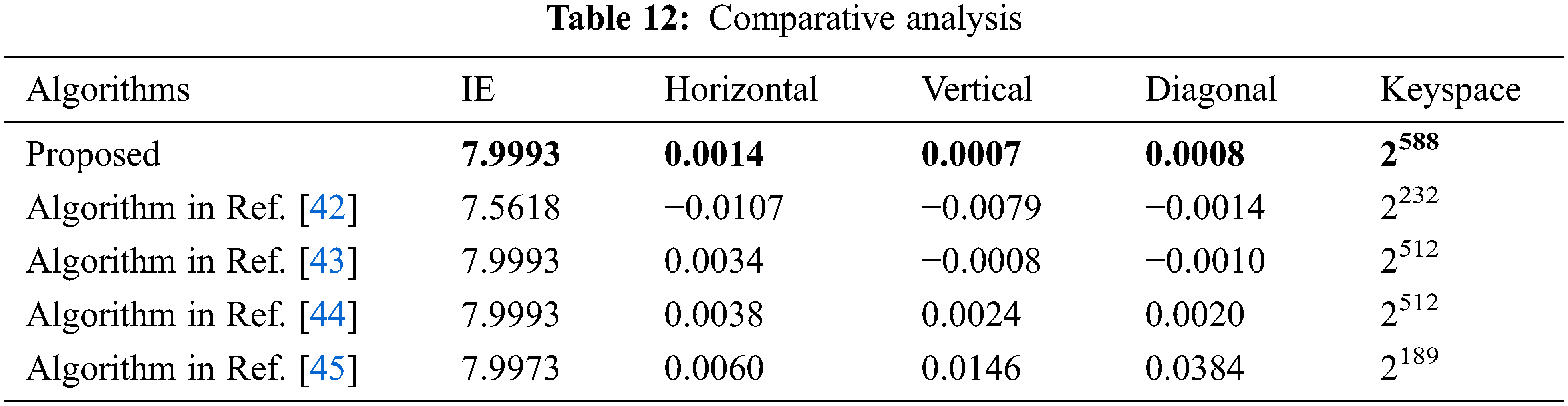
In this section, the proposed algorithm is compared with some classical algorithms, and the comparison results are shown in Table 6. The values in Table 12 are averages. The comparison results show that our algorithm is more secure than the algorithm in Ref. [42], algorithm in Ref. [43], algorithm in Ref. [44], and algorithm in Ref. [45].

5  Conclusion

In this paper, a new chaotic system, 1D-SLM, is proposed. This system has two control parameters that give the cryptosystem a larger key space. It is verified that the key stream generated by 1D-SLM has strong energy and can generate a key stream with excellent performance that is very suitable for cryptography by the Lyapunov exponent, bifurcation graph analysis, and spectral entropy analysis. We propose a new image encryption algorithm based on 1D-SLM. This encryption algorithm combines the three channels of the color image to encrypt simultaneously. In other words, during the encryption process, the three channels of the color image are interactive. This design structure reduces the correlation between image channels. Through performance analysis, it is verified that the proposed algorithm has good performance. Comparative analysis shows that the proposed algorithm has excellent security.

Funding Statement: This research was supported by the National Natural Science Foundation of China (61802212).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. Ga, J. Mou, L. Xiong, Y. W. Sha, H. Z. Yan et al., “A fast and efficient multiple images encryption based on single-channel encryption and chaotic system,” Nonlinear Dynamics, vol. 108, no. 1, pp. 613–636, 2022. [Google Scholar]

 2.  D. Jerusha and T. Jaya, “Cryptographic lightweight encryption algorithm with dimensionality reduction in edge computing,” Computer Systems Science and Engineering, vol. 42, no. 3, pp. 1121–1132, 2022. [Google Scholar]

 3.  M. A. B. Farah, R. Guesmi, A. Kachouri and M. Samet, “A novel chaos based optical image encryption using fractional Fourier transform and DNA sequence operation,” Optics and Laser Technology, vol. 121, pp. 105777, 2020. [Google Scholar]

 4.  B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]

 5.  C. Wang, B. Ma, Z. Xia, J. Li, Q. Li et al., “Stereoscopic image description with trinion fractional-order continuous orthogonal moments,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 4, pp. 1998–2012, 2022. [Google Scholar]

 6.  Q. Li, X. Wang, B. Ma, X. Wang, C. Wang et al., “Concealed attack for robust watermarking based on generative model and perceptual loss,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 8, pp. 5695–5706, 2022. [Google Scholar]

 7.  X. Wang, X. Wang, B. Ma, Q. Li and Y. Shi, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]

 8.  S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, pp. 108745, 2023. [Google Scholar]

 9.  Z. Hua, Y. Zhou and H. Huang, “Cosine-transform-based chaotic system for image encryption,” Information Sciences, vol. 480, pp. 403–419, 2019. [Google Scholar]

10. Y. Chen, S. Xie and J. Zhang, “A novel double image encryption algorithm based on coupled chaotic system,” Physica Scripta, vol. 97, no. 6, pp. 065207, 2022. [Google Scholar]

11. R. Wu, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons and Fractals, vol. 165, pp. 112770, 2022. [Google Scholar]

12. Y. Xian and X. Wang, “Fractal sorting matrix and its application on chaotic image encryption,” Information Sciences, vol. 547, pp. 1154–1169, 2021. [Google Scholar]

13. S. Wang, Q. Peng and B. Du, “Chaotic color image encryption based on 4D chaotic maps and DNA sequence,” Optics and Laser Technology, vol. 148, pp. 107753, 2022. [Google Scholar]

14. J. Arif, M. A. Khan, B. Ghaleb, J. Ahmad, A. Munir et al., “A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution,” IEEE Access, vol. 10, pp. 12966–12982, 2022. [Google Scholar]

15. Z. Man, J. Li, X. Di, Y. H. Sheng and Z. F. Liu, “Double image encryption algorithm based on neural network and chaos,” Chaos, Solitons and Fractals, vol. 152, pp. 111318, 2021. [Google Scholar]

16. Q. Wang, S. Yu, C. Li, J. H. Lu, X. L. Fang et al., “Theoretical design and FPGA-based implementation of higher-dimensional digital chaotic systems,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 63, no. 3, pp. 401–412, 2016. [Google Scholar]

17. S. Kang, Y. Liang, Y. Wang and V. I. Mikulovich, “Color image encryption method based on 2D-variational mode decomposition,” Multimedia Tools and Applications, vol. 78, no. 13, pp. 17719–17738, 2019. [Google Scholar]

18. F. Yu, X. Kong, H. Chen, Q. L. Yu, S. Cai et al., “A 6D fractional-order memristive hopfield neural network and its application in image encryption,” Frontiers in Physics, vol. 10, pp. 847385, 2022. [Google Scholar]

19. J. Xu, B. Zhao and Z. Wu, “Research on color image encryption algorithm based on bit-plane and chen chaotic system,” Entropy, vol. 24, no. 2, pp. 186, 2022. [Google Scholar]

20. S. Patel and T. Veeramalai, “Image encryption using a spectrally efficient halton logistics tent (halt) map and DNA encoding for secured image communication,” Entropy, vol. 24, no. 6, pp. 803, 2022. [Google Scholar]

21. J. Mou, F. Yang, R. Chu and Y. H. Cao, “Image compression and encryption algorithm based on hyper-chaotic map,” Mobile Networks and Applications, vol. 26, no. 5, pp. 1849–1861, 2021. [Google Scholar]

22. P. Liu, T. Zhang and X. Li, “A new color image encryption algorithm based on DNA and spatial chaotic map,” Multimedia Tools and Applications, vol. 78, no. 11, pp. 14823–14835, 2019. [Google Scholar]

23. S. Zhou, X. Wang, M. Wang and Y. Zhang, “Simple colour image cryptosystem with very high level of security,” Chaos, Solitons and Fractals, vol. 141, pp. 110225, 2020. [Google Scholar]

24. X. Wang and S. Gao, “Application of matrix semi-tensor product in chaotic image encryption,” Journal of the Franklin Institute, vol. 356, no. 18, pp. 11638–11667, 2019. [Google Scholar]

25. C. L. Li, Y. Zhou, H. M. Li, W. Feng and J. R. Du, “Image encryption scheme with bit-level scrambling and multiplication diffusion,” Multimedia Tools and Applications, vol. 80, no. 12, pp. 18479–18501, 2021. [Google Scholar]

26. H. Zhu, L. Dai, Y. Liu and L. J. Wu, “A three-dimensional bit-level image encryption algorithm with rubik’s cube method,” Mathematics and Computers in Simulation, vol. 185, pp. 754–770, 2021. [Google Scholar]

27. R. M. May, “Simple mathematical models with very complicated dynamics,” Nature, vol. 261, pp. 459, 1976. [Google Scholar]

28. A. Yahi, T. Bekkouche, M. Daachi and N. Diffellah, “A color image encryption scheme based on 1D cubic map,” Optik, vol. 249, pp. 168290, 2022. [Google Scholar]

29. A. Belazi, A. A. Abd El-Latif, “A simple yet efficient S-box method based on chaotic sine map,” Optik, vol. 130, pp. 1438–1444, 2017. [Google Scholar]

30. Y. Hu, X. Wang and L. Zhang, “1D sine-map-coupling-logistic-map for 3D model encryption,” Frontiers in Physics, vol. 10, pp. 1006324, 2022. [Google Scholar]

31. M. Turkyilmazogl, “An extended epidemic model with vaccination: Weak-immune SIRVI,” Physica A: Statistical Mechanics and its Applications, vol. 598, pp. 127429, 2022. [Google Scholar]

32. M. T. Rosenstein, J. J. Collins and C. J. De Luca, “A practical method for calculating largest lyapunov exponents from small data sets,” Physica D: Nonlinear Phenomena, vol. 65, no. 1–2, pp. 117–134, 1993. [Google Scholar]

33. D. Ravichandran, P. Praveenkumar, J. B. B. Rayappan and R. Amirtharajan, “Chaos based crossover and mutation for securing DICOM image,” Computers in Biology and Medicine, vol. 72, pp. 170–184, 2016. [Google Scholar]

34. Y. Wu, J. P. Noonan and S. Agaian, “NPCR and UACI randomness tests for image encryption,” Cyber Journals: Multidisciplinary Journals in Science and Technology, Journal of Selected Areas in Telecommunications, vol. 1, no. 2, pp. 31–38, 2011. [Google Scholar]

35. J. Zaman and R. Ghosh, “Review on fifteen statistical tests proposed by NIST,” Journal of Theoretical Physics and Cryptography, vol. 1, pp. 18–31, 2012. [Google Scholar]

36. E. Yavuz, R. Yazici, M. C. Kasapbasi and E. Yamac, “A chaos-based image encryption algorithm with simple logical functions,” Computers and Electrical Engineering, vol. 54, pp. 471–483, 2016. [Google Scholar]

37. Z. Hua, F. Jin, B. X. Xu and H. J. Huang, “2D logistic-sine-coupling map for image encryption,” Signal Processing, vol. 149, pp. 148–161, 2018. [Google Scholar]

38. Y. Wu, Y. Zhou, G. Saveriades, S. Agaian, J. P. Noonan et al., “Local shannon entropy measure with statistical tests for image randomness,” Information Sciences, vol. 222, pp. 323–342, 2013. [Google Scholar]

39. E. Yavuz, “A novel chaotic image encryption algorithm based on content-sensitive dynamic function switching scheme,” Optics and Laser Technology, vol. 114, pp. 224–239, 2019. [Google Scholar]

40. E. Yavuz, “A new parallel processing architecture for accelerating image encryption based on chaos,” Journal of Information Security and Applications, vol. 63, pp. 103056, 2021. [Google Scholar]

41. S. Amina and F. K. Mohamed, “An efficient and secure chaotic cipher algorithm for image content preservation,” Communications in Nonlinear Science and Numerical Simulation, vol. 60, pp. 12–32, 2018. [Google Scholar]

42. Y. G. Yang, B. P. Wang, Y. H. Zhou, W. M. Shi and X. Liao, “Efficient color image encryption by color-grayscale conversion based on steganography,” Multimedia Tools and Applications, 2022. https://doi.org/10.1007/s11042-022-13689-z. [Google Scholar]

43. H. Qiu, X. Xu, Z. Jiang, K. H. Sun and C. W. Xiao, “A color image encryption algorithm based on hyperchaotic map and rubik’s cube scrambling,” Nonlinear Dynamics, 2022. https://doi.org/10.1007/s11071-022-07756-1. [Google Scholar]

44. M. Demirtas, “A new RGB color image encryption scheme based on cross-channel pixel and bit scrambling using chaos,” Optik, vol. 265, pp. 169430, 2022. [Google Scholar]

45. M. Xiao, R. Tan, H. Ye, L. H. Gong and Z. Zhu, “Double-color-image compression-encryption algorithm based on quaternion multiple parameter dfrat and feature fusion with preferable restoration quality,” Entropy, vol. 24, no. 7, pp. 941, 2022. [Google Scholar]