Design of Evolutionary Algorithm Based Energy Efficient Clustering Approach for Vehicular Adhoc Networks

1  Introduction

Vehicular communication for intelligent transport systems (ITS) is a quickly rising research area. Vehicular ad hoc network (VANET) exhibits unique features to mobile ad hoc network (MANET), but the unique feature of VANET (i.e., high mobility) differentiates it from MANET. The vehicles in VANET do not suffer from energy insufficiency but face several new challenges because of high mobility. A comprises automobiles linked with one another through a temporary assembly lacking any central access point. VANETs enhance road safety and offer comfort for passengers and drivers through the sporadic sharing of messages [1]. The shared data has status information (i.e., direction, position, velocity) of each vehicle, hazard warnings, and data regarding present traffic conditions. Every automobile was armed with transceivers to interact with the help of Wireless Access for Vehicular Environments (WAVE) [2]. Owing to the high mobility of vehicles, VANET contains dynamic topologies. In dynamic topologies, recurrent interruptions between the loss of messages and vehicles were frequent, particularly under the rising quantity of vehicles [3]. Thus, it is a challenge for interaction protocol to ensure dependable interaction for vehicular applications and scalable concurrently. One such possible solution for enabling scalable interaction in VANETs is clustering. Clustering splits up the network into logical subsets termed clusters. Every cluster can be constituted between nodes with similar features [4]. A Cluster Head (CH) allows both intercluster and intracluster interaction within a cluster. Fig. 1 depicts the framework of VANET.

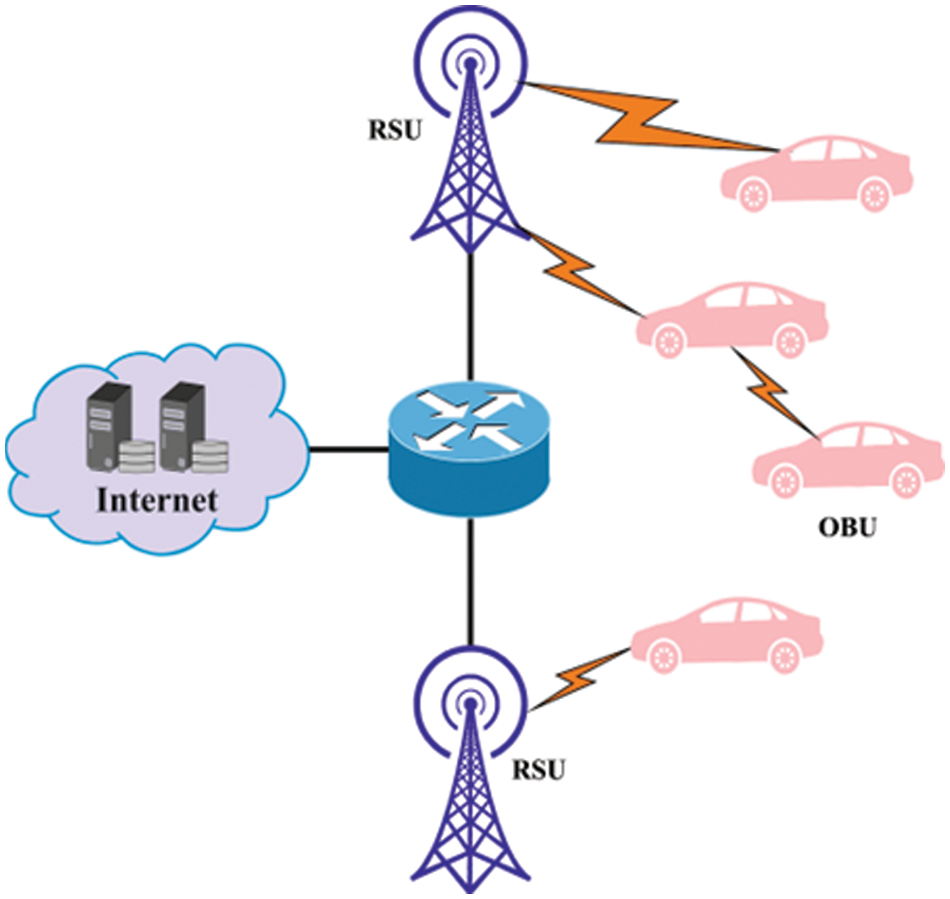
Figure 1: Structure of VANET

In VANET clustering, the cluster head (CH) is essential in the procedure of cluster formation. The cluster is made in several means related to the input metrics [5]. The cluster member vehicle is named cluster member (CMs). Apart from CM and CH, certain methods utilize 2 CMs to interact with others because CH is named cluster gateways (CGs). Until mentioned as CG, all cluster members are termed as CMs. Single CH, 0/1/2 CGs, and any number of CMs are presented in a cluster [6]. The cluster formation depends upon the metrics like the vehicle’s average speed, direction, acceleration, vehicle degree, position, vehicle density, transmitting range, and many more [7]. CH can be chosen from the vehicles that have to be very stable among the vehicles that were participating. The remaining vehicles enter the cluster as CMs [8]. Thus, choosing a CH becomes a part of the cluster formation process, and no separate CM choosing criteria is needed. CMs and CH sustain a routing table comprising data of the CMs and CH of the cluster for intracluster interaction. But CM does not sustain some of the routing tables for others that can be sustained by the CH if required [9]. One main difficulty in forming the cluster was identifying the optimal number of clusters which is needed [10]. It follows that a higher number of clusters might lead to higher delays, and lesser number of clusters might leads to intermittent connectivity.

In [11], the complexity of clustering can be creatively converted into a cutting graph issue. A new clustering technique related to the improved force-directed algorithm and the Spectral Clustering approach was devised. It will take the average lifespan of every cluster as an optimizing goal; thereby, the stability of the complete mechanism is improvised. Cheng et al. [12] present a connectivity estimation-related dynamic clustering (DC) method for VANET in an urban scene. Initially, the author devises a predictive connectivity technique (CP) under the relative features and vehicle nodes features between vehicle nodes. After that, the author designed a DC method related to connectivity between vehicle node density and vehicle nodes. At last, the author models a DC method-related routing approach for realizing stable interactions between vehicle nodes.

In [13], a novel PSO enable multihop method can be devised for helping to Select the optimal route in the VANET and finding the stable CH and eliminating the malicious nodes presented in the network to avoid false messaging. The false may happen if the malicious node is presented in a network. Clustering refers to the method in order to constitute a set of the same node types. This study depends on PSO enable clustering and its significance in VANET. In [14], a new cluster-related VANET oriented evolving graph (CVoEG) technique can be formulated through an extension of the prevailing VoEG method for enhancing the dependability of vehicular interactions. Here, link dependability can be utilized as a criterion for selecting CHs and CMs. The presented CVoEG method classifies VANET nodes into an optimal number of clusters (ONC) with the help of the Eigen gap heuristic. A vehicle is chosen as a CH if it contains maximal Eigen-centrality scores.

In [15], a two-level technique for Primary User detection from the network was formulated. The received signal energy can be sensed, and Primary User can be identified by FL, and it can also utilize a threshold for the final selection of the Primary User. Other variables like average velocity, network connectivity levels, lane weight, and average distance with reliability by cognitive radio sensing were employed for choosing the CH by SDN. In [16], an enhanced weight-based clustering algorithm (EWCA) has been presented for solving such difficulties. The author will consider some vehicles moving on similar road segments and similar road IDs and within the transmitting range of their neighbour to be appropriate for the process of cluster formation. To choose a CH, the author found certain metrics based on vehicle mobility data. Every vehicle was linked with a predefined weight value depending upon relevance.

This article introduces an Evolutionary Hide Objects Game Optimization based Distance Aware Clustering (EHOGO-DAC) Scheme for VANET. The major intention of the EHOGO-DAC technique is to portion the VANET into distinct sets of clusters by grouping vehicles. In addition, the DHOGO-EAC technique is mainly based on the HOGO algorithm, which is stimulated by old games, and the searching agent tries to identify hidden objects in a given space. The DHOGO-EAC technique derives a fitness function (FF) for the clustering process, including the total number of clusters and Euclidean distance. The experimental assessment of the DHOGO-EAC technique is performed under several aspects.

2  The Proposed DHOGO-EAC Technique

In this study, a new EHOGO-DAC scheme was introduced for the effectual clustering process in VANET. The major intention of the EHOGO-DAC technique is to portion the VANET into distinct sets of clusters by grouping vehicles.

2.1 System Model

The VANET scenarios implemented throughout this study are in desert surroundings without any of the usual transmission facilities. This study will consider a group of vehicles functioning over a particular task. The presented method would assume the number of vehicles (N) split into several clusters based on their place. Every cluster (C) contains one CM and CH. Several vehicles within a single cluster can be denoted as Nc , and the maximal number of vehicles for the single cluster is Nmax . The hops count can be indicated as M, and the maximal allowable hops count can be represented as Mmax. The primary communication distance of the ordinary VANET for 2 vehicles i,j was L, which is given as:

L=(xi−xj)2+(yi−yj)2 (1)

Here, x,y indicates the vehicle coordinates i,j, and L≤Lvmax , whereas Lvmax denotes the maximal communicating distance between 2 vehicles which can be decided per the PHY specification of the interaction system. But this interacting distance will be prolonged utilizing the VANETs multihop properties. Thus, the maximal distance Lmax is acquired by:

Lmax=MmaxLvmax (2)

For a definite number of hops M utilizing K≤Nc vehicles, the interaction distance is gained as:

LM=∑m=1M⁡Lm (3)

Here, Lm indicates the communicating distance of a particular hop m.

2.2 Overview of the HOGO Technique

HOGO can be described in 2 common phases: (i) form a time discrete artificial method in the problem, the primary position of the member, which determines the arranging parameters and governing laws, and (ii) pass the time until arriving at the stop time [17].

Assume a set of m ’ players. The position of players is a point in the space where it is a solution to optimization issues. d dimensional position of i−th player is represented by xid in Eq. (4).

Xi=(xi1,…,xid,…,xin) (4)

Firstly, the first position of the game player is randomly generated on the game fields. This player moves to the hidden object according to the governing laws.

In the study, the location of the worst and best players are represented as playerworst and playerbest , correspondingly and are denoted as follows.

playerbest=locationofmin(fitj) (5)

j∈{1:N}

playerworst=locationofmax(fitj) (6)

j∈{1:N}

Here, fiTj demonstrates the objective function j - th members, and N illustrates the player count. While playing HOGO, every player should be considered 4 points:

⋅ Paying attention to the voice generated by the coach for the player

An objective function has been used for simulating the voice generated by the coach. It implies that player with the best position is well suited, and consequently, they receive a louder voice. The voice generated by the coach is normalized, and later, it is evaluated as follows.

Voicei=fiti−fit(playerworst)∑j=1N⁡[fitj−fit(playerworst)] (7)

Now, Voice denotes a voice generated by the coach for i−th members, and it is evaluated as follows.

Pi=Voicei∑=1N⁡Voicej (8)

⋅ Getting close to the better player for whom the coach generated the louder voice

In these games, concerned the voice loudness, players try to guide the direction towards the player for whom the coach generated the louder voice and it is formulated by

dX1j,d=playerbestd−X0j,d (9)

In Eq. (9), dX1j,d denotes the movement value of j - th members d−th e dimension towards the better player position, and X0j, signifies the first position of the j - th member’s d−th e dimension.

⋅ Receding from the worst player for whom the coach generated the lowest voice

In this approach, the player tries to move away from the player who has the lowest voice and the worst position, and it is evaluated by using the following equation.

dX2j,d=X0j,d−playerworstd (10)

Here, dX2j,d implies the movement value of j - th members d−th e dimension from the worst player position.

⋅ Taking inspiration from the voice generated by the coach for others

Instead of worst and best players, every player tries to take the greatest benefit of others’ location. Now, every player measures the loudness of the voice generated for others and moves towards or away from the other players by comparing the loudness of voice. The roulette wheel operator is used for simulating this strategy. Consequently, the potential accumulation function evaluated in Eq. (5) is used for determining the influential player and it is shown as follows.

dX3j,d={X0j,d−X0select,dPj>PselectX0select,d−X0j,delse (11)

In Eq. (11), dX3j,d indicates the d−th dimension movement of j - th members viz., appropriate for the selected influential player position, X0select,d indicates the location of d−th e dimension, and Pselect denotes the potential accumulation of the selected influential player and Pj shows j - th members’ potential accumulation. Here, X′j,l indicates the primary position of j - th member d−th e dimension that is evaluated according to Eq. (12). Now, r1,r2 , and r3 denotes random number using standard distribution within [0, 1].

X′j,d=X0j,d+r1×dXj,d1+r2×dXj,d2 (12)

+r3×dXj,d3

Comparing the new voice afterward the move with the voice previous to the move and return back in case the voice gets low.

In this method, the player can be temporarily positioned on Xj place by using Eq. (12). In this state appropriate to the position, the coach will make a novel sound as voice j for the players. Now, the player determines where she or he should stand by comparing the older and newer voice of the coach. It indicates that the player will be standing in the new place when the new voice was greater when compared with the older one. Or else, the player should return back to his or her former position via this return cannot be satisfied because he or she exited the prior position. According to Eq. (13), he or she might be in a random place around the prior Xj position and rand denote random number has standard distributions within [0, 1].

X′′j,d=(0.9+0.2×rand)×X0j,d (13)

Xj={X′jVoice′j>VoicejX0j,dVoicejmax(Voice)>0.5X′′jelse (14)

Initially, players are placed at random in any portion of the game. At any time, player location is measured and later their dislocation is assessed according to Eqs. (4) to (14). The stopping criteria are defined afterward the passing of discrete time period. Fig. 2 illustrates the flowchart of HOGO technqiue. The HOGO algorithm is given in the following steps:

1. Determine the system space or atmosphere and the initial quantifying

2. Primary positioning of player

3. Evaluating the player

4. Determine the voice of all the players by the coach

5. Update the location of the worst and best players

6. Update the player location

7. Repeat steps 3 to 6 till the stopping criteria are met

8. Finish

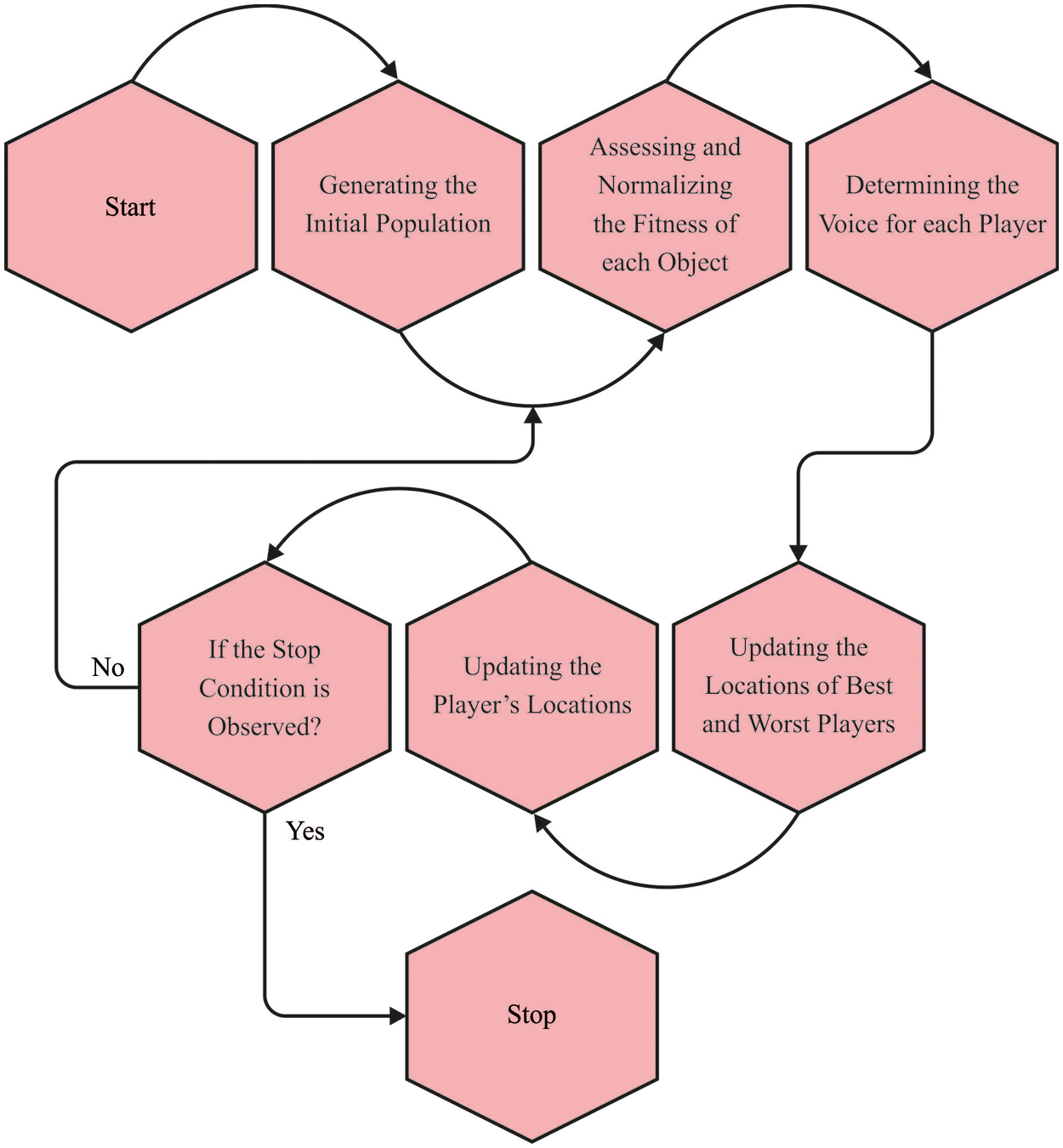
Figure 2: Flowchart of HOGO

2.3 Process Involved in DHOGO-EAC Technique

For clustering process, the DHOGO-EAC technique derives a FF, including total number of clusters and Euclidean distance [18]. The presented approach is adopted for Multiobjective optimization, where weight is allocated to all the objectives based on the condition of user preferences. The FF is calculated by the following equation:

Fn=(F1∗W1)+(F2∗W2) (15)

Let, Wl and W2 be the weight of the F1 and F2 objective functions correspondingly. The weight is allocated similar value viz., 0.5, but this value is adapted based on the condition preferred by the user.

The function F1 characterizes the delta variance of the cluster in n (overall amount of clusters) and it can be derived as follows:

F1=∑i=1n⁡abs(DeltaDegree−|CNi|) (16)

The DeltaDegree portrays the ideal degree of cluster density as stated by the user. For dense clusters, the value is greater, while it is lesser for sparse clusters. The overall amount of vehicles in cluster i can be described as CN N. The lower value of F1 implies the cluster has been created nearly optimal based on the user specification.

The function F2 signifies the sum of distance of each CH from the cluster node and it is evaluated by Eq. (17):

dCHi=∑j=1|CNi|⁡ED(CHi,CNj.i) (17)

Now, ED refers to Euclidean distance, the location of ith CH is represented as CHi , whereas the location of the jth cluster node in the ith cluster is shown as CNj,i . In the following, it can be expressed in the form as:

F2=∑i=1n⁡dCHi (18)

Now, n represents the overall amount of clusters. A lesser value of F2 function was desired. As lesser value implies the CH and the cluster node are closer to one another, thereby needing lower energy for data transmission. Then, add further objective functions to compute the FF and also by differing the weight based on the user requirement.

3  Results and Discussion

The experimental validation of the DHOGO-EAC MODEL is examined under varying levels of vehicle speed (VS). Table 1 offers a detailed clustering efficiency of the DHOGO-EAC model under all vehicle speeds.

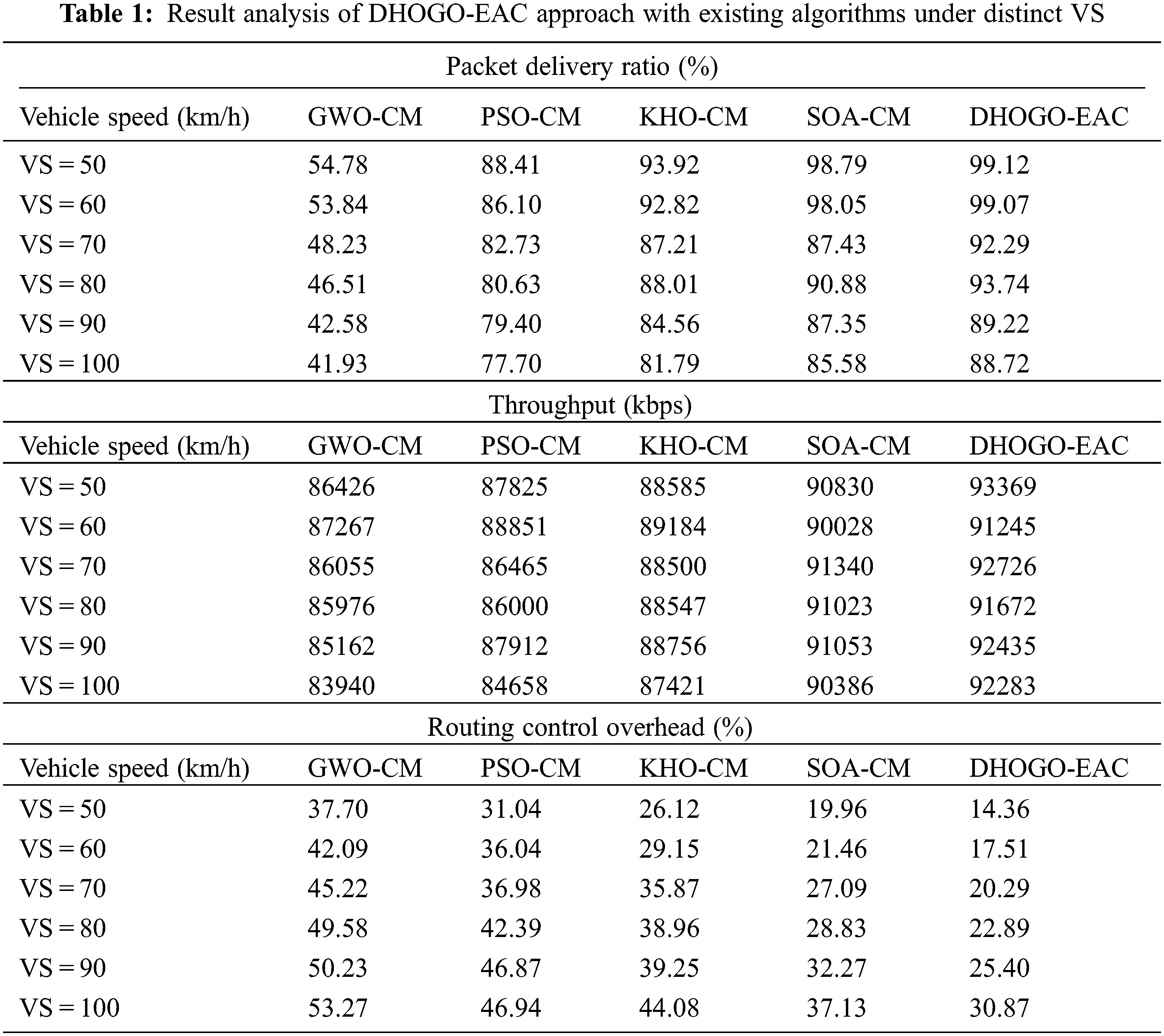
Fig. 3 depicts the comparative PDR assessment of the DHOGO-EAC model under diverse VS. The figure portrayed that the DHOGO-EAC model has exhibited increased PDR values. For instance, with VS of 50 km/h, the DHOGO-EAC model has provided enhanced PDR of 99.12% whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM models have attained reduced PDR values of 54.78%, 88.41%, 93.92%, and 98.79% respectively. Concurrently, with VS of 60 km/h, the DHOGO-EAC method has rendered enhanced PDR of 99.07% whereas the GWO-CM, PSO-CM, KHO-CM,and SOA-CM approaches have gained reduced PDR values of 53.84%, 86.10%, 92.82%, and 98.05% correspondingly. Parallelly, with VS of 70 km/h, the DHOGO-EAC technique has offered enhanced PDR of 92.29% whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM approaches have achieved reduced PDR values of 48.23%, 82.73%, 87.21%, and 87.43% correspondingly.

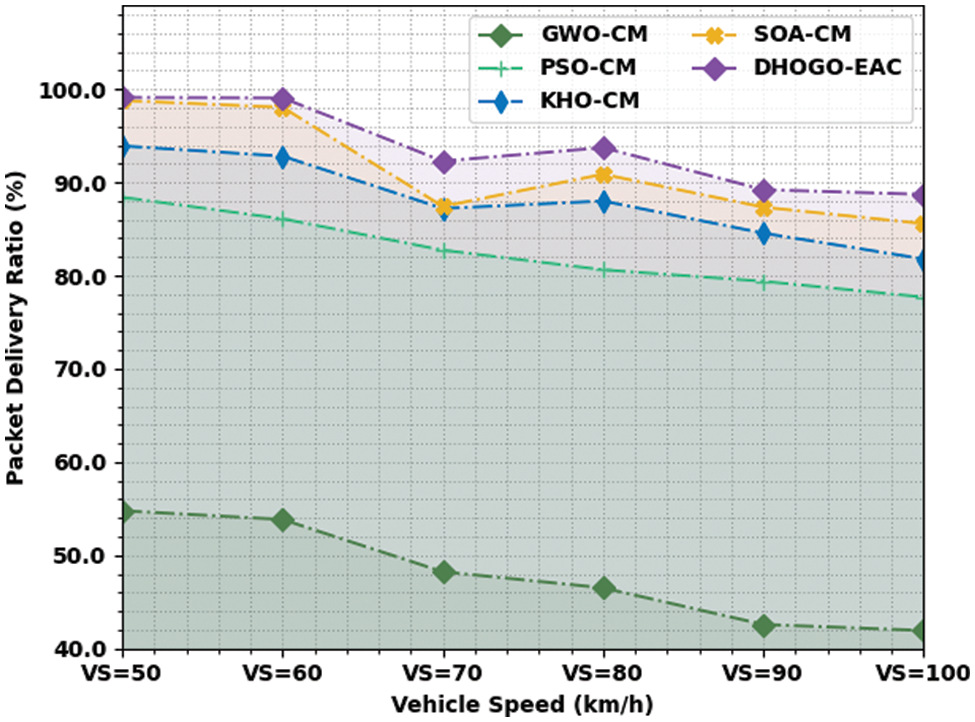
Figure 3: PDR analysis of DHOGO-EAC approach under distinct VS

Fig. 4 portrays the detailed THROP assessment of the DHOGO-EAC methodology under diverse VS. The figure depicted that the DHOGO-EAC approach has shown increased THROP values. For example, with VS of 50 km/h, the DHOGO-EAC algorithm has presented enhanced THROP of 93369 kbps whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM techniques have obtained reduced THROP values of 86426, 87825, 88585, and 90830 kbps respectively. At the same time, with VS of 60 km/h, the DHOGO-EAC method has offered enhanced THROP of 91245 kbps whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM methodologies have obtained reduced THROP values of 87267, 88851, 89184, and 90028 kbps correspondingly. Simultaneously, with VS of 70 km/h, the DHOGO-EAC algorithm has presented enhanced THROP of 92726 kbps whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM approaches have acquired reduced THROP values of 86055, 86465, 88500, and 91340 kbps correspondingly.

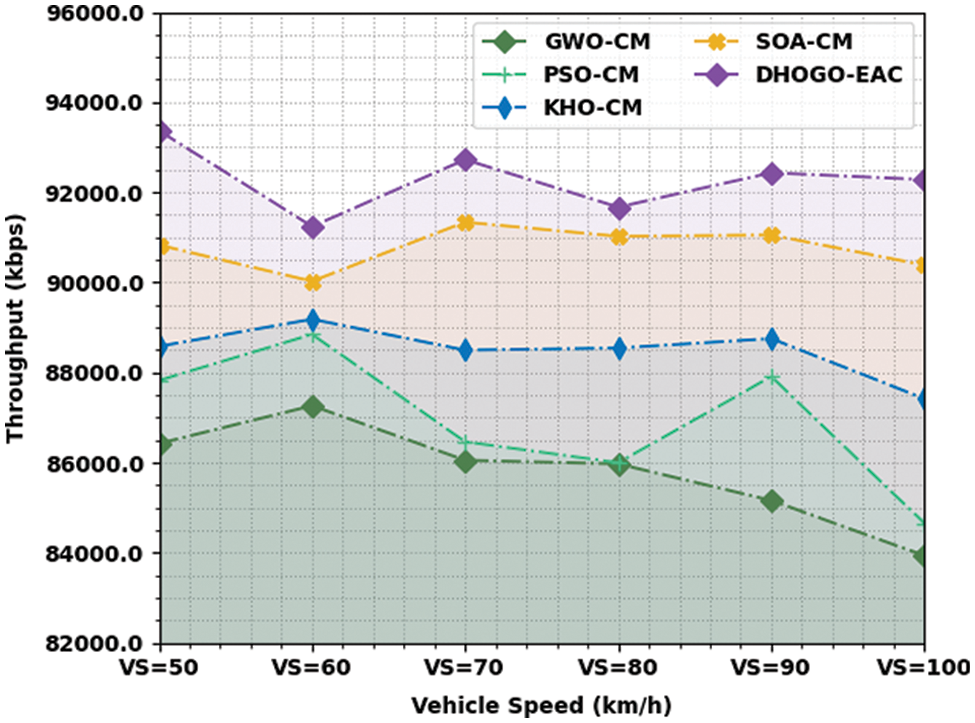
Figure 4: THROP analysis of DHOGO-EAC approach under distinct VS

A detailed routing control overhead (RCO) inspection of the DHOGO-EAC model is compared with recent models in Fig. 5. The figure represented the enhancements of the DHOGO-EAC model with minimal RCO values. For instance, with VS of 50 km/h, the DHOGO-EAC model has gained minimal RCO of 14.36% whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM models have resulted in increased RCO values of 37.70%, 31.04%, 26.12%, and 19.96% respectively. Also, with VS of 60 km/h, the DHOGO-EAC technique has obtained minimal RCO of 17.51% whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM approaches have resulted to increased RCO values of 42.09%, 36.04%, 29.15%, and 21.46% correspondingly. Additionally, with VS of 70 km/h, the DHOGO-EAC algorithm has obtained minimal RCO of 20.29% whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM approaches have resulted in increased RCO values of 45.22%, 36.98%, 35.87%, and 27.09% correspondingly.

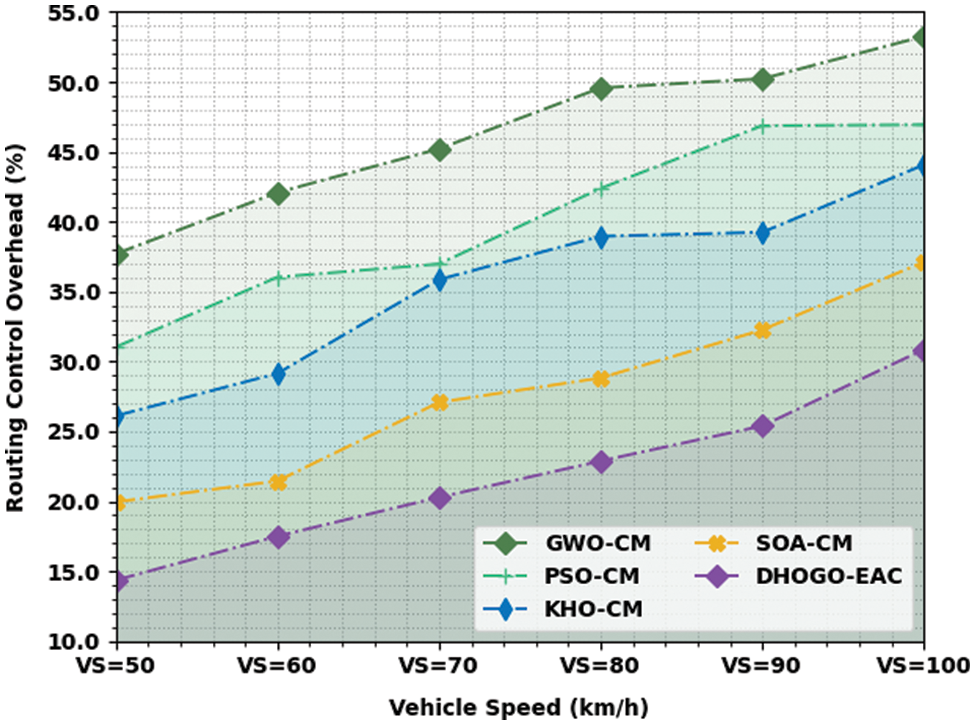
Figure 5: RCO analysis of DHOGO-EAC approach under distinct VS

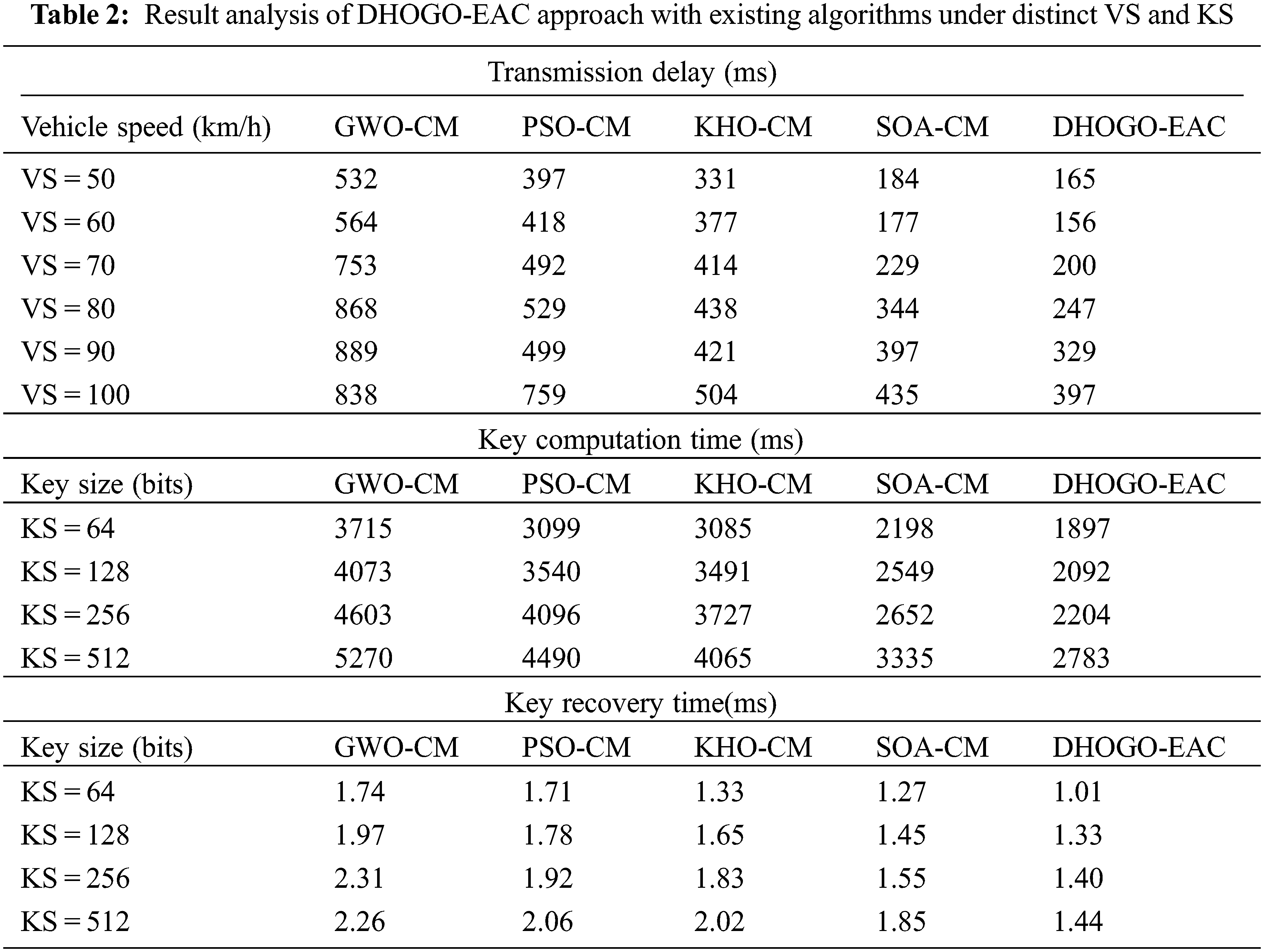
Table 2 presents a detailed clustering efficiency of the DHOGO-EAC approach under all vehicle speeds and key sizes.

A comprehensive transmission delay (TDEL) review of the DHOGO-EAC method is compared with recent algorithms in Fig. 6. The figure signified the enhancements of the DHOGO-EAC technique with minimal TDEL values. For example, with VS of 50 km/h, the DHOGO-EAC algorithm has acquired minimal TDEL of 165 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM methods have resulted in increased TDEL values of 532, 397, 331, and 184 ms correspondingly. Besides, with VS of 60 km/h, the DHOGO-EAC approach has attained minimal TDEL of 156 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM methods have resulted in increased TDEL values of 564, 418, 377, and 177 ms correspondingly. Likewise, with VS of 70 km/h, the DHOGO-EAC methodology has acquired minimal TDEL of 200 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM methods have resulted in increased TDEL values of 753, 492, 414, and 229 ms correspondingly.

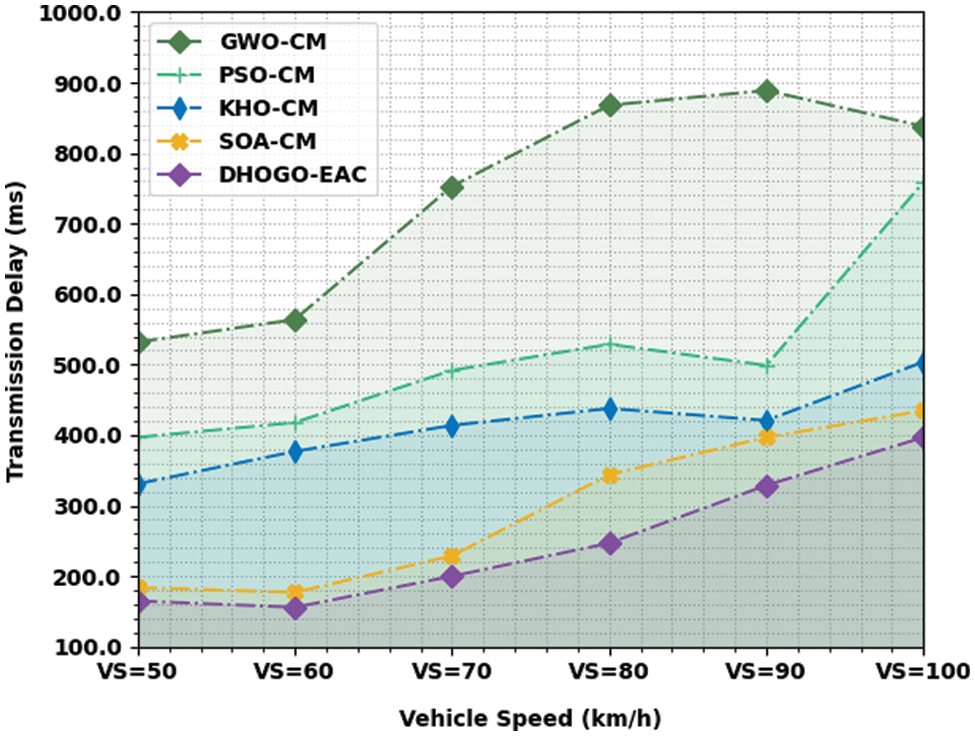
Figure 6: TDEL analysis of DHOGO-EAC approach under distinct VS

A brief key computation time (KCT) analysis of the DHOGO-EAC technique is compared with recent models in Fig. 7. The figure denoted the enhancements of the DHOGO-EAC approach with minimal KCT values. For example, with KS of 64bits, the DHOGO-EAC method has acquired minimal KCT of 1897 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM algorithms have resulted in increased KCT values of 3715, 3099, 3085, and 2198 ms correspondingly. Additionally, with KS of 128bits, the DHOGO-EAC methodology has achieved minimal KCT of 2092 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM algorithms have resulted in increased KCT values of 4073, 3540, 3491, and 2549 ms correspondingly. Furthermore, with KS of 256bits, the DHOGO-EAC approach has attained minimal KCT of 2204 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM models have resulted in increased KCT values of 4603, 4096, 3727, and 2652 ms correspondingly.

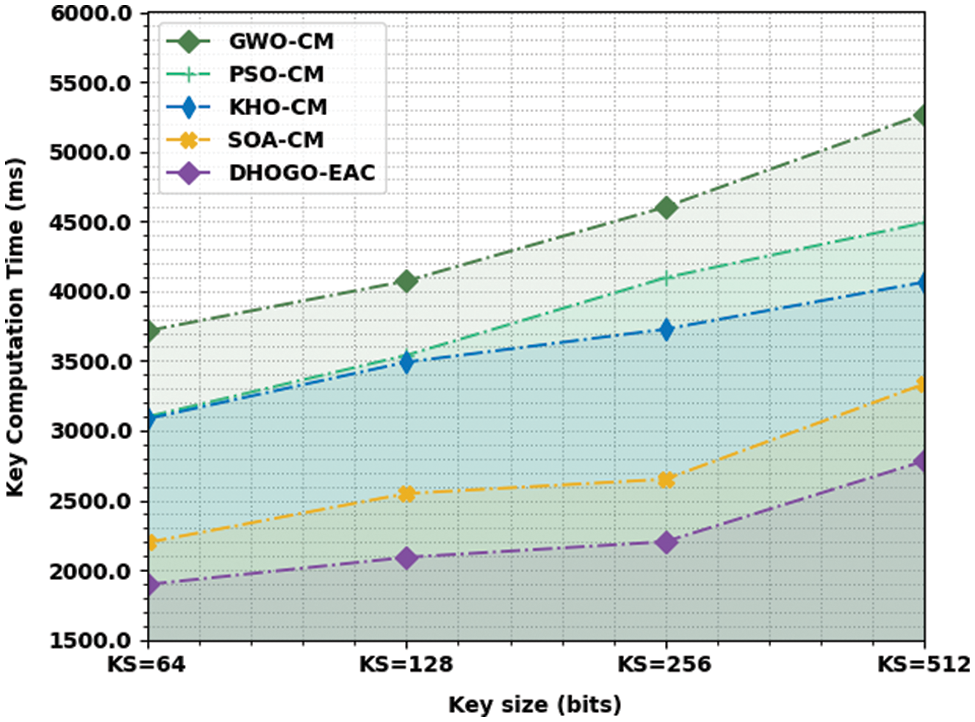
Figure 7: KCT analysis of DHOGO-EAC approach under distinct KS

A complete key recovery time (KRT) review of the DHOGO-EAC method is compared with recent models in Fig. 8. The figure represented the enhancements of the DHOGO-EAC approach with minimal KRT values. For example, with KS of 64bits, the DHOGO-EAC technique has attained minimal KRT of 1.01 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM models have resulted in increased KRT values of 1.74, 1.71, 1.33, and 1.27 ms correspondingly. Besides, with KS of 128bits, the DHOGO-EAC approach has obtained minimal KRT of 1.33 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM models have resulted in increased KRT values of 1.97, 1.78, 1.65, and 1.45 ms correspondingly. Also, with KS of 256bits, the DHOGO-EAC method has attained minimal KRT of 1.40 ms whereas the GWO-CM, PSO-CM, KHO-CM, and SOA-CM algorithms have resulted in increased KRT values of 2.31, 1.92, 1.83, and 1.55 ms correspondingly.

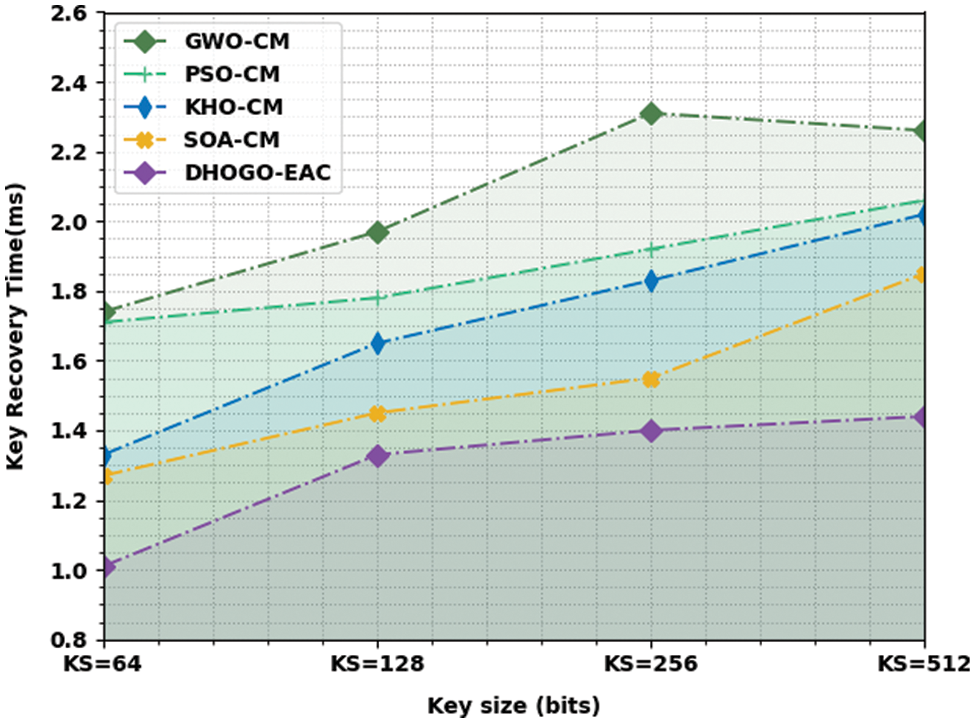
Figure 8: KRT analysis of DHOGO-EAC approach under distinct KS

4  Conclusion

In this study, a novel EHOGO-DAC scheme was introduced for effectual clustering process in VANET. The major intention of the EHOGO-DAC technique is to portion the VANET into distinct sets of clusters by the grouping of vehicles. In addition, the DHOGO-EAC technique is mainly based on the HOGO algorithm, which is stimulated by old games and the searching agent tries to identify hidden objects in a given space. For clustering process, the DHOGO-EAC technique derives a FF, including total number of clusters and Euclidean distance. The experimental assessment of the DHOGO-EAC technique was carried out under distinct aspects. The comparison outcome stated the enhanced outcomes of the DHOGO-EAC technique compared to recent approaches. In future, the performance of the DHOGO-EAC technique can be extended by the design of hybrid metaheuristic algorithms.

Funding Statement: This work was supported by the Ulsan City & Electronics and Telecommunications Research Institute (ETRI) grant funded by the Ulsan City [22AS1600, the development of intelligentization technology for the main industry for manufacturing innovation and Human-mobile-space autonomous collaboration intelligence technology development in industrial sites].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. Ahsan, M. F. Khan, F. Aadil, M. Maqsood, S. Ashraf et al., “Optimized node clustering in VANETs by using meta-heuristic algorithms,” Electronics, vol. 9, no. 3, pp. 394, 2020. [Google Scholar]

 2.  M. Ren, J. Zhang, L. Khoukhi, H. Labiod and V. Vèque, “A review of clustering algorithms in VANETs,” Annals of Telecommunications, vol. 76, no. 9, pp. 581–603, 2021. [Google Scholar]

 3.  A. Katiyar, D. Singh and R. S. Yadav, “State-of-the-art approach to clustering protocols in VANET: A survey,” Wireless Networks, vol. 26, no. 7, pp. 5307–5336, 2020. [Google Scholar]

 4.  S. A. Rashid, L. Audah, M. M. Hamdi and S. Alani, “Prediction based efficient multi-hop clustering approach with adaptive relay node selection for VANET,” Journal of Communications, vol. 15, no. 4, pp. 332–344, 2020. [Google Scholar]

 5.  A. F. M. S. Shah, H. Ilhan and U. Tureli, “CB-MAC: A novel cluster-based MAC protocol for VANETs,” IET Intelligent Transport Systems, vol. 13, no. 4, pp. 587–595, 2019. [Google Scholar]

 6.  S. Kosuru, P. Suma, M. A. Alam and M. A. Hussain, “An intelligent cluster-based energy-efficient optimization algorithm to improve the network performance in VANET,” Mathematical Statistician and Engineering Applications, vol. 71, no. 3, pp. 201–208, 2022. [Google Scholar]

 7.  M. A. Mujahid, K. A. Bakar, T. S. Darwish and F. T. Zuhra, “Cluster-based location service schemes in VANETs: Current state, challenges and future directions,” Telecommunication Systems, vol. 76, no. 3, pp. 471–489, 2021. [Google Scholar]

 8.  J. I. Z. Chen and P. Hengjinda, “Enhanced dragonfly algorithm based K-medoid clustering model for VANET,” Journal of ISMAC, vol. 3, no. 1, pp. 50–59, 2021. [Google Scholar]

 9.  G. Husnain and S. Anwar, “An intelligent cluster optimization algorithm based on whale optimization algorithm for VANETs (WOACNET),” Plos One, vol. 16, no. 4, pp. e0250271, 2021. [Google Scholar]

10. R. Kolandaisamy, R. M. Noor, I. Kolandaisamy, I. Ahmedy, M. L. M. Kiah et al., “A stream position performance analysis model based on DDoS attack detection for cluster-based routing in VANET,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 6, pp. 6599–6612, 2021. [Google Scholar]

11. G. Liu, N. Qi, J. Chen, C. Dong and Z. Huang, “Enhancing clustering stability in VANET: A spectral clustering-based approach,” China Communications, vol. 17, no. 4, pp. 140–151, 2020. [Google Scholar]

12. J. Cheng, G. Yuan, M. Zhou, S. Gao, Z. Huang et al., “A connectivity-prediction-based dynamic clustering model for VANET in an urban scene,” IEEE Internet of Things Journal, vol. 7, no. 9, pp. 8410–8418, 2020. [Google Scholar]

13. A. Temurnikar, P. Verma and G. Dhiman, “A PSO enable multi-hop clustering algorithm for VANET,” International Journal of Swarm Intelligence Research (IJSIR), vol. 13, no. 2, pp. 1–14, 2022. [Google Scholar]

14. Z. Khan, P. Fan, S. Fang and F. Abbas, “An unsupervised cluster-based VANET-oriented evolving graph (CVoEG) model and associated reliable routing scheme,” IEEE Transactions on Intelligent Transportation Systems, vol. 20, no. 10, pp. 3844–3859, 2019. [Google Scholar]

15. U. Maan and Y. Chaba, “Accurate cluster head selection technique for software-defined network in 5G VANET,” Wireless Personal Communications, vol. 118, no. 2, pp. 1271–1293, 2021. [Google Scholar]

16. A. B. Tambawal, R. M. Noor, R. Salleh, C. Chembe and M. Oche, “Enhanced weight-based clustering algorithm to provide reliable delivery for VANET safety applications,” PloS One, vol. 14, no. 4, pp. e0214664, 2019. [Google Scholar]

17. M. Dehghani, Z. Montazeri, S. Saremi, A. Dehghani, O. P. Malik et al., “HOGO: Hide objects game optimization,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 10, pp. 216–225, 2020. [Google Scholar]

18. R. Sharma, V. Vashisht and U. Singh, “EEFCM-DE: Energy-efficient clustering based on fuzzy C means and differential evolution algorithm in WSNs,” IET Communications, vol. 13, no. 8, pp. 996–1007, 2019. [Google Scholar]