Intelligent Digital Envelope for Distributed Cloud-Based Big Data Security

1  Introduction

Cloud computing is crucial in providing optimal information service to Cloud consumers from diverse places. Hybrid Cloud appears efficient in offering Cloud services; however, it has limitations. For example, it allows off-premises Cloud computing as backup data centers, which was previously believed and used. Many firms are struggling to supply services in the age of Cloud computing. Horlach’s bimodal concept helps information officers choose the best way to use Cloud computing. Rivest created the remarkable RSA Public Key Cryptosystem (PKC) in the 1970s, which is now used by millions of people worldwide. Authenticating open key endorsements before using the customer’s public key is one of the testing issues in PKI, requiring the verifier to pay a higher cost in the count. Large-key management and certificate authentication become inefficient.

Asymmetric key generation, symmetric encryption and decryption of sensitive data, and asymmetric encryption and decryption of the symmetric secret key are all included in the Digital Envelope. Encryption creates the Digital Envelope, whereas decryption is used to open the Digital Envelope. Several secure methods have been proposed; however, most rely on a single Cloud infrastructure for big data access. This paper proposes the dual Digital Envelope for distributed Cloud-based big data security for practical and real-time data management in the Cloud.

Less secure Cloud services have varying security criteria and threat levels. Cloud-dominant computing services include IaaS, PaaS, and SaaS. These include bandwidth, communication, computing power, storage, and virtualization. It is used for PaaS and SaaS. These are common IaaS threats. Scalable PaaS applications connect operating systems and server hardware. Peer-to-Peer security is rare in PaaS. The periodic software changes and interruptions are risks, including software security, data access, authentication and authorization. SaaS risks include session hijacking, data loss, and privacy violations. The SaaS model is ideal for storing sensitive viewer data in the Cloud. Encryption algorithms are used to protect the user’s privacy. An important part of network security is data integrity and authentication.

The KGS generates cryptographic keys. These keys encrypt data. For real-time applications, this KGS module must be protected. Cryptosystem keys can be symmetric or asymmetric. The KGS and cipher receivers share a secret key. The sender uses KGS’ shared public key (d, N) to encrypt plain text, and the receiver uses its private key (e, N) to decode cipher text. Asymmetric RSA KGS uses the same N-bit moduli for public and private keys. Kleinjung broke the 768 N-bit RSA modulus in 2009. NIST recommends 2048 or 2K bits. Start with two N/2 secret primes, p and q. N-bit primes and private keys. Thus, RSA KGS uses ϕ(N) = (p − 1) * (q − 1). It is possible to improve RSA’s security and key storage by breeding it.

When the private key size is small, the apt attack can hack the original message from the sent public key. Wiener demonstrated the dangers of RSA using d < N0.25. By obtaining tiny solutions to the polynomial problem using the Lattice theory, Boneh and Durfee demonstrated the Wiener Attack's vulnerability at d < N0.292. The Wiener attack is dormant when e > N1.5. These assaults are also polynomial time-bound. Dual RSA is insecure when d < N0.333, say Sun et al. In 2014, L. Peng et al. [1] extended the attack to Dual RSA with d < N0.368 [2].

The suggested technique is significant because it provides a flexible approach for businesses that want to adopt SaaS [3] but need high data storage security [4,5], like the online software training industry. The proposed solution prevents Cloud providers from directly accessing consumers’ original data. This study makes two major contributions:

•   With the proposed innovative cryptographic solution, Cloud operators cannot directly access consumers’ original data.

•   This research provides a low-cost data split approach that ensures data retrievability.

Work organized as follows: Section 2 discussed the existing PKC security architecture in detail, including key generation, encryption, and decryption; Section 3 demonstrated the dual Digital Envelope for distributed Cloud-based big data security algorithms; Section 4 discussed the experimental results, and Section 5 concluded.

2  Related Research Review

Cloud computing security has spread to network and system administration. Cloud computing's interconnection of technical applications, such as Virtual Machines (VM), raises network and data storage security concerns. Prior research examined security issues from various dimensions [6,7]. Encryption and data classification are two common data management security subsets [8]. In the Cloud, data encryption is used to save money on computers [9], and classification of data is done to determine its encryption. Data management practices assume Cloud providers do not abuse or restrict data access. Even if data is encrypted in the Cloud, it can be retrieved. Monitoring and preserving data storage is part of safeguarding Cloud data. It means Cloud operators’ actions are being watched. One option is using Attributed-Based Encryption (ABE) to protect data sent between Clouds [10]. The access scale of Cloud operators may harm data integration and integrity, increasing the risk of data loss or system failure. As a result, storing the contradictions between privacy and data processing is difficult. In order to reduce total system costs, most current solutions aim to balance these two qualities.

Mass Distributed Storage (MDS) is used in Cloud systems to store large amounts of data. Aside from security concerns, this strategy has limitations regarding storage availability, reliability, and accessibility. Large data sets make system interconnections more complicated. The main concerns in using MSD are security. Several important challenges and experiments in Cloud-based MDS are summarized as follows: First, restricted processing resources make data synchronization difficult. Smaller users can expect efficient synchronization while distributing large data. However, enormous numbers of big data consumers put computational resources to the test. Studies [11] have recently addressed this topic. For instance, local synchronization can be implemented in asynchronous spiking neural P systems and methods for increasing the processing power of distributed parallel computing systems are discussed. Other research has looked into how Cloud big data storage systems, such as mobile and agent-based computing, can be used to improve corporate processes.

Other studies examine data security issues like access control and trust management [12]. Using trust level classification to protect rapid community data access was proposed. This method worked well when users chose trust communication settings for Instant Social Networking (ISN) [13]. Multimedia large data in the Cloud is being unlocked with ontology-based authentication classifiers. These investigations focused on the security of data transmission and authentication. Control is lost when data is Cloud-stored. Cloud servers also need encryption-based technologies. Studies like Fully Homomorphic Encryption (FHE) [14] and ABE have looked into this. While these safety systems can protect data from external threats and internal inefficiencies, the extra computations can significantly slow down data processing.

Some procedures are stalled due to technical issues like FHE noise [15]. In summary, most current active Cloud-side data exploitation approaches offer two alternatives. Regulation of employee behavior frequently involves the use of regulatory compliance procedures. [16,17]. Technical solutions need to control this mindset. Alternatively, utilize encryptions like FHE and ABE to prevent data leakage. More efficient operations and unresolved issues inside the solutions prevent this type of data protection from meeting most modern industrial standards. This technology meets the demand for higher-level security in big data applications. Even though the Cloud operators have access to the data, it can be safeguarded.

The NIST believes RSA security level N-bit modulus 2048 bits are safe. So, making asymmetric keys takes longer. Three major steps define the RSA public key cryptosystem: asymmetric key generation, encryption and decryption. Thangavel et al. [18] created a key generation algorithm employing four primes that computes more than ordinary RSA encryption and decoding, which is almost always four times the encryption cost of RSA. Decryption costs are reduced using Wiener’s Rebalanced RSA. Erkamsaid ESRKGS is factorization susceptible. However, their encryption and decryption keys share the same moduli, n, which only require two primes (p, q). Hence, the message (M) can be reversed using the private key (d, n). ESRKGS and RSA are thus both vulnerable to factorization attacks. An attack on CHAN-PKC is safe when primes |p| + |q| > 750.

CHAN-PKC [19] solves the form α+Re2+2RYqe≡1%∅(N) to produce asymmetric keys. This system triples the ciphertext using the public key ( α , R, N) and decrypts them using the private key (Yq, e, N) for great security and confidentiality. The ENPKESS [20] cryptosystem is protected from side-channel attacks using a non-linear Diophantine equation. Unlike ESR and RSA, this method has three stages of encryption and decoding. To improve Cloud security, ENPKESS encryption keys apply to Knapsack. To protect Cloud operators from obtaining sensitive user data, intelligent cryptography was developed. The SA-EDS (Security-Aware Efficient Distributed Storage) effectively defends against major Cloud risks while needing minimal computation time.

3  Proposed Model

The proposed algorithms suggested are described in this section. Three primary algorithms support the proposed big data Digital Envelope security approach: Fast-PKC, Secure Data Split Distribution with Encryption (SD2E), and Fast Data Merge with Decryption (FDMD) algorithms. The sections that follow discuss the algorithms in depth.

A. Fast-PKC

As illustrated in Fig. 1, the asymmetric keys are initially produced using F-PKC for the Digital Envelope opening. This PKC’s key creation takes a collection of random positive integers r1, r2, and a huge secret prime q as input. For the Digital Envelope process, the F-PKC outputs the key variables A, D, N, and the common modulus E. Let us say the public key is A, E. The private key is D, N, and E. Similarly, if the public key is D, E, then the private key is A, N, E and so on. The F-PKC public keys are shared with the sensitive message holder to produce Digital Envelopes. For the Digital Envelope formation, the sender divides the sensitive message M into ab and P, where a and b are random constants, and P is the secret prime. The message M contains n data packets containing sensitive information, {m1, m2,…., mn}. The random symmetric key K is then used to encrypt the split messages. This symmetric secret key K is then encrypted with the received public key using F-PKC before being sent securely to the other end for opening. Algorithm 1 illustrates pseudo codes for the F-PKC algorithm. The following statement summarizes the primary steps of algorithm 1:

1.    Calculate the intermediate constant, f = r1.r2 – q, using the random positive integers r1, r2, and a huge hidden prime q.

2.    Compute the intermediate key A = q.f + r1.

3.    Compute the intermediate key D = q.A + r2.

4.    Compute the common modulus E = (AD – q)/f.

5.    Check for a relatively prime relationship between prime q and key E.

6.    At last, compute the intermediate key N = q−1 mod E.

7.    For Digital Envelope encryption and decryption, output key parameters are public (AD%E, E) and private key (N, E).

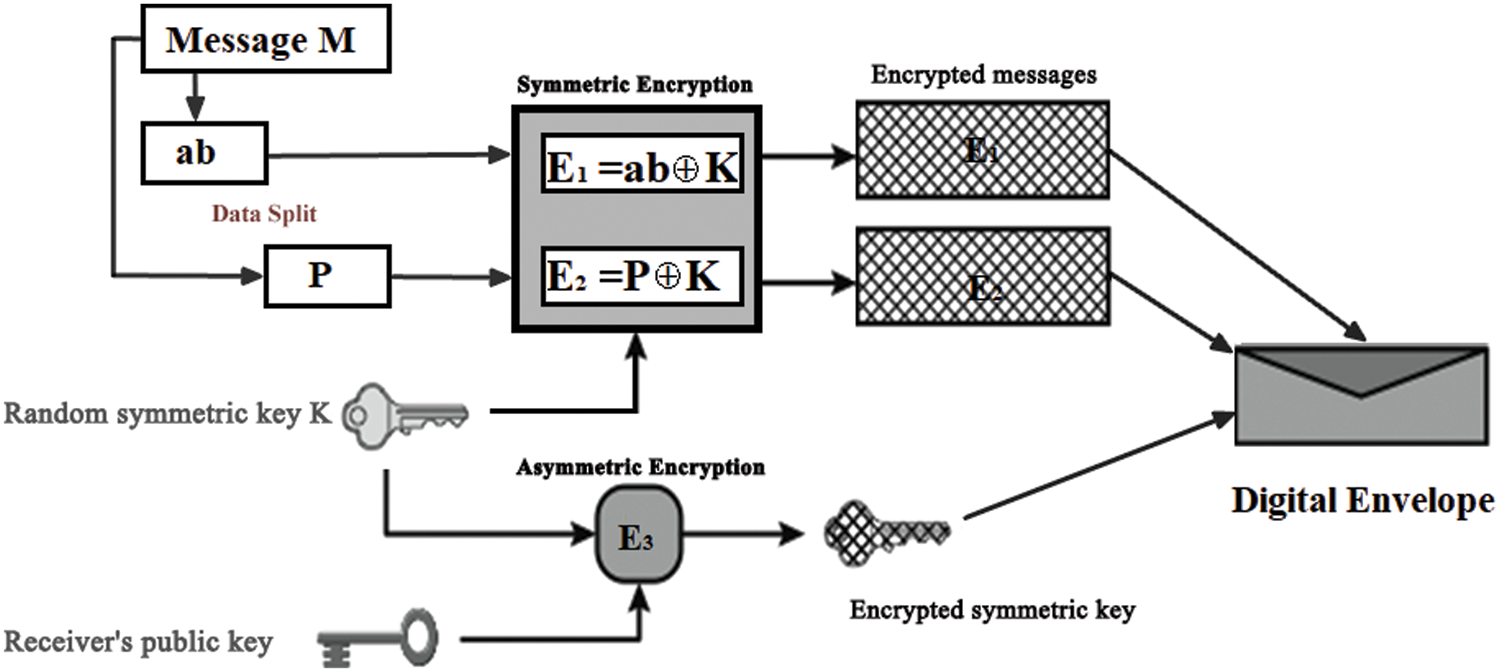
Figure 1: Creation of Digital Envelope using Data split and F-PKC encryption

B. Secure Data-split Distribution with Encryption (SD2E)

At first, the sensitive message M is divided into ab and P where a and b are random secret constants and P is secret prime b as shown in Fig. 2. Data split ab and P on sensitive message M is encrypted using symmetric key K as E1 = ab⊕K and E2 = P⊕K. After this, the encrypted messages E1 and E2 are stored in different Clouds. This data split and distributed storage of encrypted data process make it the Cloud operator difficult to access or realize the actual message M. Followed by the selected secret symmetric key K is encrypted using F-PKC public keys for the Digital Envelope. The received public key AD%E, modulus E from the key generation end, as shown in Fig. 2, is used for F-PKC encryption. Thus, the secret symmetric key K is secured using the F-PKC encryption. The above two levels of symmetric and one level of asymmetric encryption create the Digital Envelope.

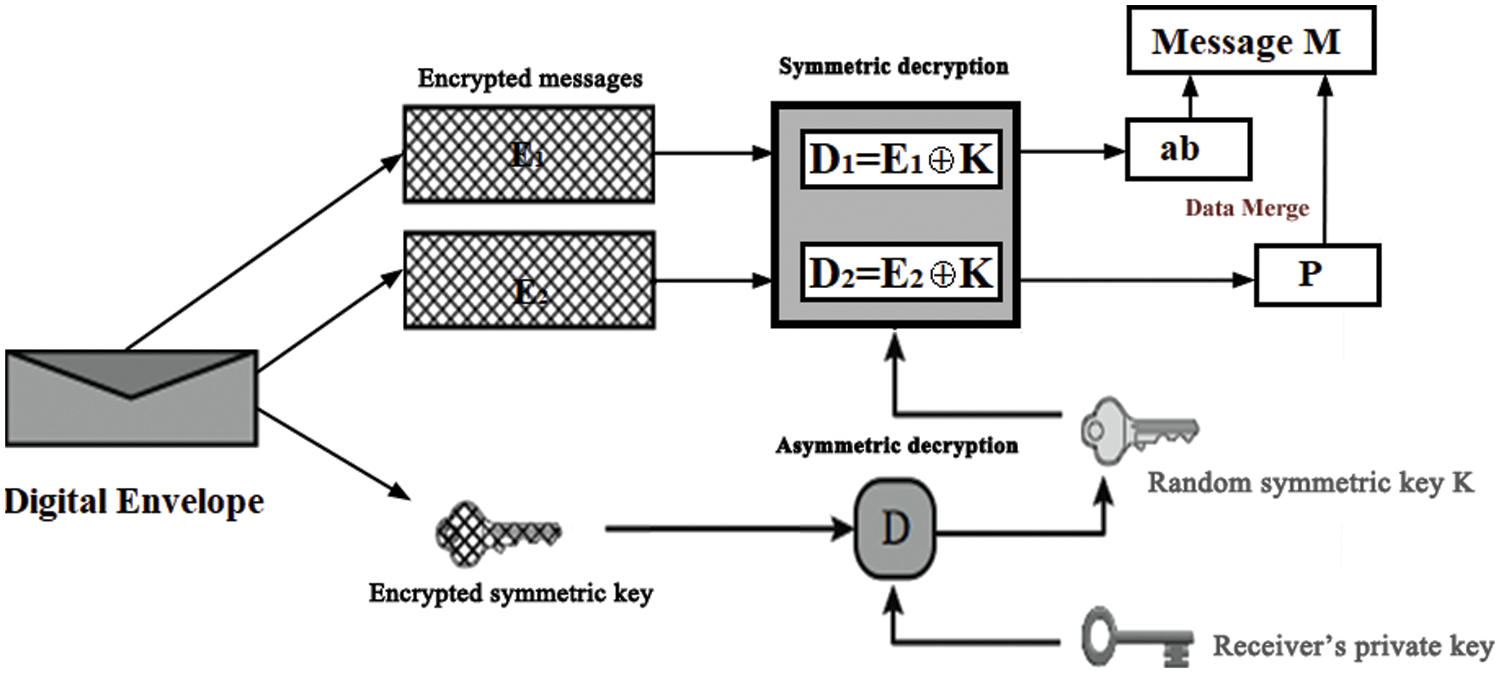
Figure 2: Opening a Digital Envelope using F-PKC decryption and data merge

Algorithm 2 illustrates pseudo codes for the SD2E algorithm. The following statement summarizes the primary steps of algorithm 2:

1.    Split the sensitive message M into ab and P, i.e., M = ab − P.

2.    Randomly select the secret symmetric key K for data split.

3.    Apply symmetric encryption on separated message ab and P as E1 = ab⊕K and E2 = P⊕K.

4.    Receive the F-PKC public key AD%E, modulus E from the Digital Envelope opener.

5.    Apply asymmetric encryption using F-PKC to secure the secret symmetric key K as E3 = (K * AD)%E.

6.    Create and share Digital Envelope using steps 3 and 5, such as E1, E2, and E3.

C. Fast Data Merge with Decryption (FDMD)

After receiving the Digital Envelope, the encrypted messages E1, E2, and E3 are decrypted using the FDMD technique. This Digital opening technique is illustrated in Fig. 2 as using F-PKC and symmetric decryption to open a Digital Envelope, followed by data merging. The symmetric key K is realized in the first stage using F-PKC decryption. For this operation, both the asymmetric F-PKC private key N, E and the incoming encrypted symmetric key E3 are used to execute the decryption form as E3*N % E, which produces symmetric key K.

The message is then created utilizing symmetric decryption and data merging. Using the symmetric key K, the encrypted messages E1 and E2 are decoded into D1 and D2 as follows: D1 = E1⊕K and D2 = E2⊕K. This decryption reveals the intermediate between the messages D1 = ab and D2 = P. The original message is finally opened with the data merging form M = ab − P. Thus, the asymmetric and symmetric decryptions described above unlock the Digital Envelope. The third algorithm depicts pseudo codes for the FDMD method. Following is a summary of the key steps of algorithm 3:

1.    Obtain the encrypted E1, E2 and E3 variables from the Digital Envelope maker.

2.    Perform F-PKC decryption on the E3 cipher to obtain the symmetric key K. Use private key N, E, and the Envelope’s E3 of the form (E3*N) % E⊕K for this process.

3.    Decrypt the encrypted messages E1 and E2 with the symmetric key from step 1 using D1 = E1⊕K and D2 = E2⊕K, respectively.

4.    Apply a data merge operation with M = ab − P to open the Envelope message where D1 = ab and D2 = P.

The subsequent section comprises the experimental evaluations and findings.

4  Experiment and Results

This section evaluates the performance of the proposed Digital Envelope schemes in terms of their computation complexity and their distributed data storage and retrieval. The experimental design is centered on the three primary phases of the proposed scheme: Fast-PKC, Secure Data Split Distribution with Encryption (SD2E), and Fast Data Merge with Decryption (FDMD). There were two assessment dimensions in this experiment. The first dimension involved investigating the Fast-PKC public and private key generation periods practically relevant to big data security. The second dimension involved evaluating the effect of the execution times of the proposed SD2E and FDMD schemes on the scale of data.

The following settings were made to the test environment: The distributed Cloud environment was emulated through this application, which was designed and created for the experiment. The experiment's hardware configuration included a 64-bit Intel Core i5 processor @ 2.42 GHz with 16 GB of memory, and the virtual machines were built using VMware Workstation. The Java language is used to build big safe keys where the bit length of modulus N is set as the prime bit length used in the respective security scheme. In RSA, the modulus bit length |N| is the product of two primes |pq|. Similarly, in the case of ESRKGS, four unique primes are generated, and lastly, for the F-PKC key generation scheme, modulus bit length is set as in q prime bits.

The generation time of the F-PKC is observed by varying the key sizes from 1 kilobit to 10 kilobits. Followed by the big data, different sizes were operated for the proposed scheme performance assessment in secure data split distribution with encryption and fast data merge with decryption. For SD2E encryption and FDMD decryption of the proposed scheme, the assessment was processed by different input data scales, such as 1 KB, 1 MB, 10 MB, 50 MB, 250 MB, and 500 MB. ESRKGS and CHAN-PKC are compared with the proposed F-PKC scheme. SED2 and AES systems are compared for SD2E big data encryption, and EDCon and AES are compared for FDMD big data decryption scheme.

The FPKC scheme significantly speeds up computation by focusing key generation on just one secret prime, q. Besides RSA and ESRKGS, two or more primes are used for generating keys. Table 1 shows that the F-PKC key generation outperforms other PKC’s by consuming less computation time than RSA and ESRKGS. The various PKC times of key generation have been evaluated by adjusting the N-bit modulus from 1 to 10 kilobits. About a thousand random samples are made for each kilobit of modulus N, and the average time for each phase’s performance evaluation is measured.

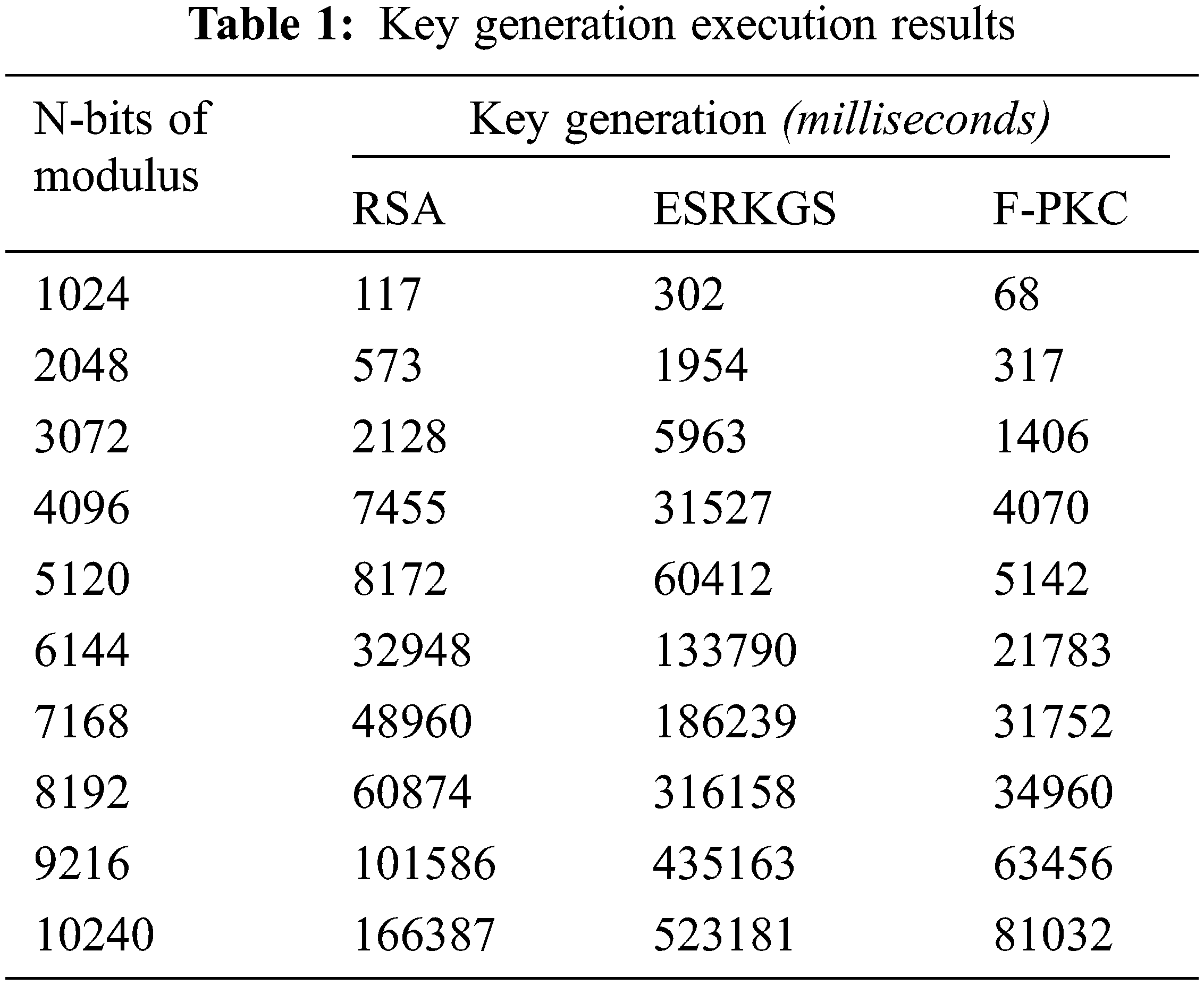
The evaluation and presentation of the F-PKC, ESRKGS, and RSA generation times are shown in Table 1 and Fig. 3. This experimental analysis demonstrates that, in terms of execution time, F-PKC outperforms other models (milliseconds). The F-PKC scheme, however, acquired at different kilobits about half as quickly as RSA and a fourth as quickly as ESRKGS. F-PKC only needs 56.83 percent of RSA and 14.40 percent of ESR durations from 1 to 10 kilobits. Like F-PKC, RSA uses 1.76 times as much F-PKC KGS and 25.33 percent more ESR generation and approximately 3.94 times as long as RSA and 6.94 times as long as F-PKC is needed for the creation of ESRKGS.

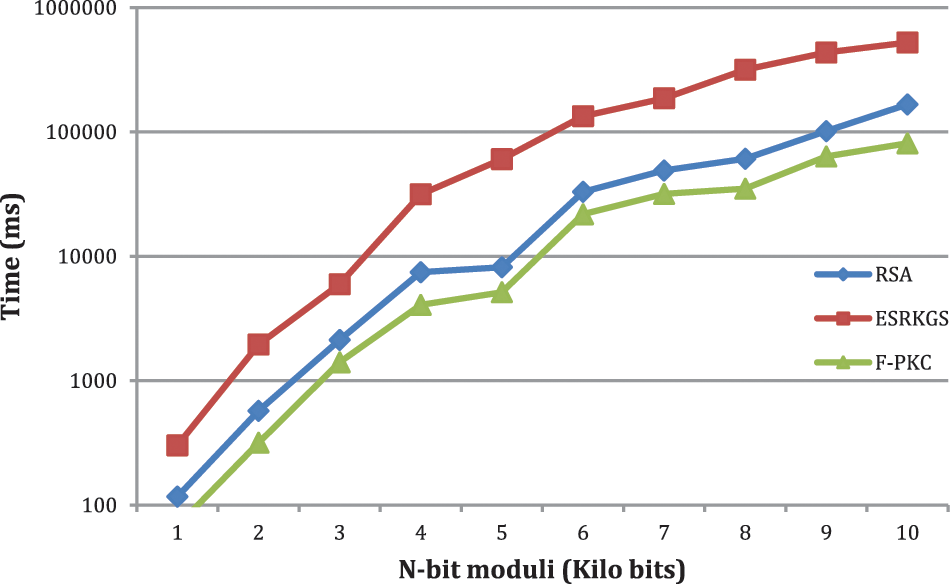
Figure 3: Comparison of the key generation time of RSA, ESRKGS, and F-PKC

Tables 2 and 3 displayed the variations in big data security encryption and decryption execution times for big data security. The data scale was changed from 1 KB to 500 MB to perform the experiment and compare the results. Comparisons of the suggested SD2E, HITAGC, SED2, and AES algorithms are included in the data encryption. The proposed FDMD, HITAGC, EDCon, and AES are then considered in the data decryption. According to the results of the big data encryption, it can be seen that the SD2E model uses only 72.95 percent of HITAGC, 57.64 percent of SED2, and 47.11 percent of AES. According to the decryption results, the proposed FDMD has only taken 30.50 percent of HITAGC, 20.44 percent of EDCon, and 16.47 percent of AES. The proposed SD2E encryption and FDMD decryption outperform other models in terms of performance, as evidenced by the results in Tables 2 and 3.

5  Conclusion

This paper focused on using hybrid intelligent cryptography to design a Digital Envelope to protect large amounts of data stored in the Cloud. The proposed method uses a secret version of a distributed equation to ensure that large amounts of data are as safe and private as possible. In order to achieve this goal, the proposed algorithms include Fast-PKC, Secure Data Split Distribution with Encryption (SD2E), and Fast Data Merge with Decryption (FDMD) schemes. Based on the proposed scheme, an application for a Digital Envelope is suggested. SD2E encryption and FDMD decryption use data split and merge operations to store and get large amounts of data across different Clouds. With this method, Cloud service providers can only get direct access to enough or encrypted data. The proposed F-PKC scheme went from 1 to 10 kilobits, about half as fast as RSA and a quarter as fast as ESRKGS. According to big data encryption results, the SD2E model uses 72.95% HITAGC, 57.64% SED2, and 47.11% AES. The proposed FDMD took 30.50% of HITAGC, 20.44% of EDCon, and 16.47% of AES. The results of the tests showed that the proposed plan is better at computing than other models.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

 1.  L. Peng, L. Hu, Y. Lu, J. Xu and Z. Huang, “Cryptanalysis of dual RSA,” Design Codes Cryptography, vol. 83, pp. 1–21, 2016. [Google Scholar]

 2.  M. Herrmann and A. May, “Maximizing small root bounds by linearization and applications to small secret exponent RSA,” in PKC 2010 LNCS, Singapore, 6056, pp. 53–69, 2010. [Google Scholar]

 3.  G. K. Shyam and R. S. S. Theja, “A survey on resolving security issues in SaaS through software-defined networks,” International Journal of Grid and Utility Computing, vol. 12, no. 1, pp. 1–14, 2021. [Google Scholar]

 4.  D. Pal, P. Khethavath and K. Utpal, “KeyPIn–mitigating the free rider problem in the distributed Cloud based on key, participation, and incentive,” Journal of Cloud Computing, vol. 11, no. 1, pp. 989–1007, 2022. [Google Scholar]

 5.  Q. Huang, Y. Yang and J. Jingyi, “Secure data group sharing and dissemination with attribute and time conditions in public Cloud,” IEEE Transactions on Services Computing, vol. 14, no. 4, pp. 1013–1025, 2021. [Google Scholar]

 6.  S. K. Kotha, M. S. Rani, B. Subedi and V. E. Sathishkumar, “A Comprehensive review on secure data sharing in Cloud environment,” Wireless Personal Communications, vol. 113, pp. 891–910, 2021. [Google Scholar]

 7.  S. Mandal and D. A. Khan, “Comprehensive survey of security issues & framework in data-centric Cloud applications,” Journal of Engineering Science and Technology Review, vol. 14, no. 1, pp. 1–24, 2021. [Google Scholar]

 8.  D. Chadwick and K. Fatema, “A privacy-preserving authorisation system for the Cloud,” Journal of Computer and System Sciences, vol. 78, no. 5, pp. 1359–1373, 2012. [Google Scholar]

 9.  N. Thillaiarasu and S. Chenthurpandian, “A novel scheme for safeguarding confidentiality in public Clouds for service users of Cloud computing,” Cluster Computing, vol. 22, pp. 1179–1188, 2019. [Google Scholar]

10. S. Belguith, N. Kaaniche and M. Hammoudeh, “Analysis of attribute-based cryptographic techniques and their application to protect Cloud services,” Transactions on Emerging Telecommunications Technologies, vol. 33, no. 3, pp. 989–1014, 2019. [Google Scholar]

11. W. Tingfang, L. Zhang, Q. Lyu and Y. Jin, “Asynchronous spiking neural P systems with local synchronization of rules,” Information Sciences, vol. 588, pp. 1–12, 2022. [Google Scholar]

12. Z. Yan, P. Zhang and A. Vasilakos, “A survey on trust management for internet of things,” Journal of Network and Computer Applications, vol. 42, pp. 120–134, 2014. [Google Scholar]

13. Z. Yan, M. Wang and P. Zhang, “A scheme to secure instant community data access based on trust and contexts,” in IEEE Int. Conf. on Computer and Information Technology, vol. 119, pp. 646–651, 2014. [Google Scholar]

14. T. Plantard, W. Susilo and Z. Zhang, “Fully homomorphic encryption using hidden ideal lattice,” IEEE Transactions on Information Forensics and Security, vol. 8, no. 12, pp. 2127–2137, 2013. [Google Scholar]

15. Z. Brakerski, C. Gentry and V. Vaikuntanathan, “(Leveled) fully homomorphic encryption without bootstrapping,” ITCS ’12: Proc. of the 3rd Innovations in Theoretical Computer Science Conf., vol. 6, no. 3, pp. 43–67, 2014. [Google Scholar]

16. E. Herrera-Viedma, F. Cabrerizo, J. Kacprzyk and W. Pedrycz, “A review of soft consensus models in a fuzzy environment,” Information Fusion, vol. 17, pp. 4–13, 2014. [Google Scholar]

17. C. Modi, D. Patel, B. Borisaniya, A. Patel and M. Rajarajan, “A survey on security issues and solutions at different layers of Cloud computing,” The Journal of Supercomputing, vol. 63, no. 2, pp. 561–592, 2013. [Google Scholar]

18. M. Thangavel, P. Varalakshmi, MukundMurrali and K. Nithya, “An enhanced and secured RSA key generation scheme (ESRKGS),” Information Security and Applications, vol. 20, no. 1, pp. 3–10, 2015. [Google Scholar]

19. C. S. Thirumalai and P. Viswanathan, “Modelling a side channel resistant CHAN-PKC cryptomata for medical data security,” Multimedia Tools and Applications, vol. 78, pp. 25977–25997, 2019. [Google Scholar]

20. T. Chandrasegar, M. Senthilkumar and S. Gautam, “An efficient public key secure scheme for Cloud and IoT security,” Computer Communications, vol. 150, pp. 634–643, 2020. [Google Scholar]