Impulsive Noise Cancellation in OFDM System Using Low Density Parity Check

1  Introduction

The Orthogonal Frequency Division Multiplexing (OFDM) is a digital modulation technique which splits single wideband into narrowband or smaller dividing into parallel bit streams. The narrow band stream of each is modulated separately on different orthogonal sub-carriers and is then frequency multiplexed. OFDM is extensively used in wireless applications due to its high data rate and higher spectral efficiency. Moreover there is more resistance of orthogonal frequency-division multiplexing (OFDM) to IN inherently than the modulation of single carrier, still performance of system is degraded if the power of IN is exceeded with specified threshold and it affects all subcarriers [1]. OFDM smartly deals with mitigating the effect of multipath, thus making it best suited for higher data rates in wireless applications [2]. Over the past decade number of wireless standards including worldwide interoperability for microwave access (WiMAX), 4G mobile systems using long term evolution (LTE) and uses OFDM technique; it is adopted for digital audio/video broadcasting due to its higher data rate [3].

OFDM based communication systems are usually corrupted by Impulsive noise, unwanted pulses of short duration that have random amplitude at random duration. Impulsive noise is human made noise having non Gaussian characteristics, exhibiting adverse effects in communication systems such as great capacity loss and poor error rate performance [4,5]. In [6–9], authors are taking benefit of the processing in analog domain whereas IN is separable and broadband. But for analog domain technique, finding thresholds s is not trivial. For reducing impulsive noise from OFDM, linear error correcting codes such as low-density parity-check (LDPC) and adaptive filters can be used. LDPC is used for transmitting a message signal over a noisy channel. One of the great uses of this code is that it performs near to Shannon limit and thus has Low Decoding Complexity. An adaptive filter, is self-optimizing filter that uses its own design by adjusting its internal parameters upon estimating the characteristics of its input output signal. Adaptive algorithms are being used for the reduction of noise.

The paper’s organization is as follows, in Section 2 related work is described. Section 3 explains proposed methodology, Section-4 presents decoding via Sum product Algorithm (SPA). Results of simulation are elaborated in Section-5, which is followed by comparative analysis of adaptive filters and LDPC codes. Finally, Section-6 gives the conclusion.

2  Related Work

Various techniques have been presented in literature for the suppressing impulsive noise from OFDM systems. Researchers are finding solutions for mitigating impulsive noise from OFDM systems, thus improving performance of the system by means of Bit Error Rate (BER) and Mean square error (MSE). Impulsive noise mitigation through conventional method is median filter with some signal degradation was proposed in [10]. In OFDM, for suppressing impulsive noise, Clipping and nulling methods was proposed in [11,12]. Moreover by the combination of clipping and nulling the BER was improved in OFDM systems [13]. Removing multiple impulsive noises from received OFDM through sample replacement algorithm was presented in [14]. Although the replica signals subtraction method for OFDM in time domain was proposed for cancellation of noise [15]. Further, for impulsive noise cancellation, copy of impulsive noise was produced and same was subtracted from received signal, is presented in [16] Impulsive Noise suppression in time as well as frequency domain has been proposed for OFDM in [16], where it has been showed that the combined time/frequency domain performs better and significantly reduces the impulsive noise than nonlinear methods under power line communication (PLC) systems. Removal of impulsive noise from multiple-input multiple-output (MIMO) fdm based system using adaptive filters NLMS, RLS and visual sequence Normalized Least Mean Square (VSNLMS) was proposed in [17]. In OFDM based OFDM, the Notch and Least Mean Square methods were proposed for reduction of impulsive noise in [18]. An impulsive noise canceller was proposed in [19] for sinusoid and state space recursive least square (SSRLS) method for ECG signals Whereas the same work in [19] was presented in time domain [20]. Another technique for reduction of impulsive noise using clipping and adaptive filters was presented in [21].

In OFDM, for correction of impulsive noise based on Reed Solomon (RS) code for broadband power line transmission has been proposed where the decoding algorithm with emphasis on low implementation and complexity [22]. The impulsive noise was reduced for OFDM based PLC systems using turbo decoding adaptive noise compensation was proposed in [23] showed good performance than well-known noise reduction methods. In [24], for OFDM based PLC, the periodic impulsive noise was suppressed with and without filtering method. Two methods have been presented i.e., adaptive notch filter and LMS algorithm. Adaptive LMS algorithm showed better result for noise mitigation.

In the [25], An approach of a deep neural network (DNN) is followed for detecting the IN, and the IN after detection has been alleviated in the suppression’s stage to cancel the harming outliers outcomes. In [24], An OFDM based system impulsive noise canceller had been proposed while comparing two different algorithms that is SSRLS and Bhagyashri algorithm. An impulsive noise suppressor for OFDM system while comparing different adaptive algorithms such as SSRLS, NLMS and RLS had been proposed in [26]. In our work we investigate impulsive noise mitigation in OFDM systems with encoding techniques: i.e., Low density parity check code and SSRLS.

3  Proposed Methodology

In this research, suppression of impulsive noise is investigated by implementing hybrid LDPC code and SSRLS on OFDM system.

3.1 SSRLS And LDPC Based OFDM System

A multicarrier modulation (MCM) system i.e Orthogonal Frequency Division Multiplexing (OFDM), with multiple sub bands and multiple sub carriers where transmission is parallel. This multi carrier transmission divides the single wideband into number of narrowband or smaller dividing into parallel bit streams. Narrow band stream of each is modulated on carrier and then is frequency multiplexed. The proposed block diagram of SSRLS and LDPC coded OFDM system is demonstrated in Fig. 1. Message signal is first coded with LDPC and using QAM technique the same is modulated. QAM modulated data symbols are converted into parallel data stream. OFDM transmitter and receiver is efficient in terms of using fast algorithms such as Fast Fourier Transform (FFT) and Inverse Fast Fourier Transform (IFFT). Modulated symbols are then converted into time domain by means of IFFT. These symbols are multiplexed and then passed through channel where the signal is deteriorated because of impulsive noise and Additive White Gaussian Noise (AWGN). Impulsive noise, an unwanted signal of short duration on/off pulses that have random amplitude produced at random duration. It is human made noise having non Gaussian characteristics, exhibiting adverse effects in communication systems [4].

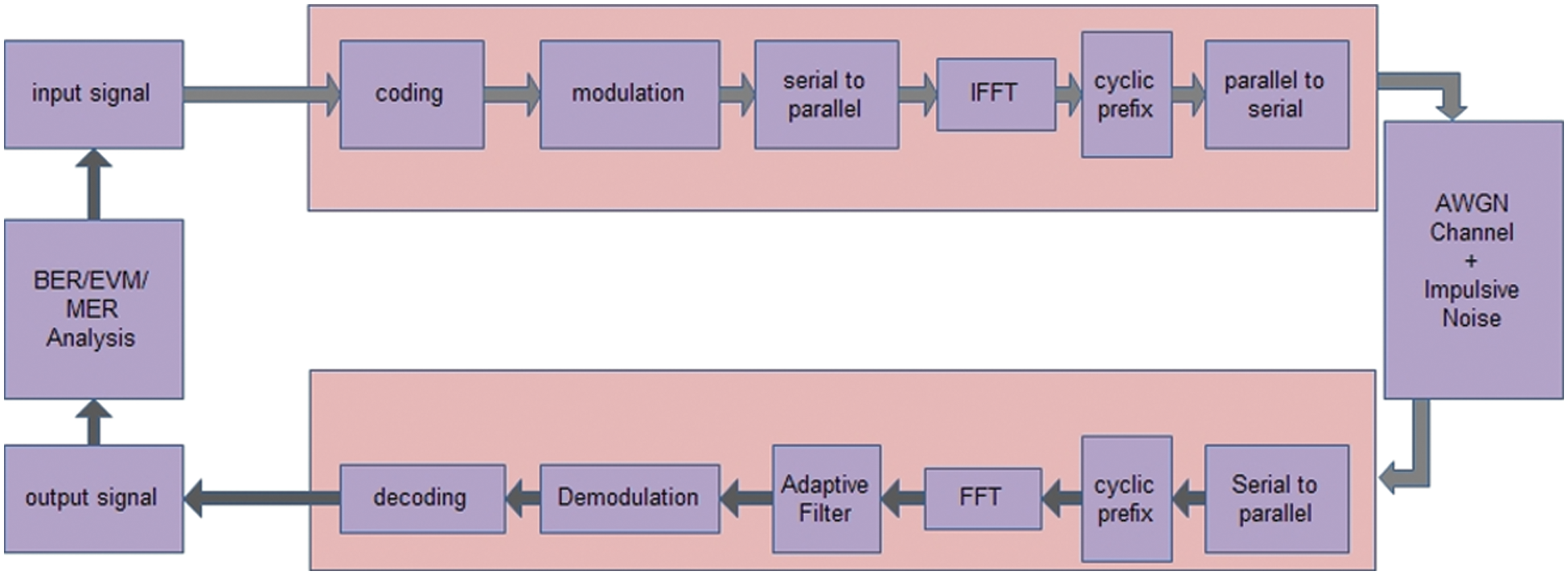
Figure 1: LDPC and SSRLS based OFDM system

Impulsive noise results in different type of sources like inadequate synchronization in communication, electromagnetic system, switching noise etc. The Impulsive noise sequence can be demonstrated by modelling it using Bernoulli Gaussian model. In this model, Gaussian distribution is used to model amplitude and occurrence of all impulses via Bernoulli distribution [10]. Mathematically,

ni(m)=n(m)b(m) (1)

From the above equation, n(m) and b (m) represents a binary Bernoulli process, which is random noise process constituting random ones and zeros. The impulsive noise ni(m) probability density function of a Bernoulli–Gaussian model can be written as [10]

fNBG(ni(m))=(1−α)δ(ni(m))+αfN(ni(m)) (2)

Probability density function of a Gaussian model of impulsive noise with zero mean having amplitudes distributed randomly and σ2n , the variance of noise amplitude is written as [10]

fN(n(m))=12πσnexp[−n2(m)2σ2n] (3)

The mean μb and variance σb2 of Bernoulli process in [5] can be expressed as

μb=E[(b(m))]=α×1+(1−α)=α (4)

σb2=E[(b(m)−μb)2]=α(1−α) (5)

Auto correlation of impulsive noise as binary state can be expressed as

rnn(k,m)=E[ni(m)ni(m+k)]=σn2δ(k)b(m) (6)

As Kronecker delta function is represented by symbol δ(k) . For a sequence of Impulsive noise, power spectrum PNINI can be achieved, by applying Fourier transform on autocorrelation function [10], thus it can be written as

PN1N2(f,m)=σn2b(m) (7)

3.2 Adaptive Filter Algorithm

Adaptive filters are used for the reduction of noise. Fig. 2 shows basic adaptive noise cancellation block diagram. There are many adaptive algorithms, the concise overview of each adaptive algorithms used in this research is discussed below.

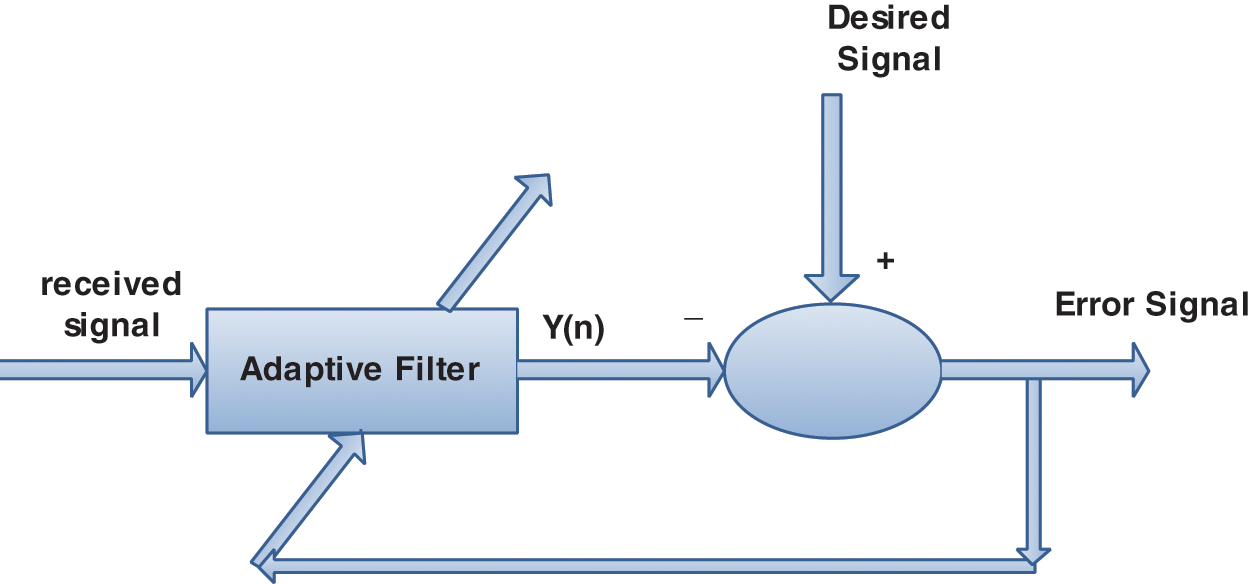
Figure 2: Adaptive noise cancellation system [16]

3.3 Recursive Least Square

The Recursive Least Square (RLS) adaptive filter finds coefficient of filter recursively, useful for minimizing a cost function that is concerning to deterministic input signal. In RLS estimation of matrix autocorrelation is utilized for de correlating the present (current) input data. RLS exhibits computational complexity and extremely fast convergence when compared with all variants of Least Mean Square. In RLS, where wt denotes the filter weights are recursively updated using the equations below [20], mathematically, it is defined as follows:

wt(n+1)=wt(n)+k(n)x(n) (8)

k(n)=λ−1∅−1(n−1)x(n)1+λ−1xT(n)∅−1(n−1)x(n) (9)

∅−1(n)=λ−1∅−1(n−1)−λ−1k(n)xT(n)∅−1(n−1) (10)

From equation, λ shows forgetting factor, ∅−1 depicts cross correlation matrix.

3.4 State Space Least Squares

An extension to RLS method is State Space Recursive Least Squares (SSRLS). Usually represented using state space and used for noise reduction. Its performance can be evaluated in presence of impulsive noise background. The sinusoidal model for implementation of SSRLS form II filter is given in [4].

x^[n]=x^[n]+ϵ[n]k[n] (11)

x^[n]=Ax^[n−1] (12)

ϵ[n]=y[n]−y¯[n] (13)

y¯[n]=Cx[n] (14)

∅[n]=λ(A−T∅[n−1])A−1+CTC (15)

K[n]=∅−1(n)CT (16)

where x^[n] denotes input state, k[n] representing the gain of observer, ϵ[n] shows the prediction error, the predicted input is denoted by n, estimated state is represented by n^ , the predicted output and correlation matrix are denoted by y¯[n]and∅[n] respectively.

3.5 Low Density Parity Check Codes

Low Density Parity Check codes (LDPC), linear error correcting codes used for purpose of transmitting an input signal over a noisy channel. One of the great uses of this code is that it performs near to Shannon limit and thus has low decoding complexity. A low-density parity-check code is one that is described by a parity-check matrix that has the following attributes: Each column has a small fixed number j geq 3 of l’s, but each row includes defined number k > j of l’s. For a fixed amount and fixed j, the usual minimum range of these codes rises linearly with block size. When combined with maximum likelihood decoding over just a sufficiently silent binary-input symmetric channel, the normal rate of decoding error decreases exponential with block length for a fixed rate and fixed j. In this paper, we consider a random sequence of bits generated and coded bits are modulated using 4 array QAM symbols and orthogonally is maintained by applying fast Fourier transform on OFDM signal. LDPC codes are represented by a matrix having almost O’s and very small number of 1’s. LDPC code mentioned here by parity check matrix H as illustrated an example in Fig. 3.

Figure 3: Parity check matrix

Suppose N(m) represent set of symbol nodes i.e., 1’s positions in the mth row parity check equation. M(n) represent the constituent nodes i.e., 1’s position in nth column of parity check equation. Consequently, the received codeword denoted by y={y1,y2,y3…….yN} equivalent to code word C={C1,C2,C3……CN} .

In this paper SPA algorithm is used for decoding, where Initialization is based on the probabilities of the modulated signal and probabilistic properties of the channel noise. The next step is to update the message, where the message bits are based on the observed value of the bit nodes by computing bit to constituent nodes and some of the messages transmitted to that bit nodes from the corresponding constituent nodes. The last step is decision, where the decoding is successfully done if and only if decision condition is satisfied or otherwise it switches direct to upcoming message update iteration.

di={1iflamda(1)>0.50elsewhere} (17)

When maximum number of iteration is done i.e., decoding is completed, the message signal is extracted.

4  Results and Discussion

Performance analysis of OFDM is done by applying LDPC code and SSRLS adaptive filter. Table 1 describes the simulating parameters for the OFDM system.

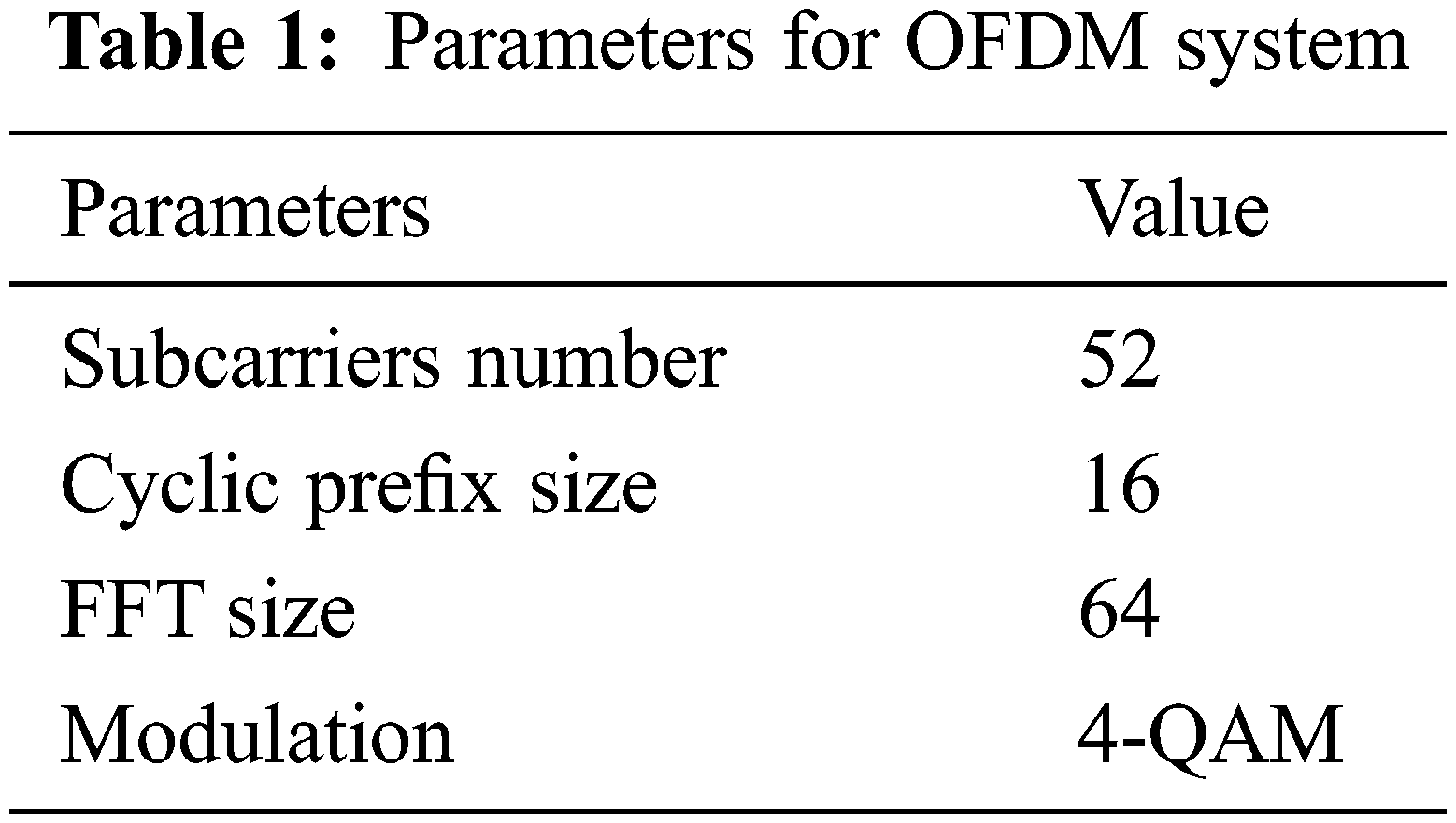
Modulation technique used is 4-QAM, by generating random data. In this paper irregular LDPC code size of 525 × 1050 is created where the H matrix has m columns and n rows. The coding rate defined here is 1/2 . The number of iteration for decoding is set to 20. Table 2 mentioned below depicts the simulation parameters of LDPC code.

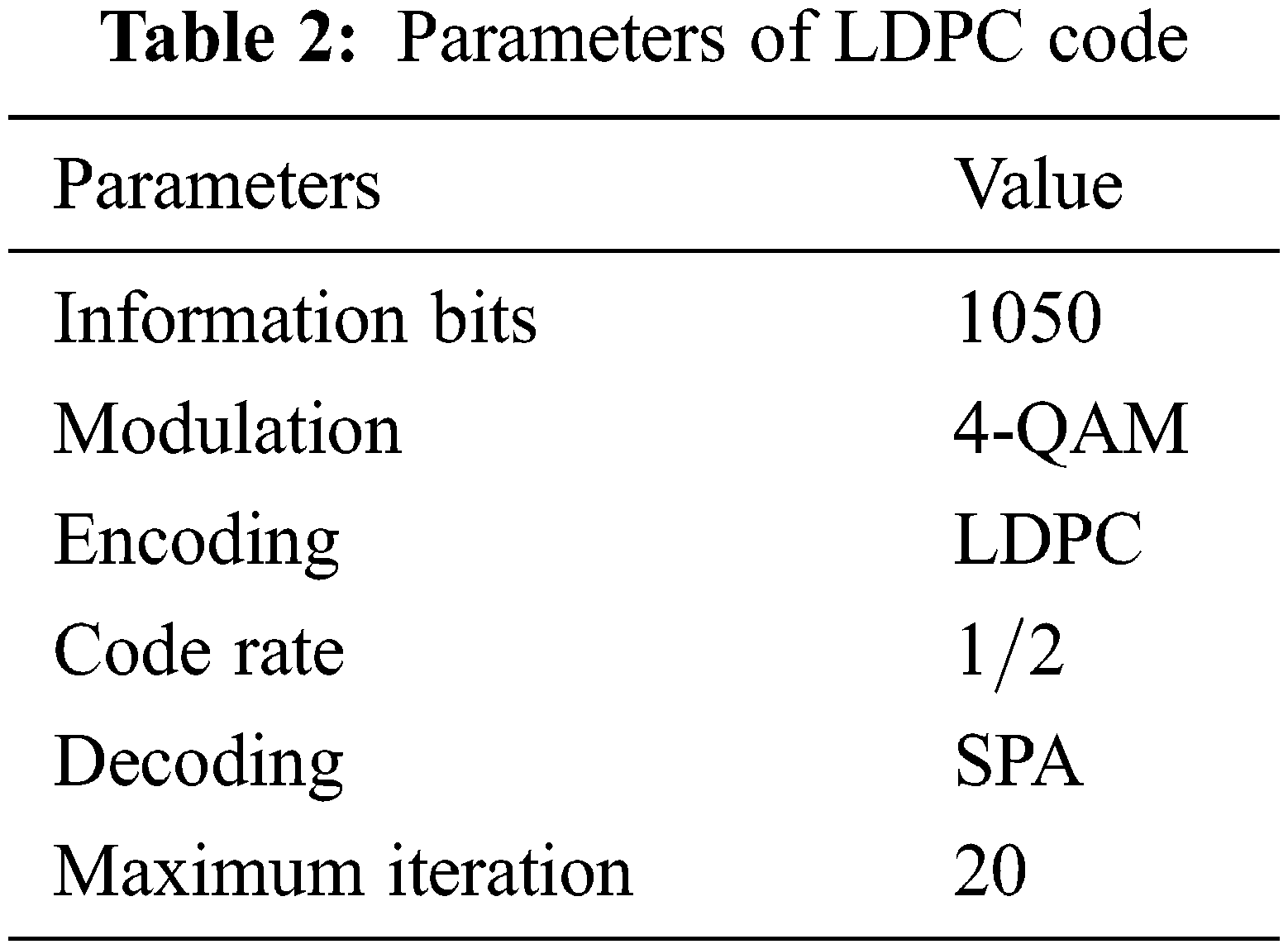
In this paper impulsive noise is generated as per the mentioned steps in [4]. Moreover, Table 3 depicts the simulated parameters to generate impulsive noise in OFDM.

In this paper, AWGN and IN (impulsive Noise) are introduced into the OFDM system. A corrupted signal is first encoded using LDPC code and then filtered using SSRLS adaptive filter to reduce noise. The results of the adaptive filter and a signal known as the required signal are compared. As a result, the difference between the two signals generates an error signal, and the filter recursively upgrades its weights to mitigate the effect of the error signal. The performance of various adaptive filters, such as LMS, NLMS, RLS, and SSRLS, is compared. For NLMS algorithm, the step size parameter’s range i.e., µ lies in between 0 to 1 and the value to be selected is 0.01. While for RLS forgetting factor i.e., λ is calculated to be 0.98 from the range 0.98 to 1.

The BER vs signal to noise ratio (SNR) of the OFDM signal is depicted in Fig. 4, by using LMS, LDPC and hybrid of both technique to reduce impulsive noise.

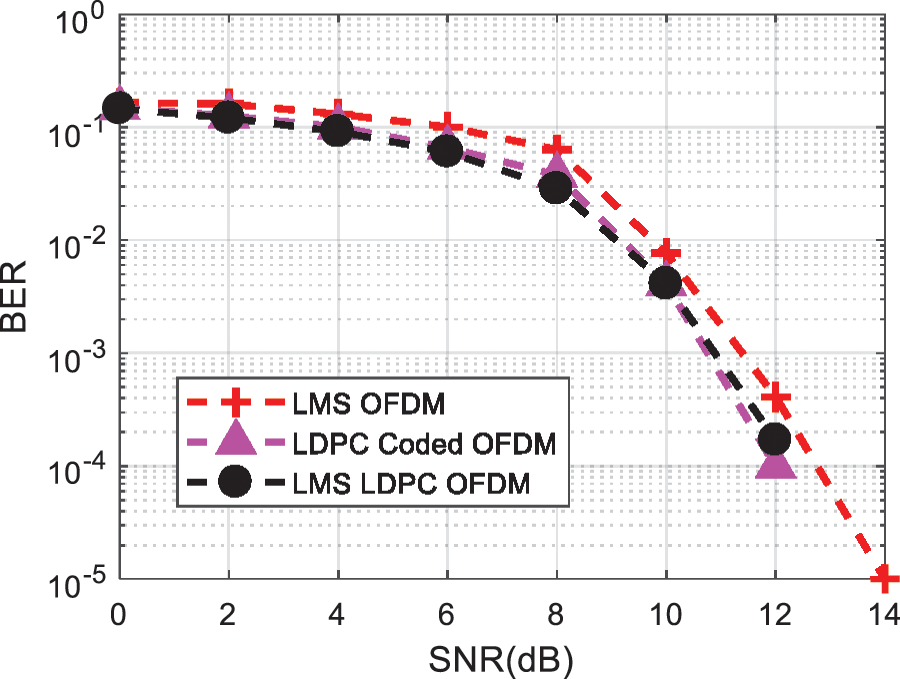
Figure 4: BER comparison of hybrid LMS and LDPC code for reduction of Impulsive Noise in OFDM signal

Performance of amalgamated LMS and LDPC is better than LMS filtering method. Furthermore Fig. 5 shows the performance analysis of NLMS and LDPC OFDM system and depicts that combination of LDPC with NLMS performs better in term of BER.

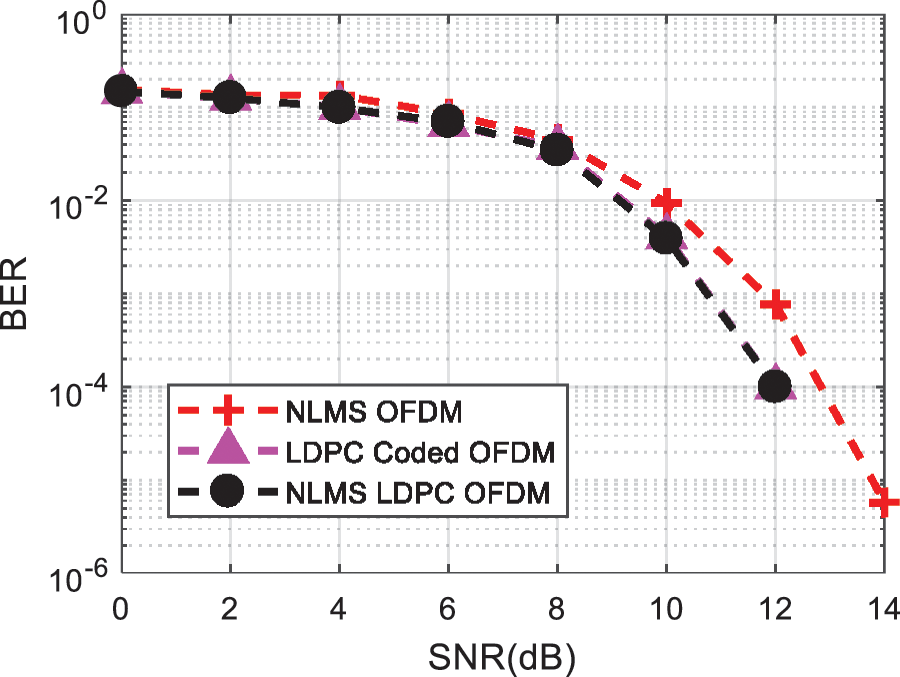
Figure 5: BER comparison of hybrid of NLMS and LDPC code for Impulsive Noise mitigation in OFDM signal

Moreover, for reduction of IN, RLS LDPC coded OFDM’s performance is compared with LDPC OFDM and RLS OFDM in Fig. 6. Results depicts that hybrid combination of RLS LDPC coded OFDM outperform the other two.

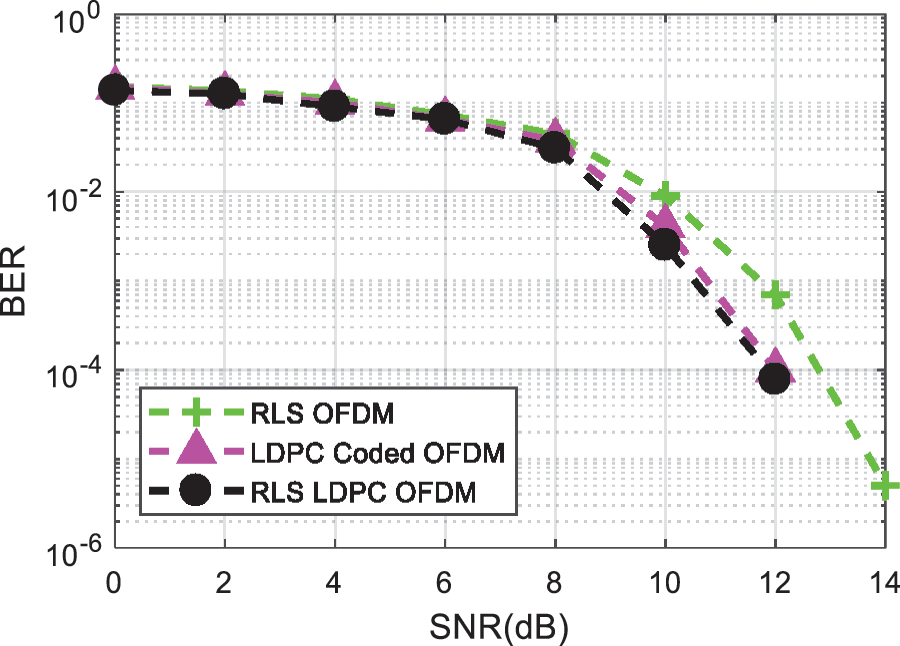
Figure 6: BER comparison of hybrid combination of RLS and LDPC code for reducing Impulsive Noise in OFDM signal

Fig. 7 illustrates the BER performance of hybrid combination of SSRLS and LDPC code for noise reduction in OFDM system.

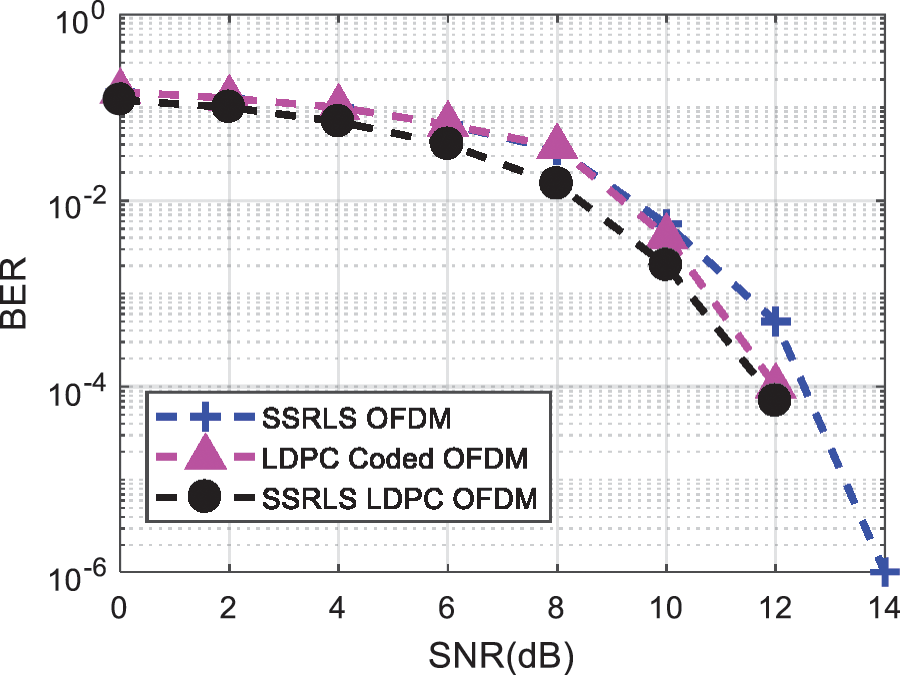
Figure 7: BER comparison of hybrid combination of SSRLS and LDPC code for Impulsive Noise reduction in OFDM signal

The hybrid method i.e., SSRLS and LDPC outperforms than RLS LDPC as well as NLMS LDPC coded OFDM system. The comparison among hybrid combination of LMS, NLMS, RLS and SSRLS based LDPC code is shown in Fig. 8. The outcomes depicts that SSRLS LDPC coded OFDM system mitigates the effect of impulsive noise far better than RLS LDPC and NLMS LDPC coded OFDM system. Further, Fig. 8 shows BER performance for all adaptive filters. Fig. 9 illustrates Uncoded OFDM along with RLS, SSRLS, LDPC and SSRLS LDPC coded OFDM system. SSRLS LDPC coded OFDM system exhibits better performance in terms of noise removal than individual filter and LDPC code in OFDM system.

Figure 8: BER comparison of hybrid combination of SSRLS LDPC, RLS LDPC NLMS LDPC and LMS LDPC for Impulsive Noise cancellation in OFDM signal

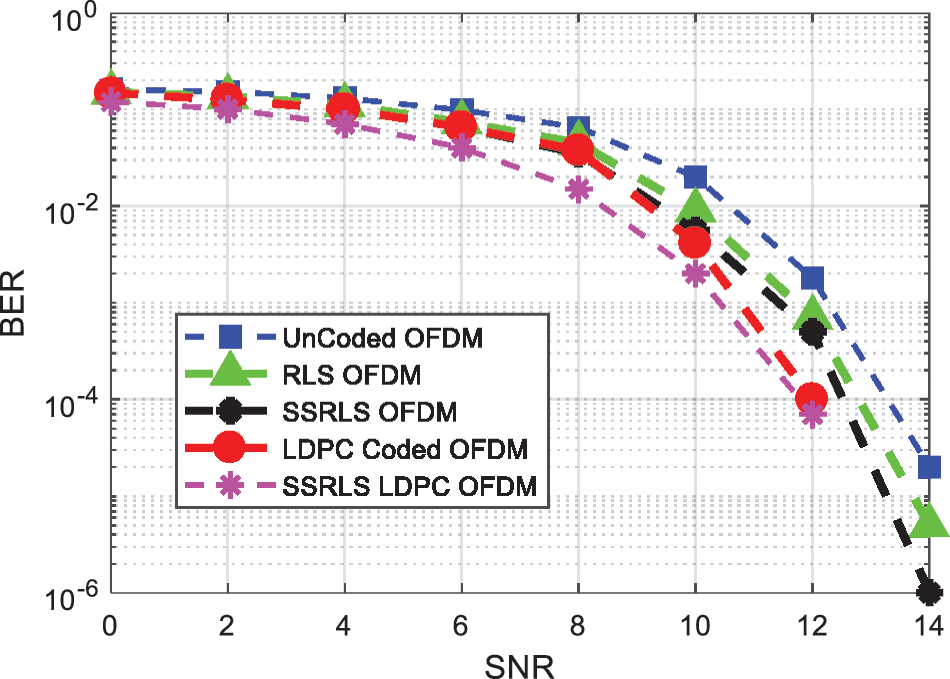
Figure 9: BER comparison of hybrid combination of SSRLS and LDPC code for Impulsive Noise reduction in OFDM signal

For Figs. 4 to 9, the modulation scheme used is 4-QAM. Moreover, for reduction of impulsive noise in OFDM, performance of SSRLS LDPC based OFDM system for different modulation scheme over BPSK, 4-QAM, 16-QAM and 32-QAM is compared in Fig. 10. Whereas, result shows that SSRLS LDPC based OFDM modulated over BPSK exhibits better performance in terms of BER.

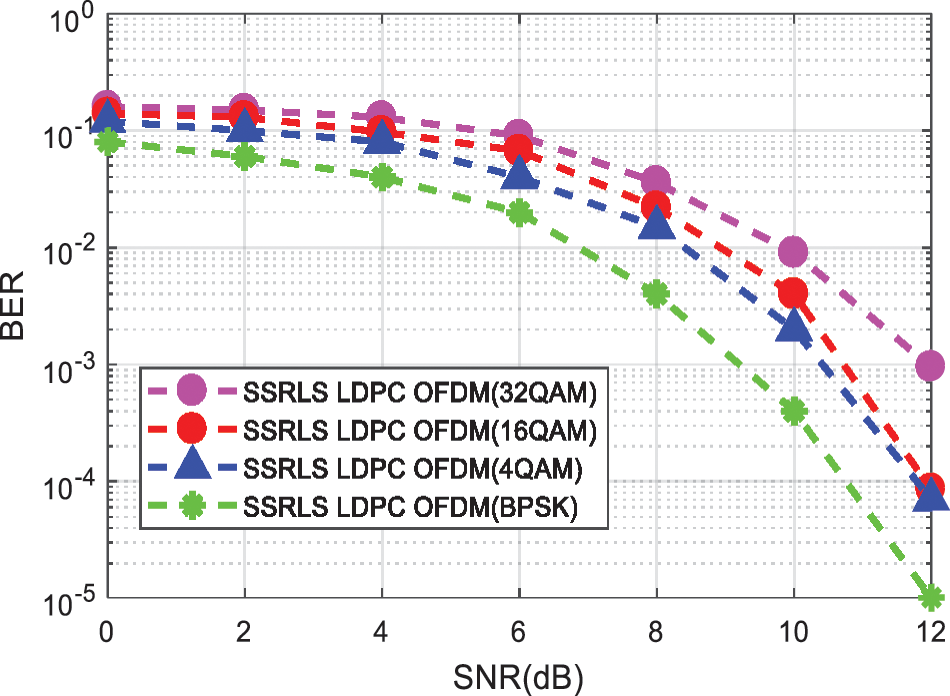
Figure 10: BER comparison of hybrid combination of SSRLS and LDPC code for Impulsive Noise mitigation in OFDM signal

5  Conclusion

This paper presents a hybrid combination of adaptive filters amalgamated LDPC coded OFDM system. Because of recursive parameters of adaptive filters such as Normalized Least Mean Square (NLMS), Recursive Least Square (RLS), State Space Recursive Least Square (SSRLS), and LDPC code, the presented scheme exhibits better impulsive noise reduction in OFDM systems. Furthermore, the comparison was made using various modulation techniques such as BPSK, 4-QAM, and 16-QAM. The results demonstrated the good performance of the hybrid technique through lower BER. The simulation results show that SSRLS LDPC coded OFDM outperforms SSRLS, RLS, and NLMS-based OFDM. Individual filters with LDPC code mitigated impulsive noise in OFDM better than the proposed technique. In the future, this technique can be applied for several computer vision research applications such as medical [27,28], agriculture [29,30], surveillance, and many more [31–36].

Funding Statement: This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ICAN (ICT Challenge and Advanced Network of HRD) program (IITP-2022-2020-0-01832) supervised by the IITP (Institute of Information & Communications Technology Planning & Evaluation) and the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Ghosh, “Analysis of the effect of impulse noise on multicarrier and single carrier QAM systems,” IEEE Transactions on Communications, vol. 44, no. 11, pp. 145–147, 1996. [Google Scholar]

 2.  R. Krishnamoorthy and N. Pradeep, “Forward error correction code for MIMO-OFDM system in AWGN and rayleigh fading channel,” International Journal of Computer Applications, vol. 69, no. 21, pp. 1–21, 2013. [Google Scholar]

 3.  W. A. Zhou and B. Xie, “Link-level simulation and performance estimation of WiMAX IEEE802. 16e,” in 2007 2nd Int. Conf. on Pervasive Computing and Applications, Beijing, China, pp. 667–671, 2007. [Google Scholar]

 4.  U. Masud, F. Jeribi, M. Alhameed, F. Akram and A. Tahir, “Two-mode biomedical sensor build-up: Characterization of optical amplifier,” Computers, Materials & Continua, vol. 70, no. 2, pp. 5487–5489, 2022. [Google Scholar]

 5.  T. Liang, Y. Li, W. Xue, Y. Li and T. Jiang, “Performance and analysis of recursive constrained least Lncosh algorithm under impulsive noises,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 68, no. 4, pp. 2217–2221, 2020. [Google Scholar]

 6.  R. Barazideh, B. Natarajan, A. V. Nikitin and R. L. Davidchack, “Performance of analog nonlinear filtering for impulsive noise mitigation in OFDM-based PLC systems,” in 2017 IEEE 9th Latin-American Conf. on Communications (LATINCOM), NY, USA, pp. 1–6, 2017. [Google Scholar]

 7.  R. Barazideh, A. V. Nikitin and B. Natarajan, “Practical implementation of adaptive analog nonlinear filtering for impulsive noise mitigation,” in 2018 IEEE Int. Conf. on Communications (ICC), NY, USA, pp. 1–7, 2018. [Google Scholar]

 8.  U. Masud, T. Saeed, F. Akram, H. Malaikah and A. Akbar, “Unmanned aerial vehicle for laser based biomedical sensor development and examination of device trajectory,” Sensors, vol. 22, no. 6, pp. 34–53, 2022. [Google Scholar]

 9.  R. Barazideh, S. Niknam, B. Natarajan and A. V. Nikitin, “Intermittently nonlinear impulsive noise mitigation and doppler shift compensation in UWA-OFDM systems,” IEEE Access, vol. 7, no. 5, pp. 36590–36599, 2019. [Google Scholar]

10. S. V. Vaseghi, Advanced Digital Signal processing and Noise Reduction. vol. 1. John Wiley & Sons, UK, pp. 1, 2008. [Google Scholar]

11. H. A. Suraweera, C. Chai, J. Shentu and J. Armstrong, “Analysis of impulse noise mitigation techniques for digital television systems,” in Proc. 8th Int. OFDM Workshop, New Delhi, India, pp. 172–176, 2003. [Google Scholar]

12. S. V. Zhidkov, “Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers,” IEEE Transactions on Communications, vol. 56, no. 5, pp. 5–9, 2008. [Google Scholar]

13. A. Mengi and A. H. Vinck, “Successive impulsive noise suppression in OFDM,” in ISPLC2010, IEEE, NY, USA, pp. 33–37, 2010. [Google Scholar]

14. T. Hirakawa, M. Fujii, M. Itami and K. Itoh, “Improving influence of impulse noise to OFDM signal by recovering time domain samples,” in 2006 Digest of Technical Papers Int. Conf. on Consumer Electronics, Beijing, China, pp. 327–328, 2006. [Google Scholar]

15. T. Umatani, K. Ohno and M. Itami, “A study on schemes of reducing influence of impulse noise in OFDM under multi-path channel,” in 2010 Digest of Technical Papers Int. Conf. on Consumer Electronics (ICCE), Beijing, China, pp. 119–120, 2010. [Google Scholar]

16. T. Kitamura, H. Ando, K. Ohno and M. Itami, “The impulsive noise reduction using it’s replica signal under class-A impulsive channel,” in The 15th Int. Symp. on Wireless Personal Multimedia Communications, NY, USA, pp. 463–467, 2012. [Google Scholar]

17. A. Hakam, N. Abou Aly, M. Khalid and S. Al-Araji, “Impulsive noise reduction in MIMO-OFDM systems using adaptive receiver structures,” in 2013 IEEE 20th Int. Conf. on Electronics, Circuits, and Systems (ICECS), Beijing, China, pp. 674–677, 2013. [Google Scholar]

18. S. Mathew and P. Murukan, “Periodic impulsive noise reduction in OFDM based power line communication,” International Journal of Research in Engineering and Technology, vol. 3, no. 2, pp. 1–20, 2014. [Google Scholar]

19. A. Mirza, S. M. Kabir and S. Ayub, “Impulsive noise cancellation of ECG signal based on SSRLS,” Procedia Computer Science, vol. 62, no. 13, pp. 196–202, 2015. [Google Scholar]

20. A. Mirza, S. M. Kabir, S. Ayub and S. A. Sheikh, “Enhanced impulsive noise cancellation based on SSRLS,” in 2015 Int. Conf. on Computer, Communications, and Control Technology (I4CT), NY, USA, pp. 31–35, 2015. [Google Scholar]

21. S. M. Kabir, A. Mirza and S. A. Sheikh, “Impulsive noise reduction method based on clipping and adaptive filters in AWGN channel,” International Journal of Future Computer and Communication, vol. 4, no. 2, pp. 341, 2015. [Google Scholar]

22. S. D. P. Farkas, “Impulsive noise cancellation in systems with OFDM modulation,” Journal of Electrical Engineering, vol. 59, no. 21, pp. 310–316, 2008. [Google Scholar]

23. Y. Himeur and A. Boukabou, “OFDM-based power-line communication enhancement using a turbo coded adaptive impulsive noise compensator,” Telecommunication Systems, vol. 62, no. 11, pp. 481–494, 2016. [Google Scholar]

24. A. Mirza, S. M. Kabir and S. A. Sheikh, “Reduction of impulsive noise in OFDM system using adaptive algorithm,” International Journal of Electronics and Communication Engineering, vol. 9, no. 4, pp. 1427–1431, 2015. [Google Scholar]

25. R. Barazideh, S. Niknam and B. Natarajan, “Impulsive noise detection in OFDM-based systems: A deep learning perspective,” in 2019 IEEE 9th Annual Computing and Communication Workshop and Conf. (CCWC), NY, USA, pp. 0937–0942, 2019. [Google Scholar]

26. A. Mirza, S. M. Kabir and S. A. Sheikh, “SSRLS based enhanced impulsive noise OFDM suppressor in AWGN channel,” in The 6th Int. Conf. on Computational Methods (ICCM2015), Toronto, Canada, pp. 1–6, 2015. [Google Scholar]

27. T. Akram, M. Sharif, S. Kadry and Y. Nam, “Computer decision support system for skin cancer localization and classification,” Computers, Material and Continua, vol. 69, no. 2, pp. 1–16, 2021. [Google Scholar]

28. F. Afza, M. Sharif, U. Tariq and H. S. Yong, “Multiclass skin lesion classification using hybrid deep features selection and extreme learning machine,” Sensors, vol. 22, no. 6, pp. 1–21, 2022. [Google Scholar]

29. M. Z. U. Rehman, F. Ahmed, S. S. Jamal and J. Ahmad, “Classification of citrus plant diseases using deep transfer learning,” Computers, Materials & Continua, vol. 70, no. 1, pp. 1401–1417, 2022. [Google Scholar]

30. U. Yasmeen, J. A. Khan and C. A. Hanif, “Citrus diseases recognition using deep improved genetic algorithm,” Computers, Material and Continua, vol. 71, no. 2, pp. 1–16, 2021. [Google Scholar]

31. S. Riaz, M. W. Anwar, I. Riaz and Y. Nam, “Visibility restoration using generalized haze-lines,” Information Technology Control, vol. 50, no. 22, pp. 188–207, 2021. [Google Scholar]

32. M. Ahmed, M. Ramzan, H. U. Khan and S. Iqbal, “Real-time violent action recognition using key frames extraction and deep learning,” Computers, Materials & Continua, vol. 70, no. 2, pp. 1–17, 2021. [Google Scholar]

33. Z. Akhtar, J. W. Lee, M. Sharif, S. A. Khan and N. Riaz, “Optical character recognition (OCR) using partial least square (PLS) based feature reduction: An application to artificial intelligence for biometric identification,” Journal of Enterprise Information Management, vol. 21, no. 4, pp. 1–26, 2020. [Google Scholar]

34. A. Iqbal, M. Sharif, W. Nisar and M. Alhaisoni, “FF-UNet: A u-shaped deep convolutional neural network for multimodal biomedical image segmentation,” Cognitive Computation, vol. 4, no. 2, pp. 1–16, 2022. [Google Scholar]

35. M. N. Akbar, F. Riaz, A. B. Awan, U. Tariq and S. Rehman, “A hybrid duo-deep learning and best features based framework for action recognition,” Computers, Material and Continua, vol. 71, no. 3, pp. 1–15, 2022. [Google Scholar]

36. M. S. Amin, J. H. Shah, M. Yasmin and U. Tariq, “A two stream fusion assisted deep learning framework for stomach diseases classification,” Computers, Material and Continua, vol. 72, no. 2, pp. 1–15, 2022. [Google Scholar]