Dynamic Analogical Association Algorithm Based on Manifold Matching for Few-Shot Learning

1  Introduction

Artificial intelligence algorithms represented by deep learning have achieved advanced performance in image classification [1–3], biometric recognition [4,5], relation extraction [6–8] and medical assisted diagnosis [9–10] by virtue of ultra-large-scale datasets and powerful computing resources. It is worth noting that although the complex hypothesis space easily contains the real mapping, it is also more difficult to find the target mapping. Therefore, deep neural networks usually require a large number of supervised samples for training.

Unfortunately, it is hard to obtain large-scale trainable data in most real scenarios because of the high cost of data labeling and the inability to obtain large amounts of data in some specific areas. In order to be able to learn in the case of limited supervised information, the research of few-shot learning has sprung up. In few-shot classification, the model is trained on a set of classes with sufficient samples, which are called base classes. When evaluating performance, further training and testing are carried out on another set of novel classes with small samples. It is worth mentioning that testing on novel classes that have not been seen before in training is called zero-shot learning.

As is known to all, human beings have rich prior knowledge and superb ability of association and analogy, so human beings can distinguish novel things from just a few or even one example. For example, as shown in Fig. 1, when people need to distinguish killer whales, doves and cats that they have never seen before, but if they have seen sharks, sparrows and dogs, people can make analogical associations and make full use of prior knowledge for classification. In other words, people can use the knowledge structure in the familiar category to make analogical associations, since some elements of the latent semantic structure already exist in other already familiar categories. Specifically, fins, wings and ears are the most obvious distinguishing features in the classification of sharks, sparrows and dogs, considering killer whales, doves and cats also have the similar structures, so people need to pay attention to these characteristics as well.

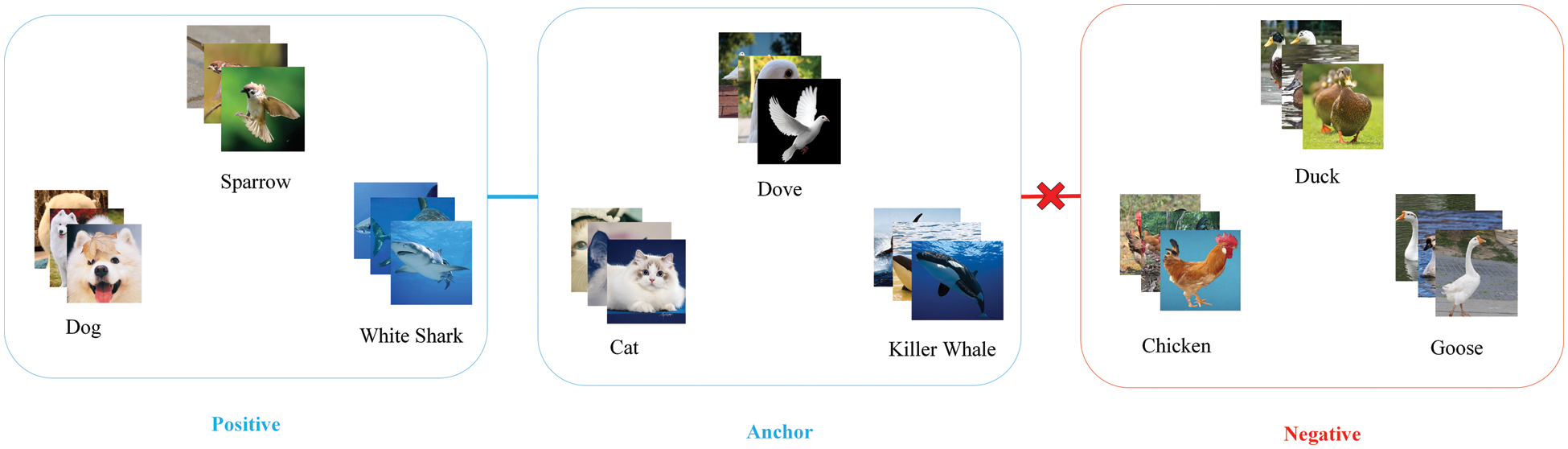
Figure 1: The similarity of knowledge structure

The Fig. 1 shows the importance of analogical association in humans’ rapid recognition of novel things. The positive represents the knowledge structure similar to the anchor, on the contrary, the negative represents the knowledge structure not similar to the anchor.

At present, the existing researches for few-shot learning mainly focus on representation learning [11–13], data generation [14–19] and learning strategies [20–34]. These methods alleviate the problem of insufficient training samples, but only consider the use of rich priors and ignore the importance of analogy and association.

Therefore, in order to make rational use of analogies and associations, the dynamic analogical association algorithm is proposed to search for knowledge structures that are similar to the current task and exist in prior knowledge. The in-depth exploration of the knowledge structure combined with the observation distribution of the current task can generate a sample that not only has high confidence but also can make the significant contribution to the classification. Our main contributions in this paper are as follows:

1.    The data generation framework which ensures the high confidence of the generated samples and significant contribution to the classification is proposed.

2.    The comparative results substantiate the superiority of the proposed method to existing data generation approaches for few-shot learning, and the effectiveness of the algorithm has been proved through ablation experiments and synthetic experiments.

3.    More importantly, we explained the importance of analogical association based on prior knowledge. Researchers need to re-examine how to make better use of prior knowledge.

2  Related Work

2.1 The Difficulty of Few-shot Learning

Suppose a problem to be learned, it has a from X to Y optimal mapping h⋆ . D is the joint distribution on X×Y . The D is the train dataset which contains the observation samples in D . The expected risk on D and the empirical risk on D are as follow [35].

R(h;D)=E(x,y)∼D(ℓ(h(x),y)) (1)

R^m(h;D)=1m∑i=1mℓ(h(xi),yi) (2)

Assuming hm=arg⁡minh∈H R^m(h) and h′=arg⁡minh∈H R(h) , where H is the given hypothetical space. The error can be decomposed [36–38] according to the following formula, as visualized in Fig. 2.

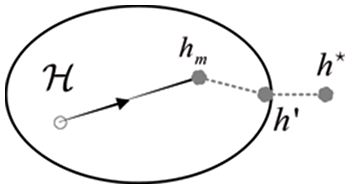
Figure 2: Illustration of the error decomposition

E[R(hm)−R(h⋆)]=E[R(hm)−R(h′)]+E[R(h′)−R(h⋆)] (3)

E[R(hm)−R(h′)] is called generalization error. The upper bound of generalization error is determined by model complexity and sample size. In general, it can be reduced by having a larger number of examples. Therefore, the difficulty of few-shot learning is that minimizing empirical risk becomes unreliable.

E[R(h∗)−R(h′)] is called approximation error, which is mainly determined by h∗ and hypothesis space H . It is worth noting that if the hypothesis space is sufficiently complex, such as h⋆∈H , then the generalization error will increase while reducing the approximation error.

The above analysis explains the reason why the algorithm is difficult to generalize with small samples, and explains the design motivation of the few-shot learning algorithm. Based on the design motivation, the existing algorithms can be divided into three categories: representation learning, data generation and learning strategy.

2.2 Representation Learning

The motivation of representation learning is to change the original data into embedding which has lower dimensions and semantic information obtained according to a priori knowledge to reduce the difficulty of learning in the latent semantic space, which can reduce the approximation error and generalization error at the same time.

The simplest idea is to learn a feature extractor through a large number of base-class dataset, so that it can adapt to the limited differences between base-class dataset and novel-class dataset, and then recognize it through a classifier. Although the pretraining and fine-tuning method [25] is intuitive and concise, it is hard to learn general features.

With the continuous development of self-supervised technology [39,40], the backbone network based on self-supervised learning can learn better representation, so as to improve the performance of few-shot learning. The augmented multiscale deep infomax algorithm (AMDIM) [11] can learn more generalized representations of images based on maximizing mutual information and achieve advanced results, which proves the importance of self-supervised learning in few-shot learning [12].

It is worth noting that robust representation is beneficial for few-shot learning. Therefore, the use of regularization technology in representation learning can improve the performance of few-shot learning. Puneet Mangla et al. [13] proposed self-supervised manifold mixup method (S2M2) that uses regularization technology based on manifold mixing, which significantly improves the performance of few-shot learning. In addition, there are some regularization techniques [41] which are beneficial for few-shot learning, such as adding penalty items, stopping early, etc.

2.3 Data Generation

The motivation of data generation is to generate non-trivial and diverse samples to increase the sample size, which can reduce the upper bound of generalization error and make the empirical risk more reliable.

Wang et al. [14] proposed a general generation algorithm based on generation network. Its motivation is to generate samples that is useful for learning classifiers, which is different from the traditional image reconstruction. Weinshall et al. [15] proposed the generation hidden condition optimization algorithm (GLICO), which generates new samples by hyperspherical interpolation of any two intra-class samples and restores them to images.

Taking into account the difficulty of image reconstruction, it is also a good choice to generate samples directly from the latent semantic space. Schwartz et al. [16] proposed Delta Encoder to generate samples through offset learning. It is worth noting that generating samples from the semantic space is dependent on the performance of the representation model.

Most of the existing data generation methods usually only consider the high confidence of the generated samples and ignore its weak contribution to the classification, or consider the significant contribution to the classification and ignore its low confidence. Therefore, we have the motivation to propose a data generation framework which ensures the high confidence of the generated samples and significant contribution to the classification.

2.4 Manifold Matching

Manifold matching usually refers to getting a distribution closest to a given distribution through optimization or selection.

How to measure the difference between distributions is very important, which can usually help model training, such as cross entropy, Kullback-Leibler divergence (KL divergence), Wasserstein distance and so on. As a special case of the optimal transport cost, the Wasserstein distance has the advantage over KL divergence in that even if the two distributions do not overlap, the Wasserstein distance can still reflect their distance, which can be used as a very suitable loss in the generative model.

Genevay et al. [42] introduced the sinkhorn loss which is the optimal transport cost with entropy regularization into the generative model and achieved better results.

Dai et al. [43] proposed a generative model based on metric learning and manifold matching. Different from the traditional method which only considers the optimal transmission distance, it performs matching based on geometric descriptors.

In addition, manifold matching is not exclusive to generative tasks, which is also commonly used in document matching [44], image-set matching [45] and other tasks. For example, Arandjelovic et al. [46] proposed an image-set matching method based on the similarity between Gaussian mixture distributions.

In this work, based on the assumption that the feature distribution of latent semantic space can reflect the knowledge structure after reasonable representation learning, manifold matching is used to select the knowledge structure in prior knowledge closest to the current task, rather than generate samples directly.

3  Dynamic Analogical Association Algorithm

3.1 Problem Definition

In the few-shot learning classification benchmark, the classes in the dataset are usually divided into two non-overlapping class sets. One class set with rich sample size is called base-class set Cbase , while the other class set with only a small number of samples is called novel-class set Cnovel , Cbase∩Cnovel=∅ . Then the dataset D can be divided according to the class set Dbase={(x,y)|(x,y)∈D,y∈Cbase} , Dnovel={(x,y)|(x,y)∈D,y∈Cnovel} .

In few-shot classification, Firstly, the model is trained on the base-class dataset Dbase with abundant examples to obtain appropriate prior knowledge. Then the few-shot learning methods are evaluated using N-way K-shot classification framework.

For each task instance of N-way K-shot Ti , including support set and query set. The labeled support set contains N classes randomly sampled from the novel-class dataset Dnovel with K examples for each class. The query set contains unseen samples similar to support set. The evaluation method of few-shot learning is mainly to accurately classify unlabeled unseen query sample set through the learning of support set.

3.2 Overview

Biologically speaking, the ability of human beings to quickly understand new things mainly comes from the fact that human beings have rich prior knowledge and superb ability of association and analogy. Therefore, they can distinguish new things from only a few or even one examples.

Based on this assumption, the dynamic analogical association algorithm in the way of sample generation for few-shot learning is proposed. Most of the existing sample generation methods usually only consider the high confidence of the generated samples and ignore its weak contribution to the classification, or consider the significant contribution to the classification and ignore its low confidence.

Different from these methods, our method tends to search for knowledge structures similar to existing tasks in prior knowledge based on manifold matching, and combine sampling distributions to generate offsets instead of two sample points, thereby ensuring the high confidence of the generated samples and significant contribution to the classification. The overall structure of algorithm is shown in Fig. 3.

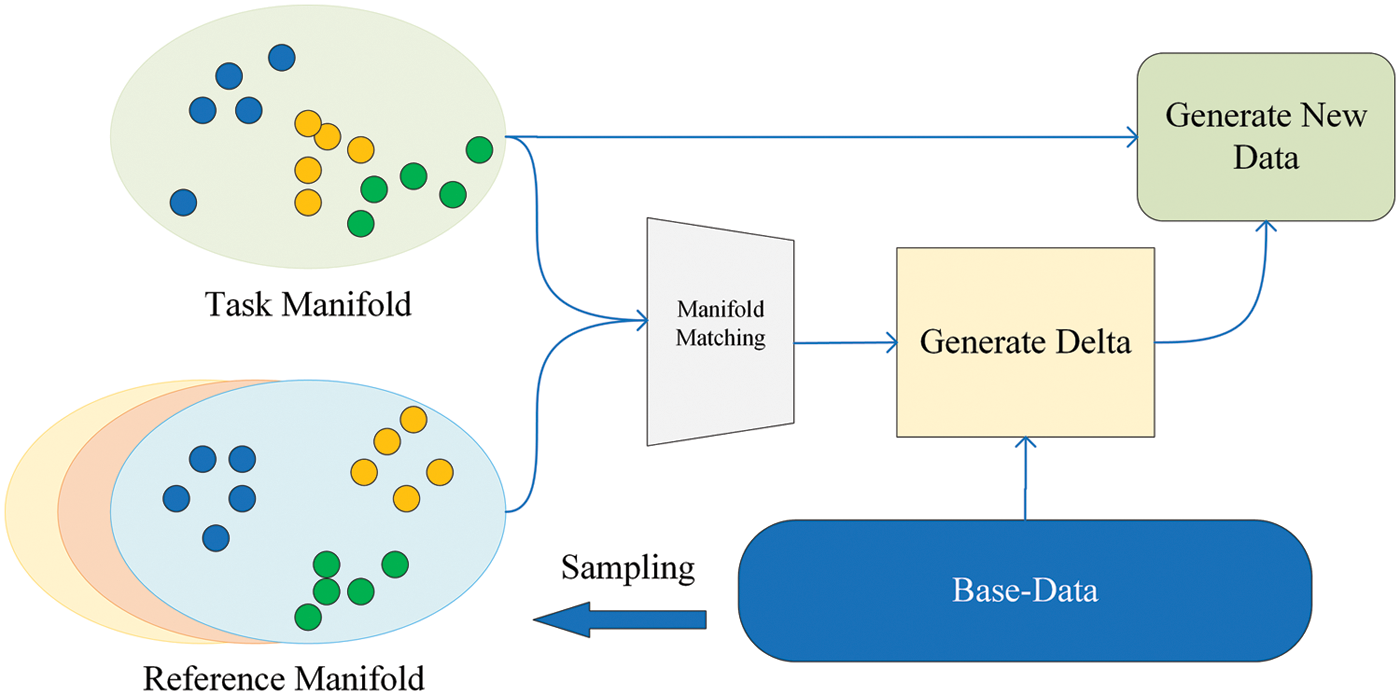
Figure 3: Framework of the proposed dynamic analogical association algorithm

The algorithm includes two core parts: manifold matching module and data generation module. The manifold matching module is responsible for finding the knowledge structure similar to the current task in the prior knowledge. The data generation module is responsible for generating the offset with the help of the knowledge structure.

3.3 Manifold Matching Based on Optimal Transportation

We regard the distribution of labeled samples in the latent semantic space in each task support set as a sampling of the knowledge structure of N-way entities. The q refers to the corresponding latent overall distribution of the data in T , which is usually assumed to be the Gaussian mixture model with unknown parameters.

The distribution with unknown parameters is difficult to sample directly. However, samples of support set can be regarded as observation data sampled from latent distribution, which is also called the observed manifold M , and M=sample(q) .

The M is a matrix, each row of which represents the feature of a sample in the support set. Therefore, for the N-way K-shot task, its dimension is NK×d , where d represents the dimension of the feature.

The optimal transportation cost between the two distributions μ,v is used to define the distance between the two distributions in the latent semantic space, so as to approximate the similarity of knowledge structure.

C(μ,v):=minγ∈Π(μ,v)∫X×Yc(x,y)dγ(x,y) (4)

In the above formula, c(x,y) represents the transportation cost function and γ(x,y) represents the joint distribution.

Furthermore, the sinkhorn algorithm [47] is used to solve the optimal transport problem. Specifically, sinkhorn algorithm uses L2 distance as the cost function and takes the manifold of the current task and the reference manifold as the input to obtain the distance, which reflects the similarity of their knowledge structure. The specific algorithm process is shown by Algorithm 1.

After the definition of knowledge structure similarity is completed, we hope to seek similar knowledge structure from prior knowledge to assist in the learning of current tasks. Therefore, Tibase from base-class dataset Dbase and corresponding manifold set {Mibase|Mibase=sample(qibase)} are generated.

M⋆base=arg minMibase C(M,Mibase) (5)

According to the optimal transport distance between manifold sets, we can find the T⋆base closest to the current T , and trace back to the corresponding category with rich samples in the base-class dataset, which can assist in sample generation. In other words, each time learning from novel-class information, the similar knowledge structure in the base-class can be referred to for knowledge transfer. For example, samples of the novel task are generated by learning the offset.

It is worth mentioning that the proposed method usually chooses Topk closest manifolds instead of only considering the closest one, which is similar to ensemble approach to make the algorithm more stable.

3.4 Data Generation Method

Based on manifold matching, for each new task T , one or more matching tasks T⋆base and its corresponding feature manifold of a large number of samples in the base-class dataset are obtained.

The traditional data generation methods in semantic space mainly utilize a pair of intra-class sample points to generate offsets. For example, methods such as Delta-Encoder [16] and DTN (Diversity Transfer Network) [17] do not consider the distribution of samples. If an offset is added to the sample points at the boundary of the distribution, it is easy to generate wrong samples, so it only considers the significant contribution to the classification and ignores its low confidence. In contrast, another type of method, such as GLICO [15], uses interpolation between two sample points to generate the new samples. The new samples exist in the convex area, with high confidence, but it is difficult to improve the classification performance. The shortcomings of the two types of existing methods are shown in Figs. 4a and 4b.

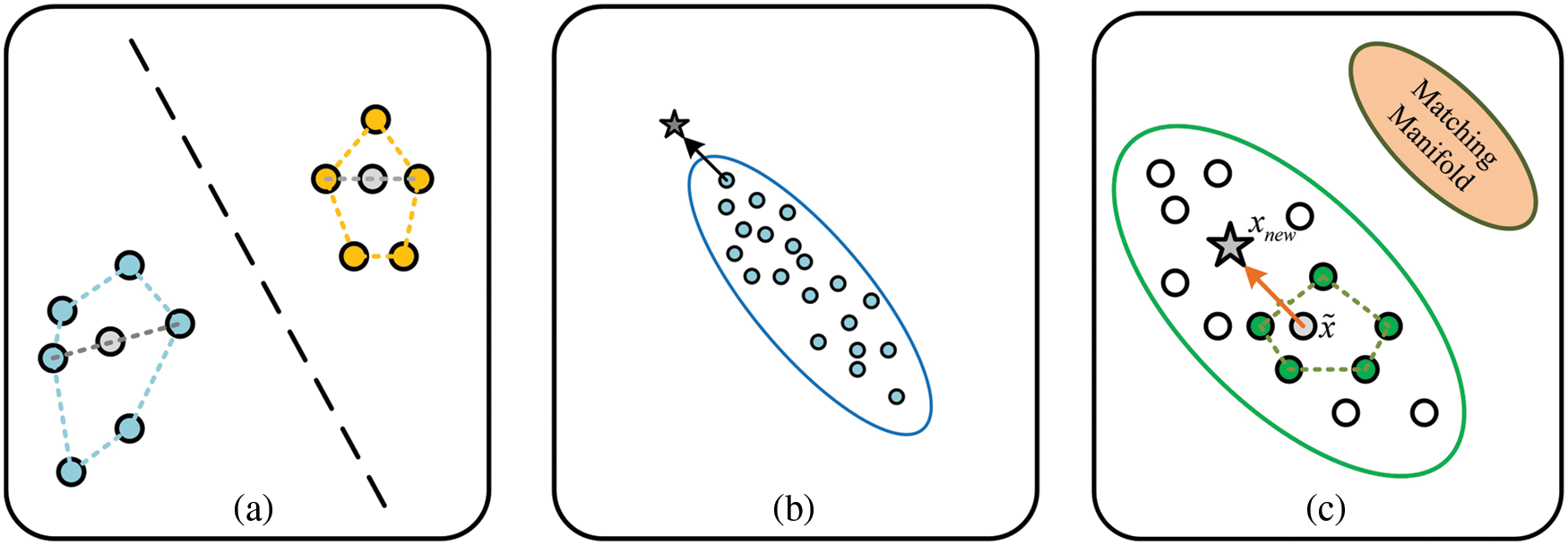
Figure 4: The figure (a) and figure (b) show disadvantages of the two existing methods. In contrast, the figure (c) illustrates the advantages of our method

Fig. 4a shows that the interpolation of the convex area is difficult to affect the interface, and Fig. 4b shows that simply considering the offset learning is easy to produce sample points that do not belong to the current distribution.

Therefore, in order to ensure high confidence of the generated samples and significant contribution to the classification at the same time, new samples are generated based on intra-class distribution. In Fig. 4c, the advantages of the proposed method are clearly demonstrated, x~ is located in the convex region, while xnew adds an offset to x~ to make it possible to rush out of the convex area and close to the latent real sample that has not been seen.

The data generation method is divided into two steps.

(1) The first step is to find the maximum variation direction within each class in base-class dataset corresponding to T⋆base and other offsets.

To be specific, assuming that there is the centralized intra-class data x , the corresponding w which is the maximum variation direction can be obtained by solving the following problem.

maxwVar(x)=1n∑i=1n(xiTw)2=wT(1n∑i=1nxixiT)ws.t.||w||22=1 (6)

The above problems can be solved by Lagrange multiplier method and transformed into solving the eigenvector corresponding to the largest eigenvalue of covariance matrix. The w is the intra-class maximum variation direction of prior knowledge structure.

Therefore, increasing training samples along this direction can effectively increase the diversity of datasets. For example, in Fig. 5, adding an offset to a silver cat can generate a golden cat. In addition, global manifold offset Δ1 and central attraction offset Δ2 are also noteworthy.

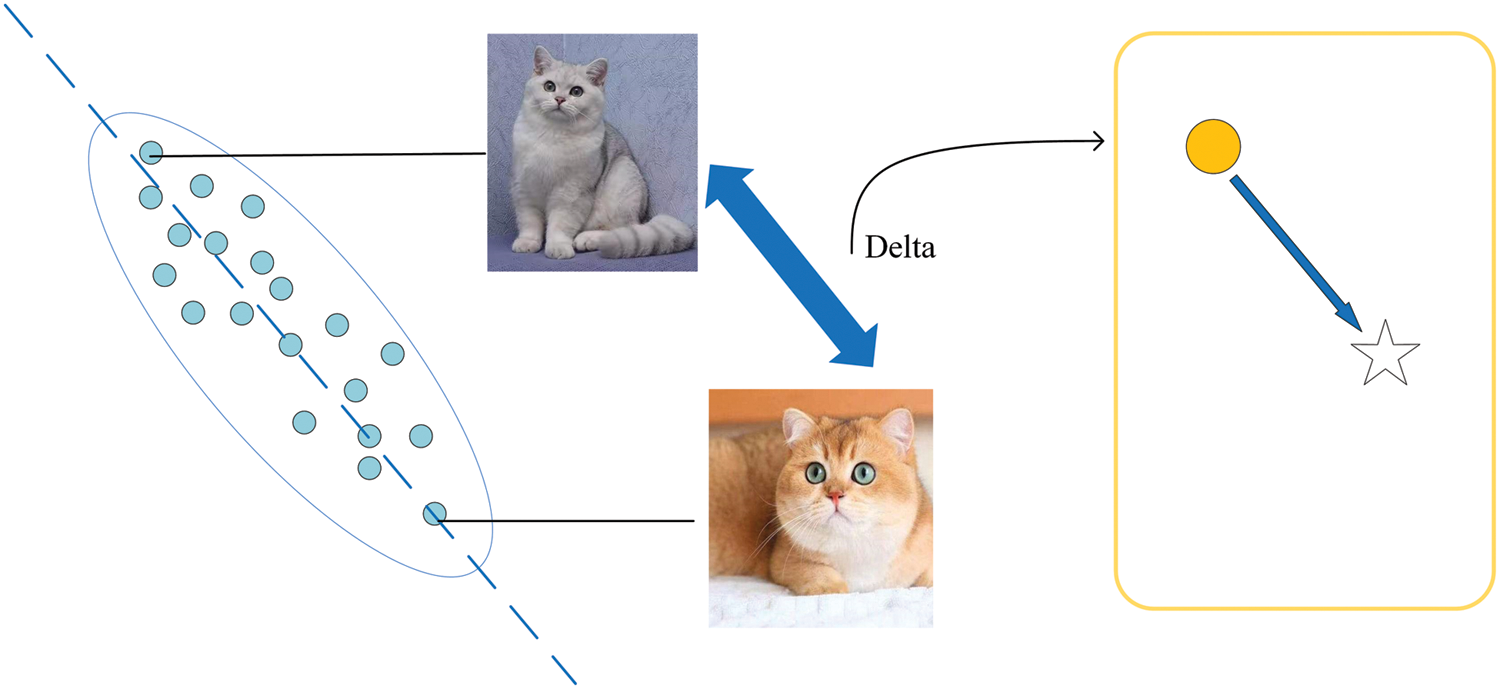
Figure 5: The intra-class maximum variation contains rich semantic information

Specifically, the Δ1 refers to the offset between the center of the current manifold and the matched manifold, and the Δ2 refers to the offset between the center of each category of the current manifold and the matched manifold.

(2) In the second step, based on the Dirichlet distribution, the basic new sample is determined by the weighted sum of intra-class sample points in current novel task to ensure that it must be inside the convex area. Then, the generated data is generated by adding an offset to the basic new sample.

To be specific, assuming θ obeys Dirichlet distribution. θ∼Dirichlet(a1,a2,…,am) , and ∑i=1mθi=1 . The basic new sample x~ is determined by the weighted sum of intra-class sample points in current novel task to ensure that it must be inside the convex area, x~=∑θixi,x~∈conv(x) .

After adding the offsets, the samples generated by this method ensure high confidence and significant contribution to the classification, as shown in Fig. 4c. Therefore, the formula for our final sample generation is as follows:

xnew=∑θixi+∑j=12αjΔj+βw (7)

3.5 Classifier

Here is a brief introduction to the PT-MAP (Power Transform-Maximum A Posteriori) algorithm [32], which will be combined with the dynamic analogical association algorithm to verify performance.

The algorithm assumes that each class distribution is a Gaussian distribution with different means, and the mean value is a prototype vector.

Therefore, the following problem needs to be solved, where f represents the representation vector of the image and μk represents the prototype vector.

{y^i},{μk}=arg⁡max{yi}{μk}∏iP(fi|yi)=arg⁡max{yi},{μk}∏ie−(fi−μk)T(Σk)−1(fi−μk)2=arg⁡min{yi}{μk}∑(fi−μk)T(Σk)−1(fi−μk) (8)

If it is assumed that the covariance matrices are equal, then the above formula is transformed into the following formula.

arg⁡min{ℓ(fi)}∈C,{μk}∑i,k(||fi−μk||2)P(ℓ(fi)=k) (9)

For labeled data {(fi,yi)} , P(ℓ(fi)=yi)=1 , and its value is fixed, for unlabeled data {(fj)} , P(ℓ(fj)) can be learned. Therefore, this method is also a transductive inference. The above problem is transformed into an optimal transportation problem, so it can be solved by the sinkhorn algorithm.

P∗=Sinkhorn(C,u,v,λ)=arg⁡minP∈U(u,v)∑ijPijCij+λH(P) (10)

When a new prototype is obtained, the original prototype vector can be updated. Then the algorithm iterates many times to obtain a reasonable prototype.

4  Experiments

The standardized few-shot classification benchmark is used to evaluate the performance of the proposed method. The effectiveness of the proposed method has been proved based on comparison with existing methods and ablation experiments. It should be noted that the proposed method emphasizes the importance of manifolds, so only experiments are conducted on 5-shot.

4.1 Implementation Details

The 1000 5-way 5-shot classification tasks on miniImageNet and CUB (Caltech-UCSD Birds) are evaluated. It should be noted that our method emphasizes the importance of manifolds, so experiments are conducted only on 5-shot setting. Query set in task contains 15 images per class. The average accuracy of these few shot tasks is reported along with the 95% confidence interval based on Gaussian distribution hypothesis.

The WRN (Wide Residual Network), which is a wide residual network of 28 layers and width factor 10, is used as backbone to obtain the features in experiments. The WRN is trained following the same settings as S2M2 [13]. For each dataset, the feature extractor is trained on base-class dataset to learn the representation of images and test the performance on novel-class dataset.

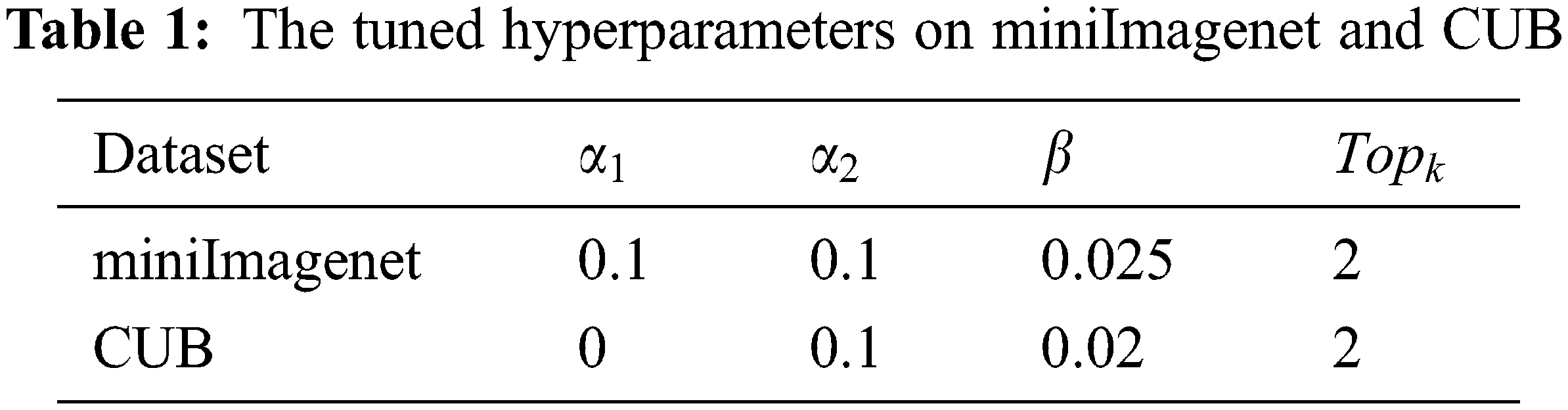
The tuned hyperparameters with validation classes for miniImageNet and CUB are shown in Table 1.

4.2 Quantitative Comparison

Following the standard setting, Table 2 provides the comparison results on the miniImagenet and CUB with the 95% confidence interval. The comparative existing methods are categorized into two groups, Non-DataGen (few-shot learning algorithm without data generation) and DataGen (few-shot learning algorithm based on data generation). It can be clearly observed that the proposed method outperforms existing methods in the 5-way 5-shot setting, with gains that are consistent across different datasets.

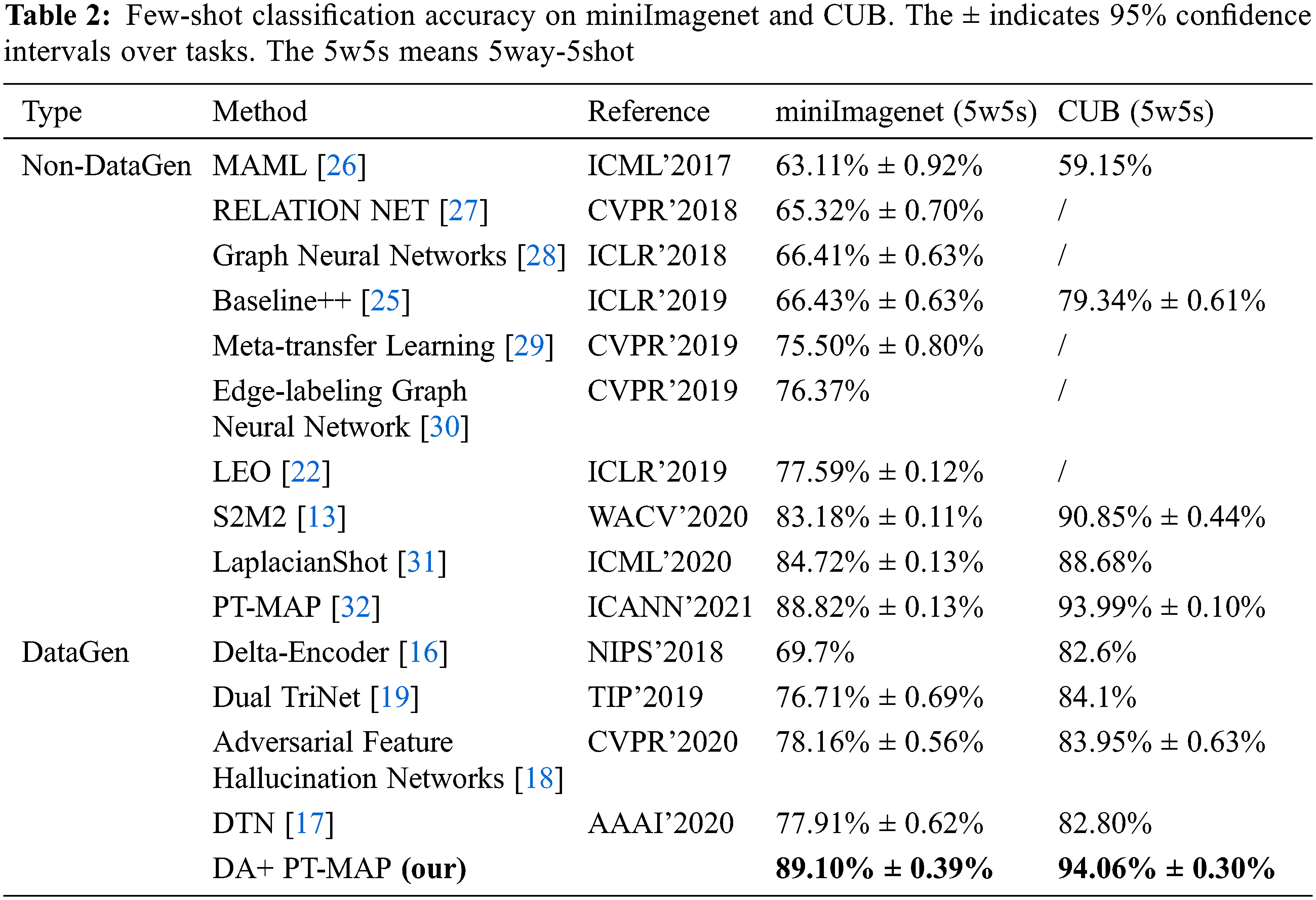
For instance, compared to well-known MAML (Model-Agnostic Meta-Learning) [26] and Delta-Encoder [16], the proposed method brings improvements of nearly 26% and 20% respectively, under the same standard setting. In addition, the WRN used in the proposed method is trained according to S2M2 [13], and good representation can be obtained without complex meta learning. Combined with dynamic analogical association, its performance is significantly better than LEO (Latent Embedding Optimization) [32] and S2M2 [13], which also use WRN as the backbone network.

More importantly, because the core of our algorithm is data generation, we need to pay more attention to the combination with state-of-the-art methods and whether it can further improve the performance. Our method surpasses the PT-MAP algorithm [32] with the same representation and the same classifier, which proves that the usefulness of dynamic analogical association. It also shows that it can be combined with the state-of-the-art methods to further improve the performance in different few-shot learning scenarios without relying on any additional information from other datasets.

4.3 Synthetic Experiments

Synthesis experiments show whether the proposed method can generate more meaningful data points. For the 5-way 5-shot task, based on t-SNE (t-distributed Stochastic Neighbor Embedding), the samples of the support set, the samples generated by the proposed method and the samples of the query set are drawn on a 2D view, as shown in the Fig. 6, in which different colors represent different categories; forks represent the samples of the support set; circles represent the synthetic samples; light colored pentagons represent the samples of the query set.

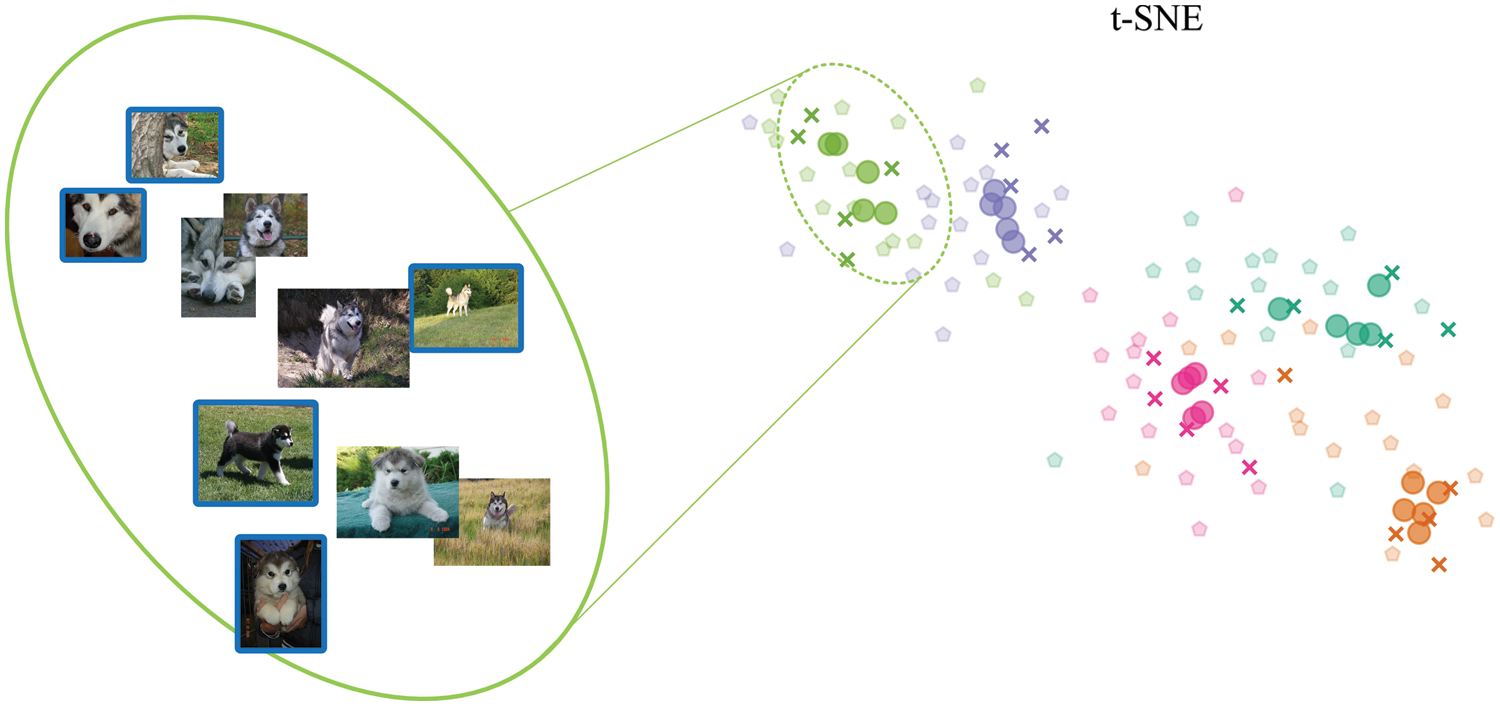
Figure 6: Synthesized samples visualization

As can be seen from the Fig. 6, the visualization of the synthesized samples reveals the following points:

1.    The synthesized samples are not concentrated in the center of the support set samples and have a certain tendency, and some synthesized sample points rush out of the convex region composed of the support set samples. This shows that non-trivial samples are generated. In addition, the results of the synthesis experiment are consistent with the expected results speculated in Fig. 4c.

2.    More importantly, the green and purple synthesized samples which rush out of the convex region are close to the samples of the query set (real latent samples) that are invisible to the proposed method, which shows that manifold matching plays a positive role and the proposed dynamic analogical association algorithm can generate meaningful samples.

4.4 Ablation Study

Considering that the proposed method is the simplest way to use prior knowledge by analogical association, the performance improvement of existing algorithms combined with dynamic analogical association should be paid attention to illustrate the importance of using prior knowledge more flexibly.

Therefore, in this subsection, the ablation studies are conducted to evaluate the performance of the proposed algorithm with quantitative results.

By comparing the accuracy of no sample generation and sample generation based on dynamic analogical association in Table 3, it can be clearly found that the proposed method improves the performance of two common classifiers, which proves the generality and effectiveness of the algorithm.

4.5 Manifold Matching Does Work

In order to verify whether the manifold matching works, the most intuitive method is to see whether the distance between our manifold sampling and the current task is significantly different.

Fig. 7 shows the maximum and minimum distances, indicating that the current task is only similar to some knowledge structures, but is significantly different from other knowledge structures.

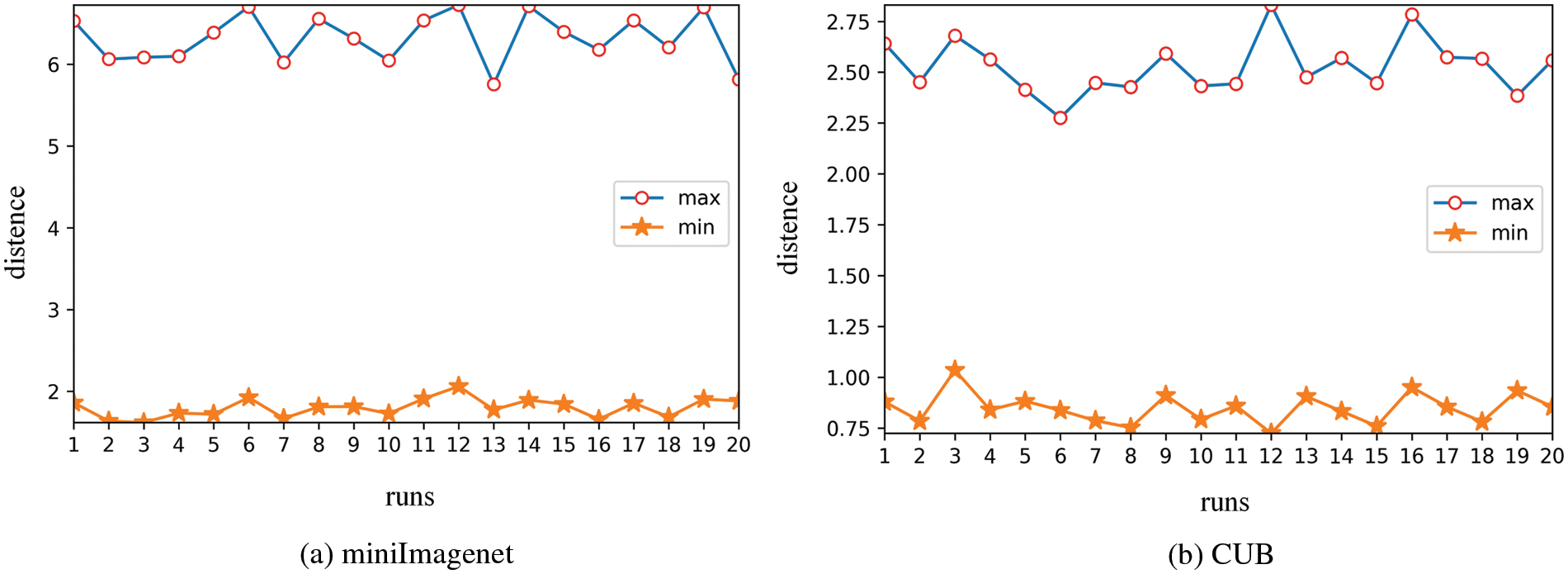
Figure 7: The max-min manifold distance in the reference manifold set

As we all know, traditional methods do not treat or use prior knowledge differently, but for a certain task, the part of the knowledge structure of prior knowledge is only needed. Therefore, it is difficult to achieve better results if only considering the use of all prior information without careful analysis.

5  Conclusion

It can be observed that our method can lead to consistent improvement of few-shot learning tasks on different image classification datasets. More importantly, we explained the importance of analogical association based on prior knowledge. Relevant researchers need to re-examine how to make better use of prior knowledge.

In the future, we believe that there will be other or more advanced methods combined with manifold matching to further improve algorithm performance, such as meta-learning. This work opens up a path for further exploration.

Funding Statement: This work was supported by The National Natural Science Foundation of China (No. 61402537), Sichuan Science and Technology Program (Nos. 2019ZDZX0006, 2020YFQ0056), the West Light Foundation of Chinese Academy of Sciences (201899) and the Talents by Sichuan provincial Party Committee Organization Department, and Science and Technology Service Network Initiative (KFJ-STS-QYZD-2021-21-001).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” in Proc. of Int. Conf. on Neural Information Processing Systems, Carson, Nevada, USA, pp. 1097–1105, 2012. [Google Scholar]

 2.  M. Tan and Q. Le, “Efficientnet: Rethinking model scaling for convolutional neural networks,” in Int. Conf. on Machine Learning, Long Beach, USA, pp. 6105–6114, 2019. [Google Scholar]

 3.  K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

 4.  P. -L. Hong, J. -Y. Hsiao, C. -H. Chung, Y. -M. Feng and S. -C. Wu, “ECG biometric recognition: Template-free approaches based on deep learning,” in Proc. of Int. Conf. of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, pp. 2633–2636, 2019. [Google Scholar]

 5.  R. D. Labati, E. Muoz, V. Piuri, R. Sassi and F. Scotti, “Deep-ECG: Convolutional neural networks for ECG biometric recognition,” Pattern Recognition Letters, vol. 126, no. 6, pp. 78–85, 2019. [Google Scholar]

 6.  Q. Wang, Z. Mao, B. Wang and L. Guo, “Knowledge graph embedding: A survey of approaches and applications,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 12, pp. 2724–2743, 2017. [Google Scholar]

 7.  H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

 8.  H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

 9.  P. R. Jeyaraj and E. R. S. Nadar, “Computer-assisted medical image classification for early diagnosis of oral cancer employing deep learning algorithm,” Journal of Cancer Research and Clinical Oncology, vol. 145, no. 4, pp. 829–837, 2019. [Google Scholar]

10. K. Guo, S. Ren, M. Z. A. Bhuiyan, T. Li, D. Liu et al., “Mdmaas: Medical-assisted diagnosis model as a service with artificial intelligence and trust,” IEEE Transactions on Industrial Informatics, vol. 16, no. 3, pp. 2102–2114, 2019. [Google Scholar]

11. P. Bachman, R. D. Hjelm and W. Buchwalter, “Learning representations by maximizing mutual information across views,” arXiv preprint arXiv:1906.00910, 2019. [Google Scholar]

12. D. Chen, Y. Chen, Y. Li, F. Mao, Y. He et al., “Self-supervised learning for few-shot image classification,” in Proc. of IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Ontario, Canada, pp. 1745–1749, 2021. [Google Scholar]

13. P. Mangla, N. Kumari, A. Sinha, M. Singh, B. Krishnamurthy et al., “Charting the right manifold: Manifold mixup for few-shot learning,” in Proc. of the IEEE/CVF Winter Conf. on Applications of Computer Vision, Snowmass Village, USA, pp. 2218–2227, 2020. [Google Scholar]

14. Y. -X. Wang, R. Girshick, M. Hebert and B. Hariharan, “Low-shot learning from imaginary data,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 7278–7286, 2018. [Google Scholar]

15. I. A. Weinshall and Daphna, “Generative latent implicit conditional optimization when learning from small sample,” in Int. Conf. on Pattern Recognition, Milano, Lombardia, Italy, 2020. [Google Scholar]

16. E. Schwartz, L. Karlinsky, J. Shtok, S. Harary, M. Marder et al., “Delta-encoder: An effective sample synthesis method for few-shot object recognition,” in Proc. of the 32nd Int. Conf. on Neural Information Processing Systems, Montreal, Canada, pp. 2850–2860, 2018. [Google Scholar]

17. M. Chen, Y. Fang, X. Wang, H. Luo, Y. Geng et al., “Diversity transfer network for few-shot learning,” in Proc. of the AAAI Conf. on Artificial Intelligence, New York, USA, pp. 10559–10566, 2020. [Google Scholar]

18. K. Li, Y. Zhang, K. Li and Y. Fu, “Adversarial feature hallucination networks for few-shot learning,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 13470–13479, 2020. [Google Scholar]

19. Z. Chen, Y. Fu, Y. Zhang, Y. -G. Jiang, X. Xue et al., “Multi-level semantic feature augmentation for one-shot learning,” IEEE Transactions on Image Processing, vol. 28, no. 9, pp. 4594–4605, 2019. [Google Scholar]

20. A. Santoro, S. Bartunov, M. Botvinick, D. Wierstra and T. Lillicrap, “Meta-learning with memory-augmented neural networks,” in Int. Conf. on Machine Learning, Vienna, Austria, pp. 1842–1850, 2016. [Google Scholar]

21. N. Mishra, M. Rohaninejad, X. Chen and P. Abbeel, “A simple neural attentive meta-learner,” in Int. Conf. on Learning Representations, Vancouver, BC, Canada, 2018. [Google Scholar]

22. A. A. Rusu, D. Rao, J. Sygnowski, O. Vinyals, R. Pascanu et al., “Meta-learning with latent embedding optimization,” in Int. Conf. on Learning Representations, Vancouver, BC, Canada, 2018. [Google Scholar]

23. L. Bertinetto, J. Henriques, P. Torr and A. Vedaldi, “Meta-learning with differentiable closed-form solvers,” in Int. Conf. on Learning Representations, New Orleans, Louisiana, United States, 2019. [Google Scholar]

24. M. A. Jamal and G. -J. Qi, “Task agnostic meta-learning for few-shot learning,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 11719–11727, 2019. [Google Scholar]

25. W. -Y. Chen, Y. -C. Liu, Z. Kira, Y. -C. F. Wang and J. -B. Huang, “A closer look at few-shot classification,” in Int. Conf. on Learning Representations, New Orleans, Louisiana, United States, 2019. [Google Scholar]

26. C. Finn, P. Abbeel and S. Levine, “Model-agnostic meta-learning for fast adaptation of deep networks,” in Int. Conf. on Machine Learning, Stockholm, Sweden, pp. 1126–1135, 2017. [Google Scholar]

27. F. Sung, Y. Yang, L. Zhang, T. Xiang, P. H. Torr et al., “Learning to compare: Relation network for few-shot learning,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 1199–1208, 2018. [Google Scholar]

28. V. G. Satorras and J. B. Estrach, “Few-shot learning with graph neural networks,” in Int. Conf. on Learning Representations, Vancouver, BC, Canada, 2018. [Google Scholar]

29. Q. Sun, Y. Liu, T. -S. Chua and B. Schiele, “Meta-transfer learning for few-shot learning,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 403–412, 2019. [Google Scholar]

30. J. Kim, T. Kim, S. Kim and C. D. Yoo, “Edge-labeling graph neural network for few-shot learning,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 11–20, 2019. [Google Scholar]

31. I. Ziko, J. Dolz, E. Granger and I. B. Ayed, “Laplacian regularized few-shot learning,” in Int. Conf. on Machine Learning, Austria, Venna, pp. 11660–11670, 2020. [Google Scholar]

32. Y. Hu, V. Gripon and S. Pateux, “Leveraging the feature distribution in transfer-based few-shot learning,” in Int. Conf. on Artificial Neural Networks, Bratislava, Slovakia, pp. 487–499, 2021. [Google Scholar]

33. J. Xie, F. Long, J. Lv, Q. Wang and P. Li, “Joint distribution matters: Deep brownian distance covariance for few-shot classification,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New Orleans, LA, USA, pp. 7972–7981, 2022. [Google Scholar]

34. P. Chikontwe, S. Kim and S. H. Park, “CAD: Co-Adapting discriminative features for improved few-shot classification,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New Orleans, LA, USA, pp. 14554–14563, 2022. [Google Scholar]

35. Koltchinskii and Vladimir, “Rademacher penalties and structural risk minimization,” IEEE Transactions on Information Theory, vol. 47, no. 5, pp. 1902–1914, 2001. [Google Scholar]

36. L. Bottou and O. Bousquet, “The tradeoffs of large scale learning,” in Proc. of the Int. Conf. on Neural Information Processing Systems, Vancouver, BC, Canada, pp. 161–168, 2007. [Google Scholar]

37. L. Bottou, F. E. Curtis and J. Nocedal, “Optimization methods for large-scale machine learning,” Siam Review, vol. 60, no. 2, pp. 223–311, 2018. [Google Scholar]

38. Y. Wang, Q. Yao, J. T. Kwok and L. M. Ni, “Generalizing from a few examples: A survey on few-shot learning,” ACM Computing Surveys, vol. 53, no. 3, pp. 1–34, 2020. [Google Scholar]

39. I. Misra and L. V. D. Maaten, “Self-supervised learning of pretext-invariant representations,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 6707–6717, 2020. [Google Scholar]

40. R. Zhang, P. Isola and A. A. Efros, “Colorful image colorization,” in European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 649–666, 2016. [Google Scholar]

41. R. Moradi, R. Berangi and B. Minaei, “A survey of regularization strategies for deep models,” Artificial Intelligence Review, vol. 53, no. 6, pp. 3947–3986, 2020. [Google Scholar]

42. A. Genevay, G. Peyre and M. Cuturi, “Learning generative models with sinkhorn divergences,” in Int. Conf. on Artificial Intelligence and Statistics, Playa Blanca, Lanzarote, pp. 1608–1617, 2018. [Google Scholar]

43. M. Dai and H. Hang, “Manifold matching via deep metric learning for generative modeling,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, Montreal, Quebec, Canada, pp. 6587–6597, 2021. [Google Scholar]

44. C. E. Priebe, D. J. Marchette, Z. Ma and S. Adali, “Manifold matching: Joint optimization of fidelity and commensurability,” Brazilian Journal of Probability and Statistics, vol. 27, no. 3, pp. 377–400, 2013. [Google Scholar]

45. M. Harandi, M. Salzmann and M. Baktashmotlagh, “Beyond gauss: Image-set matching on the riemannian manifold of pdfs,” in Proc. of the IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 4112–4120, 2015. [Google Scholar]

46. O. Arandjelovic, G. Shakhnarovich, J. Fisher, R. Cipolla and T. Darrell, “Face recognition with image sets using manifold density divergence,” in IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, San Diego, CA, USA, pp. 581–588, 2005. [Google Scholar]

47. M. Cuturi, “Sinkhorn distances: Lightspeed computation of optimal transport,” in Proc. of Int. Conf. on Neural Information Processing Systems, Carson, Nevada, USA, pp. 2292–2300, 2013. [Google Scholar]