Al-Biruni Based Optimization of Rainfall Forecasting in Ethiopia

1  Introduction

Rural life sustains almost all Ethiopians, with agriculture providing the bulk of the country’s income (about 85%). Rainfall is critical to Ethiopia’s agriculture, which relies significantly on it. The expected rainfall has a wide-ranging effect on agriculture and on people planning their vacations. It is incredibly difficult to predict rainfall, on the other hand, Precipitation is affected by a wide range of variables such as humidity, maximum and lowest temperatures, wind speed and direction, and so on [1,2]. It is possible to predict rainfall using the patterns in these factors. Decision trees (DT), k-nearest neighbors (KNN), linear regression (LR), and rule-based approaches are all examples of machine learning algorithms that can be used to forecast rainfall. For huge datasets, deep learning can provide substantial results. We are primarily interested in predicting rainfall based on six key rainfall parameters: maximum temperature, minimum temperature, relative humidity, solar radiation, wind speed, and precipitation itself. Predictive models are built using deep learning techniques [3]. In Jimma, a region in Ethiopia’s Oromia region in the southwest, we’ve developed a prediction model [4]. A cup of Arabica coffee may be traced back to Jimma, Ethiopia. Basically, too little water is never a good thing, and too much water may be either destructive or useful, depending on other environmental circumstances, to the coffee product [5]. However, despite several research on rainfall prediction using artificial neural network (ANN), multi-layer perceptron (MLP), and linear regression, there is no literature on deep-learning-based prediction for the same region in Jimma town [6]. Given that local meteorological conditions differ widely, a model built for one place might be useless in another. Exporting coffee from this region helps the country’s economy flourish financially. When water resources are poorly managed, the area is plagued by flooding and water shortages [7].

Water shortages and flooding can be prevented if people are aware of the weather forecast for the next day. A deep-learning model based on meteorological data from the country’s weather stations is used in this work to create the capacity to predict rainfall. The Ethiopian national meteorological service agency (NMSA) provided the data for this study, which covered the years 1985–2017. It is possible to employ rainfall estimation for a number of goals, including lowering traffic accidents and congestion, boosting water management, reducing floods, and so on. For a long time, meteorologists have worked to improve the accuracy and timeliness of their forecasts. Numerical weather prediction (NWP) based on theory has a number of challenges, including the inability to extract valuable information from a deluge of observational data and the requirement for extremely powerful computing resources [8–12]. It has been demonstrated that deep-learning approaches may efficiently extract temporal and spatial features from temporal data through successful implementations in a range of domains, including computer vision, speech recognition, and time series prediction. Large geographic data sets include, for example, weather forecasts. To put it another way, the conventional technique is projected to benefit greatly from deep-learning-based weather prediction (DLWP).

Precipitation forecasting relies on first-hand knowledge and measurements of various rainfall features. Researchers have employed machine learning algorithms, such as MLP, to forecast rainfall. Deep learning’s capacity to accurately forecast rainfall is severely hampered when working with sensor-based information. According to recent studies, MLP is the most used neural network model for forecasting rainfall. Data-driven deep learning is now being used in weather forecasting, and some tentative results have been produced. Research on this topic will be aided by reading these publications. Various machine-learning algorithms have been suggested by distinct researchers for various research areas. In [13], ANN was used to develop a rainfall forecasting model for South Korea’s Geum River Basin during the late spring/early summer period. For the training, validation, and testing datasets, the best ANN model exhibited relative root mean square errors of 25.84 percent, 32.72 percent, and 34.75 percent, respectively. This implies that the ANN model correctly predicted rainfall in the study region, since the hit score, which is the number of hit years divided by the total number of years, was higher than 60%. According to authors in [14], some regions of Ethiopia can benefit from the adoption of a rainfall prediction model for crop recommendation. They used ANN and KNN to build their rain forecasting model. Maximum temperature, minimum temperature, and average rainfall were the three most important factors in determining the amount of rain that fell. Meteorological stations at Gojjam and Gonder were used to perform tests on summer rainfall. The accuracy of their forecasts has to be enhanced, as they did not cover all Ethiopian seasons. The authors at [15] suggested employing KNN, ANN, and extreme learning algorithms to estimate rainfall in Kerala, India. To avoid a drought and deal with water scarcity, the rainfall forecast model for Kerala described here is crucially important. In the Indian Institute of Technology Madras (IITM), time-series meteorological data is employed. The results reveal that ANN and extreme learning machine (ELM) models beat KNN models in terms of accuracy. Using large-scale climate predictors, the authors in [16] give an ensemble forecast of semi-arid rains. A semi-arid watershed in Iran was studied for a lengthy time period (1967–2009) to determine the relationship between climatic predictions and seasonal precipitation. The seasonal ensemble precipitation time series was predictd using linear regression and two nonlinear models, the adaptive neuro-fuzzy inference system (ANFIS) and the multi-layer perceptron. It was shown that the ANFIS algorithm had a greater connection with winter predictors when predicting spring precipitation modes as an ensemble prediction. The fluctuation of the predictor is statistically linked, according to an investigation, with seasonal precipitation. In arid and semi-arid nations, where water shortages are widespread, climate modelling and prediction are essential. Authors in [17] use the adaptive neuro-fuzzy inference system (ANFIS), the M5P model tree, and MLP to simulate drought indexes based on large-scale climatic variables. In order to forecast the standardized precipitation index (SPI) one to twelve months in advance, they employed ANFIS, the M5P model tree, and MLP together with factor analysis to identify the climate signal among 25 climate signals. Error parameters and Taylor diagrams were used to evaluate the models’ performance, and the MLP came out on top.

There has been an increase in interest in semi-arid climate forecasting because of the dangers connected with precipitation amounts that are above average. Short-term extremes and a lack of data make it difficult to develop long-term projections. The Classification and Regression Trees (CART) algorithm was used to estimate precipitation across an extremely complicated semiarid climatic system utilizing climate data. CART is an acronym for Classification and Regression Trees. Precipitation may be predicted using CART, autoregressive integrated moving average (ARIMA) and ANFIS models, according to a study by [18]. The CART model was shown to be more accurate than the other two regularly used models. Inputs included various combinations of large-scale climatic signals. The CART model performed better than the ANFIS and ARIMA in predicting precipitation, according to their experimental data (NSE = 0.75). Another technique for predicting rainfall, based on an ANN model and a time series dataset, was proposed by [19]. A feed-forward neural network with a back-propagation algorithm was used to build two models using time-series data from the Indian meteorology department in Pune (one-month-ahead and two-months-ahead predictions). Model 1 had the best accuracy results in the study of (3–25–1) regression, with a (0.946) and a (0.948) on the validating and testing datasets. Model 2’s (3–50–1) regression yielded (0.913) for the validating dataset and (0.910) for the testing dataset. Research has been done to apply deep-learning approaches to time series prediction. Temperature, wind speed, and humidity may be predicted for (24) and (72) h using a multi-stacked LSTM, according to authors in [20]. For a period of fifteen years, from 2000 to 2015, they analyzed hourly weather data from nine Moroccan cities. The researchers found that deep LSTM networks were capable of accurately forecasting weather features and recommending its application for other weather-related issues. For the purpose of short-term precipitation forecasting in China, the authors in [21] employed multi-task convolutional neural network (CNN) to combine meteorological information collected from many different China-based rain gauges. Multi-site features outperformed single-site features, according to the researchers. Monthly rainfall in Thimphu’s Simtokha district has been predicted by the authors at [22]. The rainfall data was given by Bhutan’s national center for hydrology and meteorology (NCHM). They tested the forecasting power of LR, MLP, CNN, LSTM, gated recurrent unit (GRU), and bidirectional LSTM (BiLSTM) based on data from an autonomous weather station in the region. BiLSTM-GRU models outperform existing machine and deep learning models, according to the researchers [23–30]. A deep-learning algorithm can help enhance the accuracy of rainfall forecasts, according to the studies above. So we present an improved method for forecasting rainfall in Ethiopia: LSTM-based rainfall prediction for Jimma. Deep-learning algorithms are being used in this study to predict rainfall in Jimma town based on a variety of features. The following list presents the main contributions of this paper.

1.    A new approach for rainfall prediction based on LSTM and meta-heuristic optimization.

2.    An extended experiment is conducted to demonstrate the effectiveness of the proposed approach.

3.    A comparison with the other competing models to show the superiority of the proposed approach.

What follows is an outline for the remainder of the paper. In Section 2, the proposed methodology is presented in details. The outcomes of the conducted experiments are discussed in detail in Section 3. Finally, we wrap up our research and provide some recommendations for the future in Section 4.

2  The Proposed Methodology

In order to build a rain prediction model, meteorological data must be collected. Weather data from the national oceanic and atmospheric administration (NMSA) is used in this context. Data is then preprocessed, which involves things like deleting empty entries, resolving missing values, and normalizing. Deep learning uses the preprocessed data to learn from it and predict rainfall for previously unknown data. The stages depicted in Fig. 1 are used in the proposed model for predicting rainfall. The next sections provide explanation of the proposed methodology.

Figure 1: The stages of the proposed methodology

2.1 Data Preprocessing

Preprocessed NMSA data are shown with arrow heads to demonstrate the passage of data through four states. The dataset was tidied up by deleting the records that had no data. In the preparation step, the null values of the dataset are normalized. The linear regression approach was used to approximate missing precipitation data using correlation coefficients. An technique known as Markov Chain Monte Carlo (MCMC) multiple imputation, also known as fully conditional specification, was used to fill in any missing data on daily minimum and maximum temperatures, humidity and wind speed. A normal distribution with mean and standard error equal to those of the available data was used to sample the initial values of the missing values, and an imputation approach based on sampling and Ordinary Least Squares (OLS) regression was performed to each variable in the dataset with missing values. All other variables were treated as independent and the researched variable was treated as dependent. Data taken from a variety of distributions was also utilized to create disturbance. This model was used to generate new imputed values. We normalized the weather parameters using a min–max scaler in order to get the new scaled value v. The ranges of features vary, thus we used the min–max scaler to adjust the data [31–36].

v=v−min(x)max(x)−min(x) (1)

where max(x) and min(x) represent the values of x that are maximum and minimum, respectively, and v is the scaled value. As shown in Fig. 2, the steps of the preprocessing stage are depicted.

Figure 2: The steps of the preprocessing stage

It is called data reshaping when the original data is rearranged to fit the new dimensions [37–40]. Preparing sequence data for an LSTM model is tough to grasp. There is a prevalent misconception about what constitutes an LSTM input layer. LSTM’s input layer requires a 3D format, therefore we remove empty records, resolve missing values, and scale the data using the min–max scaler.

To increase the accuracy of the rainfall prediction, a new approach is proposed by adjusting the hyperparameters of the LSTM. This section begins by presenting the LSTM’s structure and describing which parameters are being improved, followed by presenting the optimization algorithm that is employed to optimize the parameters of LSTM.

2.2 Long Short-Term Memory (LSTM)

The LSTM model has lately gained favor as a recurrent neural network because it can mimic intricate time series with time delays of unknown magnitude [41–48]. Self-loops, where the gradient may flow for long periods of time without bursting or vanishing, are at the heart of LSTM. In combination with this, a forget-gate allows the LSTM to accumulate information that, depending on the input data, may be “forgotten” later. LSTM models have been used for the first time to model short-term network flow sizes with exquisite granularity. LSTMs are characterized by the following recursive equations:

ot=σ(WoXt+Uoht−1+bo)

ct=it⊙c~t+ft⊙ct−1

ft=σ(WfXt+Ufht−1+bf) (2)

ht=ot⊙tanh⁡(ct)

it=σ(WiXt+Uiht−1+bi)

c~t=tanh(WcXt+Ucht−1+bc)

where Wo , Wc , Wi , and Wf represent the weights for output gate, candidate state gate, input gate, and forget gate, respectively. The values bf , Xt , ht , ot , ct , c~t , it , ft are the bias value, input data, hidden state, output gate, current state, candidate state, input gate, and forget gate, respectively. The Hadamard product, ⊙ , refers to the sigmoid function. The values of Uo , Uc , Ui , and Uf are the recurrent weights for the output gate, current state, input gate, and forget gate, respectively. The bias terms for output gate, candidate state, input gate, and forget gate are denoted by, bo , bc , bi , and bf , respectively. As shown in Fig. 3, the LSTM unit at time t and how it relates to previous and future states to construct a neural network may be seen from this perspective.

Figure 3: Standard structure of the LSTM network

2.3 Al-Biruni Earth Radius (BER) Optimization Algorithm

It is the goal of optimization algorithms to find the best possible solution to a problem given limitations. When using BER, an individual from the population may be shown in the form of ‘S’ vector, S→={S1,S2,…,Sd}∈Rd , where Si is the size of the search space and d is the parameter or feature in the optimization problem. It is suggested that the fitness function f be utilized in order to assess a person’s performance up to a predetermined point. These steps of the optimization technique are used to search populations for an optimal vector S* that optimizes the fitness. The method begins by selecting a random group of people from the population (solutions). The fitness function, the lower and higher limits for each solution, the dimension, and the population size are all required before BER can begin the optimization process. The optimization algorithm used to optimize the parameters of LSTM is depicted in Algorithm 1.

3  Experimental Results

The evaluation of the proposed approach is performed and the results are explained in this section. The section starts with describing the dataset included in the conducted experiments followed by the evaluation criteria and explanation of the achieved results.

3.1 Dataset Description

Jimma is a tiny town located in the Oromia region of Ethiopia’s southwest. A meteorological station at Jimma provided the sensor data for this study. Its coordinates are 7°400 N 36°500 E on the compass rose. The study region is depicted in Fig. 4. As a result, this study uses a daily record of meteorological parameters from 1985 to 2017 in order to account for the length of the record, continuity of the data, and the contemporaneous time of observation The consistency of the meteorological data was verified before it was put to use. The collection contains 12,052 days of data for six different metrics. Preprocessing handled any missing values in these parameters, which had zero or a tiny number. The mean of maximum and lowest temperatures, relative humidity, solar radiation, wind speed, and precipitation were used to derive meteorological parameters from weather data. Precipitation was employed as an output, while the first five parameters were used as inputs. The dataset spans a period of more than three decades. Train-validate-test ratios of 80%, 10% and 10% were employed in this experiment. It was built using data from 1985 through 2012, and then tested using data from 2013 through the first half of this year. Evaluations were carried out using data from the second half of 2015 through 2017. The features of the weather utilized in this study are listed in Tab. 1, along with the units in which they were measured. Precipitation is predicted using the five initial weather factors.

Figure 4: The location of interest in the conducted experiments

3.2 Evaluation Metrics

The metrics used to assess the proposed methodology and their corresponding formulas are presented in Tab. 2. These metrics are: root mean square error (RMSE), normalized RMSE (NRMSE), Nash–Sutcliffe model efficiency (NSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and R2 metrics. In these formulas; Fi is the forecast daily rainfall value, Ai is the actual daily rainfall value, yi is the observed daily rainfall, xi is the model’s simulated daily rainfall, and n is the number of data points.

3.3 The Achieved Results

To prove the effectiveness and superiority of the proposed approach, several experiments were conducted to predict the rainfall. Firstly, a set of baseline experiments were conducted using six base models including LSTM, BILSTM, GRU, LSTMs, BiLSTMs, and ConvLSTMs. The results of these models were compared to the achieved results using the optimized LSTM based on BER algorithm. Tab. 3 presented the results of the training and testing for each of the base models along with the proposed approach based on the adopted evaluation criteria.

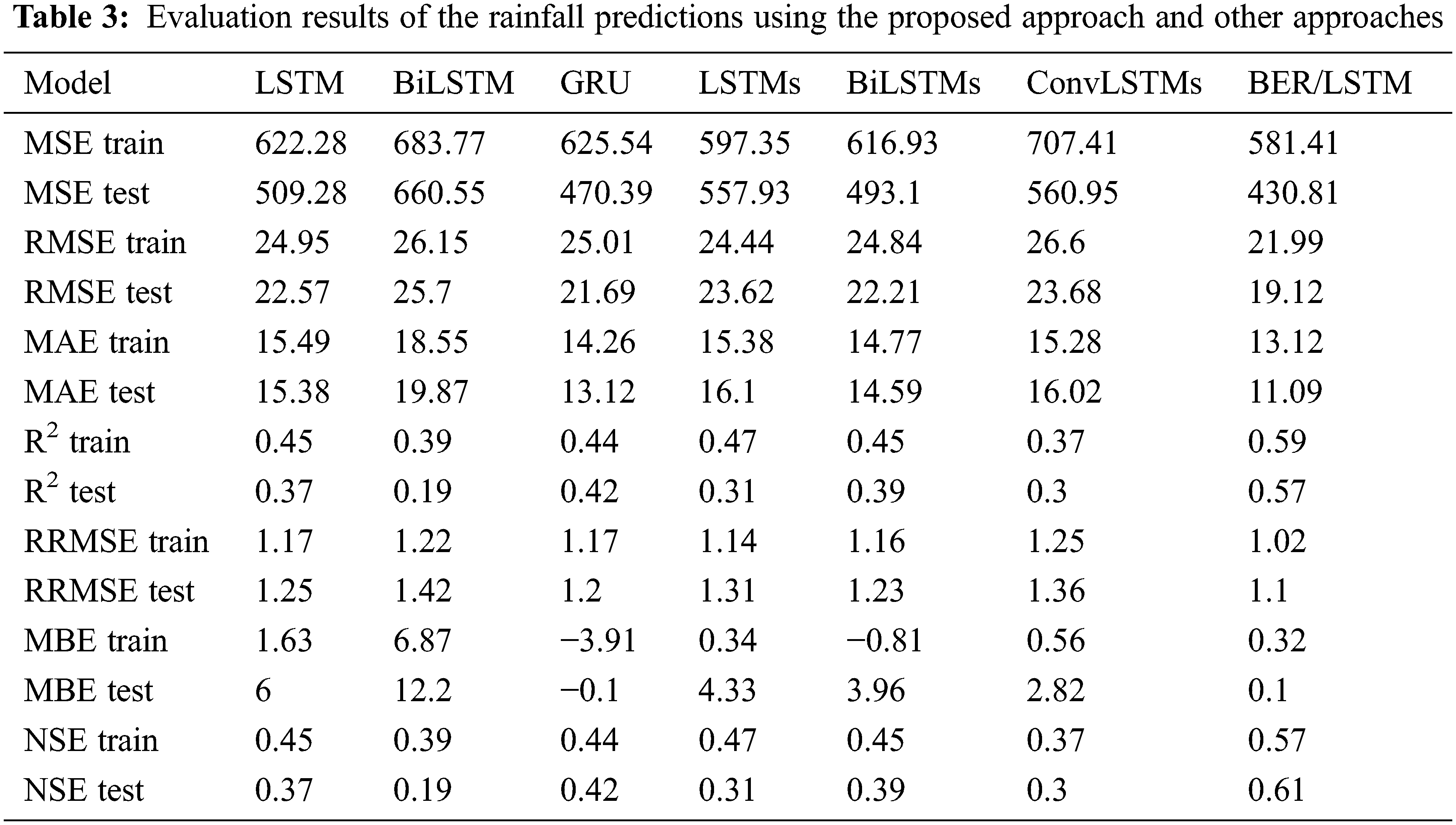
As presented in the table, the proposed approach could achieve the best values over all the evaluation criteria, which confirm the superiority of the proposed approach. The achieved MSE on the test set using the proposed approach is (430.81), whereas the best MSE achieved by the base models is (493.1). In addition, MAE, R2, MBE, and NSE of the test set using the proposed approach are (11.09), (0.57), (1.1), (0.1), and (0.61). These value prove the effectiveness of the proposed approach.

On the other hand, a statistical analysis is performed to clearly investigate the effectiveness of the proposed approach. Tab. 4 presents the results of this statistical analysis. As presented in the table, the mean and standard deviation for example are the minimum when compared to the base models. This confirms the findings of the proposed approach.

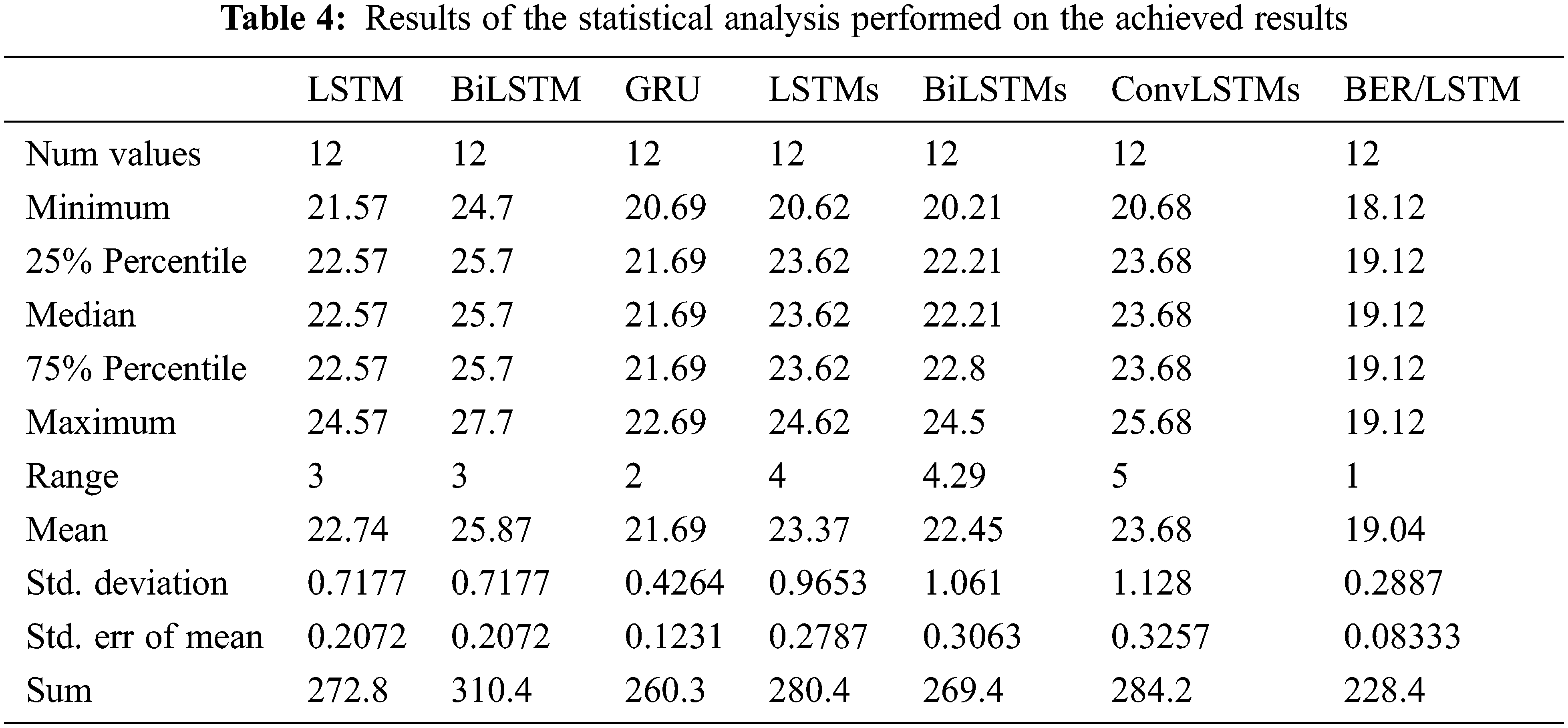
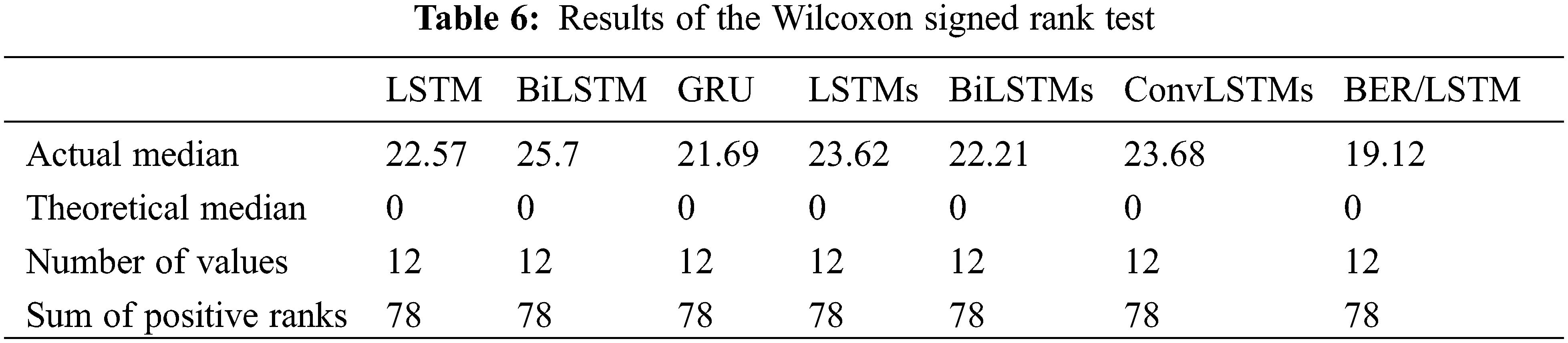
Moreover, the one-way analysis of variance (ANOVA) and the Wilcoxon singed rank tests are performed to study the stability of the proposed approach. The results of these tests are presented in Tabs. 5 and 6. The results presented in these tables show the significance and stability of the proposed approach as the value of F in the ANOVA test is (78.51) and (P < 0.0001). In addition, the significance of all methods using the Wilcoxon test is satisfied.

On the other hand, more results are shown in the plots depicted in Figs. 5 and 6. In these figures, the ranges of RMSE using the base models and the proposed approach are shown in the plot of Fig. 5a. In this plot, the range of values of RMSE using the proposed approach is the minimum, which reflects the superiority of the proposed approach. In addition, the receiver operating characteristic (ROC) curve using the proposed approach shows a promising performance.

Figure 5: Comparison between the proposed approach and the other competing approaches in terms of RMSE and ROC

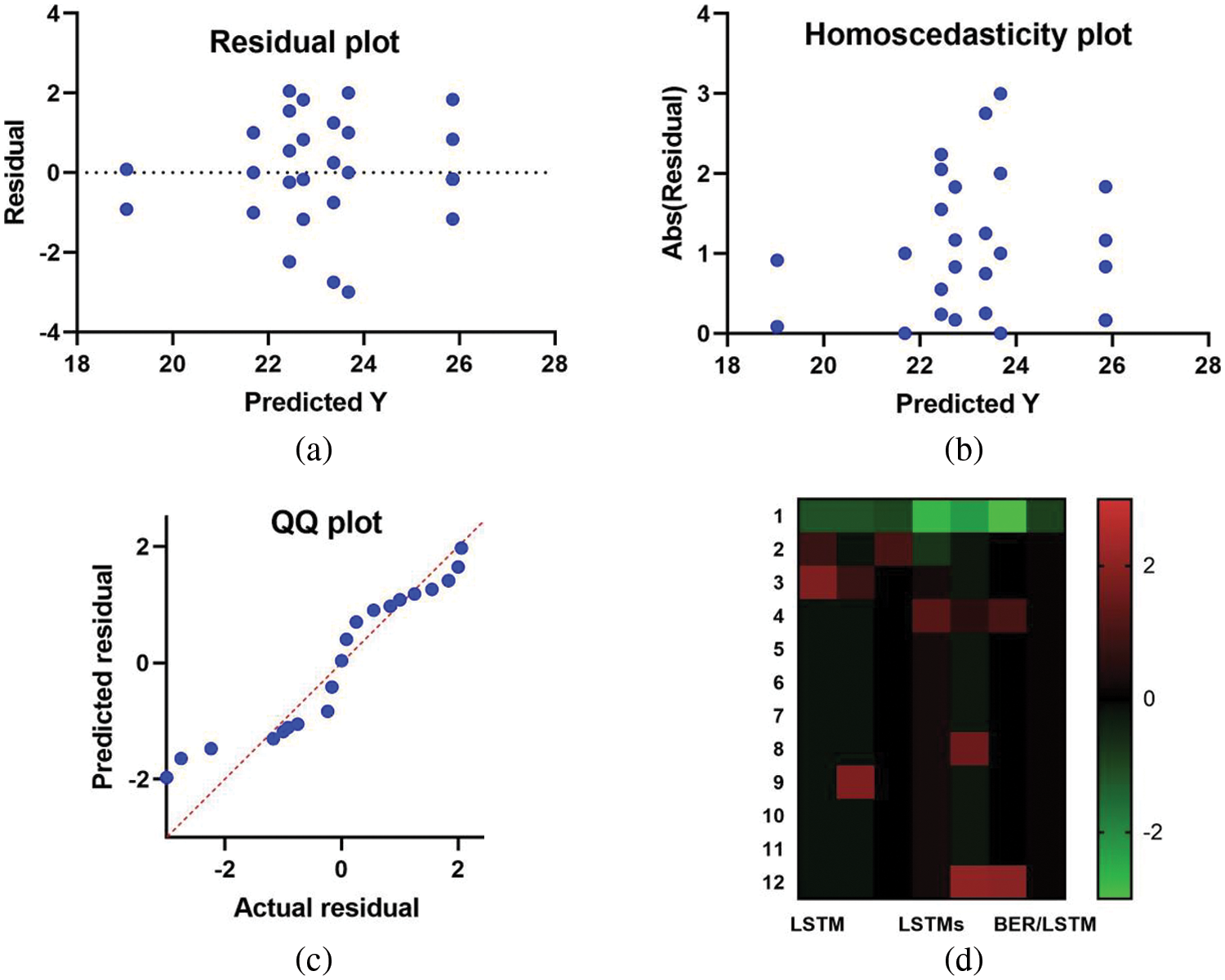
Figure 6: Analyzing the performance of the recorded predictions using the proposed approach

More plots are shown in Fig. 6 that present the behavior of the residual, homoscedasticity, quantile-quantile (QQ) and heatmap of the achieved results. In these plots, the proposed approach shows a promising performance which makes it a proper and better solution to the problem of rainfall prediction using machine learning.

4  Conclusions

Research into deep learning approaches for rain forecasting is described in this paper, and an LSTM-based model for Jimma in Ethiopia’s western Oromia region is proposed. The proposed model is optimized using Al-Biruni earth radius optimization algorithm. Data for the experiment came from Ethiopia’s NMSA. The data collection spans the years 1985 to 2017 and contains daily records of several meteorological parameters, such as maximum and minimum temperatures, relative humidity, solar radiation, wind speed, and precipitation. There are a number of tests done on this dataset to verify the predicted performance of the new machine learning-based model. Tests show that the prediction model presented by the researchers is accurate. Smart farming and other applications that need accurate rainfall forecasts might benefit from the suggested model’s ability to predict the weather based on LSTMs. There are a number of things we hope to do in the future, including the development of a model for predicting rainfall that incorporates data on sea-surface temperature, global wind circulation, and a variety of other climatic variables.

Acknowledgement: Princess Nourah Abdulrahman University Researchers Supporting Project Number (PNURSP2022R77), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R77), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Siddiqua and S. Kumar, “Heavy rainfall prediction using gini index in decision tree,” International Journal of Recent Technology and Engineering (IJRTE), vol. 8, no. 4, pp. 4558–4562, 2019. [Google Scholar]

 2.  S. Azadi, H. Amiri and G. Reza, “Evaluating the ability of artificial neural network and PCA-M5P models in predicting leachate COD load in landfills,” Waste Management, vol. 55, pp. 220–230, 2016. [Google Scholar]

 3.  N. Bahari, A. Ahmad and B. Aboobaider, “Application of support vector machine for classification of multispectral data,” in 7th IGRSM Int. Remote Sensing & GIS Conf. and Exhibition, Kuala Lumpur, Malaysia, 2014. [Google Scholar]

 4.  Y. Biyadglgn and H. Melkamu, Rainfall Prediction and Cropping Pattern Recommendation Using Artificial Neural Network: A Case Study for Ethiopia, Addis Ababa, Ethiopia: Addis Ababa University, 2016. [Google Scholar]

 5.  M. Carr, “The water relations and irrigation requirements of coffee,” Experimental Agriculture, vol. 37, no. 1, pp. 1–36, 2001. [Google Scholar]

 6.  M. Chhetri, S. Kumar, P. Roy and B. -G. Kim, “Deep BLSTM-GRU model for monthly rainfall prediction: A case study of simtokha, Bhutan,” Remote Sensing, vol. 12, pp. 3174–3190, 2020. [Google Scholar]

 7.  B. Choubin, A. Malekian and M. Golshan, “Application of several data-driven techniques to predict a standardized precipitation index,” Atmósfera, vol. 29, no. 2, pp. 121–128, 2016. [Google Scholar]

 8.  B. Choubin, A. Malekian, S. Samadi, S. Khalighi-Sigaroodi and F. Sajedi-Hosseini, “An ensemble forecast of semi-arid rainfall using large-scale climate predictors,” Meteorological Applications, vol. 24, no. 3, pp. 376–386, 2017. [Google Scholar]

 9.  B. Choubin, G. Zehtabian, A. Azareh, E. Rafiei-Sardooi, F. Sajedi-Hosseini et al., “Precipitation forecasting using classification and regression trees (CART) model: A comparative study of different approaches,” Environmental Earth Sciences, vol. 77, pp. 314–330, 2018. [Google Scholar]

10. A. Danladi, M. Stephen, B. Aliyu, G. Gaya, N. Silikwa et al., “Assessing the influence of weather parameters on rainfall to forecast river discharge based on short-term,” Alexandria Engineering Journal, vol. 57, no. 2, pp. 1157–1162, 2018. [Google Scholar]

11. Y. Dash, S. Mishra and B. Panigrahi, “Rainfall prediction for the Kerala state of India using artificial intelligence approaches,” Computers & Electrical Engineering, vol. 70, pp. 66–73, 2018. [Google Scholar]

12. H. Elwell and M. Stocking, “Rainfall parameters and a cover model to predict runoff and soil loss from grazing trials in the rhodesian sandveld,” African Journal of Range & Forage Science, vol. 9, no. 1, pp. 157–164, 1974. [Google Scholar]

13. D. Endalie and T. Tegegne, “Designing a hybrid dimension reduction for improving the performance of Amharic news document classification,” PLoS ONE, vol. 16, no. 5, pp. e0251902, 2021. [Google Scholar]

14. A. Garg and H. Pandey, “Rainfall prediction using machine learning,” International Journal of Innovative Science and Research Technology, vol. 4, no. 5, pp. 56–58, 2019. [Google Scholar]

15. E. Gelenbe and Y. Yin, “Deep learning with dense random neural networks,” in 5th Int. Conf. on Man–Machine Interactions, vol. 17, Cracow, Poland, 2017. [Google Scholar]

16. P. Hewage, M. Trovati, E. Pereira and A. Behera, “Deep learning-based effective fine-grained weather forecasting model,” Pattern Analysis and Applications, vol. 24, no. 1, pp. 343–366, 2021. [Google Scholar]

17. J. Kumar, R. Goomer and A. Singh, “Long short term memory recurrent neural network (LSTM-RNN) based workload forecasting model for cloud datacenters,” Procedia Computer Science, vol. 125, pp. 678–682, 2018. [Google Scholar]

18. J. Lee, C. Kim, J. Lee, N. Kim and H. Kim, “Application of artificial neural networks to rainfall forecasting in the Geum River Basin, Korea,” Water, vol. 10, pp. 1448–1459, 2018. [Google Scholar]

19. W. Li and Z. Liu, “A method of SVM with normalization in intrusion detection,” Procedia Environmental Sciences, vol. 11, pp. 256–262, 2011. [Google Scholar]

20. Q. Liu, Y. Zou, X. Liu and N. Linge, “A survey on rainfall forecasting using artificial neural network,” International Journal of Embedded Systems, vol. 11, no. 2, pp. 240–248, 2019. [Google Scholar]

21. M. Mengistu, M. Workie and A. Mohammed, “Physical and cup quality attributes of Arabica coffee (Coffea arabica L.) varieties grown in highlands of Amhara region, northwestern Ethiopia,” International Journal of Agronomy, vol. 2020, pp. 1–9, 2020. [Google Scholar]

22. M. Mhatre, F. Siddiqui, M. Dongre and P. Thakur, “A review paper on artificial neural network: A prediction technique,” International Journal of Scientific & Engineering Research, vol. 6, no. 12, pp. 161–163, 2015. [Google Scholar]

23. K. Miao, T. Han, Y. Yao, H. Lu, P. Chen et al., “Application of LSTM for short term fog forecasting based on meteorological elements,” Neurocomputing, vol. 408, pp. 285–291, 2020. [Google Scholar]

24. N. Mishra, H. Soni, S. Sharma and A. Upadhyay, “Development and analysis of artificial neural network models for rainfall prediction by using time-series data,” International Journal of Intelligent Systems and Applications, vol. 10, no. 1, pp. 16–23, 2018. [Google Scholar]

25. D. Nayak, A. Mahapatra and P. Mishra, “A survey on rainfall prediction using artificial neural network,” International Journal of Computer Applications, vol. 72, no. 16, pp. 32–40, 2013. [Google Scholar]

26. P. Nielsen, I. Fontana, K. Sloth, M. Guarino and H. Blokhuis, “Validation and comparison of 2 commercially available activity loggers,” Journal of Dairy Science, vol. 101, no. 6, pp. 5449–5453, 2018. [Google Scholar]

27. Z. Pu and E. Kalnay, “Numerical weather prediction basics: Models, numerical methods, and data assimilation,” in Handbook of Hydrometeorological Ensemble Forecasting, Berlin, Germany: Springer, 2018. [Google Scholar]

28. M. Qiu, P. Zhao, K. Zhang, J. Huang, X. Shi et al., “A short-term rainfall prediction model using multi-task convolutional neural networks,” in 2017 IEEE Int. Conf. on Data Mining (ICDM), Piscataway, NJ, USA, pp. 395–404, 2017. [Google Scholar]

29. X. Ren, X. Li, K. Ren, J. Song, Z. Xu et al., “Deep learning-based weather prediction: A survey,” Big Data Research, vol. 23, pp. 100178, 2020. [Google Scholar]

30. W. Ridwan, M. Sapitang, A. Aziz, K. Kushiar, A. Ahmed et al., “Rainfall forecasting model using machine learning methods: Case study Terengganu, Malaysia,” Ain Shams Engineering Journal, vol. 12, no. 2, pp. 1651–1663, 2021. [Google Scholar]

31. M. M. Eid, E. -S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf. (NCCC 2021), Taif, Saudi Arabia, IEEE, pp. 1–6, 2021. [Google Scholar]

32. Y. Song and Y. Lu, “Decision tree methods: Applications for classification and prediction,” Shanghai Archives of Psychiatry, vol. 27, no. 2, pp. 130–135, 2015. [Google Scholar]

33. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” Journal of Machine Learning Research, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]

34. T. Steichen and N. Cox, “A note on the concordance correlation coefficient,” The Stata Journal, vol. 2, no. 2, pp. 183–189, 2002. [Google Scholar]

35. N. Sundaravalli and A. Geetha, “A study & survey on rainfall prediction and production of crops using data mining techniques,” International Research Journal of Engineering and Technology (IRJET), vol. 3, no. 12, pp. 1269–1274, 2016. [Google Scholar]

36. I. Sutskever, O. Vinyals and Q. Le, “Sequence to sequence learning with neural networks,” in NIPS’14: Proc. of the 27th Int. Conf. on Neural Information Processing Systems, vol. 2, Cambridge, MA, USA, MIT Press, pp. 3104–3112, 2014. [Google Scholar]

37. A. Taravat, S. Proud, S. Peronaci, F. Del Frate and N. Oppelt, “Multilayer perceptron neural networks model for Meteosat Second Generation SEVIRI daytime cloud masking,” Remote Sensing, vol. 7, pp. 1529–1539, 2015. [Google Scholar]

38. V. Buuren, “Multiple imputation of discrete and continuous data by fully conditional specification,” Statistical Methods in Medical Research, vol. 16, pp. 219–242, 2007. [Google Scholar]

39. Y. Xue, J. Jiang and L. Hong, “A LSTM based prediction model for nonlinear dynamical systems with chaotic itinerancy,” International Journal of Dynamics and Control, vol. 8, pp. 1117–1128, 2020. [Google Scholar]

40. E. -S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

41. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” CMC-Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

42. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

43. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

44. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

45. E. -S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” CMC-Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

46. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

47. E. -S. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

48. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]