Particle Swarm Optimization for Solving Sine-Gordan Equation

1  Introduction

Whenever there is a need to optimize any one of the parameters involved in a problem there needs a tool or technique that can be implemented to solve it. The main focus is to obtain the best feasible collection of values to achieve a given goal while adhering to a set of constraints. The majority of real-world situations can be modelled as optimization problems that include large dimensions, non-linearity, multimodality, constraints, and other factors. Since traditional optimization approaches are generally incapable of resolving these complex problems, non-traditional efficient optimization tools/techniques are implemented to deal with a wide range of such problems. Nature-inspired algorithms belong to the category of optimization methods that have gained much popularity since their inception. Nature-inspired optimization algorithms are the approaches that replicate an existing natural process to find an optimum solution to a problem that can’t be handled using classical techniques. Swarm intelligence paradigm is an emerging field which simulates the social behavior of organisms. Since its inception, various algorithms have been proposed to handle complex problems arising in different spheres. Particle swarm optimization (PSO) is one of the potential global optimization techniques in the category of nature-inspired algorithms. PSO simulates the foraging process of swarm analogies such as bird flocks and fish schools. It is inspired by the well-informed social behaviour of swarms and was firstly proposed by Kennedy et al. in 1995 [1]. Fast convergence to the global optimum, a simple to implement code, and a sophisticated computation-free environment are all advantages of employing PSO. The search process in PSO is driven by the velocity and position update equations.

The present work is intended to obtain the numerical solution for the Sine-Gordan equation, which is a well-known nonlinear partial differential equation using exponential basis functions implementing the particle swarm optimization technique. The implemented optimization technique is to find the involved parameter in the exponential B-spline basis functions that was just approximated as a random number in the work reported till now in the literature.

Sine-Gordon (SG) equation is a second-order hyperbolic partial differential equation whose numerical solutions depict the soliton form and have intense applications in science and engineering. It appears in the study of optics as a solution to the classical Maxwell systems [2]. This equation also appears in the literature in the geometrical study of the soliton in view of the canonical field [3]. This study also depicts a relation between the black hole temperature and the soliton velocity. SG equation also presents a mathematical model to illustrate the fault dynamics of the phenomena of strain waves and earthquakes [4]. It plays a significant role in understanding the seismic distortion effects on the earth’s crust and the theory behind the cause of faulty natural substances. The soliton solution of the kinks form of the equation makes it a suitable equation to understand the concepts related to the different phenomena.

The equation is given by:

utt+αut=βuxx+η(x)sin⁡(u) (1)

To be solved with set of initial conditions:

u(x,0)=ϕ1(x)andut(x,0)=ϕ2(x)

And values defined at the boundaries.

Here, α and β are real constants and η(x,y) depicts the Josephson current density. The constant α represents the dissipative term that plays an important role in converting the equation from damped (α≥0) to undamped for ( α=0 ).

Researchers have investigated the SG equation to study the solution based on the properties shown by the equation. Ben-yu et al. [5] have implemented finite difference based on the concept of conserved discrete energy to discuss the solution of the equation. Albowitz et al. [6,7] discussed the equation for the unstable nature using the nonlinear spectrum. Various analytical and numerical approaches have been applied by the researchers to solve this equation for its soliton solutions including the modified decomposition method [8,9] for solving this equation 1D and 2D, the modified Adomian decomposition method [10] to solve the SG equation in (N + 1)-dimensions, homotopy analysis method [11], boundary element and boundary integral approach [12,13], Compact finite difference of order-6 (CFD6) scheme [14], tension spline-based approximation scheme [15], Modified cubic B-spline (MCB) collocation technique [16], localized method of approximate particular solutions [17], Legendre spectral element method [18], virtual element method [19], Barycentric rational interpolation and local radial basis functions [20], fourth-order collocation scheme [21] and rational radial basis function [22].

In this work, exponential basis functions with the differential quadrature method and the particle swarm optimization technique are implemented to find a numerical solution of the Sine-Gordan equation. To the authors’ knowledge, there is no such optimization method reported in the literature to calculate the value of the parameter involved in the exponential B-spline which plays a crucial role in finding the solutions.

This paper is organized in the following manner: Section 2 is concerned with the numerical scheme for the implementation of the PSO in the exponential B-spline which is implemented in the differential quadrature approach. In Section 3, two test problems of the SG equation are demonstrated with the different sets of parameters. The summary of this research paper is stated in Section 4.

2  Numerical Scheme

2.1 Differential Quadrature Method

Numerical methods have always proved as an efficient tool to solve differential equations in a programmable approach. There is a lot of mathematical software that assists researchers in obtaining the numerical solution of differential equations by a set of algorithms. Among the numerous available numerical approaches, the Differential quadrature method (DQM) is a higher-order method proposed by Bellman and Casti [23] that provides accurate results with a smaller number of grid points by discretization of the domain. One of the important characteristics of the DQM is the basis functions. Different forms of basis functions have been successfully employed to find the underlying weighting coefficients to obtain the solution [24,25].

Consider the distribution of domain x∈[a,b] as a=x1<x2<⋯<xN=b with N number of grid points. If u(x,t) is a smooth function over the solution domain, it’s rth derivative with respect to x at a grid point xi can be approximated by a linear summation of all the functional values evaluated using weighing coefficients wij(r) as follows:

d(r)udx(r)|xi=∑j=1N⁡wi,j(r)u(xj),i=1,2,…,N,r=1,2,…,N−1. (2)

2.2 Exponential B-Spline Basis Function

In the last few years, the B-Spline basis functions have been used in their different forms successfully in DQM to obtain numerical solutions to differential equations [25,26]. These functions are very popular because of the properties of continuity, compact support, orthogonality, and capability to handle the local phenomenon. B-spline functions of standard [27] and trigonometric forms [27] are successfully implemented to solve the well-known differential equations but the work reported in the literature using the exponential form of B-spline is less because of the involved parameter, whose value is taken as a hit and trial for reducing the errors [28,29].

As known the exponential B-spline functions are the generalization of the polynomial B-splines with a free parameter. The exponential B-spline of the third degree can be defined as follows [30]:

Bm(x)=1h3{β2(xm−2−x)−β2ω(sinh(ω(xm−2−x))),xε[xm−2,xm−1]α1+β1(xm−x)+γ1eω(xm−x)+δ1e−ω(xm−x),xε[xm−1,xm]α1+β1(x−xm)+γ1eω(x−xm)+δ1e−ω(x−xm),xε[xm,xm+1]β2(x−xm+2)−β2ω(sinh(ω(x−xm+2))),xε[xm+1,xm+2] (3)

here h is the uniform space partition and other parameters are reported as:

α1=ωhcωhc−s,β1=ω2(c(c−1)+s2(ωhc−s)(1−c)),β2=ω2(ωhc−s),γ1=14((1−c+s)e−ωh−s(ωhc−s)(1−c)),

δ1=14((−1+c+s)eωh−s(ωhc−s)(1−c)),c=cosh(ωh),s=sinh(ωh).

The numerical values of the function and the derivatives at nodal point can be obtained as:

Bm(xm−1)=Bm(xm+1)=s−ωh2(ωhc−s);Bm(xm)=1

Bm′(xm−1)=ω(c−1)2(ωhc−s);Bm′(xm+1)=ω(1−c)2(ωhc−s);Bm′(xm)=0

Bm′′(xm−1)=Bm′′(xm+1)=ω2s2(ωhc−s);Bm′′(xm)=−ω2s(ωhc−s)

Further before implementation of the basis function, it is modified at the boundary mesh points to satisfy the condition of a diagonally dominant matrix as follows

M1(x)=B1(x)+2B0(x),M2(x)=B2(x)−B0(x),

Mk(x)=Bk(x)fork=3,4,…,N−2,(5)

MN−1(x)=BN−1(x)−BN+1(x),MN(x)=BN(x)+2BN+1(x),

2.3 Particle Swarm Optimization Algorithm

Particle swarm optimization (PSO) algorithm is developed on the communal actions of birds in searching for food [31,32]. In this algorithm, particles are entities whose routine is measured by their locations. Each location presents a part of the solution that needs to be optimized. The search process is driven by changing particle’s velocity and positions at every time step. In the swarm, position of each particle is a solution in D-dimensional space. The updating rules for velocity and position of each particle is given by

vidt+1=χ[vidt+c1r1(pidt−xidt)+c2r2(pgdt−xidt)] (4)

xidt+1=xidt+vidt+1 (5)

where, xidt , represents c particle’s position and vidt represents ith particle’s velocity in d dimension at time step t, pgd represents the particle having the best fitness value, pid is the particle’s best position visited so far, c1,c2 are acceleration coefficients which quantifies particle personal and global experience respectively, χ is called constriction coefficient which evaluates a value in the range [0, 1] and is given by

χ=2κ|2−φ−φ(φ−4)|

With φ=φ1+φ2,φ1=c1r1,φ2=c2r2 and κ≈1 .

To start with the parameter optimization the first step is to initialize the parameter by assigning random positions to the particles in the defined range. The next step is to randomly assign velocity for all particles. After this, the values of the function are evaluated for the particles and then the information is collected from the particles regarding their updated values and the velocity and position are again updated to search for the global optimum value. The working of PSO is shown below by the algorithm.

The solution thus obtained by the implementation of the approach is reliable as it is being searched for the number of iterations with the selected number of parameters with a predetermined population size. This approach has been successfully implemented in calculating the solution of equations using radial basis functions [31]. The parameters considered here are as: swarm size: 20; maximum iterations: 50; inertia weight is linearly decreased and social and cognitive coefficients are taken as c1=c2=2.05 . Some recent and interesting studies on the theory, parameters and application of PSO are presented in [33–35].

In the present work selection of the value of the parameter in the basis function rests on certain factors such as the degree of the function, the number of knot points and the precision of computations. It plays a vital role in the accuracy of numerical methods. The objective of this study is to obtain the parameter based on the optimization of the L∞ error.

2.4 The Scheme’s Implementation

To solve the SG equation a transformation ut=v is used to reduce the equation in the following system of differential equations:

ut=v

vt+αv=βuxx+η(x)sin(u)

Substituting the approximations of the space derivatives using the DQM with exponential B-Spline basis functions results in an ordinary differential equation (ODE) that can be solved by any appropriate numerical method. Once the solutions are obtained for the equation with the known initial condition, then after the PSO technique is implemented to reduce the obtained error by comparing the numerical and exact solutions to minimize the errors. Once the value of the parameter is obtained for the minimum error, numerical results can be calculated on predefined domain and time intervals.

The numerical scheme can be summarized and visualized as follows: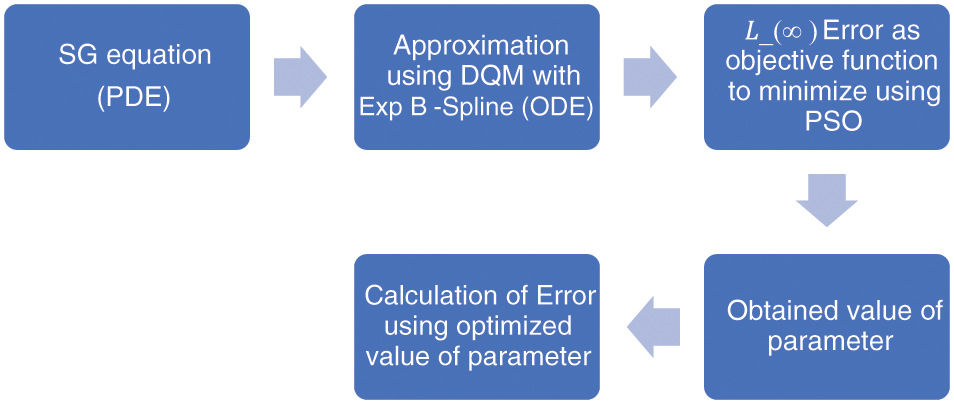

3  Numerical Observations

The Sine-Gordon equation has been solved numerically for two different problems to authenticate the effectiveness and precision of the proposed method by computing the errors.

Example 1:

The numerical solutions of Sine-Gordon equation are obtained in the computational domain x∈[−3,3] for α=0,β=1 and η(x)=−1 with initial conditions:

ϕ1(x)=4tan−1(exp(γx))

and

ϕ2(x)=−2γexp(γx)1+exp(2γx)

The boundary conditions are computed from the exact solution given as:

u(x,t)=4tan−1(exp(γx−0.5t))

Here γ is a parameter that depends on velocity of solitary wave given as:

γ=1√(1−c2)

For numerical computation, c is taken as 0.5 with the time step as k=0.0001 and space step size is h=0.02 and 0.04 compared with results as reported in the literature [16,21,36]. The number of iteration used in the PSO is 50. As presented in Tab. 1, the results show the efficiency of the present approach as compared to that available in the literature for the parameter ω  = 0.5579.

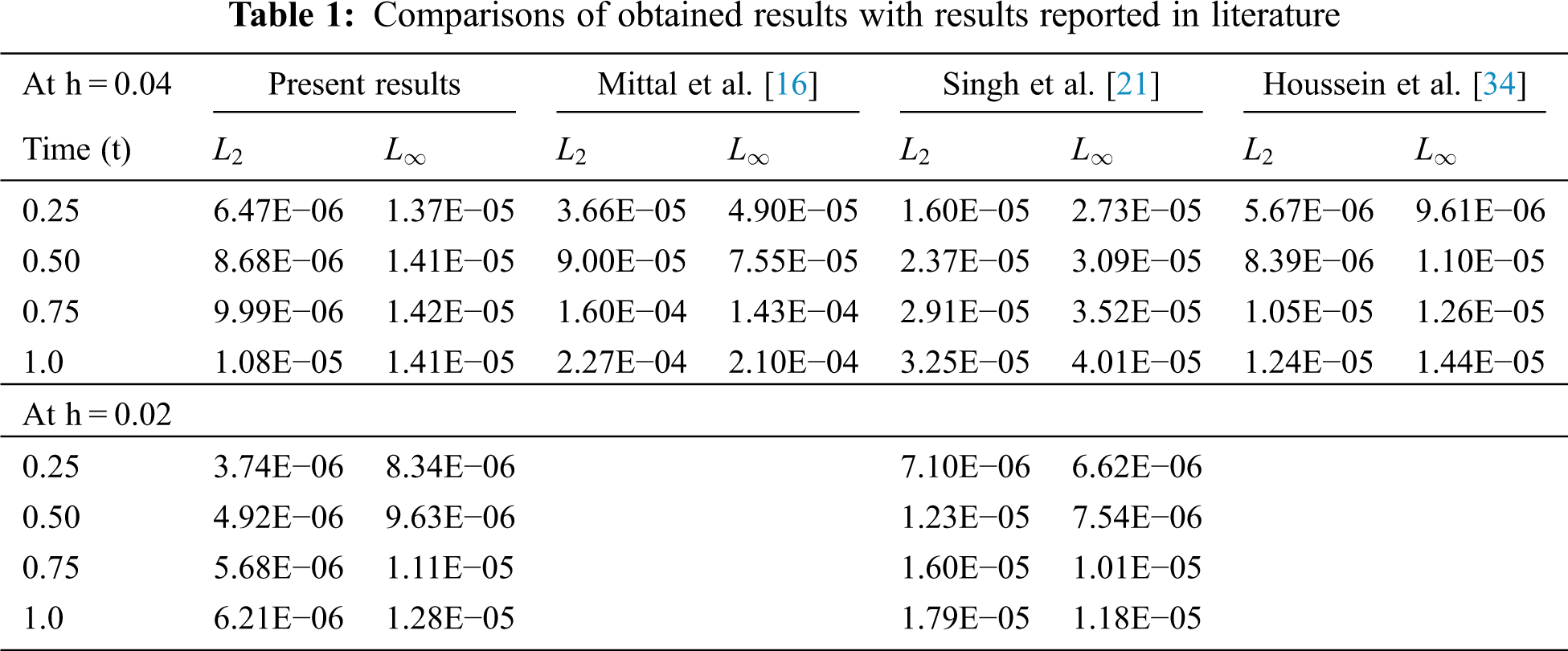
It can be concluded that obtained results are in good agreement and even superior as compared to results given by other researchers. The program is created and compiled on MATLAB 2014b on Intel Processor 64 bit, the CPU time for the algorithm is presented in Tab. 2. Numerical and the exact solutions are also depicted in the Fig. 1 at different time levels.

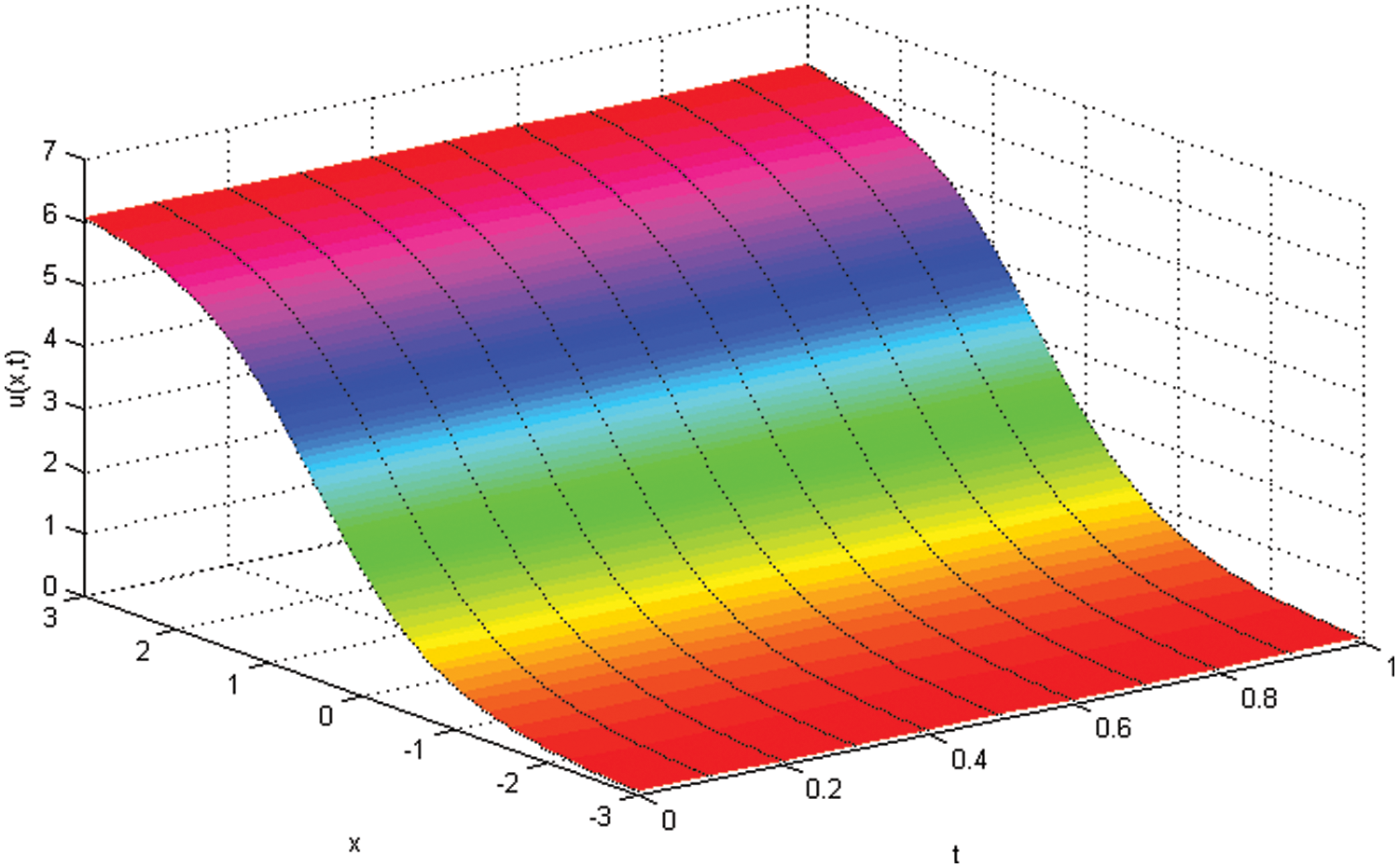
Figure 1: Physical profile of the SG equation example 1

Example 2:

Another example of Sine-Gordon equation to validate the algorithm is considered with x∈[−20,20] for α=0,β=1 and η(x)=−1 with initial conditions:

ϕ1(x)=4tan−1(csinh⁡(γx))

and

ϕ2(x)=0

Here,

γ=1√(1−c2)

The boundary conditions are computed from the exact solution given as:

u(x,t)=4tan−1(csinh⁡(γx) sech(γct))

The results are calculated at c=0.5,k=0.001 and number of node points as N=300 . From the results given in Tab. 3 it can be seen that the present approach is efficiency and is comparable to results in literature for the parameter ω  = 1. The results are obtained for 1oo iterations with 5 as particle swarm size. To validate the obtained results the errors are presented and compared with results given in the literature [16,37]. To present the behavior of the solution the results are presented at various time in Figs. 2–5. A three-dimensional plot is given to showcase the behavior for time 1≤t≤20.

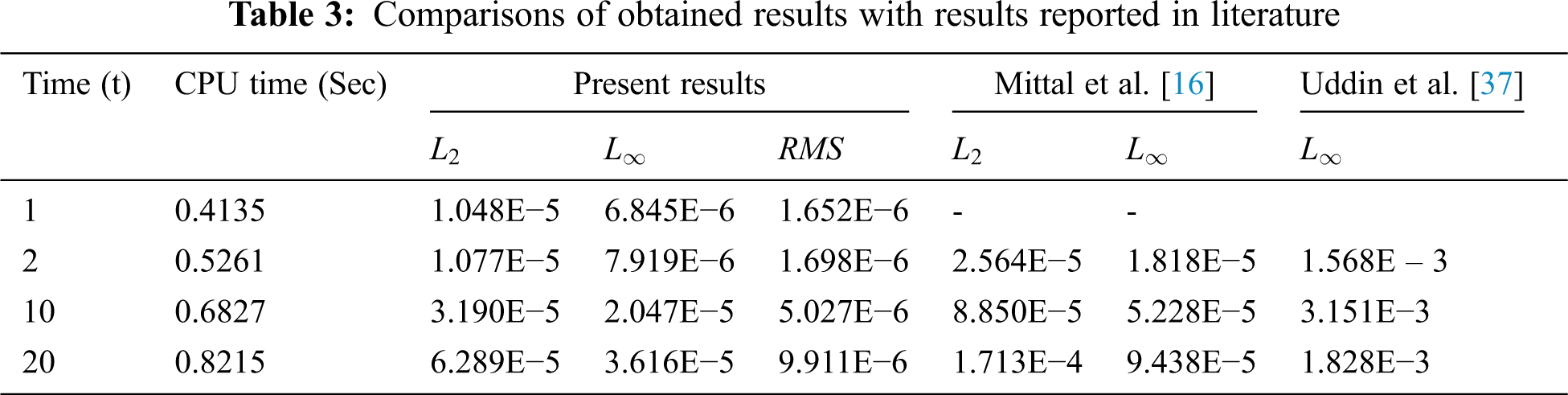
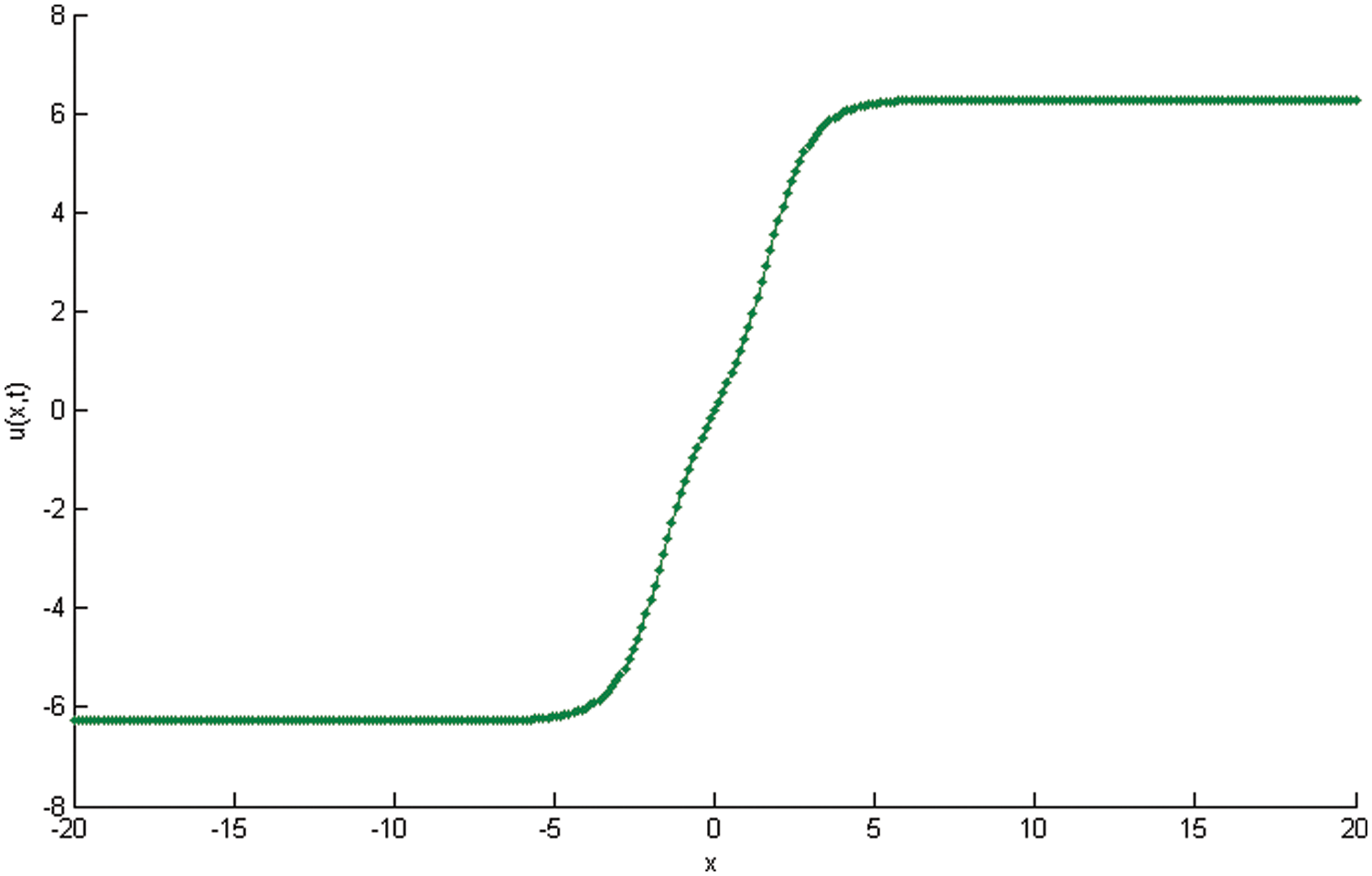
Figure 2: Physical profile of the SG equation example 2 at t = 2

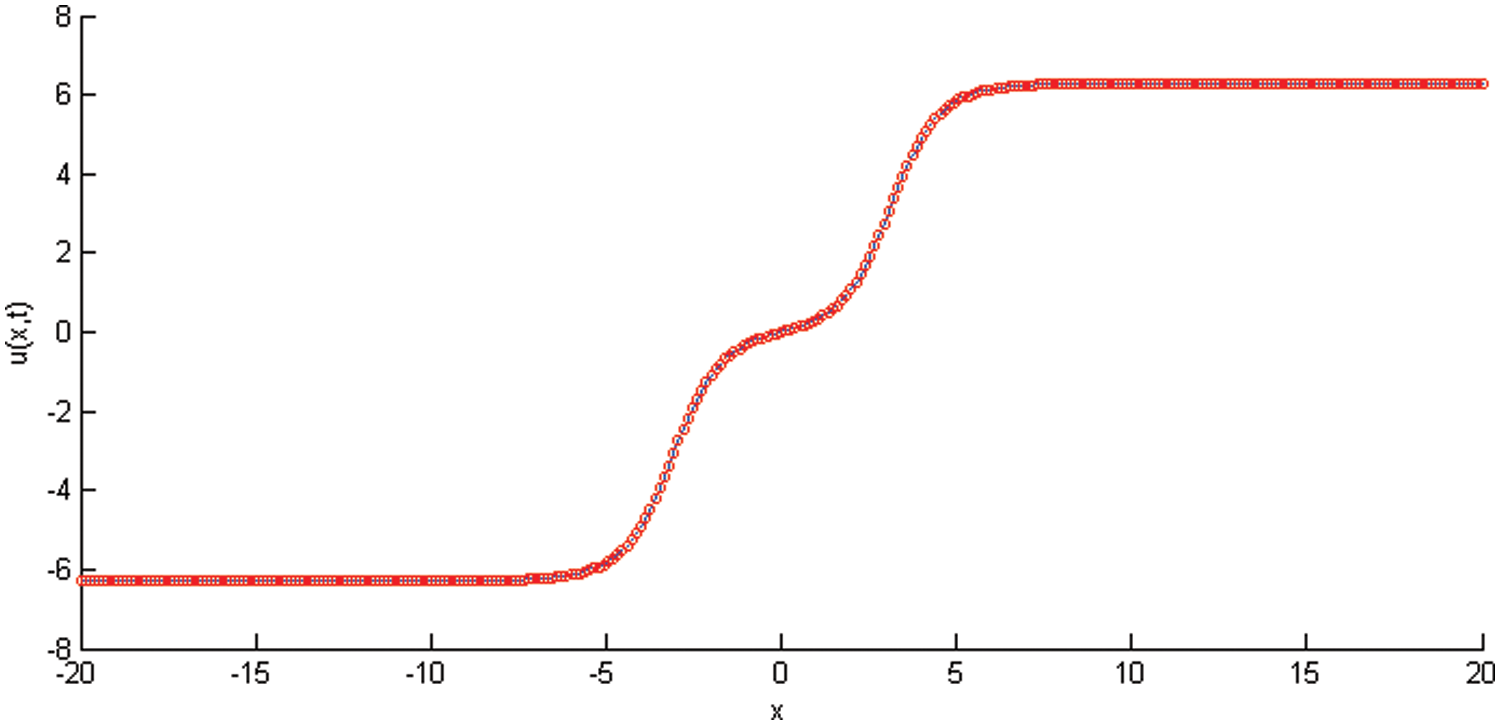
Figure 3: Physical profile of the SG equation example 2 at t = 5

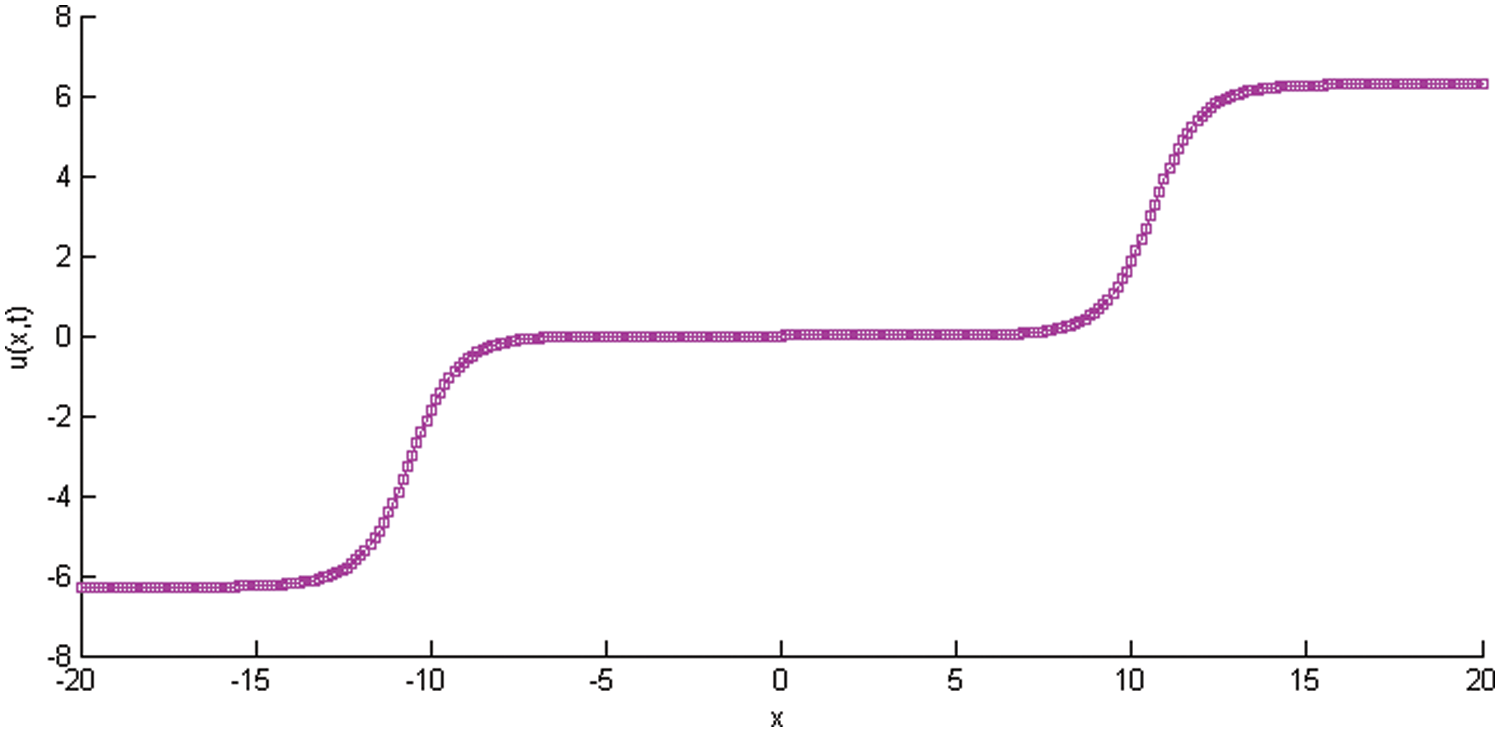
Figure 4: Physical profile of the SG equation example 2 at t = 20

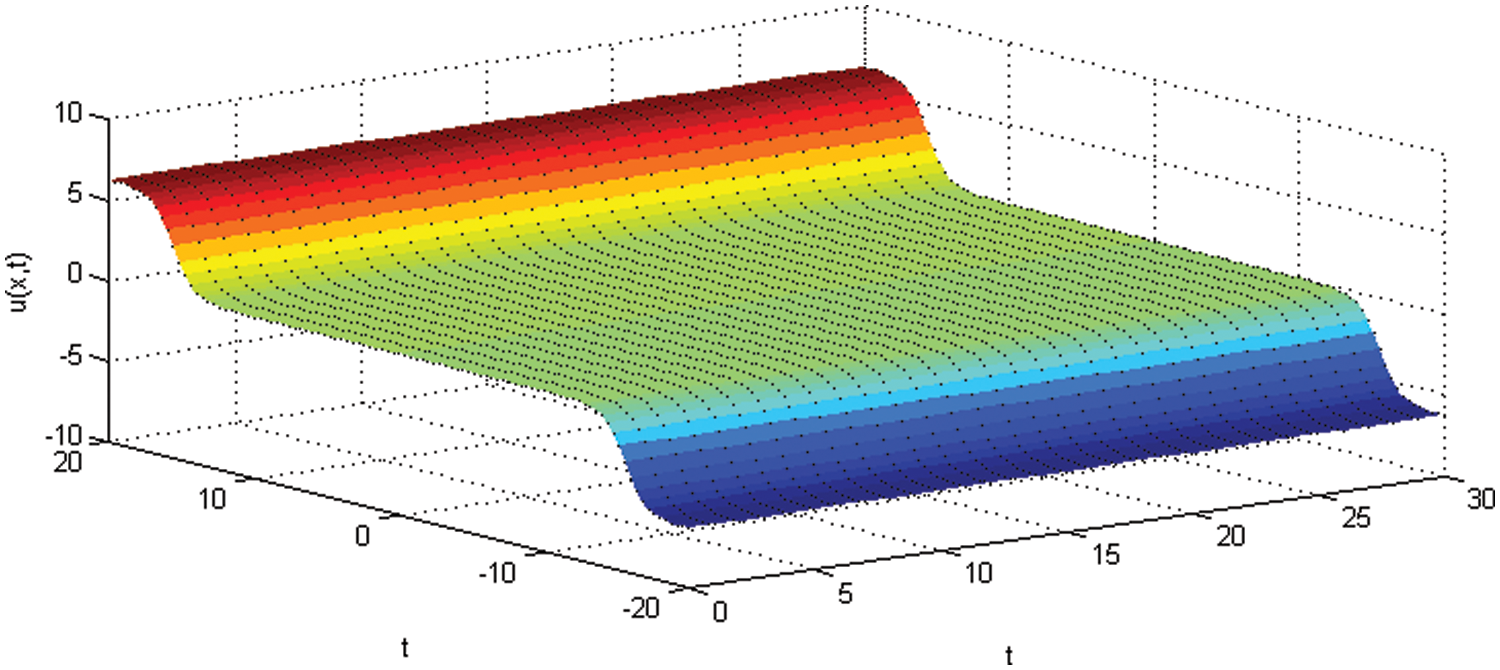
Figure 5: Physical profile of the SG equation example 2 at t = 2

4  Conclusion

Inspired by the success of PSO in optimization tasks, this approach is implemented to obtain an optimal value of the parameter involved in the exponential B-spline basis function to solve the SG equation. The advantage of PSO is to find the parameter value that aids in reducing the error involved in the function evaluations. The PSO-based method is capable of evaluating the parameter in a search space with global search ability. The obtained results are found encouraging and the scheme can be implemented to solve linear and nonlinear partial differential equations efficiently.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Kennedy and R. C. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]

 2.  T. Povich and J. Xin, “A numerical study of the light bullets interaction in the (2 + 1) Sine-Gordon equation,” Journal of Nonlinear Science, vol. 15, no. 1, pp. 11–25, 2005. [Google Scholar]

 3.  L. D. M. Villari, G. Marcucci, M. C. Braidotti and C. Conti, “Sine-Gordon soliton as a model for hawking radiation of moving black holes and quantum soliton evaporation,” Journal of Physics Communications, vol. 2, no. 55016, pp. 1–10, 2018. [Google Scholar]

 4.  V. G. Bykov, “Sine-Gordon equation and its application to tectonic stress transfer,” Journal of Seismology, vol. 18, no. 3, pp. 497–510, 2014. [Google Scholar]

 5.  G. Ben-Yu, P. J. Pascual, M. J. Rodriguez and L. V´azquez, “Numerical solution of the Sine-Gordon equation,” Applied Mathematics and Computation, vol. 18, no. 1, pp. 1–14, 1986. [Google Scholar]

 6.  M. J. Ablowitz, B. M. Herbst and C. M. Schober, “On the numerical solution of the Sine-Gordon equation, I. Integrable discretization and homoclinic manifolds,” Journal of Computational Physics, vol. 126, no. 2, pp. 299–314, 1996. [Google Scholar]

 7.  M. J. Ablowitz, B. M. Herbst and C. M. Schober, “On the numerical solution of the Sine-Gordon equation. II. Performance of numerical schemes,” Journal of Computational Physics, vol. 131, no. 2, pp. 354–367, 1997. [Google Scholar]

 8.  D. Kaya, “An application of the modified decomposition method for two dimensional Sine-Gordon equation,” Applied Mathematics and Computation, vol. 159, no. 1, pp. 1–9, 2004. [Google Scholar]

 9.  S. S. Ray, “A numerical solution of the coupled Sine-Gordon equation using the modified decomposition method,” Applied Mathematics and Computation, vol. 175, no. 2, pp. 1046–1054, 2006. [Google Scholar]

10. Q. Wang, “An application of the modified adomian decomposition method for (N + 1)-dimensional Sine-Gordon field,” Applied Mathematics and Computation, vol. 181, no. 1, pp. 147–152, 2006. [Google Scholar]

11. U. Yucel, “Homotopy analysis method for the Sine-Gordon equation with initial conditions,” Applied Mathematics and Computation, vol. 203, no. 1, pp. 387–395, 2008. [Google Scholar]

12. M. Dehghan and D. Mirzaei, “The dual reciprocity boundary element method (DRBEM) for two-dimensional Sine-Gordon equation,” Computer Methods in Applied Mechanics and Engineering, vol. 197, no. 6–8, pp. 476–486, 2008. [Google Scholar]

13. M. Dehghan and A. Shokri, “A numerical method for one dimensional nonlinear Sine-Gordon equation using collocation and radial basis functions,” Numerical Methods for Partial Differential Equations, vol. 24, no. 2, pp. 687–698, 2008. [Google Scholar]

14. M. Sari and G. Gurarslan, “A sixth-order compact finite difference method for the one-dimensional Sine-Gordon equation,” International Journal for Numerical Methods in Biomedical Engineering, vol. 27, no. 7, pp. 1126–1138, 2011. [Google Scholar]

15. J. Rashidinia and R. Mohammadi, “Tension spline solution of nonlinear Sine-Gordon equation,” Numerical Algorithms, vol. 56, no. 1, pp. 129–142, 2011. [Google Scholar]

16. R. C. Mittal and R. Bhatia, “Numerical solution of nonlinear Sine-Gordon equation by modified cubic B-spline collocation method,” International Journal of Partial Differential Equations, vol. 2014, pp. 1–8, 2014. [Google Scholar]

17. L. Su, “Numerical solution of two-dimensional nonlinear Sine-Gordon equation using localized method of approximate particular solutions,” Engineering Analysis with Boundary Elements, vol. 108, no. 2, pp. 95–107, 2019. [Google Scholar]

18. M. Lotfi and A. Alipanah, “Legendre spectral element method for solving Sine-Gordon equation,” Advances in Difference Equations, vol. 2019, no. 1, pp. 1–15, 2019. [Google Scholar]

19. D. Adak and S. Natarajan, “Virtual element method for semi linear Sine–Gordon equation over polygonal mesh using product approximation technique,” Mathematics and Computers in Simulation, vol. 172, pp. 224–243, 2020. [Google Scholar]

20. R. Jiwari, “Barycentric rational interpolation and local radial basis functions based numerical algorithms for multidimensional Sine-Gordon equation,” Numerical Methods for Partial Differential Equations, vol. 37, no. 3, pp. 1965–1992, 2021. [Google Scholar]

21. B. K., Singh and M. A. Gupta, “New efficient fourth order collocation scheme for solving sine–Gordon equation,” International Journal of Applied and Computational Mathematics, vol. 7, no. 4, pp. 1–18, 2021. [Google Scholar]

22. M. Shiralizadeh, A. Alipanah and M. Mohammadi, “Numerical solution of one-dimensional Sine-Gordon equation using rational radial basis functions,” Journal of Mathematical Modeling, Article in press, pp. 1–19, 2021. [Google Scholar]

23. R. Bellman, B. G. Kashef and J. Casti, “Differential quadrature: A technique for the rapid solution of nonlinear differential equations,” Journal of Computational Physics, vol. 10, no. 1, pp. 40–52, 1972. [Google Scholar]

24. G. Arora and V. Joshi, “A computational approach for one and two dimensional fisher’s equation using quadrature technique,” American Journal of Mathematical and Management Sciences, vol. 40, no. 2, pp. 145–162, 2021. [Google Scholar]

25. G. Arora and B. K. Singh, “Numerical solution of burgers’ equation with modified cubic B-spline differential quadrature method,” Applied Mathematics and Computation, vol. 224, pp. 166–177, 2013. [Google Scholar]

26. P. Devshali and G. Arora, “Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method,” Nonlinear Engineering, vol. 11, no. 1, pp. 135–142, 2022. [Google Scholar]

27. R. C. Mittal and G. Arora, “Efficient numerical solution of fisher’s equation by using B-spline method,” International Journal of Computer Mathematics, vol. 87, no. 13, pp. 3039–3051, 2010. [Google Scholar]

28. W. Imtiaz, A. Muhammad, I. M. Kashif and H. A. Mubashir, “Exponential B-spline collocation method for solving the generalized Newell-Whitehead-Segel equation,” Journal of Mathematics and Computer Science, vol. 20, no. 4, pp. 313–324, 2020. [Google Scholar]

29. M. Reza, “Exponential B-spline collocation method for numerical solution of the generalized regularized long wave equation,” Chinese Physics B, vol. 24, no. 5, pp. 050206, 2015. [Google Scholar]

30. I. Dag and O. Ersoy, “The exponential cubic B-spline algorithm for Fisher equation,” Chaos, Solitons and Fractals, vol. 86, pp. 101–106, 2016. [Google Scholar]

31. J. A. Koupaei, M. Firouznia and S. M. Hosseini, “Finding a good shape parameter of RBF to solve PDEs based on the particle swarm optimization algorithm,” Alexandria Engineering Journal, vol. 57, no. 4, pp. 3641–3652, 2018. [Google Scholar]

32. J. Kennedy, “The particle swarm: Social adaptation of knowledge,” in Proc. of IEEE Int. Conf. on Evolutionary Computation, Indianapolis, IN, USA, pp. 303–308, 1997. [Google Scholar]

33. Y. Belkourchia, L. Azrar and E. M. Zeriab, “Hybrid optimization procedure applied to optimal location finding for piezoelectric actuators and sensors for active vibration control,” Applied Mathematical Modelling, vol. 62, pp. 701–716, 2018. [Google Scholar]

34. E. H. Houssein, A. G. Gad, K. Hussain and P. N. Suganthan, “Major advances in particle swarm optimization: Theory, analysis, and application,” Swarm and Evolutionary Computation, vol. 63, pp. 100868, 2021. [Google Scholar]

35. A. P. Piotrowski, J. J. Napiorkowski and A. E. Piotrowska, “Population size in particle swarm optimization,” Swarm and Evolutionary Computation, vol. 58, pp. 100718, 2020. [Google Scholar]

36. H. S. Shukla and M. Tamsir, “Numerical solution of nonlinear sine–Gordon equation by using the modified cubic B-spline differential quadrature method,” Beni-Suef University Journal of Basic and Applied Sciences, vol. 7, no. 4, pp. 359–366, 2018. [Google Scholar]

37. M. Uddin, S. Haqand and G. Qasim, “A meshfree approach for the numerical solution of nonlinear Sine-Gordon equation,” International Mathematical Forum, vol. 7, no. 24, pp. 1179–1186, 2012. [Google Scholar]