Small-World Networks with Unitary Cayley Graphs for Various Energy Generation

1  Introduction

Complex networks have recently gained popularity in a variety of disciplines and research areas. The Internet has altered the way we deal with everything in our daily lives. Computer experts were fascinated by the idea of mastering the wheel of controlling the Internet’s complexity and massive expansion. The data magnitude of social networks is unpredictable and unmanageable by social scientists. The biological interactions that characterize a cell metabolism are believed to establish its pathways and supply biologists with information [1]. To be able to manage networks before networks manipulate our needs, new science is required [2].

The small-world phenomenon has recently become a hot area of theoretical and practical research, attracting the attention of multidisciplinary academics. “Short chains of acquaintances” or “six degrees of separation” are synonymous with the term “small world.” [3,4] refers to the graph of a human social network, in which nodes replace people and edges between nodes simulate if the two matching people know each other by first name [5]. Because any two random pairs of nodes are separated by a small number of nodes, usually less than 6, the graph is known as a “small world.” Although the first-name basis criterion for edge definition is just a little naive, the resulting graph acts as a real-world network.

Because of the adoption of the constraints of either of the end extreme network types, random networks and regular lattices, small-world networks are extremely important. Small-world networks have shown that they can be utilized as frameworks for studying complex system interaction networks [6]. The most significant goal of the small-world study is to confirm the notion that all networks have a qualitatively similar structure across different areas. Although nodes in the network exhibit a high degree of clustering, a common aspect of vast networks is the existence of short pathways between most node pairs. Nodes can be reached and navigated without requiring a comprehensive of the entire network. Such qualities aided in the description of large-scale social network behaviour, as well as providing vital insights into the internal architecture of decentralized peer-to-peer systems.

The main contribution of this research, works a new small world network-based unitary Cayley graphs is proposed to design and analyse the communication of the network and also it reduces the delay and gives better reliability. The remainder of the research is organized as follows: Section 2 shows the connected research efforts as well as the research work basis. The explained various energy generation theorems in Section 3. Section 4 clearly illustrates the proposed small world network-based unitary Cayley graph. Section 5 shows the result and discussion of the small-world network. Section 6 depicts the conclusion.

2  Literature Survey

This section explains various surveys related to small-world networks studied throughout the years. The present state of the small-world network is discussed and an overview is provided in this study.

Baysal et al. [7] presented the autapse effects on the chaotic resonance (CR) phenomena in single neurons and small world neural networks. When the autaptic delay time matches the half period signal, the multiple CR develops when the autaptic time delay for ideal chaotic current. The autapse considerably improves the chaotic resonance of the suitable autaptic values, according to the results. Dhaya et al. [8] presented the topology of the deep learning (DL) design is changed in such a way that optimal cross-layer connection is achieved. This modification takes advantage of our crucial insight that a Small-World Network’s topology crosses the border convergence is fastest for a given level of accuracy. The results show that the proposed strategy is both accurate and quick to respond to for training.

Qiu et al. [9] presented a data propagation strategy with the small world characteristics used for data transfer in IoV. As the hop distance decreases, the time required to disseminate a message decrease. The suggested methodology has a low average data packet delay, according to simulation results. Furthermore, because of the increased robustness, the packet delivery ratio is higher. Pandey et al. [10] presented the small-world network for data transfer with minimal latency and energy balance based on a wireless sensor network. The average path length of a small world wireless sensor network (SW-WSN) is short, and the average clustering coefficient is large. The suggested small world network accomplishes power exchanging, boosts the network, increases power economy as well as minimises data, according to experimental outcomes.

Qi et al. [11] presented the small-world network is linked to decreased alert attention after total sleep deprivation. The findings show that topological features of networks are disturbed, and that abnormal temporal and salience network topology may operate as neural markers underpinning vigilant attention problems following total sleep deprivation (TSD). Gu et al. [12] presented the small-world network model to explain how a small-world network with a select group of people. The addition of theories boosted the network model prediction capacity greatly, it helped to reveal factors which influence an establishment of a small-world industrial network focused on exclusive groups.

3  Various Energy Generation

The various energies generations are Seidel matrix, Seidel Signless Laplacian matrix, Seidel energy, Seidel Signless Laplacian energy, Maximum and Minimum energy, Degree Sum energy and Distance Degree energy of the Unitary Cayley graph have been calculated.

3.1 Seidel Energy of UnitaryCayleyGraphXn

Here, [13] we obtain Seidel eigenvalues and Seidel energy of Xn .

The Seidel matrix SM(Xn)=(sij) of a UnitaryCayleygraph Xn on n vertices and nϕ(n)2 edges is a real symmetric matrix as

sij={−1if viandvjareadjacentvertices1if viandvjarenotadjacentvertices0elsewhere (1)

Let s1 , s2 ,…, sn be the eigenvalues of SM(Xn) .The Seidel energy of Xn is defined as

SE(Xn)=∑i=1n⁡|si| .

Theorem 1: The Seidel eigenvalues of the UnitaryCayleygraph Xn are n−1−2ϕ(n) and

−1−2ϕ(n)μ(ti)ϕ(ti),1≤i≤n−1 where ti=ngcd(i,n) .

Also, the Seidel energy SE(Xn) is |n−1−2ϕ(n)|+∑i=1n−1⁡|1+2ϕ(n)μ(ti)ϕ(ti)| .

Proof: The Seidel matrix SM(Xn)=A(Xn)¯−A(Xn) , where A(Xn¯) is the adjacency matrix of the

complement of UCG Xn.

The eigenvalues of Xn are ϕ(n)μ(ti)ϕ(ti),0≤i≤n−1 , where ti=ngcd(i,n) .

Let η0≥η1≥,…,≥ηn−1 be the eigenvalues of Xn .

Let η0 = ϕ(n) .

The eigenvalues of the complement of the UCG Xn¯ are n−1−η0 , −1−η1 , −1−η2 …, −1−ηn−1 .

Hence the eigenvalues of SM(Xn) are n−1−2ϕ(n) and −1−2ϕ(n)μ(ti)ϕ(ti),1≤i≤n−1

TheSeidelenergyofXn isSE(Xn)=∑i=0n−1⁡|ηi| (2)

=|η0|+∑i=1n−1⁡|ηi| (3)

=|(n−1)−2ϕ(n)|+∑i=1n−1⁡|−1−2ϕ(n)μ(ti)ϕ(ti)| (4)

=|n−1−2ϕ(n)|+∑i=1n−1⁡|1+2ϕ(n)μ(ti)ϕ(ti)| (5)

3.2 Seidel Signless Laplacian Energy of UCG Xn

The Seidel matrix of UnitaryCayleygraphXn on n vertices and nϕ(n)2 edges are S(Xn) .

Let DS(Xn)=diag(n−1−2ϕ(n),n−1−2ϕ(n),…,n−1−2ϕ(n)) be the diagonal matrix.

The Seidel Signless Laplacian matrix SSLM(Xn)=DS(Xn)+S(Xn) of a UnitaryCayleyGraph Xn on n vertices and nϕ(n)2 edge is a real symmetric matrix defined as [14]:

aij={−1ifi≠jandvi,vjareadjacent1ifi≠jandvi,vjarenotadjacentn−1−2ϕ(n)ifi=j (6)

Let σ0 , σ1 ,…, σn−1 be the eigenvalues of SSLM(Xn) . The spectrum of the SSLM(Xn) is the set of

its eigenvalues together with their multiplicities.

The Seidel Signless Laplacian energy of Xn is defined as SSLE(Xn)=∑i=0n−1⁡|σi+2ϕ(n)−n+1|.

Theorem 2: Seidel Signless Laplacian eigenvalues of the UnitaryCayleyGraph Xn are 2( −1−2ϕ(n)) and n−2−2ϕ(n)(1+μ(ti)ϕ(ti)),1≤i≤n−1 where ti=ngcd(i,n) . Also, the Seidel Signless Laplacian energy SSLE(Xn) is |n−1−2ϕ(n)|+∑i=1n−1⁡|1+2ϕ(n)μ(ti)ϕ(ti)| .

Proof: The Seidel Signless Laplacian matrix SSLM(Xn)=DS(Xn)+S(Xn) where S(Xn) is the Seidel matrix of UCG Xn . DS(Xn)=diag(n−1−2ϕ(n),n−1−2ϕ(n),…,n−1−2ϕ(n)) is a diagonal matrix.

The eigenvalues of Xn are ϕ(n)μ(ti)ϕ(ti),0≤i≤n−1 , where ti=ngcd(i,n) .

The eigenvalues of DS(Xn) are n−1−2ϕ(n) (n times).

The Seidel Signless Laplacian energy of Xn is

SSLE(Xn)=∑i=0n−1⁡|σi+2ϕ(n)−(n−1)| (7)

=|n−1−2ϕ(n)|+∑i=1n−1⁡|1+2ϕ(n)μ(ti)ϕ(ti)|. (8)

3.3 Maximum Degree Energy of UCG Xn

The Maximum Degree of energy of UCG Xn is the sum of the absolute eigenvalues of the Maximum

Degree matrix, [15] where Maximum Degree matrix MDM(Xn)=(mij) of a UnitaryCayleyGraph Xn on n vertices and nϕ(n)2 edge is a real symmetric matrix as

mij={ max(di,dj) if vi,vj are adjacent  0      elsewhere

where di,dj are the degree of vertices vi and vj .

Theorem 3: The Maximum degree energy of UnitaryCayleyGraph Xn is 2ϕ(n)(n−1).

Proof: The Maximum degree matrix of Xn is

MDM(Xn)=(0ϕ(n)ϕ(n)…ϕ(n)ϕ(n)0ϕ(n)…ϕ(n)⋮⋮⋮⋮⋮ϕ(n)ϕ(n)ϕ(n)…0)n×n (9)

=ϕ(n)(011…1101…1⋮⋮⋮⋮⋮111…0) (10)

=ϕ(n)[(111…1111…1⋮⋮⋮⋮⋮111…1)−(100…0010…0⋮⋮⋮⋮⋮000…1)] (11)

=ϕ(n)(Jn−In) (12)

The spectrum of Jn is (0nn−11) . The spectrum of In is (1n) .

Hence the spectrum of (Xn ) is ϕ(n)(−1n−1n−11) .

The Maximum Degree of energy of UCG Xn is 2ϕ(n)(n−1).

3.4 Minimum Degree Energy of UCG

The Minimum Degree of energy of UCG Xn is the sum of the absolute eigenvalues of the Minimum Degree matrix [16], where the Minimum Degree matrix Min(Xn)=(mij) of a UnitaryCayleyGraph Xn on n vertices and nϕ(n)2 edges is a real symmetric matrix as

mij={ max(di,dj) if vi,vj are adjacent  0      elsewhere where di,dj are the degree of vertices vi and vj .

Theorem 4: Minimum Degree energy of the UnitaryCayleyGraph Xn is 2ϕ(n)(n−1).

Proof: The UnitaryCayleygraph Xn is a ϕ(n) regular graph.

Therefore, the maximum degree of Xn is equal to the minimum degree. Hence the Minimum Degree

of energy of Xn is 2ϕ(n)(n−1).

3.5 Degree Sum Energy of UCG Xn

The sum of the absolute eigenvalues of the [17] Degree Sum matrix is the Degree Sum energy of UCG Xn , where the Degree Sum matrix DSM(Xn)=(mij) of a UnitaryCayleyGraph Xn on n vertices and nϕ(n)2 edge is a real symmetric matrix as {2ϕ(n)ifi≠j0elsewhere .

Theorem 5: The Degree Sum energy of UnitaryCayleyGraphXn is 4ϕ(n)(n−1).

Proof: The Degree sum matrix of Xn is

DSM(Xn)=(02ϕ(n)2ϕ(n)…2ϕ(n)2ϕ(n)02ϕ(n)…2ϕ(n)⋮⋮⋮⋮⋮2ϕ(n)2ϕ(n)2ϕ(n)…0)n×n (13)

=2ϕ(n)(011…1101…1⋮⋮⋮⋮⋮111…0) (14)

=2ϕ(n)[(111…1111…1⋮⋮⋮⋮⋮111…1)−(100…0010…0⋮⋮⋮⋮⋮000…1)] (15)

=2ϕ(n)(Jn−In) (16)

The spectrum of Jn is (0nn−11) . The spectrum of In is (1n) .

Hence the spectrum of (Xn ) is 2ϕ(n)(−1n−1n−11) .

The Degree Sum energy of UCG Xn is 4ϕ(n)(n−1).

3.6 Degree Distance Energy of UnitaryCayleyGraphs Xn

Computed distance energy of UnitaryCayleygraphs . Motivated by these papers we determine the degree of distance energy of UnitaryCayleyGraphs (UCG) [18].

The degree distance matrix of Xn , denoted by DDM(Xn) can be defined as

DDM(Xn)={(di+dj)d(vi,vj),ifvi≠vj0if vi=vj where di = degree of vi and d(vi,vj) is the shortest distance between the vertices vi and vj . Let λ1,λ2,…,λn be the degree distance eigenvalues of DDM (Xn). The degree of distance energy of Xn , DDE(Xn)=∑i=1n⁡|λi| .

Theorem 6: Let Xn be the UCG, where n is a prime number. The spectrum of a degree distance

matrix Xn is (−2(n−1)2(n−1)2n−11) . The degree of distance energy is 4(n−1)2 .

Proof: For UCG Xn , n being prime, Xn is a complete graph.

Therefore, di=degree(vi)=n−1,∀i .

d(vi,vj)=1,∀vi,vj , di+dj=degree(vi)+degree(vj) = 2 (n−1)

The degree distance matrix

DDM(Xn)=(02(n−1)2(n−1)…2(n−1)2(n−1)02(n−1)…2(n−1)⋮⋮⋮⋮⋮2(n−1)2(n−1)2(n−1)…0)n×n (17)

=2(n−1)(Jn−In) (18)

The spectrum of Jn is (0nn−11) . The spectrum of In is (1n) .

Hence the Spectrum of (Jn−In ) is (−1n−1n−11)

ThedegreeofdistanceenergyDDE(Xn)=∑i=1n⁡|λi| (19)

=|−2(n−1)|(n−1)+|2(n−1)2|×1 (20)

=2(n−1)2+2(n−1)2=4(n−1)2. (21)

4  Small-World Network Based on the Unitary Cayley Graph

Cayley graphs are well-known for being good models for computer networks with multiple connections. Cayley graphs are used to create a variety of well-known and practical connectivity networks. To begin, define a few terms and symbols. V vertices and E arcs or directed edges make up a digraph=(V,E).V×V′s elements are a subset of (u,v)E. If the subset E is symmetric, (u,v)E implies (v,u) E, the undirected edge can be used to identify two opposing arcs (u,v)and(v,u) . Assume G is a finite group with S as a subset. (This study does not address infinite groups.)

For g∈G,s∈S,Cay(G,S) is a Cayley graph of a group G and its subset S with G elements at the vertices and ordered pairs (g,gs) at the arcs. Cay (G, S) is a simple (undirected) graph if 1∉S represents the identity member of S=S−1,Cay(G,S) . It is recommended that additional concepts and fundamental outcomes on graphs and groups, as well as connectivity networks. G is a finite group; hence the clustering coefficient is 3. Consider the situation when 1∉ S,S=S−1,=Cay for some G generating set S.

Then there is a Cayley graph with constant degree d=|S|, in which each node v has precisely d neighbours, and these d neighbours have at most d(d−1)2 edges between them. As a result, the only thing we need to think about is node 1’s clustering coefficient, which is G’s identity element.

Node 1 has S neighbours. If s1,s2∈S, then s1ands2 are adjacent if and only if s2=s1s . Assume H is a subset of S and H∪1 is a subgroup of G. Then s1s2∈H when s1,s2∈H . As a result, the set S of neighbours of node 1 has at least | H|(|H|−1)/2 edges. As a result, if H can be set to a big value, the clustering coefficient will be high.

5  Experimental Results

Numerical simulations are used to examine the performance of small world network-based Unitary Cayley graphs.

Fig. 1 depicts the delay of regular node density at the various sectors. When delay increases as the number of regular nodes increases. Furthermore, the small world network-based unitary Cayley latency is reduced. The latency grows as the value increases when the regular node is fixed. The maximum delay of small world network-based Unitary Cayley graphs has been reduced by 40%, according to simulation data.

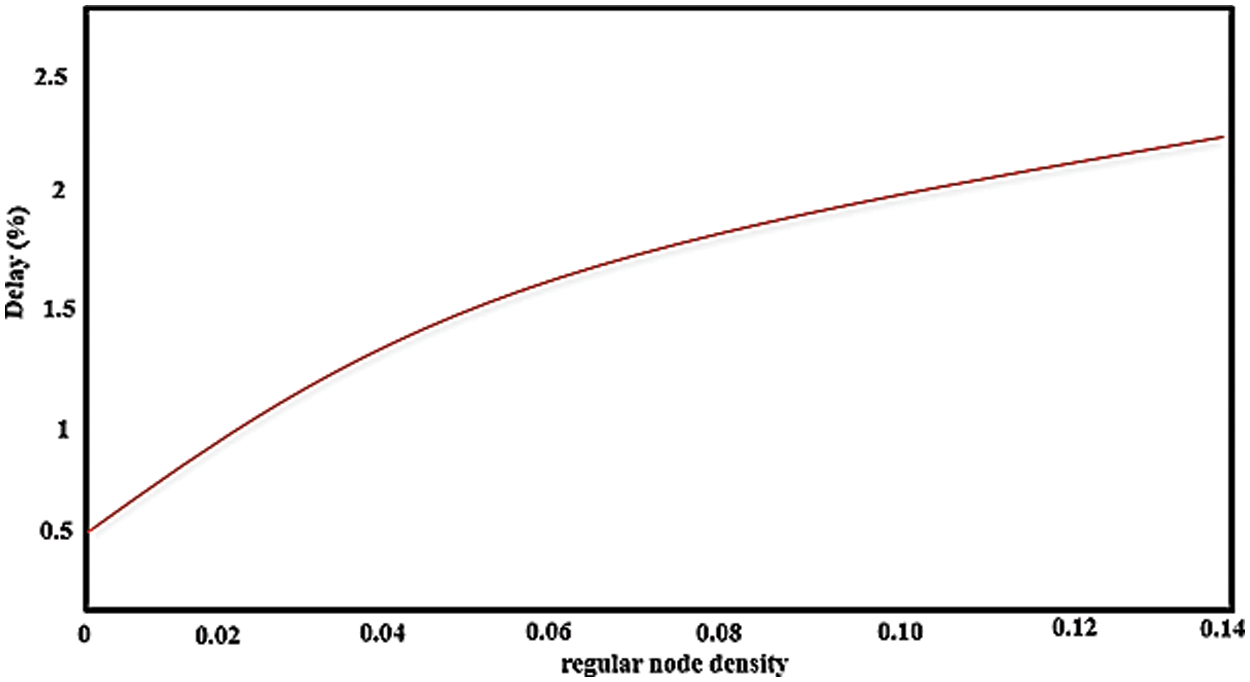
Figure 1: Delay function of regular node density in proposed small world network-based Unitary Cayley graphs

The reliability factor of a regular node with varying sectors is shown in Fig. 2. The reliability factor drops as regular node density improves. Furthermore, the small world network-based unitary Cayley has a greater reliability factor. When the regular node density is kept constant, the reliability factor drops.

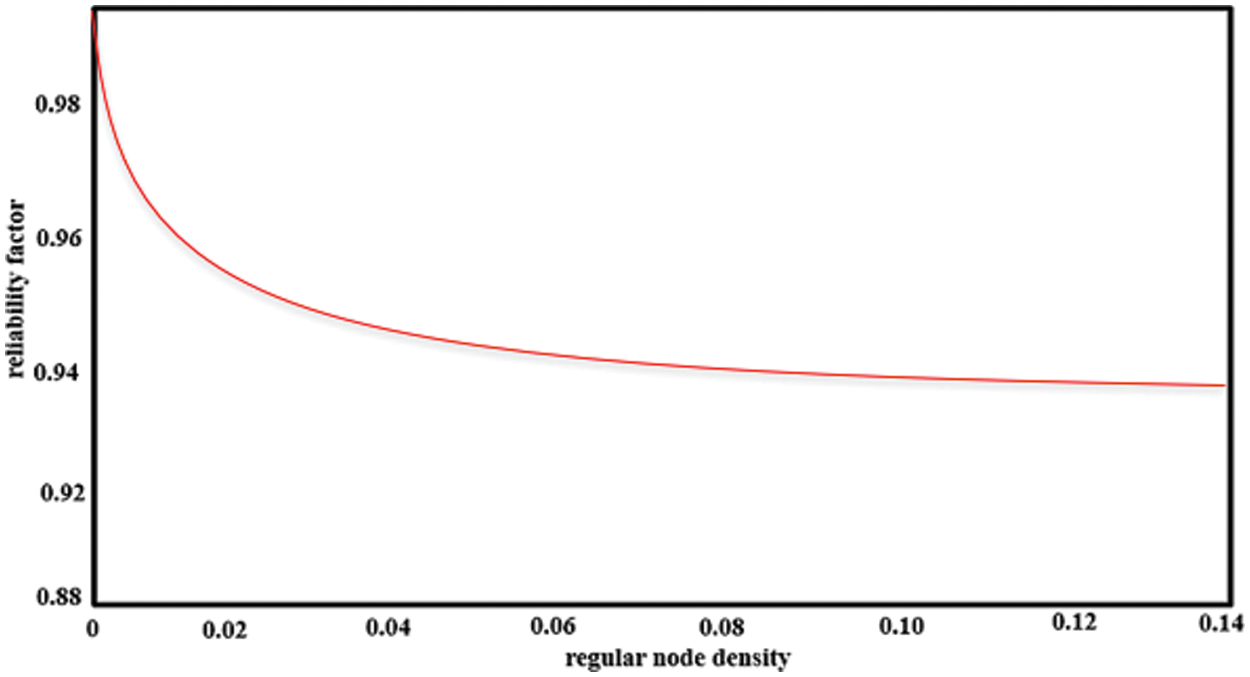
Figure 2: Reliability factor as a function of a regular node with proposed small world network-based Unitary Cayley graphs

The consensus speed and power consumption of our proposed topology control solutions were assessed. The simulations were run on 100 host graphs, each with sensors evenly and randomly spread throughout a 100 m 100 m region.

Fig. 3 depicts the consensus protocol’s energy consumption. With power model 0 and power model 1, BCG-1 used 2% less energy than BCG-0. With power model 1, BCG-1 used 2% less energy than BCG-0.

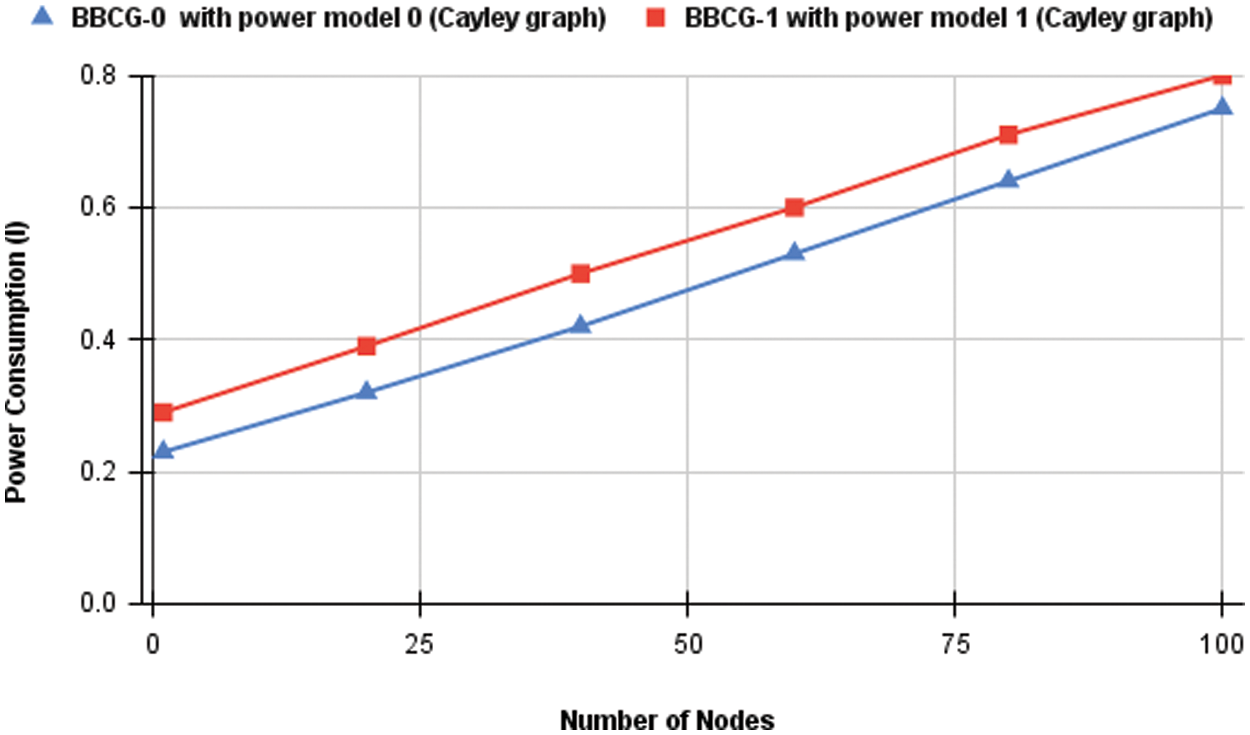
Figure 3: Power consumption

For N = 1081, the distance created by the suggested node ID assignment approaches is shown in Fig. 4. The right-skewed distribution of the CR assignment (BCG-1) histogram shows a significant frequency of short edges. All connection distances are under 80 meters, according to the Dist-swap assignment (BCG-2).

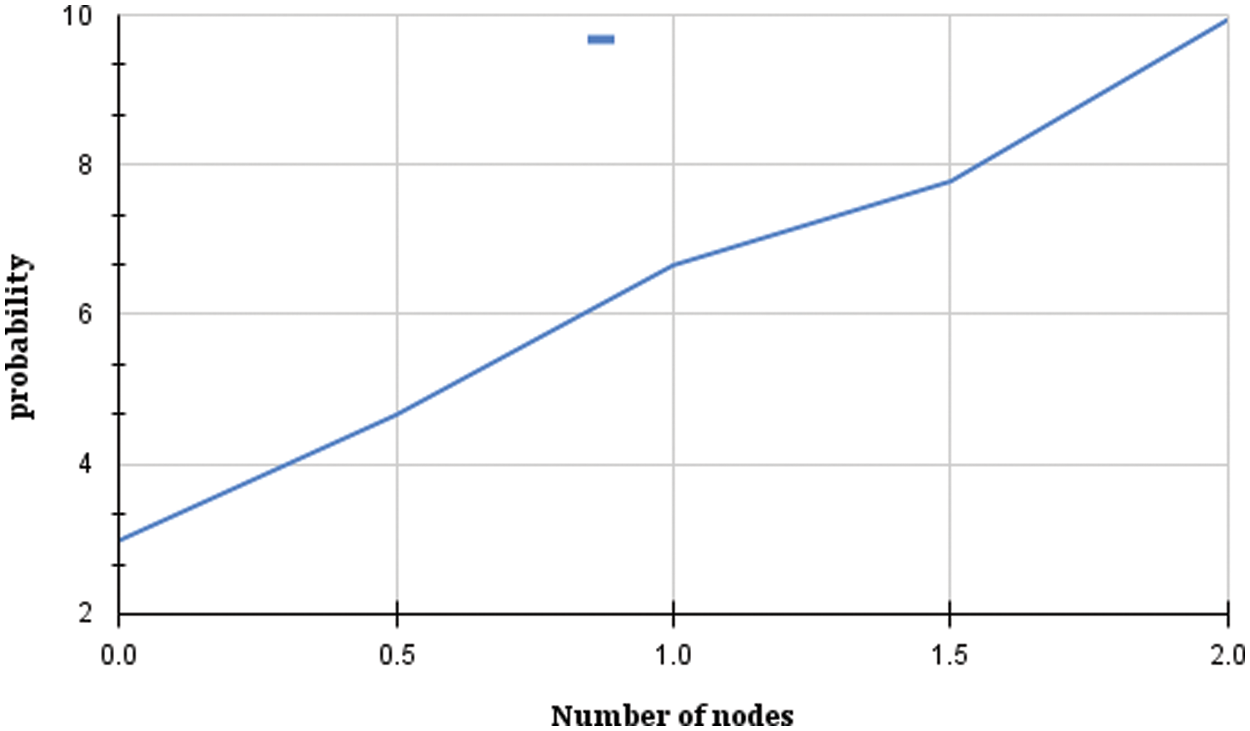
Figure 4: Distance of probability

6  Conclusion

One of the key concepts of spectral graph theory, which integrates organic chemistry with mathematics, is graph energy. Graph energies and limits have been determined using eigenvalues of graph matrices. In this paper, small-world computer networks, for which Cayley graphs have been demonstrated to be good models. Small-world networks based on the Cayley graphs have a straightforward topology and are very adaptable. Furthermore, small-world computer networks based unitary Cayley graph have a 40% lower delay and higher reliability. The Cayley-graph model can be used to design, analyse, and train communication and other real-world networks. Cayley graphs are therefore useful method for small-world computer networks. This graph method is easy to conceptualize, construct and compare since they have a simpler structure. Cayley-graph employed to recreate a broad variety of real-life networks in the biological, social, and technological domains by carefully defining the parameters.

Acknowledgement: The Author with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. H. Strogatz, “Exploring complex networks,” Nature, vol. 410, no. 6825, pp. 268–276, 2001. [Google Scholar]

 2.  P. Kumar and A. Sinha, “Information diffusion modeling and analysis for socially interacting networks,” Social Network Analysis and Mining, vol. 11, no. 1, pp. 1–18, 2021. [Google Scholar]

 3.  M. N. Hallquist and F. G. Hillary, “Graph theory approaches to functional network organization in brain disorders: A critique for a brave new small-world,” Network Neuroscience, vol. 3, no. 1, pp. 1–26, 2018. [Google Scholar]

 4.  J. Kleinberg, “Complex networks and decentralized search algorithms,” in Proc. Int. Congress of Mathematicians (ICM), Madrid, Spain, vol. 3, pp. 1019–1044, 2006. [Google Scholar]

 5.  B. J. Zubillaga, A. L. Vilela, M. Wang, R. Du, G. Dong et al., “Three-state majority-vote model on small-world networks,” Scientific Reports, vol. 12, no. 1, pp. 1–12, 2022. [Google Scholar]

 6.  A. Appathurai and P. Deepa, “Design for reliability: A novel counter matrix code for FPGA based quality applications,” in Proc. 6th Asia Symp. on Quality Electronic Design (ASQED), Kula Lumpur, Malaysia, pp. 56–61, 2015. [Google Scholar]

 7.  V. Baysal, E. Erkan and E. Yilmaz, “Impacts of autapse on chaotic resonance in single neurons and small-world neuronal networks,” Philosophical Transactions of the Royal Society A, vol. 379, no. 2198, pp. 20200237, 2021. [Google Scholar]

 8.  R. Dhaya, R. Kanthavel and A. Ahilan, “Developing an energy-efficient ubiquitous agriculture mobile sensor network-based threshold built-in MAC routing protocol (TBMP),” Soft Computing, vol. 25, no. 18, pp. 12333–12342, 2021. [Google Scholar]

 9.  T. Qiu, X. Liu, K. Li, Q. Hu, A. K. Sangaiah et al., “Community-aware data propagation with small world feature for internet of vehicles,” IEEE Communications Magazine, vol. 56, no. 1, pp. 86–91, 2018. [Google Scholar]

10. O. J. Pandey and R. M. Hegde, “Low-latency and energy-balanced data transmission over cognitive small world WSN,” IEEE Transactions on Vehicular Technology, vol. 67, no. 8, pp. 7719–7733, 2018. [Google Scholar]

11. J. Qi, B. Z. Li, Y. Zhang, B. Pan, Y. H. Gao et al., “Disrupted small-world networks are associated with decreased vigilant attention after total sleep deprivation,” Neuro Science, vol. 471, pp. 51–60, 2021. [Google Scholar]

12. W. Gu and J. Liu, “Exploring small-world network with an elite-clique: Bringing embeddedness theory into the dynamic evolution of a venture capital network,” Social Networks, vol. 57, no. 4, pp. 70–81, 2019. [Google Scholar]

13. N. H. Sarmin, A. F. A. Fadzil and A. Erfanian, “Seidel energy for cayley graphs associated to dihedral group,” Journal of Physics: Conference Series, vol. 1988, no. 1, pp. 12066, 2021. [Google Scholar]

14. H. S. Ramane, K. Ashoka, D. Patil and B. Parvathalu, “On the seidel laplacian and seidel signless laplacian polynomials of graphs,” Kyungpook Mathematical Journal, vol. 61, no. 1, pp. 155–168, 2021. [Google Scholar]

15. V. Salah, N. Sarmin and H. Hassim, “Maximum degree energy of the non-commuting graphs associated to the dihedral groups,” Advances and Applications in Mathematical Sciences, vol. 21, no. 4, pp. 1913–1923, 2022. [Google Scholar]

16. Z. Yan, C. Liu, Y. Pan and J. Li, “Energy, randic index and maximum degree of graphs,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 86, pp. 539–542, 2021. [Google Scholar]

17. S. Mondal, N. De and A. Pal, “Neighborhood degree sum-based molecular descriptors of fractal and Cayley tree dendrimers,” The European Physical Journal Plus, vol. 136, no. 3, pp. 1–37, 2021. [Google Scholar]

18. J. Gurjar and S. R. Jog, “Degree sum exponent distance energy of some graphs,” Journal of the Indonesian Mathematical Society, vol. 27, no. 1, pp. 64–74, 2021. [Google Scholar]