A Load-Fairness Prioritization-Based Matching Technique for Cloud Task Scheduling and Resource Allocation

1  Introduction

Cloud computing is an information technology concept that meets the demands of users based on their requests and requirements. It offers a variety of services as web services to registered users, which removes the need for consumers to invest in computing infrastructure. Through the use of a network in an autonomous self-serviced process, consumers are given completely prepared hardware and software in a cloud environment [1]. The responsibility of handling the needed resources to satisfy consumers’ requests is managed by Cloud Service Provider (CSP). Moreover, various scheduling algorithms are used by CSPs to schedule user tasks and properly allocate their computing resources. CSPs are looking to increase their profits and resource utilization to their maximum capacity by efficient task scheduling and resource management. Task scheduling is about managing incoming tasks with respect to identified criteria to reach an effective resource utilization. Criteria such as task size, task load, task execution time task queue, and the availability of the resources should be considered during the task scheduling process [2]. On the other hand, the procedure of assigning available resources to cloud services via the Internet with taking into consideration infrastructure availability, Service Level Agreements (SLA), price, and energy aspects is known as resource allocation [3].

A resource management system capable of dynamically scheduling and assigning these resources is essential to manage the resources efficiently [4]. Cloud consumers are seeking the most resources possible for a certain task that will improve performance and must be completed on time. Similarly, the resource allocator is responsible for addressing the issue of application starvation by appropriate resource allocation, allowing CSPs to allocate resources for each particular component at a minimal cost. The expanding popularity of cloud computing has resulted in increased benefits for both cloud consumers and CSPs. The resource management process became more sophisticated as a result of this expansion, which necessitates additional resource provisioning and scheduling. Because several cloud service vendors use a pay-as-you-use model, consumers are looking for vendors who can provide high-quality services at a reduced cost. The cost of the provided services is determined by a number of factors, including response time, throughput, and resource cost [5]. This allows cloud consumers to search for the most suitable CSP from various options. In addition, the remarkable innovation and rise in the use of cloud computing necessitates efficient and precise cloud service selection techniques because the accurate selection of a CSP is essential to improving the reliability level between vendors and consumers [6]. Furthermore, the complexity of selecting the best CSP increases due to the similarity in the proposed services by various service providers; therefore, cloud consumers need a selection framework that helps them in specifying the most appropriate CSP.

Cloud consumers should evaluate criteria such as performance, reliability, and other management and technical Quality-of-Service (QoS) factors to determine the best CSP. In addition, choosing the best CSP is based on matching the needs of consumers with the cloud services characteristics offered by various CSPs. Also, trade-offs among selecting criteria should be considered (e.g., performance and cost). Therefore, to choose the most suitable CSP that precisely meets consumers’ demands, a multitude of different assessment factors that characterize numerous cloud services provided by several CSPs should be tackled. As a result, determining the appropriate CSP is a Multi-Criteria Decision Making (MCDM) problem where various related factors need to be evaluated to select the suitable one. Adopting MCDM approaches based on pre-defined criteria can lead to optimal decisions on selecting or prioritizing various alternatives or CSPs. Different investigations have indeed been published in the literature that address the efficacy of MCDM techniques to tackle the task scheduling and resource allocation problems with considering various related criteria. For example, the Best Worst Method (BWM) is adopted by Youssef [7] and the Analytical Hierarchy Process (AHP) by Kumar et al. [8] to select the best service providers.

The paper is organized as follows: Section 2 presents related work of task scheduling algorithms. Section 3 presents the proposed framework to select the best service provider for cloud tasks. In Section 4, the matching process within the framework is presented and explained. Section 5 illustrate an example to motivate utilizing the proposed framework with the domain of cloud tasks prioritization and provisioning. Section 6 presents the details of the experiments, while Section 7 presents the results and findings. Finally, the conclusion and future enhancements to the proposed model is presented in Section 8.

2  Related Work

Cloud computing is defined as the delivery of services and resources to consumers via the internet. Consumers can also buy and use services and resources virtually through the service. Software as a Service (SaaS), Platform as a Service (PaaS), and Infrastructure as a Service (IaaS) are the three basic service-based models for the cloud, according to the National Institute of Standards and Technology (NIST) [9]. These cloud models necessitate an efficient task scheduling and resource allocation mechanism. Consumers and providers are significant players in cloud computing models. Moreover, pay-per-use is the most common method of delivering cloud services and resources, with the goal of maximizing resource use and profit for the provider while lowering costs for the consumer [10]. To avoid over-provisioning expenditures, cloud computing encourages the offer of powerfully shared resources that are stored on a single or multiple physical machines, which is referred to as a data center [11]. The wide concept of resource management encompasses both resource provisioning and resource scheduling. Consumer requests represent the primary Quality of Service (QoS) requirements for both provisioning and scheduling procedures, which are completed using various algorithms and strategies. A broker, in general, allocates an appropriate resource depending on these requirements, and then sends a request for scheduling [12].

Multiple distinct techniques and models have been presented for task scheduling and resource allocation. The benefits of applying various optimization approaches to the resource allocation problem in cloud computing have been highlighted by Shyam and Chandrakar [13]. Ant Colony Optimization Algorithms (ACO) [14], game theory [15], Particle Swarm Optimization (PSO) [16], and Genetic Algorithms (GA) [17] are some of the approaches that are investigated by various researchers. However, tools and research to determine the impact of these approaches on consumer workload and computing resources are still lacking [13]. Each technique’s adoption is guided by the aim of achieving a specific goal in the cloud computing environment. An-Ping and Chun-Xiang, for example, proposed PSO for effective energy utilization in multi-resource allocation [18], while Devarasetty and Reddy suggested GA to accomplish QoS with respect to consumer requirements within a specified cost [19].

Wang et al. [20] introduced two models to overcome the Virtual Machine (VM) allocation problem. The first model is designed to minimize load unfairness, while the second is designed to optimize resource usage and limit energy consumption. In addition, for effective VM placement, Re-sampled Binary Particle Swarm Optimization (RBPSO) was introduced with the aim of preserving diversity of the population, decreasing duplicate calculations, and hence enhancing the algorithm’s ability and efficiency. GA based on VM placement for task allocation problem was introduced by Akintoye and Bagula [21]. The cost criteria was used as QoS features, and the findings exhibited improving the service quality in the cloud environment.

Halabi et al. [22] presented a broker-based model for resource allocation problem with respect to service security satisfaction. The resource allocation problem was designed as an optimization problem and heuristic solution was introduced to enhance security. The GA showed a satisfactory approximation of the optimum solution and is computationally effective, which makes it appropriate for use in online mode and dealing with the the cloud environment scalability.

A hierarchical multi-agent optimization (HMAO) algorithm for cloud computing that increases resource utilization while lowering bandwidth costs is proposed by Gao et al. [23]. The proposed HMAO method integrates two algorithms: The genetic algorithm (GA) and the multi-agent optimization (MAO). The results show that the HMAO algorithm is more effective than available options at solving the resource allocation problem when a high number of tasks are required. Tseng et al. [24] propose GA for estimating resource use in a data center, and based on the prior data, the GA estimates the resource requirements. Simulation results are used to demonstrate the strategy’s validity and applicability. The findings indicate that GA outperforms other methods in terms of accuracy. It also optimizes CPU and memory utilization as well as energy consumption.

Several issues regarding provisioning resources and scheduling tasks in the cloud computing domain have been identified. Consumers and CSPs have various needs, which necessitates the use of the best technique to ensure superior efficiency. Singh and Chana [25] explored the issue and its ramifications for providers and consumer profits, including both sides’ unwillingness to disclose information, unpredictability, uncertainty, and resource heterogeneity. Moreover, maximizing resource utilization effectiveness by determining the most suitable resources to guarantee the services quality and the lowest completion time for a workload is the primary aim of resource scheduling. Furthermore, modern computing characteristics such as optimum task scheduling, resource allocation, and enhanced security are becoming more essential as computing systems’ capabilities and speed increase [26] and [27]. Conflict of interest among cloud service stakeholders (i.e., consumer, vendor, and operator) is a key concern, according to Liu et al. [28], because each participant has their interests and preferences.

Selecting the best vendor, which has an impact on the organization’s growth and efficacy, is one of the major objectives for enhancing the companies’ effectiveness. Several researches have been conducted to study this issue and offer potential solutions. One or more of the MCDM approaches have been used in a variety of suggested algorithms. In addition, these algorithms examined the use of the MCDM to prioritize resources based on their QoS, as well as the viability of prioritizing tasks based on various factors [29,30] and [31]. Krishankumar et al. [32] address that the most commonly used MCDMs for CSPs selection are AHP, Preferences Ranking Organization Method for Enrichment Evaluation (PROMETHEE), and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS). Youssef [7], for example, integrated the BWM with TOPSIS in terms of determining the best CSP. Many CSPs have been compared by the author based on criteria like cost, sustainability, response time, usability, and security.

Kumar et al. [8] proposed a hybrid of the AHP and TOPSIS frameworks for selecting the most suited cloud service. The AHP important scale was used to indicate the significance of each cloud service over the other based on a variety of factors including reliability, stability, auditability, accuracy, and data privacy. The overall prioritization of cloud services was then determined using the TOPSIS approach.

A model for selecting the best CSP based on the Analytic Network Process (ANP) was presented by Chung and Seo [33]. Different criteria and sub-criteria have been identified such as provider point of view, service point of view, support point of view, service availability and performance, service scalability and security, and service level agreement. The ANP pairwise comparisons were made based on the judgments of 7 domain experts to obtain the weight for each criterion. Jatoth et al. [34] looked at a hybrid multi-criteria decision-making methodology that involved ranking cloud services among the available options. The proposed methodology uses a novel extended Grey TOPSIS method integrated with the AHP to assign various priorities to cloud services based on quantified quality-of-service metrics. Alashaikh and Alanazi [35] presented a methodology for determining the best service based on the application of Conditional Preference Networks (CP-nets) regarding a collection of criteria with complex interdependencies.

To consider the internal process of resource allocation, different criteria have been identified to evaluate service providers. Costa et al. [36] have combined these criteria into seven categories and identified all criteria that belong to each category based on the literature. The identified categories are Accountability, Assurance, Agility, Performance, Security and Privacy, Financial, and Usability. These criteria play a major role in maximizing providers’ profit and increasing consumers’ satisfaction.

3  Framework

The proposed framework incorporates prioritizing tasks and resources with a matching process to ensure a balanced task scheduling among available resources with respect to their capabilities. The main components of the framework are depicted in Fig. 1.

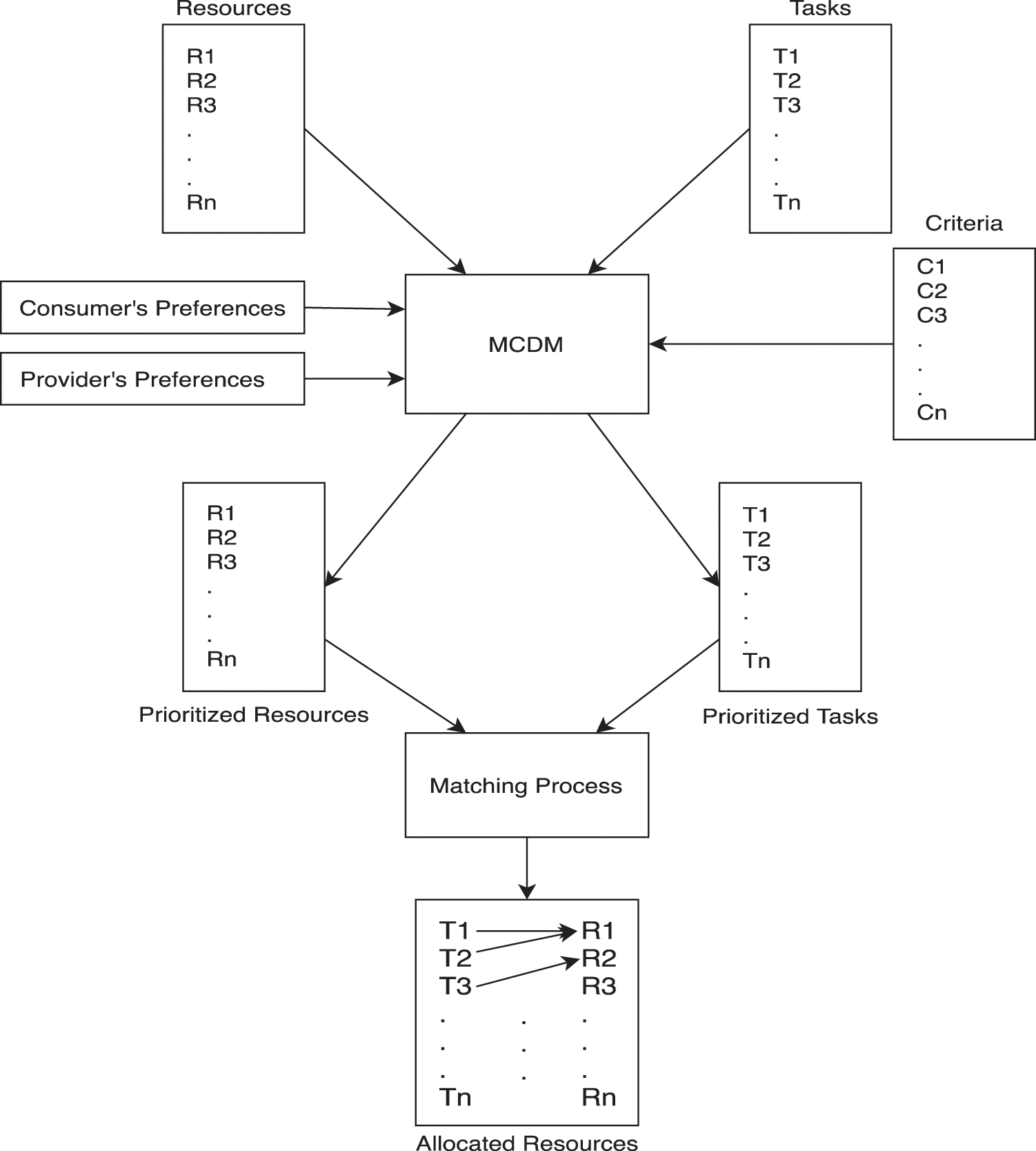
Figure 1: Framework for prioritizing and matching tasks and resources

The first part of the proposed framework takes a number of inputs to enable prioritizing process. These inputs are 1) List of available tasks, 2) List of available resources, 3) criteria for evaluation, and 4) preferences of both consumers and CSPs.

We enable acquiring preferences of both CSPs and consumers to service their preferences of a CSP will differ than others based on their goal such as building reputation, maximizing net profit, or minimizing resource wastage. Further, CSPs differ in their capabilities such as resources availability, performance, cost, and agility. Similarly, a consumer differs than others based on targeted goal such as minimized ongoing cost, increased agility, or minimized completion time of tasks.

To enable achieving targets of both parties, we cover a wide spread of criteria in cloud which are adopted from the literature and can be found in [36]. The main categories of these criteria are accountability, security and privacy, agility, performance, usability, management.

The ability to represent the tasks allocation problem by prioritizing tasks and resources into a hierarchical and mathematical problem to consider different preferences of decision-makers, i.e., consumers and CSPs, has enabled the successful adoption of different MCDM methods. Our proposed framework takes all criteria and produces the criteria weights based on all provided preferences for both tasks and resources. To do that, the framework adopts the AHP as the most common MCDM method, which was proposed by Saaty [37], as depicted in Fig. 2.

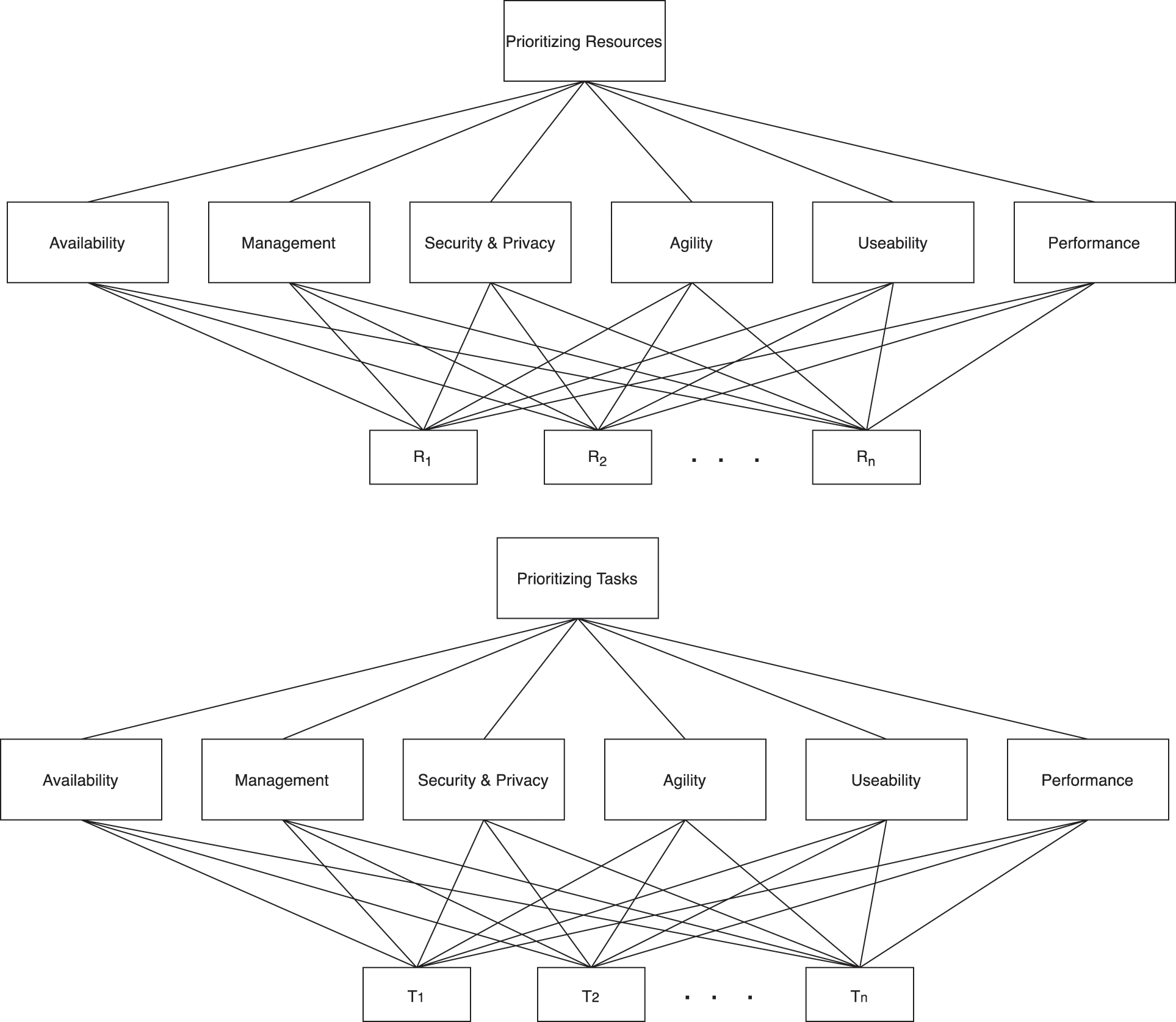
Figure 2: The proposed AHP model for prioritizing tasks and resources

The AHP is executed on the evaluations of consumers’ preferences to yield prioritized tasks and on the evaluations of providers’ preferences to yield prioritized resources. The AHP interprets complicated decision problems with numerous competing factors into a hierarchical decision structure. The hierarchical structure comprises an objective for decision making, the primary criteria and sub-criteria, and the rundown of alternatives accessible to assess the result of the objective.

In the AHP, all the problem’s components are orchestrated in a hierarchic structure of several prioritization sub-problems and afterward, after all sub-problems are unraveled, the amassed ranking of the decision-alternatives is made. The consequences of prioritization sub-problems are consistently expressed in the form of ranking vectors that comprise the appraisals of ranking weights; for example, numbers that advise to what degree a given option fulfills considered measure. The prioritization methods that are utilized inside the AHP system depend on the pairwise comparison matrix. The pairwise comparison matrix contains decision-makers’ assessments of the ranking weights. These assessments are regularly called decision maker’s judgments and are normally based on a predefined scale that was introduced by Saaty in [37]. In this scale, the decision-maker gives a number (between 1 to 9) among two criteria or alternatives which represents the level of importance of a criterion or alternative over the other; where 1 denotes equal importance while 9 denotes extreme importance of the first criterion or alternative over the other. Within the proposed framework, adopting the AHP requires conducting the following steps:

1.    Breaking down the problem into a hierarchical structure.

2.    Identifying the related criteria and structuring criteria pairwise comparisons. In this step, the weight for every criterion will be determined.

3.    Structuring alternatives pairwise comparisons as for the control criterion in every matrix.

4.    Calculating the consistency ratio.

5.    Selecting the most noteworthy weighted rating after finding the weight for every alternative.

The last part of the framework is the matching process. We propose a matching technique that enables an efficient process of tasks scheduling among the available resources. The matching process takes the prioritized tasks and divides them among the available resources based on their capabilities as explained in the following section.

4  Matching Process Among Tasks and Resources

The outputs of the prioritization process (prioritized resources and prioritized tasks) are processed by the proposed algorithm 1 to assign each set of tasks to the best match resource in a way that effectively maximizes the benefits for both CSPs and consumers.

4.1 The Proposed Algorithm for Matching Process Among Tasks and Resources

The proposed algorithm is described in steps as shown in Algorithm 1 which uses an auxiliary procedure for distribution of the tasks among resources in each category which is described in steps and depicted in procedure 1.

First, the algorithm defines two two-dimensional arrays (Rs_Arr [NR][2] and Ts_Arr [NT][2]) which contain the prioritized resources and prioritized tasks respectively. The algorithm produces the final assignment of tasks by assigning each set of tasks to each resource based on its belonging to one of three ranks (Low, Medium, and High); thus, three arrays are produced (HR_Arr [], MR_Arr [], and LR_Arr []). The test condition in for loop of line 2 is evaluated n times as true for its successful iteration. The execution falls under one of three cases where the weight of R is: 1) > = 0.5, 2) < 0.5 & > = 0.3, or 3) < 0.3. We proposed these thresholds based on Saaty’s scale where an evaluation of value 5 between any two alternatives is considered “high importance”, value 3 is considered “medium importance”, and values < 3 are considered either “slight” or “equal importance” between the two alternatives. The goal of proposing the thresholds and traversing all resources is to compute their importance level. Therefore, the total number of High rank resources with Weight > = 0.5 is calculated and stored in HR (line 4). Similarly, the number of Medium and Low rank resources are calculated and stored in MR (line 6) and LR (line 8) respectively.

Lines 9–15 calculate the cumulative weight of all resources belonging to each rank. Thus, the cumulative weight is calculated and stored in HR_values, MR_values, and LR_values for High, Medium, and Low ranks respectively. Therefore, the test condition in for loop of line 9 is evaluated n times as true for its successful iteration.

The algorithm sums the total weights and calculates the rate of tasks for resources. Then, the total tasks for each of the Low, Medium, and High ranks are calculated in lines 19, 20, and 21 respectively. As a final step, the procedure 1 is called to wisely assign a suitable number of Ts without exceeding the total number of tasks allocated for each rank. Interestingly, the algorithm is assured that the important tasks will be assigned to the best resources because all tasks and resources were prioritized (from the most important to the least important) and processed by the algorithm. Thus, it is significant and efficient to call R_Share to assign the tasks for High rank, Medium rank, and Low rank respectively. Generally, the worst-case time complexity of the proposed algorithm 1 and the associated procedure 1 is O(m + n2). In Section 7.4, we will run different sets of inputs and measure the time required to assign each set of tasks to the best available resources.

4.2 Analysis of the Proposed Algorithm

The proposed algorithm is described in steps as shown in Algorithm 1 which uses an auxiliary procedure as a procedure for distribution of the tasks among resources in each category which is described in steps and depicted in Procedure 1. The analysis of the Algorithm 1 cannot be completed without knowing the complexity of Procedure 1 which is described in Tab. 1.

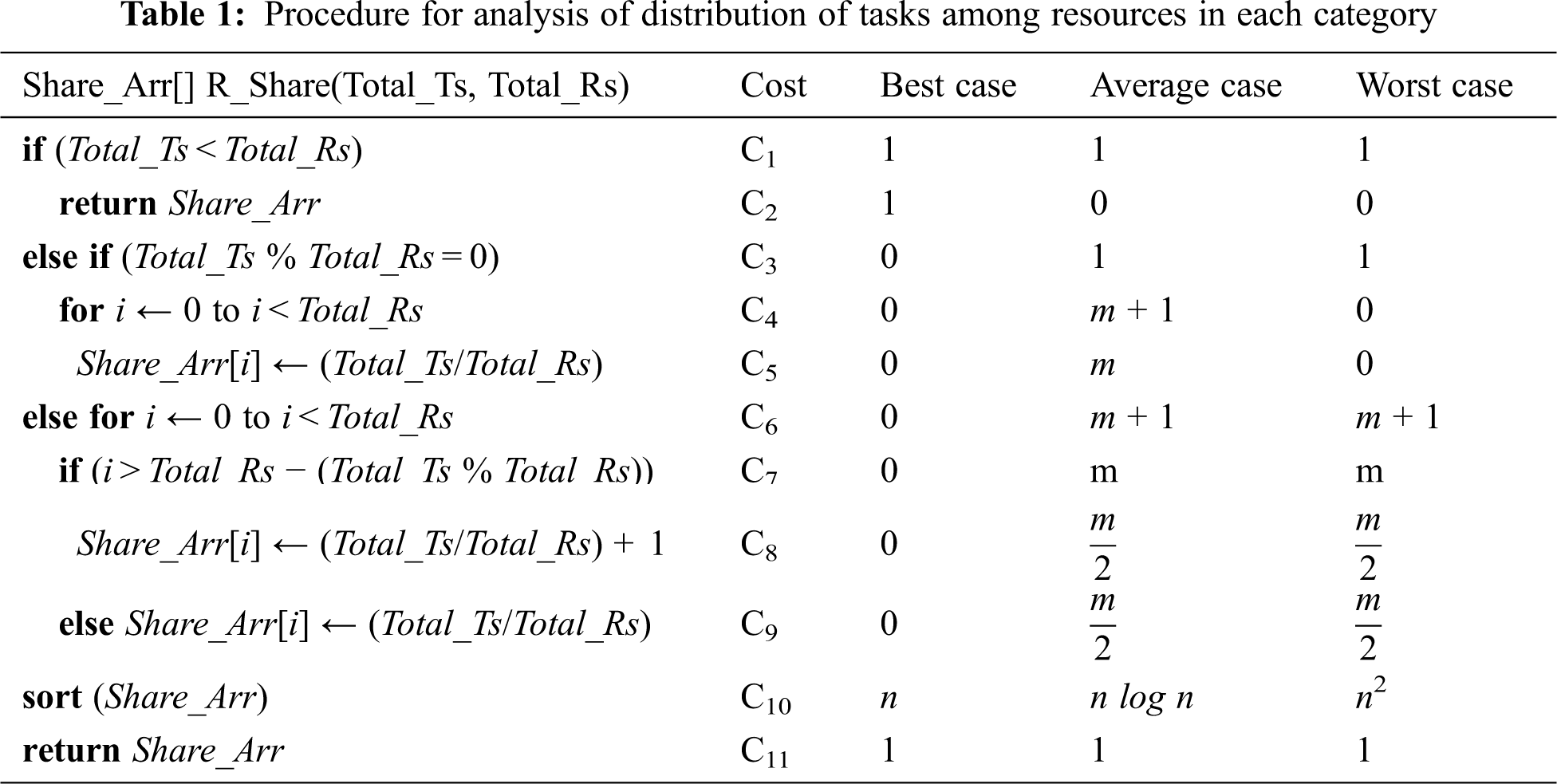
4.2.1 Best Case Analysis of Procedure 1

T(n)=C1+C2+C11+C10n=C10n+(C1+C2+C11)

T(n)=An+B (1)

where, A=C10 , B=C1+C2+C11

Since Eq. (1) is a linear equation, therefore, the coefficient of the highest order term and the constant term are neglected to get the asymptotic notation of the algorithm, which is Ω(n). Therefore, the time complexity of Procedure 1 in the best-case is Ω(n).

4.2.2 Average Case Analysis of Procedure 1

T(n)=C1+C3+C4(m+1)+C5m+C6(m+1)+C7m+C8m2+C9m2+C10nlogn+C11=(C4+C5+C6+C7+C82+C92)m+C10nlogn+(C1+C3+C4+C6+C11)

T(n)=Am+Bnlogn+C (2)

where, A=C4+C5+C6+C7+C82+C92 , B=C10,C=C1+C3+C4+C6+C11

Eq. (2) is a sub-linear equation. The coefficients of the highest order terms and the constant term are neglected to get the asymptotic notation of the algorithm, which is ϴ(m + nlogn). Therefore, the time complexity of Procedure 1 in the average-case is ϴ(m + nlogn).

4.2.3 Worst Case Analysis of Procedure 1

T(n)=C1+C3+C6(m+1)+C7m+C8m2+C9m2+C10n2+C11=(C6+C7+C82+C92)m+C10n2+(C1+C3+C6+C11)

T(n)=Am+Bn2+C (3)

where, A=C6+C7+C82+C92 , B=C10,C=C1+C3+C6+C11

Eq. (3) is a quadratic equation. The coefficients of the highest order terms and the constant term are neglected to get the asymptotic notation of the algorithm, which is O(m + n2). Therefore, the time complexity of Procedure 1 in the worst-case is O(m + n2).

Analysis of the proposed algorithm has been done in the form of the general expression of the asymptotic notations Ω, Θ, and O, with respect to the size of input data. The computational complexity for each step is expressed in Tab. 2 that corresponds to the algorithm provided in Algorithm 1 (Balanced Allocation of Tasks in Three Categories).

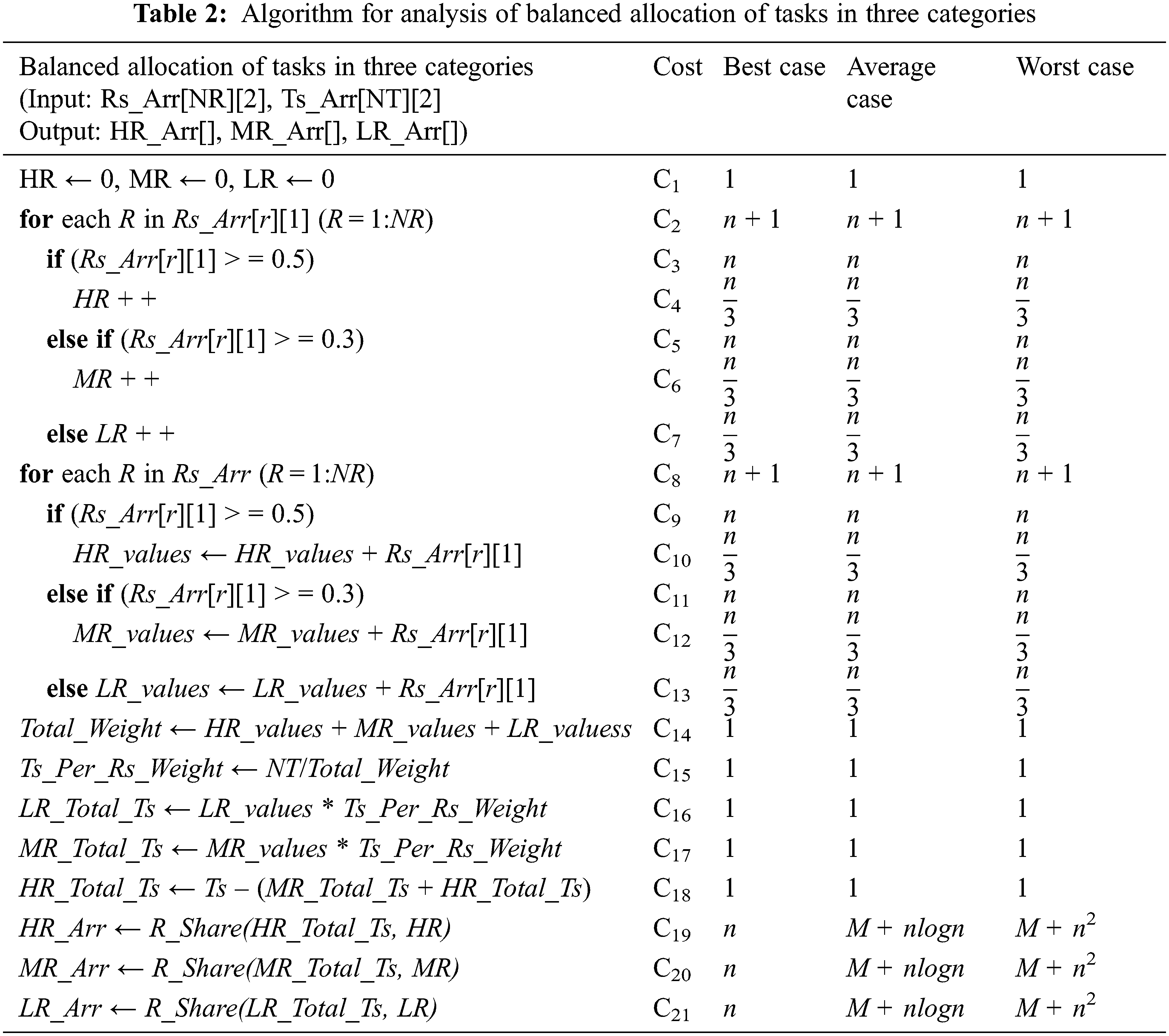
4.2.4 Best Case Analysis of Algorithm 1

T(n)=C1+C2(n+1)+C3n+C4n3+C5n+C6n3+C7n3+C8(n+1)+C9n+C10n3+C11n+C12n3+C13n3+C14+C15+C16+C17+C18+C19n+C20n+C21n=(C2+C3+C5+C8+C9+C11+C19+C20+C21+C43+C63+C103+C123+C133)n+(C1+C2+C8+C14+C15+C16+C17+C18)

T(n)=An+B (4)

where, A=C2+C3+C5+C8+C9+C11+C19+C20+C21+C43+C63+C103+C123+C133,B=C1+C2C8+C14+C15+C16+C17+C18

Eq. (4) is a linear equation. The coefficient of the highest order term and the constant term are neglected to get the asymptotic notation of the algorithm, which is Ω(n). Therefore, the time complexity of Algorithm 1 in the best-case is Ω(n).

4.2.5 Average Case Analysis of Algorithm 1

T(n)=C1+C2(n+1)+C3n+C4n3+C5n+C6n3+C7n3+C8(n+1)+C9n+C10n3+C11n+C12n3+C13n3+C14+C15+C16+C17+C18+C19(m+nlogn)+C20(m+nlogn)+C21(m+nlogn)=(C19+C20+C21)m+(C19+C20+C21)nlogn+(C2+C3+C5+C8+C9+C11+C43+C63+C103+C123+C133)n+(C1+C2+C8+C14+C15+C16+C17+C18)

T(n)=Am+Bnlogn+Cn+D (5)

where, A=C19+C20+C21,B=C19+C20+C21,C=C2+C3+C5+C8+C9+C11+C43+C63+C103+C123+C133,D=C1+C2+C8+C14+C15+C16+C17+C18

Eq. (5) is a sub-linear equation. The coefficients of the highest order terms and the lower order term as well as the constant term are neglected to get the asymptotic notation of the algorithm, which is ϴ(m + nlogn). Therefore, the time complexity of Algorithm 1 in the average-case is ϴ(m + nlogn).

4.2.6 Worst Case Analysis of Algorithm 1

T(n)=C1+C2(n+1)+C3n+C4n3+C5n+C6n3+C7n3+C8(n+1)+C9n+C10n3+C11n+C12n3+C13n3+C14+C15+C16+C17+C18+C19(m+nlogn)+C20(m+nlogn)+C21(m+nlogn)=(C19+C20+C21)m+(C19+C20+C21)n2+(C2+C3+C5+C8+C9+C11+C43+C63+C103+C123+C133)n+(C1+C2+C8+C14+C15+C16+C17+C18)

T(n)=Am+Bn2+Cn+D (6)

where, A=C19+C20+C21,B=C19+C20+C21,C=C2+C3+C5+C8+C9+C11+C43+C63+C103+C123+C133,D=C1+C2+C8+C14+C15+C16+C17+C18

Eq. (6) is a quadratic equation. The coefficients of the highest order terms and the lower order term as well as the constant term are neglected to get the asymptotic notation of the algorithm, which is O(m + n2). Therefore, the time complexity of Algorithm 1 in the worst-case is O(m + n2).

5  Example

Suppose we have a pool of prioritized tasks (PTs = 250), and a pool of prioritized resources (PRs = 7). Suppose the PTs are ordered (T1, T2, …, T250) where T1 has the highest priority and T250 has the lowest priority. Both tasks and resources have been prioritized based on the AHP, where the weight of the PRs is shown in Tab. 3. By adopting Algorithm 1, we first store PTs in Ts_Arr and PRs in Rs_Arr along with their weights. The algorithm traverses all Rs to calculate how many resources are in each category (High, Medium, or Low) based on the given threshold. From this example, no Rs falls under HR category, Two Rs fall under MR category, and Five Rs fall under LR category. Thus, we come up with the total number of Ts for each category as follows:

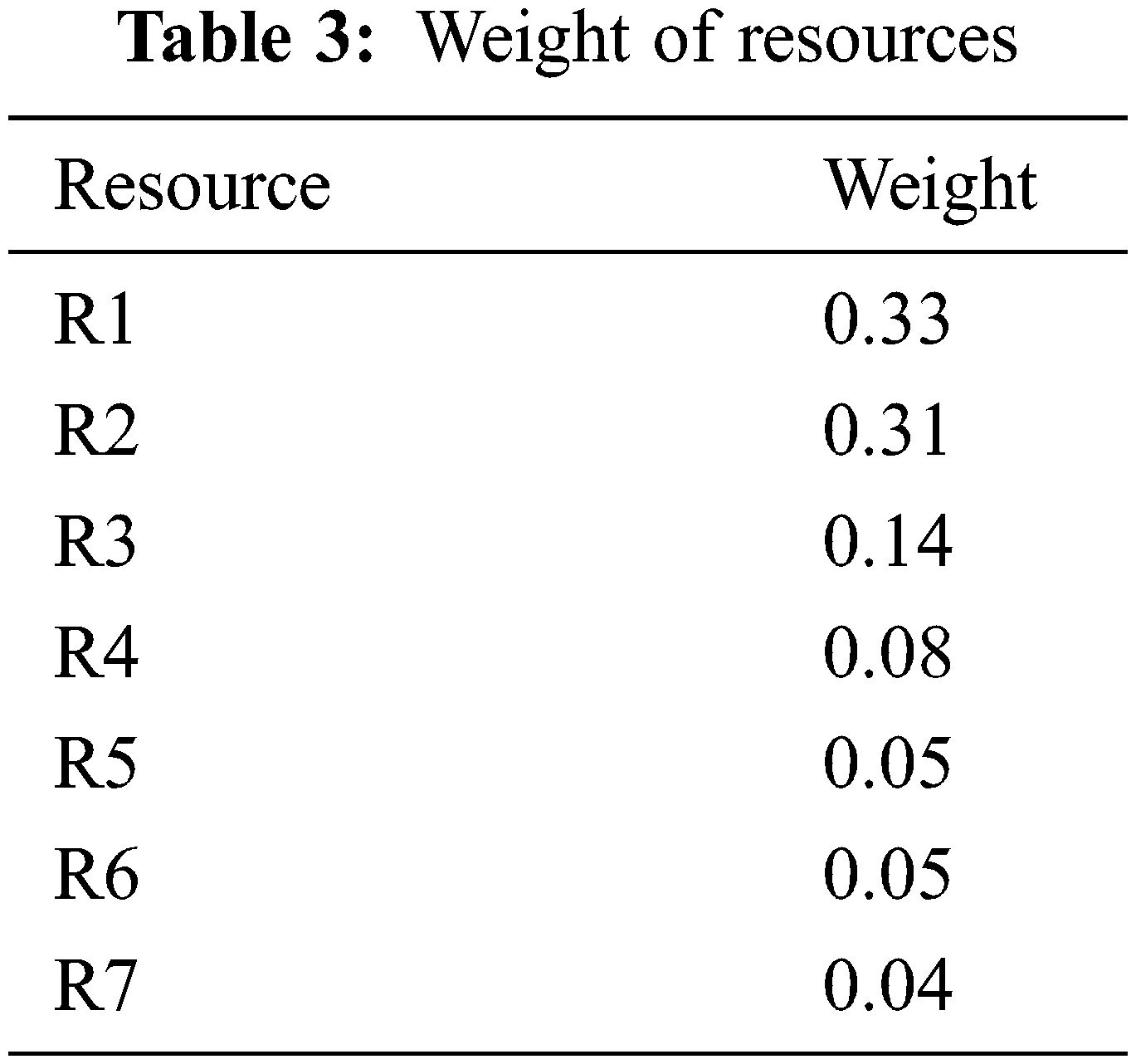
LR_Total_Ts = 250 * 0.64 = 160 Ts

MR_Total_Ts = 250 * 0.36 = 90 Ts

HR_T otal_T s = 250-(160 + 90) = 0 Ts

Now, we pass the number of Ts assigned for each category to Procedure 1 in order to assign and return the suitable number of Ts for each R as follow:

HR_Arr ← {0}

M R_Arr ←{R1{T 1, T 2, …T 80}, R2{T 81, T 82, …, T 160}}

LR_Arr ← {R3{T 161, T 162, …T 178}, R4{T 179, T 180, …T 196}, R5{T 197, T 198, …T214},

     R6{T215, T 216, …T 232}, R7{T 233, T 234, …T 250}}

The maximum number of T s for each R in Medium rank are 80 Ts, while the maximum number of Ts for each R belong to Low rank are 18 Ts. Therefore, the first 80 Ts in Ts_Arr are assigned to R1, and the second 80 Ts are assigned to R2. The rest of T s are sequentially assigned to R3, R4, R5, R6, and R7 where 18 T s are assigned to each R respectively.

6  Experiment

To validate the effectiveness of the proposed framework, we test a various number of tasks, resources, and criteria and provide the evaluation and analysis of the results. The successful application of the AHP in cloud environment has been done by many researches, for example, [38] and [39]. Thus, we build our testing on the second part of the model where we create various sets of prioritized tasks and resources based on various sets of cloud criteria.

6.1 The Setup

The algorithm 1 has been designed to support the research work. It has been implemented in Java language due its elegance and efficiency. developing and testing were conducted on IntelliJ IDEA Community Edition 2019.2.3 x64, PC with processor Intel(R) Core(TM) i7-4600U CPU @ 2.10 GHz 2.70 GHz, RAM 8.00 GB, Windows 10: 64-bit operating system, and x64-based processor.

6.2 Dataset

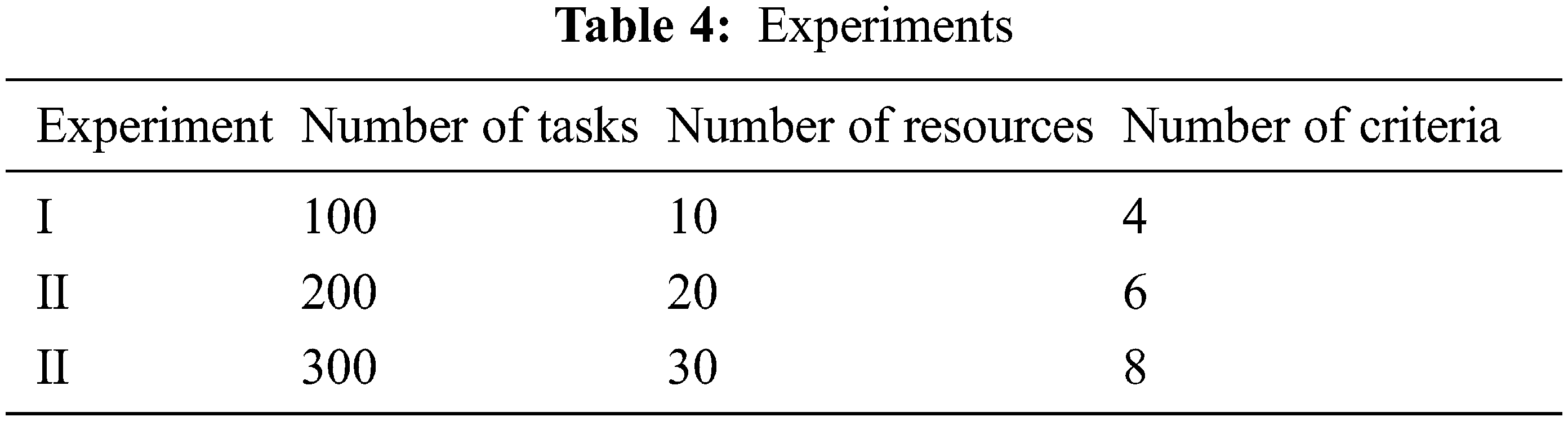
We have randomly created various sets of tasks, resources, and criteria, as shown in Tab. 4, to measure the efficiency of the proposed framework.

7  Finding and Results

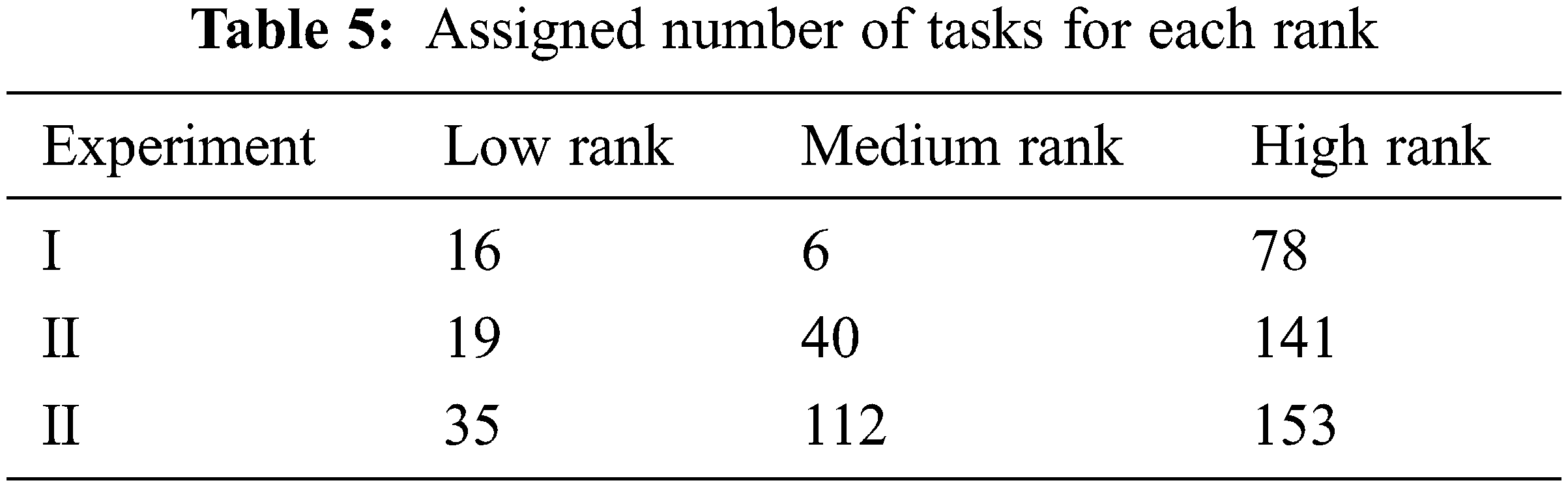
We have run the algorithm on the three sets of tasks. Tab. 5 exhibits the maximum number of tasks that can be assigned for each rank in order to have a well-balanced and efficient execution of the assigned tasks. To have deeper explanations on the results, we explain the results of each experiment as follow:

7.1 Experiment I

The approximate rate for Low rank is 5.33% and the number of Rs in Low rank is 3 (cumulative rate is 16%) which allows for each R in Low rank to have a maximum of 6 Ts, see Tab. 6. The rate for Medium rank is 6% and the number of Rs in Medium rank is one, which allows for the only R in Medium rank to have a maximum of 6 Ts. Similarly, the approximate rate for each R in High rank is 13%, and the number of Rs in this rank is six. Therefore, the average cumulative rate for all six Rs is 78% which allows for each R to have up to 13 Ts.

After dividing Rs into the appropriate rank and calculating the maximum number of Ts for each R, the final results of assigning Ts for each R is depicted in Tab. 7.

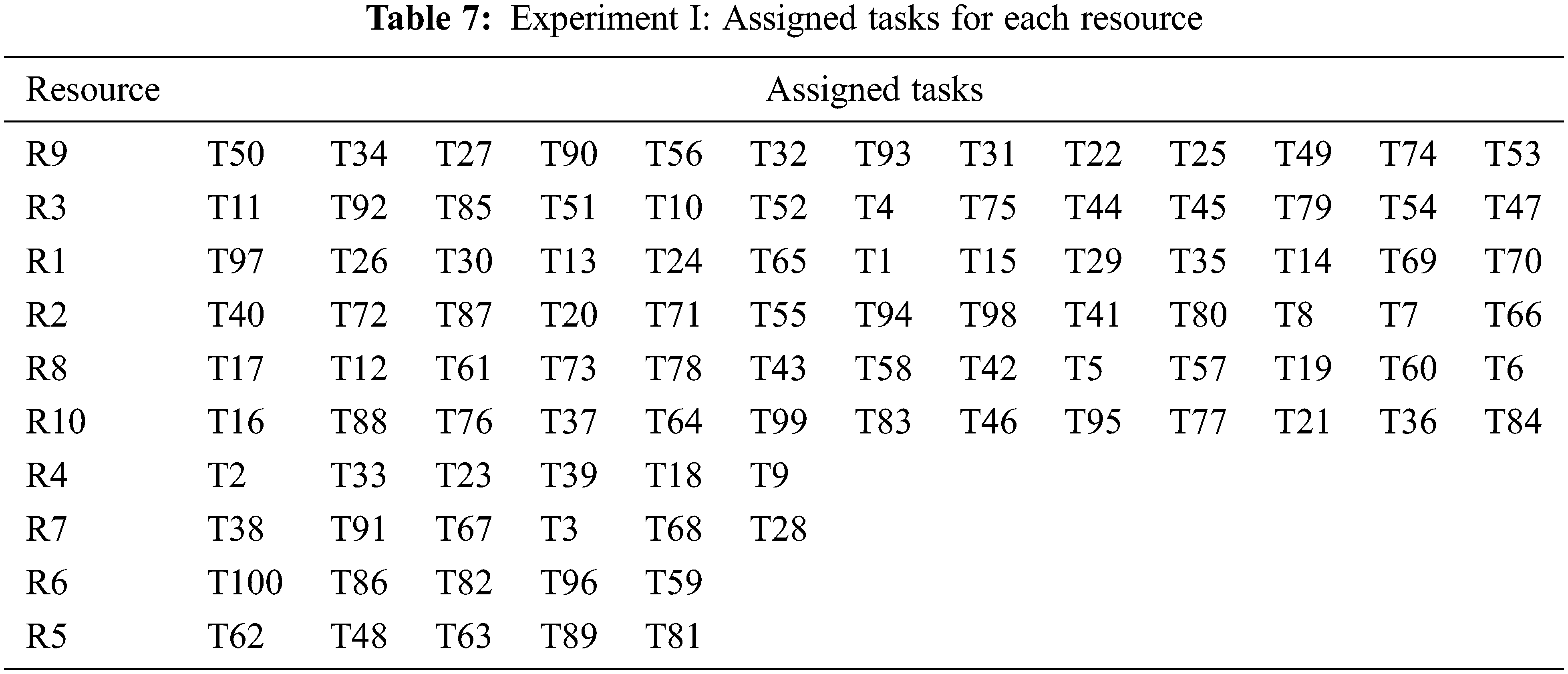
The results in Tab. 7 show that six Rs that are R9, R3, R1, R2, R8, and R10, belong to the High rank; thus, each of these Rs was assigned 13 Ts. R4 belongs to the Medium rank where six Ts are assigned to it. Finally, R7, R6, and R5 belong to the Low rank where 16 Rs are divided among them. Six Ts are assigned to R7 while five Ts are assigned to each of R6 and R5.

7.2 Experiment II

In Experiment II, the approximate rate for Low rank is 1.6% and the number of Rs in Low rank is six (cumulative rate is 9.6%) which allows for each R in Low rank to have a maximum of four Ts, see Tab. 8. The rate for Medium rank is 4% and the number of Rs in Medium rank is five (cumulative rate is 20%) which allows for each R in Medium rank to have a maximum of eight Ts. Similarly, the approximate rate for each R in High rank is 7.8%, and the number of Rs in this rank is nine. Thus, the average cumulative rate for all nine Rs is 70.2% which allows for each R to have up to 16 Ts.

The results in Tab. 9 show that nine Rs, that are R20, R9, R8, R17, R14, R7, R3, R12, and R19, belong to the High rank; thus, each of these Rs can be assigned up to 16 Ts. However, because only 141 Ts are assigned to the high rank, each of R20, R9, R8, R17, R14, and R7 is assigned 16 Ts, and each of R3, R12, and R19 is assigned 15 Ts. Five Rs, that are R11, R18, R6, R2, and R13, belong to the Medium rank where eight Ts are assigned to each R. Finally, R15, R4, R10, R5, R16, and R1, belong to the Low rank where a maximum of four Ts can be assigned to each R. Because only 19 Ts should be assigned to the six Ts, only R15 is assigned four Ts, while each of R4, R10, R5, R16, and R1 is assigned three Ts.

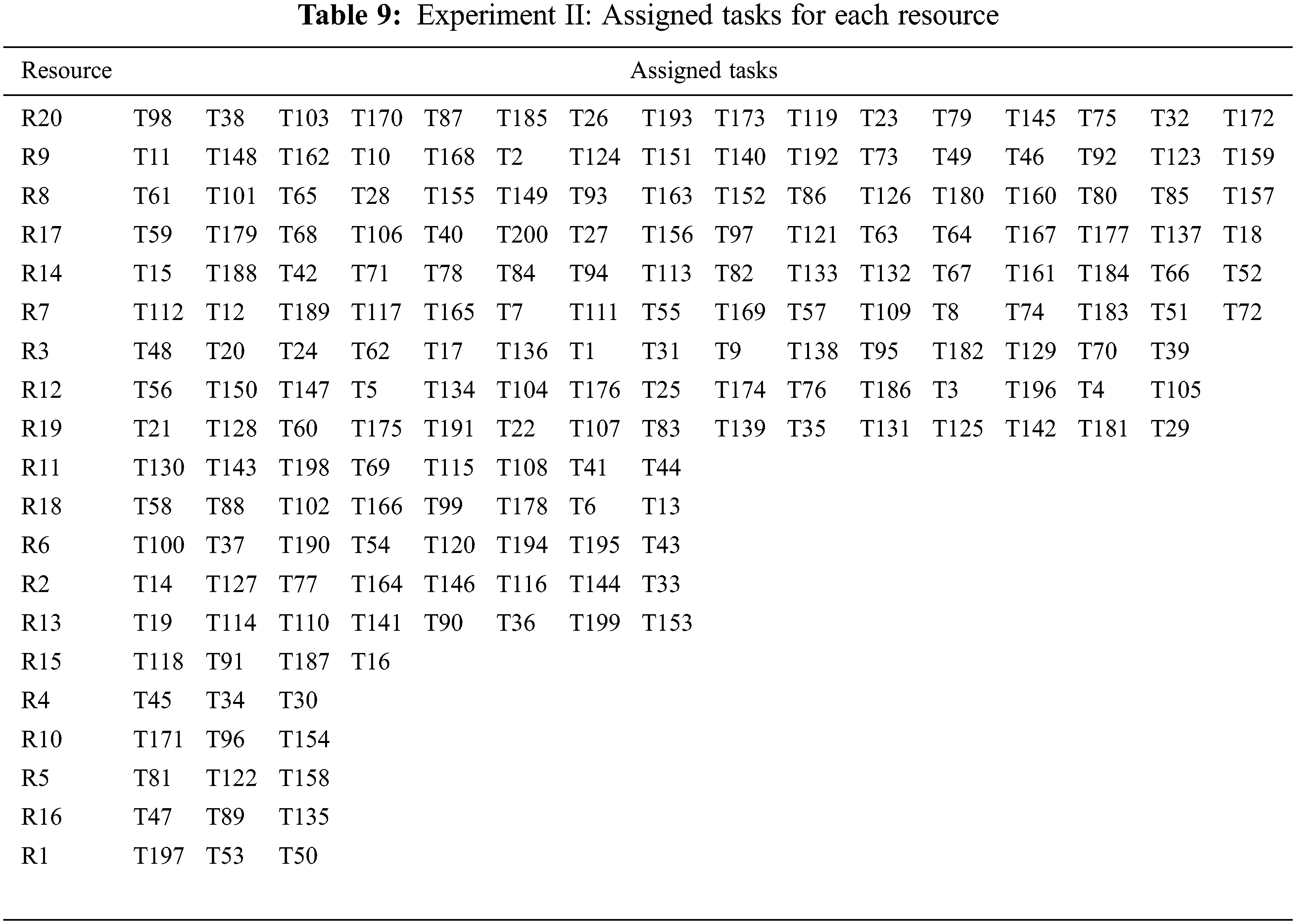
Note that all Ts are assigned based on their weight where our model considers assigning Ts based on their priority/importance. Also, all Rs are prioritized even if they belong to the same rank. To illustrate this, both R15 and R4 in experiment II belong to the Low rank but R15 comes prior to R4. Therefore, we find that the most important Rs within the same rank have a higher chance to be assigned the maximum number of Ts compared to less important Rs. Thus, after the run of the algorithm 1 on Experiment II, we find that R15 is assigned the maximum number of Ts, while R4 is assigned less Ts.

7.3 Experiment III

In Experiment III, the approximate rate for Low rank is 0.8% and the number of Rs in Low rank is 14 (cumulative rate is 11.2%) which allows for each R in Low rank to have a maximum of three Ts, see Tab. 10. The rate for Medium rank is 4.2% and the number of Rs in Medium rank is nine (cumulative rate is 37.8%) which allows for each R in Medium rank to have a maximum of 13 Ts. Similarly, the approximate rate for each R in the High rank is 7.3%, and the number of Rs in this rank is seven. Thus, the approximate average cumulative rate for all seven Rs is 51.1% which allows for each R to have up to 22 Ts.

The results in Tab. 11 show that seven Rs, that are R15, R29, R10, R26, R1, R20, and R5, belong to the High rank; thus, each of these Rs was assigned 22 Ts except R5 is assigned only 21 Ts to avoid exceeding the maximum number of Ts allowed for the High rank. Nine Rs, that are R9, R19, R8, R28, R22, R14, R27, R11, and R16, belong to the Medium rank where 13 Ts are assigned to each of R9, R19, R8, and R28, and 12 Ts are assigned to each of R22, R14, R27, R11, and R16. Finally, R4, R2, R21, R12, R18, R7, R25, R23, R13, R17, R24, R30, R6, and R3, belong to the Low rank where three Ts are assigned to each of the first seven Rs, and two Ts are assigned to each of the remaining seven Rs. As in Experiment II, note that only two Ts are assigned to the least important Rs.

7.4 Time Complexity Measurement

The time complexity of the proposed algorithm 1 and the associated procedure 1 are estimated in the worst case to be O(m + n2). However, to illustrate the average time taken to find the best match between the tasks and resources, we have run the algorithm on different combinations of inputs (Tasks and Resources). A total of six combinations have been run on the proposed implementation of the algorithm. The six combinations are illustrated in Tab. 12.

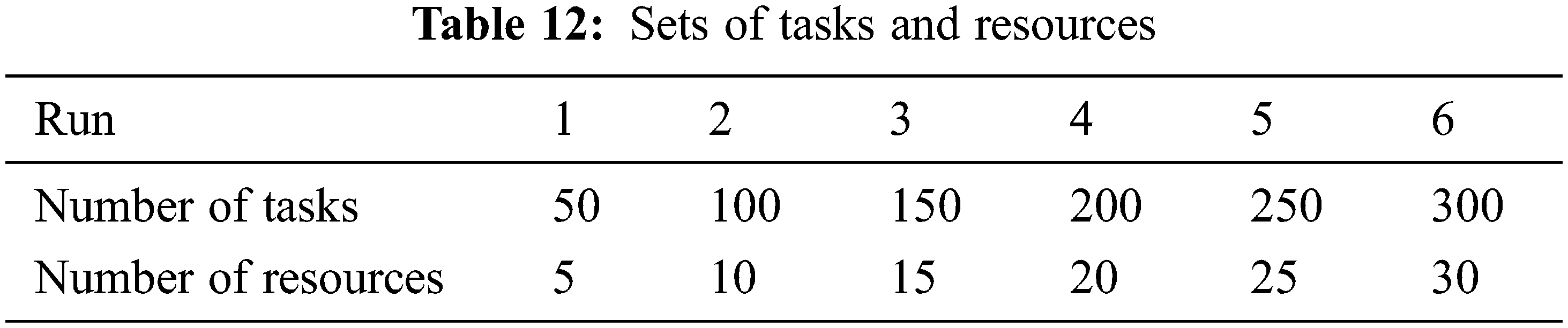
Fig. 3 depicts the run time for each combination where the results show higher growth of the required time whenever the number of tasks exceeds 200 Ts. Therefore, results confirm that time complexity is O(m + n2).

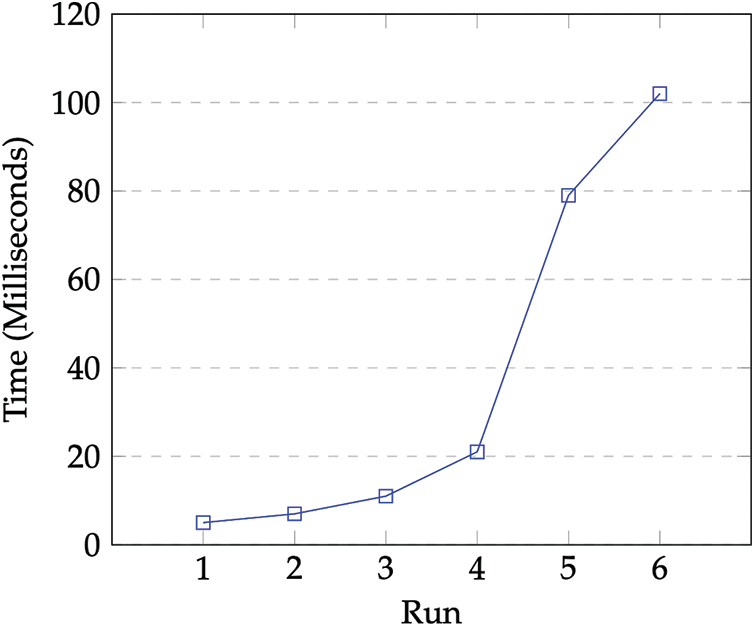
Figure 3: Average time taken to assign the tasks to the best resource

8  Conclusion

A trade-off between a variety of criteria and attributes in the cloud leads to complicating the efficiency and effectiveness of task scheduling and resource allocation process. Both consumers and CSPs have their preferences which should be taken into consideration to maximize the profit of both parties. The paper introduces a model that acquires and manipulates consumers’ and providers’ preferences considering a set of criteria that influence the task scheduling and resource allocation process. The manipulation of the preferences is done by adopting the AHP. Then, the model proposes a matching process based on thresholds to categorize the prioritized resources before the actual assignment of the prioritized tasks.

The proposed model was tested by conducting three experiments, each with a set of tasks and a set of resources. Each of the tasks and resources was assigned a random weight/priority which represents the weight of the task/resource after processing the consumers’ and providers’ preferences by the AHP. The results of the three experiments show the effectiveness of assigning a high number of tasks to the available resource with the consideration of both consumers’ and providers’ preferences. Further, the results reflect the load-fairness technique where all available resources are assigned a suitable amount of tasks based on the priority/importance of each resource. The proposed algorithm will be very suitable and robust one to implement the model for a big scale cloud-based task scheduling and resource allocation problem.

In the future, multifaceted improvements can be done to the current model. First, we will extend the model by including criteria related to not only consumers’ and CSPs’ preferences, but also actual measurements of the quality of services and other resource-related criteria. Also, different recent techniques can be utilized to automatically evaluate the criteria of new CSPs and resources. For example, machine learning techniques can be utilized to extract important criteria and produce a model to evaluate CSP and their resources. Finally, various MCDM methods, such as ANP and BWM, can be adopted; then, analytical comparisons can be done to identify the most suitable MCDM method that provides reliable and consistent results with less processing time.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Liu, F. T. Chan and W. Ran, “Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes,” Expert Systems with Applications, vol. 55, pp. 37–47, 2016. [Google Scholar]

 2.  M. B. Gawali and S. K. Shinde, “Task scheduling and resource allocation in cloud computing using a heuristic approach,” Journal of Cloud Computing, vol. 7, no. 1, pp. 1–16, 2018. [Google Scholar]

 3.  A. Abid, M. F. Manzoor, M. S. Farooq, U. Farooq and M. Hussain, “Challenges and issues of resource allocation techniques in cloud computing,” KSII Transactions on Internet and Information Systems (TIIS), vol. 14, no. 7, pp. 2815–2839, 2020. [Google Scholar]

 4.  J. Kumar, A. K. Singh and R. Buyya, “Ensemble learning based predictive framework for virtual machine resource request prediction,” Neurocomputing, vol. 397, pp. 20–30, 2020. [Google Scholar]

 5.  R. R. Kumar, S. Mishra and C. Kumar, “A novel framework for cloud service evaluation and selection using hybrid mcdm methods,” Arabian Journal for Science and Engineering, vol. 43, no. 12, pp. 7015–7030, 2018. [Google Scholar]

 6.  R. R. Kumar, S. Mishra and C. Kumar, “Prioritizing the solution of cloud service selection using integrated MCDM methods under fuzzy environment,” The Journal of Supercomputing, vol. 73, no. 11, pp. 4652–4682, 2017. [Google Scholar]

 7.  A. E. Youssef, “An integrated MCDM approach for cloud service selection based on TOPSIS and BWM,” IEEE Access, vol. 8, pp. 71 851–71 865, 2020. [Google Scholar]

 8.  R. R. Kumar and C. Kumar, “A multi criteria decision making method for cloud service selection and ranking,” International Journal of Ambient Computing and Intelligence (IJACI), vol. 9, no. 3, pp. 1–14, 2018. [Google Scholar]

 9.  P. Mell, and T. Grance, “The nist definition of cloud computing,” National Institute of Standards and Technology, vol. 800–145, pp. 7, 2011. [Google Scholar]

10. S. H. H. Madni, M. S. A. Latiff, Y. Coulibaly and S. M. Abdulhamid, “Recent advancements in resource allocation techniques for cloud computing environment: A systematic review,” Cluster Computing, vol. 20, no. 3, pp. 2489–2533, 2017. [Google Scholar]

11. M. O. Agbaje, O. B. Ohwo, T. G. Ayanwola and O. Olufunmilola, “A survey of game-theoretic approach for resource management in cloud computing,” Journal of Computer Networks and Communications, vol. 2022, pp. 1–13, 2022. [Google Scholar]

12. S. Singh and I. Chana, “Q-Aware: Quality of service based cloud resource provisioning,” Computers & Electrical Engineering, vol. 47, pp. 138–160, 2015. [Google Scholar]

13. G. K. Shyam and I. Chandrakar, “Resource allocation in cloud computing using optimization techniques,” In Mishra, B., Das, H., Dehuri, S., Jagadev, A. (eds) Cloud Computing for Optimization: Foundations, Applications, and Challenges. Studies in Big Data, vol. 39. Cham: Springer, 2018, https://doi.org/10.1007/978-3-319-73676-1_2. [Google Scholar]

14. K. Li, G. Xu, G. Zhao, Y. Dong and D. Wang, “Cloud task scheduling based on load balancing ant colony optimization,” in 2011 Sixth Annual ChinaGrid Conf., Liaoning, China, pp. 3–9, 2011. [Google Scholar]

15. J. Yang, B. Jiang, Z. Lv and K. -K. R. Choo, “A task scheduling algorithm considering game theory designed for energy management in cloud computing,” Future Generation Computer Systems, vol. 105, pp. 985–992, 2020. [Google Scholar]

16. A. Awad, N. El-Hefnawy and H. Abdel_kader, “Enhanced particle swarm optimization for task scheduling in cloud computing environments,” Procedia Computer Science, vol. 65, pp. 920–929, 2015. [Google Scholar]

17. S. H. Jang, T. Y. Kim, J. K. Kim and J. S. Lee, “The study of genetic algorithm-based task scheduling for cloud computing,” International Journal of Control and Automation, vol. 5, no. 4, pp. 157–162, 2012. [Google Scholar]

18. A. -P. Xiong and C. -X. Xu, “Energy efficient multiresource allocation of virtual machine based on PSO in cloud data center,” Mathematical Problems in Engineering, vol. 2014, pp. 1–8, 2014. [Google Scholar]

19. P. Devarasetty and S. Reddy, “Genetic algorithm for quality of service based resource allocation in cloud computing,” Evolutionary Intelligence, vol. 14, no. 2, pp. 381–387, 2021. [Google Scholar]

20. X. Wang, H. Gu and Y. Yue, “The optimization of virtual resource allocation in cloud computing based on RBPSO,” Concurrency and Computation: Practice and Experience, vol. 32, no. 16, pp. e5113, 2020. [Google Scholar]

21. S. B. Akintoye and A. Bagula, “Improving quality-of-service in cloud/fog computing through efficient resource allocation,” Sensors, vol. 19, no. 6, pp. 1267, 2019. [Google Scholar]

22. T. Halabi, M. Bellaiche and A. Abusitta, “Online allocation of cloud resources based on security satisfaction,” in 17th IEEE Int. Conf. on Trust, Security and Privacy in Computing and Communications/12th IEEE Int. Conf. on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, pp. 379–384, 2018. [Google Scholar]

23. X. Gao, R. Liu and A. Kaushik, “Hierarchical multi-agent optimization for resource allocation in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 3, pp. 692–707, 2020. [Google Scholar]

24. F. -H. Tseng, X. Wang, L. -D. Chou, H. -C. Chao and V. C. Leung, “Dynamic resource prediction and allocation for cloud data center using the multiobjective genetic algorithm,” IEEE Systems Journal, vol. 12, no. 2, pp. 1688–1699, 2017. [Google Scholar]

25. S. Singh and I. Chana, “A survey on resource scheduling in cloud computing: Issues and challenges,” Journal of Grid Computing, vol. 14, no. 2, pp. 217–264, 2016. [Google Scholar]

26. S. H. H. Madni, M. S. Abd Latiff, M. Abdullahi, S. M. Abdulhamid and M. J. Usman, “Performance comparison of heuristic algorithms for task scheduling in IaaS cloud computing environment,” PloS One, vol. 12, no. 5, pp. e0176321, 2017. [Google Scholar]

27. S. Iqbal, M. L. M. Kiah, B. Dhaghighi, M. Hussain, S. Khan et al., “On cloud security attacks: A taxonomy and intrusion detection and prevention as a service,” Journal of Network and Computer Applications, vol. 74, pp. 98–120, 2016. [Google Scholar]

28. Y. Liu, L. Wang, X. V. Wang, X. Xu and L. Zhang, “Scheduling in cloud manufacturing: State-of-the-art and research challenges,” International Journal of Production Research, vol. 57, no. 15–16, pp. 4854–4879, 2019. [Google Scholar]

29. A. Singh and K. Dutta, “Apply AHP for resource allocation problem in cloud,” Journal of Computer and Communications, vol. 3, no. 10, pp. 13–21, 2015. [Google Scholar]

30. D. Ergu, G. Kou, Y. Peng, Y. Shi and Y. Shi, “The analytic hierarchy process: Task scheduling and resource allocation in cloud computing environment,” The Journal of Supercomputing, vol. 64, no. 3, pp. 835–848, 2013. [Google Scholar]

31. A. Alhubaishy and A. Aljuhani, “The best-worst method for resource allocation and task scheduling in cloud computing,” in 2020 3rd Int. Conf. on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, pp. 1–6, 2020. [Google Scholar]

32. R. Krishankumar, K. S. Ravichandran and S. K. Tyagi, “Solving cloud vendor selection problem using intuitionistic fuzzy decision framework,” Neural Computing and Applications, vol. 32, no. 2, pp. 589–602, 2020. [Google Scholar]

33. B. Do Chung and K. -K. Seo, “A cloud service selection model based on analytic network process,” Indian Journal of Science and Technology, vol. 8, no. 18, pp. 1–5, 2015. [Google Scholar]

34. C. Jatoth, G. Gangadharan, U. Fiore and R. Buyya, “Selcloud: A hybrid multi-criteria decision-making model for selection of cloud services,” Soft Computing, vol. 23, no. 13, pp. 4701–4715, 2019. [Google Scholar]

35. A. Alashaikh and E. Alanazi, “Conditional preference networks for cloud service selection and ranking with many irrelevant attributes,” IEEE Access, vol. 9, pp. 131214–131222, 2021. [Google Scholar]

36. P. Costa, J. P. Santos and M. M. da Silva, “Evaluation criteria for cloud services,” in 2013 Sixth Int. Conf. on Cloud Computing, Santa Clara, CA, USA, pp. 598–605, 2013. [Google Scholar]

37. T. L. Saaty, “How to make a decision: The analytic hierarchy process,” European Journal of Operational Research, vol. 48, no. 1, pp. 9–26, 1990. [Google Scholar]

38. Z. urRehman, F. K. Hussain and O. K. Hussain, “Towards multi-criteria cloud service selection,” in 2011 Fifth Int. Conf. on Innovative Mobile and Internet Services in Ubiquitous Computing, Seoul, Korea (Southpp. 44–48, 2011. [Google Scholar]

39. S. C. Nayak and C. Tripathy, “Deadline sensitive lease scheduling in cloud computing environment using AHP,” Journal of King Saud University-Computer and Information Sciences, vol. 30, no. 2, pp. 152–163, 2018. [Google Scholar]