Tricube Weighted Linear Regression and Interquartile for Cloud Infrastructural Resource Optimization

1  Introduction

In cloud computing, resource allocation takes part in a pivotal part in deciding the performance, utilization of resources, and data center power consumption. The pertinent VM allocation in cloud data centers is also one of the main optimization issues as far as cloud computing is concerned. A load-balancing algorithm called, Priority Aware Longest Job First (PA-KJF) was proposed in [1] to enhance the VM utilization and fulfill users’ requirements in cloud infrastructure. Here, the priority of tasks was first identified. VIP tasks were first executed followed by which the normal tasks were executed. Next, the heuristic-based dynamic load-balancing algorithm was employed that monitored VMs in a continuous manner resulting in significant resource utilization. With this various QoS parameters like processing time, throughput, and task acceptance ratio were found to be improved.

Despite improvement observed in three different QoS parameters, less focus was made on VM migration, energy consumption. To address this issue, an Inter Quartile Range is introduced in the TWLR-IQ method that efficiently predicts overloading hosts, therefore, minimizing the number of migrations. Cloud workflow scheduling strategy employing intelligent algorithm called D-JStorm, a dynamic resource scheduling was proposed in [2]. In addition, a strategy for aligning the fusion of recognized cloud service resources to attain scheduling of cloud workflow tasks in a two-tier manner was designed. With the implementations of a fusion i.e., cloud workflow scheduling based on an intelligent algorithm, the response time was shortened in addition to optimal memory utilization. Despite improvement observed in optimal memory utilization, the energy consumed in cloud workflow scheduling was less focused. To address this issue, a Tricube Weighted Linear Regression model is designed that estimates the history of usage in each cloud server (i.e., energy consumption). To solve the above problems, this work proposes a cloud infrastructural resource optimization algorithm for ensuring high QoS.

The main contributions of this paper are as follows.

•   We propose a novel priority of resource allocation based on the history of usage or resource demands (i.e., CPU utilization, memory, and network bandwidth utilization) for each requested task in a cloud environment, which guarantees the estimated resource demand to be allocated resources in a computationally efficient and accurate manner.

•   We propose a model of virtual allocation, which selects more suitable physical servers to provide resources with better performance for VM requests based on resource performance matching between VMs and physical servers employing Tricube Locality Quarter Weight.

•   We propose a model of VM migration, using Markov Inter Quartile-based VM Migration which performs between VM migrations to ensure balanced utilization between different types of resources of physical servers.

•   Conduct extensive simulation and performance analysis of the proposed method. In addition, we investigate how the three cloud resource optimization methods have an impact on the performance in terms of resource optimization time, resource optimization accuracy, energy usage, and a number of migrations.

The rest of this paper is organized as follows. Section 2 discusses related works. Section 3 introduces the system model presented in this study, followed by which the proposed Tricube Weighted Linear Regression-based Inter Quartile (TWLR-IQ) method is elaborated. Section 4 presents an experimental evaluation of the proposed method. Section 5 discusses the comparative analysis with two state-of-the-art methods. We conclude the paper in Section 6.

2  Related Work

An end-to-end Price-Aware Congestion Control Protocol (PACCP) was designed in [3] for cloud service provisioning. However, predicting demand for resource estimation is a vital task as it permits optimized resource estimation. A novel method employing anomaly detection and machine learning was proposed in [4] to achieve cost-optimized and QoS-constrained cloud infrastructural resource estimation. Yet another hybrid cloud environment consistency management employing Graph Partitioning Algorithm was presented in [5].

Brokering model for Service Selection (BSS) was proposed in [6] utilizing integrated weighting selection of cloud services. In this work, both subjective and objective weights of QoS features were integrated into the measured integrated total weight. However, congestion causes an interruption in the allocation of tasks with the respective resource. To address this issue, a pre-allocation algorithm was designed in [7] employing access point resource utilization, therefore enhancing the overall task execution with a minimum time overhead. However, estimating the best-performing resource is a difficult task. This is owing to the reason that the optimality depends on both the topology and workload collocation.

To address this aspect, a framework called, DRMaestro has proposed in [8] that with the assistance of a novel flow-network model determined optimal placement in several phases and prevented workload performance interference. However, with the huge executions involved in scientific workflows, the overall process is said to be time-consuming. In order to address workflow issues, a Cost Optimized Heuristic Algorithm (COHA) was proposed in [9] employing novel workflow scheduling called, Multi-Objective Workflow Optimization Strategy (MOWOS). Yet another resource allocation algorithm ensuring timeliness and optimization employing an improved evolutionary algorithm was proposed in [10].

With the increased load in data centers, energy consumption is also said to be high. To address this aspect, a hybrid approach combining Genetic Algorithm and Random Forest was proposed in [11] that in turn not only reduced power consumption but also maintained better load balance. To ensure the QoS and time consumed in the execution of the user requested task, an improved particle swarm optimization algorithm was designed in [12]. However, customarily designed as single objective issues and solutions are proposed. For handling multi-objective issues, a method called, multi constraint multi-objective resource scheduling optimization method was proposed in [13] for ensuring cloud infrastructure services to the user requested tasks. However, this multi-objective optimization model was not found to be suitable for high-performance computing platforms. To concentrate on this issue, artificial neural networks were employed in [14] therefore ensuring optimization time and cost.

A holistic approach concentrating on scheduling methods for cloud computing was investigated in [15]. In [16], an improved particle swarm optimization (IPSO) algorithm was designed with the purpose of enhancing resource scheduling efficiency. Yet another QoS constrained cloud resource configuration model employing machine learning was proposed in [17], therefore causing an improvement in prediction efficiency. To address this aspect, a Hierarchical Multi-Agent Optimization (HMAO) algorithm was proposed in [18] to not only ensure maximal resource utilization but also reduce bandwidth cost for cloud computing. In [19], a multi-objective optimization algorithm to ensure performance and cost-efficiency for Big Data applications running on Cloud was proposed. An Enhanced Heterogeneous Earliest Finish Time based on Rule (EHEFT-R) for efficient task scheduling was designed in [20] to ensure task efficiency, improve QoS and minimize energy consumption.

Cost-Effective Optimal Task Scheduling Model (CEOTS) was introduced in [21] for minimizing the cost and make span. However, the energy usage was not considered. Genetic simulated annealing fusion algorithm named GSA-EDGE was developed in [22] for minimizing the time delay of task processing. But, the resource optimization accuracy was not focused. An efficient virtual machine placement strategy (VMP-SI) was developed in [23] to guarantee the QoS. But, the execution time was not reduced. Resource-aware dynamic task scheduling approach was introduced in [24] to improve resource utilization and minimum execution time. But, the computational complexity was not minimized. Cloud computing multi-objective task scheduling optimization method was developed in [25] for selecting the global optimal solution. An enhanced sunflower optimization (ESFO) algorithm was introduced in [26] for determining the optimal scheduling. However, the accuracy was not improved. Motivated by the above state-of-the-art methods, in this work, a cloud infrastructural resource optimization method called, Tricube Weighted Linear Regression-based Inter Quartile (TWLR-IQ) is proposed. The elaborate description of the TWLR-IQ is presented in the following sections.

3  Methodology

Cloud computing is a type of distributed computing that introduces utility models to produce quantifiable and scalable resources in a remote fashion. Significant computing potentiality and extensive storage capacity permit the users to access cloud services anytime and anywhere. On the other hand, Cloud Infrastructural Resource Optimization refers to the process of resource planning, with the objective of minimizing overall costs, while attaining the highest performance in terms of resource allocations under a set of given constraints.

In this section, a method called, the Tricube Weighted Linear Regression-based Inter Quartile (TWLR-IQ) for Cloud Infrastructural Resource Optimization is designed with the objective of ensuring high QoS (i.e., minimizing energy and power consumption). Fig. 1 shows the block diagram of Tricube Weighted Linear Regression-based Inter Quartile (TWLR-IQ) method.

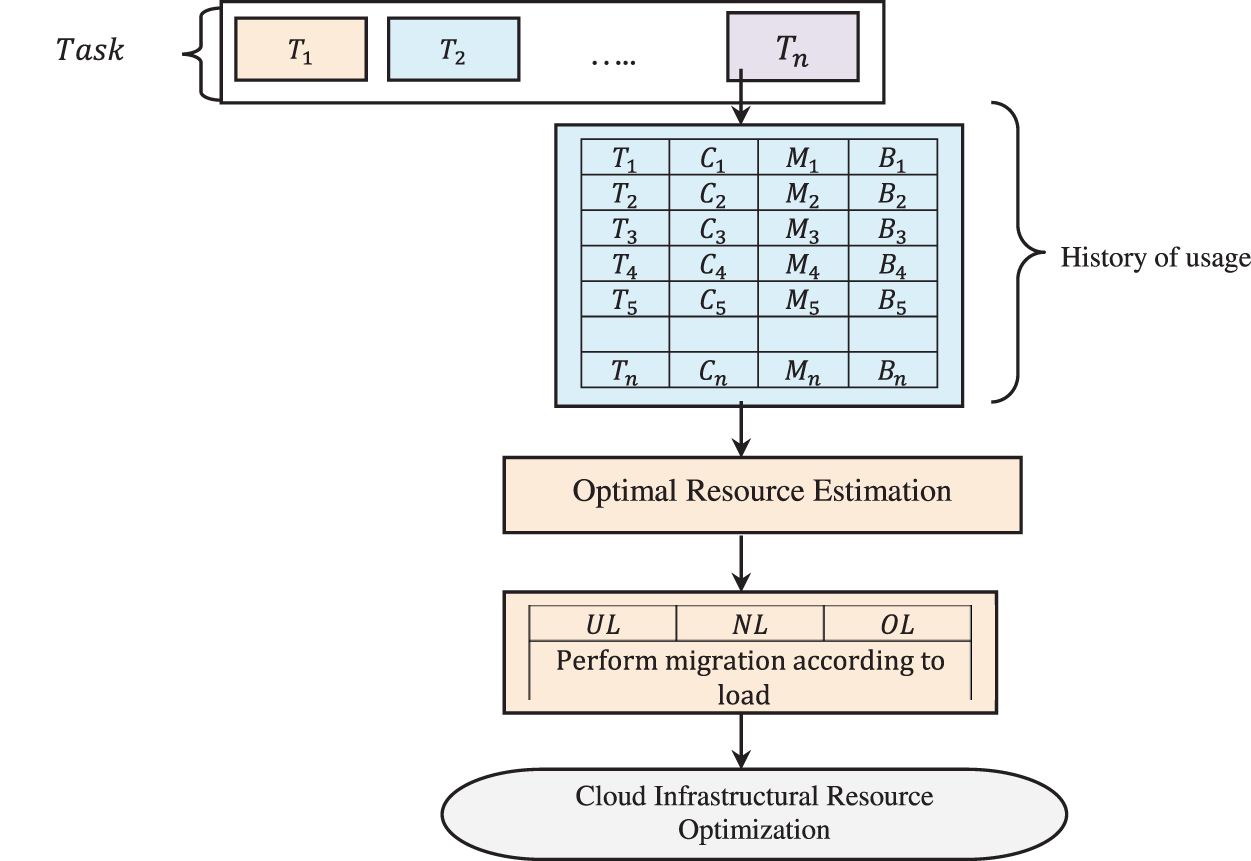
Figure 1: Block diagram of tricube weighted linear regression-based inter quartile

First, a system model for resource optimization in cloud computing environment is presented. Second, Tricube Weighted Linear Regression-based Resource Estimation model is designed to allocate the tasks based on the estimation of resources. Finally, with the incoming user request tasks resource estimation made, Inter Quartile Range-based Cloud Infrastructural Resource Optimization is ensured with maximum accuracy and minimum number of migrations, energy usage, resource optimization time. To start with a system model is presented, followed by which the proposed methodology is explained in detail.

3.1 Cloud Computing System Model

This section provides the cloud computing system model of the proposed method in the cloud computing environment.

Fig. 2 given below shows the system model of cloud infrastructural resource optimization in cloud computing environment. As shown in the figure let us consider set of tasks represented as ‘ T={T1,T2,….,Tn} ’, where ‘ i∈[1,n] ’ and ‘ n ’ represents the total number of tasks. Each task ‘ Ti ’ is expressed as ‘ Ti(CPUi,Mi,Bi) ’, here ‘ CPUi ’, ‘ Mi ’ and ‘ Bi ’ represents the CPU utilization, memory consumed and network bandwidth utilization respectively. The objective here remains in optimizing the resources with minimal energy, migrations and maximal accuracy. The elaborate description of the proposed method is given in the following sections.

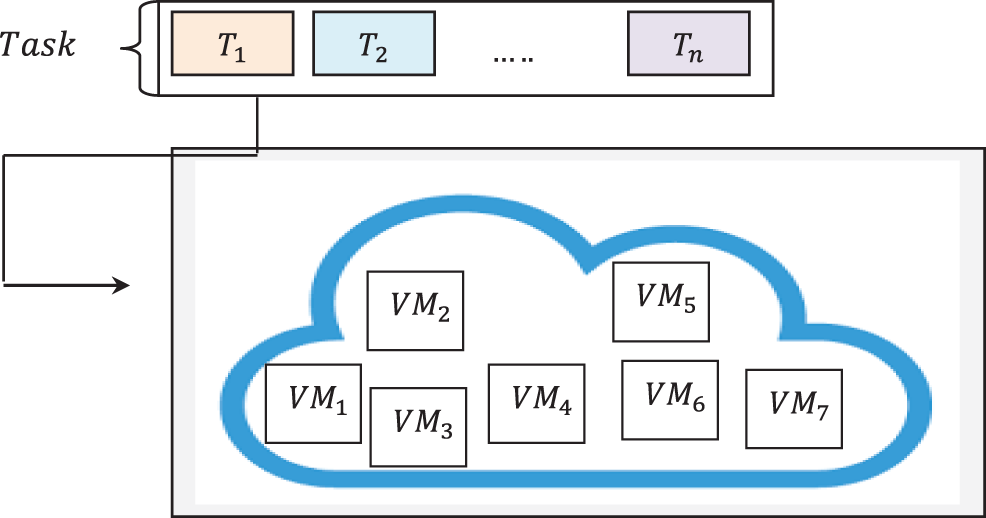
Figure 2: Proposed system model

3.2 Tricube Weighted Linear Regression-based Resource Estimation Model

Weighted Linear Regression-based Resource Estimation involves a statistical representation for quantitative resource analysis that is used to predict the future values of resources. In our work, multiple linear regressions are employed involving more than one input (i.e., a task in hand and the history or usage in terms of CPU utilization, RAM, and network bandwidth utilization). Multiple Linear Regression in our work models an approximation of a regression function by evaluating the relationship between input variable ‘ T={T1,T2,…,Tn} ’, ‘ UtilHistory={CPUi,Mi,Bi} ’ (i.e., tasks and utility history), and output variable ‘ R ’ (i.e., resource estimation) via linear regression line. The proposed Tricube Weighted Linear Regression-based Resource Estimation uses a simple weighted linear regression to predict future host utilization. This proposed model estimates the resources (CPU, RAM, and network bandwidth utilization) on the basis of the history of usage or utilization (i.e., utilization history) in each cloud server. Fig. 3 shows the structure of the Tricube Weighted Linear Regression-based Resource Estimation model.

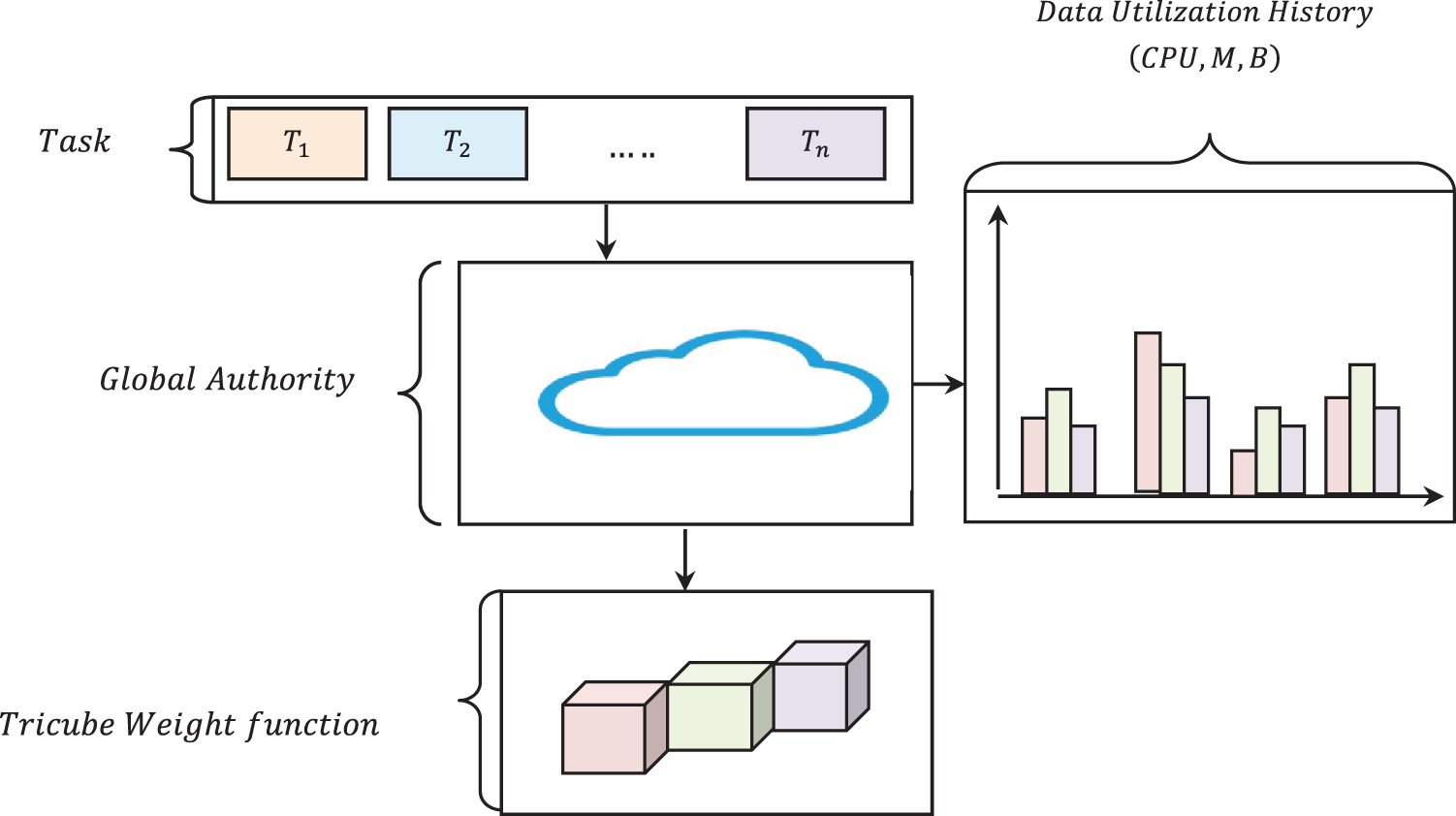
Figure 3: Structure of tricube weighted linear regression-based resource estimation model

As shown in the above figure, initially to start with the process of resource estimation in cloud computing environment, multiple regressions line for resource estimation is mathematically stated as given below.

S=α0+α1T[UtilHistory] (1)

From the above Eq. (1), ‘ S ’ represent the dependent variable, whereas ‘ T ’ and ‘ UtilHistory ’ denotes the independent variables with the regression coefficients being ‘ α0 ’ and ‘ α1 ’ respectively. The regression coefficients are then obtained via multiple regressions least square technique. This is mathematically expressed as given below

α0′=S−α1T[UtilHistory] (2)

α1′=∑i=1n⁡(Ti[UtilHistory]−T′)(Si−S′)∑i=1n⁡(Ti[UtilHistory]−T)2 (3)

From the above Eqs. (2) and (3), ‘ T′ ’, ‘ S′ ’ denotes the averages of ‘ T ’ and ‘ S ’ observations, and ‘ α0′ ’, ‘ α1′ ’ are resource estimations of ‘ α0 ’ and ‘ α1 ’ respectively. For each observation (i.e., Cloud Infrastructural Resourceestimation), ‘ Si,Ti ’, a locality quarter weight is allocated with the aid of Tricube weight function as given below.

Tri(CS)={(1−|v|3)3,if|v|<10,if|v|>1 (4)

Based on the above Tricube weight function ‘ Tri ’ for each task in the cloud server ‘ CS ’, the locality quarter weight is mathematically represented as given below.

Wi(T)=Tri(Tn−TiTn−T1)=[1−(Tn−TiTn−T1)3]3 (5)

From the above Eq. (5), ‘ Ti ’ and ‘ Tn ’, represents the ‘ i−th ’ and ‘ n−th ’, observations respectively. Let further the demand requirement of resource represented as ‘ (Tic,Tim,Tib) ’ and the available resource denoted as ‘ (CSic,CSim,CSib) ’. Then, the final cloud infrastructural optimized resource is mathematically represented as given below.

FTic=TicCSic (6)

FTim=TimCSim (7)

FTib=TibCSib (8)

From the above Eqs. (6)–(8), final cloud infrastructural resources, i.e., CPU utilization, ‘ FTic ’, memory consumption ‘ FTim ’ and bandwidth network utilization ‘ FTib ’ is measured based on the demand requirement of resource ‘ Tic,Tim,Tib ’ and the available resource ‘ CSic,CSim,CSib ’ respectively. The pseudo code representation of Tricube Locality Quarter Weight-based Cloud Infrastructural Resource estimation is given below.

The smaller requirement between requested tasks and the cloud server in the history, the higher the possibility of resources being optimized in the cloud computing environment between VMs.As given in the above Tricube Locality Quarter Weight-based Cloud Infrastructural Resource estimation algorithm, the objective remains in assigning the VM with the respective task in a queue by minimizing resource optimization time and maximizing resource optimization accuracy. With this objective, first, a multiple regressions line for resource estimation is obtained via multiple regressions least based on the utilization history. As a result, the resource estimation for each task is made in a computationally efficient manner, therefore reducing resource optimization time. Next, with the utilization of the Tricube weight function by estimating a locality quarter weight Cloud Infrastructural Resource estimation is made accurately, therefore improving the resource optimization accuracy.

3.3 Markov Inter Quartile-Based Virtual Machine Migration

At cloud Data Centers (DCs), the suitable optimization in power consumption via VM consolidation is perceived as prospective procedure for minimizing energy consumption. The prospective procedure synchronizes in an arbitrary fashion that in turn complements the active machines to the resource requirements while keeping others in sleep mode to conserve energy. The significant ascertainment of overloaded and under-loaded hosts is the paramount step in VM consolidation. On the basis of this, the significant options like VM migration to other hosts can be done, therefore reducing the energy and ensuring minimum number of migrations.

The objective of this work is to propose the Load Detection model Dynamic VM Consolidation based on Markov Inter Quartile-based VM Migration and provide the optimization for better performance and environment. The concentration of this work is on designing efficient VM consolidation employing flexible thresholds of load at hosts. The measurement of flexible threshold is obtained on the basis of the Markov Inter Quartile-based VM Migration. Fig. 4 shows the structure of Markov Inter Quartile-based VM Migration.

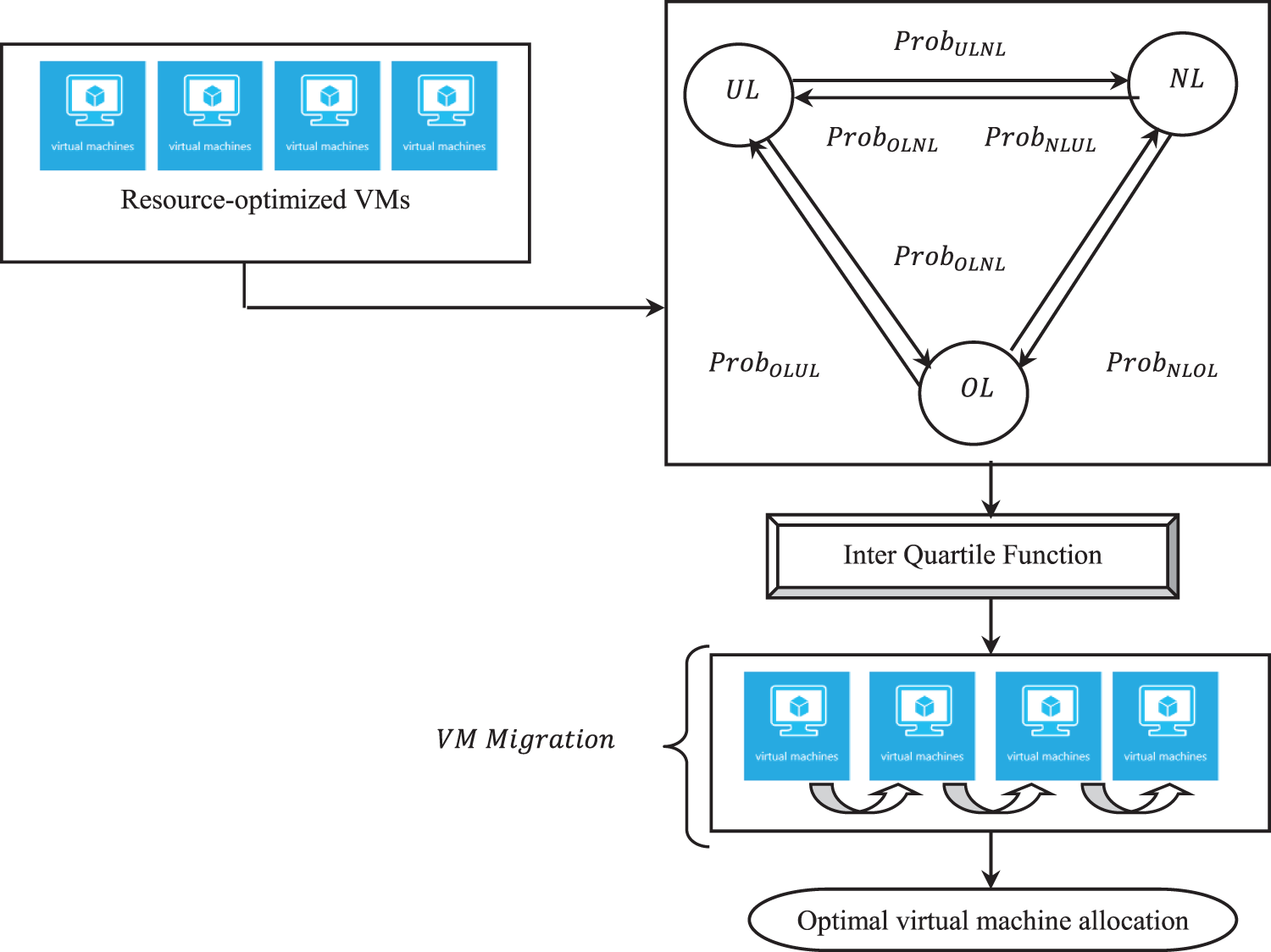
Figure 4: Structure of Markov Inter Quartile-based VM Migration

As illustrated in the above figure, to start with, in the Markov chain, the observed task ‘ T ’, discretized, so the observation task sequence ‘ T1,T2,….,Tn ’, where each of the variables ‘ Tn ’ may take one of ‘ n ’ distinct states ‘ {S1,S2,…,Sn} ’. In our work, three distinct states for a given host are feasible, Under-loaded ‘ UL ’, Normal-loaded ‘ NL ’ and Over-loaded ‘ OL ’ respectively. With this based on the results of the distinct states, either migration takes place or not by means of Inter Quartile Deviation function. Initially, the historical observations are obtained as given below.

Prob(Tn|Tn−1,Tn−2,…,T1)≈Prob(Tn|Tn−1) (9)

With the above historical observation of distinct task sequences ‘ Tn−1,Tn−2,…,T1 ’, the joint probability of ‘ n ’ observations are mathematically stated as given below.

Prob(T1,T2,…,Tn)=∏i=1n⁡Prob(Ti|Ti−1) (10)

Next, the state transition probability for each distinct task sequences is mathematically stated as given below.

Prob(Tn=Si|Tn−1=Sj) (11)

With the above result, the state transition probability matrix is represented as given below.

STPM=[ProbULULProbULNLProbULOLProbNLULProbNLNLProbNLOLProbOLULProbOLNLProbOLOL] (12)

The Inter Quartile Deviation function is defined as the difference between the ‘ 75−th ’ and ‘ 25−th ’ percentiles of data (i.e., host’s task). To calculate the ‘ IQD ’ function, the resource-optimized VMs task is split into quartiles. These quartiles are represented by ‘ Q1 ’ (i.e., lower quartile denoting the ‘ 25−th ’ percentiles of data), ‘ Q2 ’ (i.e., median) and ‘ Q3 ’ (i.e., upper quartile denoting the ‘ 75−th ’ percentiles of data). The overall function is mathematically stated as given below.

IQ3={[Q3(Hi[Ti])]−[Q1(Hj[Tj])]} (13)

Finally, with the results of the state transition probability matrix ‘ STPM ’ as given above (12), a threshold employing Inter Quartile Deviation ‘ IQD ’ function is utilized to see to that whether the host is over-loaded ‘ OL ’, under-loaded ‘ UL ’ or normally-loaded ‘ NL ’. Accordingly, migrations or either performed or not, therefore ensuring minimum energy and minimum number of migrations. The pseudo code representation of Markov Inter Quartile-based VM Migration is given below.

As given in the above algorithm, in addition to the Cloud Infrastructural Resource estimation using Tricube Locality Quarter Weight-based Cloud Infrastructural Resource estimation algorithm ensuring optimized resource-oriented VM allocation for each task, migration process for predicting overloading hosts using Inter Quartile Range is also designed. Upon detection of a host being overloaded, one of several VMs is distributed to other hosts to minimize host utilization followed by which the host is reversed to minimize power consumption by employing Inter Quartile Range function.

4  Experimental Settings

The efficiency of the proposed method is validated by conducting simulation with Cloud Simulator using Native Java Codes. Experimental evaluation is carried out using factors such as number of migrations, energy usage, resource optimization time and resource optimization accuracy with respect to number of user requests and iterations. To perform fair comparison simulation number of user requests and iterations are performed with the proposed TWLR-IQ method and two existing methods, Fuzzy-based Multidimensional Resource Scheduling and Queuing Network (F-MRSQN) [1] and D-JStorm [2].

The Cloud Infrastructural Resource Optimization is performed with the aid of Personal Cloud Datasets acquired from http://cloudspaces.eu/results/datasets. The dataset comprises of 17 attributes with an overall of 66245 instances. Among 17 attributes, two attributes namely time zone and capped are not utilized in our work, whereas the remaining attributes are employed for Infrastructural Resource Optimization with multiple user tasks. An overall of 10 simulation runs are performed for four distinct performance metrics number of migrations, energy usage, resource optimization time and resource optimization accuracy respectively.

5  Performance Metrics

In order to compare the efficiency of the TWLR-IQ method we use several metrics to evaluate their performance. The following metrics are used:

•   Resource optimization time

•   Resource optimization accuracy

•   Energy usage

•   Number of migrations

• Resource Optimization Time

Resource optimization time refers to the time consumed in optimally allocating the resources to the user requested tasks. This is mathematically formulated as given below.

ROT=∑i=1n⁡Ti∗Time(FTic+FTim+FTib) (14)

From the above Eq. (14), the resource optimization time ‘ ROT ’ is measured on the basis of the number of user requested tasks in queue in cloud environment ‘ Ti ’ and the time consumed in analyzing final cloud infrastructural optimized resource based on ‘ Time(FTic) ’, ‘ Time(FTim) ’ and ‘ Time(FTib) ’ respectively.

• Resource Optimization Accuracy

Resource optimization accuracy refers to the number of user requested tasks allocated with the accurate resources as requested. The resource optimization accuracy is mathematically stated as given below.

ROA=∑i=1nRAATi (15)

From the above Eq. (15), the resource optimization accuracy ‘ ROA ’, is measured based on the number of user requested tasks in queue in cloud environment ‘ Ti ’ to be allocated with the requested resources and the resources that has been actually allocated ‘ RAA ’. It is measured in terms of percentage (%).

• Energy Usage

Total energy usage is defined as the sum of energy consumed by physical resources (i.e., the tasks involved in the request process in cloud environment) of a data center as a result of application workloads (i.e., allocation of VMs). Total energy consumption is defined as the sum of energy consumed by physical resources (i.e., the tasks involved in the request process in cloud environment) of a data center as a result of application workloads (i.e., allocation of VMs).

EU=∑i=1n⁡Ti∗Energy(VMalloc) (16)

From the above Eq. (16), the energy usage ‘ EU ’ is measured based on the tasks involved in the request process in cloud environment ‘ Ti ’ and the energy usage involved in allocation of VMs ‘ Energy(VMalloc) ’ respectively. It is measured in terms of kilo watt hour (Kwh).

• Number of Migrations

For VM consolidation upon successful identification of the overloaded or under-loaded, the VMs are then selected for migration process. The minimization of VM migration time being the most significant restriction in migration and it is arrived at by the minimization of total number of migrations.

• Computational Complexity

Computational Complexity is determined as the different between the ending time and starting time measured for resource allocation in scheduling. The computational complexity is mathematically estimated as given below.

ComputationalComplexity=Endingtime−Startingtime (17)

From the above Eq. (16), the Computational Complexity is evaluated. It is measured in terms of milliseconds (ms).

5.1 Performance Analysis of Resource Optimization Time

Initially we start by evaluating the resource optimization time across different methods, TWLR-IQ, F-MRSQN [1] and D-JStorm [2] utilizing random workload traces as it is the easiest type of workload to begin our experiments without affecting operation. Fig. 5 shows the comparison of the PA-KJF [1] and D-JStorm [2] and the proposed method, TWLR-IQ based on their resource optimization time. Let us consider ‘100’ number of user requested task for experimentation, the time consumed by TWLR-IQ based to allocate the resources is 255 ms ’, whereas ‘ 315ms and ’ 485ms of time consumed by existing techniques F-MRSQN [1] and D-JStorm [2]. As revealed in the chart, the resource optimization time is gradually increased for all three methods while raising the number of user-requested tasks since the counts of data get increased for each run. But proposed TWLR-IQ method achieves better performance on average resource optimization time when compared to existing methods. To improve the average resource optimization time, the TWLR-IQ method uses Tricube Weighted Linear Regression-based Resource Estimation that estimates resources according to the Tricube Weight function.

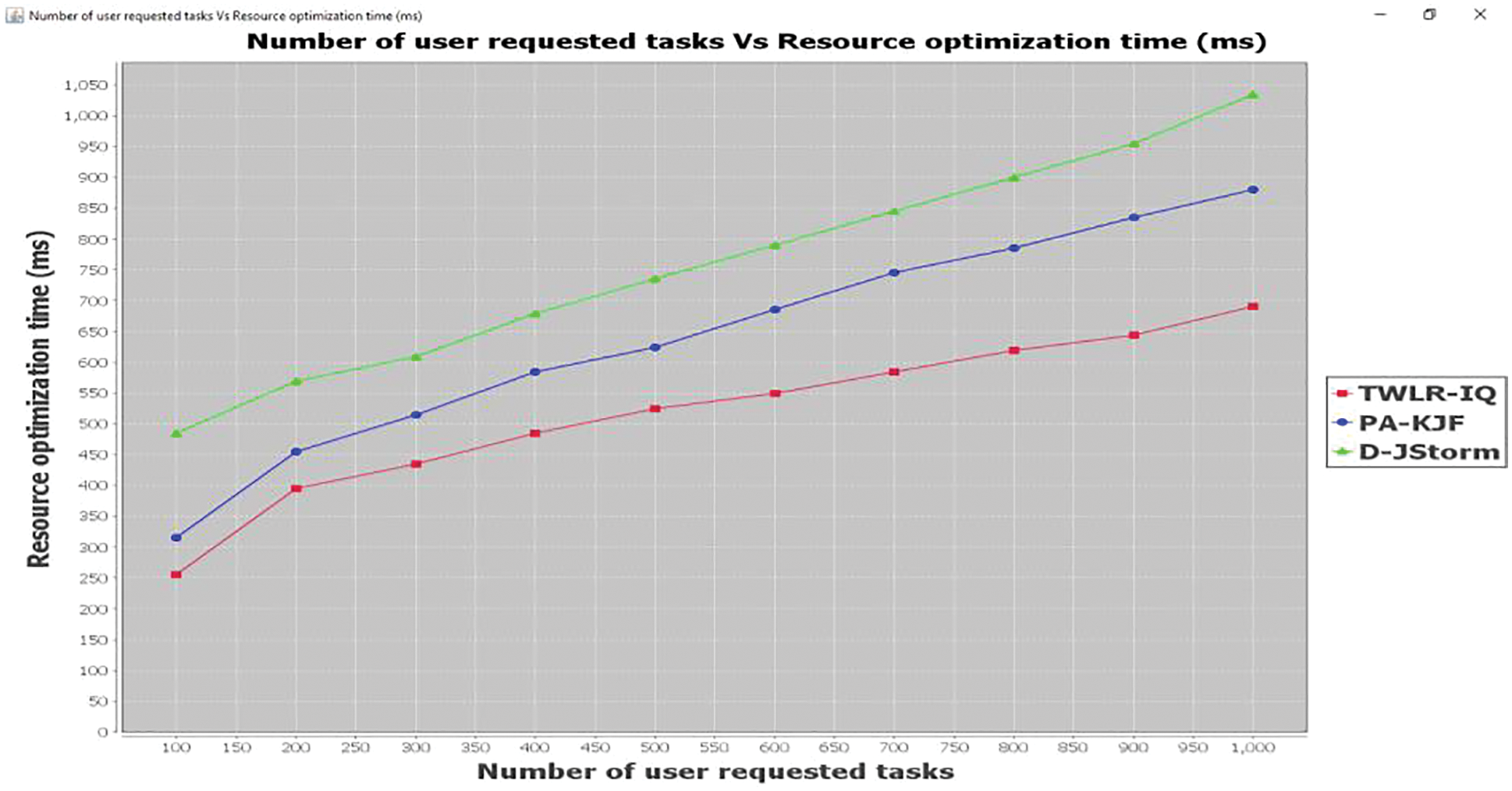
Figure 5: Graphical representation of resource optimization time

The Tricube Weight function performs efficient resource estimation. Hence TWLR-IQ method reduces average resource optimization time by 19%when compared to existing PA-KJF [1] and 32% when compared to existing D-JStorm [2] respectively.

5.2 Performance Analysis of Resource Optimization Accuracy

Second, we have evaluated the resource optimization accuracy using the proposed method, TWLR-IQ, and two state-of-the-art methods, F-MRSQN [1] and D-JStorm [2] with the assistance of random workload traces in the range of 100 and 1000. Let us considers 100 number of user requested for conducting the experiments in the first iteration. By applying the TWLR-IQ method, 95 resources are actually allocated and the resource optimization accuracy is 95% whereas the accuracy percentage of the existing [1] and [2] are 90% and 87% respectively. Followed by, various performance results are observed for each method. For each method, ten different results are observed. The performance result of resource optimization accuracy as given in Fig. 6.

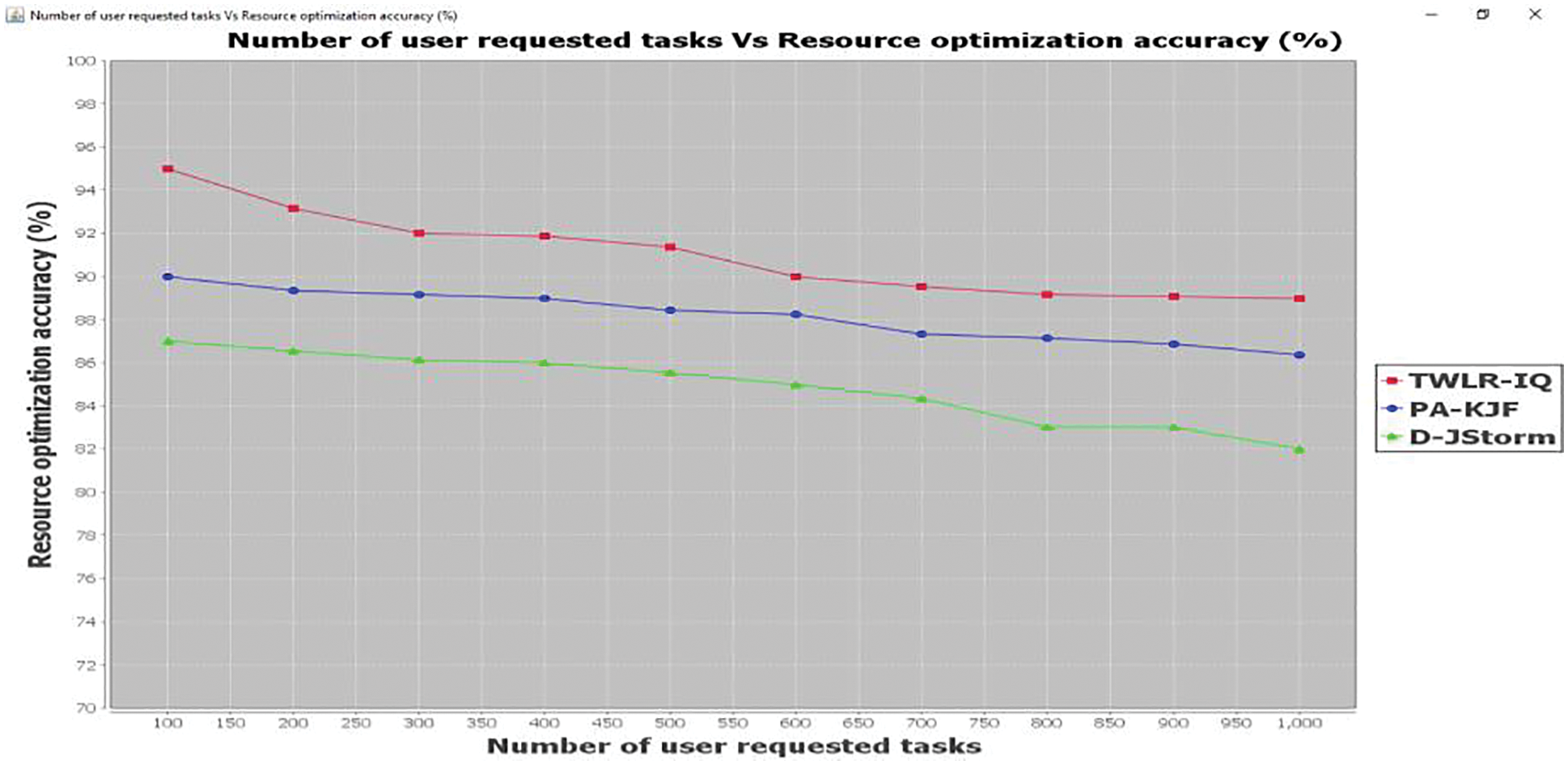
Figure 6: Graphical representation of resource optimization accuracy

This is because the multiple regressions least square technique using TWLR-IQ method schedules all user requested tasks based on the locality quarter weight. This in turn improves the resource optimization accuracy efficiency by 3% compared to PA-KJF [1] and 7% compared to D-JStorm [2] respectively.

5.3 Performance Analysis of Energy Usage

Third, the energy usage involved in the process of cloud infrastructural resource optimization is estimated employing the proposed method, TWLR-IQ, and two state-of-the-art methods, F-MRSQN [1] and D-JStorm [2]. With ‘100’ number of user requested task as input, the energy consumed by TWLR-IQ based to allocate the resources is 69.63 kwh, whereas ’ 72.35kwh and ’ 76.85kwh of time consumed by existing techniques F-MRSQN [1] and D-JStorm [2]. As revealed in the chart, the energy usage is gradually increased for all three methods while raising the number of user requested task since the counts of data get increased for each run.

Fig. 7 shows the performance of energy usage calculated using proposed TWLR-IQ method and compared with existing methods namely F-MRSQN [1] and D-JStorm [2]. This efficient reduction on energy usage is achieved using Markov Inter Quartile-based VM Migration algorithm. Hence energy usage is reduced in proposed TWLR-IQ method by 9% when compared to existing F-MRSQN [1] and 13% when compared to D-JStorm [2] respectively.

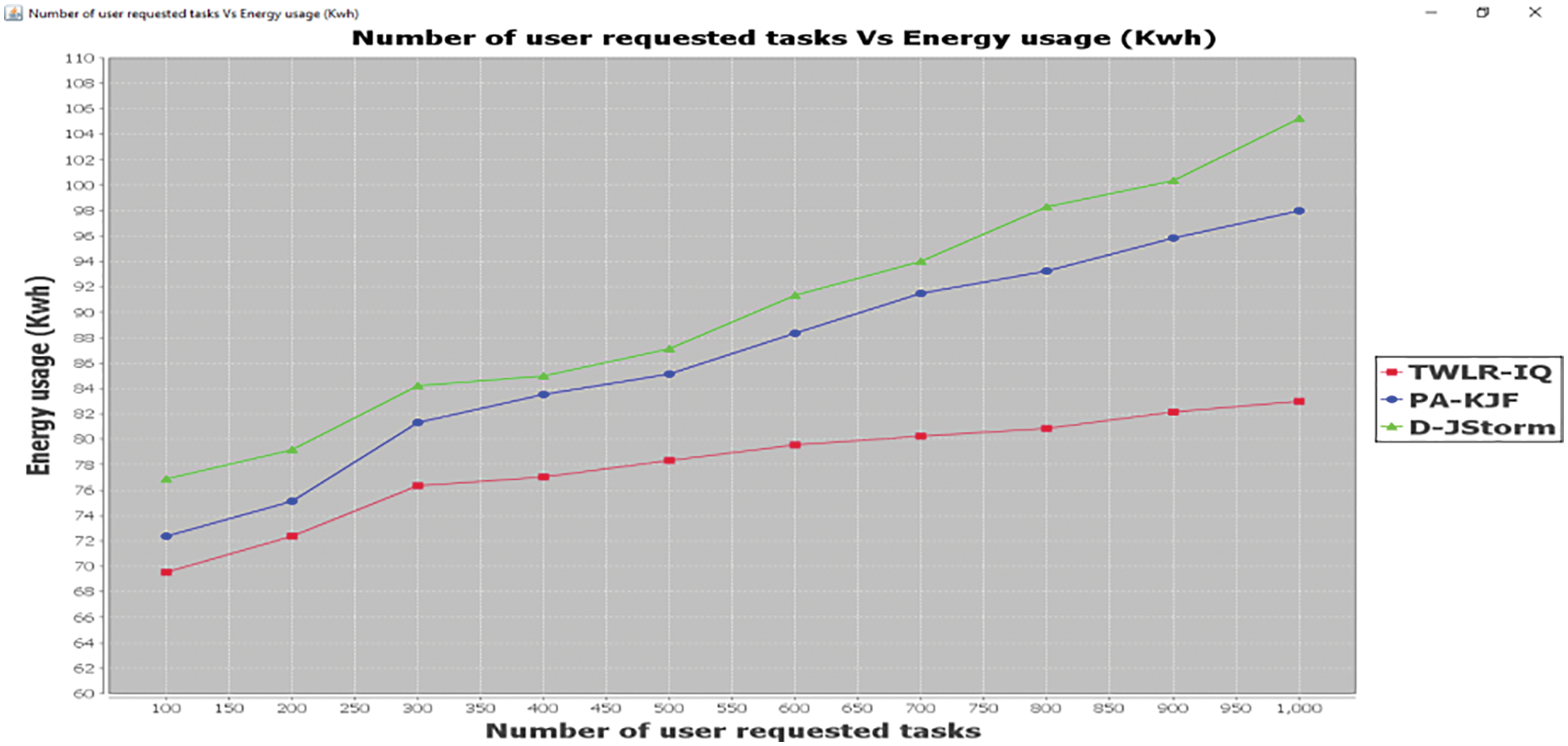
Figure 7: Graphical representation of energy usage

5.4 Performance Analysis of Number of Migrations

Fourth, the number of migrations involved during the process of cloud infrastructural resource optimization is provided in Fig. 8.

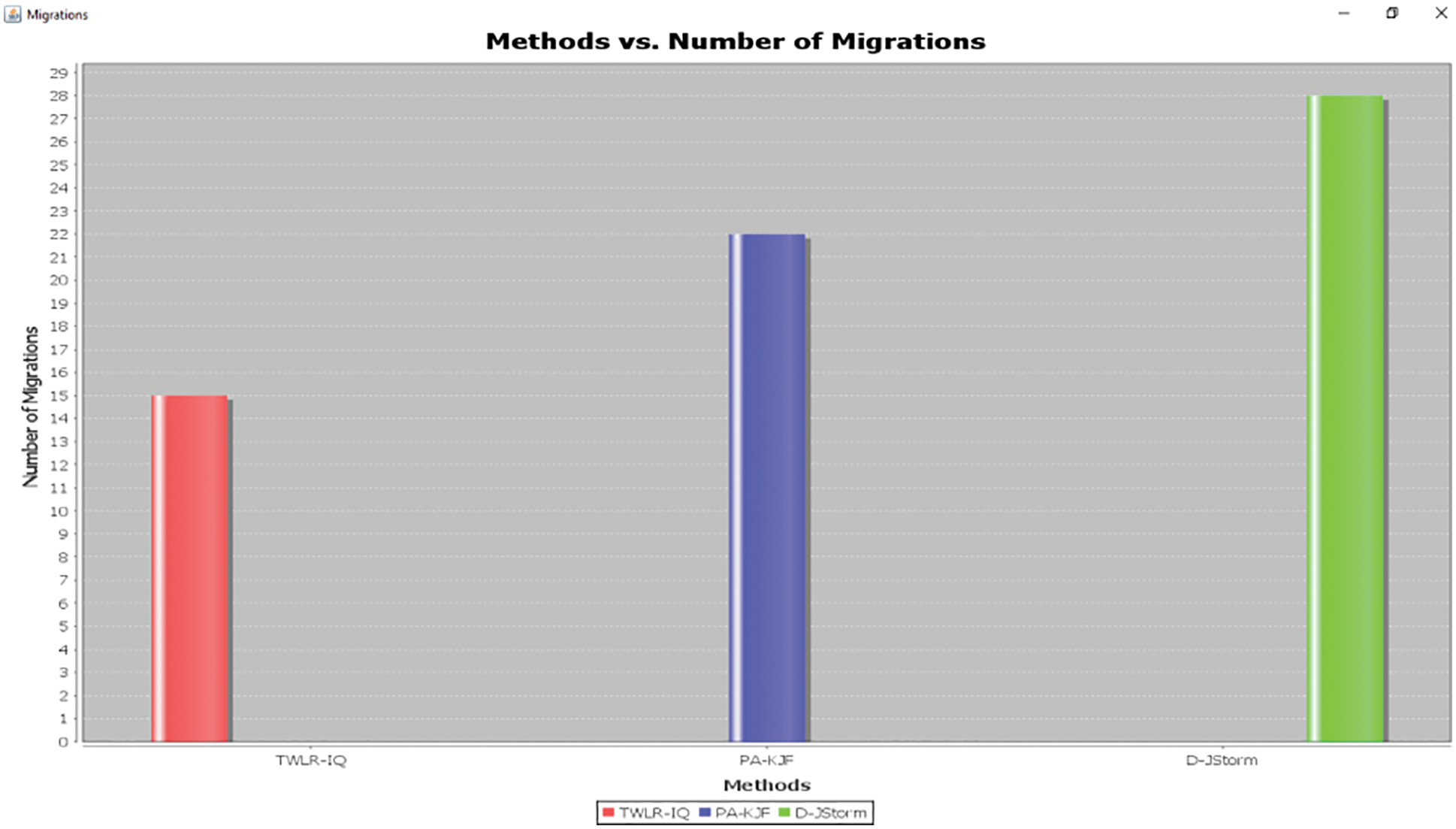
Figure 8: Graphical representation of number of migrations

Finally, Fig. 8 given above illustrates the number of migrations involved during cloud infrastructural resource optimization process. The reason behind the minimum number of migrations using TWLR-IQ method is due to the application of Tricube Locality Quarter Weight-based Cloud Infrastructural Resourceestimation algorithm. Therefore minimizing the overall number of migrations. This is said to be reduced using TWLR-IQ method by 53% compared to [1] and 27% compared to [2].

5.5 Performance Analysis of Computational Complexity

Finally, the computational complexity involved in the process of cloud infrastructural resource optimization is measured by using the proposed method, TWLR-IQ, and conventional methods, F-MRSQN [1] and D-JStorm [2].

Fig. 9 demonstrates the graphical results of computational complexity for three methods such as TWLR-IQ method, existing PA-KJF [1] and D-JStorm [2]. The different number of user requested tasks is taken as input to estimate evaluating the performance of computational complexity in cloud. However, proposed TWLR-IQ method comparatively minimizes the computational complexity than the existing works. Let us consider 100 number of user requested task. In the first iteration, computational complexity is observed as 28 ms for proposed TWLR-IQ method whereas 28 ms and 38 ms of computational complexity is observed in existing PA-KJF [1] and D-JStorm [2] respectively. The reason for minimizing the computational complexity in cloud is to perform the efficient resource estimation by using Tricube Weighted function. Also, Data utilization history is applied to measure the resource estimation depended on the prior with aid of multiple regressions. As a result, the resource estimation for all tasks is done with minimum resource computational complexity.

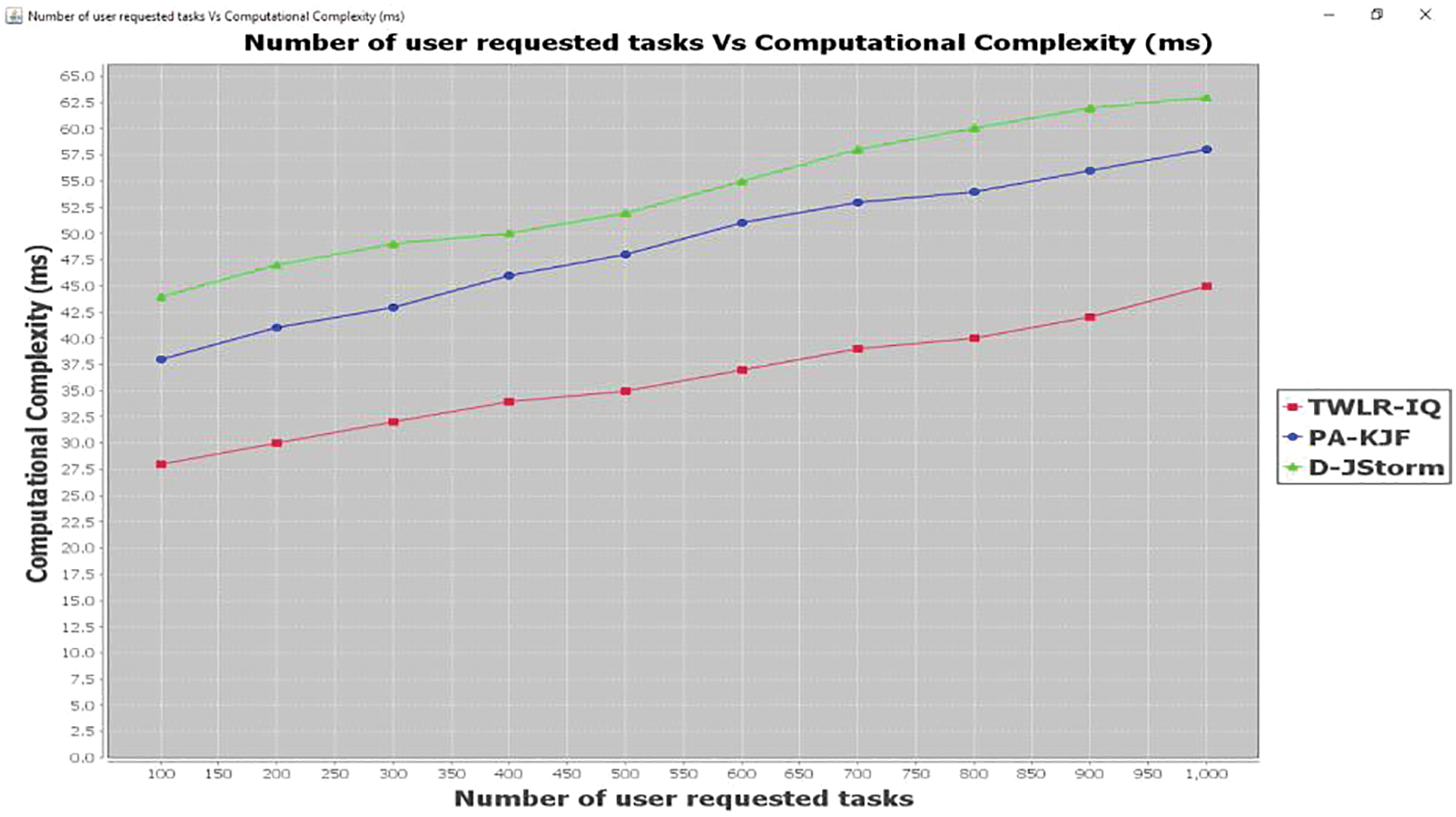
Figure 9: Graphical representation of computational complexity

6  Conclusion

With the development of cloud computing, machine learning, and artificial intelligence, cloud infrastructural resource demands demonstrate the characteristics of high energy utilization, time, and a maximum number of migrations owing to the overloaded nature. Unquestionably, cloud infrastructures frequently experience such emergent resource optimizations which require to be allocated resources swiftly and optimally. This paper proposes a Tricube Weighted Linear Regression-based Inter Quartile (TWLR-IQ) for Cloud Infrastructural Resource Optimization for resource estimations. The priority of resource allocation is initially designed to respond to resource estimations, and resource performance based on the history of utilization and resource proportion matching are entrenched to perceive resource optimization and balanced utilization of all types of resources. Then, a Markov Inter Quartile-based VM Migration algorithm for analyzing load is presented to guarantee the timeliness and optimization of resource allocation. Experiments are performed to compare our proposed TWLR-IQ method with the state-of-the-art methods. The results of this study verify the efficiency of our method to meet the emergent demands in cloud computing with maximum accuracy by reducing the energy and time involved during migrations. The proposed TWLR-IQ method failed to measure the throughput, makespan metric. In the future, the proposed method is further extended to estimate the throughput, makespan for optimized resource utilization VM.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Priya, C. S. Kumar and R. Kannan, “Resource scheduling algorithm with load balancing for cloud service provisioning,” Applied Soft Computing Journal, Elsevier, vol. 76, no. 1, pp. 416–424, 2019. [Google Scholar]

 2.  Y. Hu, H. Wang and W. Ma, “Intelligent cloud workflow management and scheduling method for big data applications,” Journal of Cloud Computing: Advances, Systems and Applications, Springer, vol. 9, no. 39, pp. 1–13, 2020. [Google Scholar]

 3.  X. Sun, Z. Wang, Y. Wu, H. Che, H. Jiang et al., “A price-aware congestion control protocol for cloud services,” Journal of Cloud Computing: Advances, Systems and Applications, vol. 10, no. 55, pp. 1–15, 2021. [Google Scholar]

 4.  P. Nawrocki and P. Osypanka, “Cloud resource demand prediction using machine learning in the context of QoS parameters,” Journal of Grid Computing, Springer, vol. 19, no. 20, pp. 1–20, 2021. [Google Scholar]

 5.  J. Dizdarevic, Z. Avdagic, F. Orucevic and S. Omanovic, “Advanced consistency management of highly-distributed transactional database in a hybrid cloud environment using novel R-TBC/RTA approach,” Journal of Cloud Computing: Advances, Systems and Applications, Springer, vol. 10, no. 27, pp. 1–31, 2021. [Google Scholar]

 6.  S. S. Chauhan, E. S. Pilli and R. C. Joshi, “BSS: A brokering model for service selection using integrated weighting approach in cloud environment,” Journal of Cloud Computing: Advances, Systems and Applications, vol. 10, no. 26, pp. 1–14, 2021. [Google Scholar]

 7.  L. Tang, B. Tang, L. Zhang, F. Guo, H. He et al., “Joint optimization of network selection and task offloading for vehicular edge computing,” Journal of Cloud Computing: Advances, Systems and Applications, vol. 10, no. 23, pp. 1–13, 2021. [Google Scholar]

 8.  M. Amaral, J. Polo, D. Carrera, N. Gonzale, C. C. Yang et al., “DRMaestro: Orchestrating disaggregated resources on virtualized data-centers,” Journal of Cloud Computing: Advances, Systems and Applications, vol. 10, no. 22, 2021. [Google Scholar]

 9.  J. KokKonjaang and L. Xu, “Multi-objective workflow optimization strategy (MOWOS) for cloud computing,” Journal of Cloud Computing: Advances, Systems and Applications, Springer, vol. 10, no. 11, pp. 1–19, 2021. [Google Scholar]

10. J. Chen, T. Du and G. Xiao, “A multi-objective optimization for resource allocation of emergent demands in cloud computing,” Journal of Cloud Computing: Advances, Systems and Applications, Springer, vol. 10, no. 20, pp. 1–17, 2021. [Google Scholar]

11. H. S. Madhusudhan, S. T. Kumar, S. M. F. D. SMustapha, P. Gupta, R. P. Tripathi et al., “Hybrid approach for resource allocation in cloud infrastructure using random forest and genetic algorithm,” Scientific Programming, Hindawi, vol. 2021, no. 4924708, pp. 1–10, 2021. [Google Scholar]

12. W. Qi, “Optimization of cloud computing task execution time and user QoS utility by improved particle swarm optimization,” Microprocessors and Microsystems, Elsevier, vol. 80, no. 1, pp. 103529, 2021. [Google Scholar]

13. S. Ramamoorthy, G. Ravikumar, B. S. Balaji, S. Balakrishna, K. Venkatachalam et al., “MCAMO: Multi constraint aware multiobjective resource scheduling optimization technique for cloud infrastructure services,” Journal of Ambient Intelligence and Humanized Computing, Springer, vol. 12, no. 6, pp. 5909–5916, 2020. [Google Scholar]

14. V. Simic, B. Stojanovic and M. Ivanovic, “Optimizing the performance of optimization in the cloud environment–An intelligent auto-scaling approach,” Future Generation Computer Systems, Elsevier, vol. 101, no. 1, pp. 909–920, 2019. [Google Scholar]

15. M. Kumar, S. C. Sharma, A. Goel and S. P. Singh, “A comprehensive survey for scheduling techniques in cloud computing,” Journal of Network and Computer Applications, Elsevier, vol. 143, no. 2, pp. 1–33, 2019. [Google Scholar]

16. H. Yu, “Evaluation of cloud computing resource scheduling based on improved optimization algorithm,” Complex & Intelligent Systems, Springer, vol. 7, pp. 1817–1822, 2020. [Google Scholar]

17. P. Nawrocki and P. Osypanka, “Cloud resource demand prediction using machine learning in the context of QoS parameters,” Journal of Grid Computing, vol. 19, no. 20, pp. 1–20, 2021. [Google Scholar]

18. X. Gao, R. Liu and A. Kaushik, “Hierarchical multi-agent optimization for resource allocation in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 3, pp. 677–692, 2021. [Google Scholar]

19. W. Dai, L. Qiu, A. Wu and M. Qiu, “Cloud infrastructure resource allocation for big data applications,” IEEE Transactions on Big Data, vol. 4, no. 3, pp. 313–324, 2018. [Google Scholar]

20. H. Zhang, Y. Wu and Z. Sun, “EHEFTR: Multiobjective task scheduling scheme in cloud computing,” Complex & Intelligent Systems, Springer, pp. 1–8, 2021. [Google Scholar]

21. M. Manikandan, R. Subramanian, M. S. Kavitha and S. Karthik, “Cost effective optimal task scheduling model in hybrid cloud environment,” Computer Systems Science & Engineering, vol. 42, no. 3, pp. 935–948, 2022. [Google Scholar]

22. S. Wang, W. Wang, Z. Jia and C. Pang, “Flexible task scheduling based on edge computing and cloud collaboration,” Computer Systems Science & Engineering, vol. 42, no. 3, pp. 1241–1255, 2022. [Google Scholar]

23. D. Zhang and G. Yin, “A Virtual Machine Placement Strategy Based on Virtual Machine Selection and Integration,” Journal on Internet of Things, vol. 3, no. 4, pp. 149–157, 2021. [Google Scholar]

24. S. Nabi, M. Ibrahim and J. M. Jimenez, “DRALBA: Dynamic and resource aware load balanced scheduling approach for cloud computing,” IEEE Access, vol. 9, pp. 61283–61297, 2021. [Google Scholar]

25. X. Guo, “Multi-objective task scheduling optimization in cloud computing based on fuzzy self-defense algorithm,” Alexandria Engineering Journal, Elsevier, vol. 60, no. 6, pp. 5603–5609, 2021. [Google Scholar]

26. H. Emami, “Cloud task scheduling using enhanced sunflower optimization algorithm,” ICT Express, Elsevier, vol. 8, no. 1, pp. 97–100, 2021. [Google Scholar]