Dipper Throated Algorithm for Feature Selection and Classification in Electrocardiogram

1  Introduction

High fatality and morbidity rates are caused mainly by the heart disease as one of the most common diseases in the world with over 385,000 individuals dying each year. A heart attack happens every 34 s [1,2] in the United States alone. An erratic heartbeat, also known as cardiac arrythmia, is the most noticeable indication of heart disease. The ECG, which records electrical impulses produced by the heart from electrodes put on the body and visually visualizes the patterns of activity, is the most routinely used technique for assessing heart function [3]. P, Q, and QRS complex waves are the primary variables produced by ECG signals. The interval, form, and correlations of P, Q, and QRS complex wave characteristics in heart disease patients may be studied using a variety of basic factors. Any abrupt change in these limitations implies a cardiac condition in which the heartbeat is irregular, either quicker or slower than normal. Arrythmia can be caused by a number of different things [4]. As a result, arrythmia should be identified and treated as quickly as feasible. Arrhythmia is most commonly associated with the start of a cardiac disease such as insufficient blood flow from the heart, shortness of breath, chest discomfort, tiredness, or unconsciousness. An aberrant ECG signal can be seen [5,6]. Both bradycardia and tachycardia are types of arrhythmias. Bradycardia is defined as a heartbeat that is less than 60 beats per minute (bpm), whereas tachycardia is defined as a pulse that is greater than 100 bpm [7]. The need of efficient and precise arrhythmia categorization and detection is becoming clear with the advent of remotely managed healthcare systems for heart disease patients. In the last few years, diagnostic systems based on various machine learning (ML) algorithms have been developed to increase the accuracy of arrhythmia classification from ECG recorded signals, which is a difficult problem [8]. It is difficult to choose appropriate procedures for detecting and classifying cardiac disease. It entails taking into account the setting, data analysis, and the individual requirements of patients [9]. ML methods employ techniques that let a computer to learn from its own experiences rather than having to be explicitly programmed. The goal is to create an algorithm that can take a group of patterns and automatically generalize from them without the need for human intervention. Cluster analysis, or clustering, is an unsupervised ML technique. Clustering is a technique for categorizing observations into different groups depending on how similar the objects in each category are. Several intelligent disease diagnostic systems [10–15] have implemented clustering methods.

Electrocardiogram (ECG) represents the electrical activity of the heart and picked up using electrodes placed around the heart of the patient. ECG signal provides information about heart beats, regularity of heart rhythm, and detection of heart failure along with disorders that affects performance of the heart. A normal ECG signal is showing in Fig. 1.

Figure 1: Normal electrocardiogram signal

The normal ECG signal can be divided into three waves (P-QRS, T), two segments (PR, ST), and four intervals (PR, QRS, ST, QT). P wave represents the contraction of the atria it’s amplitude lies between (0.2–0.25 mV) while it’s duration lies between (0.06–0.12 s). The QRS complex marks the start of the contraction of the ventricles, it’s amplitude between (0.5–3 mV) and duration between (0.06–0.1 s). The T wave corresponding to the relaxation of the ventricles, it’s amplitude in range of (0.1–0.8 mV) and duration between (0.05–0.25 s). In Normal ECG recording PR interval is between (0.12–0.2 s) while normal QRS duration lies between (0.06–0.10 s), QT interval lies between (0.36–0.44 s). the QT interval between (0.36–0.44 s) and ST segment between (0.08–0.12 s). ECG is a non-stationary signal; it has multiple frequencies. The QRS wave oscillates faster than the T wave which is also faster than P wave. The ECG signal acquires noise from the power supply and interference from breathing muscle, which have to be removed before processing of ECG signals. So it’s very difficult to analyze ECG signal, beside that the clinical observation takes long time. According to this automatic analysis of ECG signal is preferred to done by computers. Arrhythmias is the oddity of the ECG signal from the above normal measurements and specifications, it reflects a fast or slow heart beats (tachycardia, bradycardia) or irregular ECG patterns.

Ventricular arrhythmias are the popular type of cardiac arrhythmias leading to abnormal heartbeat causing approximately 79% of sudden death. As soon as the arrhythmia is detected the cardiac arrest can be avoided. Therefore, it is safe to conclude that regular heart rate monitoring is essential to prevent cardiovascular disease. Arrhythmia detection in ECG signals has attracted many researchers [4]. Nowadays, automated diagnostic systems of heart disease are widespread, ranging from choosing the most powerful suffering factors to physicians in making independent decisions. In addition to the unseen morphological features, wavelet, and mathematical features have also been proven to be effective in diagnosis [16]. During last years, different algorithms of machine learning provide accurate ECG signal analysis [17], making ECG analysis more brilliant and effective [18]. Many methods have been proposed for identifying cardiac arrhythmias with advantages and drawbacks. The next section of the paper presents a literature review of arrythmias classification.

We present a new approach to improve arrhythmia classification prediction accuracy. We employed the dipper throated optimization algorithm for optimizing the feature selection and the K-nearest neighbors’ classifier for categorizing patients into one of 16 arrhythmia types. The medical industry can benefit greatly from this approach to arrhythmia categorization. The categorization helps in determining if an arrhythmia exists or not. The dataset for the simulation came from the UCI Machine Learning arsenal, and the results showed a significant improvement in classification accuracy.

The following is how the rest of the paper is organized. The basis of arrhythmia categorization is discussed in Section 2. The method and strategy proposed are explained in Section 3. The simulation results for the suggested technique are presented in Section 4. Section 5 concludes this work by summarizing the results and suggesting areas for further investigation.

2  Literature Review

Several methods for detecting and classifying cardiac arrhythmia have been presented in the last two decades. Simple statistical learning, traditional machine learning, and more contemporary deep learning techniques are all examples of these approaches.

Filtering to remove noise from ECG [19], signal segmentation [20], and feature extraction [21] are the most used methods to detect arrhythmia. Different researchers classify arrhythmias using machine learning (ML) and data mining, we will now discuss several proposed algorithms. The first research used discrete wavelet transform to identify QRS, reduce the noise using empirical modern distribution and classify five types of arrythmias using support vector machine (SVM) with 98% accuracy of 99% sensitivity [22]. Another research used statistics and Hermite coefficient in detection of QRS and SVM to classify 5 different types of arrhythmia with 98% averaging accuracy. Although the high accuracy but this method suffers from high computation cost. Another Algorithm used higher order multidimensional Fourier transform for feature extraction, and SVM to classify five different types of arrhythmia with 99% accuracy [23]. Also, a higher order multidimensional Fourier transform for feature extraction, and SVM for classification are used in [24]. A new idea used a least square support vector machine in the classification process suggested in [25].

Particle swarm optimization (PSO)is used to increase the performance of SVM in classification of five types of arrhythmia by fine tune the discriminator function for selecting the best features is introduced in [26]. The authors adopted their algorithm to two existing classifiers the first one is K-nearest neighbors (KNN) while the second is radial basis function neural networks. Genetic algorithm is used to optimize the discriminator function, and modified SVM for classification of arrythmia is used in [27]. Authors in [28] proposed a least square SVM classifier to classify heartbeat with 96% accuracy. Discrete wavelet transform is used for feature representation with SVM classifier to classify five types of arrhythmias with 98% accuracy is proposed in [29]. A random decision forest classifier and discrete cosine transform for detecting R-R interval are proposed as a new classifier for arrythmia classification in [30].

A novel classifier is proposed to classify seventeen different types of arrhythmias [30]. It works in two steps; the first by identifies the P wave and the QRS complex using the Pan-Tompkins method, while the second step KNN classifier is used to classify them. A Graphic Processing Unit based cloud system used for arrhythmia classification with two stages as in [31] is presented in [32]. Machine learning model are strongly affected by feature architecture and extraction. Basic idea after learning to incorporate all data in ECG signals for the ML algorithm to read and select functions. This theory also supports the deep learning model, especially convolutional neural network and its 1-D equivalent [33]. As a result of the power and optimism of deep learning strategies, researchers [34–36] use these methods for the classification of different types of diseases. A conventional neural network (CNN) model for prediction of heart attack with 95% is presented in [37]. A proposed automated classifier for arrhythmias introduces in [38]. Another proposed automated CNN model is built for classification of ventricular arrhythmias with 93% accuracy, 95% sensitivity is presented in [39].

A suggested algorithm used short term Fourier transform and wavelet transform for the classification of arterial fibrillation. Also, a CNN model is built to interpret ECG segments [40]. Another proposed algorithm uses 5-layer CNN to classify arrhythmias which provides accuracy but have a problem of vanishing gradient [41]. A proposed end to end CNN model is built for the classification of cardiac arrest during cardiopulmonary resuscitation with 89% accuracy for ventricular fibrillation [42]. Another research used convolution deep neural network for the classification of arrythmia and optimization using random search is presented in [43]. Two deep neural network architectures are used to classify electrical activity and generating rhythm using ECG reading and used Bayesian optimizer and provide 93% accuracy proposed in [44]. A proposed algorithm for classification of atrial fibrillation that includes connections in CNN, which increase the speed of data transmission and reduces the dependencies between data presented in [45]. three different algorithms: CNN, CNN+LSTM and CNN+ LSTM+ attention is proposed for the arrhythmia classification presented in [46,47]. Another algorithm proposed a CNN-LSTM model with converting the ECG signal into the time and frequency domain to train his model presented in [48] and achieves 89% accuracy. Tab. 1 presents a summary of the electrocardiogram classification methods in the literature.

3  Methodology

In this paper, we propose the application of the dipper throated optimization (DTO) algorithm to select the significant features of the given dataset. In addition, we employed DTO algorithm to optimize the parameters of the K-NN classification algorithm. Practically, the process starts with preprocessing the records of the dataset to ensure the consistency and integrity of the recorded data. The coming sections present the main steps of the proposed approach.

3.1 Preprocessing

In contrast to those characteristics with tiny numeric values, the features in the arrythmia dataset have huge numeric values, which have a significant impact on classification accuracy. For many attributes in the dataset utilized in this research, there is an inclusive numeric fluctuation. For these sorts of characteristics, data normalization is employed to limit the effect of the response variables. Data normalization aims to improve the classification model's performance by limiting the impact of higher-valued features. The numeric stability of the proposed approach is improved by using a scaling and centering strategy for data normalization [49].

3.2 Dipper Throated Optimization Algorithm

This algorithm is proved as an efficient metaheuristic optimization algorithm inspired by the hunting dipper throated bird that performs rapid bowing movements. The main formulation of this algorithm is expressed in terms of the following equations [50].

X=[X1,1X1,2X1,3…X1,dX2,1X2,2X2,3…X2,dX3,1X3,2X3,3…X3,d……………Xm,1Xm,2Xm,3…Xm,d] (1)

Y=[Y1,1Y1,2Y1,3…Y1,dY2,1Y2,2Y2,3…Y2,dY3,1Y3,2Y3,3…Y3,d……………Ym,1Ym,2Ym,3…Ym,d] (2)

h=[h1(X1,1,X1,2,X1,3,…,X1,d)h2(X2,1,X2,2,X2,3,…,X2,d)h3(X3,1,X3,2,X3,3,…,X3,d)…hm(Xm,1,Xm,2,Xm,3,…,Xm,d)] (3)

X(i+1)={Xbest(i)−K1.|K2.Xbest(i)−X(i)|ifR<0.5X(i)+Y(i+1)otherwise (4)

Y(i+1)=K3Y(i)+K4r1(Xbest(i)−X(i))+K5r2(XGbest−X(i)) (5)

where the location and speed of the ith bird in the jth dimension are denoted by Xi,j and Yi,j for i∈1,2,3,…,m and j∈1,2,3,…,d . For each bird, the values of the fitness functions h=h1,h2,h3,…,hn are used to find the best values of locations and speed of each bird, which is used to find the best solution. The steps of the dipper throated optimization algorithm are depicted in Fig. 2.

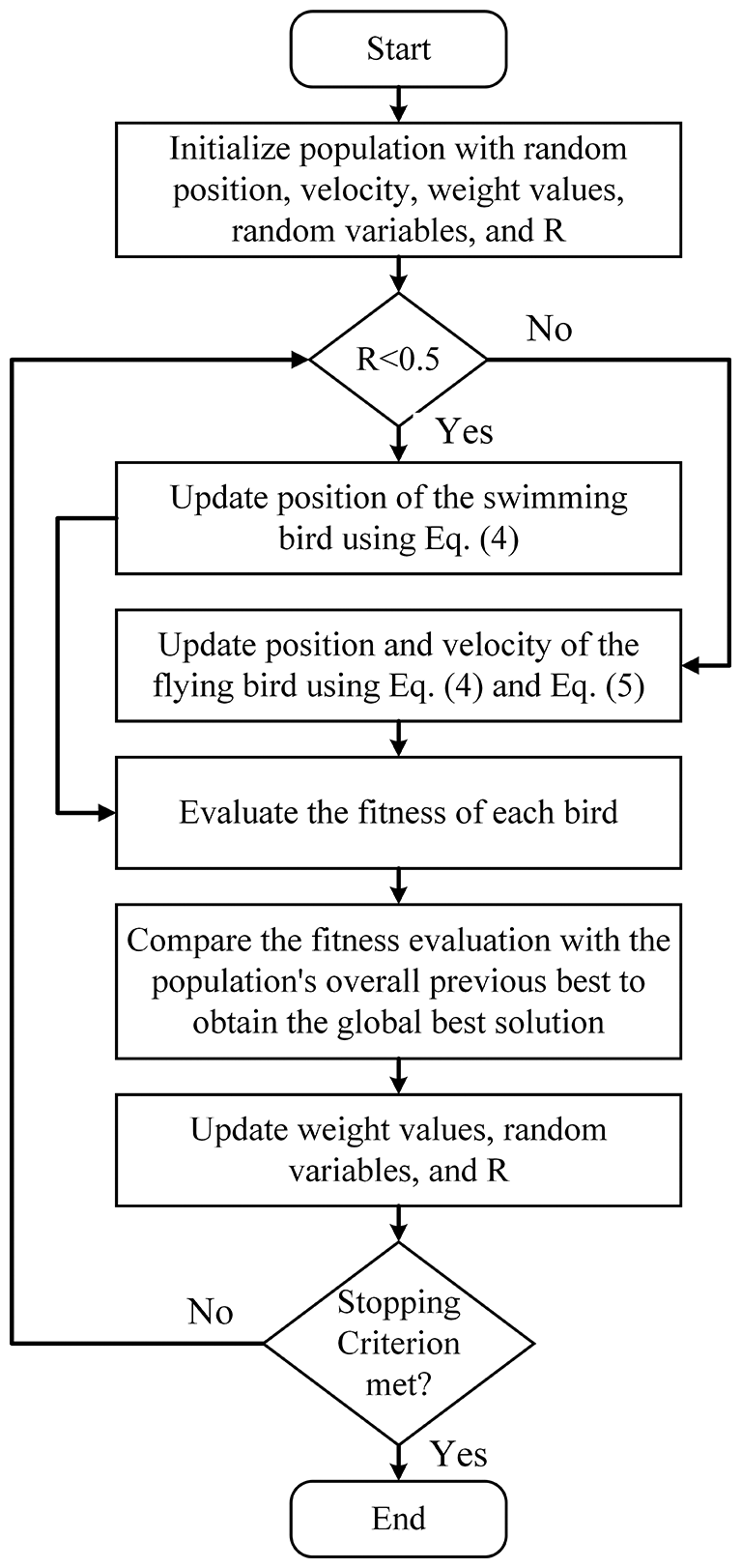
Figure 2: The steps of the dipper throated optimization algorithm

3.3 Feature Selection

The challenge in selecting features is unique since the search space is limited to two binary values, 0 and 1. Consequently, we used the sigmoid function to turn the normal optimizer’s output into something that works for our purpose. To fit the feature selection problem, we apply the following equation to transform the continuous solution to binary.

S(i+1)={0ifSigmoid(SBest)<0.51otherwiseSigmoid(SBest)=11+e−10(SBest−0.5) (6)

where S(i+1) is the updated binary position at iteration i and SBest is the best position retrieved by the dipper throated optimization algorithm.

3.4 K-Nearest Neighbors Classifier

The query instance’s KNN prediction is based on the category of nearest neighbors’ simple majority. To calculate the K-nearest neighbors, it uses the shortest distance between the query instance and the training examples. Euclidean distance, which is defined in the following equation, is a widely used distance metric.

d2ij(n)=∑m=1M⁡{xi(n,m)−xj(n,m)}2 (7)

where the training set is denoted by xi(n, m) and the testing set is denoted by xj(n, m) for nth sample and mth feature dimension. The detailed steps of KNN classifier are shown in Fig. 3.

Figure 3: The steps of the K-nearest neighbors’ classifier

4  Experimental Results

The UCI ML Repository [27] provided the dataset. There is a total of 452 of them. Each row represents a separate patient’s medical data. 279 characteristics, including as weight, height, and age, are included in the electrocardiography-related dataset. Our major objective was to classify arrhythmia recordings into 16 different types based on their presence or absence. The normal ECG was represented by class 01 of arrhythmia, whereas classes 02 through 15 indicated various pathological classes of arrhythmia, and class 16 represented an unidentified group of patients. As illustrated in Fig. 4, a considerable number of classes are uncategorized, with 245 examples belonging to class 01 and 185 instances dispersed among 14 different types of arrhythmia classes [51,52].

Figure 4: Arrhythmia instances distribution in several classes

To prove the effectiveness of the proposed approach, a set of experiments were conducted to assess the performance of the steps of the proposed approach. The first experiment was conducted to assess the feature selection process using the dipper throated optimization algorithm. The results presented in Tab. 2 records the achieved findings using the proposed approach with comparison to other six feature selection algorithms. As shown in this table, the results achieved by the proposed approach outperform those achieved by the other algorithms.

On the other hand, to chose the classifier that is best convenient for the task in hand, three classifiers were evaluated to find the best classifier. Tab. 3 presents the assessment of the three classifiers. As shown in the table, the best performance was achieved by the KNN classifier. Therefore, this classifier is adopted for the optimization and classification of the dataset in hands.

Another set of experiments is conducted to evaluate the performance of the optimization applied to the KNN classifier. In these experiments, five optimization approaches were used to optimize the parameters of KNN classifier, and the results are recorded in Tab. 4. In this table, a statistical analysis is presented. The results achieved by the proposed approach are shown as the best results among the other results achieved by the other approaches.

The Wilcoxon signed rank test is performance to measure the statistical difference between the proposed approach and the other approaches. Tab. 5 presents the results of this analysis. The recorded results emphasize our expectations and show that there is no statistical difference between the proposed and other approaches.

In addition, the one-way analysis of variance (ANOVA) test is performed to study difference between the proposed approach and the other approach using different hypothesis. The results are shown in Tab. 6.

Moreover, Fig. 5 shows six plots that deeply investigate the performance of the proposed approach. The first three plots Figs. 5a–5c depict the robustness of the proposed approach. The other three plots Figs. 5d–5f depict the superiority of the proposed approach in comparison to the other approaches.

Figure 5: Performance evaluation of the proposed approach with comparison to the other approaches

5  Conclusions

In this paper, we proposed a new approach for categorization of arrhythmia based in the dipper throated optimization algorithm. This algorithm is used for both feature selection and optimization of the parameter of the KNN classifier. The proposed approach outperformed the earlier ML and optimization frameworks in terms of accuracy. The UCI ML repository provided the arrhythmia dataset. It planned to use this optimization approach with clustering and noise reduction methods in other domains in the future. Because the majority of the examples in the dataset utilized in this study belong to class 1 and the other classes only contain two to three instances, the risk of misclassification is increased when applying different methods. Because Class 1 has the most impact on the prediction model's output, obtaining as many cases in the other classes as feasible is required to improve forecasts in the future. If the arrhythmia dataset characteristics were categorized based on their physical similarity, the algorithm's result would be more helpful. Cases with aberrant P waves, for example, may be grouped together, whereas all variables with abnormal Q waves could be grouped together. After then, the results of various methods might be compared.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R308), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Luthra, ECG Made Easy, 6th ed., New Delhi: Jaypee Brothers Medical Publishers, 2020. [Google Scholar]

 2.  S. Jones, ECG Mastery : Improving Your ECG Interpretation Skills, 2nd ed., Philadelphia: F. A. Davis Company, 2019. [Google Scholar]

 3.  E. Prystowsky and B. Padanilam, “Cardiac conduction system disordersm,” Cardiac Electrophysiology Clinics, vol. 13, no. 4, pp. i, 2021. [Google Scholar]

 4.  S. Manoj, P. Dinakarrao and G. Mason, “Computer-aided arrhythmia diagnosis with bio-signal processing,” Survey of Trends and Techniques, vol. 52, no. 2, pp. 1–37, 2019. [Google Scholar]

 5.  D. S. Khafaga, A. A. Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

 6.  A. Pinho, “Towards an accurate sleep apnea detection based on ECG signal: The quintessential of a wise feature selection,” Applied Soft Computing, vol. 83, no. 2, pp. 105568, 2019. [Google Scholar]

 7.  A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

 8.  A. Abdelhamid, E. M. El-Kenawy, B. Alotaibi, G. Amer, M. Abdelkader et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]

 9.  S. Oh, E. Ng, R. San Tan and U. Acharya, “Automated diagnosis of arrhythmia using combination of CNN and LSTM techniques with variable length heart beats,” Computational Biology Medicine, vol. 102, no. 4, pp. 278–287, 2018. [Google Scholar]

10. T. Mar, S. Zaunseder, J. Martínez, M. Llamedo and R. Poll, “Optimization of ECG classification by means of feature selection,” IEEE Transactions on Biomedical Engineering, vol. 58, no. 8, pp. 2168–2177, 2011. [Google Scholar]

11. A. Londhe and M. Atulkar, “Semantic segmentation of ECG waves using hybrid channel-mix convolutional and bidirectional LSTM,” Biomedical Signal Processing Control, vol. 63, no. October (10), pp. 102162, 2021. [Google Scholar]

12. C. Ye, B. Kumar and M. Coimbra, “Heartbeat classification using morphological and dynamic features of ECG signals,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 10, pp. 2930–2941, 2012. [Google Scholar]

13. S. Sahoo, B. Kanungo, S. Behera and S. Sabut, “Multiresolution wavelet transform based feature extraction and ECG classification to detect cardiac abnormalities,” Measurement, vol. 108, no. 1, pp. 55–66, 2017. [Google Scholar]

14. E. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

15. P. Pławiak, “Novel methodology of cardiac health recognition based on ECG signals and evolutionary-neural system,” Expert Systems Applications, vol. 92, no. 3, pp. 334–349, 2018. [Google Scholar]

16. S. Yang, K. Hao, Y. Ding and J. Liu, “Vehicle driving direction control based on compressed network,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 32, no. 8, pp. 1850025, 2018. [Google Scholar]

17. K. Polat and S. Güne, “Detection of ECG Arrhythmia using a differential expert system approach based on principal component analysis and least square support vector machine,” Applied Mathematics and Computation, vol. 186, no. 1, pp. 898–906, 2007. [Google Scholar]

18. F. Melgani and Y. Bazi, “Classification of electrocardiogram signals with support vector machines and particle swarm optimization,” IEEE Transactions on Information Technology in Biomedicine, vol. 12, no. 5, pp. 667–677, 2008. [Google Scholar]

19. J. Nasiri, M. Naghibzadeh, H. Yazdi and B. Naghibzadeh, “ECG arrhythmia classification with support vector machines and genetic algorithm,” in Proc. of the 2009 Third UKSim European Symp. on Computer Modeling and Simulation, Athens, Greece, pp. 187–192, 2009. [Google Scholar]

20. S. Dutta, A. Chatterjee and S. Munshi, “Correlation technique and least square support vector machine combine for frequency domain based ECG beat classification,” Medical Engineering Physics, vol. 32, no. 10, pp. 1161–1169, 2010. [Google Scholar]

21. U. Desai, R. Martis, C. Nayak, K. Sarika and G. Seshikala, “Machine intelligent diagnosis of ECG for arrhythmia classification using DWT, ICA and SVM techniques,” in Proc. of the 2015 Annual IEEE India Conf. (INDICON), New Delhi, India, pp. 1–4, 2015. [Google Scholar]

22. R. Kumar and Y. Kumaraswamy, “Investigating cardiac arrhythmia in ECG using random forest classification,” International Journal of Computer Applications, vol. 37, no. 4, pp. 31–34, 2012. [Google Scholar]

23. J. Park, K. Lee and K. Kang, “Arrhythmia detection from heartbeat using K-nearest neighbor classifier,” in Proc. of the 2013 IEEE Int. Conf. on Bioinformatics and Biomedicine, Shanghai, China, pp. 15–22, 2013. [Google Scholar]

24. T. Jun, H. Park, H. Yoo, Y. Kim and D. Kim, “GPU based cloud system for high-performance arrhythmia detection with parallel K-NN algorithm,” in Proc. of the 2016 38th Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, pp. 5327–5330, 2016. [Google Scholar]

25. S. Kiranyaz, T. Ince and M. Gabbouj, “Real-time patient-specific ECG classification by 1-D convolutional neural networks,” IEEE Transaction on Biomedical Engineering, vol. 63, no. 3, pp. 664–675, 2015. [Google Scholar]

26. U. Acharya, S. Oh, Y. Hagiwara, J. Tan, M. Adam et al., “A deep convolutional neural network model to classify heartbeats,” Computational Biology and Medicine, vol. 89, no. 1, pp. 389–396, 2017. [Google Scholar]

27. U. Acharya, H. Fujita, S. Oh, Y. Hagiwara, J. Tan et al., “Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals,” Information Science, vol. 415, no. 2, pp. 190–198, 2017. [Google Scholar]

28. M. Kachuee, S. Fazeli and M. Sarrafzadeh, “ECG heartbeat classification: A deep transferable representation,” in Proc. of the 2018 IEEE Int. Conf. on Healthcare Informatics (ICHI), New York, NY, USA, pp. 443–444, 2018. [Google Scholar]

29. G. Altan, Y. Kutlu and N. Allahverdi, “A multistage deep belief networks application on arrhythmia classification,” International Journal Intelligent Systems and Application Engineering, vol. 4, no. Special Issue-1, pp. 222–228, 2016. [Google Scholar]

30. U. Acharya, H. Fujita, O. Lih, Y. Hagiwara, J. Tan et al., “Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network,” Information Sciences, vol. 405, no. 1, pp. 81–90, 2017. [Google Scholar]

31. U. Acharya, H. Fujita, S. Oh, U. Raghavendra, J. Tan et al., “Automated identification of shockable and non-shockable life-threatening ventricular arrhythmias using convolutional neural network,” Future Generation in Computer Systems, vol. 79, no. 1, pp. 952–959, 2018. [Google Scholar]

32. Y. Xia, N. Wulan, K. Wang and H. Zhang, “Detecting atrial fibrillation by deep convolutional neural networks,” Computational Biology and Medicine, vol. 93, no. 5, pp. 84–92, 2018. [Google Scholar]

33. S. Savalia and V. Emamian, “Cardiac arrhythmia classification by multi-layer perceptron and convolution neural networks,” Bioengineering, vol. 5, no. 2, pp. 35, 2018. [Google Scholar]

34. I. Jekova and V. Krasteva, “Optimization of end-to-end convolutional neural networks for analysis of out-of-hospital cardiac arrest rhythms during cardiopulmonary resuscitation,” Sensors, vol. 21, no. 12, pp. 4105, 2021. [Google Scholar]

35. V. Krasteva, S. Ménétré, J. Didon and I. Jekova, “Fully convolutional deep neural networks with optimized hyperparameters for detection of shockable and non-shockable rhythms,” Sensors, vol. 20, no. 10, pp. 2875, 2020. [Google Scholar]

36. A. Ibrahim, H. A. Ali, M. M. Eid and E.-S. M. El-Kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, pp. 153–158, 2020. [Google Scholar]

37. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]

38. M. M. Eid, E.-S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf. (NCCC 2021), IEEE, Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

39. A. A. Salamai, E.-S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4. 0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

40. E.-S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

41. E.-S. M. El-kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

42. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

43. E.-S. M. El-kenawy, A. Ibrahim, N. Bailek, K. Bouchouicha, M. A. Hassan et al., “Sunshine duration measurements and predictions in Saharan Algeria region: An improved ensemble learning approach,” Theoretical and Applied Climatology, vol. 2021, pp. 1–17, 2021. [Google Scholar]

44. E.-S. M. El-kenawy, A. Ibrahim, N. Bailek, K. Bouchouicha, M. A. Hassan et al., “Hybrid ensemble-learning approach for renewable energy resources evaluation in Algeria,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5837–5854, 2022. [Google Scholar]

45. E. El-kenawy, A. Ibrahim, S. Mirjalili, Y. Zhang, S. Elnazer et al., “Optimized ensemble algorithm for predicting metamaterial antenna parameters,” Computers, Materials & Continua, vol. 71, no. 3, pp. 4989–5003, 2022. [Google Scholar]

46. A. Ibrahim, H. Abutarboush, A. Mohamed, M. Fouad and E. El-kenawy, “An optimized ensemble model for prediction the bandwidth of metamaterial antenna,” Computers, Materials & Continua, vol. 71, no. 1, pp. 199–213, 2022. [Google Scholar]

47. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-Ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]

48. E.-S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

49. E. S. M. El-Kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]

50. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

51. A. Takieldeen, E. El-kenawy, E. Hadwan and M. Zaki, “Dipper throated optimization algorithm for unconstrained function and feature selection,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1465–1481, 2022. [Google Scholar]

52. H. A. Guvenir, B. Acar, G. Demiroz and A. Cekin, “A supervised machine learning algorithm for arrhythmia analysis,” IEEE Computers in Cardiology, vol. 24, pp. 433–436, 1997. [Google Scholar]