Improved Metaheuristic Based Failure Prediction with Migration Optimization in Cloud Environment

1  Introduction

Cloud Computing (CC) is a platform that provides on-demand access to computer system resources to its users while the resources are vigorously provisioned together to meet customer demands [1]. In general, service providers provide three services to customers such as Software as a Service (SaaS), Infrastructure as a Service (IaaS), and Platform as a Service (PaaS) through cloud data centers. With increasing volume of customer demands for the services rendered by data centers, the volume of energy used by such data centers also increases simultaneously [2]. Between 2010 and 2040, global power utilization is expected to increase up to 48% whereas it is 34% increase in case of CO2 emissions. So, service providers have made multiple attempts to minimize the cost incurred upon energy in data centers owing to laws and regulations framed by global nations [3]. Further, the service providers are also working on service cost mitigation followed by increased profit rate. At the same time, consumers also need quality service at a minimum cost that can be defined via Service Level Agreement (SLA). As a result, it becomes essential to assess the performance of service delivered to the users in association with target achievements such as cost mitigation and low power utilization [4]. However, these objectives are challenging to achieve by the providers who are expected to meet the user’s demands as well.

The optimization of data centers, in terms of energy efficiency, has gained substantial interest in recent times [5,6]. When cloud data centers work with less number of computing devices excluding optimization, it may result in high energy dependency [7]. Numerous researches have suggested that the computational elements of running servers must exhibit maximum capability to increase the energy efficiency. However, this scenario result in performance degradation. In order to resolve the performance degradation issue that arose as a result of functioning at maximum capacity, static optimum consumption threshold is described for all types of resources which is inclusive of bandwidth, processing, etc [8]. But, static threshold method results in switching off the machines or else the much-needed resources are not considered. In literature, alternative methods have been proposed, one of which is server consolidation in which the number of energetic Physical Machines (PM) is reduced by compiling Virtual Machines (VMs) as small sets of Physical Machines (PMs) or it is achieved through VM migration as well [9]. But, server consolidation and VM migration methods yield less output from a service user’s perspective whereas the service provider experiences the energy overhead [10]. It is possible to mitigate energy utilization by decreasing the number of active, underutilized sources and conversely, it reduces the dependability of the system. This scenario forms a crucial trade-off between the metrics considered.

The current study develops an Improved Metaheuristic Based Failure Prediction with Virtual Machine Migration Optimization (IMFP-VMMO) model in cloud environment. The major intention of the proposed IMFP-VMMO model is to reduce energy utilization and maximum performance in terms of failure prediction. The proposed IMFP-VMMO model primarily employs Gradient Boosting Decision Tree (GBDT) classification model for effectual prediction of VM failures. At the same time, optimal VM migration process is also carried out using Quasi-Oppositional Artificial Fish Swarm Algorithm (QO-AFSA), which in turn reduces energy consumption. The performance of the proposed IMFP-VMMO technique was validated to confirm the enhanced performance of the proposed model.

2  Related Works

The current section provides a comprehensive survey of existing VM migration and failure prediction models in cloud environment. Huang et al. [11] presented an allocation system for optimization based on user requirements from the cloud data center. At first, large number of application requests, raised from mobile devices and phones, are considered as a set of VM lists from data center which are then submitted to cloud platform. The proposed method allocates the received VMs to applicable PMs, according to the current throughput of PMs from the data center and their usage of hardware resources. In line with dynamic workload, a load of PM that host the VMs might be relatively high. In the study conducted earlier [12], the authors presented an Enhanced Artificial Bee Colony (E-ABC) approach to reduce the total energy consumption with limited number of migrations. The proposed method migrates the VMs from the overloaded host to underloaded host, thus saving energy. Witano et al. [13] presented a neural network-based VM consolidation algorithm that adoptively selects an effective approach based on cloud provider, goal priority and environmental parameters. Performance evaluation results and dataset generation using simulation on real-time PlanetLab VM workload trace infer that adoptive selector can achieve remarkable outcomes.

Zhou et al. [14] developed a new algorithm called EEOM (Energy Efficacy Optimization of VM Migration). In line with memory and CPU factors, the proposed method augments three primary phases such as host location, trigger time, and VM selection. Further, the presented method uses virtualization process and migrates some of the VMs from over-loaded hosts and medium- and under-loaded hosts. In literature [15], the authors proposed a New Linear Regression (NLR) prediction system i.e., VM placement policy and host overload/underload in order to minimize SLAV and EC. The presented algorithm is capable of predicting CPU consumption. Gholipour et al. [16] developed a cloud resource management process according to multi-criteria decision-making process. In this method, a joint VM and container migration process are used simultaneously. The outcomes of the simulation with ContainerCloudsim simulator confirmed the feasibility of the projected method in terms of prominent reduction in energy consumption.

3  The Proposed Model

VM migration is performed by starting with one PM and then moving on to another machine. It can be employed to stack, adjust and achieve PM blame tolerance too. VMs are migrated in order to ensure sensibility, implementation, and optimum variation in non-critical structural failure. To be specific, it supports ‘heap-adjusting datacenter’ through migration of VMs from over-loaded servers to under-loaded servers/PM. In this work, VMM cloud datacenters, energy saving and machine learning based creative method are concentrated. The unit prepared from cloud condition i.e., Virtual Machine is employed in the fabrication of cloud foundation with huge volumes of interconnected virtualization datacenters. In this regard, the benefits of VM migration is mostly offered to the client on web as an on-demand service.

3.1 Failure Prediction Module

Prediction model, in machine learning, is used to forecast the participation of different data incidences. It performs the assignment based on the outstanding infrastructure that is applied to retrieve novel data. The presented GBDT classification is a failure prediction method for logical work process in which proactive adaptation for non-critical failure is considered. The failure effect of work process assignment, on cloud asset amid implementation, is minimized by ML technique. The failed VM is then repositioned to a new region so as to spare the asset. [17]

Here, the data is provided with n samples and m features, D={(xi,yi)}i=1n , whereas xi∈Rm and yi∈R , the forecasts in the GBDT method, y^i , is determined as a tree-based additive ensemble method, φ(xi) includes K additive function, fk , which are demonstrated as follows

y^i=φ(xi)=∑k=1Kfk(xi),fk∈F (1)

whereas F={f(x)=wq(x)} is a group of Classification and Regression Trees (CART) in which q(x) maps all the input feature x to one of the T leaves from the tree by weighted vector, w∈RT.

To provide the function determined above, GBDT technique reduces the following regularization objective function [18]:

L~=∑il(yi,y^i)+∑kΩ(fk) (2)

Here, l(yi,y^i) implies the loss function of ith instance between the forecasted value y^i and target value yi , and Ω(fk)= γT+1/2λ‖W‖2 signifies the regularized element. This element discourages all kth tree, fk denotes the over-fitting with hyperparameter λ , the regularized parameter penalized the weighted vector w , and γ denotes the term which penalizes the tree in further leaf development. In order to approximate the loss function, a second-order Taylor expansion function is utilized as follows.

L(t)≃∑i=1n[l(yi,y^i)+gift(xi)+12hift2(xi)]+Ω(ft) (3)

While the tree is trained from an additive approach, all the iteration indices of the trained procedure are represented through t . Therefore, L(t) signifies the tth loss of the trained procedure. At this point, it can also determine the gradient, gi=∂y^i(t−1)l(yi,y^i(t−1)) , and hessian, hi=∂y^2l(yi,y^i(t−1)) based on the determined loss function. To provide the derived gradient and hessian so as to yield (x) , an optimum weight of the leaf j is calculated using the formula given below.

wj∗=−GjHj+λ (4)

whereas Gj=∑i∈Igi and Hj=∑iεhi refers to the entire summation of gradient and hessians to the data sample index i.e., Ij . But, in order to effectually calculate the optimum weight wj∗ , it can greedily maximize the subsequent gain score to search for optimum splits in the leaf node during all the iterations as given below.

Gain=12[GL2HL+λ+GR2HR+λ−(GL+GR)2(HL+HR)+λ]−γ (5)

At this point, L and R denote the sum of gradient and hessians which depend upon certain indices of left and right children of the provided leaf nodes, IL and IR , correspondingly. Minkowski distance, one of the uniqueness measures that is increasingly used in recent years, is measured by adding the difference between two data focus to the extent that each machine is concerned. The distance between two concentrations such as resilience and settled edge esteems are described below.

md(i,j)=∑(|mij−mjk|)1/q (6)

The intention to select Eq. (6) is to make the presented algorithm adaptable, because Naïve Bayes classification is a fast predictor as per the literature. The underlying motive behind the selection of GBDT classification is that it has high predictive performance with less computation time. So, it is used in cloud architecture that mainly necessitates the earlier prediction of VM failure.

3.2 VM Migration Optimization Module

VM approach is the most commonly employed approach in CC to actualize these three services in addition to VM migration processes that have been employed in supporting virtualized CC datacenters. The primary objective of offering cloud services is to reduce the energy consumption of data centers. VM, at the source host, is stopped after every condition of the source host is replaced with an objective or purpose host. Then, the working of VM is resumed at objective host. Fig. 1 illustrates the processes involved in VM migration under cloud environment. This migration process has two imperative parameters which are explained herewith.

Figure 1: The proposed Virtual Machine migration process in cloud environment

Down Time: Downtime denotes the time in which the VMs’ service cannot be reached. The migration process ensures that the VMs do not face much downtime.

Migration Time: It refers to the entire amount of time required for migration of VMs from source to the purpose hub with no control on its accessibility. Virtualization is the real idea of CC and it has obtained significance from mainstream CC environment.

QO-AFSA technique is explained in a typical manner to determine an optimum solution in the model within constraints. Cloud service providers focus mainly upon minimizing the energy utilization of servers from the failed VMs. The heuristic i is optimized with a concern to settle for unique workload target choice while the energy utilization is assumed based on the selection of VMs. The method presented in this study helps in energy saving through migration of VMs to the ideal target with particular edge.

Through natural simulation of swarming, preying and random behaviors of fish, AFSA completes the process of finding the optimum solution. Artificial Fish (AF) swarming process is composed of location Xi(i=1,2,3….,N) of the fish swarming, the population size ‘N’ of fish swarming, the crowd factor δ of the fish swarming, the Yc=f(xi) food concentration of the existing location of fish swarming, the step size of the fish swarming, the visual of the fish swarming, the try-number of the fish swarming, the maximal amount of iterations, and the distance between fish Xi and Xj i.e., dij=‖Xi−Xj‖ . [19].

Prey Behavior: This is a primary behavior in FSA in which Artificial Fish (AF) arbitrarily chooses a position Xj in the fields of vision and compares the food concentration of existing positions Xi and Xj . When the Yj food concentration of the arbitrary location is lesser than the Yi food concentration of the existing location, Xj position is re-elected. Till the selection number is higher than the try-number of AF, and no location with high concentration, than the existing location, iterations are done. Then, the arbitrary behavior is implemented as shown in the following equation.

Xi(t+1)=Xi(t)+step∗Xj(t)−Xi(t)‖Xj(t)−Xi(t)‖∗rand() (7)

Swarm Behavior: This is an important fish survival model and is utilized for cooperative foraging and avoiding the enemy. It comprises of two essential conditions for aggregated behaviors such as one is closer to the center of fish group and next is the lower crowding degree of fish group. With regards to the position Xj and number nf of each fish in the field of vision, the central location Xc=∑j=1nfXj/nf can be defined, and the concentration Y is evaluated. Fig. 2 depicts the steps involved in AFSA.

Figure 2: Steps in AFSA

When the crowding degree nf/N≤δ of the existing fish population and the concentration Y of the central location are higher than Y , the scenario indicates that the central location Xc is superior and not crowded. So, cluster behavior is implemented or else foraging behavior is implemented as given below.

Xi(t+1)=Xi(t)+step*Xc−Xi(t)‖ Xc−Xi(t) ‖*rand (8)

Follow Behavior: AF observes the fish with the field of vision, defines the Yj optimum food concentration and their location Xj which are closer to the location. When Yj is higher than the concentration Yi of the existing location and density nf/N≤δ of the existing fish, then the scenario denotes that the superior location of Xj can follow pursuit behavior or else foraging behavior too.

Xi(t+1)=Xi(t)+step*Xj(t)−Xi(t)‖ Xj(t)−Xi(t) ‖*rand (9)

Random Behavior: It is a default behavior in fish swarming. In AF visual field, the arbitrary election of orientation for migration can avoid the fish which exhibits low efficacy and local optimal since these two characteristics are highly advantageous for global optimal. The formulation is shown below.

Xi(t+1)=Xi(t)+visual∗rand (10)

Metaheuristics generally create the primary solution on an arbitrary basis from the searching range; when the primary solution is distant from the global optimum solution, the convergence speed of population can be developed slowly and is trapped into local optimum solution. In order to bypass this difficulty, QO-AFSA technique is developed in which the arbitrary solution is placed at distant position from the global optimum solution compared to opposite solution which has 50% chance.

According to this method, the optimum N individuals are chosen from the population that contains N arbitrary individuals and the opposite solution of these individuals [20]. Assume that X=(X1,X2,…,XD) refers to the point from D-dimension space, and their opposite point is XOBL=(X1OBL,X2OBL,…,XDOBL) which is computed using Eq. (11); their quasi-opposite point XQOBL=(X1QOBL,X2QOBL,…,XDQOBL) is calculated by Eq. (12).

XdOBL=lbd+ubd−Xd (11)

XdQOBL={lbd+ubd2+rand(0,1)×(XdOBL−lbd+ubd2)Xd<lbd+ubd2XdOBL+rand(0,1)×(lbd+ubd2−XdOBL)Xd≥lbd+ubd2 (12)

Here Xd, XdOBL , and XdQOBL stand for dth dimensional of X , their opposite point XOBL , and their quasi-opposite point XQOBL correspondingly. Also, lbd and ubd illustrate the dth dimensional of lesser boundary lb and upper boundary ub correspondingly.

QO-AFSA technique focuses on energy utilization. The purpose of utility capacity is to increase VM arrangement by reducing the energy utilization as described herewith. Low estimation of energy utilization helps in reduced consumption.

ECi=min{energyidealmachine,i+energyrunningmachine,i} (13)

4  Performance Validation

The current section shows the performance of the proposed IMFP-VMMO model in terms of failure prediction and VM migration optimization. Tab. 1 provides the clear overview in terms of failure prediction outcomes accomplished by IMFP-VMMO model and other existing models [21–23]. The experimental values imply that the proposed IMFP-VMMO model achieved effectual outcomes than all other models.

Fig. 3 demonstrates a brief overview on accuracy analysis results achieved by IMFP-VMMO model and other recent models. The figure indicates that fuzzy classifier model demonstrated ineffectual prediction outcome with a low accuy of 86.12%. Followed by, k-nearest neighbor (KNN) model achieved a slightly enhanced performance with a moderate accuy of 90.47%. At the same time, Naïve Bayes (NB) classifier accomplished near optimal accuy value of 97.41%. However, the proposed IMFP-VMMO model attained better results with a maximum accuy of 98.78%.

Figure 3: Accuy analysis results of IMFP-VMMO technique and other existing approaches

Fig. 4 illustrates the brief sensy , specy , precn , and Fscore analysis results accomplished by the proposed IMFP-VMMO algorithm and other recent methods. The figure shows that fuzzy classifier method demonstrated ineffectual prediction outcomes with low sensy , specy , precn , and Fscore values such as 93.35%, 89.75%, 89.95%, and 93.39% respectively. Next, KNN model attained a slightly enhanced performance with moderate sensy , specy , precn , and Fscore values such as 89.34%, 86.98%, 92.84%, and 86.32% respectively. Simultaneously, NB classifier accomplished near optimal sensy , specy , precn , and Fscore values such as 96.11%, 97.23%, 97.17%, and 97.89% respectively. But, the proposed IMFP-VMMO algorithm surpassed all other models and achieved maximum sensy , specy , precn , and Fscore values such as 98.26%, 98.02%, 98.42%, and 99.12% respectively.

Figure 4: Comparative analysis results of IMFP-VMMO technique in terms of (a) Sensy , (b) Specy , (c) Precn , and (d) Fscore

Tab. 2 and Fig. 5 shows the migration level performance achieved by IMFP-VMMO model under varying number of failed VMs. The results infer the enhanced migration level of IMFP-VMMO model. For instance, with 10 failed VMs, the proposed IMFP-VMMO model offered a migration level of 2. At the same time, with 20 failed VMs, IMFP-VMMO methodology obtained a migration level of 3. Along with that, with 40 failed VMs, IMFP-VMMO system attained a migration level of 8. Moreover, with 50 failed VMs, the proposed IMFP-VMMO algorithm achieved a migration level of 9.

Figure 5: Migration level analysis results of IMFP-VMMO method under distinct number of failed VMs

Tab. 3 and Fig. 6 show the detailed Energy Consumption (ECM) examination results achieved by the proposed IMFP-VMMO model and other existing models under distinct number of failed VMs. The table values highlight that IMFP-VMMO model produced the least ECM values under all number of failed VMs. For instance, with 5 failed VMs, IMFP-VMMO model obtained a low ECM of 891 KWh, whereas Artificial Bee Colony (ABC) with Bat Algorithm (BA) named ABC-BA, ABC, BA, Particle Swarm Optimization (PSO), and Dynamic Adaptive Particle Swarm Optimization (DAPSO) models demanded high ECM of 1131 KWh, 1259 KWh, 2292 KWh, 2462 KWh, and 1528 KWh respectively. Along with that, with 15 failed VMs, the proposed IMFP-VMMO technique obtained a low ECM of 1825 KWh, whereas ABC-BA, ABC, BA, PSO, and DAPSO models reached superior ECM values such as 2179 KWh, 2419 KWh, 3679 KWh, 4769 KWh, and 2419 KWh correspondingly. Simultaneously, with 30 failed VMs, the proposed IMFP-VMMO approach attained a low ECM value of 2646 KWh, whereas ABC-BA, ABC, BA, PSO, and DAPSO models required high ECM values such as 3000 KWh, 4457 KWh, 3169 KWh, 4231 KWh, and 3608 KWh respectively. Concurrently, with 40 failed VMs, the proposed IMFP-VMMO model demanded the least ECM of 1584 KWh, whereas ABC-BA, ABC, BA, PSO, and DAPSO algorithms required high ECM of 1853 KWh, 4344 KWh, 3254 KWh, 4726 KWh, and 4330 KWh correspondingly.

Figure 6: ECM analysis results of IMFP-VMMO technique under distinct number of failed VMs

A comprehensive Success Rate (SUR) analysis was conducted between IMFP-VMMO model and other recent models and the results are shown in Tab. 4 and Fig. 7. The figure implies that the proposed IMFP-VMMO model obtained effectual outcomes with maximum SUR. For instance, with 10 testing VMs, the proposed IMFP-VMMO model exhibited a high SUR of 99.28%, whereas ABC-BA, ABC, BA, PSO, and DAPSO models portrayed the least SUR values such as 97.87%, 70.77%, 47.89%, 78.86%, and 19.38% respectively. Then, with 20 testing VMs, the proposed IMFP-VMMO model exhibited a high SUR of 92.24%, whereas ABC-BA, ABC, BA, PSO, and DAPSO models accomplished the least SUR values such as 86.61%, 49.65%, 29.94%, 35.92%, and 56.69% respectively.

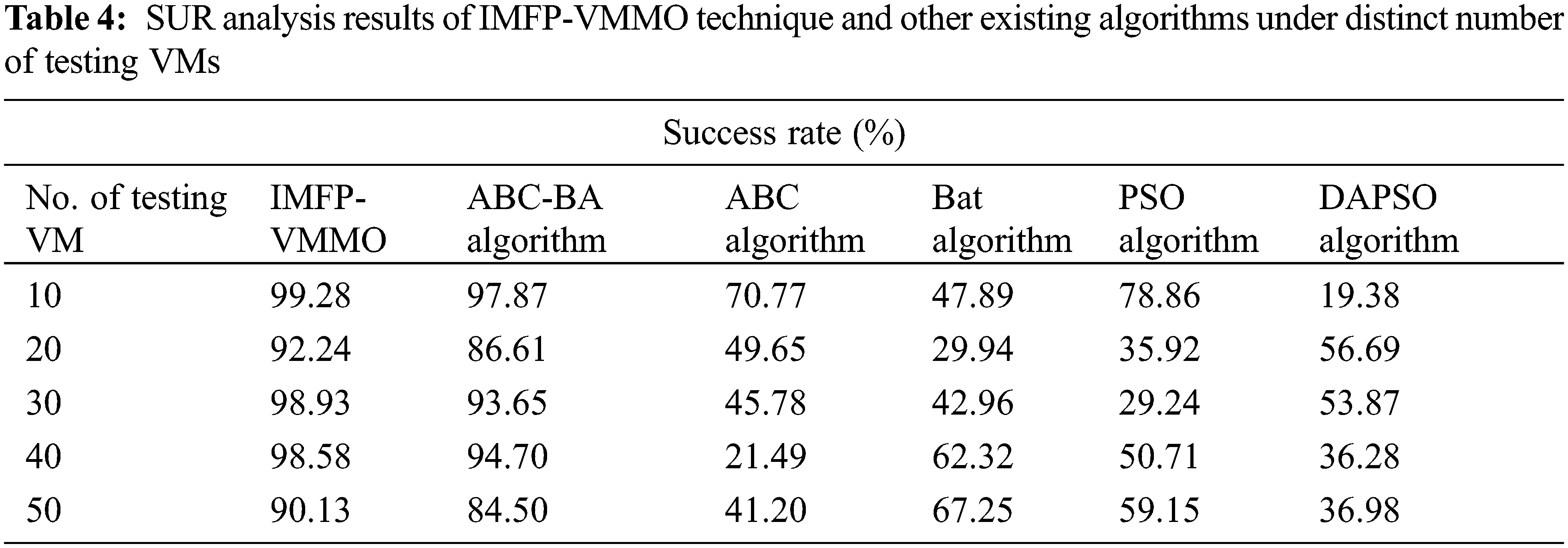
Figure 7: SUR analysis results of IMFP-VMMO technique under distinct number of testing VMs

Tab. 5 and Fig. 8 provide an overview on the Failure Rate (FR) analysis results accomplished by IMFP-VMMO method and other existing approaches under distinct number of testing VMs. The table values highlight that the proposed IMFP-VMMO model produced the least FR value under all testing VMs. For instance, with 10 testing VMs, IMFP-VMMO algorithm obtained a minimal FR of 0.72%, whereas ABC-BA, ABC, BA, PSO, and DAPSO models reached high FR values such as 2.13%, 29.23%, 52.11%, 21.14%, and 80.62% correspondingly. Followed by, with 30% testing VMs, the proposed IMFP-VMMO model obtained a low FR of 1.07%, whereas ABC-BA, ABC, BA, PSO, and DAPSO approaches achieved high FR values such as 6.35%, 54.22%, 57.04%, 70.76%, and 46.13% correspondingly. Simultaneously, with 50 testing VMs, the proposed IMFP-VMMO system obtained the least FR of 9.87%, whereas ABC-BA, ABC, BA, PSO, and DAPSO models reached high FR values such as 15.50%, 58.80%, 32.75%, 40.85%, and 63.02% respectively.

Figure 8: FR analysis results of IMFP-VMMO technique under distinct number of testing VMs

From the detailed results and discussion, it is clear that the proposed IMFP-VMMO model accomplished the maximum performance in terms of failure prediction and VM migration optimization.

5  Conclusion

In this article, a novel IMFP-VMMO model has been developed for minimizing the energy utilization and maximum failure prediction performance in cloud environment. The proposed IMFP-VMMO model uses GBDT classification model for effectual prediction of VM failures. In addition, optimal migration of VMs is also carried out using QO-AFSA technique which in turn reduced the energy consumption. The performance of the proposed IMFP-VMMO technique was validated while the comparative study results inferred that the proposed IMFP-VMMO model is superior to other recent approaches. Thus, IMFP-VMMO technique can be used as an effectual tool for failure prediction and VM migration optimization in cloud environment. In future, hybrid deep learning models can be applied to improve VM failure prediction performance in cloud environment.

Funding Statement: The authors are very grateful to acknowledge their Deanship of Scientific Research at Prince sattam bin abdulaziz university, Saudi Arabia for technical and financial support in publishing this work successfully.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Torquato, I. M. Umesh and P. Maciel, “Models for availability and power consumption evaluation of a private cloud with VMM rejuvenation enabled by VM live migration,” Journal of Supercomputing, vol. 74, no. 9, pp. 4817–4841, 2018. [Google Scholar]

 2.  R. Yadav, W. Zhang, O. Kaiwartya, P. R. Singh, I. A. Elgendy et al., “Adaptive energy-aware algorithms for minimizing energy consumption and SLA violation in cloud computing,” IEEE Access, vol. 6, pp. 55923–55936, 2018. [Google Scholar]

 3.  S. K. Pande, S. K. Panda, S. Das, K. S. Sahoo, A. K. Luhach et al., “A resource management algorithm for virtual machine migration in vehicular cloud computing,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2647–2663, 2021. [Google Scholar]

 4.  M. J. Moghaddam, A. Esmaeilzadeh, M. Ghavipour and A. K. Zadeh, “Minimizing virtual machine migration probability in cloud computing environments,” Cluster Computing, vol. 23, no. 4, pp. 3029–3038, 2020. [Google Scholar]

 5.  J. A. Jeba, S. Roy, M. O. Rashid, S. T. Atik and M. Whaiduzzaman, “Towards green cloud computing an algorithmic approach for energy minimization in cloud data centers,” in Research Anthology on Architectures, Frameworks, and Integration Strategies for Distributed and Cloud Computing. I. R. Management Association, Ed. IGI Global, pp. 846–872, 2021. [Google Scholar]

 6.  R. Yadav, W. Zhang, K. Li, C. Liu, M. Shafiq et al., “An adaptive heuristic for managing energy consumption and overloaded hosts in a cloud data center,” Wireless Networks, vol. 26, no. 3, pp. 1905–1919, 2020. [Google Scholar]

 7.  M. Ibrahim, M. Imran, F. Jamil, Y. J. Lee and D. H. Kim, “EAMA: Efficient adaptive migration algorithm for cloud data centers (CDCs),” Symmetry, vol. 13, no. 4, pp. 690, 2021. [Google Scholar]

 8.  I. Mohiuddin and A. Almogren, “Workload aware VM consolidation method in edge/cloud computing for IoT applications,” Journal of Parallel and Distributed Computing, vol. 123, no. 10, pp. 204–214, 2019. [Google Scholar]

 9.  X. Xiao, W. Zheng, Y. Xia, X. Sun, Q. Peng et al., “A workload-aware VM consolidation method based on coalitional game for energy-saving in cloud,” IEEE Access, vol. 7, pp. 80421–80430, 2019. [Google Scholar]

10. S. Basu, G. Kannayaram, S. Ramasubbareddy and C. Venkatasubbaiah, “Improved genetic algorithm for monitoring of virtual machines in cloud environment,” in Smart Intelligent Computing and Applications, Smart Innovation, Systems and Technologies book series. vol. 105. Singapore: Springer, pp. 319–326, 2019. [Google Scholar]

11. Y. Huang, H. Xu, H. Gao, X. Ma and W. Hussain, “SSUR: An approach to optimizing virtual machine allocation strategy based on user requirements for cloud data center,” IEEE Transactions on Green Communications and Networking, vol. 5, no. 2, pp. 670–681, 2021. [Google Scholar]

12. S. Talwani and J. Singla, “Enhanced Bee Colony Approach for reducing the energy consumption during VM migration in cloud computing environment,” IOP Conference Series: Materials Science and Engineering, IOP Publishing, vol. 1022, no. 1, pp. 012069, 2021. [Google Scholar]

13. J. N. Witanto, H. Lim and M. Atiquzzaman, “Adaptive selection of dynamic VM consolidation algorithm using neural network for cloud resource management,” Future Generation Computer Systems, vol. 87, no. 4, pp. 35–42, 2018. [Google Scholar]

14. Z. Zhou, J. Yu, F. Li and F. Yang, “Virtual machine migration algorithm for energy efficiency optimization in cloud computing,” Concurrency and Computation: Practice and Experience, vol. 30, no. 24, pp. e4942, 2018. [Google Scholar]

15. N. K. Biswas, S. Banerjee, U. Biswas and U. Ghosh, “An approach towards development of new linear regression prediction model for reduced energy consumption and SLA violation in the domain of green cloud computing,” Sustainable Energy Technologies and Assessments, vol. 45, no. 4, pp. 101087, 2021. [Google Scholar]

16. N. Gholipour, E. Arianyan and R. Buyya, “A novel energy-aware resource management technique using joint VM and container consolidation approach for green computing in cloud data centers,” Simulation Modelling Practice and Theory, vol. 104, pp. 102127, 2020. [Google Scholar]

17. D. Saxena and A. K. Singh, “OFP-TM: An online VM failure prediction and tolerance model towards high availability of cloud computing environments,” Journal of Supercomputing, vol. 78, no. 6, pp. 8003–8024, 2022. [Google Scholar]

18. H. Rao, X. Shi, A. K. Rodrigue, J. Feng, Y. Xia et al., “Feature selection based on artificial bee colony and gradient boosting decision tree,” Applied Soft Computing, vol. 74, no. 4, pp. 634–642, 2019. [Google Scholar]

19. M. Neshat, G. Sepidnam, M. Sargolzaei and A. N. Toosi, “Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications,” Artificial Intelligence Review, vol. 42, no. 4, pp. 965–997, 2014. [Google Scholar]

20. S. Rahnamayan, H. R. Tizhoosh and M. M. A. Salama, “Quasi-oppositional differential evolution,” in 2007 IEEE Congress on Evolutionary Computation, Singapore, pp. 2229–2236, 2007. [Google Scholar]

21. K. Karthikeyan, R. Sunder, K. Shankar, S. K. Lakshmanaprabu, V. Vijayakumar et al., “Energy consumption analysis of Virtual Machine migration in cloud using hybrid swarm optimization (ABC-BA),” Journal of Supercomputing, vol. 76, no. 5, pp. 3374–3390, 2020. [Google Scholar]

22. A. F. S. Devaraj, M. Elhoseny, S. Dhanasekaran, E. L. Lydia and K. Shankar, “Hybridization of firefly and Improved Multi-Objective Particle Swarm Optimization algorithm for energy efficient load balancing in Cloud Computing environments,” Journal of Parallel and Distributed Computing, vol. 142, no. 4, pp. 36–45, 2020. [Google Scholar]

23. N. Krishnaraj, M. Elhoseny, E. L. Lydia, K. Shankar and O. ALDabbas, “An efficient radix trie -based semantic visual indexing model for large-scale image retrieval in cloud environment,” Software: Practice and Experienc, vol. 51, no. 3, pp. 489–502, 2021. [Google Scholar]