Coherence Based Sufficient Condition for Support Recovery Using Generalized Orthogonal Matching Pursuit

1  Introduction

Compressed sensing will aid to recover a P-sparse (P-non zero elements) unknown signal x∈Rn using the linear equation

y=Hx+v (1)

where y∈Rm is an observation vector, H∈Rm×n(m<<n) is a sensing matrix, v is a noise vector. Though the above equation is under determined, P-sparse x can be recovered from under determined measurements y by imposing condition on matrix H using Restricted Isometric Property (RIP). Greedy algorithms are popular to recover the support vector indices for example Orthogonal Matching Pursuit (OMP), Compressive SAmpling Matching Pursuit (CoSAMP), Basis Pursuit. The condition to recover any P-sparse vector x, Restricted Isometric Constant (RIC) δ∈(0,1) is the smallest constant that satisfy the relation given below

(1−δp)||x||22≤||Hx||22≤(1+δp||x||22) (2)

The smallest constant δ satisfying Eq. (2) is referred as RIC. Greedy approach is most popular and lesser computational complexity than the state-of-the-art algorithms like OMP, and CoSAMP. Most of the recovery guarantee has been proposed based on the RIC which accurately recovers all the support indices of the sparse signal with the help of the RIP [1–4]. In general, it is Non-deterministic Polynomial-time (NP)-hard to evaluate RIC for a given matrix H in the expression to satisfy the stringent conditions. Recovery conditions based on the mutual coherence have been proposed in the literature earlier for the OMP algorithm (special case where a number of support elements selected in this algorithm is equal to one (Q = 1) [5,6]. Coherence statistics will be helpful in solving many signal processing problems including support detection and vector quantization [7–10]. In this paper, a sufficient condition has been derived to guarantee the recovery performance based on coherence for Generalized Orthogonal Matching Pursuit (GOMP). In recent years recovery conditions based on the RIC have been proposed to ensure recovery of the accurate P-sparse signal with GOMP [11–15]. Furthermore in, the author [11,16] proposes sufficient condition has been improved to δNK+1<1K/N+1 . Though the conditions are tighter bounds it is NP-hard to find out the RIC of the matrix H [11, 17–19]. Sufficient condition based on the mutual coherence to accurately recover the support indices of the P-sparse signal with GOMP in noisy case has been proposed. GOMP algorithm has the choice to choose number elements to be selected in each iteration Q≤(m−1)/P . As a generalized case if the number of selection element is equal to 1, it converges to OMP whose performance is inferior to the GOMP.

1.1 Contributions

Sufficient condition to guarantee the support recovery for GOMP algorithm has been derived using the coherence of the sensing matrix H.

GOMP can select Q≤(m−1)/P elements in each iteration. When Q=(m−1)/P , GOMP algorithm recovery performance is better than the OMP where Q = 1.

μ≤1|ω|Q+1(Q|ω|) is a sufficient condition based on coherence statistics to recover the support vectors of P-sparse signal in ‘P’ iterations using GOMP for noisy case. Simulations have been carried out to validate the theoretical results and compare with the other greedy algorithms.

GOMP Algorithm:

Step 1: Input: H∈Rm×n,y∈Rn,P,Q≤(m−1)/P

Step 2: Initialize: rt=y=0

Step 3: For Each t≤P

Step 4: Compute the correlation and find the first Q indices where correlation is it=arg⁡maxn∈st|Hnrt−1|

Step 5: Select the first ‘Q’ largest value indices it={i1…iQ}

Step 6: Update sub band support indices St=St−1∩it

Step 7: Estimate the signal vector Z^t=arg⁡minzsupp(z)||y−Hstz||22

Step 8: Update residual rt=y−HstZ^st

Step 9: t=t+1 ;

Step 10: Go to step 2

Step 11: End For Return index set of sub band support indices S˙¨=St;

Step 12: Output: Support vector indices S⌢

Step 13: end

1.2 Preliminaries: Generalized Orthogonal Matching Pursuit (GOMP)

Algorithm for generalized orthogonal matching pursuit shown in GOMP algorithm has three parts identification, augmentation and residual update. In the step 4, magnitude of the correlation between each column of matrix H and residual is found and the values are arranged in descending order. Step 5: First Q largest column indices it={i1…iQ} has been chosen. Step 6: Active support indices is concatenated with the previous iteration support sets.

Line 7 finding the least square estimate of the signal vector, to find the residual rt is updated after eliminating the active column indices from the measurements is shown in line 8. In other words, least square will ensure projection of y on to the complement space PStL , this will ensure that the indices in St in the current iteration cannot be selected repetitively in the upcoming iterations. The selected support indices in the current iteration is projected to the orthogonal space in that way we can avoid the same support indices will be chosen in the upcoming iterations.

2  Sufficient Condition

Coherence of sensing matrix H is maximum of absolute correlation between the two columns of H and it is given by μ(H)=^maxp≠q|hp∗hq|, where h∗ is conjugate of h. To analyze the performance of the support recovery algorithm some of the useful lemmas have been derived in the literature [12].

Lemma 1: Let H∈Rm×n satisfies the RIP of orders P1 and P2 with P1<P2 , then δP1≤δP2 .This is the monotonocity property of the RIC.

Lemma 2: For any matrix H, the RIP constant δP bounded by δP≤μ(P−1) where P is the sparsity of the signal x(t) and μ is the mutual coherence of matrix H.

Lemma 3: Suppose a matrix H satisfy RIP of order P and Q≤P , then for any signal

x∈Rn||HQTx||22≤(1+δP)||x||22

In this lemma 3 lower bound can be defined with the help of coherence μ and sparsity of the signal P

maxi∈ω∖SHiTPSLHω∖s−1N∑j∈W|HjTPSLHω∖sxω∖S|. (3)

The above expression plays a key role in proving the theorem 1. It holds good for generalized case of OMP.

Remark 1: The condition N(k+1)+|ω|−k≤m in lemma 1 is to ensure the assumption that H satisfies the RIP of order N(k+1)+|ω|−1 makes sense.

Theorem 1: Let H satisfy the coherence with μ≤11−|ω|Q+1[(Q(P+1)+|ω|−P)−1]μ for an integer N with 1≤Q≤(m−1)P . Then GOMP either identifies at least t0 indices in ω if GOMP terminates after performing t0 iterations with 1≤t0≤P or recovers ω in P iterations provided that

mini∈S||x[i]||2>2s1−|ω|Q+1[(Q(P+1)+|ω|−P)−1]μ

The proof for the special case ω=P−1 using Lemma 3 is as follows:

First we need to prove that the selection of Q elements contains at least one support index in iterations will be considered as success. The proof for the first iteration should be carried at first. Let us assume

V={j1,j2…,jN} (4)

Instead of proving Pt+1∖Pt∩ω≠ϕ we will show

|Hj11Trt|≥….≥|HjNTrt|≥|Hj∈ωc∖VTrt| (5)

maxj∈ω⁡|HiTrt|>|HjNTrt| (6)

By expression (5), HjQTrt≤1Qmaxj∈ω⁡|HiTrt| Thus, to show Pt+1∖Pt∩ω=φ , it suffices to show

maxi∈W|HiTrt|>1Qmaxj∈ω⁡|HjTrt| (7)

residual in the algorithm at tth iteration can be expressed as

rt=y−Hstxst=(I−Hst(HstTHst)−1HStT)y=PStL(Hωxω+v)=PStL(Hω∩St+Hω∖Stxω∖st+v)=PStLHω∖stxω∖st+PstLv (8)

Thus, by Eq. (8) and the triangular inequality

maxi∈ω|HiTrt|≥maxi∈ω∖st(|HiTPStTHω∖Stxω∖St|−|HiTPStLv|) (9)

1N∑j∈W|HjTrt|≤1N∑j∈W|HjTPStLHω∖Stxω∖St|+maxj∈W|HiTPStLv| (10)

It is a two-step process to fond the lower bound. To find the lower bound on maximum of IT is a two step process to find the lower bound on maxiω|HiTrt|. A lower bound on maxi∈ω|HiTrt| will be derived, and it requires Q≤P . Thus, to show (10), it suffices to show

β1>β2 (11)

β1=maxi∈ω∖st|HiTPStLHω∖st|−1N∑j∈W|HjTPStLHω∖stxω∖St| (12)

β2=maxi∈ω∖st|HiTPStLv|+maxj∈ω⁡|HjTPStLv (13)

maxi∈ω∖st|HiTPStLv|=|Hi0TPStLv (14)

maxj∈W|HiTPStLv|+maxj∈ω⁡|Hj0TPStLv (15)

β2=||Hi0∩j0TPStLv||

≤2||Hi0∪j0TPStLv||2

≤2(1+δQ(P+1)+|ω|−p)||v||2 (16)

Lower bound on β1 will be derived

0≤t≤|ω∩St|=l≤|ω|−1

β1≥1−|ω|Q+1δQ(P+1)+|ω|−l)||xω∖st||2|ω|−l (17)

||xω∖st||2≥|ω−1|P(1+δQ(P+1)+|ω|−P)MAVR.SNR||v||2 (18)

||xω∖st||2≥|ω|−lmini∈ω|xi| (19)

=|ω|−l(MAVR||x||2/K)

≥|ω−1|P(1+δQ(P+1)+|ω|−P)MAVR||Hx||2

≥|ω−1|P(1+δQ(P+1)+|ω|−P)MAVR.SNR||v||2

||Hx||=||Hωxω||2 (20)

≤(1+δQ(P+1)+|ω|−P)

β1≥(1−|ω|Q+1δQ(P+!)+|ω|−P)MAVR.SNR||v||2P(1+δQ(P+1)+|ω|−P) (21)

(1−|ω|Q+1δQ(P+!)+|ω|−P)MAVR.SNR||v||2P(1+δQ(P+1)+|ω|−P)>2(1+δQ(P+1)+|ω|−P||v||2 (22)

mini∈S||x[i]||2>2s1−|ω|Q+1δQ(P+1)+|ω|−P (23)

Hence the proof.

Remark: from the expression (23) it has been proved that if elements of the sparse signal satisfy the constraint, then the GOMP algorithm will identify at least one support index in t iterations. Figs. 2 and 3 show the performance comparison of GOMP and OMP algorithms at various Signal to Noise Ratio (SNR) level for different sparsity. It shows that GOMP has superior performance over the OMP at every SNR levels for the same sparsity. A sufficient condition has been derived in the previous section. Simulations have been carried out to validate the performance of the GOMP algorithm.

3  Numerical and Simulations

In the simulation, the unknown sparse signal is defined as

x(t)=∑j=1LEjWjsin⁡c(Wj(t−tj)cos⁡Wj(t−tj)) (24)

where L is the number of occupied bands, Ej is the energy coefficient, Wj is the jth sub-band in the wide bandwidth, tj is the time offset between tj and t = 0, and ωj is the carrier frequency. Simulations have been carried out in MATLAB 2019a. In all the trials tj in Wj is randomly chosen in MHz, and Ej is randomly chosen. Elements of sensing matrix are identical, independent Gaussian distribution. Non zero elements in the P-sparse vector x are evenly distributed in all possible locations. Support recovery performance of the GOMP algorithm has been evaluated over 500 independent trials for different sparsity levels and Signal to Noise ratio (SNR). We evaluate the performance for support recovery with GOMP over 500 independent trails for different sparsity levels and SNR. The measurement matrices involved in this paper are all Gauss random matrices while the reconstruction algorithms considered for the comparison are OMP, Subspace Pursuit (SP), and CoSAMP algorithms.

Number of support indices selected in each iteration should satisfy the constraint Q≤(m−1)/P . Support recovery performance of GOMP algorithm has been plotted for different number selection elements in every iteration range from 1 to 7 at various SNR levels, sparsity P = 6. In Fig. 1 number of selections varied and the performance of the GOMP algorithm has been studied. The number selection element Q = 7 has the superior support recovery performance than that of the traditional OMP (Q = 1). In Fig. 4 computation time has been plotted for different sparsity. It is obvious that computational time is slightly higher than the OMP, CoSAMP.

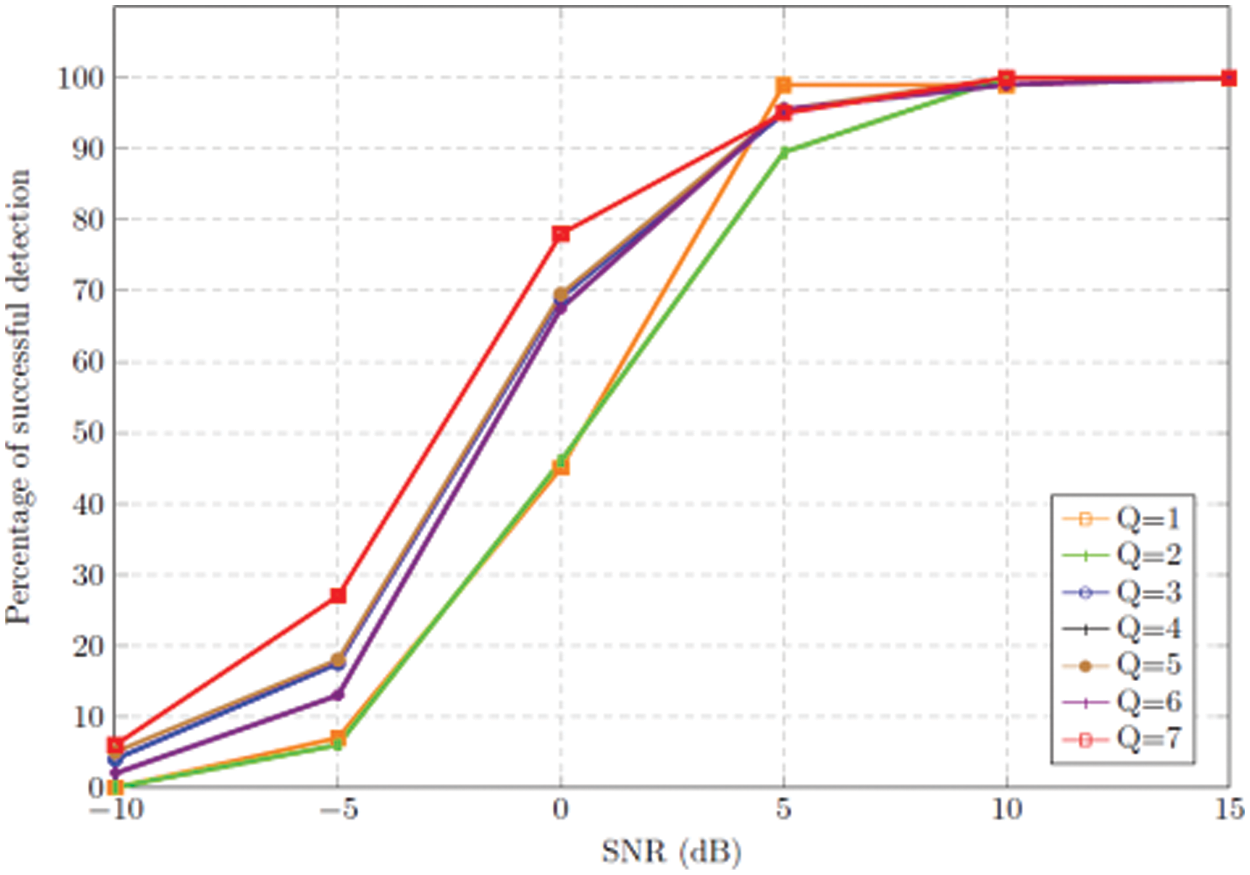
Figure 1: Detection performance of GOMP algorithm for different number of selection indices in each iteration at various signal to noise ratio levels

In this paper, successful recovery of support vector indices with respect to SNR for given sparsity of P using generalized orthogonal matching pursuit is shown in the Fig. 2. Sparsity of the signal x will be varied between 2 and 22. It is evident from the Fig. 3 that the algorithm can able to recover the signal support successfully only when there are few non-zero elements.

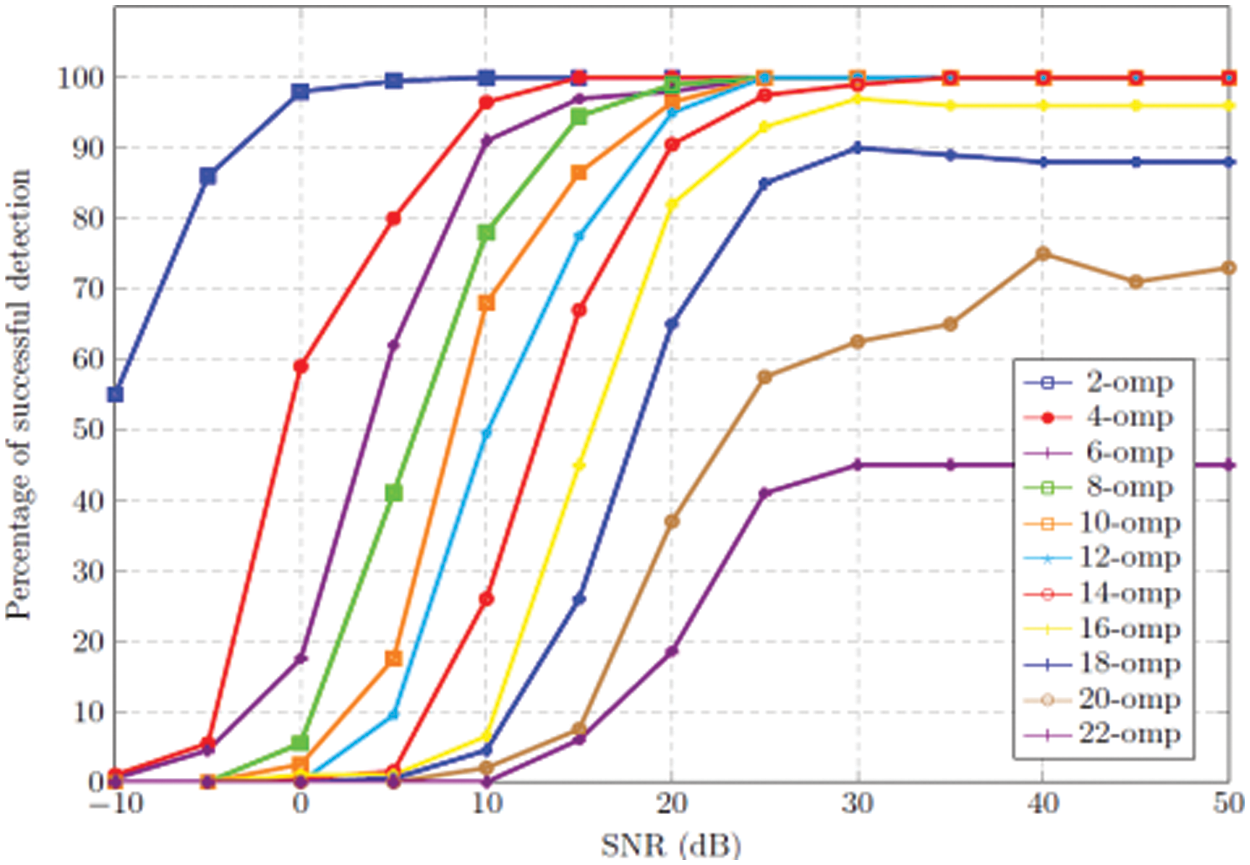
Figure 2: Detection performance of the OMP (Special case where number of selection element per iteration Q = 1) algorithm for different sparsity P varies from 2 to 22 at various SNR levels

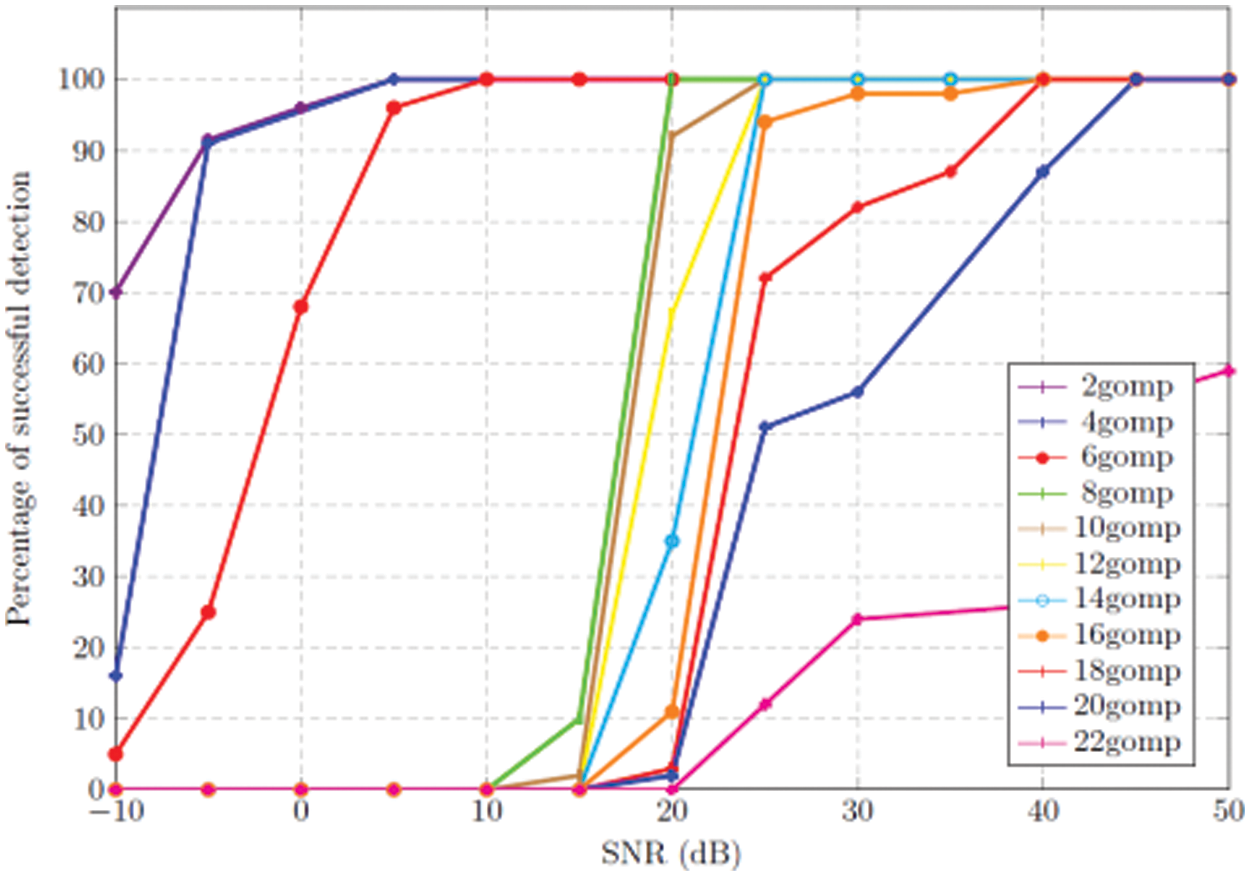
Figure 3: Detection performance of the GOMP algorithm for different sparsity P varies from 2 to 22 at various SNR levels

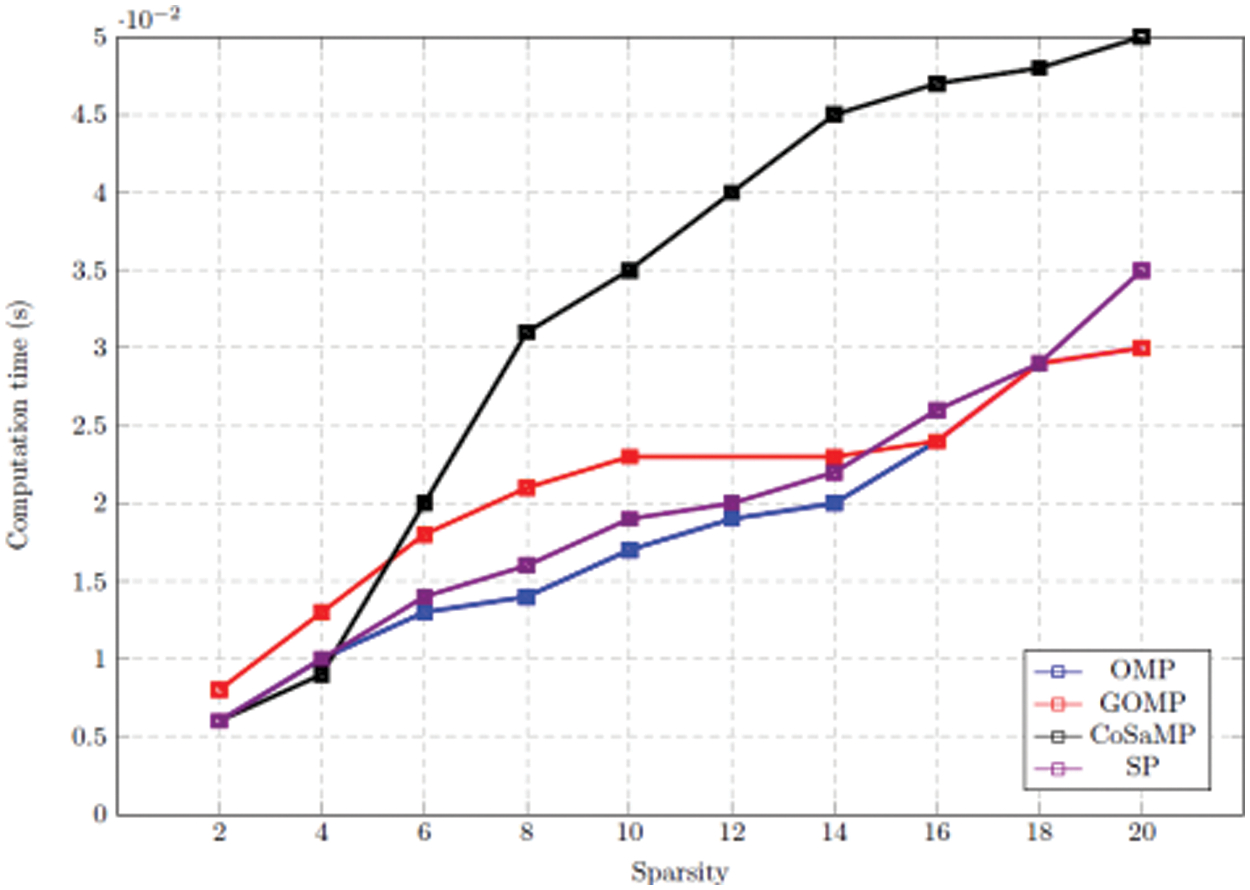
Figure 4: Graph between different sparsity level and computation time for different greedy algorithms

We note that the precise reconstruction probability and the computation time of the sparse signal vary with the level of sparsity. Reconstruction results for the different algorithms are presented in Fig. 5, where the x and y axes represent the level of sparsity and probability of exact recovery, respectively. Percentage of successful detection of support vectors at lower SNR range in GOMP is better compared to the other algorithm because GOMP recovers at least one true support vector in each iteration.

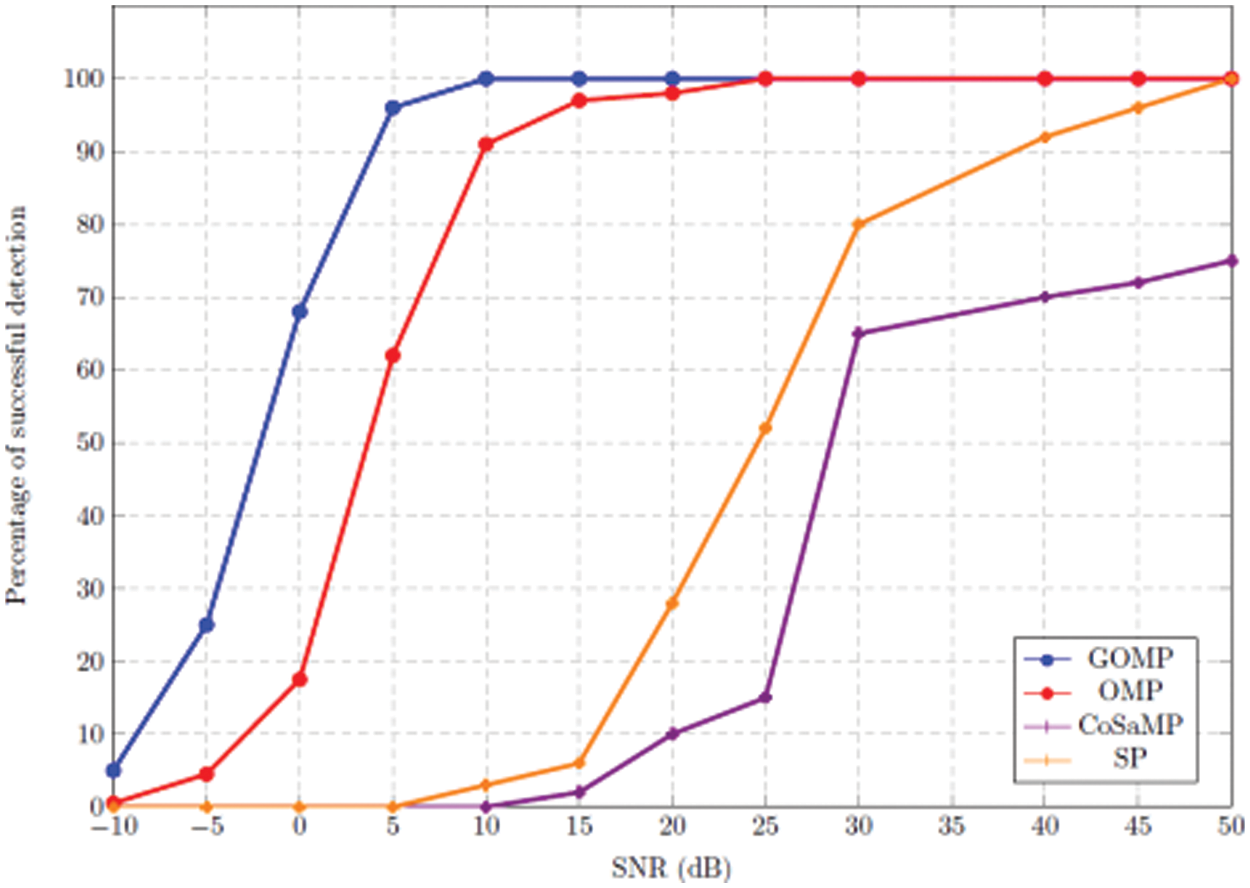
Figure 5: Detection performance of various greedy algorithm plotted between signal to noise ratio in deciBel and percentage of successful detection

4  Conclusions

In this paper, it has been proved that μ≤1(|ω|Q+1)(Q(P+1)+|ω|−P−1) with a condition on signal amplitude for the accurate support recovery of P-sparse signal based on the coherent statistics. Further number of support index chosen in each iteration is Q≤(m−1)/P . This condition is more flexible than the Q≤P . When the number of elements chosen is equal to 1, the GOMP converges to OMP. In the noisy case, it is a sufficient condition based on the coherence statistics to recover the support vector accurately in t iterations. Simulation has been carried out GOMP algorithm support recovery performance superior to the other methods at different SNR and sparsity levels. It is evident from the simulation that the GOMP has superior detection performance over other greedy algorithms like OMP, CoSAMP, and SP at different sparsity and SNR.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Wang, Z. Tian and C. Feng, “Sparsity order estimation and its application in compressive spectrum sensing for cognitive radios,” IEEE Transactions on Wireless Communications, vol. 11, no. 6, pp. 2116–2125, 2012. [Google Scholar]

 2.  E. Liu and V. N. Temlyakov, “The orthogonal super greedy algorithm and applications in compressed sensing,” IEEE Transactions on Information Theory, vol. 58, no. 4, pp. 2040–2047, 2011. [Google Scholar]

 3.  S. Satpathi, R. L. Das and M. Chakraborty, “Improving the bound on the RIP constant in generalized orthogonal matching pursuit,” IEEE Signal Processing Letters, vol. 20, no. 11, pp. 1074–1077, 2013. [Google Scholar]

 4.  Y. Shen, B. Li, W. Pan and J. Li, “Analysis of generalised orthogonal matching pursuit using restricted isometry constant,” Electronics Letters, vol. 50, no. 14, pp. 1020–1022, 2014. [Google Scholar]

 5.  Z. Ben-Haim, Y. C. Eldar and M. Elad, “Coherence-based performance guarantees for estimating a sparse vector under random noise,” IEEE Transactions on Signal Processing, vol. 58, no. 10, pp. 5030–5043, 2010. [Google Scholar]

 6.  Q. Duan, T. Kim, L. Dai and E. Perrins, “Coherence statistics of structured random ensembles and support detection bounds for OMP,” IEEE Signal Processing Letters, vol. 26, no. 11, pp. 1638–1642, 2019. [Google Scholar]

 7.  J. A. Tropp and A. C. Gilbert, “Signal recovery from random measurements via orthogonal matching pursuit,” IEEE Transactions on Information Theory, vol. 53, no. 12, pp. 4655–4666, 2007. [Google Scholar]

 8.  C. K. Au-Yeung and D. J. Love, “On the performance of random vector quantization limited feedback beamforming in a MISO system,” IEEE Transactions on Wireless Communications, vol. 6, no. 2, pp. 458–462, 2007. [Google Scholar]

 9.  X. R. Zhang, W. Z. Zhang, W. Sun, H. L. Wu, A. G. Song et al., “A Real-time cutting model based on finite element and order reduction,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]

10. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]

11. J. Wen, Z. Zhou, D. Li and X. Tang, “A novel sufficient condition for generalized orthogonal matching pursuit,” IEEE Communications Letters, vol. 21, no. 4, pp. 805–808, 2016. [Google Scholar]

12. A. S. Bandeira, M. Fickus, D. G. Mixon and P. Wong, “The road to deterministic matrices with the restricted isometry property,” Journal of Fourier Analysis and Applications, vol. 19, no. 6, pp. 1123–1149, 2013. [Google Scholar]

13. J. Weed, “Approximately certifying the restricted isometry property is hard,” IEEE Transactions on Information Theory, vol. 64, no. 8, pp. 5488–5497, 2017. [Google Scholar]

14. D. Cohen, S. Tsiper and Y. C. Eldar, “Analog-to-digital cognitive radio: Sampling, detection, and hardware,” IEEE Signal Processing Magazine, vol. 35, no. 1, pp. 137–166, 2018. [Google Scholar]

15. R. Neelakandan, “Sub-optimal low-complexity detector for generalised quadrature spatial modulation,” Electronics Letters, vol. 54, no. 15, pp. 941–943, 2018. [Google Scholar]

16. Y. C. Eldar and T. Michaeli, “Beyond bandlimited sampling,” IEEE Signal Processing Magazine, vol. 26, no. 3, pp. 48–68, 2009. [Google Scholar]

17. M. Mishali and Y. C. Eldar, “Blind multiband signal reconstruction: Compressed sensing for analog signals,” IEEE Transactions on Signal Processing, vol. 57, no. 3, pp. 993–1009, 2009. [Google Scholar]

18. M. Jia, Y. Shi, X. Gu, X. Wang and Y. Yin, “Improved algorithm based on modulated wideband converter for multiband signal reconstruction,” EURASIP Journal on Wireless Communications and Networking, vol. 2016, no. 1, pp. 1–9, 2016. [Google Scholar]

19. P. Qi, Z. Li, H. Li and T. Xiong, “Blind sub-nyquist spectrum sensing with modulated wideband converter,” IEEE Transactions on Vehicular Technology, vol. 67, no. 5, pp. 4278–4288, 2018. [Google Scholar]