 Open Access
Open Access
ARTICLE
Competitive Multi-Verse Optimization with Deep Learning Based Sleep Stage Classification
1 Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam Bin Abdulaziz University, AlKharj, Saudi Arabia
2 Department of Information Systems, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, P. O. Box 84428, Riyadh, 11671, Saudi Arabia
3 Department of Industrial Engineering, College of Engineering at Alqunfudah, Umm Al-Qura University, Saudi Arabia
4 Department of Information Systems, College of Science & Art at Mahayil, King Khalid University, Saudi Arabia
5 Department of Computer Science, College of Sciences and Humanities-Aflaj, Prince Sattam Bin Abdulaziz University, Saudi Arabia
6 Department of Electrical Engineering, Faculty of Engineering and Technology, Future University in Egypt, New Cairo, 11835, Egypt
* Corresponding Author: Anwer Mustafa Hilal. Email:
Computer Systems Science and Engineering 2023, 45(2), 1249-1263. https://doi.org/10.32604/csse.2023.030603
Received 29 March 2022; Accepted 18 May 2022; Issue published 03 November 2022
Abstract
Sleep plays a vital role in optimum working of the brain and the body. Numerous people suffer from sleep-oriented illnesses like apnea, insomnia, etc. Sleep stage classification is a primary process in the quantitative examination of polysomnographic recording. Sleep stage scoring is mainly based on experts’ knowledge which is laborious and time consuming. Hence, it can be essential to design automated sleep stage classification model using machine learning (ML) and deep learning (DL) approaches. In this view, this study focuses on the design of Competitive Multi-verse Optimization with Deep Learning Based Sleep Stage Classification (CMVODL-SSC) model using Electroencephalogram (EEG) signals. The proposed CMVODL-SSC model intends to effectively categorize different sleep stages on EEG signals. Primarily, data pre-processing is performed to convert the actual data into useful format. Besides, a cascaded long short term memory (CLSTM) model is employed to perform classification process. At last, the CMVO algorithm is utilized for optimally tuning the hyperparameters involved in the CLSTM model. In order to report the enhancements of the CMVODL-SSC model, a wide range of simulations was carried out and the results ensured the better performance of the CMVODL-SSC model with average accuracy of 96.90%.Keywords
Sleep plays a vital role in the optimal performance of both the brain and the body [1]. But, a larger number of individual severely suffers from sleeping disorder, namely narcolepsy, insomnia, and sleep dyspnoea [2]. Efficient and feasible sleep assessment is made mandatory for analyzing nap related issues and making timely interference. Assessment of sleep commonly depends on the manual phasing of overnight polysomnography (PSG) signal, including electrocardiogram (ECG), electroencephalogram (EEG), blood oxygen saturation electrooculogram (EOG), electromyogram (EMG), and respiration [3], by well trained and authorized technicians. The more time-taking characteristics of manual doze phasing hamper the application zones on very huge datasets and restrict related research in this domain [4]. In addition to this, the inter-scorer accord is comparatively lesser than 90%, and its development remains a challenge. The several channel ranges of PSG also represent disadvantages in prevention of broader use for the general population, on account of difficult groundwork and acts as a disruption to participant’ normal nap. Hence, the past decades have made evident that the development of automated nap phasing depends on one-channel EEG. These methodologies may eventually result in adequately exact, powerful, worthwhile, and fastest ways of doze scoring [5].
The conduct of most sleep stage classification (SSC) techniques mainly depends on choosing representative characteristics for various nap phases [6]. Frequency, time period, and time-frequency field decays are the few general steps for processing and functioning of time signals and extraction of characteristics straightforwardly. Several numerical designs have been well-established in the procedure of finding hidden characteristics. After the extraction of features, several machine learning algorithms were commonly used for categorization [7], namely ensemble learning, nearest neighbour classifier, linear discriminate analysis (LDA), support vector machine (SVM), random forest (RF), and so on. It also depicts the good outcomes with combinatorial machine learning (ML) techniques [8]. In recent times, deep learning (DL) methodology namely recurrent neural network (RNN), convolution neural network (CNN), and other forms of deep neural networks (DNN) have become a common tool in pattern identification in biomedical signal processing. Long short-term memory (LSTM) method that has taken advantageous factor of sequential data learning to advance categorization performance was highly recommended for automatic nap phase [9,10].
Eldele et al. [11] present new attention based DL framework named AttnSleep for classifying sleep stages utilizing single channel EEG signal. This infrastructure begins with the feature extracting element dependent upon multi-resolution CNN (MRCNN) and adaptive feature recalibration (AFR). The MRCNN is extracting minimal as well as maximal frequency features and the AFR is capable of improving the quality of extracting features by modeling the inter-dependency among the features. The authors in [12] present the primary DL technique to SSC which learn end-to-end with no computing spectrograms or removing handcrafted feature which activities every multi-variate and multi-modal PSG signals and exploits the temporal context of all 30-s window of data. The authors in [13] establish a new multi-channel method dependent upon DL network and hidden Markov model (HMM) for improving the accuracy of SSC in term neonates. The feature space dimensionality is then decreased by utilizing a developmental FS approach named MGCACO (Modified Graph Clustering Ant Colony Optimization) dependent upon the significance and redundancy analysis. The authors in [14] examine the strategy of deep RNNs to detect sleep stages in single channel EEG signals recorded at home by non-expert users. It can be reported the outcome of dataset size, infrastructure selections, regularization, and personalization on the classifier efficiency.
The authors in [15] presented an effectual approach for signal-strength-based combining (SSC) dependent upon EEG signal analysis utilizing ML techniques with assuming 10s of epochs. The EEG signal has played important role in automatic SSC. EEG signal is filtered and decomposed as to frequency sub-bands utilizing band-pass filter. In [16], a flexible DL method was presented utilizing raw PSG signal. A one-dimensional CNN (1D-CNN) was established utilizing EOG and EEG signals to classifier of sleep stages. The efficiency of the model was estimated utilizing 2 public databases. Fan et al. [17–19] present a novel sleep staging method utilizing EOG signals that are further convenient for obtaining than EEG. A 2-scale CNN initial extracting epoch-wise temporary-equal features in raw EOG signal. The RNN then captured the long-term sequential data.
This study focuses on the design of Competitive Multi-verse Optimization with Deep Learning Based Sleep Stage Classification (CMVODL-SSC) model using EEG signals. The proposed CMVODL-SSC model intends to effectively categorize different sleep stages on EEG signals. Primarily, data pre-processing is performed to convert the actual data into useful format. Besides, a cascaded long short term memory (CLSTM) model is employed to perform classification process. At last, the CMVO algorithm is utilized for optimally tuning the hyperparameters involved in the CLSTM model. In order to report the enhancements of the CMVODL-SSC model, a wide range of simulations was carried out and the results ensured the better performance of the CMVODL-SSC model interms of different metrics.
In this study, a new CMVODL-SSC model has been introduced to effectively categorize different sleep stages on EEG signals. Primarily, data pre-processing is performed to convert the actual data into useful format. Besides, a CLSTM model is employed to perform classification process. At last, the CMVO algorithm is utilized for optimally tuning the hyperparameters involved in the CLSTM model. Fig. 1 illustrates the overall process of CMVODL-SSC technique.
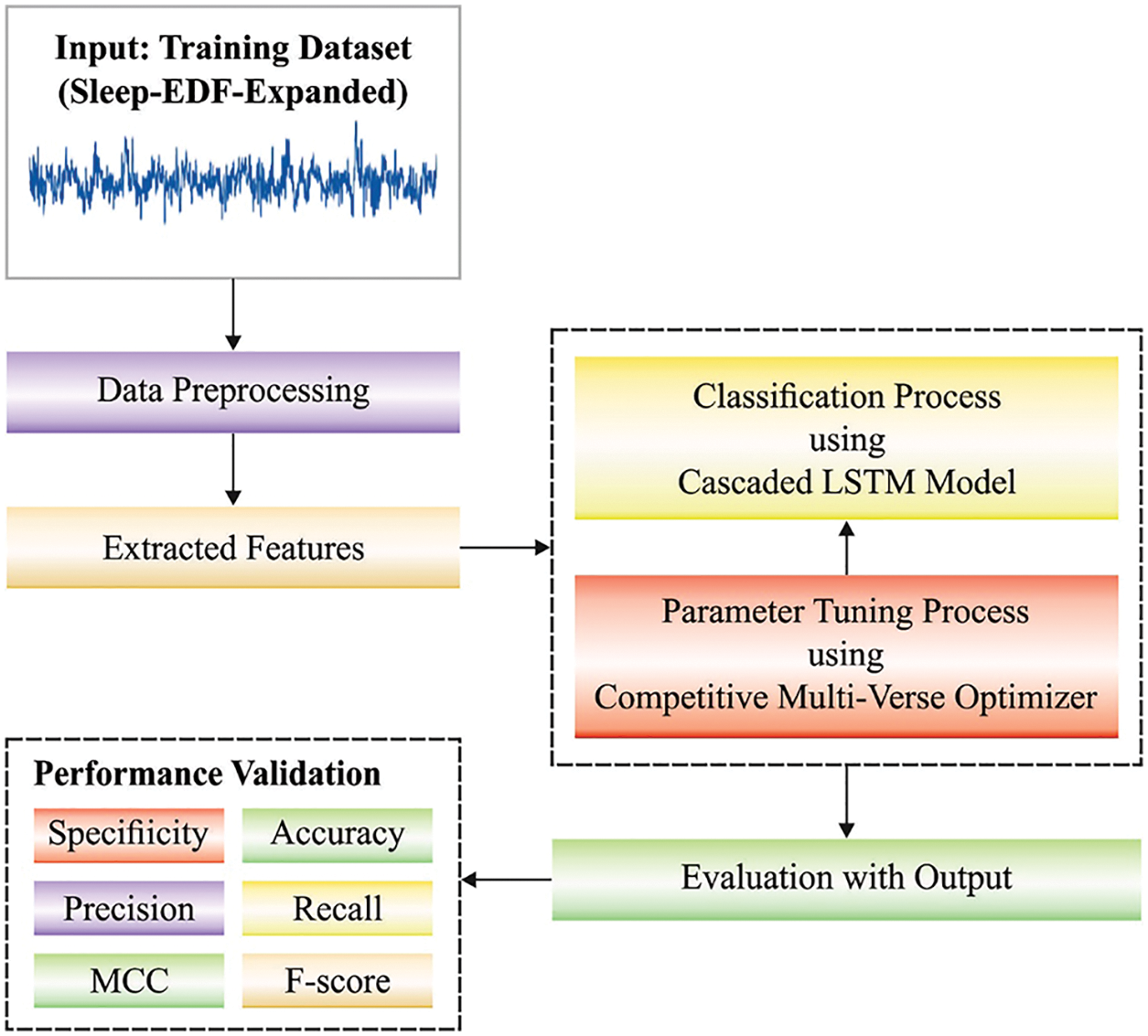
Figure 1: Overall process of CMVODL-SSC technique
At the initial stage, data pre-processing is performed to convert the actual data into useful format. The neural network (NN) trained develops further effectual on the reaching of few pre-processing steps on the network target and input. Usually, the feature was rescaled in the interval of 0 to 1 or from −l to 1. It could be formulated as:
whereas
2.2 CLSTM Based Sleep Stage Classification
Once the sleep stage data is pre-processed, the next level is to perform classification process using the CLSTM model [20]. A RNN is a sort of artificial neural network (ANN) neural network (NN) that comprises output, input, and hidden layers. There are two variances among traditional networks and RNN namely feed forward neural network (FFNN). In a similar hidden state, there are links among the nodes in RNN, while in the FFNN there is no one. The input of the hidden state in the present time contains the input neuron in the present time and the hidden state in the preceding time. The specific architecture of the RNN enables the best explanation of the temporal dynamic performance since it employs the preceding data it learns to design the pattern of the existing stage, i.e., advantageous for satisfactorily examining the feature of the existing time sequence. Consequently, in our work, RNN with memory process has been examined and employed in the time sequence predicting. Generally, an RNN could not preserve a better memory when the time interval is larger and has a vanishing gradient issue. Consequently, enhanced RNN model has been presented namely an LSTM with the easy architecture that is extensively employed for time sequence predicting in different domains. The LSTM calculates the memory unit through activation function. But, the application to hydrological information was constrained.
The LSTM unit using peephole connection comprises forget gate (FG), input gate (IG), and output gate (OG). Through the specific interaction process amongst three gates using a memory cell that assists an accumulator of the cells, the LSTM mitigates the vanishing gradient effects of long term dependency. The computation procedure of the LSTM using peephole connection is discussed in the following.
Simultaneously, the FG assesses that data to remove from the preceding cell state, through
The older cell state
(4) The upgraded cell status
Here,
Currently, the LSTM method was illustrated to be efficient at managing temporal correlation, even though certain limitation unavoidably exists. For example, the targeted value in the present time
(1) Rescale and Collect the new information.
(2) Divide the information into testing (10%) and training (90%) datasets.
(3) Training the
(4) Testing the trained
2.3 CMVO Based Hyperparameter Optimization
Finally, the CMVO algorithm is utilized for optimally tuning the hyperparameters involved in the CLSTM model [21]. The presented method's aim is to attain solution with better quality and prevent early convergence of MVO approach. The presented method is inspired by the preceding study of CSO algorithm. In the modified approach, the dynamic method of object exchange among universes varies from that in the normal form of MVO where universe presents a competitive process.
The competition method is executed by the universe is attuned instead of based on the personal best universes and global. The competition model guarantees to prevent early convergence by maintaining population variety. In CMVO, the population is arbitrarily gathered according to bi-competition to generate two sets, losers, and winners. In all the competitions, the location of loser from the competition is attuned through learning from the winner instead of from the personal best and global locations. Followed by all the competitions, winner enters the following generation. Fig. 2 depicts the flowchart of CMVO technique.
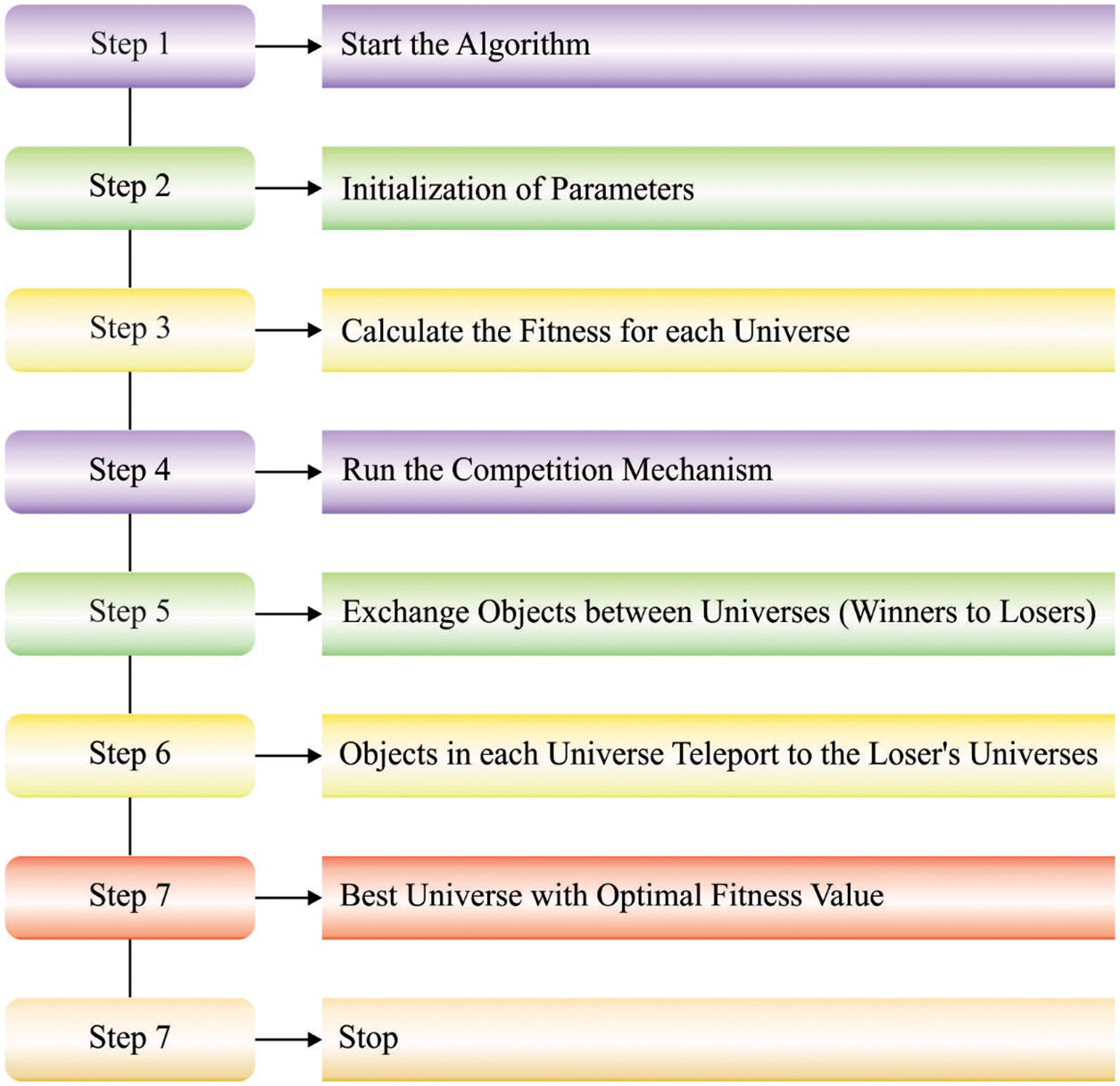
Figure 2: Flowchart of CMVO technique
Accordingly, universe might collectively converge toward the optimum solution. The competition conserves the best balance among exploitation and exploration as well as assist them to converge on optimum solution and preserve the diversity of every population. In the presented method, arithmetical equation of updating location are attuned by the subsequent approach:
In which
Step 1 (Initial step): arbitrary universe is initialized according to the population size and dimension of searching region. Next, all the universes involved in population would be arbitrarily separated.
Step 2 (Bicompetition step): two sets of population at all the iterations (whereas CMVO chooses) are allowable to contribute to the bicompetition.

In this section, the experimental assessment of the CMVODL-SSC model is carried out using the Sleep-EDF-Expanded dataset [22] comprises of 238976 samples with 71197 samples under W class, 25169 samples under N1 class, 88975 samples under N2 class, 19454 samples under N3 class, and 34181 samples under REM class as shown in Tab. 1. The proposed model is simulated using Python tool.
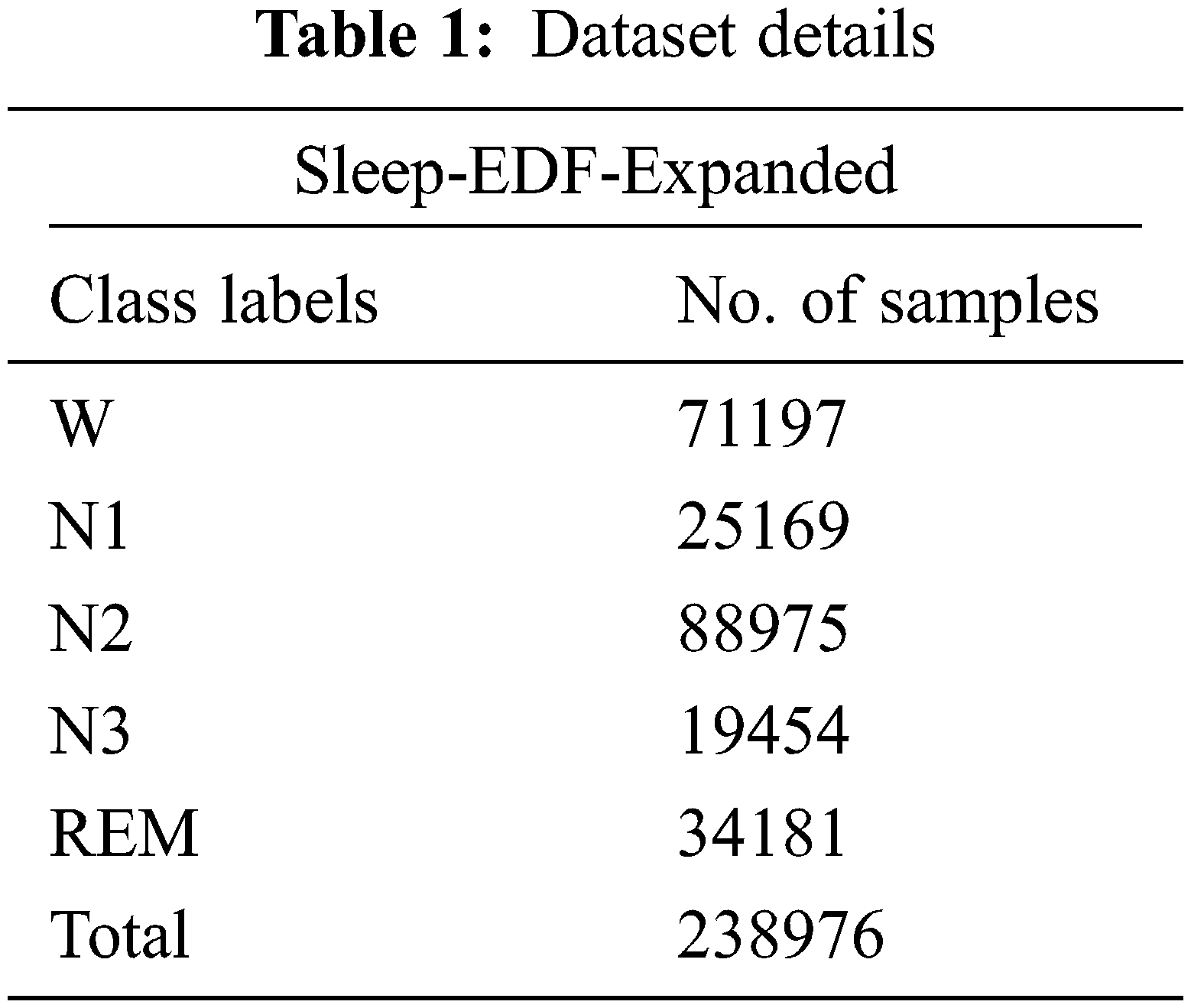
Fig. 3 shows the confusion matrices produced by the CMVODL-SSC model on 70% of training set (TRS) and 30% of testing set (TSS). On 70% of TRS, the CMVODL-SSC model has identified 48451 samples into W class, 16343 samples into N1 class, 60495 samples into N2 class, 12218 samples into N3 class, and 22486 samples into REM class. Similarly, on 30% of TSS, the CMVODL-SSC model has recognized 20786 samples into W class, 6949 samples into N1 class, 26097 samples into N2 class, 5345 samples into N3 class, and 9557 samples into REM class.
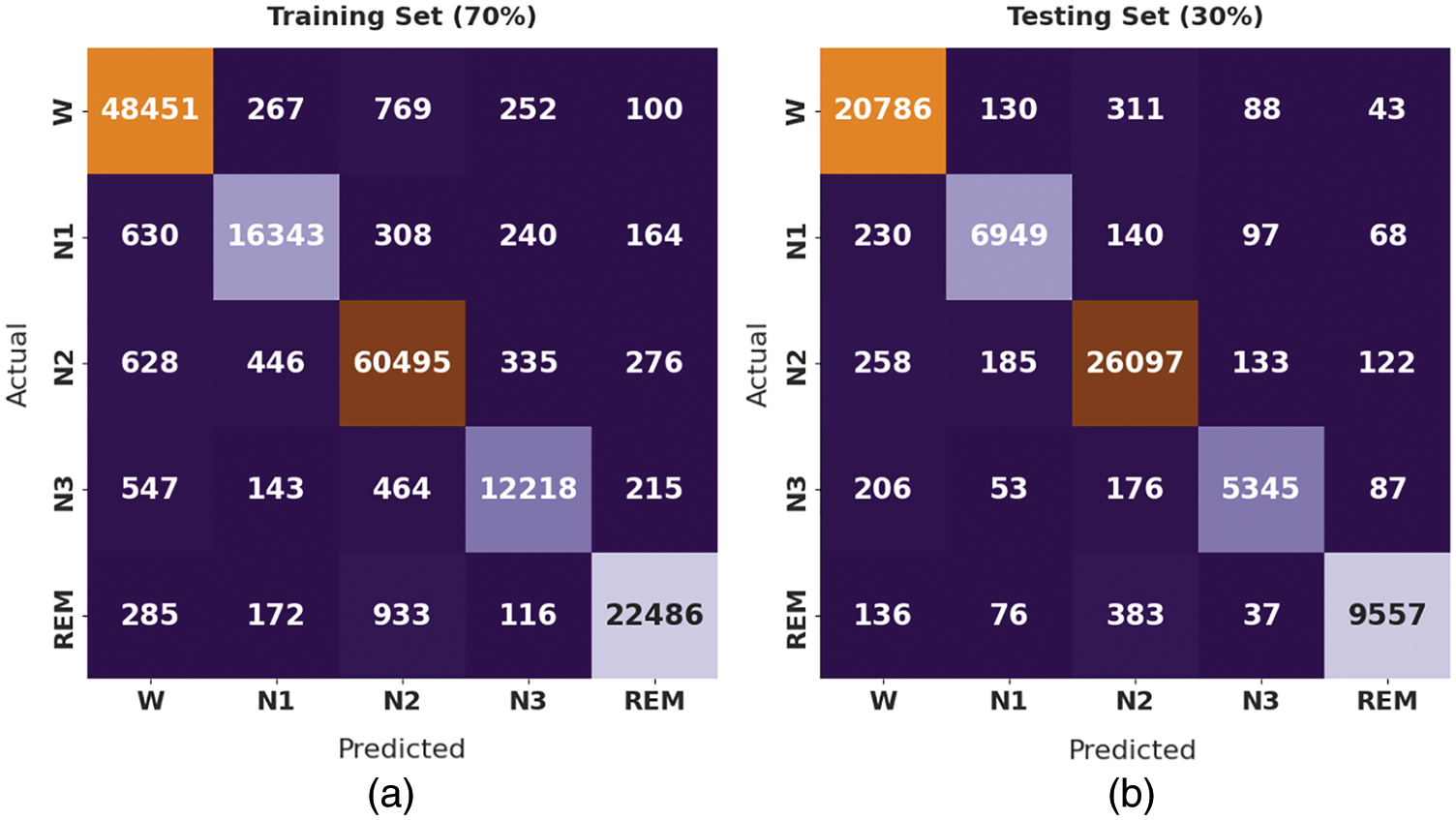
Figure 3: Confusion matrix of CMVODL-SSC technique on 70% of TRS and 30% of TSS
Tab. 2 highlights the performance of the CMVODL-SSC model on 70% of TRS and 30% of TSS.
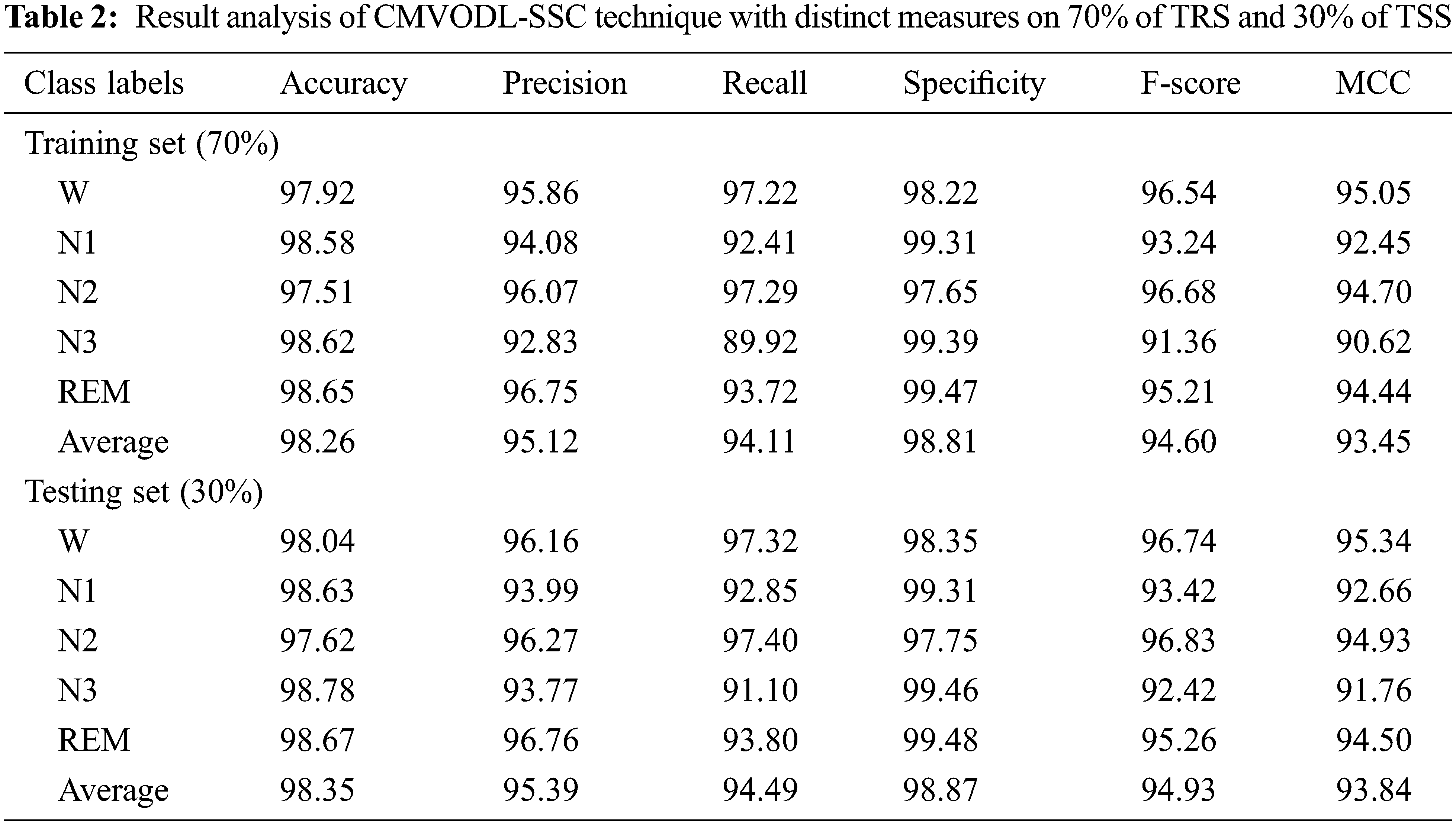
Fig. 4 reports a detailed result of the CMVODL-SSC model offered on 70% of TRS. The CMVODL-SSC model has identified samples under W class with
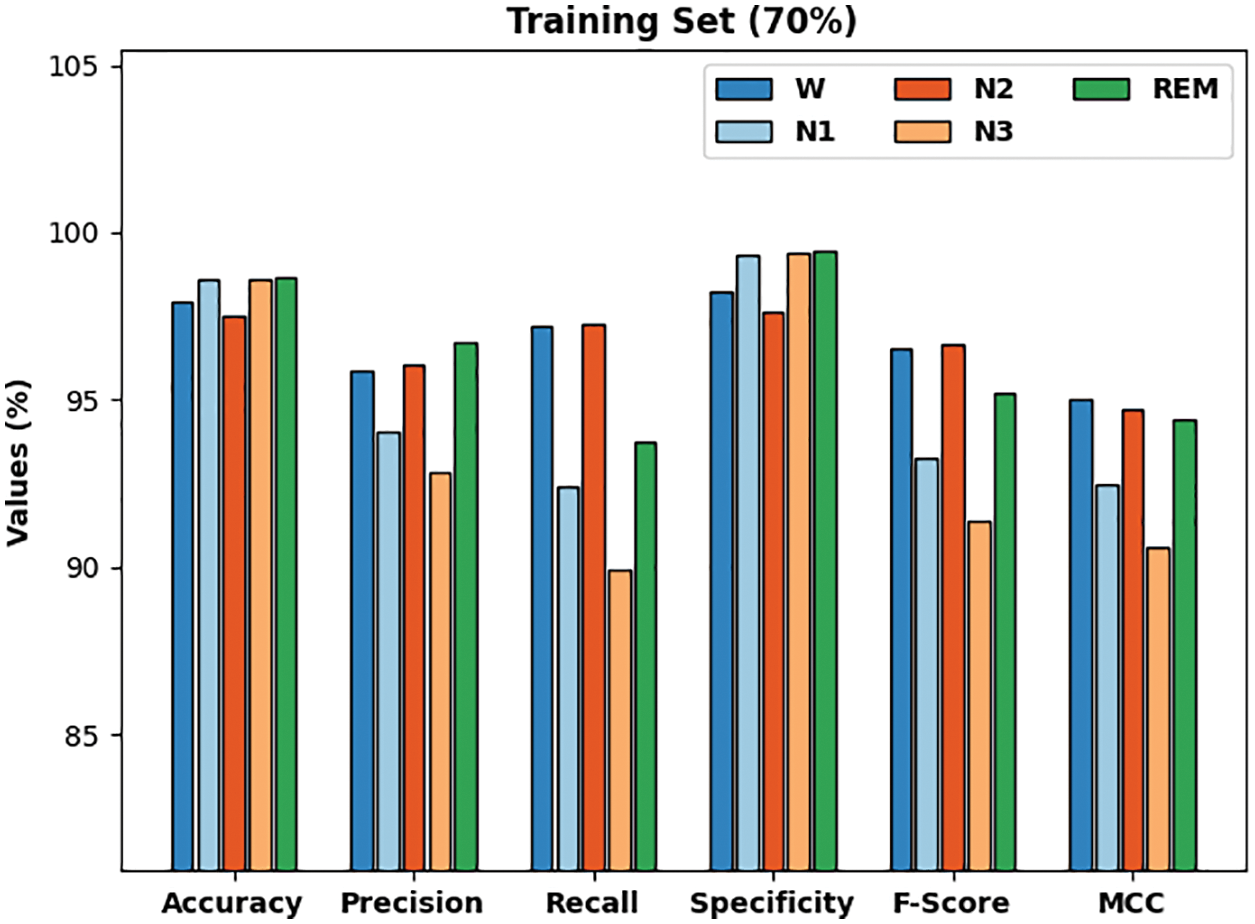
Figure 4: Result analysis of CMVODL-SSC technique on 70% of TRS
Fig. 5 demonstrates a detailed results of the CMVODL-SSC model offered on 30% of TSS. The CMVODL-SSC model has identified samples under W class with
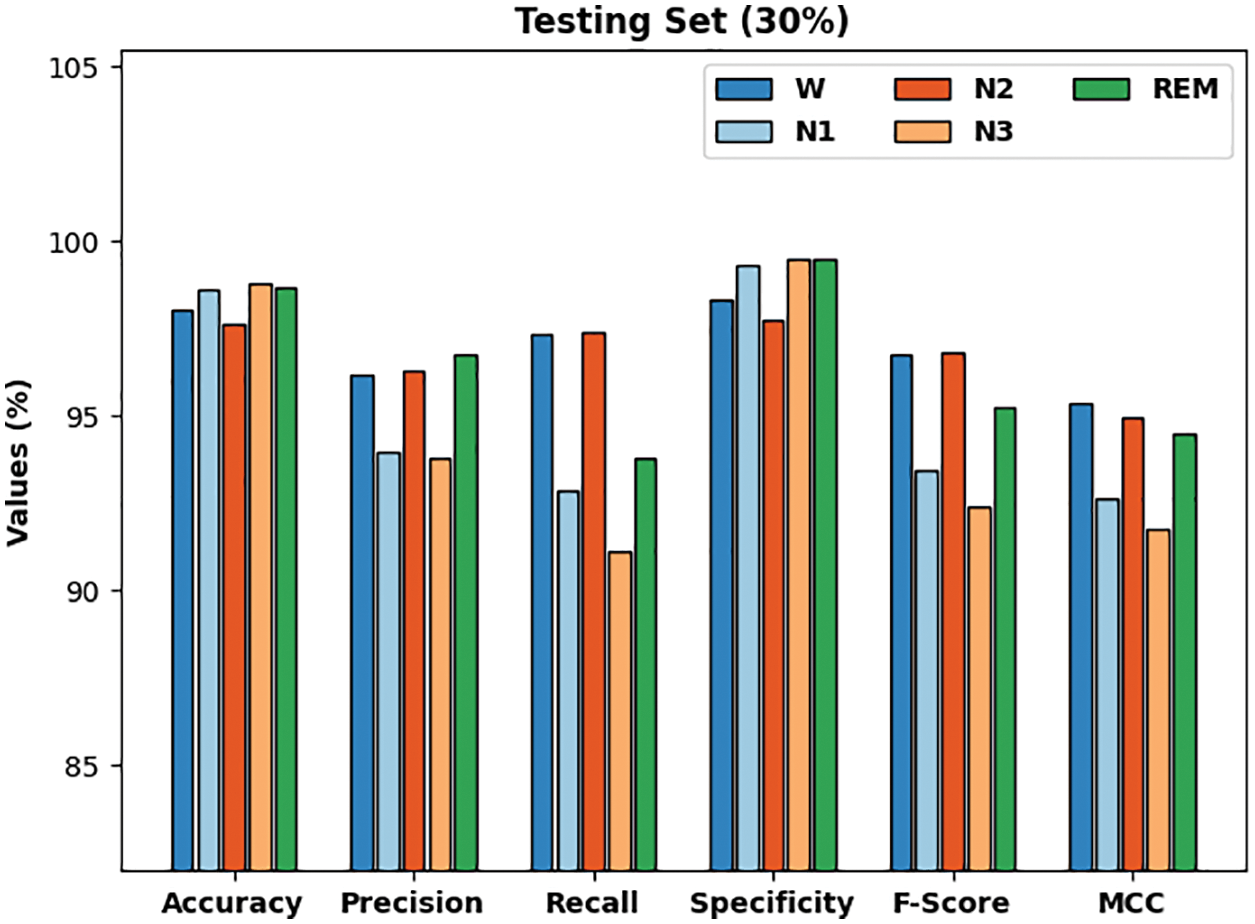
Figure 5: Result analysis of CMVODL-SSC technique on 30% of TSS
Fig. 6 illustrates the confusion matrices produced by the CMVODL-SSC approach on 80% of training set (TRS) and 20% of testing set (TSS). On 80% of TRS, the CMVODL-SSC model has identified 55198 samples into W class, 16564 samples into N1 class, 68645 samples into N2 class, 10829 samples into N3 class, and 25104 samples into REM class. Also, on 20% of TSS, the CMVODL-SSC technique has recognized 13988 samples into W class, 4203 samples into N1 class, 16986 samples into N2 class, 2689 samples into N3 class, and 6233 samples into REM class.
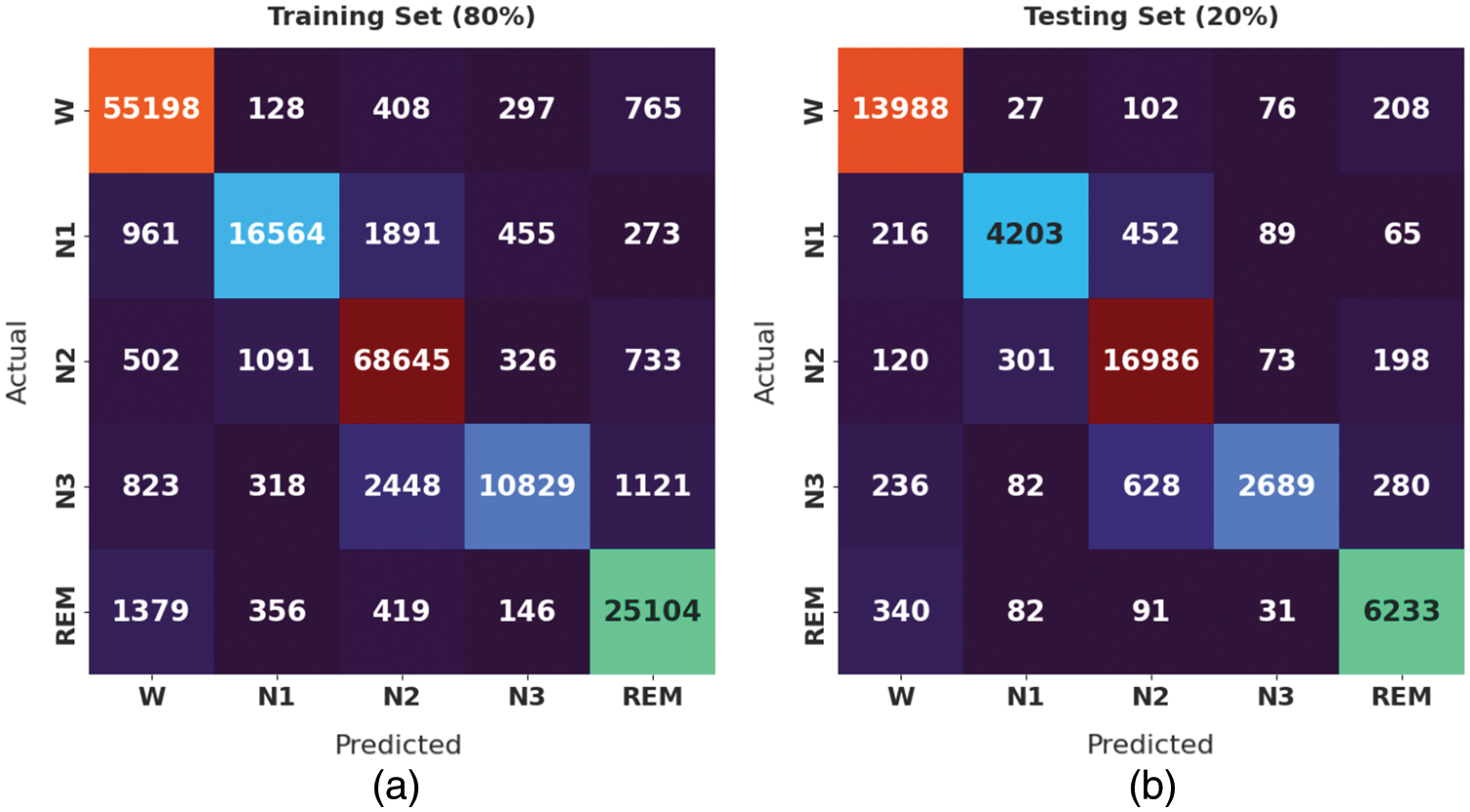
Figure 6: Confusion matrix of CMVODL-SSC technique on 80% of TRS and 20% of TSS
Tab. 3 examines the performance of the CMVODL-SSC technique on 80% of TRS and 20% of TSS. Fig. 7 defines a detailed results of the CMVODL-SSC model offered on 80% of TRS. The CMVODL-SSC model has identified samples under W class with
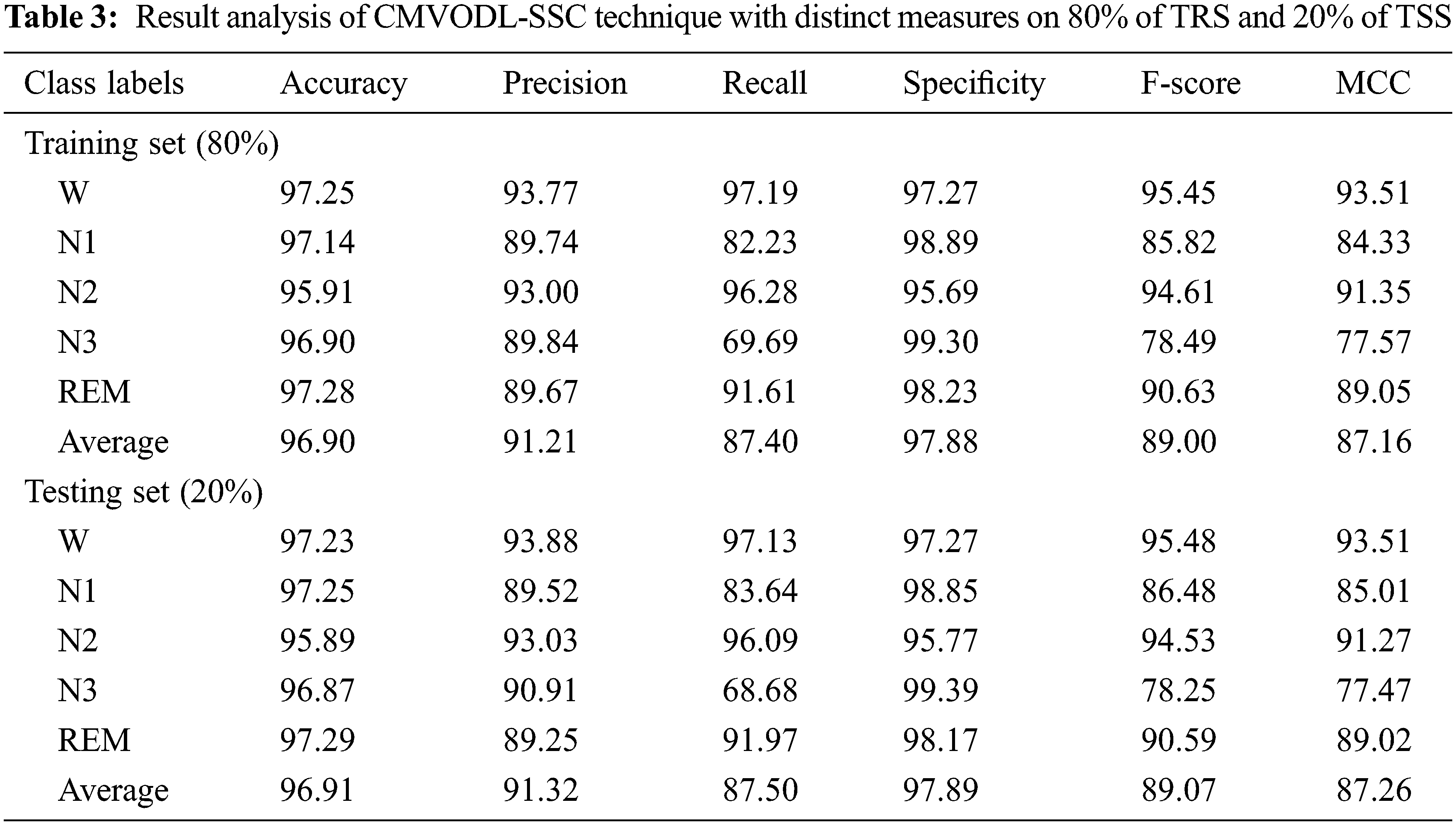
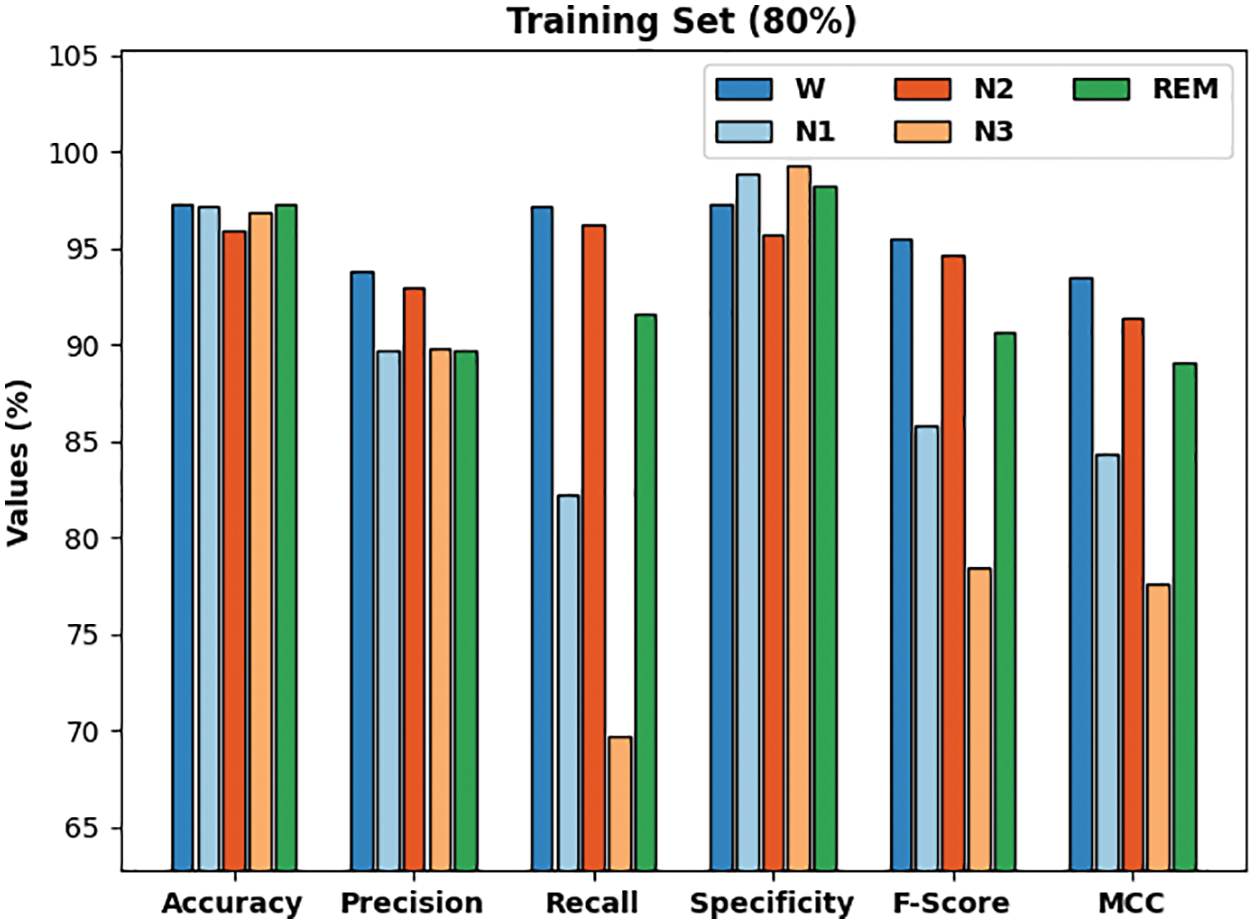
Figure 7: Result analysis of CMVODL-SSC technique on 80% of TRS
Fig. 8 demonstrates a detailed results of the CMVODL-SSC approach offered on 20% of TSS. The CMVODL-SSC model has identified samples under W class with
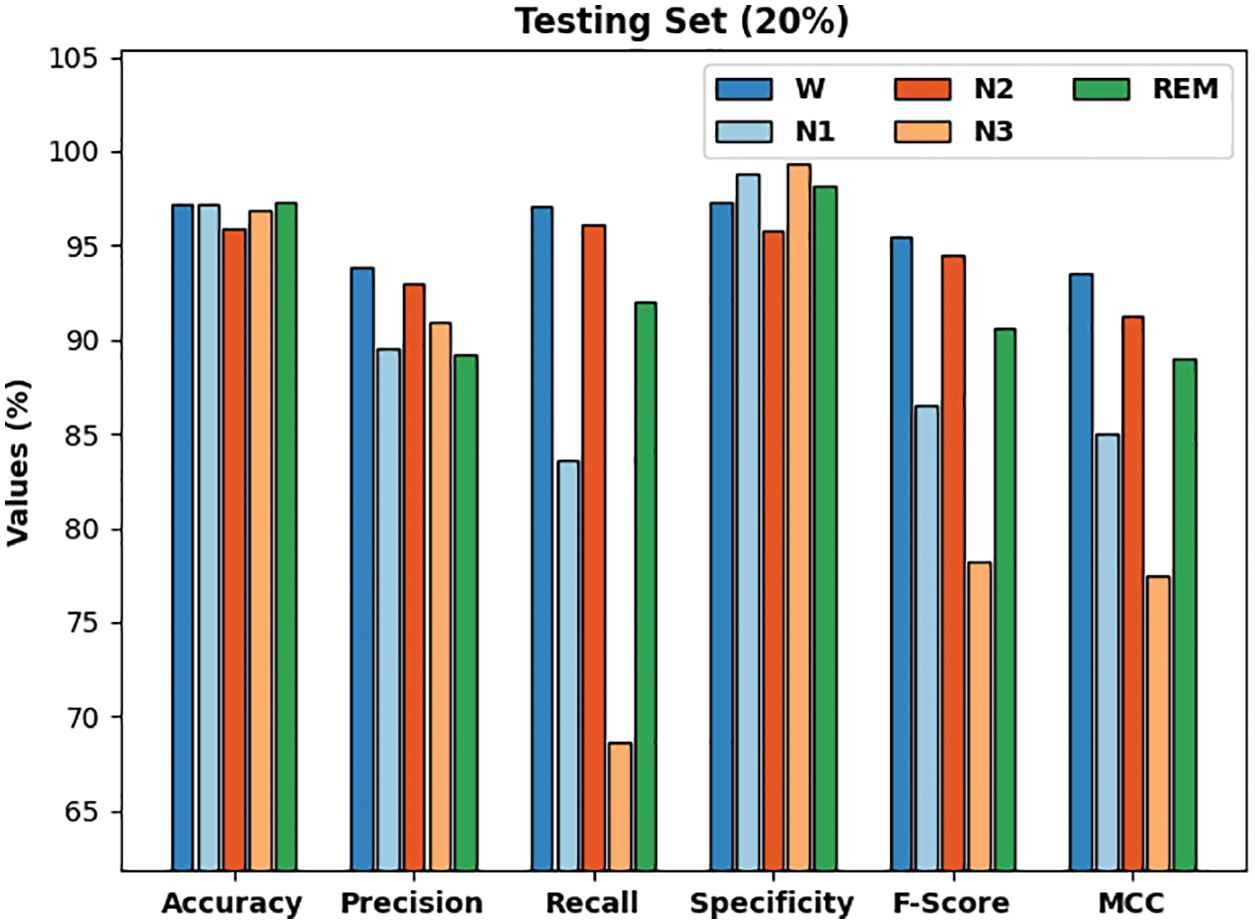
Figure 8: Result analysis of CMVODL-SSC technique on 20% of TSS
For ensuring the enhanced performance of the CMVODL-SSC model, a comparative analysis with MRCNN model interms of
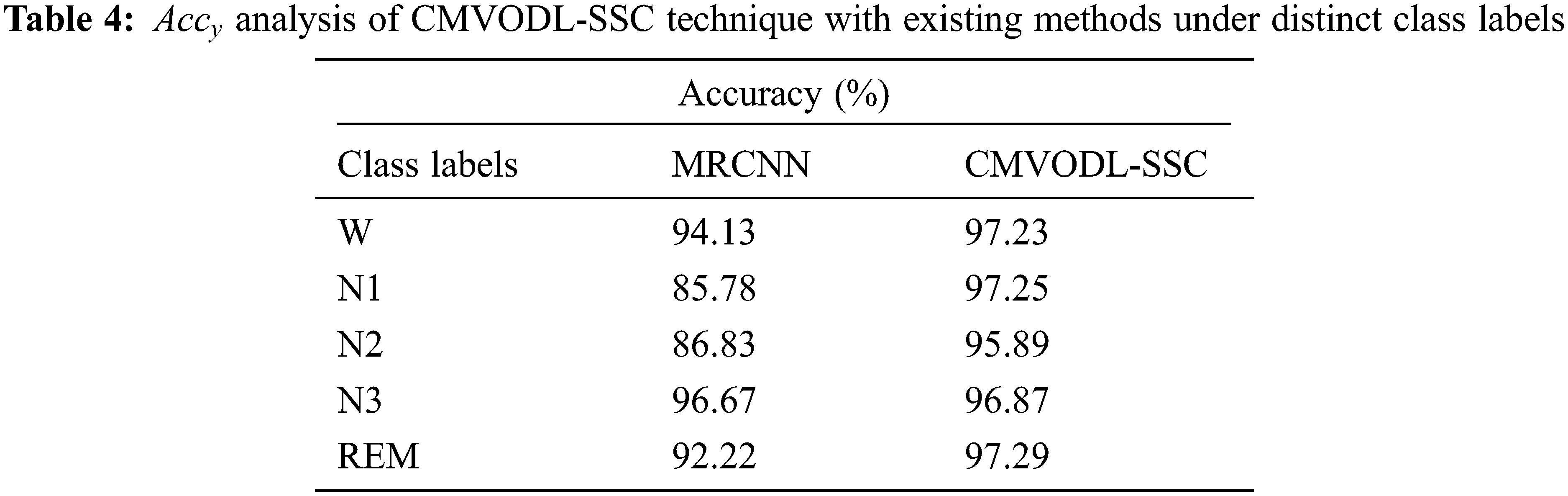
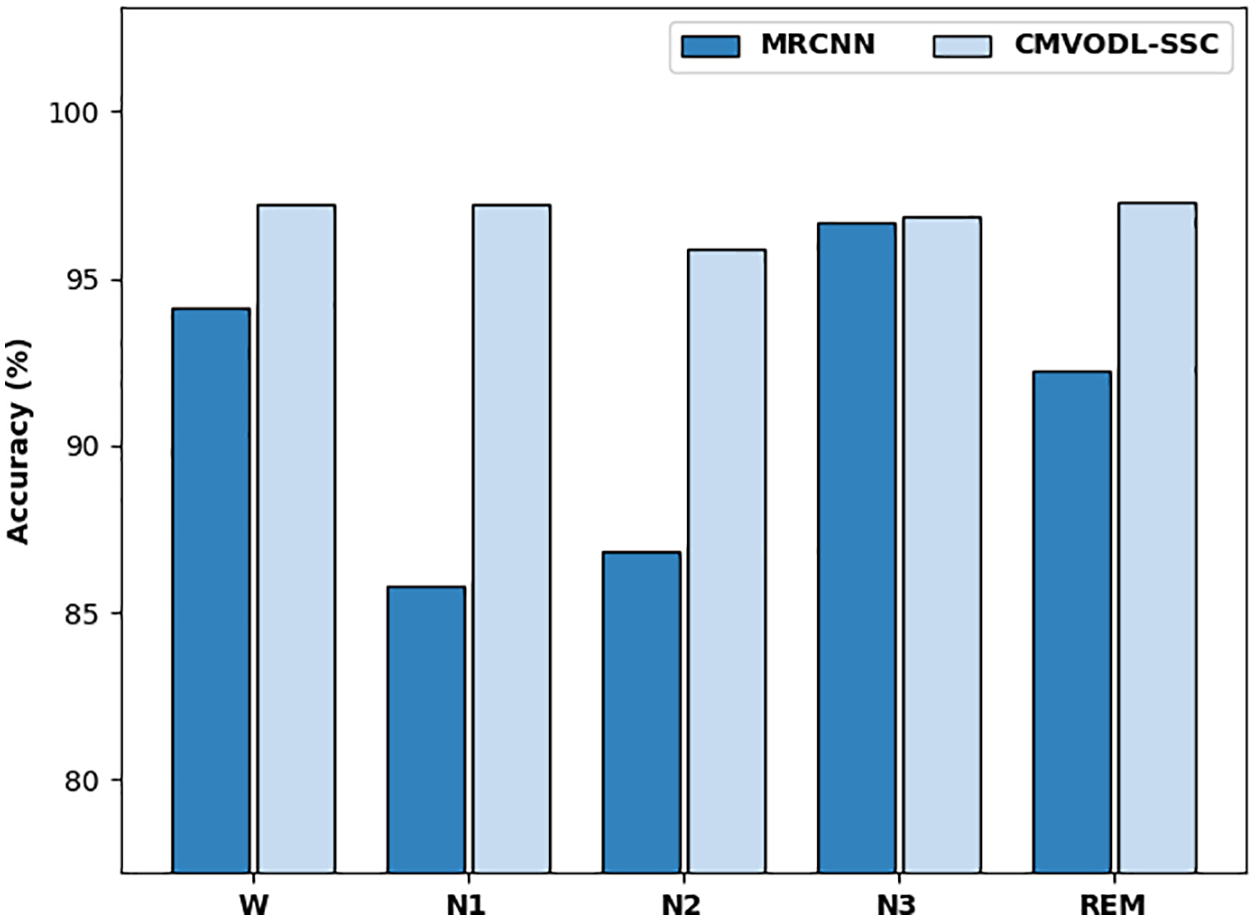
Figure 9:
In order to ensure the enhanced performance of the CMVODL-SSC model, a comparative analysis with MRCNN model with respect to
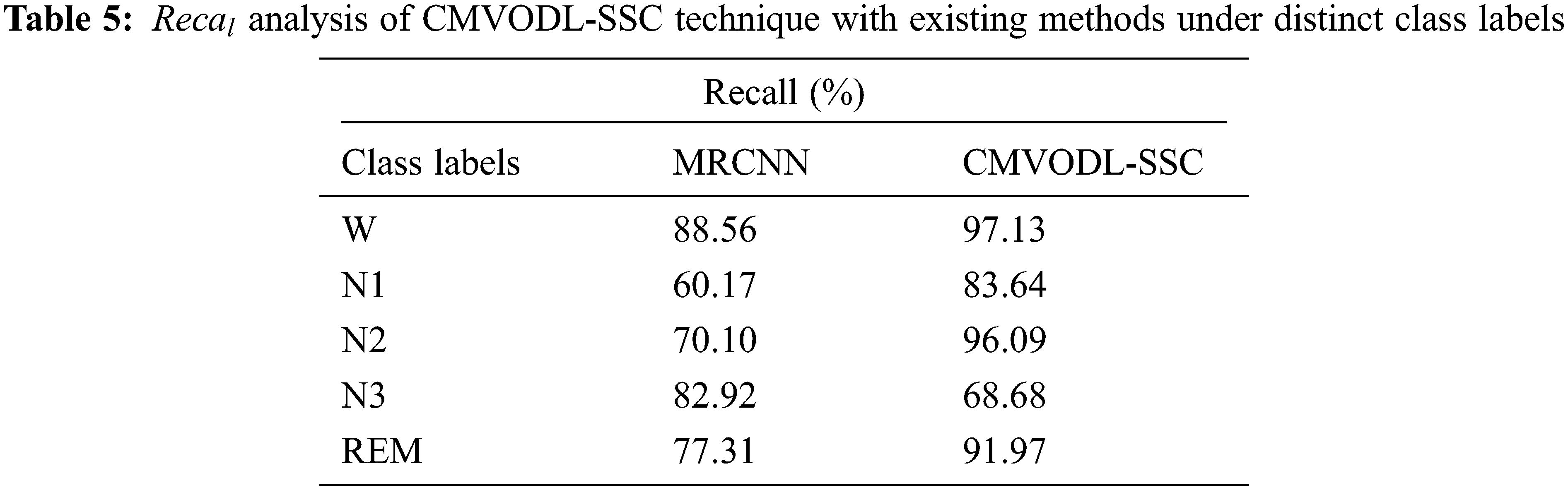
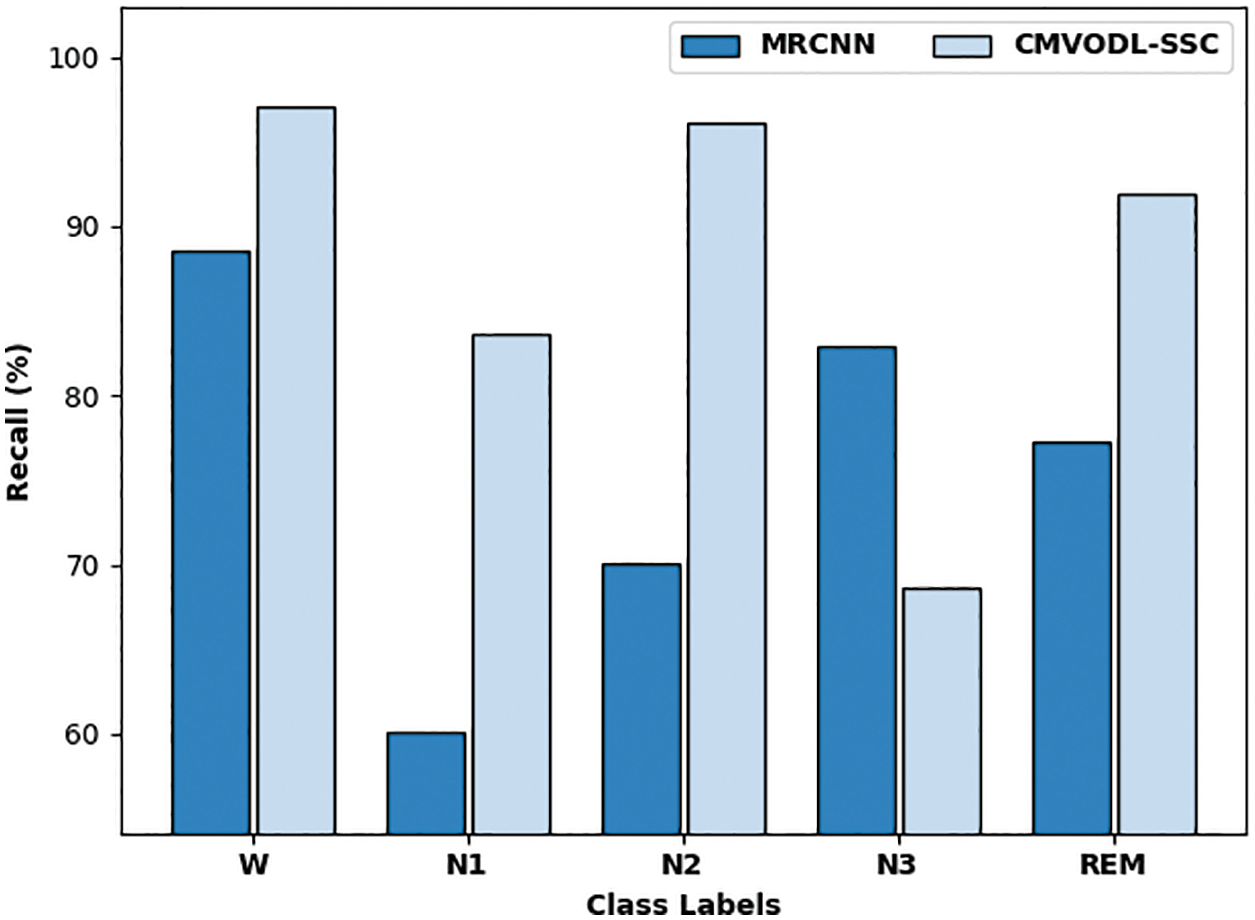
Figure 10:
For demonstrating the enhanced performance of the CMVODL-SSC model, a comparative analysis with MRCNN technique interms of
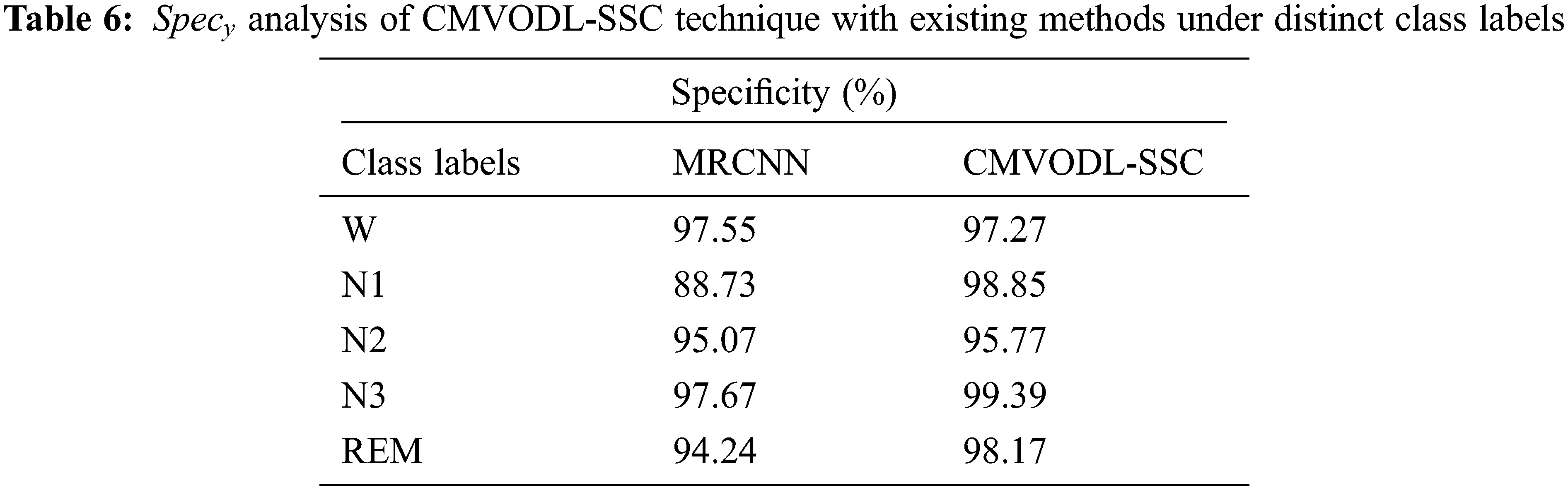
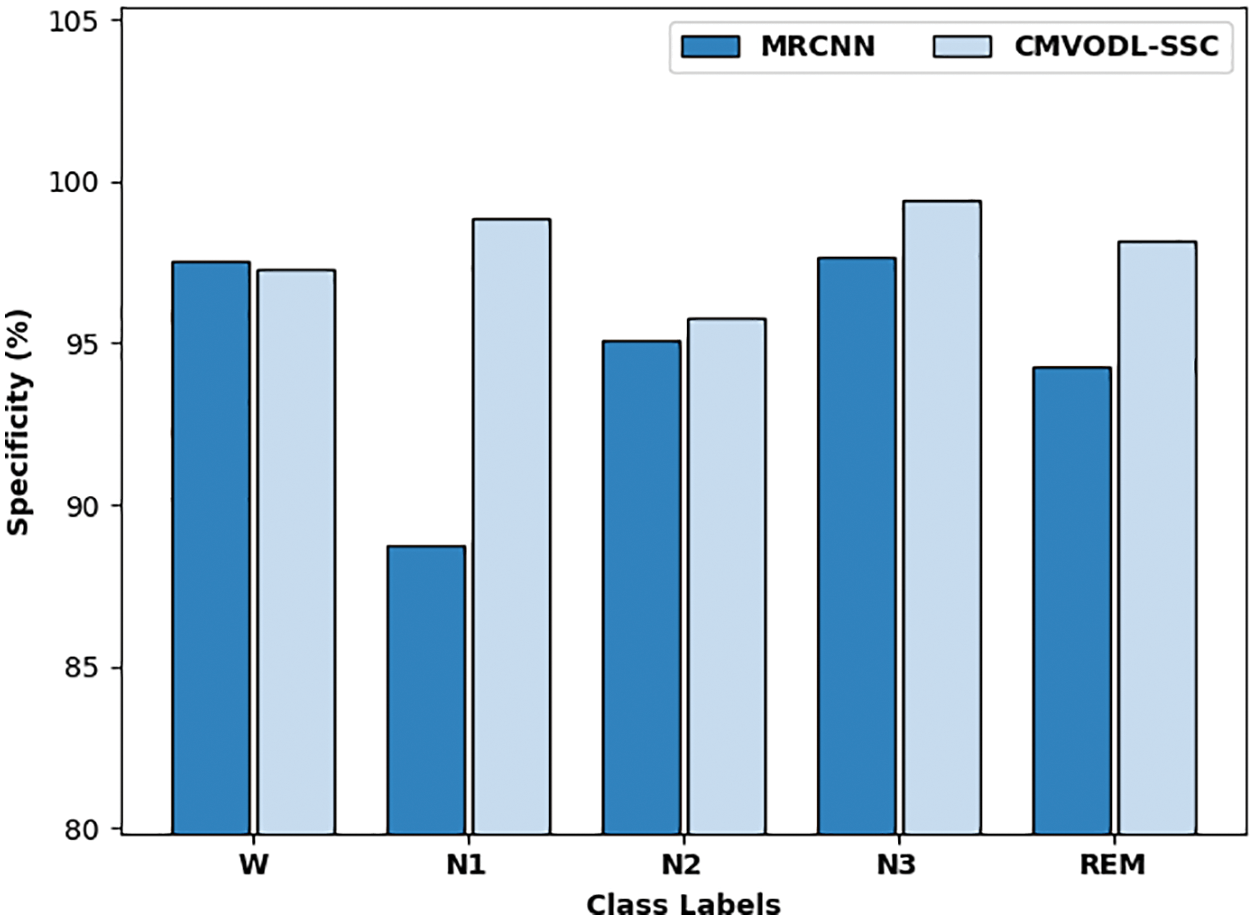
Figure 11:
After looking into the above mentioned tables and discussion, it can be concluded that the CMVODL-SSC model has outperformed the other methods on sleep stage classification.
In this study, a new CMVODL-SSC model has been introduced to effectively categorize different sleep stages on EEG signals. Primarily, data pre-processing is performed to convert the actual data into useful format. Besides, a CLSTM model is employed to perform classification process. At last, the CMVO algorithm is utilized for optimally tuning the hyperparameters involved in the CLSTM model. In order to report the enhancements of the CMVODL-SSC model, a wide range of simulations was carried out and the results ensured the better performance of the CMVODL-SSC model interms of different metrics. In future, the performance of the CMVODL-SSC model can be improved by the design of hybrid metaheuristic optimization algorithms.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under grant number (RGP 2/158/43). Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R235), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4340237DSR10).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Mousavi, F. Afghah and U. R. Acharya, “SleepEEGNet: Automated sleep stage scoring with sequence to sequence deep learning approach,” PLOS ONE, vol. 14, no. 5, pp. e0216456, 2019. [Google Scholar]
2. H. Korkalainen, J. Aakko, S. Nikkonen, S. Kainulainen, A. Leino et al., “Accurate deep learning-based sleep staging in a clinical population with suspected obstructive sleep apnea,” IEEE Journal of Biomedical and Health Informatics, vol. 24, pp. 1, 2019. [Google Scholar]
3. W. Neng, J. Lu and L. Xu, “CCRRSleepNet: A hybrid relational inductive biases network for automatic sleep stage classification on raw single-channel eeg,” Brain Sciences, vol. 11, no. 4, pp. 456, 2021. [Google Scholar]
4. R. Zhao, Y. Xia and Q. Wang, “Dual-modal and multi-scale deep neural networks for sleep staging using EEG and ECG signals,” Biomedical Signal Processing and Control, vol. 66, no. 11, pp. 102455, 2021. [Google Scholar]
5. E. Khalili and B. M. Asl, “Automatic sleep stage classification using temporal convolutional neural network and new data augmentation technique from raw single-channel eeg,” Computer Methods and Programs in Biomedicine, vol. 204, no. 3, pp. 106063, 2021. [Google Scholar]
6. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]
7. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]
8. S. K. Satapathy, A. K. Bhoi, D. Loganathan, B. Khandelwal and P. Barsocchi, “Machine learning with ensemble stacking model for automated sleep staging using dual-channel EEG signal,” Biomedical Signal Processing and Control, vol. 69, no. 1, pp. 102898, 2021. [Google Scholar]
9. Y. You, X. Zhong, G. Liu and Z. Yang, “Automatic sleep stage classification: A light and efficient deep neural network model based on time, frequency and fractional Fourier transform domain features,” Artificial Intelligence in Medicine, vol. 127, no. 11, pp. 102279, 2022. [Google Scholar]
10. B. Yang, X. Zhu, Y. Liu and H. Liu, “A single-channel EEG based automatic sleep stage classification method leveraging deep one-dimensional convolutional neural network and hidden Markov model,” Biomedical Signal Processing and Control, vol. 68, no. 2, pp. 102581, 2021. [Google Scholar]
11. E. Eldele, Z. Chen, C. Liu, M. Wu, C. K. Kwoh et al., “An attention-based deep learning approach for sleep stage classification with single-channel eeg,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 29, pp. 809–818, 2021. [Google Scholar]
12. S. Chambon, M. N. Galtier, P. J. Arnal, G. Wainrib and A. Gramfort, “A deep learning architecture for temporal sleep stage classification using multivariate and multimodal time series,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 26, no. 4, pp. 758–769, 2018. [Google Scholar]
13. H. Ghimatgar, K. Kazemi, M. S. Helfroush, K. Pillay, A. Dereymaker et al., “Neonatal EEG sleep stage classification based on deep learning and HMM,” Journal of Neural Engineering, vol. 17, no. 3, pp. 36031, 2020. [Google Scholar]
14. E. Bresch, U. Großekathöfer and G. G. Molina, “Recurrent deep neural networks for real-time sleep stage classification from single channel eeg,” Frontiers in Computational Neuroscience, vol. 12, pp. 85, 2018. [Google Scholar]
15. S. Santaji and V. Desai, “Analysis of EEG Signal to classify sleep stages using machine learning,” Sleep Vigilance, vol. 4, no. 2, pp. 145–152, 2020. [Google Scholar]
16. O. Yildirim, U. Baloglu and U. Acharya, “A deep learning model for automated sleep stages classification using psg signals,” International Journal of Environmental Research and Public Health, vol. 16, no. 4, pp. 599, 2019. [Google Scholar]
17. J. Fan, C. Sun, M. Long, C. Chen and W. Chen, “EOGNET: A novel deep learning model for sleep stage classification based on single-channel eog signal,” Frontiers in Neuroscience, vol. 15, pp. 573194, 2021. [Google Scholar]
18. Q. Shahzad, S. Raza, L. Hussain, A. A. Malibari, M. K. Nour et al., “Intelligent ultra-light deep learning model for multi-class brain tumor detection,” Applied Sciences, vol. 12, pp. 1–22, 2022. [Google Scholar]
19. A. M. Hilal, I. Issaoui, M. Obayya, F. N. Al-Wesabi, N. Nemri et al., “Modeling of explainable artificial intelligence for biomedical mental disorder diagnosis,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3853–3867, 2022. [Google Scholar]
20. Y. Bai, N. Bezak, B. Zeng, C. Li, K. Sapač et al., “Daily runoff forecasting using a cascade long short-term memory model that considers different variables,” Water Resources Management, vol. 35, no. 4, pp. 1167–1181, 2021. [Google Scholar]
21. I. Benmessahel, K. Xie and M. Chellal, “A new competitive multiverse optimization technique for solving single-objective and multiobjective problems,” Engineering Reports, vol. 2, no. 3, pp. 1–33, 2020. [Google Scholar]
22. B. Kemp, A. H. Zwinderman, B. Tuk, H. A. C. Kamphuisen and J. J. L. Oberye, “Analysis of a sleep-dependent neuronal feedback loop: the slow-wave microcontinuity of the EEG,” IEEE Transactions on Biomedical Engineering, vol. 47, no. 9, pp. 1185–1194, 2000. [Google Scholar]
23. Q. Zhong, H. Lei, Q. Chen and G. Zhou, “A sleep stage classification algorithm of wearable system based on multiscale residual convolutional neural network,” Journal of Sensors, vol. 2021, no. 2, pp. 1–10, 2021. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools