Block Verification Mechanism Based on Zero-Knowledge Proof in Blockchain

1  Introduction

With the rise of cryptocurrency, blockchain technology has attracted significant attention from the global information industry, financial institutions, and academia. There are a variety of blockchain-based cryptocurrencies in the world, among which the most representative cryptocurrencies are Bitcoin [1] and Ethereum [2]. However, the openness and transparency of blockchain have also brought tremendous pressure and challenges to protecting users’ privacy. So far, experts and scholars at home and abroad have researched blockchain privacy protection and presented many solutions. The ZKP is among the many solutions.

The blockchain is essentially a decentralized, distributed database. In blockchain technology, valuable information is stored permanently in data, forming blocks [3]. Technically, a block is a data structure that records transactions, reflects money flow to commerce, and cryptographically ensures that the records are immutable and unfalsifiable. Blockchain is characterized by decentralization, openness, autonomy, and anonymity. The decentralization of blockchain can well achieve scalability, robustness, privacy, and load balancing, and avoid the risk of a single point of failure in the centralized structure [4,5]. Therefore, blockchain has solved some security and privacy problems from different aspects at the beginning of its emergence, but it still has security problems.

ZKP solution is a proof system that can solve the transaction trust problem, privacy protection problem, data encryption problem, and interaction problem in the blockchain. ZKP was proposed by Goldwasser et al. [6] in the early 1980s and is defined explicitly as the prover can make the prover believe that a particular assertion is correct without providing any valuable information to the prover. In essence, ZKP is an agreement involving two or more parties, a series of steps that two or more parties need to take to complete a task. The prover convinces the verifier that it knows or owns a message, but the proof process cannot reveal any information about the proven message to the verifier.

With more and more applications based on blockchain technology, application scenarios are also extensive, which can be combined with edge cloud computing, 5G network, Internet of Vehicles, Unmanned Aerial Vehicle, wireless sensors, and Internet of everything [7–9]. Users have an increasing demand for data privacy protection, and the processing of ciphertext data has become a critical link [10]. How to solve the deficiency of zero-knowledge, a branch of cryptography has become an urgent demand. ZKP technology, as an essential part of modern cryptography, can play a critical role in data security, privacy security, supervision, and inspection. The perfect combination of ZKP and blockchain can provide an excellent solution to the current dilemma of blockchain. On the one hand, the nature of blockchain is open and transparent, which makes it limited in terms of privacy and data security. On the other hand, how to solve the problem of algorithm performance, such as improving throughput and response speed are the biggest problems facing the large-scale implementation of blockchain [11].

2  Related Work

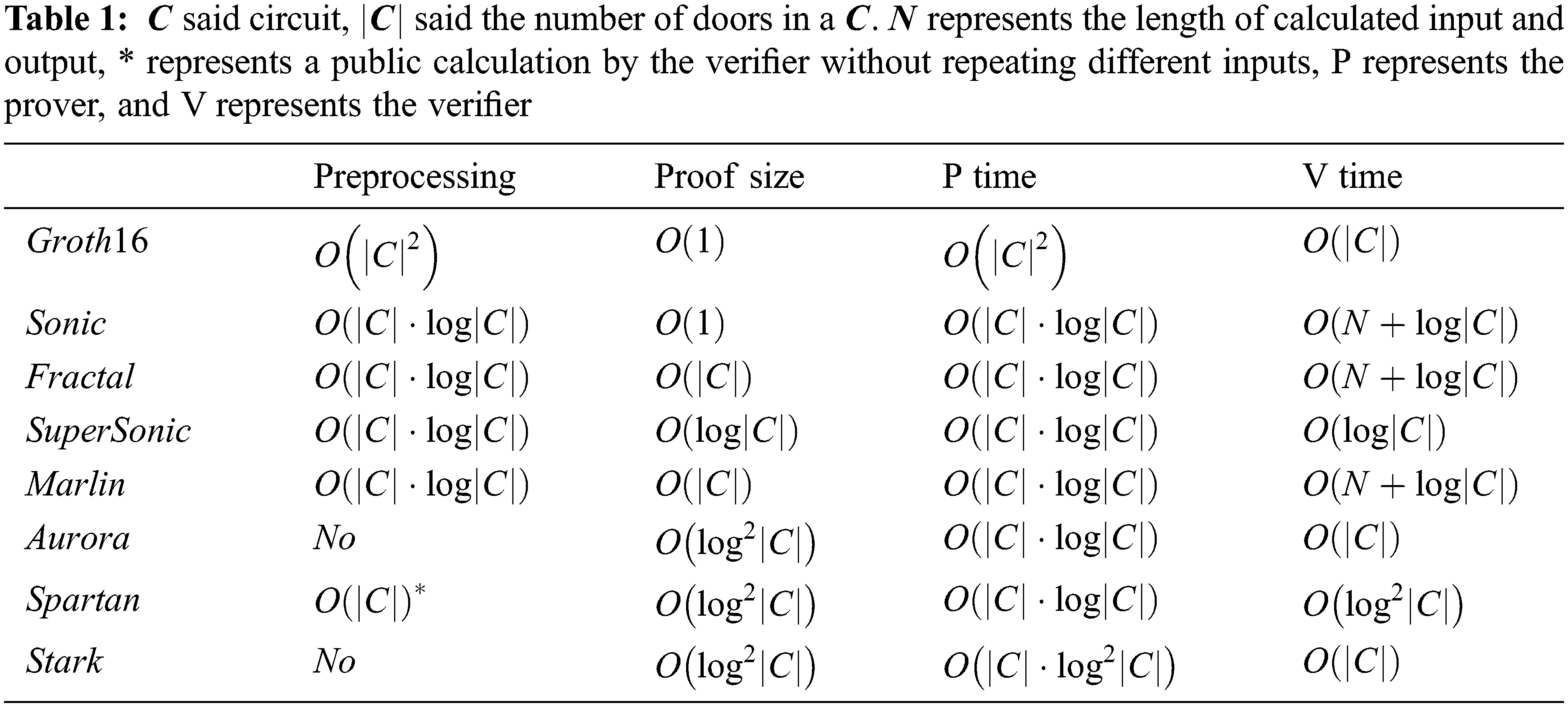
In recent years, ZKP has attracted much attention as a privacy-enhancing technology in various fields, especially in the cryptocurrency industry and verifiable computing. However, the ZKP protocol has remained in the theoretical stage for a long time because of its poor operational efficiency and generality. These academic ZKP protocols have their characteristics. Some protocols are interactive, requiring the prover and verifier to send multiple rounds of messages back and forth. In contrast, others are non-interactive, requiring the prover to send only one letter to the verifier according to the protocol. In some protocols, the size of the proof is related to the size of the problem, and the more complex the situation, the lower the guarantee. In other protocols, the proof size is the same regardless of the complexity of the problem. A universal, non-interactive, constant size ZKP protocol has been the goal of cryptography researchers for many years.

In the era of big data [12], ZKP is widely used as a tool because of its advantages, and people have higher and higher requirements for its communication complexity and efficiency. The concept of zero-knowledge Succinct non-interactive Arguments of knowledge (zk-snark) was also proposed and studied extensively by many scholars at home and abroad. The Probabilistic Checkable Proofs (PCP) theorem states that NP assertions have probabilistic proofs verified in average proof size and logarithmic polynomial time. Kilian [13] realized this NP language’s first ZKP of sublinear communication scale and verification time. This scheme is an Interactive Proof System (IPS) constructed using a collision-proof hash function and probabilistic verifiable Proof. The prover and verifier interact in multiple rounds of communication. Kilian scheme was the first structure where the total traffic was less than the traffic required to transmit an NP witness, and such an argument system was called succinct. However, the proof in Kilian construction is a polynomial-time algorithm, which cannot achieve asymptotically optimal linear time through (non-compact) ZKP. Whether a wireless sensor network scheduling scheme can optimize the time cost is a problem worth studying [14]. The Stark scheme is based on interactive oracle proofs with ordinary randomness. In the Random Oracle model, non-interaction can be implemented using the Fiat-Shamir paradigm, and the construction is post-quantum safe. Aurora is a Succinct Non-interactive Argument (SNARG) based on STARK, explicitly designed for the rank-1 constraint system (R1CS). It proposes a new univariate Sumcheck protocol to implement efficient validation. Although the traffic volume is the same as STARK in a progressive sense, it is much shorter in practice. Fractal [15] is a Succinct non-interactive Argument of knowledge (SNARK) based on IOP and R1CS. Fractal is a recursive implementation of zk-SNARKs that implements a transparent setup by preprocessing the circuit, which can be considered post-quantum secure in a random oracle model.

In 2010, Groth implemented the first all-in-one, non-interactive, constant-size ZKP protocol; based on elliptic curve bilinear mapping; he proposed pairing’s Non-interactive Zero-Knowledge proof (NIZK). It is the first proof of linear communication scale under the standard hypothesis. SNARKs, the ZKP protocol known for blockchain, is a continual refinement of this protocol. In 2013, a protocol called Pinocchio [16] implemented minute-level proofs, millisecond-level verification that was less than 300 bytes in size, bringing ZKPs from theory to application. The SNARKs used by Zcash [17] are based on a modified version of Pinocchio. In 2016, Groth was optimized again based on 2010, enjoying the most efficient Verifier algorithm and the shortest proof string, making Groth16 [18] the most widely used zk-snark scheme. Groth16 applied elliptic curve pairing and exponential knowledge hypothesis. The method can achieve constant proof length. Bulletproofs [19] is based on BCCGP technology; the protocol is designed to prove that communications are valid, primarily through scope evidence, and that confidential transactions can be effectively aggregated. Sonic [20] is a zero-knowledge scheme based on Groth renewable CRS model. It uses a polynomial commitment scheme, pairing scheme, an arithmetic circuit. The size of Sonic proofs is fixed, but the verification cost is high. Marlin is an improved version of Sonic; CRS is updatable and universal; Marlin’s proof time is ten times faster than Sonic, and verifier time is three times faster than Sonic. For maximum efficiency, Marlin can be implemented under standard assumptions or algebraic group models. Plonk [21] is also an optimization of Sonic. Based on Sonic, Plonk uses a permutation argument about the multiplicative method group of univariate evaluation rather than the permutation argument of binary polynomial coefficients. The whole scheme only sets a single confidence setting, and multiple parties can participate in the confidence set. Kate polynomial commitment scheme [22] is used to replace the zero-knowledge verification step in Sonic. Supersonic [23] introduced a new and efficient polynomial commitment scheme for existing polynomial IOPs. This scheme eliminates the initial trust setup in SNARKs and is the first practical, concise, and verifiable ZKP that does not require a trust setup.

Researchers at home and abroad have carried out extensive research on blockchain privacy protection schemes. However, the current research results still cannot meet the needs of reality in terms of real-time and space overhead, and ZKP still needs further research in its application. ZKP is traditionally an interactive online protocol, but in practical application scenarios, we need offline capabilities, such as non-interactive verification of blockchain applications. Choosing the most effective solution for a particular task requires the skills and knowledge of the developer. At present, no ZKP scheme is superior to the others under any circumstances. We need to choose an appropriate ZKP protocol to improve and optimize our block validation efficiency.

3  Problem Statement

Blockchain combines distributed database, cryptography, consensus mechanism, smart contract, and other technologies as a distributed ledger technology. It has the characteristics of de-neutralization and non-tampering. In the uncertain network space of the new generation of wireless communication (5G) [24], it is necessary to establish a set of peer-to-peer trust mechanisms to realize asset transaction, transfer, payment, data security transmission, and other functions. In blockchain technology, consensus mechanisms and cryptography are mainly used to achieve. The popularization and large-scale use of blockchain technology still need time to wait, and many problems have not been solved.

Blockchain mainly relies on distributed consensus mechanism to establish mutual trust between point-to-point nodes. The current consensus mechanism includes Proof of Work (Pow), Proof of Stake (PoS), Practical Byzantine Fault Tolerance (PBFT), and Delegated Proof of Stake (DPoS). Bitcoin adopts Pow and faces the problem of being attacked in actual operation. If the attacker’s computing power exceeds half of the whole blockchain network, it can cancel actual transactions. Attackers can control the entire blockchain, which seriously threatens the security and stability of the blockchain. At the same time, Bitcoin mining consumes a lot of power resources, which is undoubtedly a waste of resources. PoS is more environmentally friendly than PoW and does not consume a lot of computing resources. However, due to the lack of industrial-grade applications of Pos, the PoS consensus mechanism does not operate independently at this stage but is combined with PoW. Currently, Ethereum uses a hybrid mechanism of Pow and PoS.

Due to its technological advantages plus strong prospects, blockchain technology has been used by all walks of life [25], most of which are in the financial field. However, the frequent transaction demands of financial businesses cannot be fully met. In theory, Bitcoin is around seven transactions per second, but it may be even less in practice. Faster Ethereum is about 20 transactions per second, while mobile payments in China (Alipay, WeChat) can reach tens of thousands of transactions per second at peak. This huge efficiency gap is not mature enough to apply blockchain technology in the payment field. The blockchain code is open source, making the project more trustworthy. However, there is a risk that open source code will make hacking easier. At the same time, the quality of the code is directly related to the ability of the blockchain system to resist external attacks, and the code with many loopholes is easy to be used and attacked by hackers. In addition, user privacy is a big challenge because all transaction information in the blockchain is public. The problems of blockchain itself need to be improved by the continuous up and progress date of new technologies.

As more blocks become available, data will pile up and consume more space, affecting the information transfer rate across the entire blockchain. In the Bitcoin system, the Pow consensus algorithm is time-consuming and inefficient. The average time for a new block to be generated is 10 minutes. It takes about 2 minutes for each transaction to wait for verification, which is unacceptable from the users’ perspective. The consensus mechanism can be optimized, and new technologies such as ZKP and the intelligent contract can shorten the verification time, improve the system’s throughput, and improve the overall efficiency. Smart contracts have the advantages of a trust, security, efficiency, and no need for third-party arbitration. It is perfectly combined with blockchain technology. However, if the design is not reasonable, it will fail to provide safe and effective technical results and may be attacked. Therefore, this paper designs a scheme that combines ZKP and smart contract to improve the verification efficiency of the blockchain system to protect user privacy and security.

4  Data Privacy Protection and Efficient Verification Mechanism in Blockchain

This paper combines blockchain, smart contracts, and zk-snark algorithm to build a transaction system based on blockchain and ZKP privacy protection to achieve privacy protection and efficient verification of blocks in the transaction system. It is shown in Fig. 1.

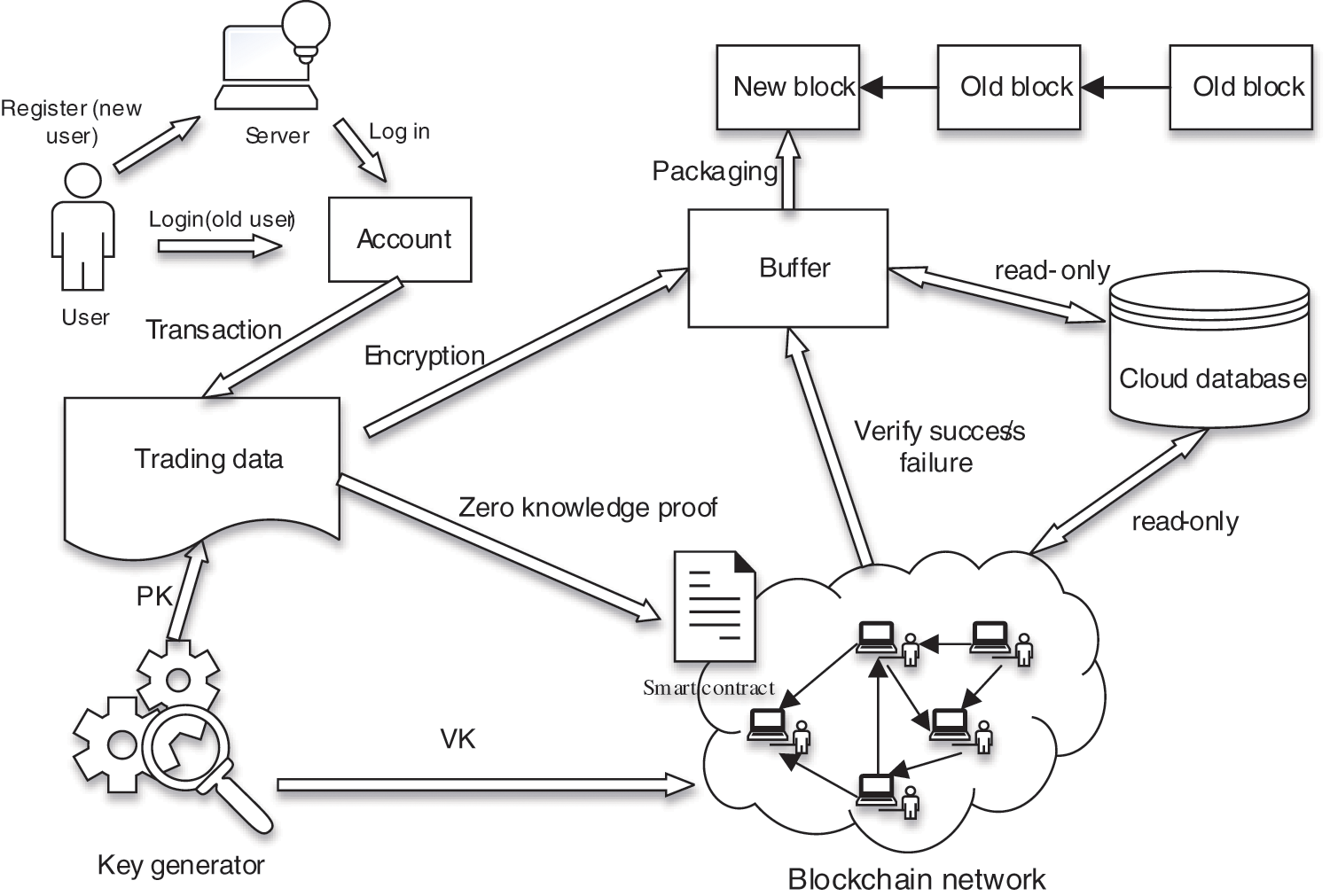
Figure 1: Data privacy protection and efficient verification mechanism based on blockchain

The data privacy protection and efficient verification scheme based on blockchain include six entities: user, key generator, smart contract, blockchain, cloud database, and buffer. Their respective functions in the system are as follows.

1)    Users: All systems are designed to provide users with more convenient services. The user registers an account through the system, and then the accountancy is hashed with a random number to get an address. The address is the receiving address of each user and the transfer address used for transactions with other users.

2)    Key generator: The key generator is a third party that can be fully trusted. Its primary function is to generate a pair of keys Pk (proving key) and Vk (verification key), which are used by provers. The Vk is used by the verifier and is called the authentication key.

3)    Smart contract: Smart contract is a “computer transaction agreement that implements the contract terms.” It can be simply understood as a computer program, which can be automatically executed after it is set up and put on the blockchain. Unlike traditional protocols, a smart contract is immutable and transparent. When a transaction occurs in a user’s account, the root hash value related to the transaction tree and ZKP needs to be written into the smart contract and uploaded to the blockchain network for verification to prevent malicious users from modifying relevant information during verification.

4)    Blockchain: Blockchain is the core of this solution. It is a technology that realizes the characteristics of decentralization and is tamper-proof. In the blockchain network, other nodes use the authentication secret key Vk to conduct zero-knowledge verification of the whole network for the newly occurring transactions, and the transactions that pass the guarantee are packaged and connected to the chain.

5)    Cloud database: The cloud database records the details of each transaction. It can interact with the buffer and blockchain network, but it is read-only and cannot modify the data. After the transaction occurs, the balance of each corresponding account will change accordingly. We did not adopt the Unspent Transaction Outputs (UTXO) structure model but the account/balance model. Each legitimate transaction will be accompanied by a change in the corresponding account balance, which will be described later.

6)    Buffer: All transaction information is stored in the buffer before the data is packaged and chained. To ease the pressure on blocks on the chain, only transactions that the blockchain network has verified will be packaged up by the buffer. At the same time, the cloud database updates the transaction’s status and broadcasts it to the whole network. Unsuccessful transactions are discarded.

5  Construction of Data Privacy Protection and Efficient Verification Scheme in Blockchain

5.1 Overview

We use the Merkle tree model to realize the storage and verification of user data. Most digital currencies use the tree data structure or data verification to control the time cost at the O(log⁡n) level. Suppose a user registers and makes a transaction on his account. The transaction should include the transaction amount, the transaction address, the root hash of the transaction tree, the destruction number, the transaction number, and a ZKP written into the smart contract.

It is assumed that Alice and Bob make a transaction. The details are as follows:

(1) User registration and authentication: The user must go to the authorization center to register their identity information sent to the authorization center, according to the authorization center RSA key generation algorithm RSA public key and a private key, and then the public key digital signature, the final authorization center will be digital signatures, and the private key is sent to the user, the user to save a digital signature and a private key. The digital signature must be sent to the server before the next user authentication. The transaction can start only after the signature is verified to be valid.

(2) Transaction amount: The transaction between two accounts needs to realize equivalent trade according to the amount. Alice transfers a sum of money to Bob, assuming five coins, then Alice’s account will lose five coins correspondingly, and Bob’s account will gain five coins simultaneously. Secondly, the transaction amount should not be greater than the corresponding balance of the account. We need to prove this relationship when the transaction occurs, called scope proof.

(3) Transaction address: Alice needs a plaintext address to transfer money to Bob. If the address is unknown, the transaction cannot be carried out. If the transaction address is filled in incorrectly, the funds will be transferred to another account and cannot be returned because there is no way to know who the other person is. To determine the validity of a transaction, obtain the account balance based on the address to prevent the transaction amount from exceeding the account balance.

(4) The root hash of the Merkle tree: As shown in Fig. 2, according to the Merkle tree principle, the transaction occurs in Alice’s account; we calculate the hash value of A and store it to the leaf node. When we want to get H1 , we must know the hash value of another transaction B. The hash value of the intermediate node H1=Hash(A,B) is calculated again by the Hash value of transaction A and transaction B, and so on. Finally, we can get the Hash value of the root node root=Hash(H1,H2) . The Hash value of the root node is public. If the user is cheating or the deal is fake, at last, the computation will change the hash value of the root, which will not be as before to hash value, thus ensuring that Alice did not dare to cheat. Otherwise, the deal will be refused because the entire network authentication, illegal trade in the validation phase will be rejected; transactions are also not packaged onto the blockchain.

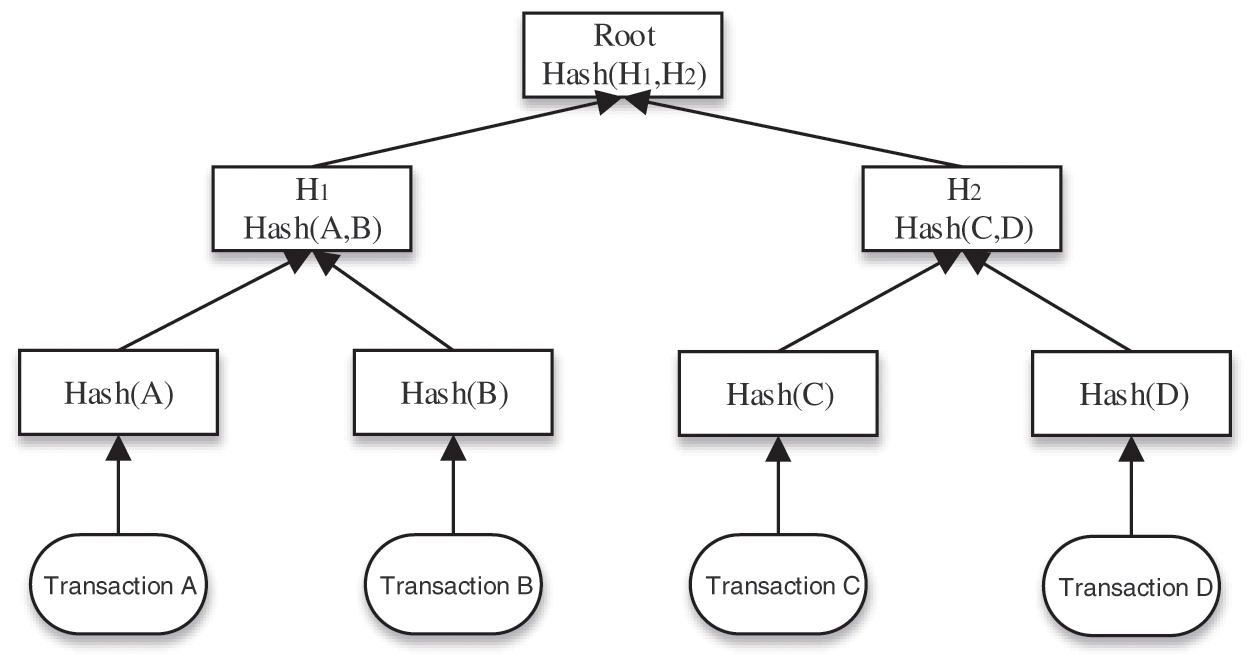
Figure 2: Merkle hash tree

(5) Destruction number: The primary function of the destruction number is to prevent the problem of double spending, which simply means that the same money cannot be used twice. Alice transfers an account to Bob. If the transaction is legal, it will be packaged onto the blockchain, and the marketing will also generate a destruction number to record that the money has been consumed and cannot be consumed again. The destruction number is open to the whole network. Every legitimate transaction will have a destruction number, and it is unique. There will be multiple transactions in an account so that the destruction number will change, and only the balance corresponding to the account’s latest destruction number is the account’s natural balance.

(6) Transaction number: Each transaction generates a number that is bound to ZKP. ZKP only proves that the marketing is legal and does not reveal any information about the transaction. If it is a legitimate transaction, the buffer will accept the encrypted transaction. We separate the receipt of transactions from the verification of transactions. After the transaction is verified in the blockchain network, the buffer receives the encrypted transaction, but it needs to confirm that the transaction has just passed the verification. We use ZKPs to bind transactions, and buffers use binding relationships to distinguish transactions.

(7) Zero-knowledge proof: After a transaction occurs in Alice’s account, the transaction will contain much private information about Alice, such as the amount of Alice’s transfer, the address of the transfer, the identity of the transfer, and other information; It is highly unsafe to expose these data on the blockchain. For example, to prove that the block contains transaction A in Fig. 2, we need to construct the Merkle tree and publish the hash values of the root, B, and the intermediate node H2 . The owner of transaction A can prove that transaction A is included in the block by verifying that the generated root is consistent with the published one without knowing the actual content of other transactions.

(8) Smart contract: Advantages of using smart contract: First of all, it is decentralized. The execution of a smart contract does not rely on the participation or intervention of a third party, and computers complete the supervision and arbitration of the contract. Secondly, it cannot be tampered with and is open and transparent. Once the smart contract is deployed, all contents cannot be modified, and no party can interfere with the execution of the contract. Everything will run according to the designed code, and anyone can view it with a high degree of transparency. Last but not least, smart transparency can view contracts have lower costs than traditional contracts because they do not require supervision by a third-party intermediary and can be enforced once the contract is broken.

5.2 Construction of Privacy Protection Scheme Based on ZKP

In the ZKP system, the prover accepts a proof key Pk , a private input W (also known as a witness), and a public input X. In this case, a function F exists such that F(x,w)=0 . The prover proved such a conclusion but did not expose private information W. Anyone can verify that F is true but can’t get any information about W. The prover generates a proof π through the ZKP algorithm and sends it to the verifier. The verifier accepts the authentication key Vk , the common input X, and the proof π sent by the prover, which is computed and output (“accept” or “reject”). The privacy information exposed in the transaction process is encrypted to generate ZKP and then put into the smart contract. The verification process is completed in the smart contract.

5.2.1 Concrete ZKP Scheme

In ZKP algorithms, we use the zk-snark approach of first converting an original computational problem into an arithmetic circuit, which can then be further converted into a mathematical model called Arithmetization. The process of transforming an Arithmetic circuit into a Quadratic Arithmetic Program (QAP) problem describes the constraints of each gate in the course, the Rank-1 Constraint System (R1CS). The QAP problem is defined as given a series of polynomials and given a target polynomial, finding the combination of polynomials divisible by the target polynomial.

We adopt the idea of the Groth16 algorithm to achieve this, and the specific steps are as follows:

(1) Pretreatment: The statements of “ownership” and “scope proof” are transformed into QAP problems to realize the proof and verification of NP problems based on arithmetic circuits in the trading field. We translate the proof of ownership and proof of scope into a circuit problem and obtain an example of R1CS, namely, three m row and n column matrices Um×n,Vm×n,Wm×n . There exists a solution vector α→ , which makes these three matrices satisfy Eq. (1).

(∑i,jm,n⁡Uij⋅a→)∗(∑i,jm,n⁡Vij⋅a→)=∑i,jm,n⁡Wij⋅a→ (1)

In Eq. (1), when i=1 , j=1,2,…,n ; when i=2 , j=1,2,…,n , and so on, until i=m . each row in the matrix represents a constraint. Then the Lagrange difference theorem is used to calculate the formula Eq. (2). We can transform the R1CS matrix problem into the QAP problem and obtain a polynomial equation Eq. (3).

Pn(x)=∑i=1n⁡yi(∏j≠i1≤j≤n(x−xj)(xi−xj)) (2)

∑i=0m⁡aiui(x)⋅∑i=0m⁡aivi(x)=∑i=0m⁡aiwi(x)+h(X)t(X) (3)

(2) Setup phase: In finite field F randomly selected α,β,γ,δ,x , and defines the τ=(α,β,r,δ,x) , computing σ=([σ1]1,[σ2]2) , the σ1,σ2 are points on groups G1 and G2 respectively.

σ1={a,β,γ,δ,{xi}i=0n−1,{βui(x)+αvi(x)+wi(x)γ}i=0l,{βui(x)+αvi(x)+wi(x)δ}i=l+1m,{xit(x)δ}i=0n−2} (4)

σ2=(β,γ,δ,{xi}i=0n−1) (5)

Through Eqs. (4) and (5) we can calculate the generation key Pk and the authentication key Vk . The part of Pk is Eqs. (6) and (7), The Vk part is Eqs. (8) and (9).

σ1={a,{βui(x)+αvi(x)+wi(x)γ}i=0l} (6)

σ2=(β,γ,δ) (7)

σ1={β,γ,δ,{xi}i=0n−1,{βui(x)+αvi(x)+wi(x)δ}i=l+1m,{xit(x)δ}i=0n−2} (8)

σ2=({xi}i=0n−1) (9)

(3) Prover generates proof π : The polynomial obtained in the QAP problem can be obtained by deformation Eq. (10). The coefficients of ui(x),vi(x),wi(x) , and polynomial h(x) can be calculated by Fast Fourier Transform (FFT). Randomly select r and S in finite field F to obtain A, B, and C through formula calculation. See Eqs. (11)–(13).

h(x)=∑i=0m⁡aiui(x)⋅∑i=0m⁡aivi(x)−∑i=0m⁡aiwi(x)t(x) (10)

A=α+∑i=0m⁡aiui(x)+rδ (11)

B=β+∑i=0m⁡aivi(x)+sδ (12)

C=∑i=l+1m⁡ai(βui(x)+αvi(x)+wi(x))+h(x)t(x)σ+As+Br−rsδ (13)

(4) Verifier verification proof π : Given the authentication key Vk , we can verify that Eq. (14) is valid using the pairing function and the proof π sent by the prover. The output then accepts or rejects, and the computation can be controlled in the millisecond.

[A]1⋅[B]2=[α]1⋅[β]2+∑i=0l⁡ai[βui(x)+avi(x)+wi(x)γ]1⋅[γ]2+[C]1⋅[δ]2 (14)

5.2.2 Designed Smart Contract Scheme

In the smart contract, we need to verify two problems: the first is the ownership problem. The balance of the user’s account for the exchange operation must be his own to prevent malicious users from operating other people’s accounts for trading. The second problem is the scope proof problem. We adopt the account balance model. When an account has a transaction, the transaction amount cannot be greater than the corresponding balance of the report. secondly, the transaction amount cannot be negative. If any of the above problems are not met, the transaction is illegal.

Suppose a transaction has been made in Alice’s account, and all we need to do is prove that the transaction is legitimate. A legitimate transaction should meet two conditions at the same time. The first condition is that we need to confirm that Alice’s account (all warrants) makes the transaction. Second, we need to know that the balance of Alice’s account must be greater than or equal to the amount of the transaction (proof of scope). If the transfer is successful, the corresponding amount will be deducted from Alice’s account, and the receiving address will be added with the corresponding amount; otherwise, the transfer will fail. After that, we can update the transaction in the cloud database and broadcast it all over the web. The contract design is shown in Fig. 3 below.

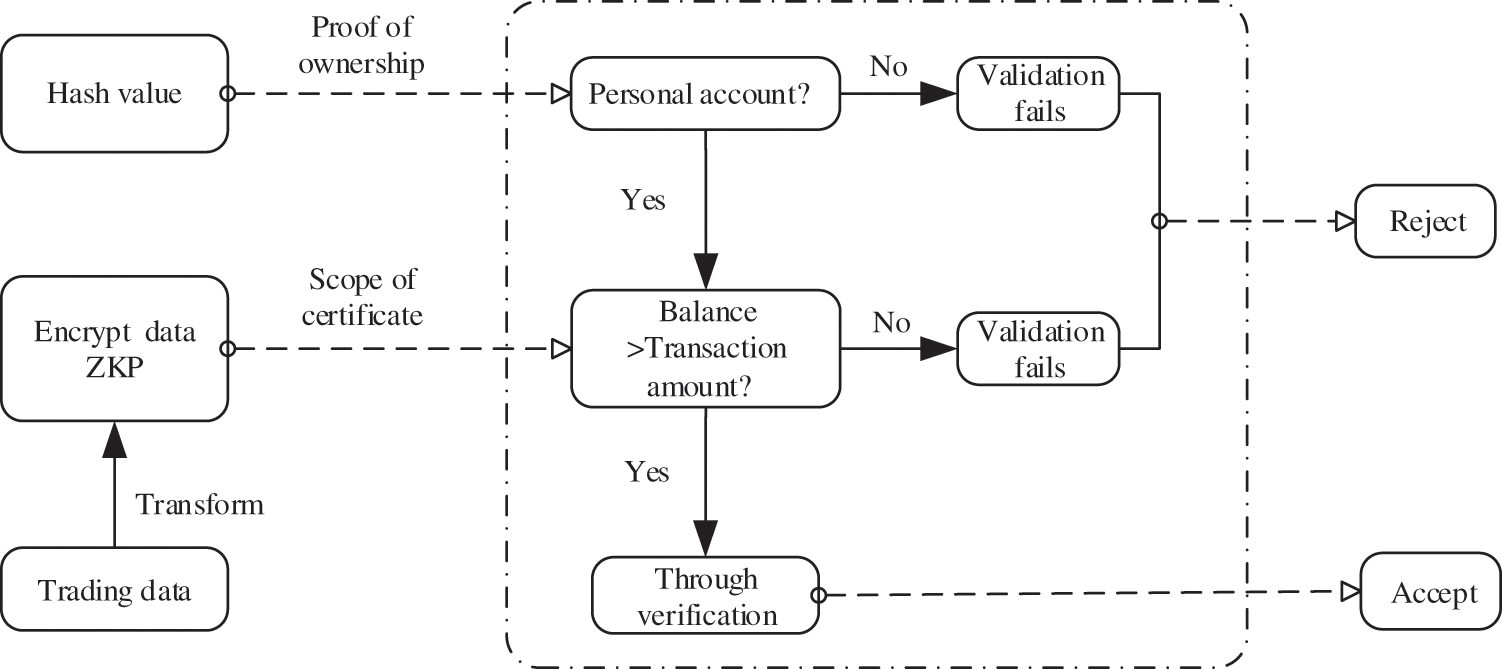
Figure 3: Smart contract design

First, we need to prove that the money is Alice’s (proof of ownership). Alice uses the private key to generate a public address and the receipt address. Then hash a generated number based on the public key and a random number. Each account will have a generated number, considered a world tree. A generated number is a leaf node that hashes with other leaf nodes to get the node’s value at the next level and so on to get the value of the root hash. The root hash before and after execution is stored in the smart contract; If the root hashes are inconsistent, it can be determined that the money is not Alice’s. Therefore, when a transaction occurs in Alice’s account, we can judge that the money belongs to Alice according to the generation number. Meanwhile, Alice’s transfer address has not been disclosed.

Secondly, we need to prove that Alice’s transfer can pass the scope proof. When checking the ownership in the above steps, in the smart contract, we will check whether the balance of Alice’s account is greater than or equal to the amount of transfer according to Alice’s address. Here we make a judgment, and we do not know the balance of the address and the amount of transfer. Because they are encrypted, we protect the sender’s address and the amount.

Therefore, the primary function of ZKP is to prove whether the transaction is legal or not. The zk-snark algorithm can be used to compress the proof size and obtain an ideal time cost when verifying smart contracts. The ZKP is bound to the transaction number. If the zero-knowledge evidence is accepted, the transaction bound to the proof is also accepted. The legitimate transaction is updated in the cloud database, and the buffer packages the transaction onto the blockchain.

5.3 Construction of Account/Balance Scheme

We use the account balance model to construct our scheme. We use some symbols to represent information about a user’s transaction for ease of understanding. Let us assume that the symbol tx means a transaction, Z represents the transfer address, S represents the billing address, V represents the transfer amount, Sn represents the destruction number, T represents the transaction number, and R represents the root hash. Sn , T , and R are public. Fig. 4 shows the transaction update process. Assume that both sides of the transaction are Alice and Bob, and the specific algorithm is as follows:

1.    Trading generates: tx←(Z,S,V,Sn,T,r) . Alice initiates a transfer transaction to Bob’s account, the contents of which include: transaction amount V , Alice’s transfer address Z , Bob’s receipt address S , transaction number T , destruction number Sn , and the corresponding Merkle hash r of this transaction will also be updated.

2.    Key generation: (Pk,Vk)←KeyGen . The key generator generates the keys Pk,Vk through the KeyGen function.

3.    Zero knowledge proof generation: π←(S,Z,V,Pk,x) . Alice inputs her transfer address S , transfer amount V , and receipt address Z as private data and accepts the proof key Pk given by the key generator and the public input X to generate a ZKP π.

4.    Transaction binding: SmartContract←(π,T,r) . The ZKP is bound to the transaction number and then written into the smart contract with the transaction’s root hashes (both before and after the transaction) and uploaded to the blockchain network for verification.

5.    Verify transactions: 0/1←(π,Vk,r,x) . The validation key Vk obtained by the blockchain network verifier from the key generator and the proof π sent by Alice and the standard input X and the root hash of Merkle are computed and output to accept or reject.

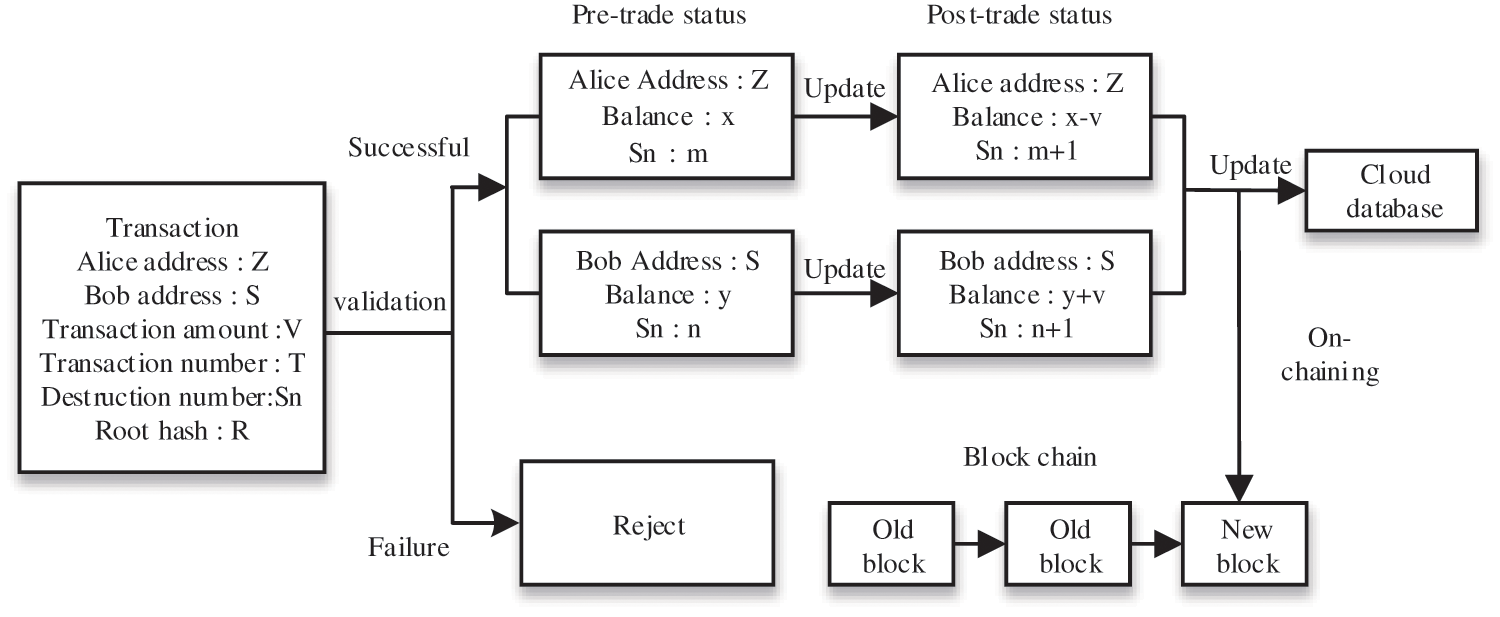
Figure 4: Account/balance scheme design

If the validation is successful, the buffer accepts the ZKP-bound transaction, at which point the destruction number is updated, and the chain is packaged. The transaction is sent encrypted, so it is known that a legitimate transaction has been made, but not the details of the transaction, which is also updated by the cloud database.

6  Theoretical Analysis of Scheme

6.1 Privacy Protection Capability

The user identity authentication uses the private key and digital signature to prevent others from using some unique means and plaintext information on the block to pretend to be oneself for identity authentication [26]. At the same time, every transaction has the root hash value of the Merkel tree stored in the ZKP, which can verify the transaction’s validity. In this way, it can effectively prevent the third party from illegally obtaining ZKP to pretend to be the user to confirm the signature so that others can not forge the user signature.

The user registers an account through the system, which hashes a random number generated by the system to obtain an address. When a user makes a transaction, the transaction information and the Pk sent by the key generator will generate a ZKP π and put it into the smart contract for the complete network verification. After passing the verification buffer, the encrypted transaction will be accepted and packaged onto the chain. In the whole process, the user’s transaction information is completely encrypted, and the block records an encrypted legal transaction. According to the nature of ZKP, the knowledge leaked to the outside is zero. Malicious users cannot track and obtain user information through the information on the block, so the scheme in this paper can ensure user anonymity.

To sum up, this scheme can ensure user privacy.

6.2 Efficiency and Safety Analysis

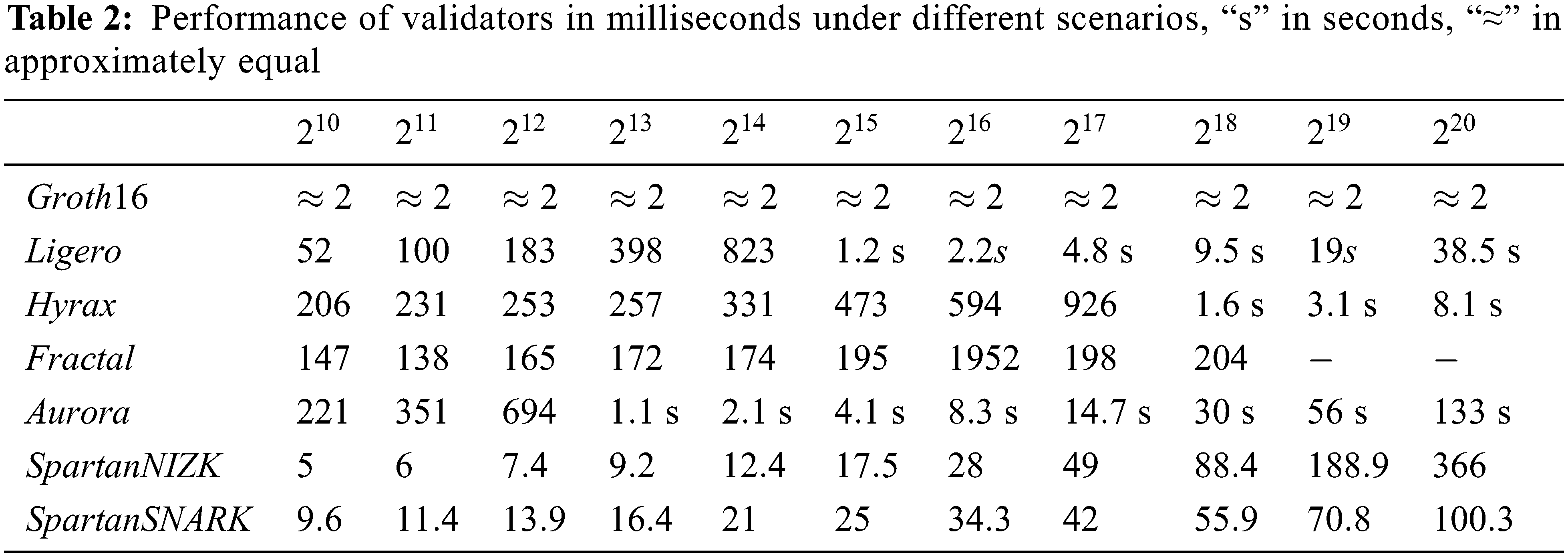
The performance indicators of blockchain mainly include transaction throughput and latency. Transaction throughput refers to the number of transactions that can be processed in a fixed time, and latency refers to transactions’ response and processing time. There are many reasons for low throughput efficiency, such as block capacity. The delay has a great relationship with algorithm performance, but the core reason is the limitation of network bandwidth rather than the problem of blockchain itself. Increasing the block output speed can improve the throughput, but it will also lead to the fork of the blockchain and threaten the security of the blockchain system. ZKP is one of the best solutions to improve block throughput without reducing system security. A good ZKP algorithm can minimize latency as much as possible. ZKP can ensure the integrity of a remote computing process and ensure the correctness of the algorithm without disclosing private information.

This scheme is based on a zk-snark algorithm to achieve privacy protection. Groth16 algorithm is based on the security of the difficulty concern solving the discrete logarithm problem on elliptic curves. The problem can be simply expressed as: given a prime number p and a positive integer g , knowing the value of y=gx(mod)p , solve x . So far, you cannot solve for x in polynomial time, but if you know x , you can solve for y=gx(mod)p very fast. zk-snark is a rapidly growing field, with several breakthrough zk-snark solutions announced in just a few years. Since there is no uniform benchmark for the construction of each solution, they are analyzed solely from the size of the solution construction proof, based on the benchmark metrics in the paper, or estimates based on data provided by the inventor: The Fractal evidence is about 250KB, the Halo proof is about 20KB, the SuperSonic proof is about 8KB, the Plonk proof is about 1KB, the Marlin proof is about 1KB, the Sonic proof is about 2KB, and the Groth16 evidence is about 0.2KB. The proof size of ZK-Stark is more sig than 100KB, etc. Partala et al. [27] made statistics, and the time complexity of specific schemes was shown in Tab. 1. Each solution had its significant advantages and disadvantages, but Groth16 was still the best in proving data size and speed.

All ZKP algorithms have the following three essential properties:

1)    Completeness: if the prover’s statement is correct, it passes the verifier’s verification with the probability of 1−ϵc . ϵc is called the completeness error.

2)    Soundness: If the prover’s statement is incorrect, the probability of passing the verifier’s verification is no greater than ϵs , which is called the soundness error.

3)    Zero-knowledge: during the interaction, the prover only discloses to the prover the statement whether edge he has relevant knowledge or not and does not disclose any additional information about knowledge.

Therefore, the ZKP algorithm meets the above conditions. Its core purpose is to hide and prove all kinds of secrets that need to be hidden k-snark algorithm is cleverly designed by combining complex problems in the field of mathematics. Backed by difficult problems in mathematics, the security of the scheme is guaranteed at the beginning of design.

6.3 Performance Analysis

The corresponding code will be automatically executed when the smart contract is deployed and relevant transactions are carried out, which will cause specific consumption of the smart contract in the execution process. The cost of the smart contract in this scheme is mainly the time required by ZKP. During verification, the verifier needs to verify that [A]1,[B]2,[C]1 are valid group elements, and at the same time, it needs to confirm whether Eq. (14) is good.

Validation: L exponential operation and a small number of group multiplications are performed in the group G1 (s), three pairing calculations (s), running time are about 1-10 ms. Different programming languages and different compilers may produce slightly different experimental data. Using the C++ libsnark library for testing, In the hardware environment of Inter(R) Core (TM) I7-4770 CPU (3.4 GHz) processor, the verification time of the BN128 elliptic curve is 1.3 ms. In the smart contract, the verification time is at milliseconds, so the block verification speed is considerable. Setty [28] used a Microsoft Surface Laptop 3 on a single CPU core of Intel Core i7-1065G7 with 16 GB RAM running Ubuntu 20.04 atop Windows 10. Under different constraints, Spartan was compared with the most advanced zk-snark and the simple proof of non-interactive ZKP for tests. For specific data, please refer to Tab. 2. We found that the experimental results were consistent with our theoretical analysis, and the validation time of the Groth16 scheme was in milliseconds.

7  Conclusion

The paper designed a block verification mechanism using ZKP and smart contract technology. The mechanism can encrypt the transaction amount and address and provide privacy protection function. Without disclosing the privacy information of both sides of the transaction, the full network node can verify the transaction confidentially, effectively solving the privacy and efficiency problems existing when users complete the transaction in the blockchain. Compared with the existing privacy protection scheme, this scheme has the advantages of high efficiency, high speed, and strong security. Moreover, how to protect privacy while reducing transaction length and verification time with more advanced technologies is still a problem worth studying in the future. The proposed scheme provides a certain reference.

Funding Statement: This work was supported by China’s National Natural Science Foundation (No. 62072249, 62072056). Jin Wang and Yongjun Ren received the grant and the URLs to sponsors’ websites are https://www.nsfc.gov.cn/. This work was also funded by the Researchers Supporting Project No. (RSP-2021/102) King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. Zaghloul, T. Li, M. W. Mutka and J. Ren, “Bitcoin and blockchain: Security and privacy,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 10288–10313, 2020. [Google Scholar]

 2.  T. Wang, C. Zhao, Q. Yang, S. Zhang and S. C. Liew, “Ethna: Analyzing the underlying peer-to-peer network of Ethereum blockchain,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 3, pp. 2131–2146, 2021. [Google Scholar]

 3.  Y. J. Ren, Y. Leng, Y. P. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]

 4.  C. Liu, K. Li and K. Li, “A game approach to multi-servers load balancing with load-dependent server availability consideration,” IEEE Transactions on Cloud Computing, vol. 9, no. 1, pp. 1–13, 2021. [Google Scholar]

 5.  G. Xiao, K. Li, Y. Chen, W. He, A. Y. Zomaya et al., “CASpMV: A customized and accelerative spMV framework for the sunway taihulight,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 1, pp. 131–146, 2021. [Google Scholar]

 6.  G. Shafi, S. Micali and C. Rackoff, “The knowledge complexity of interactive proof-systems (extended abstract),” in Proc. Proceedings of the 17th Annual ACM Symp. on Theory of Computing, Providence, Rhode Island, USA, pp. 6–8, 1985. [Google Scholar]

 7.  Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]

 8.  J. Wang, Y. Gao, K. Wang, A. K. Sangaiah and S. J. Lim, “An affinity propagation-based self-adaptive clustering method for wireless sensor networks,” Sensors, vol. 19, no. 11, pp. 2579–2595, 2019. [Google Scholar]

 9.  J. Wang, X. J. Gu, W. Liu, A. K. Sangaiah and H. J. Kim, “An empower hamilton loop based data collection algorithm with mobile agent for WSNs,” Human-centric Computing and Information Sciences, vol. 9, no. 1, pp. 1–14, 2019. [Google Scholar]

10. Y. J. Ren, F. J. Zhu, S. P. Kumar, T. Wang and J. Wang, “Data query mechanism based on hash computing power of blockchain in Internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]

11. Y. M. Xu, K. L. Li, J. T. Hu and K. Q. Li, “A genetic algorithm for task scheduling on heterogeneous computing systems using multiple priority queues,” Information Sciences, vol. 270, no. 1, pp. 255–287, 2014. [Google Scholar]

12. J. G. Chen, K. L. Li, Z. Tang, K. Bilal, S. Yu et al., “A parallel random forest algorithm for big data in a spark cloud computing environment,” IEEE Transactions on Parallel and Distributed Systems, vol. 28, no. 4, pp. 919–933, 2017. [Google Scholar]

13. J. Kilian, “A note on efficient zero-knowledge proofs and arguments (extended abstract),” in Proc. ACM Symp. on Theory of Computing (STOC), Victoria, Canada, pp. 723–732, 1992. [Google Scholar]

14. J. Wang, Y. Gao, C. Zhou, R. Simon Sherratt and L. Wang, “Optimal coverage multi-path scheduling scheme with multiple mobile sinks for WSNs,” Computers Materials & Continua, vol. 62, no. 2, pp. 695–711, 2020. [Google Scholar]

15. A. Chiesa, D. Ojha and N. Spooner, “Fractal: Post-quantum and transparent recursive proofs from holography,” in Proc. of the Int. Conf. on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, Springer, pp. 769–793, 2020. [Google Scholar]

16. B. Parno, J. Howell, C. Gentry and M. Raykova, “Pinocchio: Nearly practical verifiable computation,” in Proc. IEEE Symp. on Security and Privacy, California, CA, USA, pp. 238–252, 2013. [Google Scholar]

17. Z. Zhang, W. Li, H. Liu and J. Liu, “A refined analysis of Zcash anonymity,” IEEE Access, vol. 8, pp. 31845–31853, 2020. [Google Scholar]

18. J. Groth, “On the size of pair-based non-interactive arguments,” in Proc. of the Int. Conf. on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, Springer, pp. 305–326, 2016. [Google Scholar]

19. B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille et al., “Bulletproofs: Short proofs for confidential transactions and more,” in Proc. IEEE Symp. on Security and Privacy (SP), California, CA, USA, pp. 315–334, 2018. [Google Scholar]

20. M. Maller, S. Bowe, M. Kohlweiss and S. Meiklejohn, “Sonic: Zero-knowledge snarks from linear-size universal and updatable structured reference strings,” in Proc. ACM Conf. on Computer and Communications Security, London, UK, pp. 2111–2128, 2019. [Google Scholar]

21. A. Gabizon, Z. J. Williamson and O. Ciobotaru, “Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge,” in Proc. Stanford Blockchain Conf., Stanford, CA, USA, pp. 953, 2019. [Google Scholar]

22. A. Kate, G. M. Zaverucha and I. Goldberg, “Constant-size commitments to polynomials and their applications,” in Proc. Int. Conf. on the Theory & Application of Cryptology & Information Security, Singapore, Singapore, pp. 177–194, 2010. [Google Scholar]

23. B. Bünz, B. Fisch and A. Szepieniec, “Transparent SNARKs from DARK compilers,” in Proc. of the Int. Conf. on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, Springer, pp. 677–706, 2020. [Google Scholar]

24. J. Wang, C. Y. Jin, Q. Tang, N. X. Xiong and S. Gautam, “Intelligent ubiquitous network accessibility for wireless-powered MEC in UAV-assisted B5G,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]

25. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip and J. Wang, “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 3, pp. 304–313, 2021. [Google Scholar]

26. J. Wang, H. Han, H. Li, S. He, P. Kumar Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]

27. J. Partala, T. H. Nguyen and S. Pirttikangas, “Non-interactive zero-knowledge for blockchain: A survey,” IEEE Access, vol. 8, pp. 227945–227961, 2020. [Google Scholar]

28. S. Setty, “Spartan: Efficient and general-purpose zksnarks Without Trusted Setup,” in Proc. Int. Association of Cryptological Research (IACR), California, CA, USA, pp. 704–737, 2020. [Google Scholar]