Image Enhancement Using Adaptive Fractional Order Filter

1  Introduction

Fractional calculus is widely used in research foundation in different domains such as engineering, computer science and others [1]. It is a well-known fact, that Fractional calculus is a method that results from the function to a non-integer order. A fruitful outcome of the discussion between Leibniz and L’Hospital lead to the idea of fractional calculus [2,3], therefore, this concept started in the year 1695.

Echocardiographic images are one of the most widely used imaging techniques for heart-related problems diagnosis. The main drawback of these images is that they have very low contrast [4] which hinders the job of doctors/technicians/physicians in giving accurate results. Hence, image enhancement becomes a necessary preprocessing step to make use of this modality. Enhancement is a process of improving the contrast which in turn results in the improvement of image visual quality and assessing doctors/technicians/physicians in a proper and accurate diagnosis to improve patient’s health. Methods that have been proposed earlier for image enhancement [5,6] like integer-order differential calculus or fixed order filters based on fractional differentiation or histogram equalization have their drawbacks such as computational complexities in the case of integer order differential calculus used for enhancement, also when fixed order filters are used for enhancement of images fails to give considerable amount of enhancement resulting in poor or low average gradient. Histogram equalization, which is commonly used for image enhancement has two major drawbacks i.e., over enhancement or under enhancement. The features of the texture smooth area might be attenuated significantly and also its differential results might be very near to zero. This is one of the reasons, why the integral differential filter linearly attenuates the features of the texture and this will also fail to preserve these in the given area. To preserve the textural features in the smooth areas, a non-linear operator based on the fractional differential technique is much more effective than that of the integer derivative-based methods and other enhancement methods [7]. Fractional operators particularly defined as differential and integral operators have been widely used in various applications, where integral operators are capable of attenuating the components corresponding to high frequency and differential operators are good for enhancing high-frequency components with an increase in the differential order of the filter and preserves components corresponding to low frequency with a small order of the differential filter. But if the higher-order filter is applied to the entire image it will result in only enhancing of edges of the image and fails to preserve the texture details of the image. Whereas if only small differential order is applied to the entire image, smooth details in the image are preserved. However, edges and high-frequency details are washed out. This leads to a need for a filter that could be adaptive and can be implemented for overall enhancement of the image, improve contrast and preserve texture details as well.

The objectives of the paper and findings are as follows:

•   The proposed filter is a fractional-order differential filter designed for image enhancement to improve the contrast of the image, consequently helpful to doctors/physicians in diagnosis.

•   Since echocardiographic images have intensity inhomogeneity, the algorithm is based on firstly partitioning images in terms of homogenous regions, details and edges.

•   The order of the filter is adaptive stating that it automatically chooses order which is a fractional value for pixels. This implies the feasibility of different order of the filter used as a fractional differential mask to above mentioned three different partitions of the image.

•   Also, the filter selects higher-order fractional values for a large magnitude of the gradient and vice versa, helps in fast implementation of the filter with appropriate selection of the order of the filter for the entire image, consequently speed up the entire processing of medical images.

Organization of the paper:

The following paper has been organized as follows, Section 2 discusses the related work with background, preliminary studies and literature review. Section 3 describes the materials and methods of the proposed work. Section 4 focuses on experimentation and analysis with experimental setup and parameters followed by results and discussions and Section 5 concludes.

2  Related Work, Background, Preliminary Studies and Literature Review

Fractional order calculus, although proposed in history long back decades ago, the significance lies in various aspects of image processing. For the measure of a Euclidean, the frequently used common definitions are R_L, G-L and Caputo definitions. The Euclidean measure is a very frequently used and commonly applied definition for fractional calculus. The computationally complex equations are always the R–L and Caputo definitions, which are Cauchy equations. The weighted sum around the function is used to express the G_L definition. This is an obvious way to show the appropriate applications of image processing. The differential of signal s (t) according to the G_L definition [8] is written below:

 DGaVS(X)=Δtlimh→0h−ν(−1)m[ ∑m=0n−1Γ(ν+1)Γ[ (m+1)(ν−m+1) ] ](s(t)−mh))(1)

In this equation s (t), is [a, t], ν∈R (and it can also be a fraction), h=(t−a)/(n) , represents the step size and Γ(x)=(x−1)! , will be the gamma function of the x. The Euclidean measure in the definition of the G-L function ranges the step of fractional numbers from integer, and hence it also extends the concepts from integer to fractional differentiation. The fractional calculus which is defined by the G-L algorithm can be calculated easily. It has its dependency only on the sampling values that are discrete of S(t−k((t−a)/(n))) and its never related to the vital values of the derivative.

The next is to analyze the influence that fractional order differentiation has on a signal. The resultant Fourier transformation of the signal s (t) is given in Eq. (2).

FT[Dνs(x)]=(iω)νFT[s(t)]−∑k=0n−1(iω)kdν−1−kdxν−1−ks(0) (2)

The even function in this is the amplitude characteristic and the odd function denotes the phase characteristic. The analysis of all the characteristics that belong to the fractional differential filter is for ω > 0. The response for the fractional differential filter is shown in Fig. 1.

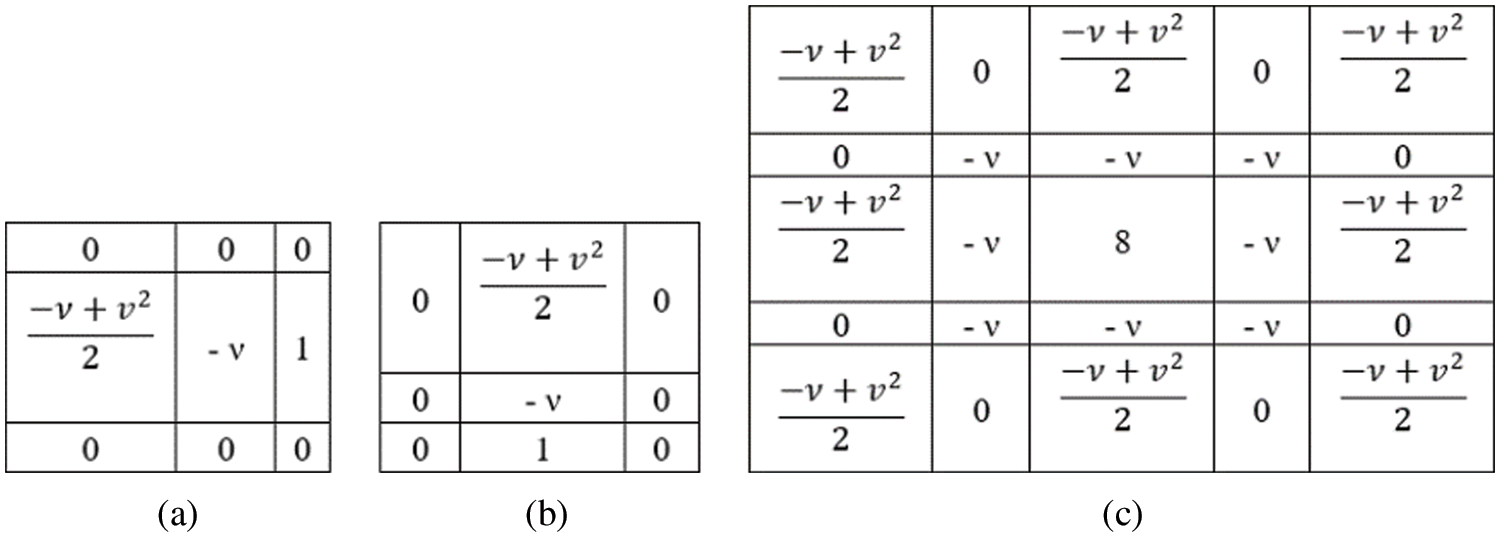
Figure 1: (a), (b) 3 × 3 fractional integral mask. (c) 5 × 5 fractional integral mask

According to the observation, the frequency response for the fractional differential filter is nonlinear when the value of ν=0 . In addition to that, the frequency response of ν -order of an all-pass filter and its response towards the frequency is d→v(ω)= (iω)v forv <0 . The singular high pass differential filter is denoted as limω→∞⁡|d→v(ω)|→∞ . The characteristics of High pass become stronger and result in a narrow transmission band i.e., d→v(ω) if there is an increase in the value of ν . In the section of low-frequency where0<ω<1 , the conservation of magnitude of low-frequency contours that uses the fractional differential is far better than that of the first-order derivative. The consideration is made that in the smooth area of the image there will be no significant changes in the grayscale.

G–L, R–L, and Caputo are the very famous and popular definitions of fractional calculus. Normally R-L and G-L are the most famous definitions that are used in digital image processing (DIP) [9]. Many scholars and researchers use the G-L based differential operator [10]. The fractional problems are solved in an effective mathematical method using fractional differentials [11]. Image processing is paving a growing path for fractional calculus [12]. Pu et al. prove that the contour features in the low frequency in the smooth areas are preserved in the fractional differential-based methods [13,14]. This also proves that there is a marginal retainment of the high frequency in the areas with large variabilities in the gray levels, this will result in enhancement of the details of texture where there are no noticeable changes in gray levels [15,16]. The trend of imaging is presently having the significance of the three-dimensional (3-D) images which are increased in its number. In image processing applications the 3-D objects have a biological mechanism, and this mechanism is studied using magnetic resonance images (MRIs) and functional MRIs (fMRIs). Accordingly in a 3-D object, the slices are obtained and these slices are 2-D images in nature [17,18]. Again the 2-D images are used to reconstruct the 3-D object. This is well known as 3-D image reconstruction. There are reasons why 3-D images contain noise; one such reason is hardware imperfection [19]. One of the widespread techniques in image processing that is grounded on reducing the total variation (TV) [20] is 3-D image denoising. To denoise, the 3-D image algorithm [20] is been developed. Spare representation [21] non-local means [22,23], and many other techniques [24–26] are used to denoise the images. Tab. 1 gives a comparison of the proposed method with state-of-the-art methods. In [27] A. Heena et al. discussed the design and implementation of fractional-order filters used for denoising of images. The filter used is fractional order integral filter and designed for noise removal as preprocessing filter. Muresan et al. in the most recent paper discussed the review of advances in fractional order filtering [28] where a detailed review of how fractional-order analogue and digital filters are given, fractional-order calculus is well exploited for both sensing and filtering, a detailed description of fractional filters used in different applications including biomedical applications are highlighted. Mashat et al. proposed a novel technique for medical image transmission where the paper focuses on security aspects of medical information during transmission to authenticate and protect the information over public networks. The technique is robust and assures the prevention of stealing of medical data over transmission network [29]. Bhatia [30] has given a comparative analysis of opinion summarization techniques paper covers both abstractive and extractive approaches where extractive approaches use Principal component analysis for summarization of the text resulting in a reduction of dimensions in data aspects without any loss of information irrespective of domain. All work done earlier uses fractional filters or fractal derivatives but the proposed work uses a fractional-order differential filter for echo image enhancement and the filter is adaptive which is the highlight of the paper. Enhancement of the images with no loss of information is a novelty of the present work.

3  Materials and Methods

This section discusses the stepwise procedure required to achieve image enhancement and a block diagram of the proposed algorithm is given in Fig. 3. The block diagram of the proposed method comprises of the input image which gets partitioned into three parts, the homogenous regions, details and edges so that effectively the order of the enhancement filter gets adaptively adjusted to enhance each one of them.This adaptiveness of the fractional-order differential filter is a novel approach discussed in the methodology. The process explains the details of the image data, feature extraction, second-order derivative for a fractional differential filter which is adaptive and fractional order differential enhancement.

3.1 Explanation of Dataset

In this paper, standard clinical database from the MIMIC (Medical Information Mart for Intensive Care) is an openly available dataset developed by the MIT Lab for Computational Physiology, comprising identified health data associated with ∼40,000 critical care patients are used for analysis. The MIMIC-III Clinical Database is available on Physio Net (doi: 10.13026/C2XW26). The analysis of the proposed method is carried out by testing and applying on the database of the images i.e., six different images are described in the next section.

3.2 Methods

An important characteristic that is used to identify the objects for any region is the texture. Based on the spatial dependencies, earlier many authors proposed computational texture features. The texture (details) of the image is characterized by major components such as the co-occurrence Matrix feature. In addition to the co-occurrence matrix, it is also required to define a few internal factors of the medical images such as the Contrast, Homogeneity (H), entropy & Local Homogeneity (LH).

If I represents the grayscale image at level m, the position of each pixel is given by s≡(x,y) in I and t=(Δx,Δy). The co-occurrence matrix M is the m x m matrix. The pair of gray levels (i, j) is

M(i,j)=card(s,s+t)ϵR2|I(s)=I,I(s+t)=j (3)

M → concurrent matrix.

Card → predefined mat lab function for the data exchange.

s → position of the pixel.

I → image data under consideration.

t → translation vector.

i, j → gray level.

The Contrast, when the scale of local texture is larger the distance

C=∑k=0m−1k2∑|i−j|=kM(i,j) (4)

k → neighboring pixels

Homogeneity is represented as

H=∑i∑j(M(i,j))2 (5)

Entropy is the measure of randomness: close to either 0 or 1.

E=∑i∑j(M(i,j)logM(i,j)) (6)

Local Homogeneity (LH) is given as

LH=∑i∑jM(i,j)1+(i−j)2 (7)

These various features/parameters of the medical image are very essential for the advanced image processing which will be done at the pixel level for the query and reference pixel, in this regard the first parameter contrast is given by the Eq. (4) in which the texture decision is done on the contrast of the test image with the neighboring pixels. The second parameter is homogeneity which decides the pixel region and the background of the image which is not a concern, on the other hand, it is most required for the data extraction from the region of interest in the medical image data which is given by the Eq. (5). The next parameter is the entropy which is given by the Eq. (6) in which it plays a decision parameter for the 1 or 0 for pixel exchange. Last parameter Local Homogeneity which is similar to the homogeneity which is done among the inter and intra pixel of analysis given by Eq. (7).

3.3 Proposed Technique with Second Order Derivative for Adaptive Fractional Differential Filter

It is also relevant to select every pixel from the f (x, y) image into their relevant classifications such as its edges, homogenous content and details of the image for the classification of the image data requires the operation of signal convolution with suitable mask value which is pre-defined.

With the various regions of the input data for operation, there exists further classification of pixels depending upon the intensity values of the pixels for exact differentiation. Hence providing the scope for the various embedded image features raises the requirement to be particular about the classification based on its intra and inter-pixel values of it. As an appropriate solution, this entire process demands the setting of suitable threshold values as a boundary condition for the feature extraction among the pixels. The threshold values are given by the following equations:

τa=max(λ1)−λ¯ (8)

τb=max(λ2)+τa2. (9)

In which λ¯  = mean values of λ1 of all the pixels of the input image. λ1, λ2 = Eigenvalues of the image pixel. To analyze and improve the contrast of the image it is required to approach the derivative technique by defining a square matrix condition to compare inter and intra pixel levels which is defined as the Hessian matrix of the order of 2 × 2, in which the four different elements of the matrix under consideration are; the two elements correspond to the inter-pixel values and other two corresponds to the intra-pixel values which are always the second-order partial derivative function of f(x, y) which is given as a Hessian form of f(x, y) as:

[fxxfxyfyxfyy]=f(x,y) (10)

In which ( fxx,fyy ) = intra pixel value in the same direction. ( fxy,fyx ) = intra pixel value determination in the two different directions. Each functional value of the matrix defines the intensity values of the pixel in which these values are minimum if the pixel belongs to the same region. The pixel value will be maximum if and only if when the adjacent pixels belong to the different regions comparatively. The pixel classification in turn depends on the boundary variables such as τa and τb as defined previously for region classification such as the edge of the image, homogenous pixel region or details of the image. The defined 2 × 2 Hessian matrix is proportionally relative to the two Eigenvalues λ1 and λ2 which will be given based on the second-order derivative function of every pixel value which will be given by:

λ1=12[fxx+fyy+(fxx+fyy)2+4fxy2] (11)

λ2=12[fxx+fyy−(fxx+fyy)2+4fxy2] (12)

with the above Eqs. (11) and (12) for pixel classification the normalized Eigenvalues are very small if the pixel belongs to the homogenous region of the image, whereas λ2 will be comparatively small than λ1 for the pixels falling in the region of edges of the image but both the values λ1&λ2 are very essential for the region of details as per classification. Hence with the above observation, it can be noted that by considering only λ1 value it will be sufficient for the classification of the image into different regions.

3.4 System Model

Generally, two different types of derivative functions namely integer order and fractional order methods exist for the image processing applications. Due to the higher-order accuracy, fractional-order derivative is more preferable than integer-order derivative. The fractional-order derivatives are defined by three definitions namely:

•   Grunwald–Letnikov fractional derivative (G-L).

•   Riemann-Liouville fractional derivative (R-L) and

•   Caputo (Li & Xie) et al. fractional derivative.

Out of the above-mentioned G-L fractional derivative plays a vital role in the processing of medical images without affecting their properties as represented in Eq. (1). The other two algorithms defined can be used relevantly for other signal processing implications, but this G-L based derivative method has a vital role in the medical image processing in which this algorithm processes by segmenting the available medical image. This algorithm processing is done by defining the variable size image enhancement mask, for the algorithm under consideration, it is done with 3 × 3 and 5 × 5 masks, for region-based segmenting of the input medical image data by defining the parameters such as Average gradient and Entropy, it is also discussed with the variance of the respective data.

The image enhancement is carried out by defining the enhancement factor ‘ν’: which acts as the deciding factor for the fuzzy logic to classify the three different regions of the pixel as a homogenous region or edge-based data or detailed data for the pixel. Which will be given by fuzzy decision logic comprising the thresholds λ1 and λ2 which are Eigenvalues of the derivative, the decision matrix values are decided with τa and τb respectively. Initially, the resultant enhanced image is defined by Eq. (13), by finding the value of the ‘ν’ the corresponding mask is chosen with the gradient of ‘ν’ defined by Eq. (14).

f′(x,y)=f(x,y)∗(n×n). (13)

f’ (x, y) = enhanced resultant image.

f (x, y) = partial derivative as defined by Eq. (8).

(*) = convolution operator.

(n × n) = mask value with the order 3 or 5 depending on the ‘ν’ value.

ν={−0.5forλ1<τa−0.2forτa<λ2<τb0.5forλ1>τb (14)

The value of ‘ν’ defines the mask value in different directions of the pixel if the 3 × 3 mask is selected two different mask values are defined to perform masking in 8 different directions of pixel processing as shown in Figs. 1a and 1b and if the mask value is 5 × 5 a fixed mask as shown in Fig. 1c is used.

As described in Fig. 1 the value ν for various boundary regions of the medical image are considered, after applying the mask the data in the medical image is designed and desired as shown in Fig. 2 with the two boundary conditions that are τa=e and τb=g , hence thereby focusing the medical image in which it is rich in the extraction of image parameters by suppressing the artefacts, hence by minimizing the boundary conditions with the consideration of the Eigenvalues and its mean values are considered.

For the recovery of the signal by the application of the mask and its coefficients, the interval values desired are shown in Fig. 2, lets’s define the unitary signal f(s), which belongs to the coefficients (x, y), for the initial synthesis of the medical image in equal intervals which will be given by Eq. (15).

dνf(s)dsν≈f(s)+(−ν)f(s−1)+(−ν)(ν+1)2f(s−2)+⋯+Γ(−ν+1)n!Γ(−ν+n+1)f(s−m)

dνs(x,y)dxν≈s(x,y)+(−ν)s(x−1,y)+(−ν)(ν+1)2s(x−2,y)+⋯+Γ(−ν+1)n!Γ(−ν+n+1)s(x−m,y)

dνs(x,y)dyν≈s(x,y)+(−ν)s(x,y−1)+(−ν)(ν+1)2s(x,y−2)+⋯+Γ(−ν+1)n!Γ(−ν+n+1)s(x,y−n) (15)

3.5 Architecture and Working of Algorithm

Step by step working of the Proposed algorithm:

In this proposition, there is a proposal of a method that can improve contrast, conserve the edges and major edge features of an image, that is fractional-order image enhancement. The algorithm consists of 3 important steps.

•   Step-1: The enhancement method of fractional order is done based on G–L definition.

•   Step-2: An improved numerical method is implemented (adaptive filter order) and G–L image enhancement masks are derived.

•   Step-3: In the final step, the capabilities of the image enhancement process are just demonstrated using the proposed method. The contour in the low-frequency features in a smooth area is protected as shown in experimental results. In addition to that, the nonlinear method is used to maintain the texture and the high-frequency edge details in the areas, where the levels of the gray are not changing significantly.

Fig. 3 gives a complete overview of the proposed algorithm where the input echocardiographic image is partitioned into three different categories homogeneous part, detail’s part and edges in the image for pixels being inhomogeneous. Then each of these regions is masked with different order fractional filter which is adaptive to enhance the entire image irrespective of inherent inhomogeneity in the echocardiographic images. A complete flow chart of the entire algorithm which is proposed and implemented in the paper is based on Fig. 2 where the partitioning of the image is λ1  <  τa characterized as a homogeneous region, λ1 between τa and τb is corresponding to details in the image and λ1  >  τb is referring to edges. Filter designed to adapt to this and correspondingly adjust the order for each partition and then each processed partition combined corresponds to an enhanced output image. λ1 is Eigen value as defined in Eq. (11).

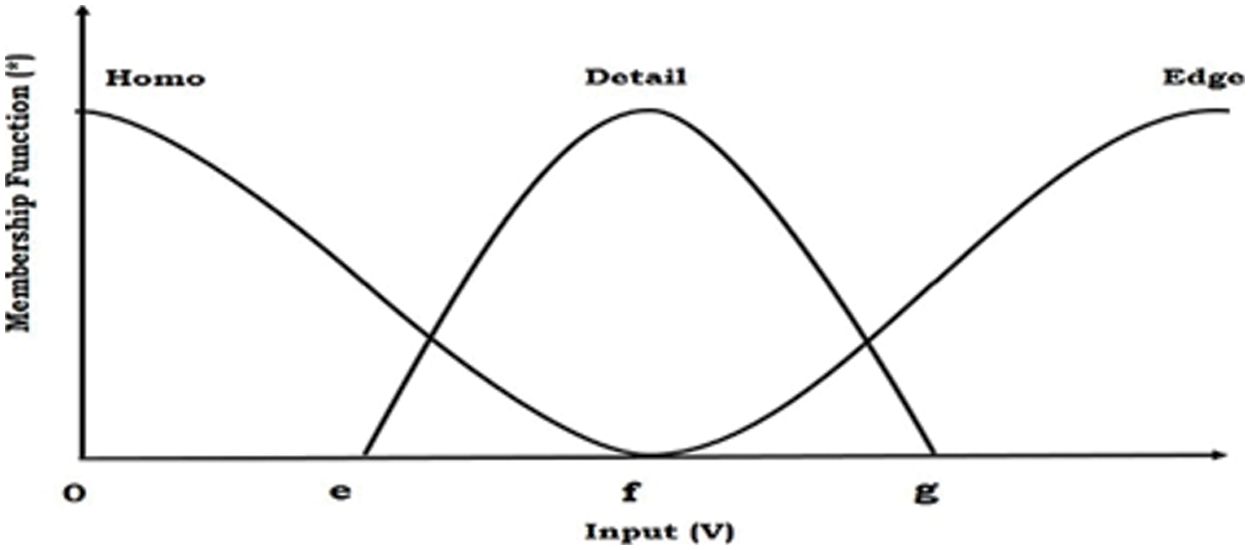
Figure 2: Fuzzy based 3 region segmentation with the condition τb  = e and τa  = g

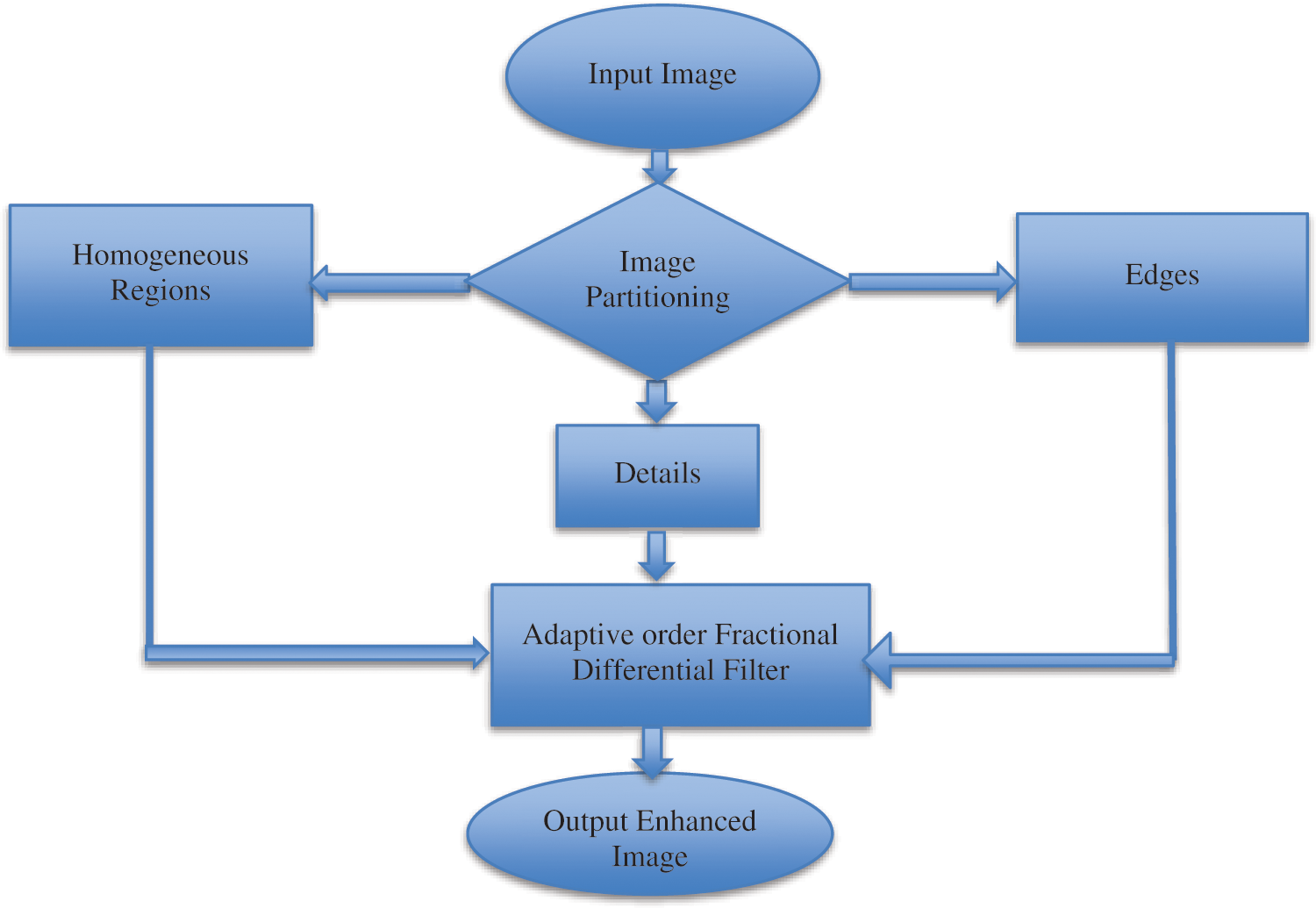
Figure 3: Diagram of the proposed algorithm

4  Experimentation and Analysis

4.1 Experimental Setup and Parameters

The effectiveness of the proposed method is tested using a set of echocardiographic images which are tested both in terms of quantitative and qualitative metrics. The performance metric used for quantitative analysis is Average gradient, entropy and SSIM. Entropy is defined by an Eq. (6) gives the information content in the image and also measures randomness whether close to either 0 or 1. The information content of the image is preserved by the proposed algorithm. Since Entropy is increased means no loss of information and from the tables, it is clear that entropy obtained using the proposed method is close to the original entropy of the image.

The average gradient decides the measure of improvement in image quality. It also decides how clear the image is. Where the increased value in AG indicates an increase in enhancement and also improvement in clarity achieved in the proposed method.

AG=1M×N∑i=1M∑j=1N(∂f∂x)2+(∂f∂y)22 (16)

AG reflects the ability to express the details of an image and can be used to measure the relative clarity of the image. AG is calculated as shown in Eq. (16). Where numerator in the square root has first term representing partial derivative of image w.r.t ‘x’ and the second term is a partial derivative of an image

w.r.t ‘y’.

SSIM is a newer measurement tool that is designed based on three factors i.e., luminance, contrast, and structure as given in Eq. (17) to better suit the workings of the human visual system. This metric is widely used in image quality assessment.

SSIM(x,y)=[l(x,y)]α⋅[c(x,y)]β⋅[s(x,y)]γ (17)

If α = β = γ = 1 (the default for Exponents) then, l (x, y) is luminance, c (x, y) is contrast and s (x, y) is structure.

4.2 Results and Discussions

The proposed method uses filters for the enhancement of echocardiographic images using adaptive fractional order differentiation. The filter designed is capable of enhancing the image significantly and also preserves the structure of an input image. The proposed filter has the advantage of faster implementation of this method compared to other methods. This filter suitably adopts the fractional order of the masks concerning membership of the current pixel. The analytical test on the input echo images has proved and revealed enough the strengths and sustainability of the designed co-efficient.

If an order of the filter is integer order it is not suitable for images also when an order of the filter is fixed, in some parts of the image improvement is observed but other details in the image regions are affected. As given in Fig. 2 every image can be considered to be comprised of homogenous regions, details and edges. Higher orders are suitable for edges, low orders are for smooth regions and intermediate orders are for texture details in images. Hence fixed order filters when applied to the whole image the results are not good as the adaptive fractional order filter proposed in the paper. Each pixel in an image has a gradient magnitude which can be used to categorize regions or details or edges. However, a minimum value of gradient represents regions, a maximum value of gradient represents edges and intermediate values indicate details. Thresholds are computed using Eqs. (8) and (9). It is reflected from the tables that the proposed filter exhibited better results in comparison to state-of-the-art methods (as mentioned earlier in the paper) by not only increasing AG value but also information content in images is preserved as indicated by the value of entropy being close to the original value of information in images. Hence it can be concluded that the adaptiveness of the filter results in improvement and enhancement by appropriately selecting fractional-order for edges, details and regions as given by Eq. (14).

After partitioning the image into three regions accordingly order of the filter is selected for pixels in different regions and an enhanced image with improved contrast is suitable for physicians’ inaccurate diagnoses. Tabs. 1 and 2 show the proposed algorithm is a better method of image enhancement.

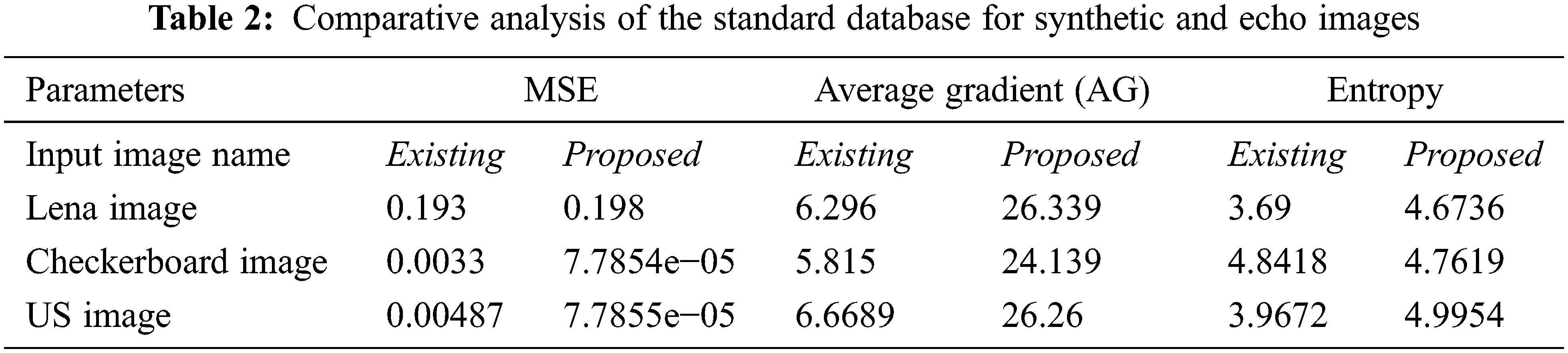
The desired algorithm is also tested with the non-medical image database, and its comparative analysis is done with the existing and proposed algorithms as shown in Figs. 4 and 5 and its tabulated values are as shown in Tab. 2. For analysis, it is considered only with three types of test input images, Lena, Checkerboard and US image. Fig. 6 shows windows exhibiting the variation in the MSE performance metric and can be seen how the error becomes minimum almost near to zero which is a requirement for achieving enhancement and Fig. 7 gives a summary of tested images from the dataset.

Figure 4: Result of enhancement achieved through denoising of noisy Lena image

Figure 5: Result of enhancement achieved through denoising of the noisy checkerboard image

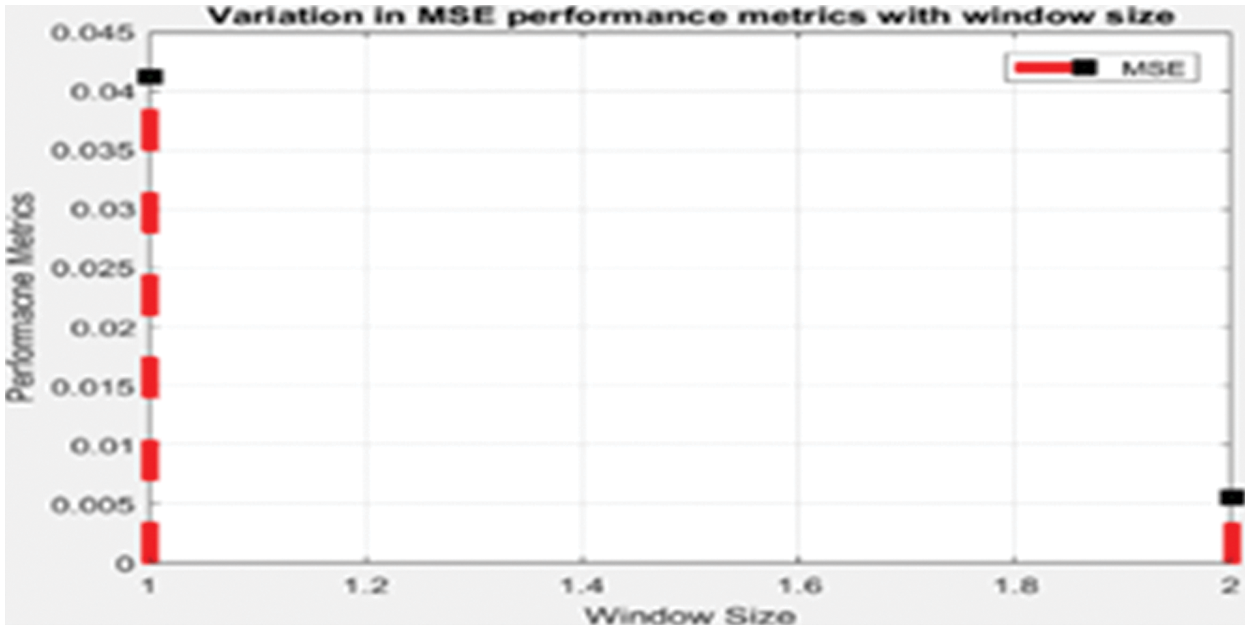
Figure 6: Window showing variation in MSE performance metric

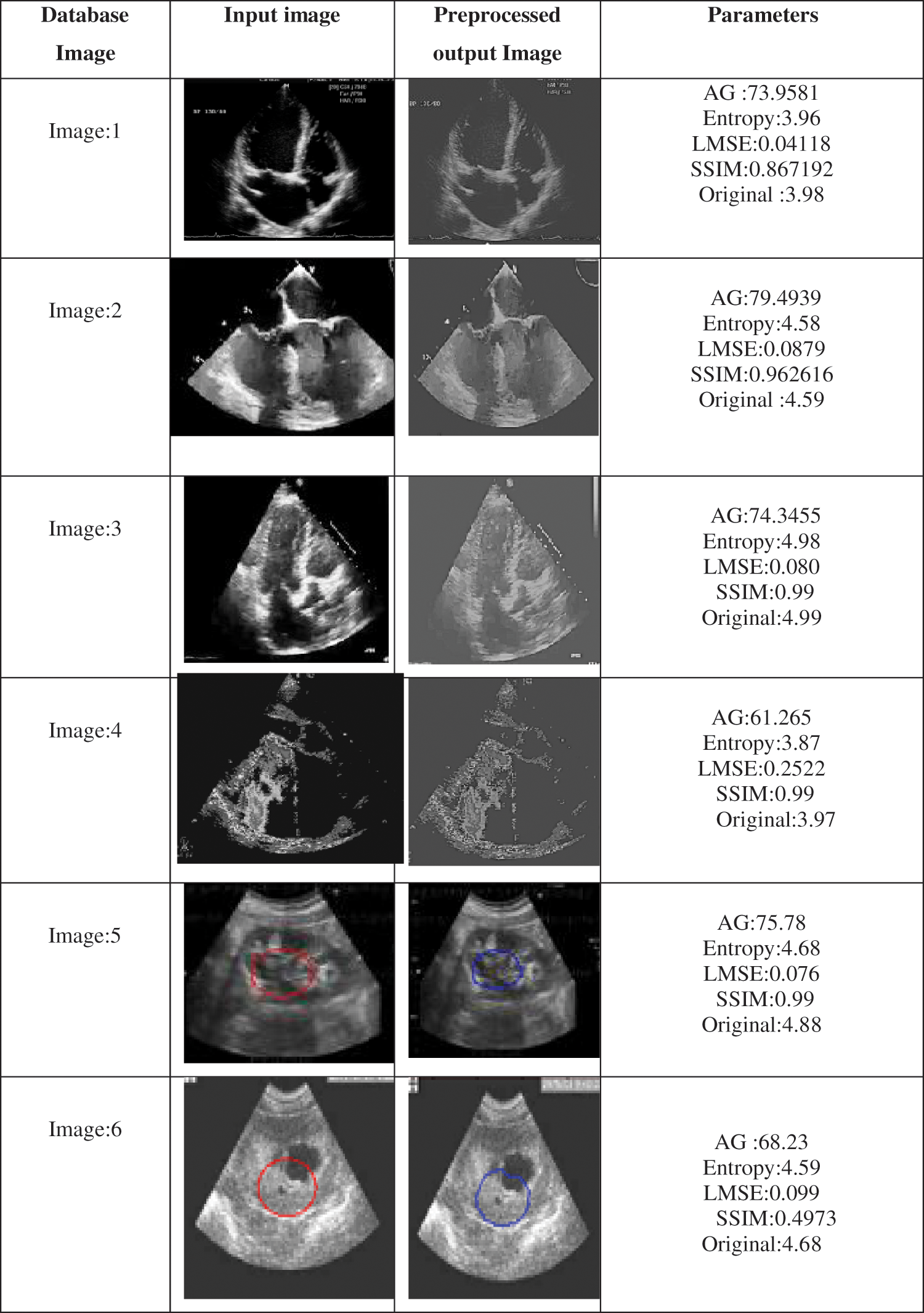
Figure 7: Results summary for the tested database with parameter metric of qualitative analysis

5  Conclusion and Future Directions

In any digital signal processing, concerning the synthetic image or medical images, it is noted that Fractional differentiation plays a vital role in the analysis of enhanced research in the domain. In this research article, improved quality of images is presented with a differentiation technique and algorithm processed with the G-L based technique for enhancement. Finally, it is demonstrated that the algorithm successfully enhanced different regions in an image resulting in increased Average gradient, entropy and SSIM with an adaptive fast selection of the order of the filter as compared to distinct image content, experimental results and analysis have proven that the algorithm is better than the existing with the various standard medical image database and other image databases. The proposed algorithm would make medical image processing speed up further and assess doctors in clinical diagnosis as a result of enhancement achieved. The adaptive nature of the filter is the novelty of the algorithm.

As a future enhancement, the applications of fractional order calculus can be used in other fields of image processing and can explore for segmentation, image restoration, image analysis etc. Also, fractional-order calculus can be a field of research for various advanced image processing techniques as discussed earlier. It has to be noted that the improvement of the proposed algorithm could have an addition of the neural network as a classifier which plays a very important role. With the developed algorithm the performance is measured using the Structural Similarity Index Matrices (SSIM), this similarity index is used as the similarity tool for the measurement of the performance and efficiency, it has to be noted that, there exists a remarkable enhancement of the similarity index among the standard database. It should also be noted that the developed algorithm can also be applied to any of the real-time Images (such as Echocardiographic images) or other untrained databases for the applications. As a future enhancement, an advanced algorithm can be designed for the video applications, satellite images and other formats of images, even as the next improvement it can also be extended to the comparative analysis among other image datasets. As every research ends with some limitations the work carried out in this paper also resulted in some limitations. Availability of the data sets that too real-time echocardiographic images used in the work are the major limitation in the work carried out.

Funding Statement: This research is supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R195), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest.

References

 1.  A. Heena, N. Biradar and N. M. Maroof, “Comparative analysis of fractional-order calculus in image processing,” in Proceedings of ICAIT in IEEE Digital Explore, pp. 180–183, china, 2020. [Google Scholar]

 2.  Li, D. Qian and Y. Q. Chen, “On riemann–Liouville and caputo derivatives,” Discrete Dynamics in Nature and Society, vol. 2011, pp. 15, 2011. https://doi.org/10.1155/2011/562494. [Google Scholar]

 3.  J. V. Garg and K. Singh, “An improved grünwld–Letnikov fractional differential mask for image texture enhancement,” Int. Adv. Comput. Sci. Appl, vol. 3, no. 3, pp. 130–135, 2012. [Google Scholar]

 4.  Q. Chen, H. Guo and X. Zhang, “A fractional differential approach to low contrast image enhancement,” International Journal of Knowlengde Language Process, vol. 3, no. 2, pp. 20–29, 2012. [Google Scholar]

 5.  C. Gao, J. Zhou, Z. Zheng and F. Lang, “Image enhancement based on improved fractional differentiation,” Journal of Computer Information System, vol. 7, no. 1, pp. 257–264, 2011. [Google Scholar]

 6.  Y. Pu, J. Zhou and X. Yuan, “Fractional differential mask: A fractional differential-based approach for multiscale texture enhancement,” Image Processing, IEEE Transactions, vol. 19, no. 2, pp. 491–511, 2009. [Google Scholar]

 7.  S. Huang and C. Yeh, “Image contrast enhancement for preserving mean brightness without losing image features,” Engineering Applications of Artificial Intelligence, vol. 26, pp. 1487–92, 2013. [Google Scholar]

 8.  K. Diethlm and N. J. Ford, “Analysis of fractional differential equations,” Journal of Mathematical Analysis and Applications, vol. 265, no. 2, pp. 229–248, 2002. [Google Scholar]

 9.  S. Ayesha and R. Adnan, “Fractional order integration and fuzzy logic-based filter for denoising of echocardiographic image,” Computer Methods and Programs in Biomedicine, vol. 137, pp. 65–75, 2016. [Google Scholar]

10. Y. Liu, Y. Pu and J. Zhou, “Design of image denoising filtering based on fractional integral,” Journal of Computer Information System, vol. 6, no. 9, pp. 2839–2847, 2010. [Google Scholar]

11. Q. Yu, F. Liu, I. Turner, K. Burrage, V. Vegh et al., “The use of a riesz fractional differential-based approach for texture enhancement in image processing,” ANZIAM Journal, vol. 54, pp. C590–C607, 2012. [Google Scholar]

12. Chen, D. Xue and Y. Chen, “Fractional differential-based approach for CT image enhancement,” Advanced Materials Research, vol. 634, AMR 634–638, pp. 3962–3965, 2013. https://doi.org/10.4028/www.scientific.net/amr.634-638.3962. [Google Scholar]

13. Y. Pu, W. Wang, J. Zhou, Y. Wang, H. Jia et al., “Fractional differential approach to detecting texture features of digital image and its fractional differential filter implementation,” Science in China Series F: Information Sciences, vol. 51, no. 9, pp. 1319–1339, 2008. [Google Scholar]

14. Y. Zhang, Y. Pu, J. Hu, Q. Chen, J. Zhou et al., “Efficient CT metal artifact reduction based on fractional-order curvature diffusion,” Computational and Mathematical Methods in Medicine, vol. 2011, pp. 173748–173757, 2011. [Google Scholar]

15. J. R. H. Chan, A. Lanza, S. Morig and F. Sgallari, “An adaptive strategy for the restoration of textured images using fractional order regularization,” Numerical Mathematics: Theory, Methods and Applications, vol. 6, pp. 276–296, 2013. [Google Scholar]

16. J. Hu, Y. Pu and J. Zhou, “A novel image denoising algorithm based on riemann–Liouville definition,” Journal of Computers, vol. 6, no. 7, pp. 1332–1338, 2011. [Google Scholar]

17. Y. Gao, M. Wang, D. Tao, R. Ji, Q. Dai et al., “3-D object retrieval and recognition with hypergraph analysis,” IEEE Trans. Image Process, vol. 21, no. 9, pp. 4290–4303, 2012. [Google Scholar]

18. Y. Gao, M. Wang, R. Ji, Z. Wu, Q. Dai et al., “3-D object retrieval with hausdorff distance learning,” IEEE Transactions on Industrial Electron, vol. 61, no. 4, pp. 2088–2098, . 2014. [Google Scholar]

19. S. Khan. W. Yin Chai, W. Soo See and A. Khan, “X-Ray image enhancement using a boundary division wiener filter and wavelet- based image fusion approach,” Journal of Information Processing Systems, vol. 12, pp. 35–45 2016. [Google Scholar]

20. A. Chanbolle, “An algorithm for total variation minimization and applications,” Journal of Mathematical Imaging and Vision, vol. 20, no. 1, pp. 89–97, 2004. [Google Scholar]

21. J. Zhang and Z. Wei, “A class of fractional-order multi-scale variational models and alternating projection algorithm for image denoising,” Applied Mathematical Modelling, vol. 35, no. 5, pp. 2516–2528, 2011. [Google Scholar]

22. Chen, Da Li, Ding Yu Xue, and Yang Quan Chen. “Fractional differential-based approach for CT image enhancement.” In Advanced Materials Research, vol. 634, pp. 3962–3965. Trans Tech Publications Ltd, 2013. [Google Scholar]

23. L. Ruding, S. Osher and E. Fatemi, “Nonlinear total variation-based noise removal algorithms,” Physics D: Nonlinear Phenom, vol. 60, no. 1, pp. 259–268, 1992. [Google Scholar]

24. J. Machado, V. Kiryakova and F. Mainardi, “Recent history of fractional calculus,” Communications in Nonlinear Science and Numerical Simulation, vol. 16, pp. 1140–53, 2011. [Google Scholar]

25. B. Li and W. Xie, “Image denoising and enhancement based on adaptive fractional calculus of small probability strategy,” Neurocomputing, vol. 175, pp. 704–14, 2016. [Google Scholar]

26. Kaur, Ramandeep; Kaur, Kamaljit. International Journal of Engineering and Manufacturing; Hong Kong Vol. 6, no. 6, 38, 2016, https://dx.doi.org/10.5815/ijem.2016.06.04. [Google Scholar]

27. A. Heena, N. Biradar and N. M. Maroof, “Design and implementation of fractional order integral filter for denoising of echocardiographic images,” in Published in Elsevier SSRN, ISMAC CVB 2020 as Conf. Proc., Elsevier SSRN, Tirunelveli, India. pp. 506–515, 2020, https://ssrn.com/abstract=3735736. [Google Scholar]

28. C. I. Muresan, I. R. Birs, E. H. Dulf, D. Copot and L. Miclea, “A review of recent advances in fractional-order sensing and filtering techniques,” Sensors 2021, vol. 21, pp. 1–26, 2021. [Google Scholar]

29. A. Mashat, S. Bhatia, A. Kumar, P. Dadheech and A. Alabdali, “Medical image transmission using novel crypto-compression scheme,” Intelligent Automation and Soft Computing, vol. 32, pp. 841–857, 2021. [Google Scholar]

30. S. Bhatia, “A comparative study of opinion summarization techniques,” IEEE Transactions on Computational Social Systems, vol. 8, pp. 110–117, 2020. [Google Scholar]