WACPN: A Neural Network for Pneumonia Diagnosis

1  Introduction

Community-acquired pneumonia (CAP) is considered a sort of pneumonia [1] developed outside hospitals, and clinics, along with infirmaries [2]. CAP may affect people of any age, but it is more prevalent in very young and elderly groups, which may need hospital treatment if they develop CAP [3]. Chest computed tomography (CCT) is a crucial way to help radiologists/physicians to diagnose CAP patients. Recently, automatic diagnosis models based on artificial intelligence (AI) have gained promising performances and attracted researchers’ attention. For example, Heckerling, et al. [4] employed the genetic algorithm for neural networks to foresee CAP. This approach is shortened to the genetic algorithm for pneumonia (GAN). Afterward, Liu, et al. [5] proposed a computer-aided detection (CADe) model to uncover lung nodules in the CCT slides. Strehlitz, et al. [6] presented several prediction systems by means of support vector machines (SVMs) together with Monte Carlo cross-validation. Dong, et al. [7] proposed an improved quantum neural network (IQNN) for pneumonia image recognition. Ishimaru, et al. [8] proposed a decision tree (DT) model to foresee the atypical pathogens of CAP. Zhou [9] introduced the cat swarm optimization (CSO) method to recognize CAP. Wang, et al. [10] proposed an advanced deep residual dense network for the image super-resolution problem. Wang, et al. [11] proposed a CFW-Net for X-ray based COVID-19 detection.

However, the above methods still have room to improve. Their recognition performances, for example, the accuracies, are no more than or barely above 91.0%. We analyze their models and believe the reason is their training algorithms. After comparing recent global optimization algorithms, we find that particle swarm optimization (PSO) is one of the most successful optimization algorithms, compared to otheroptimization algorithms such as artificial bee colony [12] and bat algorithm [13]. Hence, we use the framework in Zhou [9] but replace CSO with an improved PSO. In addition, we introduce the two-dimensional wavelet-entropy (2d-WE) layer, introduce an improved PSO method—adaptive chaotic PSO (ACP) [14], and combine it with a feed-forward neural network. The final combined model is named WE-layer ACP-based network (WACPN). The experiments show the effectiveness of this proposed WACPN model. In all, we exhibit three contributions:

(a) The 2d-WE layer is managed as the feature extractor.

(b) ACP is utilized for training the neural network to gain a robust classifier.

(c) The proposed WACPN is proven to give better results than six state-of-the-art models.

2  Dataset and Preprocessing

The dataset is described in Zhou [9], where we have 305 CAP images and 298 healthy control (HC) images. The detailed demographical information can be found in Ref. [9]. Assume the raw CCT dataset is signified as FA , within which each image be signified as fa , and the number of entire images of both classes is |F|=603 , we get FA={fa(i),i=1,2,⋯,|F|} . The size of each image can be obtained as:

hsize[fa(i)]=W0×H0×3, (1)

where (W0,H0) connotes the width and height of the image set FA and hsize(x) outputs the size of x. Here W0=H0=1024 . Figs. 1a and 1b depicts the schematic for preprocessing, which aims to grayscale the raw images, enhance their contrasts, cut the margins and texts, and resize the images.

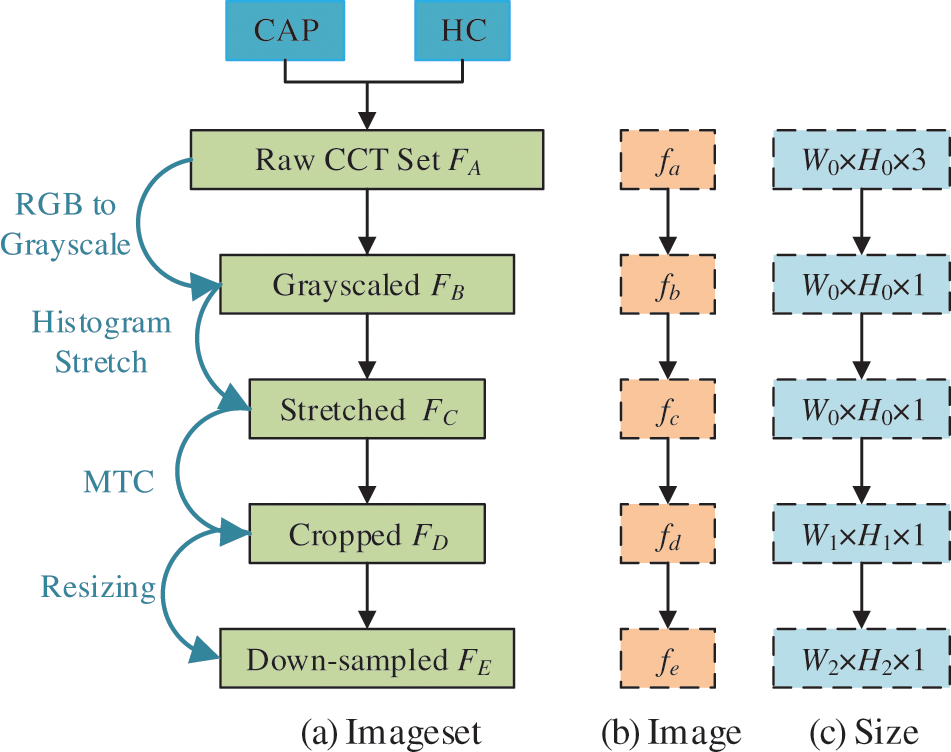
Figure 1: Diagram of preprocessing

Initially, the color CCT image set FA is transformed into grayscale images by holding the luminance channel. The grayscaled CCT image set is symbolized as FB={fb(i),i=1,2,⋯,|F|} .

Second, we use histogram stretching (HS) on all images FB={fb(i)} to enhance the contrast. Take the i-th image fb(i) as a case, its image-wise minimum, and maximum grayscale value fbl(i) and fbh(i) are calculated as:

{fbl(i)=minpw=1W0minph=1H0fb(i|pw,ph)fbh(i)=maxpw=1W0maxph=1H0fb(i|pw,ph), (2)

where (pw,ph) are temporary variables signifying the index of width and height along with the image fb(i) , respectively. The HSed image set FC={fc(i),i=1,⋯,|F|} can be determined as:

fc(i)=fb(i)−fbl(i)fbh(i)−fbl(i) (3)

Third, margin & text cropping (MTC) is implemented to eradicate (a) the checkup bed at the bottom zone, (b) the privacy-related scripts at the margin or corner zones, and (c) the ruler adjacent to the right-side and bottom zones. The MTCed image set FD={fd(i),i=1,⋯,|F|} can be determined as fd(i)=fc(i;pw,ph),pw∈[p1+1,W0−p2],ph∈[p3+1,H0−p4] , where (p1,p2,p3,p4) stand for pixels to be cut from four directions (left, right, top, and bottom) with the unit of pixels. Note here the size of fd(i) is hsize[fd(i)]=W1×H1 . By means of straightforward maths calculation, we reckon that

{W1=W0−p1−p2H1=H0−p3−p4 (4)

Lastly, each image in FD is resized to the extent of [W2,H2] , acquiring the resized image set FE={fe(i),i=1,⋯,|F|} as fe(i)=hresize[fd(i);(W2,H2)] , where hresize signifies the resizing function.

Fig. 1c shows the extent of every raw image in FA is W0×H0×3 , and that of the final preprocessed image in FE is reduced to W2×H2 . In addition, the value of data-compression ratio (DCR) z1 is obtained as z1=W0×H0×3/(W2×H2) =48 . The value of space-saving ratio (SSR) z2 is calculated as z2=1−W2×H2/(W0×H0×3)=97.92 . Fig. 2 shows two examples of the preprocessed image set. We use 10-fold cross-validation in our experiment.

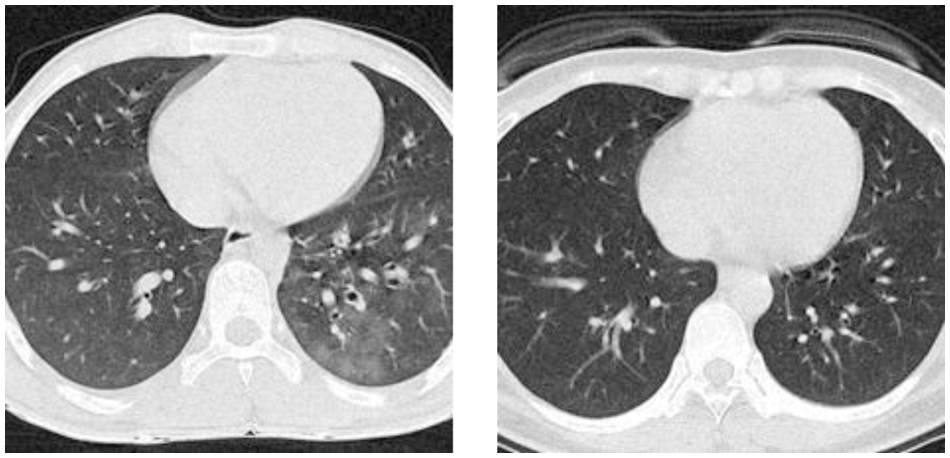
Figure 2: Examples of the preprocessed image set

3  Methodology of WACPN

3.1 Discrete Wavelet Transform

Tab. 1 enumerates all abbreviations and their associated meanings. The advantage of wavelet transform (WT) is that it holds both time/spatial and frequency information of the given signal/image. Nevertheless, the discrete wavelet transform (DWT) is chosen to convert the raw signal r(t) into the wavelet coefficient domain [15] in reality. Suppose the signal r(t) is one-dimension, first, we define the continuous wavelet transform (CWT) Eγ(sa,st) of r(t) as:

Eγ(sa,st)=∫−∞∞⁡r(t)×γ(t|sa,st)dt, (5)

in which E stands for the wavelet coefficient, γ the mother wavelet. γ(t|sa,st) is defined as:

γ(t|sa,st)=1saγ(t−stsa),sa>0,st>0, (6)

where the sa signifies the scale factor (SF) and st the translation factor (TF).

Now, we deduct the definition of DWT from CWT. The Eq. (5) is discretized by substituting sa and st with two discrete variables (DVs) c and v,

{sa=2cst=v×2c (7)

where c signifies the DV of the SF sa , and v the DV of the TF st [16]. Moreover, the original signal r(t) is a DV to r(q) , of which q signifies the DV of t. Like this, two subbands (SBs) can be calculated. The approximation SB EA(q|c,v) is determined as:

EA(q|c,v)=SD[∑o⁡r(q)×fA∗(q−2cv2c)], (8)

where fA(q) signifies the low-pass filter. SD is the down-sampling operation. The detail SB ED(q|c,v) is determined as:

ED(q|c,v)=SD[∑o⁡r(q)×fD∗(q−2cv2c)]. (9)

where fD(q) signifies the high-pass filter.

3.2 2d-WE Layer

Suppose we handle a two-dimensional (2d) image Q; the 2d-DWT [17] is worked out by processing row-wise and column-wise 1d-DWT in succession [15]. Initially, the 2d-DWT operates on the original image Q. Later, four SBs (Z1,O1,F1,A1) are generated, where the subscript i means i -th level decomposition. Tab. 2 itemizes the description of four SBs. Note here MDL means the maximum decomposition level.

Assuming h2d−DWT signifies a 2D-DWT decomposition operation, we deduce

(A1Z1O1F1)=h2d−DWT(Q). (10)

The subsequent decompositions run as:

(AmZmOmFm)=h2d−DWT(Am−1),m=2,…M, (11)

where M is the MDL and m the current decomposition level [18].

The subband A1 is further decomposed into four SBs (A2,Z2,O2,F2) at the 2nd level. The SB A2 is later decomposed to (A3,Z3,O3,F3) , and then SB A3 is decomposed accordingly. Fig. 3 portrays a diagram of 5-level 2d-DWT, whose pseudocode is represented in Algorithm 1. This study chooses a M -level decomposition. The optimal value of M is found via trial-and-error approach [19] and related in Section 4.1.

Figure 3: Diagram of a 2d-DWT (M=5)

The (3M+1) SBs (AM,ZM,OM,FM,ZM−1,OM−1,FM−1,…,Z1,O1,F1) may contain redundant features. Here we use the db4 wavelet. To decrease the number of features, we employ two-dimensional wavelet entropy (2d-WE) layer. The pseudocode of 2d-WE is illustrated in Algorithm 2. For each SB s in the generated (3M+1) SBs, we imagine s to be a random DV S with H quantization values (s1,s2,…,sh,…,sH) . In the beginning, we gauge the matching probability mass function (PMF) p(s)={ph(s)} .

ph(s)=hPr(S==sh),h=1,2,⋯H, (12)

where hPr signifies the probability function.

Second, the entropy of the PMF p(s) is calculated as fe(s) :

fe(s)=−∑h=1H⁡ph(s)×log⁡ph(s), (13)

where fe is the entropy function.

Lastly, the entropy values of the whole SBs are concatenated to grow a feature vector I.

I=[fe(AM)fe(ZM)fe(OM)fe(FM)fe(ZM−1)fe(OM−1)fe(FM−1)………fe(Z1)fe(O1)fe(F1)], (14)

where the number of the features in I is NI=(3M+1) , which equals the number of SBs.

3.3 ACP Network

The NI features are thrown into a feed-forward neural network (FNN)—in which its inner connections do not make a loop. One-hidden-layer FNN (OFNN), represented in Fig. 4, is established due to the universal approximation theory. Assume (x,t) stands for a training case as: x=[x1,x2,…,xi,…,xNI]T signifies the input feature vector with NI -dimension, i denotes the neuron index at the input layer, t is the corresponding target label t=[t1,t2,…,tk,…,tNO]T, where NO signifies the number of prediction categories and k the node index at the output layer. Assuming n is the case index and N the number of entire training cases, this study symbolizes the training case (x,t) as {x(n),t(n)|n=1,,…,N} . The training of the weights/biases (WBs) of OFNN is considered an optimization problem that minimizes the loss between the target t and the real output y. This study chooses the loss as the sum of the mean-squared error (MSE) E :

E=∑n=1N⁡∑k=1NO⁡[yk(n)−tk(n)]2. (15)

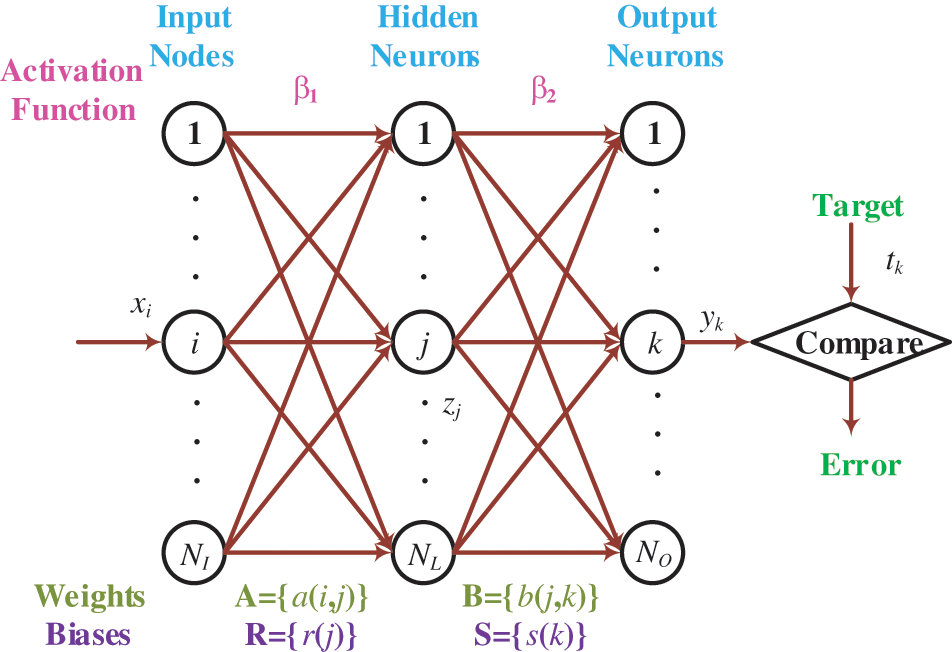
Figure 4: Diagram of an FNN

Assume β2 is the activation function (AF) in the output layer, and (B,S) are the WBs of neurons that connect the hidden layer (HL) to the output layer. B={b(j,k)},j=1,…,NL,k=1,…NO, and S={s(k)},k=1,…,NO. It is easy to reckon the output yk as

yk(n)=β2[∑j=1NL⁡b(j,k)zj(n)+s(k)], (16)

where zj(n),j=1,…,NH signifies the output of j -th neuron in the HL. The description of zj(n) is

zj(n)=β1[∑i=1NI⁡a(i,j)xi(n)+r(j)]. (17)

where A={a(i,j)},i=1,…,NI,j=1,…,NL and R={r(j)},j=1,…,NL are the WBs of the neurons that connect the input layer with the HL, and β1 the AF linked to the HL.

The parameter training is an optimization problem that guides us to search for the optimal WB parametric vector θ=(A,B,R,S) . The length of θ is the number of parameters we need to optimize and is calculated as Nθ=NI×NL+NL×NO+NL+NO . The training algorithm we choose is adaptive chaotic PSO (ACP) [14].

Recap that two attributes (position x and velocity v ) are linked with each particle p in the standard PSO algorithm. Those two attributes are defined as the position of the particle (PoP) and the velocity of the particle (VoP). In each epoch, the fitness function E is re-calculated for the entire particles {p} in the swarm. The VoP v is re-evaluated by keeping track of the two best positions (BPs).

The first is the BP a particle p has traversed till now. It is dubbed pBest and symbolized as xpB . The second is the BP that any neighbor of p has traversed till now. It is a neighborhood best and is named nBest and symbolized as xnB .

If p takes the entire swarm as its neighborhood, the nBest turns to the global best and is for that reason named gBest. In standard PSO, the VoP v of particle p is updated as:

v←ωv+b1r1(xPB−x)+b2r2(xnB−x) (18)

where ω signifies the inertia weight (IW) controlling the influence of the preceding velocity of the particle on its present one. b1 and b2 stand for two positive constants named acceleration coefficients. r1 and r2 mean two random numbers, uniformly distributed in the range of [0,1]. r1 and r2 are re-calculated whenever they occur. The PoP x of the particle p is updated as:

x←x+vΔt (19)

where Δt is the assumed time step and always equals 1 for simplicity.

The ACP algorithm proposed an adaptive IW factor (AIWF) strategy. It uses ωAIWF to replace ω .

ωAIWF=ωmax−ωmax−ωminkmax×k (20)

Here, ωmax signifies the maximum IW, ωmin the minimum IW, kmax the epoch once the IW goes to the final minimum IW, and k the present epoch.

Another improvement in ACP is upon the two random numbers (r1,r2) . In reality, (r1,r2) are created by pseudo-random number generators (RNG), which cannot guarantee the optimization’s ergodicity in solution space since they are pseudo-random. Rossler attractor (RA) is a good choice to calculate the random numbers (r1,r2) . RA equations are defined:

{dxdt=−(y+z)dydt=x+δay    dzdt=δb+xz−δcz, (21)

where δa , δb , and δc are inherent parameters of RA. We choose δa=0.2,δb=0.4,δc=5.7 via the trial-and-error method [20]. The corresponding curve is drawn in Fig. 5a.

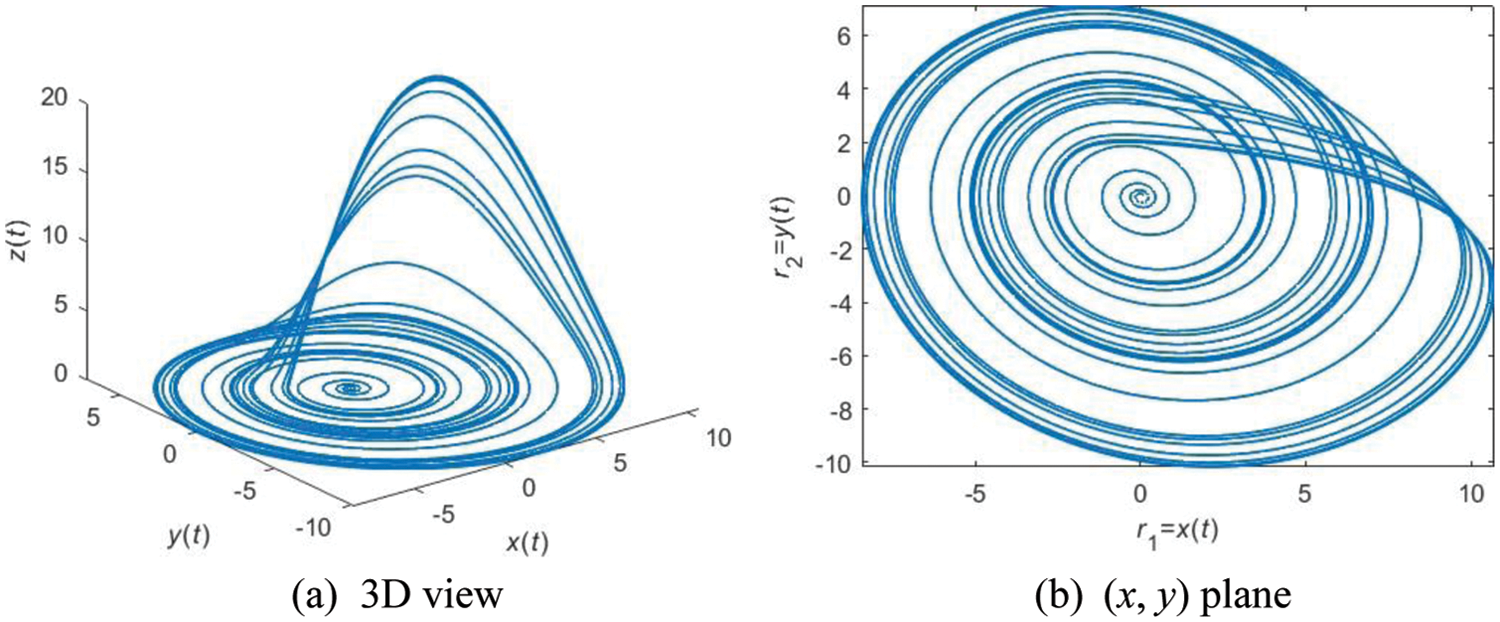
Figure 5: An example of RA with parameters of (δa = 0.2, δb = 0.4, δc = 5.7)

4  Experiments, Results, and Discussions

Ten runs of 10-fold cross-validation are used to relate a reliable performance of our WACPN model. Besides, we use the following measures—sensitivity (Sen, symbolized as η1 ), specificity (Spc, symbolized as η2 ), precision (Prc, symbolized as η3 ), accuracy (Acc, symbolized as η4 ), F1 score (symbolized as η5 ), Matthews correlation coefficient (MCC, symbolized as η6 ), Fowlkes–Mallows index (FMI, symbolized as η7 ), and the area under the curve (AUC)—to appraise the performances of different models.

4.1 Parameter Configuration

The parameters of this study are listed in Tab. 3. The sizes of the original images are 1024×1024 if we do not consider the number of color channels. The sizes of MTCed images are 624×624 , and the sizes of preprocessed images are 256×256 . The DCR is z1=48 , and the SSR is z2=97.92 . The MDL is M=4 . The number of features is NI=13 . The number of neurons in HL is NL=8 . The number of output neurons is NO=2 . The number of parameters to be optimized is Nθ=130 . The parameters in RA are δa=0.2,δb=0.4,δc=5.7 .

4.2 Wavelet Decomposition

Fig. 6 shows the wavelet decomposition results with M=4 . The raw image is shown in Fig. 2a. The reason why we choose M=4 is the trial-and-error method. We test other values of M and find M=4 can obtain the best result.

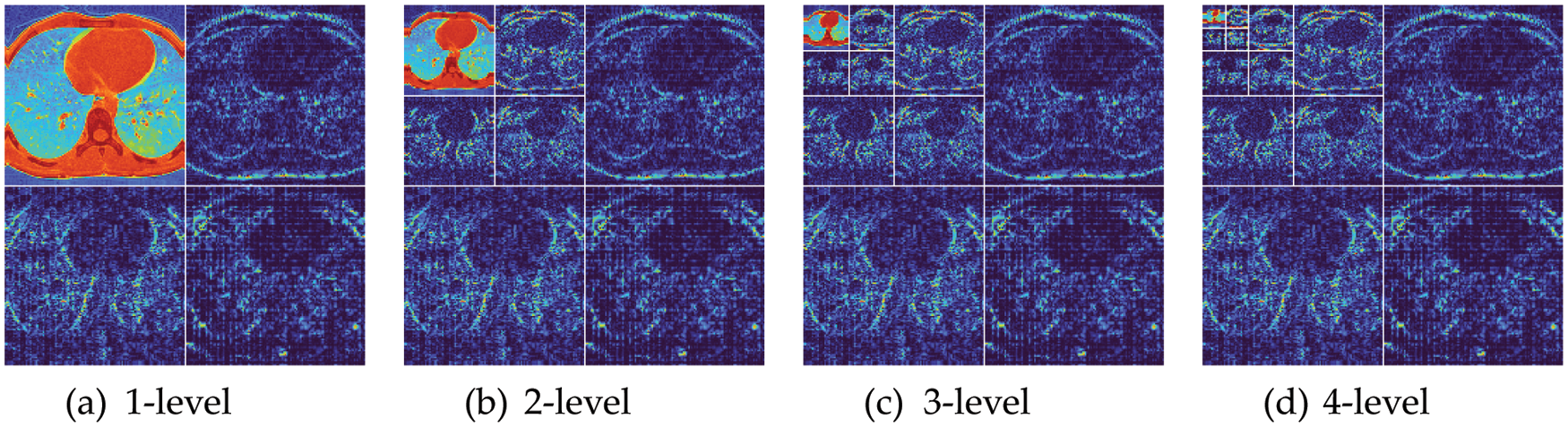
Figure 6: Wavelet decomposition results

4.3 Results of Proposed WACPN Model

Tab. 4 shows the ten runs of 10-fold CV via the parameters shown in Tab. 3, where pr=1,2.,..,10 means the run index. The final row in Tab. 4 presents the mean and standard deviation (MSD) of the results of 10 runs. WACPN attains a sensitivity of 91.87 ± 1.37%, a specificity of 90.70 ± 1.19%, a precision of 91.01 ± 1.12%, an accuracy of 91.29 ± 1.09%, an F1 score of 91.43 ± 1.09%, an MCC of 82.59 ± 2.19%, and an FMI of 91.44 ± 1.09%.

4.4 Effects of AIWF and RA

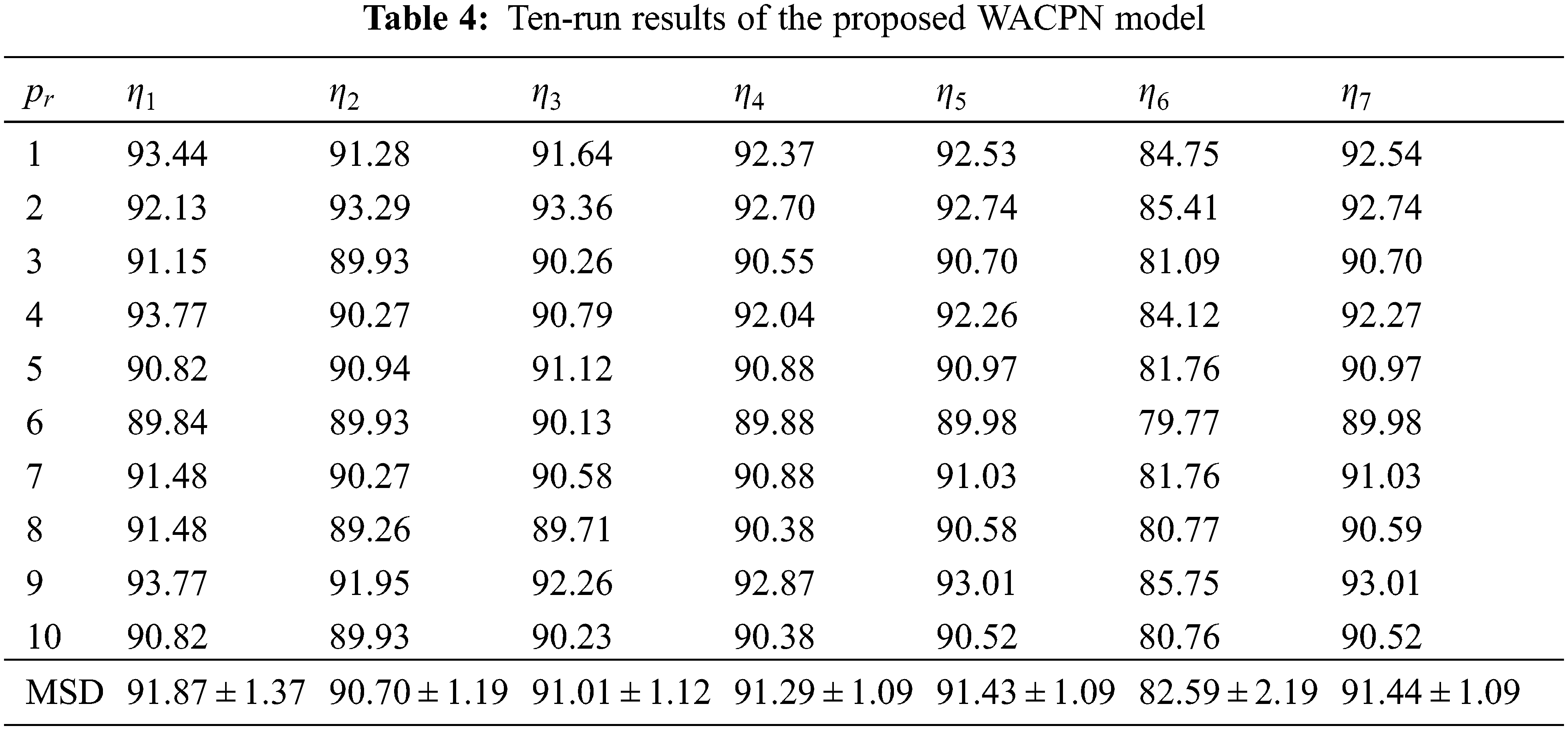
If we remove the AIWF from our WACPN model, the results using the same configuration are shown in Tab. 5. Similarly, the results of removing RA from our WACPN model are shown in Tab. 6. After comparing the results in Tab. 4 against the results in Tabs. 5 and 6, we can deduce that both strategies—AIWF and RA—are beneficial to our WACPN model.

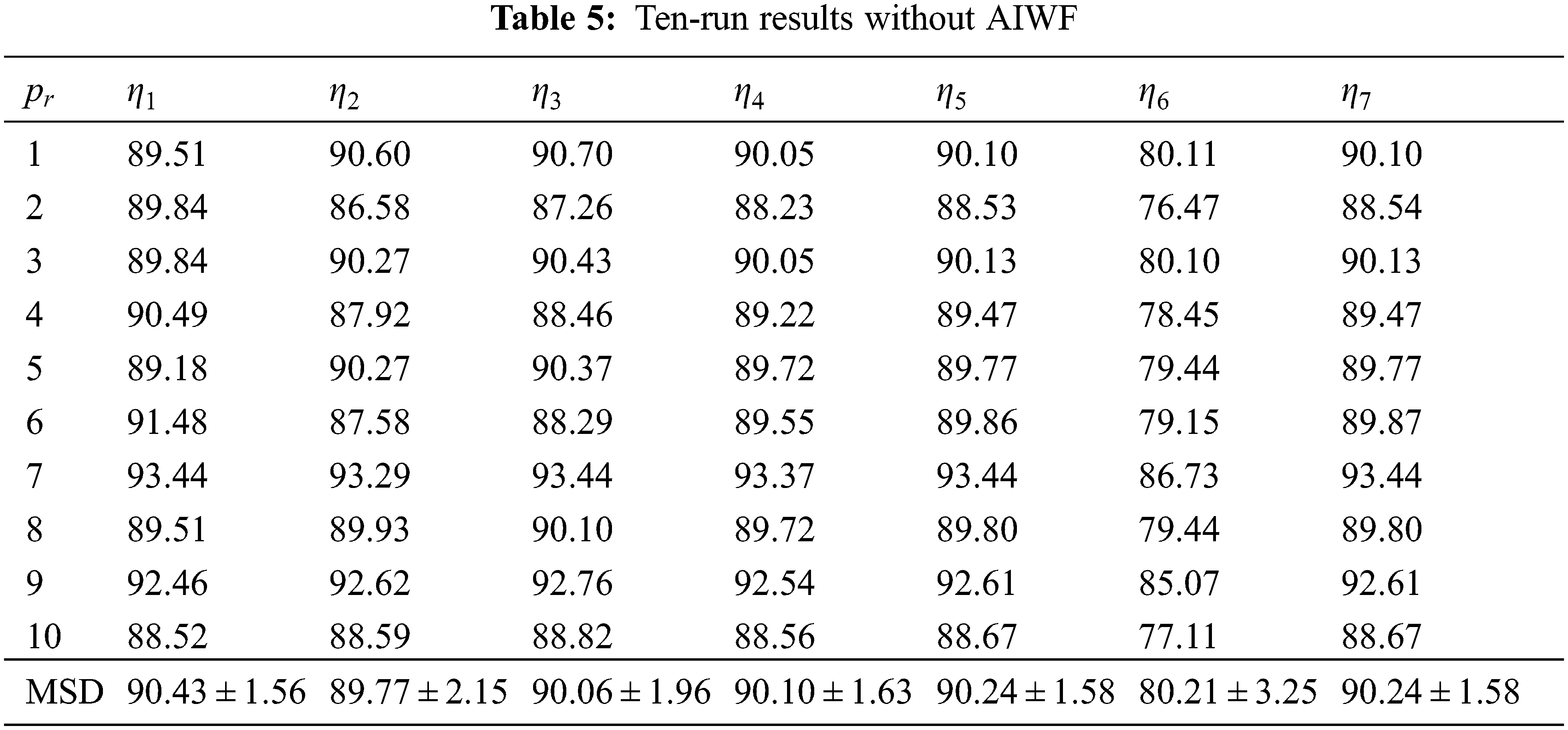
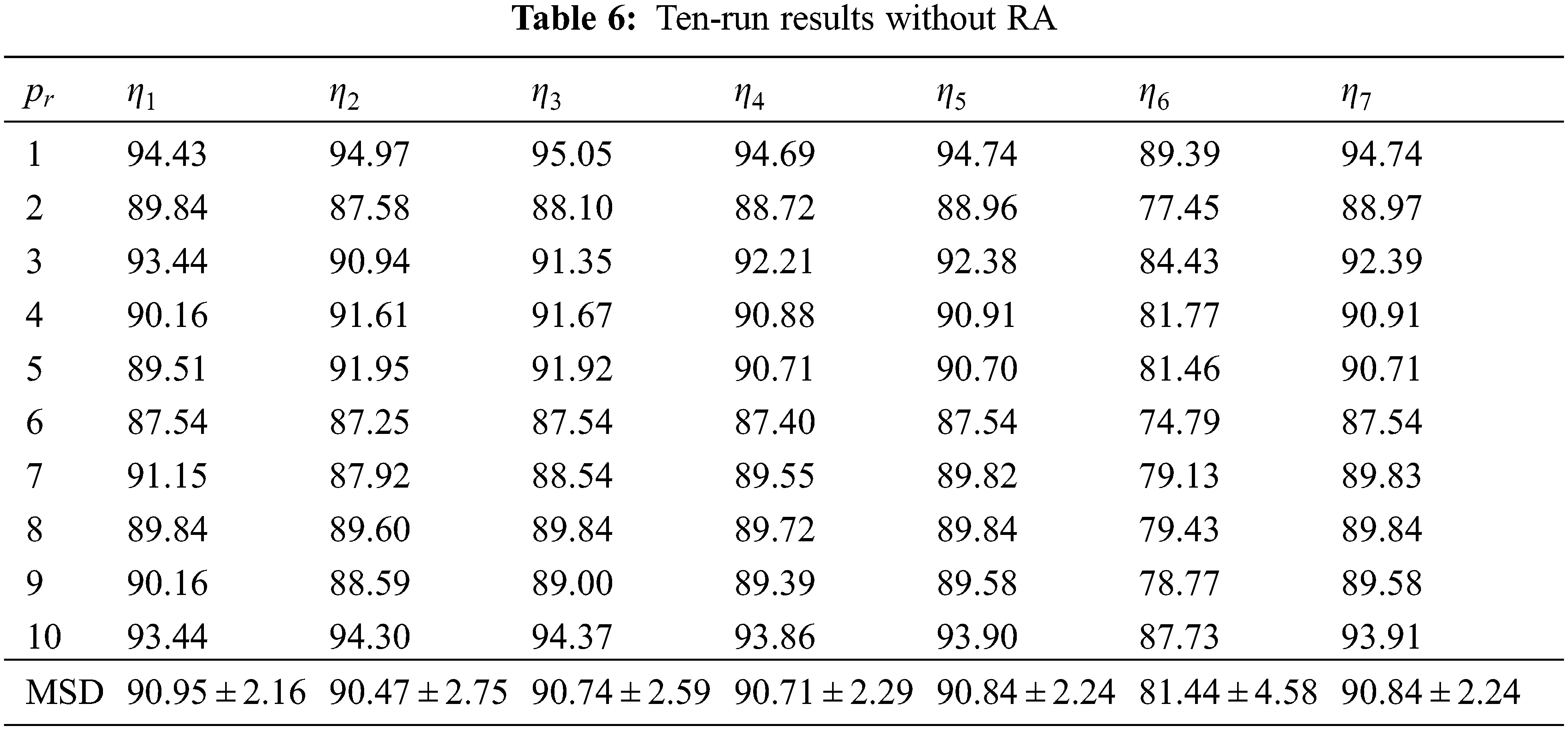
Fig. 7 represents the ROC curves together with their upper and lower bounds of the proposed WACPN model and its two ablation studies (without AIWF and without RA). The AUC of WACPN model is 0.9577. The AUCs of the models removing AIWF or RA are only 0.9319 and 0.9456, respectively, demonstrating that both AIWF and RA help improve the standard PSO.

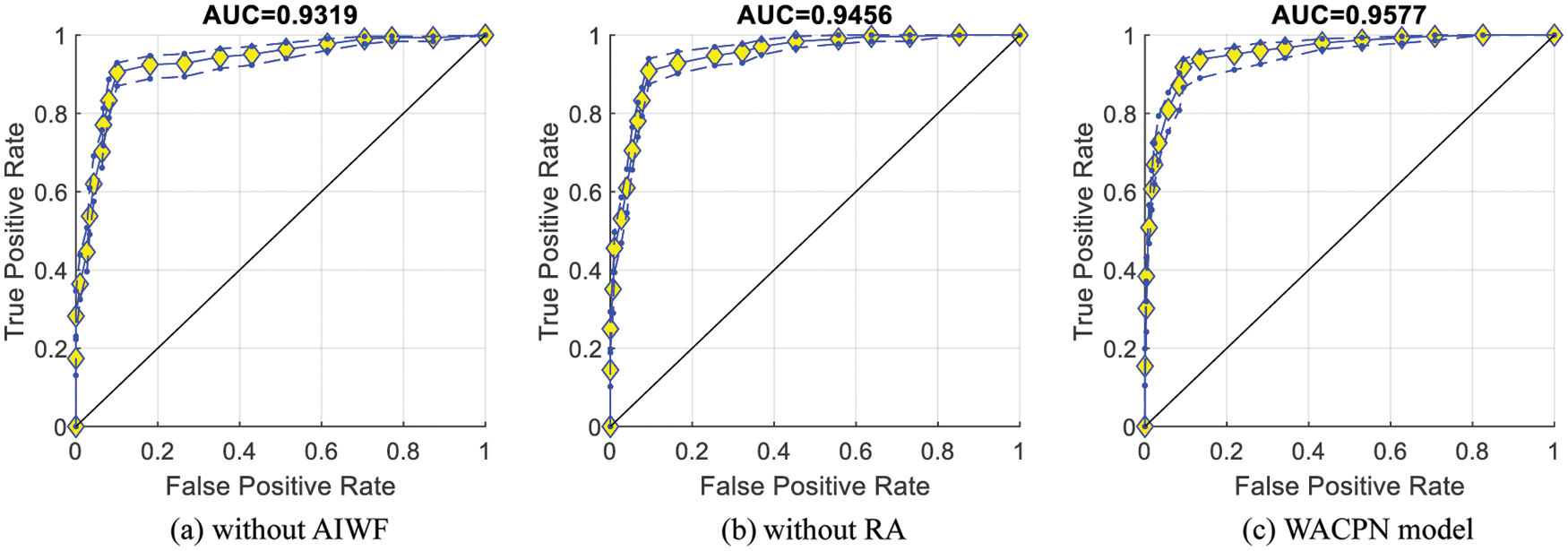
Figure 7: ROC curves

4.5 Comparison with State-of-the-Art Models

The proposed WACPN model is judged with six state-of-the-art models: GAN [4], CADe [5], SVM [6], IQNN [7], DT [8], and CSO [9]. The evaluation results on the same dataset via ten runs of 10-fold CV are listed in Tab. 7.

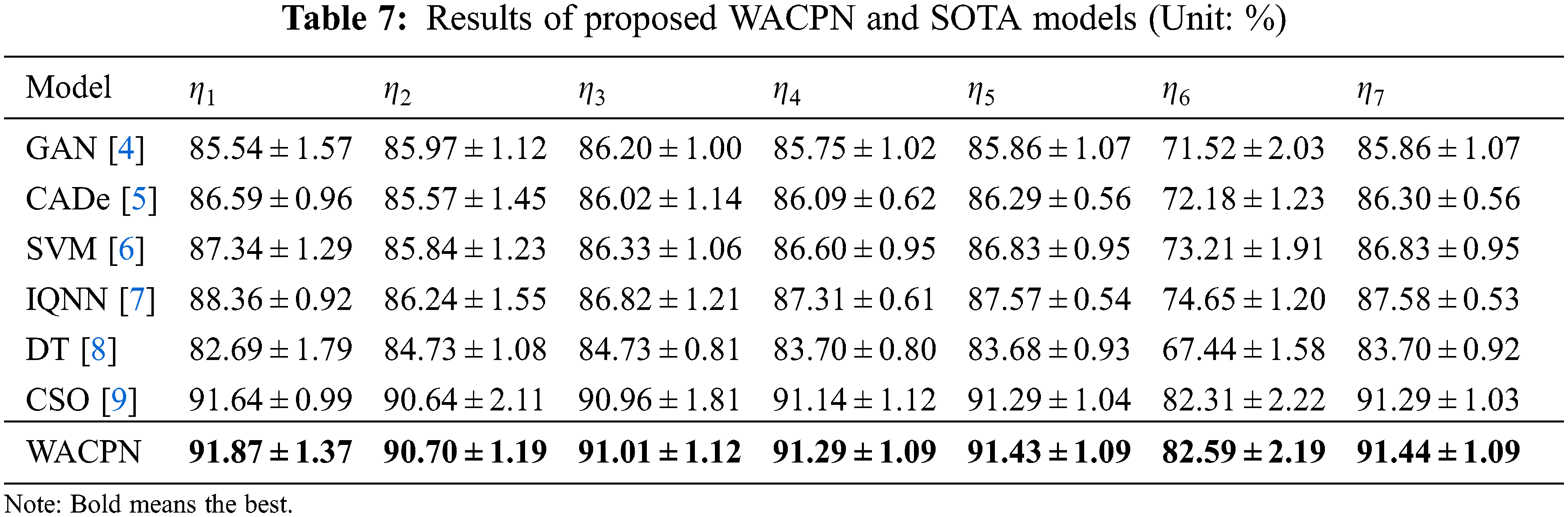
Error bar (EB) is an excellent tool for ease of visual evaluation. Fig. 8 presents the EB of model comparison, from which we can observe that the proposed WACPN model is superior to six state-of-the-art models. The causes are triple. First, the 2d-WE layer stands as a proficient way to designate CCT images. Second, ACP is efficient in training FNN. Third, we fine-tune and select the best parameters for the RA. In the future, our model may be applied to other fields [21,22].

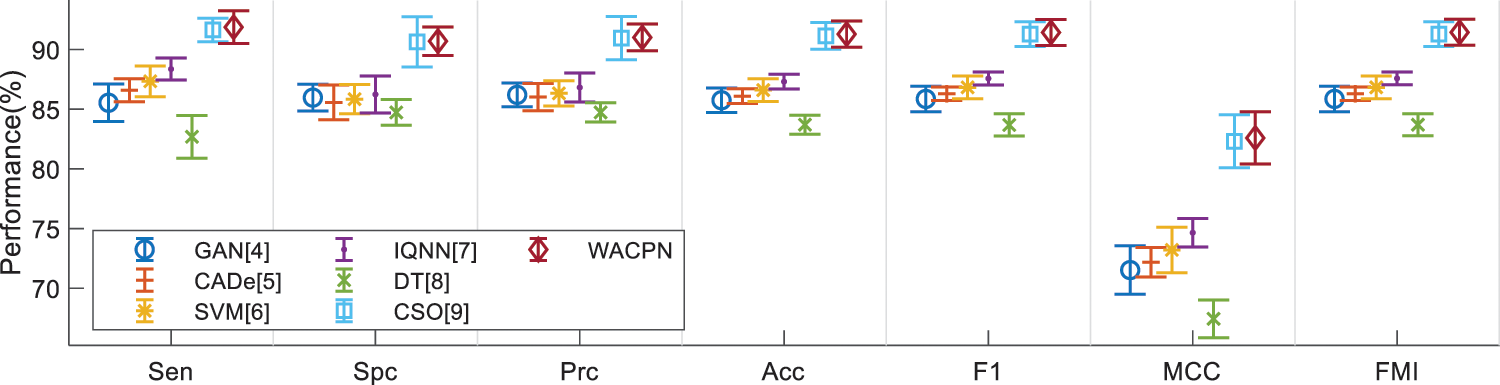
Figure 8: EB of model comparison

5  Conclusions

A novel WACPN method is proposed for diagnosing the CAP in CCT images. In WACPN, the 2d-WE layer works as feature extraction, and the optimization algorithm—ACP—is exercised to optimize the neural network. This proposed WACPN model is verified to have better results than six state-of-the-art models.

Three defects of the proposed WACPN model exist: (i) Deep learning models are not exercised. The reason is the small amount of our image set. (ii) Strict clinical validation is not tested either on-site or in cloud computing (CC) environments. (iii) The model is a black box, which does not go well with patients and doctors.

To work out the three limitations, first, we shall utilize the data augmentation method to enlarge the number of images in the dataset. Second, our team shall circulate the proposed WACPN model to the online CC environment (such as Azure) and summon specialists, clinicians, and physicians to examine its efficiency. Third, trustworthy or explainable Ais, which may provide the heatmaps pointing out the lesions, are two optional models to assist in adding explainability to the proposed WACPN model.

Funding Statement: This paper is partially supported by Medical Research Council Confidence in Concept Award, UK (MC_PC_17171); Royal Society International Exchanges Cost Share Award, UK (RP202G0230); British Heart Foundation Accelerator Award, UK (AA/18/3/34220); Hope Foundation for Cancer Research, UK (RM60G0680); Global Challenges Research Fund (GCRF), UK (P202PF11); Sino-UK Industrial Fund, UK (RP202G0289); LIAS Pioneering Partnerships award, UK (P202ED10); Data Science Enhancement Fund, UK (P202RE237).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Guarnieri, L. B. De Marchi, A. Marcon, S. Panunzi, V. Batani et al., “Relationship between hair shedding and systemic inflammation in covid-19 pneumonia,” Annals of Medicine, vol. 54, pp. 869–874, 2022. [Google Scholar]

 2.  J. E. Schneider and J. T. Cooper, “Cost impact analysis of novel host-response diagnostic for patients with community-acquired pneumonia in the emergency department,” Journal of Medical Economics, vol. 25, pp. 138–151, 2022. [Google Scholar]

 3.  M. T. Olsen, A. M. Dungu, C. K. Klarskov, A. K. Jensen, B. Lindegaard et al., “Glycemic variability assessed by continuous glucose monitoring in hospitalized patients with community-acquired pneumonia,” Bmc Pulmonary Medicine, vol. 22, Article ID: 83, 2022. [Google Scholar]

 4.  P. S. Heckerling, B. S. Gerber, T. G. Tape and R. S. Wigton, “Use of genetic algorithms for neural networks to predict community-acquired pneumonia,” Artificial Intelligence in Medicine, vol. 30, pp. 71–84, 2004. [Google Scholar]

 5.  X. L. Liu, F. Hou, H. Qin and A. M. Hao, “A cade system for nodule detection in thoracic ct images based on artificial neural network,” Science China-Information Sciences, vol. 60, pp. 15, Article ID: 072106, 2017. [Google Scholar]

 6.  A. Strehlitz, O. Goldmann, M. C. Pils, F. Pessler and E. Medina, “An interferon signature discriminates pneumococcal from staphylococcal pneumonia,” Frontiers in Immunology, vol. 9, Article ID: 1424, 2018. [Google Scholar]

 7.  Y. M. Dong, M. Q. Wu and J. L. Zhang, “Recognition of pneumonia image based on improved quantum neural network,” IEEE Access, vol. 8, pp. 224500–224512, 2020. [Google Scholar]

 8.  N. Ishimaru, S. Suzuki, T. Shimokawa, Y. Akashi, Y. Takeuchi et al., “Predicting mycoplasma pneumoniae and chlamydophila pneumoniae in community-acquired pneumonia (cap) pneumonia: Epidemiological study of respiratory tract infection using multiplex pcr assays,” Internal and Emergency Medicine, vol. 16, pp. 2129–2137, 2021. [Google Scholar]

 9.  J. Zhou, “Community-acquired pneumonia recognition by wavelet entropy and cat swarm optimization,” Mobile Networks and Applications, https://doi.org/10.1007/s11036-021-01897-0, 2022 (Online First). [Google Scholar]

10. W. Wang, Y. B. Jiang, Y. H. Luo, J. Li, X. Wang et al., “An advanced deep residual dense network (drdn) approach for image super-resolution,” International Journal of Computational Intelligence Systems, vol. 12, pp. 1592–1601, 2019. [Google Scholar]

11. W. Wang, H. Liu, J. Li, H. S. Nie and X. Wang, “Using cfw-net deep learning models for x-ray images to detect covid-19 patients,” International Journal of Computational Intelligence Systems, vol. 14, pp. 199–207, 2021. [Google Scholar]

12. K. Thirugnanasambandam, M. Rajeswari, D. Bhattacharyya and J. Y. Kim, “Directed artificial bee colony algorithm with revamped search strategy to solve global numerical optimization problems,” Automated Software Engineering, vol. 29, Article ID: 13, 2022. [Google Scholar]

13. W. Z. Al-Dyani, F. K. Ahmad and S. S. Kamaruddin, “Binary bat algorithm for text feature selection in news events detection model using markov clustering,” Cogent Engineering, vol. 9, Article ID: 2010923, 2022. [Google Scholar]

14. L. Wu, “Crop classification by forward neural network with adaptive chaotic particle swarm optimization,” Sensors, vol. 11, pp. 4721–4743, 2011. [Google Scholar]

15. M. Sahabuddin, M. F. Hassan, M. I. Tabash, M. A. Al-Omari, M. K. Alam et al., “Co-movement and causality dynamics linkages between conventional and islamic stock indexes in Bangladesh: A wavelet analysis,” Cogent Business & Management, vol. 9, Article ID: 2034233, 2022. [Google Scholar]

16. S. Kavitha, N. S. Bhuvaneswari, R. Senthilkumar and N. R. Shanker, “Magnetoresistance sensor-based rotor fault detection in induction motor using non-decimated wavelet and streaming data,” Automatika, vol. 63, pp. 525–541, 2022. [Google Scholar]

17. A. K. Gupta, C. Chakraborty and B. Gupta, “Secure transmission of eeg data using watermarking algorithm for the detection of epileptical seizures,” Traitement Du Signal, vol. 38, pp. 473–479, 2021. [Google Scholar]

18. A. Meenpal and S. Majumder, “Image content based secure reversible data hiding scheme using block scrambling and integer wavelet transform,” Sadhana-Academy Proceedings in Engineering Sciences, vol. 47, pp. 1–11, Article ID: 54, 2022. [Google Scholar]

19. O. Kammouh, M. W. A. Kok, M. Nogal, R. Binnekamp and A. R. M. Wolfert, “Mitc: Open-source software for construction project control and delay mitigation,” Softwarex, vol. 18, Article ID: 101023, 2022. [Google Scholar]

20. J. M. Malasoma and N. Malasoma, “Bistability and hidden attractors in the paradigmatic rossler'76 system,” Chaos, vol. 30, Article ID: 123144, 2020. [Google Scholar]

21. X. R. Zhang, X. Sun, W. Sun, T. Xu, P. P. Wang et al., “Deformation expression of soft tissue based on bp neural network,” Intelligent Automation and Soft Computing, vol. 32, pp. 1041–1053, 2022. [Google Scholar]

22. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Cmc-Computers Materials & Continua, vol. 71, pp. 3035–3050, 2022. [Google Scholar]