Multi-Agent Dynamic Area Coverage Based on Reinforcement Learning with Connected Agents

1  Introduction

1.1 Background, Definition and Motivation

Due to the size and complexity of the problems, a system can be designed through processes run by more than one subsystem in a coordinated, interactive, dependent, or independent manner. In this context, unmanned aerial vehicles (UAVs) have a great opportunity to design a complex system in unstructured environments such as search and rescue [1], target tracking [2], and environment mapping [3]. Small, lightweight, low-cost platforms can incorporate many types of sensors adapted to detect targets in outdoor environments. However, due to limited endurance, low computing power, and limited detection, UAVs can be configured as a team (multi-UAVs), which has multi-agent coordination algorithms, to perform missions in a scalable, reliable, and robust manner [4]. In this regard, using UAVs as mobile nodes is a way to compose easy-to-deploy, time-efficient, and flexible communication systems. For multi-UAV applications used as mobile nodes, deployment strategies of UAVs should supply optimal coverage with minimal energy consumption [5]. The deployment strategies for optimal area coverage can be classified into two categories: (1) static strategies, (2) dynamic strategies. Unlike static strategies, dynamic strategies enable adaptivity to the environment [6]. Thus, dynamic strategies are preferred by researchers to guide autonomously performing UAVs for optimal area coverage [7]. The dynamic strategies are classified into behavior-based methods and automated design methods.

In behavior-based methods, the individual behavior of each agent is practiced iteratively until the desired collective behavior is achieved [8]. Agents perform predefined behaviors, such as avoiding obstacles, moving to a target, and keeping formation. Behavior-based methods for dynamic area coverage problems are decomposed as grid-based, and optimization approaches.

1.2 Literature Review

Grid-based approaches [9–18] mainly divide the area into sub-areas to solve dynamic area coverage problems. In [9], Choset presented a strategy dividing the space into cell regions covered with back-and-forth motions. Cell decomposition methods can be applied to a system that is coordinated with a central controller. It is applicable to multi-UAV systems in that each UAV gets information from the others or has direct access to others’ observations. Studies in [10–12] use multiple vehicles that focused on partitioning the area into sub-areas and then each sub-area assigned to a vehicle. Cho et al. [13] proposed a method which creates a search path to cover an area. A mixed-integer linear programming (MILP) model has been used to determine a coverage path planning for visiting all generated nodes in the shortest amount of time. Voronoi partitions have been used for optimum area coverage task [14–16]. The connection is established on a cell which is selected by a closest-point search on decomposed area. In [17], the area coverage problem was adopted to multiple traveling salesman (MTSP) problem that multiple UAVs have been assigned to the decomposed target area. While distributing the cells in grid-based methods, the distance between UAV and cell, area to be covered and energy consumption should be taken into consideration [18]. Grid-based methods are suitable for fully observable environments or systems that have a centralized controller or decision-maker. Consequently, it is difficult to apply them to complex and continuous environments.

The studies [19–23] that considered area coverage problem as an optimization problem proposed swarm intelligence (SI) as a solution. In [19,20], agents move through the pheromones left by robots acting like ants to cover the target area. Tao et al. [21] proposed an algorithm based on Artificial Fish Swarm (AFS) for optimizing the area coverage by setting optimal sensing directions of directional sensors. In [22], the meta-heuristic Artificial Bee Colony (ABC) algorithm with Binary Detection Model and Probabilistic Detection Model has been applied for dynamic deployment of wireless sensor networks (WSNs). Multi-Objective Particle Optimization (MPSO) algorithm has been used to discover the best location for energy efficiency [23], which evaluates the area coverage problem by optimizing the network coverage rate. Sequential Quadratic Programming (SQP) algorithms have been applied to optimal placement for UAVs guided by a leader [24]. Virtual Force (VF) algorithms and techniques have been employed for the formation and placement of mobile sensors [25,26]. Traditional optimization methods and learning-based intelligent optimization algorithms (LIOAs) [27] can be applied to distributed systems optimizing the actions of each UAV in the multi-agent system (MAS). However, there is no certain illustration of the MAS behavior [28]. Therefore, it can be difficult to place the UAVs to optimum location for dynamic area with maximal coverage.

Automated design methods are successfully applied to develop multi-agent systems [29,30]. Multi-agent systems implemented with automated design methods are divided into two sub-categories: reinforcement learning (RL) [31] and evolutionary algorithms [32]. Evolutionary strategy (ES) is an automatic design method that applies evolutionary computational techniques to single and multi-agent systems [33]. In the ES method, a population of individual behavior is randomly generated [34]. At each iteration, a series of experiments are performed for each individual behavior. The same individual behavior is used by all agents in the experiment. In each experiment, a fitness function is used to evaluate the collaborative behavior of the agents resulting from this individual behavior. At this point, the selection of the highest scoring individual behavior, such as crossover and mutation, are modified by genetic operators and used for subsequent iterations. In RL, an agent learns behavior through interactions with an environment by receiving positive and negative feedback for each action. For systems developed with multi-agent reinforcement learning (MARL), the task is handled at the collective level, but learning is usually handled at the individual level. It is advantageous for a multi-agent system because of the low calculation cost for real-time operations. Usually, negative, or sub-optimal solution information is discarded in evolutionary algorithms, but a RL agent learns both positive and negative actions [35]. It is also advantageous because of the ability to adapt to the dynamic environment for multi-agent systems. Although RL is widely used in many areas, there are not many studies applied to dynamic area coverage with multi-agent systems. The main reason is that it is difficult for the individual learning ability to adapt to collaborative learning in distributed systems. Using a joint learning strategy helps to improve the performance and reliability of systems using data in different fragments [36]. As a solution, Xiao et al. [37] proposed an algorithm for dynamic area coverage with path planning problems based on Q-learning. In [38], trajectory planning with multi-vehicle was studied using Q-learning as well. While the previous methods that applied Q-learning algorithm focused on path planning challenges, we investigate maximizing covered area using UAVs. Moreover, we use an actor-critic method to avoid disadvantages from Q-learning, because an exploration strategy is not specified in Q-learning so that agents should try all possible actions for any state [39]. It causes quite substantially in policy space even though the estimated value is slightly changed [40]. In [41], the coverage of the point of interest (PoI) was investigated based on MARL with connectivity constraints that use the Laplacian matrix to build an undirected graph. Liu et al. [42] suggested an energy-efficient UAV control algorithm based on deep reinforcement learning (DRL) algorithm for area coverage with connectivity constraint, and it is a type of actor-critic RL method based on the deep deterministic policy gradient (DDPG). The algorithm, which is called DRL-EC3, uses one actor-critic network to maximize coverage score, while considering communication coverage, minimum energy consumption, and fairness with maintaining connectivity between UAVs. Liu et al. [43] designed a DRL method for maximizing coverage by a group of UAVs in a decentralized way (D-DRL). The method aims to increase fairness of targeted PoIs while consuming minimum energy with connected UAVs. They modelled each UAV as an agent using DNNs according to the action space, state, reward, and observation. In [44], a novel decentralized decision algorithm for the placement of UAVs in the target area was researched to maximize the coverage score in an energy-efficient way with high fairness. The algorithm, which is called state-based game with actor–critic (SBG-AC), is a type of actor-critic RL method using a state-based potential game. For the coverage problem, it aims to provide a distributed decision capabilities with minimum interactions to a group of UAVs. Pham et al. [45] proposed an algorithm based on Q-learning to maximize full coverage using homogeneous UAVs which have the same action and state spaces. Q-function is decomposed using the approximation techniques Fixed Sparse Representation (FSR) and Radial Basis Function (RBF). The fully distributed behavior cannot be obtained because of the decomposition technique since the joint state and action spaces orient the functions. The proposed methods based on actor-critic RL methods aim to improve fairness of targeted PoIs with connected UAVs in fully observable environment. Our suggested method aims to determine the optimum location of UAVs to get maximal area coverage on the target area. In addition to that, as real applications, we use a partially observable environment for simulations.

1.3 Contribution of the Paper

Even though these works mentioned in literature review section are effective for optimal area coverage, there are still gaps for improvements since the environment and characteristics of agent changes in MAS pose another kind of challenge. While working on the area coverage method, it can be considered that UAVs may become inoperable due to environmental conditions or hardware failures. With this assumption, the solution of the positioning problem, which will be performed adaptively and independently of the central orientation, becomes more complex according to the changing number of UAVs. Moreover, situations such as an interruption in communication between agents and/or base station, unexpected hardware and software failures of agents make the MAS weak are needed to be handled in a more sophisticated manner. Such cases can occur often in practical applications. In this respect, agents mounted intelligent behavior with high tolerance for failures can deal with a continuous task. In this connection, we studied such challenges concerning optimal area coverage: model-free policy to adapt to an unknown environment, decentralized execution to increase robustness, connection strategy, independent of the number of agents to keep reliable area coverage process.

In this paper, for the effective area coverage, we propose a method for MAS named decentralized decision-making dynamic area coverage (DDMDAC) based on the Multi-agent Deep Deterministic Policy Gradient (MADDPG) algorithm [46]. DDMDAC consists of decentralized UAV agents, which primarily rely on learning with a centralized critic at training-time, and then apply learned policies at execution-time. The UAVs motivated with decentralized decision-making capabilities increase the distance between each other without going beyond their communication distance to obtain maximal coverage. In this way, uncovered areas would be minimized, and resources can be used efficiently. It is assumed that the MAS is an undirected connected graph that includes UAVs as vertices. UAV vertices ask their neighbors, which vertices they are neighbors with. This process continues recursively until there are no vertices left or loops to the same vertices occur. Therefore, a UAV vertex will have a list of reachable UAVs. At each step, the UAV merges overlaps of every reachable UAV and then calculates the rate of the total overlapped area on the target area. Thus, the main idea of the DDMDAC is to construct a model-free MAS motion model to place the undirected graph into the target area with maintaining the connectivity of UAVs. In this way, not only a UAV vertex learns to increase the number of reachable vertices but also learns to determine optimal positions in an interactive manner with the vertices in contact with it.

The main contributions of the proposed method can be summarized as follows:

(1)An area coverage method with model-free policy based on MARL is proposed to provide maximal area coverage. The model-free policy is represented independently of the value function using a separate memory structure that allows agents to select an action time-efficiently with minimal computation cost.

(2)We present a decentralized-execution scheme that each agent, which considers actions of agents nearby it, learns through rewarding desired collaborative behavior and punishing undesired ones based on online training process and executes without the need for a central controller.

(3)A connected agent strategy based on the number of agents available in the target area is proposed and used to keep reliable area coverage process.

(4)We propose a reward structure based on agent-specific and collective reward for arranging agents’ location to improve coverage performance.

1.4 Organization of the Paper

The rest of this paper is organized as follows. In Section 2, we describe the proposed method, present the MAS model for dynamic area coverage problems. Section 3 describes the experiments and simulation results. Section 4 presents our conclusions and discusses possible directions for future research.

2  Problem Formulation

In this section, we describe the system framework, give brief definition of MADDPG, build a multi-agent system model based on MADDPG, and then outline details of connected graph with UAV vertices. Finally, we provide a detailed overview and the pseudo-code of DDMDAC.

2.1 System Framework

In the MAS, each UAV is represented by an agent. Agents can take action out of the five possible actions: north, west, south, east, or stay in the current state.

As shown in Fig. 1, an agent can go out or enter the area of influence of the group after moving at each timestep. In the MAS, the proposed method guaranties the continuity of network communication with moving agents.

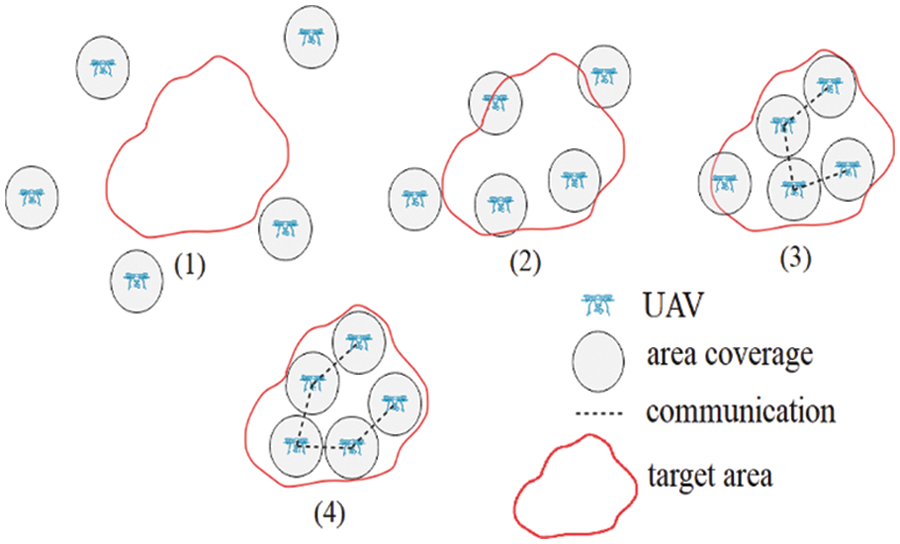
Figure 1: The MAS motion model

Agents with mobile and limited coverage capabilities adjust their positions according to environmental conditions and other agents’ locations. This concept enables us to build a connected undirected agent graph (Fig. 2).

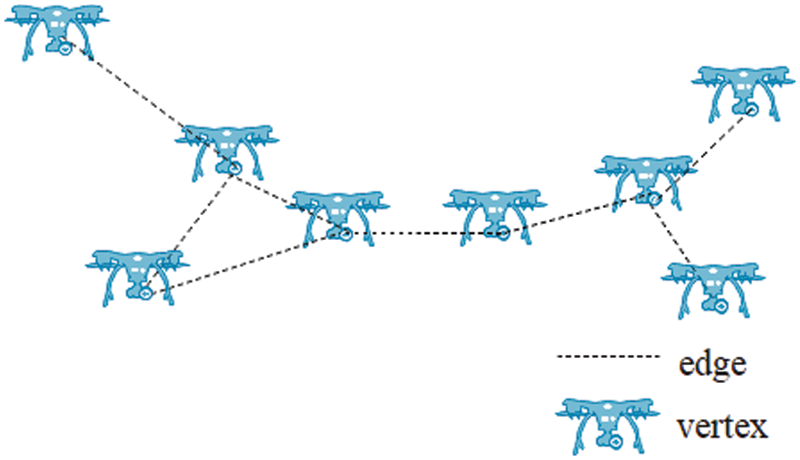
Figure 2: Connected undirected agent graph

Assumption 1: It is assumed that each agent knows its location. The proposed method uses geographical approach to be able to reach target area, explore other agents in target area, and connect agents within communication range to share information.

An agent in the MAS is represented by Ai such that Ai∈A for all i=1,...,N . At the time t , the location of the agent is defined as (xiA(t),yiA(t)).

GN={(x1A(t),y1A(t)),(x2A(t),y2A(t)),...,(xmA(t),ymA(t))} (1)

where GN denotes the set of all agents.

Assumption 2: We assume that the homogenous agents are randomly deployed in a 2 dimensions (2D) region of interest. The altitude of an agent is not considered within constraints.

We represent the distance dij between Ai and Aj by |AiAj| . GiC is the set of the connected agents with Ai , GiC⊆GN , and Eq. (2) is needed to satisfy that Ai and Aj are connected.

|(xiA(t),yiA(t)),(xjA(t),yjA(t))|≤dij (2)

Assumption 3: It is assumed that each agent creates a same size circle sensing region using communication range.

We use Depth-First-Search (DFS) algorithm to get connected agents [32]. In DFS, it is explored throughout each edge before backtracking. The pseudo-code for DFS is given in Algorithm 1.

Agents take the union of the covered area of reachable agents, which they are connected at each step. The formula for the calculation of the process π is defined as:

π[i]=x∈⋃M⇔∃U∈M,x∈U, (3)

M={c(A1),c(A2),...,c(AM)},A∈GiC (4)

where c(Ai) denotes the covered area by the agent i in the target area. Moreover, at each step, each agent modifies its knowledge (covered area) with all agents with which it can reach. Therefore, the process becomes a sequence of the sub-process π[i...L]={π[1],π[2],...,π[L]} such that L∈{1,...,N} for all AL∈GiC . Finally, for the agent i , we define the total area coverage as follows:

πiL=⋃π[i...L] (5)

The goal of the DDMDAC is to maximize the intersection of the target area and the covered area of MAS:

z=T⋂π (6)

where T denotes the target area. In addition, it is needed each agent to organize its next position to avoid collisions. To achieve that the agent receives less reward whereas the distance between an agent and another is less than the sum of their radius f .

pi=∏jw(ij),j∈{1,...,N} forallAj∈GiC (7)

w(ij)={1,fi+fj≤dijγr,fi+fj>dij (8)

where γr denotes the area coverage discount factor for collision. The reward function for coverage rate is defined as follows:

ri=1μ(T)pi∗μ(z)∗100 (9)

where μ(t) is used to calculate the area of t .

2.2 MADDPG Method

Using RL methods, which allows for learning and navigate the changing environment, is a good approach to overcome the area coverage problem. The RL agent reacts to the environments it encounters and receives a numerical reward signal in return. The agent works to maximize the reward signals it receives. This process is called the Markov Decision Process (MDP). The MDP process is mainly designed for single-agent systems. In classical MDPs, it is assumed that an agent has direct access to the system state. In Partially Observable MDPs (POMDPs), the system state is estimated by the agent via local observations and history of actions. If the agent is more than one, this process is called Multi-agent MDP (MMDP).

Decentralized POMDPs (Dec-POMDPs) are used for multi-agents to create collaborative behaviors like MMDP. However, in Dec-POMDPs, each agent has local observations of the environment and system status. Since the agent cannot access the observations of other agents, an agent does not have enough information to decide on the whole system. In Dec-POMDPs, super-exponential time is needed to solve the worst case. For this reason, the proposed method is based on MADDPG algorithm, which has the central learning with the decentralized-execution scheme.

MADDPG is a multi-agent learning algorithm that extends DDPG, which is a type of simple actor-critic policy gradient method, where the critic network uses joint actions executed by agents, while the actor-network uses a single state action executed by an agent via local observations.

Training experiences are stored in a replay buffer to be used by the critic network to improve the performance of actions in the training time. Centralized module is not used during execution time. It is expected that the proper information is taken from centralized module to guide local policy training.

2.3 MAS Model Based On MADDPG

We construct the MAS model to solve the complexity of cooperation between UAVs. In this model, each agent stands for a UAV, which has the same motion model as a real UAV.

The agent policy is represented by μ and the parameter of the policy θ is directly adjusted by single-agent Policy Gradient methods. In our MAS model deployed with N agents, the transition μ={μ1,μ2,...,μN,} is used for the set of agents’ policies parameterized by θ={θ1,θ2,...θN} . Also, the MAS model uses a replay buffer for off-policy training. The agent stores the tuples (x,x′,a1,...,aN,r1,...,rN) at each step where x,x′,a and r denote the joint state, next joint state, joint action, and rewards received by each agent respectively. Then, a series of tuples is sampled from the replay buffer to train the agent. To update an agent’s centralized critic using the sampled tuples, the model learns an approximation of the optimum action-value function by minimizing the loss. The loss function using sampled temporal difference error (TD-error) is defined as the following:

L(θi)=1S∑j(yj−Qiμ(xj,a1j,...,aNj))2,y=ri+γQiμ′(x′,a1′,...,aN′)|aj′=μj′(oj) (10)

where a′,γ,S,o and Qiμ denote the next joint action, discount factor, the size of random samples from the replay buffer, partial observations of the environment, and centralized action-value function respectively.

The sampled policy gradient for updating actor is defined as follows:

∇θiJ≈1S∑j∇θiμi(oji)∇aiQiμ(xj,aji,...,aNj)|ai=μi(oij) (11)

For agent i , Q -value is obtained as output using Qiμ that uses as input the set of each agent action with the state.

2.4 The MAS With UAV Vertices

We design a reward structure to find the optimum locations and to avoid collisions. An agent represents a moving vertex, which seeks to connect any agent within communication distance. Each agent observes the location and area coverage information of the agents connected after each step. Thus, each agent indirectly has a list of agents that it can reach. The greater the area coverage of reachable agents overlaps the target area, the greater reward it gets. The pseudo-code of reward is given in Algorithm 2.

Note that increasing the number of connected agents may not be sufficient to increase the total coverage. There can be many common areas covered by agents close to each other.

2.5 MADDPG Construction Of DDMDAC

DDMDAC is a dynamic-area coverage method consisting of training layer and execution layer. In the training layer, the reward structure is used for policy training according to actions. Each agent has only local observations within its coverage, and it can communicate with any other agent within communication distance to share its state. A policy is learned to determine optimum placement in a fully decentralized manner by each agent. Moreover, it can change its position with actions using shared states. Furthermore, the experience of the MAS is handled at the collaborative level.

Inspired by [47], we use fight-or-flight response approach for ad-hoc strategies, where fighting leads to moving towards to target, which flight are about moving away from collision. An agent gets a positive reward while connecting and increasing the covered area on target area. On the other hand, a negative reward is taken when an agent is too close to another. Thus, each agent aims to get a positive reward being in desired distance to others and avoids getting a negative reward being in too close to others.

The designed reward structure as shown in Algorithm 2 enforces collective behavior and thus, there is no need to share an explicit reward. Inspired by [48], merging an agent’s overlap with connected agents overlaps represents local attention (agent-specific) and global attention (collective) respectively. Placement of agents on the target area depends on this collective reward. This approach eliminates the need to consider shared reward, e.g., taking average of rewards of all agents. Therefore, agents are affected by the reward function shared by their own share.

The proposed method learns from experience using replay buffer due to model-free design. The centralized module guides the agents on how to update their policies during training time. The training process is divided into episodes, and at the beginning of each episode, the agents’ state will be re-initialized. In training process, agents store the tuple consist of action, state, and reward to replay buffer. At each time step, sample a minibatch taken from replay buffer, and then actors are modified policy gradient using Eq. (11), while critics are modified using Eq. (10). Each agent should determine the optimum joint action to increase the area coverage. Then, the agents will evaluate their performance based on the reward structure. The pseudo-code of DDMAC is given in Algorithm 3.

The centralized module is removed during execution time. In execution process, actor network is used for an action because of its local observation capabilities. Agents aim that it has been taken enough information to guide policy training.

3  Experiment

We designed an environment for the simulation process based on the multi-agent actor-critic platform implemented by OpenAI team [35]. For the area coverage process, the designed environment interaction with the DDMDAC framework is shown as Fig. 3.

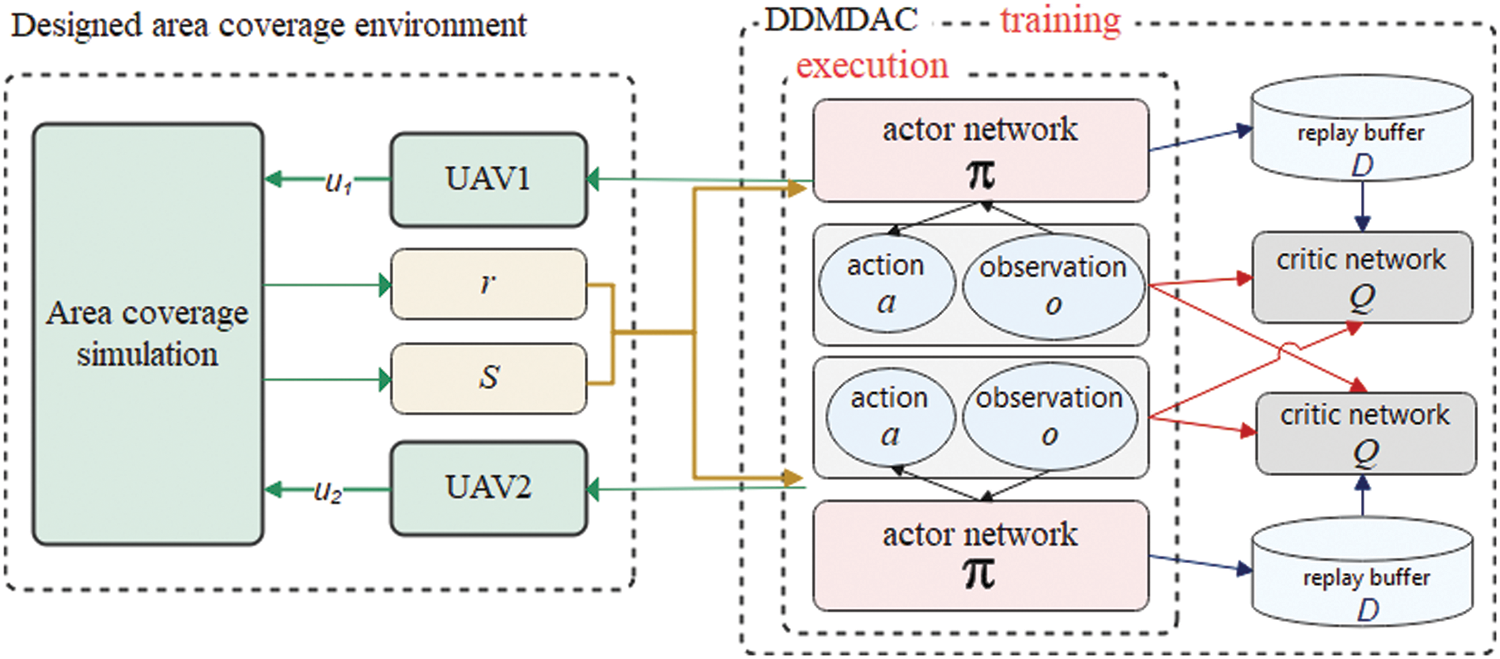
Figure 3: The overall framework of area coverage process

In this section, we present the environment setting together with the training process, and then discuss results of the simulations.

3.1 Environment Settings

The simulation environment is a coordinate plane in which each quadrant is set up as 1 unit while geometric center is the origin. The plane consists of agents and a target area which is constructed according to training settings. A circle around the agent is used to represent area coverage. In addition, an agent is represented by node in the simulation environment. Communication distance, coverage circle radius, and shape of the target area are set at the beginning of the training episode. Within the coverage radius, the agent can observe the local environment while the agent can communicate with any other agent in the communication distance. The target area can be any free shape. At each training episode, the agents’ locations, and the location of the target area are randomly generated.

3.2 Training Process

In the DDMDAC, collaborative reward is shared by the agents. For agents that can be reached in the target area, the reward is affected negatively by collision and positively by coverage. As shown in Fig. 4, overlaps are merged to get collaborative reward where the green area represents the covered area. It is assumed that the agents are identical.

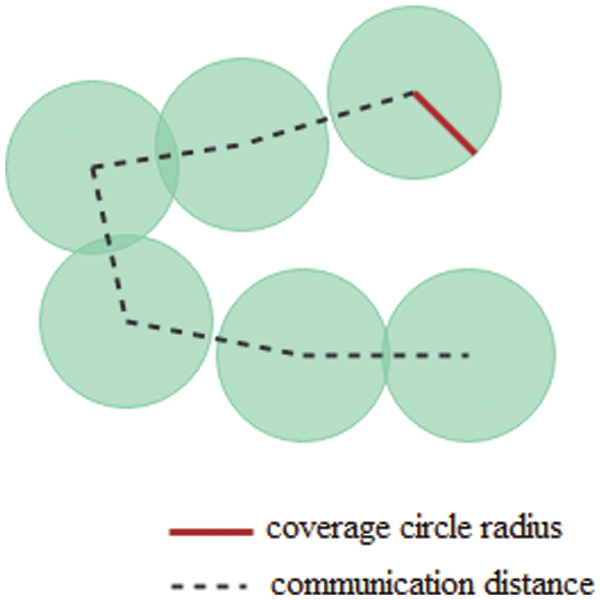
Figure 4: Merged overlaps for collaborative reward

For training, we set the number of episodes to 10000 and in each episode, an agent can take 150 actions. The average results of the training in each episode are used to evaluate performance. The number of samples that will be propagated through (batch size) network is defined as 1024. Other parameters are defined as follows: the number of units in the multilayer perceptron (MLP) is 64, the discount factor is 0.95, and the learning rate is 0.01.

At the end of each training step, the reward is calculated according to the coverage rate on the target area. In addition, for each collision, the reward is reduced by 1 percent (area coverage discount factor).

3.3 Experimental Results

In experiment 1, as shown in Fig. 5, we obtain the area coverage of the environment by changing the number of agents from 4 to 8. The coverage circle radius of each agent and the communication range are 0.12 and 0.5 units, respectively, while the target area is set as 0.5 × 1 units.

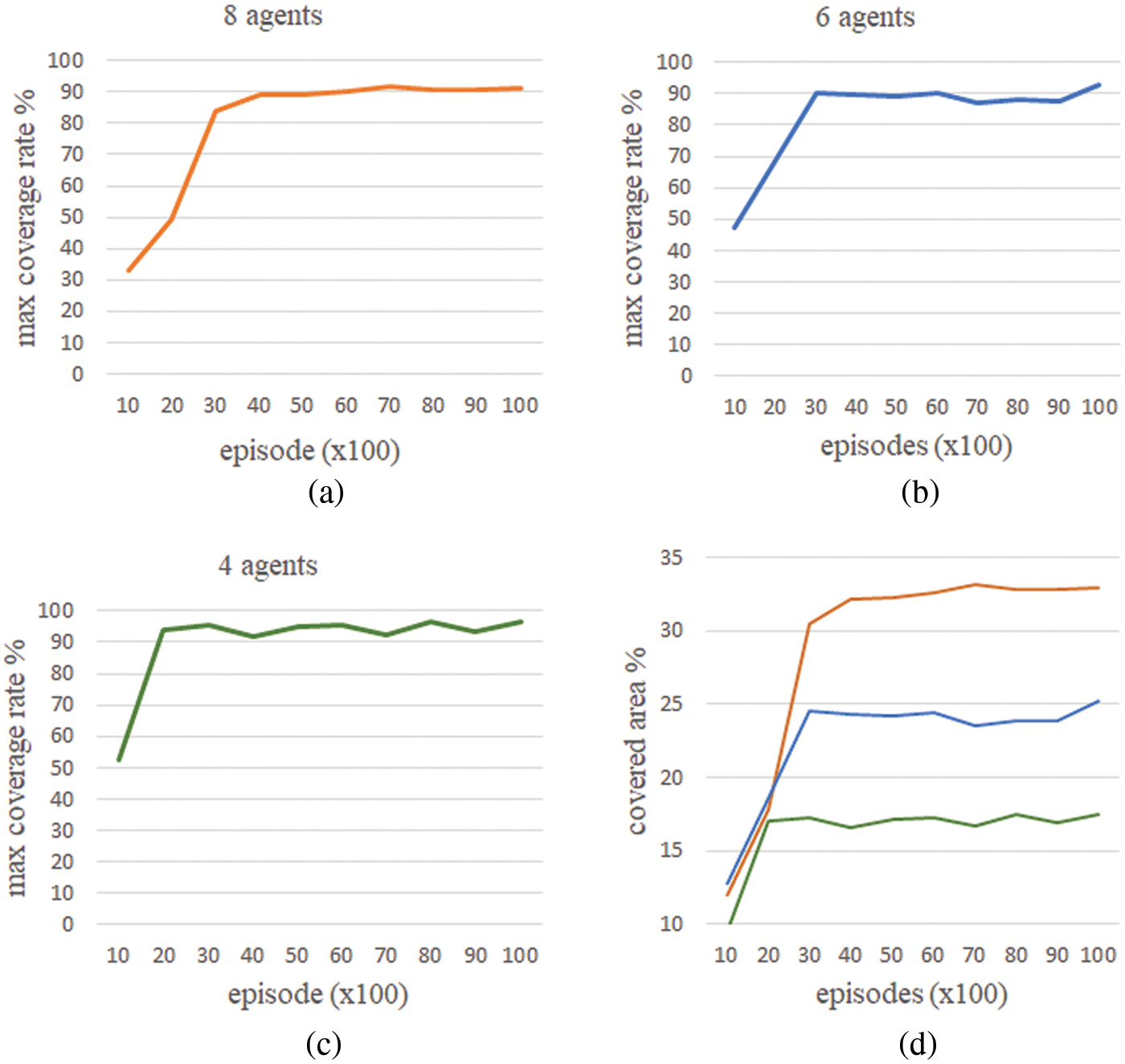
Figure 5: Area coverage results by changing number of agents

Changes in the number and variety of interactions can affect the quality of the experience. Max coverage rate represents the rate where the MAS achieves maximum coverage over the target area. According to the results of experiment 1, as expected, it is observed that as the number of agents increases, the coverage performance improves even if the environment settings are the same. Eight agents achieved better coverage rate compared to six agents and four agents by an average increment approximately equal to 30.9% and 88.3%, respectively. For instance, when the number of episodes was 5k, the team composed of eight agents reached a coverage rate equal to 32.3%, while the team composed of six agents achieved a coverage rate equal to 24.2% and the team composed of four agents a coverage rate equal to 17.1%. In contrast, by increasing coverage rate performance, even in the case of lower number of agents MAS can reach a maximum coverage rate in fewer episodes. Agents operated the process model-independently and produced new policies according to the number of active agents in the target area.

In experiment 2, we use 6 agents to analyze the effect of target area size on coverage performance in the system. Agents can communicate if the distance between agents is less than or equal to 0.5 units.

Fig. 6 shows area coverage results by changing the size of target area. Increasing the size of area to be covered brings about different formation types for connected agents. Agents found different optimum locations without the need for a centralized guidance. The agents have various alternative actions to avoid commonly covered areas and to reduce the size of uncovered areas. In the case where the number of agents does not change but the target area expands, the agents can more easily increase the distance between them without exceeding the communication distance. Using the target area with 1 × 1 unit provided better max coverage rate compared to the target area with 0.75 × 1 units and the target area with 0.5 × 1 units by an average increment approximately equal to 1.4% and 3%, respectively. For instance, when the number of episodes was 3k, the target area with 0.5 × 1 units had a max coverage rate equal to 90.3%, while the target area with 0.75 × 1 units had a max coverage rate equal to 93.1% and the target area with 1 × 1 units a max coverage rate equal to 95.9%. In addition, the results obtained in this case are helpful in determining the optimal number of agents to be used depending on the size of the target area.

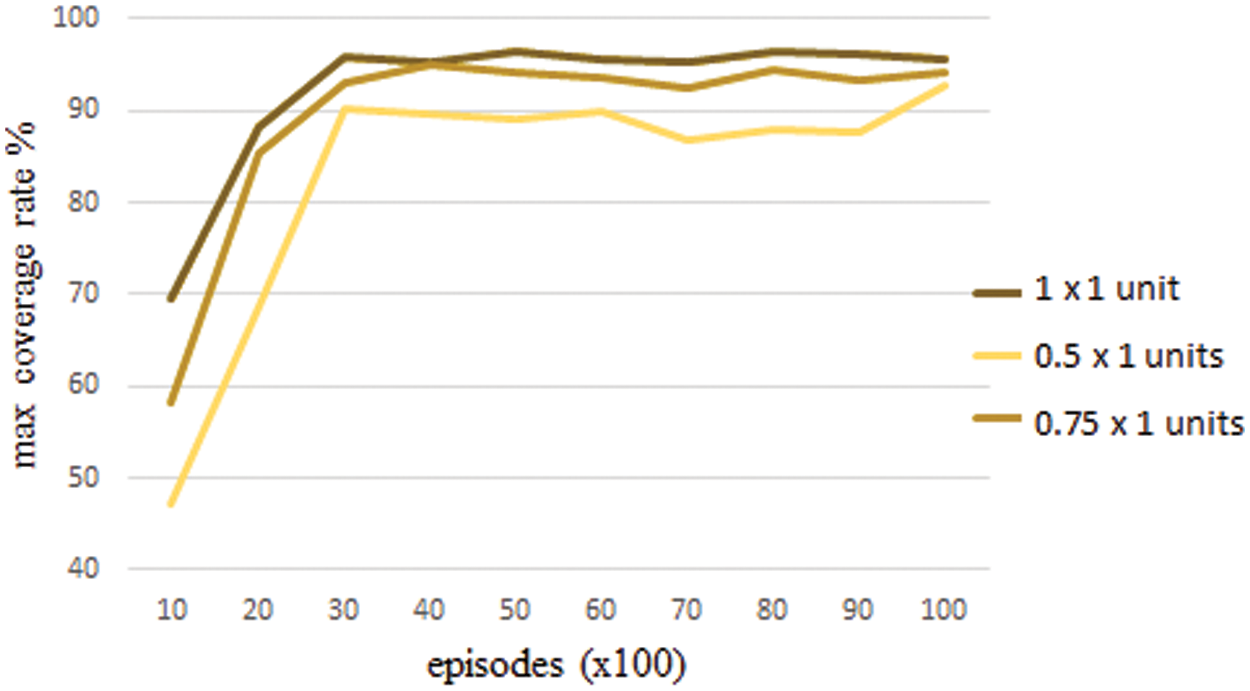
Figure 6: Area coverage results by changing the size of target area

In experiment 3, we analyze the coverage performance by changing the communication distance of each agent from 0.35 units to 1 unit. The target area is set as 0.5 × 1 units, and the number of agents in the system is 8. As shown in Fig. 7, the communication distance has a significant effect on coverage performance.

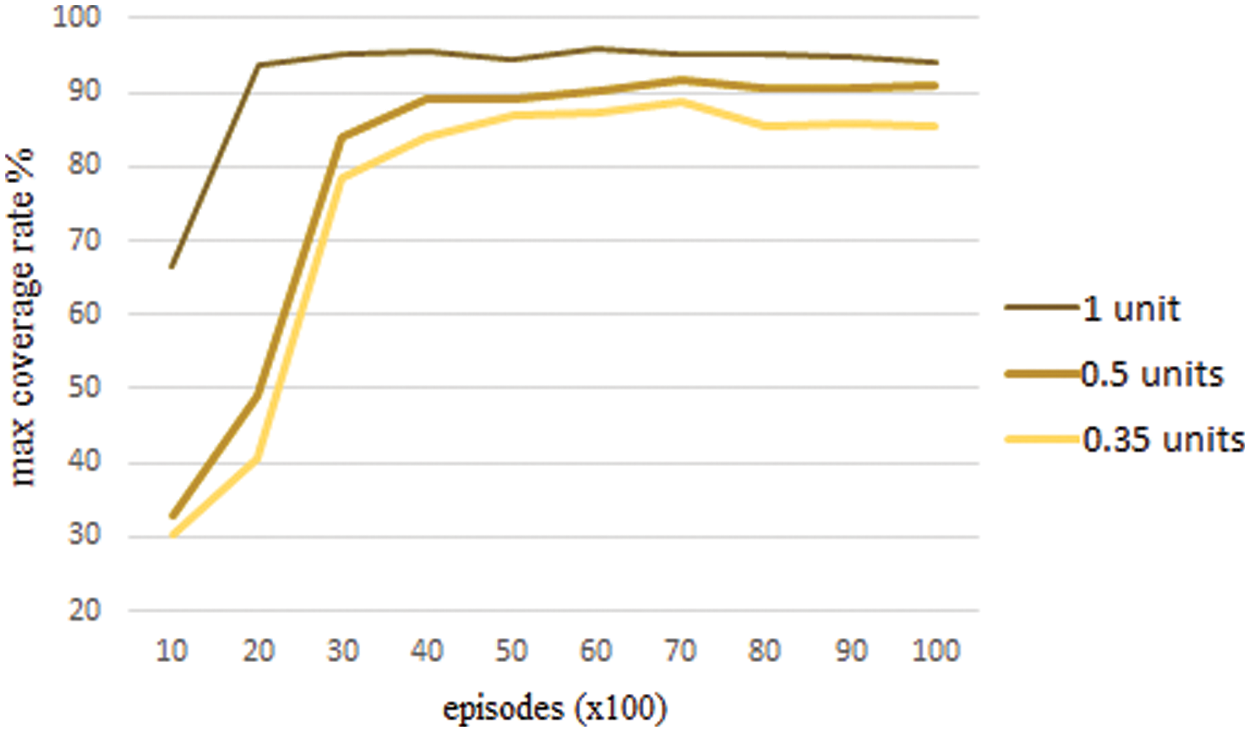
Figure 7: Area coverage results by changing communication distance

When the communication distance is long enough, the agents that reach the target area are not required to be closer to connect. They can take fewer actions to be a member of the connected graph as possible action-state space increases. Using communication distance with 1 unit provided better max coverage rate compared to using communication distance with 0.5 units and using communication distance with 0.35 units by an average increment approximately equal to 3.4% and 10.1%, respectively. In the case of 2k episodes, the scenario using 1 unit had a max coverage rate equal to 93.9%, while the scenario using 0.5 units had a max coverage rate equal to 49.1% and the scenario using 0.35 units a max coverage rate equal to 40.7%. In addition, the computational complexity for finding reachable agents decreases when agents directly reach others instead of using a hub. Furthermore, agents that must move close to each other increase the risk of collision within the system.

According to experimental results, we noticed that the DDMDAC algorithm can complete the task of dynamic coverage efficiently in unknown conditions. To achieve this, the proposed method is modeled in model-free policy gradient manner using local observations unlike many existing research in RL which employ location-based strategies. In location-based strategies, state space depends on covered part, mostly covered a grid cell, of target area. It causes inconsistent rewards and inaccurate Q-values when the covered area is covered again with another agent, and thus it is needed to have fully observed environment to be able to place agents to near optimum locations. On the other hand, in our approach, state space depends on local observations, thus, it eliminates growing up action-state space. For MAS, this strategy mainly benefits producing accurate policy in training process. In real applications, the environment is usually unknown, and it causes that agents explore to get to know it. Our proposed method allows for a real-world formulation of the area coverage problem because agents learn and acts only based on the surrounding area they can observe. The designed reward structure enforces collective behavior without the need sharing an explicit reward. Therefore, exploring the environment can be handled in decentralized way based on surrounding area they sense.

4  Conclusions and Future Work

In this paper, we present a DDMDAC method to create collaborative behavior for multi-agent systems, which aim to accomplish maximal area coverage in varying shapes. In DDMDAC, the area coverage problem is modeled as an actor-critic MARL approach with continuous action-space and state-space.

The simulation results show that the MAS with DDMDAC is suitable for dynamic area coverage problems. The performance of the proposed method was tested by choosing different scenarios in the simulations. Test results reveal that DDMDAC can perform area coverage without exceeding the communication distance by adapting to the changing number of agents in the dynamic area. Agents were positioned adaptively according to the positions of other UAVs in the target area using a model-independent policy. Agents do not need centralized routing at runtime since DDMDAC addresses the dynamic range coverage problem based on central learning with the decentralized-execution scheme. Moreover, for the MAS, it provides adaptability for agents with limited communication range to effectively cover areas in unknown environments.

For future investigation, we will focus on two subjects to improve our proposed method:

(1)In this paper, the proposed method is only applied to 2D motion model. In future, our proposed method will be extended to 3D motion model that the altitude of a UAV will be taken into consideration. Therefore, each UAV will have a circle sensing region using a conical field of view which depends on the altitude of the UAV.

(2)In the DDMDAC method, agents use the DFS algorithm to find reachable agents. DFS algorithm requires traversing all vertices to have a list of reachable agents. Therefore, finding available agents may take longer when the number of agents is large. We will focus on reducing the complexity for finding reachable agents by a UAV.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Valsan, B. Parvaty, D. G. H. Vismaya, R. S. Unnikrishnan, P. K. Reddy et al., “Unmanned aerial vehicle for search and rescue mission,” in 2020 4th Int. Conf. on Trends in Electronics and Informatics (ICOEI) (48184), Tirunelveli, India, pp. 684–687, 2020. [Google Scholar]

 2.  W. Zhang, K. Song, X. Rong and Y. Li, “Coarse-to-fine UAV target tracking with deep reinforcement learning,” IEEE Transactions on Automation Science and Engineering, vol. 16, no. 4, pp. 1522–1530, 2018. [Google Scholar]

 3.  M. Sanfourche, B. Le Saux, A. Plyer and G. Le Besnerais, “Environment mapping & interpretation by drone,” in 2015 Joint Urban Remote Sensing Event (JURSE). Lausanne, Switzerland, pp. 1–4, 2015. [Google Scholar]

 4.  O. Khan, A. Din, A. Khalid, A. Khan, A. Ahmed et al., “Online adversarial coverage for multi-agent systems,” in 2019 15th Int. Conf. on Emerging Technologies (ICET), Peshawar, Pakistan, pp. 1–6, 2019. [Google Scholar]

 5.  R. Tang, X. Qian and X. Yu, “On virtual-force algorithms for coverage-optimal node deployment in mobile sensor networks via the two-dimensional Yukawa Crystal,” International Journal of Distributed Sensor Networks, vol. 15, no. 9, pp. 155014771986488, 2019. [Google Scholar]

 6.  B. Omoniwa, B. Galkin and I. Dusparic, “Energy-aware optimization of UAV base stations placement via decentralized multi-agent Q-learning,” arXiv [2106.00845], 2021. [Google Scholar]

 7.  G. Wang, G. Cao and T. F. La Porta, “Movement-assisted sensor deployment,” IEEE Transactions on Mobile Computing, vol. 5, no. 6, pp. 640–652, 2006. [Google Scholar]

 8.  A. Din, M. Jabeen, K. Zia, A. Khalid and D. K. Saini, “Behavior-based swarm robotic search and rescue using fuzzy controller,” Computers & Electrical Engineering, vol. 70, no. 339, pp. 53–65, 2018. [Google Scholar]

 9.  H. Choset, “Coverage for robotics-a survey of recent results,” Annals of Mathematics and Artificial Intelligence, vol. 31, no. 1, pp. 113–126, 2001. [Google Scholar]

10. Y. Kang and D. Shi, “A research on area coverage algorithm for robotics,” in 2018 IEEE Int. Conf. of Intelligent Robotic and Control Engineering (IRCE), Lanzhou, China, pp. 6–13, 2018. [Google Scholar]

11. M. T. Nguyen, C. S. Maniu and S. Olaru, “Control invariant partition for heterogeneous multi-agent dynamical systems,” in 2015 19th Int. Conf. on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, pp. 354–359, 2015. [Google Scholar]

12. S. Ann, Y. Kim and J. Ahn, “Area allocation algorithm for multiple UAVs area coverage based on clustering and graph method,” IFAC-PapersOnLine, vol. 48, no. 9, pp. 204–209, 2015. [Google Scholar]

13. S. W. Cho, J. H. Park, H. J. Park and S. Kim, “Multi-UAV coverage path planning based on hexagonal grid decomposition in maritime search and rescue,” Mathematics, vol. 10, no. 1, pp. 83–98, 2022. [Google Scholar]

14. M. Santos, U. Madhushani, A. Benevento and N. E. Leonard, “Multi-robot learning and coverage of unknown spatial fields,” in 2021 Int. Symp. on Multi-Robot and Multi-Agent Systems (MRS), Cambridge, United Kingdom, pp. 137–145, 2021. [Google Scholar]

15. J. Li, R. Wang, H. Huang and L. Sun, “Voronoi based area coverage optimization for directional sensor networks,” in 2009 Second Int. Symp. on Electronic Commerce and Security, Nanchang, China, pp. 488–493, 2009. [Google Scholar]

16. J. N. Portela and M. S. Alencar, “Cellular coverage map as a voronoi diagram,” Journal of Communication and Information Systems, vol. 23, no. 1, pp. 1–6, 2008. [Google Scholar]

17. C. Yang and K. Y. Szeto, “Solving the traveling salesman problem with a multi-agent system,” in 2019 IEEE Congress on Evolutionary Computation (CEC). Wellington, New Zealand, pp. 158–165, 2019. [Google Scholar]

18. R. Almadhoun, T. Taha, L. Seneviratne and Y. Zweiri, “A survey on multi-robot coverage path planning for model reconstruction and mapping,” SN Applied Sciences, vol. 1, no. 8, pp. 1–24, 2019. [Google Scholar]

19. M. Rosalie, M. R. Brust, G. Danoy, S. Chaumette and P. Bouvry, “Coverage optimization with connectivity preservation for UAV swarms applying chaotic dynamics,” in 2017 IEEE Int. Conf. on Autonomic Computing (ICAC), Columbus, OH, USA, pp. 113–118, 2017. [Google Scholar]

20. M. Antal, I. Tamas, T. Cioara, I. Anghl and I. Salomie, “A swarm-based algorithm for optimal spatial coverage of an unknown region,” in 2013 IEEE 9th Int. Conf. on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, pp. 7–13, 2013. [Google Scholar]

21. D. Tao, S. Tang and L. Liu, “Constrained artificial fish-swarm based area coverage optimization algorithm for directional sensor networks,” in 2013 IEEE 10th Int. Conf. on Mobile Ad-Hoc and Sensor Systems, Hangzhou, China, pp. 304–309, 2013. [Google Scholar]

22. C. Öztürk, D. Karaboğa and B. Gorkemli, “Artificial bee colony algorithm for dynamic deployment of wireless sensor networks,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 20, no. 2, pp. 255–262, 2012. [Google Scholar]

23. J. Akram, A. Javed, S. Khan, A. Akram, H. S. Munawar et al., “Swarm intelligence-based localization in wireless sensor networks,” in Proc. of the 36th Annual ACM Symp. on Applied Computing, Virtual Event Republic of Korea, pp. 1906–1914, 2021. [Google Scholar]

24. Z. Zhang, X. Xu, J. Cui and W. Meng, “Multi-UAV area coverage based on relative localization: Algorithms and optimal UAV placement,” Sensors, vol. 21, no. 7, pp. 2400–2414, 2021. [Google Scholar]

25. K. Liang, C. Y. Chung and C. F. Li, “A virtual force based movement scheme for area coverage in directional sensor networks,” in 2014 Tenth Int. Conf. on Intelligent Information Hiding and Multimedia Signal Processing, Kitakyushu, Japan, pp. 718–722, 2014. [Google Scholar]

26. C. Yang and J. Wen, “A hybrid local virtual force algorithm for sensing deployment in wireless sensor network,” in 2013 Seventh Int. Conf. on Innovative Mobile and Internet Services in Ubiquitous Computing, Taichung, Taiwan, pp. 617–621, 2013. [Google Scholar]

27. W. Li, G. -G. Wang and A. H. Gandomi, “A survey of learning-based intelligent optimization algorithms,” Archives of Computational Methods in Engineering, vol. 28, no. 5, pp. 3781–3799, 2021. [Google Scholar]

28. D. Xu, X. Zhang, Z. Zhu, C. Chen and P. Yang, “Behavior-based formation control of swarm robots,” Mathematical Problems in Engineering, vol. 2014, no. 1, pp. 1–13, 2014. [Google Scholar]

29. F. Rossi, S. Bandyopadhyay, M. Wolf and M. Pavone, “Review of multi-agent algorithms for collective behavior: A structural taxonomy,” IFAC-PapersOnLine, vol. 51, no. 12, pp. 112–117, 2018. [Google Scholar]

30. Y. Cao, W. Yu, W. Ren and G. Chen, “An overview of recent progress in the study of distributed multi-agent coordination,” IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 427–438, 2013. [Google Scholar]

31. M. Vidyasagar, “Recent advances in reinforcement learning,” in 2020 American Control Conf. (ACC), Denver, CO, USA, pp. 4751–4756, 2020. [Google Scholar]

32. P. A. Vikhar, “Evolutionary algorithms: a critical review and its future prospects,” in 2016 Int. Conf. on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, pp. 261–265, 2016. [Google Scholar]

33. S. Van Rijn, H. Wang, M. van Leeuwen and T. Bäck, “Evolving the structure of Evolution Strategies,” in 2016 IEEE Symp. Series on Computational Intelligence (SSCI), Athens, Greece, pp. 1–8, 2016. [Google Scholar]

34. Z. Zhang, X. Sun, L. Hou, W. Chen, Y. Shi et al., “A cooperative co-evolutionary multi-agent system for multi-objective layout optimization of satellite module,” in 2017 IEEE Int. Conf. on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, pp. 147–151, 2017. [Google Scholar]

35. A. Nowé, P. Vrancx and Y. M. De Hauwere, “Game theory and multi-agent reinforcement learning,” in Adaptation, Learning, and Optimization, vol. 12, Berlin, Heidelberg, Germany, Berlin Heidelberg: Springer, pp. 441–470, 2012. [Google Scholar]

36. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

37. J. Xiao, G. Wang, Y. Zhang and L. Cheng, “A distributed multi-agent dynamic area coverage algorithm based on reinforcement learning,” IEEE Access, vol. 8, pp. 33511–33521, 2020. [Google Scholar]

38. M. Samir, D. Ebrahimi, C. Assi, S. Sharafeddine and A. Ghrayeb, “Trajectory planning of multiple dronecells in vehicular networks: A reinforcement learning approach,” IEEE Networking Letters, vol. 2, no. 1, pp. 14–18, 2020. [Google Scholar]

39. S. Jiang, Z. Huang and Y. Ji, “Adaptive UAV-assisted geographic routing with Q-Learning in VANET,” IEEE Communications Letters, vol. 25, no. 4, pp. 1358–1362, 2021. [Google Scholar]

40. R. H. Crites and A. G. Barto, “An actor/critic algorithm that is equivalent to Q-learning,” in Proc. of the 7th Int. Conf. on Neural Information Processing Systems, Denver, CO, USA, pp. 401–408, 1994. [Google Scholar]

41. S. Meng and Z. Kan, “Deep reinforcement learning-based effective coverage control with connectivity constraints,” IEEE Control Systems Letter, vol. 6, pp. 283–288, 2022. [Google Scholar]

42. C. H. Liu, Z. Chen, J. Tang, J. Xu and C. Piao, “Energy-efficient UAV control for effective and fair communication coverage: A deep reinforcement learning approach,” IEEE Journal on Selected Areas in Communications, vol. 36, no. 9, pp. 2059–2070, 2018. [Google Scholar]

43. C. H. Liu, X. Ma, X. Gao and J. Tang, “Distributed energy-efficient multi-UAV navigation for long-term communication coverage by deep reinforcement learning,” IEEE Transactions on Mobile Computing, vol. 19, no. 6, pp. 1274–1285, 2020. [Google Scholar]

44. I. A. Nemer, T. R. Sheltami, S. Belhaiza and A. S. Mahmoud, “Energy-efficient UAV movement control for fair communication coverage: A deep reinforcement learning approach,” Sensors, vol. 22, no. 5, pp. 1919–1946, 2022. [Google Scholar]

45. H. X. Pham, H. M. La, D. Feil-Seifer and A. A.Nefian, “Cooperative and distributed reinforcement learning of drones for field coverage,” arXiv [1803.07250], 2018. [Google Scholar]

46. R. Lowe, Y. Wu, A. Tamar, J. Harb, P. Abbeel et al., “Multiagent actor-critic for mixed cooperative-competitive environments,” in Proc. of the 31st Int. Conf. on Neural Information Processing Systems, Long Beach, California, USA, pp. 6379–6390, 2017. [Google Scholar]

47. A. Suresh, S. S. Latha, P. Nair and N. Radhika, “Prediction of fight or flight response using artificial neural networks,” American Journal of Applied Sciences, vol. 11, no. 6, pp. 912–920, 2014. [Google Scholar]

48. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]