Blockchain-based Privacy-Preserving Group Data Auditing with Secure User Revocation

1  Introduction

Cloud computing has proved its value through the widespread practice these years [1]. More and more enterprises and organizations outsource their data to cloud storage, in order to obtain the improved features of third-party storage service with the pay-as-you-go model. With the scale of research and development expanding, users start to work together in a group to share data with each other. To be more specific, a user uploads its data to cloud storage [2,3], and other members of group can easily access and work on shared data. This group-sharing model employs cloud service as collaboration platform and is particularly common in software development. In scenario of software development, a number of users work on different parts of the same source code and sometimes modify snippets created by other collaborators. Just like all the infrastructures in cloud environment [4], cloud-based group data sharing is also confronted with challenge to data integrity and reliability [5]. Integrity of data shared via cloud storage may be compromised due to hardware/software failures and human errors. Even worse, increasing number of users adds to the complexity of data integrity protection.

Checking integrity of data [6,7] is the basis of ensuring data reliability in cloud storage. Considering the scale of data in cloud, works [8] have been proposed, which implement a method enabling verifiers to check data integrity without downloading, namely Provable Data Possession (PDP). In these works, data is often divided into blocks and its owner signs signatures attached to each block with private key. These signatures, also called tags or meta data, are the evidences that decide the correctness of data blocks being checked. Thus, for fairness to cloud service providers, quite a number of researchers [9–18] proposed schemes that allows a third-party auditor (TPA) to execute the process of integrity verification. Since TPA uses the public key of data owner, it is convinced that the signatures of challenged blocks are definitely authentic.

When the number of users changes from single to multiple, unfortunately, simply extending of aforementioned works is no longer appropriate for group sharing. Because the public keys of users may leak data owner identity and visitor activity to TPA. Some researchers [19–22] noticed the importance of protect identity privacy when auditing group-shared data. By introducing group or ring signature, these schemes enabled integrity verification without identity of data owners revealed. However, not so many researchers considered a basic and practical problem, a dynamic group with user affiliation and revocation.

No matter employing group or ring signature, when data owner uploads or modifies a block, it computes a tag using public keys of multiple other group members to construct a privacy-preserving signature. Just like all groups in real society, sometimes a user may quit group due to personal will or misbehavior, called revocation of this user. As a result, all the signatures relevant to the revoked user must be re-signed. The re-signing caused by revocation can be divided into two cases: signatures signed by the revoked user, and other ones merely using its public key.

A straightforward method to re-compute these revoked signatures is to ask other users to download the original data blocks and generate signatures in the old way. Nevertheless, considering the scale of cloud data, the consequent communication for signer is overwhelmed. Some researchers [23] noticed the problem and proposed a few schemes based on proxy re-signing. Wang et al. [20] proposed a new model: a user quits its group and transfer the data possession to another user, using cloud service to re-sign the blocks for proxy. They also put forward a new re-signing method that enables cloud service to complete such re-computing, without asking for the private keys of both two users. This work is based on a disclosed-identity model. That is to say, all the relationship of group members is public, not only ownership of data blocks but also user activity. Aware of the risk that TPA is able to pry into the identities of group users, Wang et al. [19] have also published another work about privacy-preserving data auditing scheme for group sharing, which is based on ring signature. This work did not discuss how to deal with user revocation, though.

Besides the risk of identity privacy leakage, collusion attack existing in group sharing data auditing must be considered as well. Most PDP schemes share an assumption-TPAs are all semi-trusted, which means that they will be only curious about user privacy, but always honest for verification results. This wishful assumption, of course, does not always stand in reality. What is more, in the scenario of group sharing, revoked users may collude with cloud storage or TPA to endanger the security of other members. They can leak their keys to malicious cloud service or TPA in order to tamper with the re-signed signatures. Noticing this problem, Yuan et al. [24] proposed a dynamic public PDP scheme with collusion-resistant group user revocation. However, security of this scheme is merely a kind of partial collusion-resistance. Possibility of malicious TPA colluding with revoked user was still left out of consideration. Following this work, Jiang et al. [21] continued to make some improvement. They constructed a user revocation scheme based on vector commitment, Asymmetric Group Key Agreement and group signature, focusing on a dynamic PDP scheme on encrypted database. This work focused on a narrower scenario and made some improvements on security and performance, but cannot solve the problem of identity privacy leakage. On the other hand, there are already some works [25,26] against the threat of collusion attack, but a clear solution for group sharing scenario is still absent.

Imperfections of the aforementioned works constitute the motivation for our work. In this paper, we try our best to propose a novel privacy-preserving public PDP scheme with group user revocation. We construct the new scheme on the basis of blockchain technique to resist collusion attack, and use ring signature to solve the problem of identity privacy. We discuss each case of user revocation and complete related method to implement reliable signature re-signing. Our proposal is a generic solution, which can be applied to both plaintext data and encrypted data.

Constructions. 1) We introduce a construction of blockchain-based PDP scheme, which enables secure user revocation for group shared data. 2) We propose a novel linkable ring signature re-signing method to protect identity privacy. 3) We analyze the security of our proposed scheme and evaluate its performance.

2  Problem Statement

In this section, we will describe our system model of cloud data group sharing. Then we will give the definition of threat model and design goals for our proposed scheme.

2.1 System Model

A system model of cloud data group sharing is shown in Fig. 1. The entities in the system are described as below.

•   Cloud Service Provider (CSP): cloud provides storage service for every group user, and will respond to integrity challenge of data blocks.

•   Group Users: every user may play two roles in group: data owner or visitor. Data owner uploads data blocks, and visitors access its data with authorization. A user can be owner of some blocks and visitor of other ones. For the sake of clarity, if a visitor modifies a data block, we call the visitor ‘’owner’’ of the new modified replica, distinguished from the original one.

•   Third Party Auditor (TPA): TPA has enough computing and storage resource to execute integrity verification for every group user.

•   Blockchain: To resist collusion attack, we employ blockchain network based on Hyperledger Fabric. The entities above play different roles of blockchain. Group users and cloud service act as client peer, while TPA undertakes the job of endorsement peer. All the work of auditing scheme is performed in the form of smart contracts already installed in each peer.

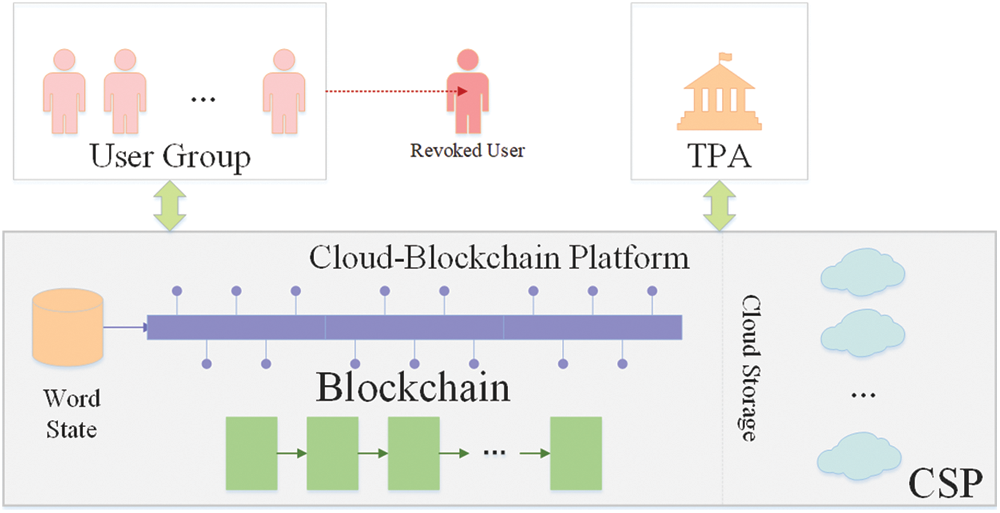
Figure 1: System model

2.2 Threat Model and Design Goals

Besides the common threat of normal PDP schemes discussed in many works before [11], in this part we focus on the specific threat in user revocation scenario. A user u1 quits its group due to some reason, leaving data blocks {mi} to be transferred to user u2 . Original signatures of these blocks are σi and TPA needs to authenticate the re-signed signatures {σi′} with the help of CSP. In this process, there are two kinds of attack threatening group sharing data auditing:

1)   The revoked user may collude with CSP and try to introduce incorrect or even harmful information into re-signed signatures.

2)   The revoked user may collude with TPA, to slander certain honest user by misleading the ownership of revoked data.

Here we omit the common threat such as an external malicious adversary forging signatures, and focus on the discussion of threat in user revocation. Different from previous works [20], we try to loosen the security assumption that CSP and TPA must be semi-trusted. They can be untrusted, just like real entities in real society. The most difficult point to resist collusion attack is that malicious revoked user may leak the secret key of group to TPA or CSP, leading to weakening of group security. Considering the factors above, we propose the following goals necessary for a secure user revocation scheme:

•   Correctness: A group sharing data PDP scheme holds the property of correctness if and only if for any polynomial adversary, integrity proof cannot pass verification unless it is generated by intact data blocks and signatures.

•   Unforgeability: A group sharing data PDP scheme is unforgeable if for any internal or external adversary, signature cannot pass verification unless it is generated from correct blocks and secret key.

•   Privacy-Preserving: A group sharing data PDP scheme is privacy-preserving if for any TPA, the identity of real signer cannot be inferred from given signatures and public keys.

•   Collusion-Resistance: A group sharing data PDP scheme can resist collusion attack if for any revoked user colluding with TPA or CSP, cannot generate valid signatures without correct data blocks and private keys.

•   Traceability: When a user is revoked from group, all the signatures it signed before can be traced.

3  Preliminaries

3.1 Bilinear Maps

Denote two multiplicative cyclic groups of prime order q as G1 and G2 , and their generators as g1,g2 respectively. Bilinear map e:G1×G2→GT holds properties as follows:

•   Bilinearity: for all u∈G1,v∈G2,a,b∈Zq , there holds e(ua,vb)=e(u,v)ab .

•   Non-degeneracy: e(g1,g2)≠1 .

•   Computability: there exists an efficient algorithm for computing mapping e in polynomial time.

3.2 Security Assumptions

Computational Diffie-Hellman Assumption. Consider a cyclic group G of prime order q. Let g be a random generator of G and choose two random elements a,b from Zq . Value of gab is computationally intractable when (g,ga,gb) is given.

Discrete Logarithm Assumption. Given a cyclic group G of order q and any two random elements a,b of G , choosing an integer k∈Zq that solves the equation bk=a is termed a discrete logarithm. If prime number q is a sufficiently large, computing k in polynomial time is hard.

3.3 Linkable Ring Signature

Ring signature is a kind of digital signature cryptography firstly introduced in 2001, which is named after its ring-like structure of algorithm. Ring signature can be performed by any member in a set of users connected by shared keys. When checking validity of ring signature, verifiers can learn whether the signature comes from certain set of users, but cannot reveal the identity of real signer. Ring signature ensures that it is highly computationally infeasible to determine the real signer identity, which makes the scheme well suited for ad hoc group.

Ring signature has high anonymity, which brings another problem: it is quite hard for a user to prove a certain signature is signed by itself without breaking the anonymity. To solve this problem, linkable ring signature is proposed [27]. It enables proving two signatures signed by the same user sharing some kind of link, which is called that these signatures are linked.

3.4 Smart Contracts in Blockchain Network

Although the first blockchain network is born for cryptocurrency, the progress of technology has already enabled blockchain network to be used for non-financial fields. In this work, we take that advantage and design a blockchain-based group data auditing scheme. We build our work on the basis of a well-known platform, Hyperledger Fabric.

Fabric is a customizable blockchain system, which allows different users join the network and make transactions via installed smart contracts. The workflow of a transaction in Fabric is as below:

•   Propose: Clients propose requests of transactions to blockchain network.

•   Endorsement: Endorsement peers simulate transaction results following the method defined in smart contracts. If passed, endorsement peers send its approval to client.

•   Submission: When a client collects enough endorsements, it submits the transaction to blockchain network, which will write this transaction into block later.

4  Scheme Construction

4.1 Definition of Scheme

In this part, we will introduce the basic definition of our proposed group PDP scheme.

a)   Setup Phase

KeyGen(1κ)→(sk,pk,param) Let κ be secure length of the proposed scheme. Every user should invoke this algorithm when joining group. And the algorithm will output their private and public keys (sk,pk) as well as common secure parameter param.

b)   Preprocessing Phase

SigGen(m,sk,pk)→(σ,L) Denote data block as m. Before uploading m, its owner uo invokes SigGen to choose a ring L and generate signature σ . L is a list of public keys from n members of group, including uo . Thus, the real identity of data owner for m will be hidden in L.

c)   Verification Phase

ChalGen({idxi})→(chal) . A group user run this algorithm to generate challenge request chal for TPA. {idxi} are the indices of blocks to be checked, denoted as K indices in total.

ProofGen(chal,{mi})→(P) . When CSP receives challenge request chal , it firstly queries required blocks {mi} in storage, then invokes ProofGen to compute the integrity proof P in response.

ProofVerify(P,σ,L)→(TRUE,FALSE) . Once receiving integrity proof P from CSP, TPA will parse block signature σ and related ring L from blockchain-based ledger. Then it runs algorithm ProofVerify to check the proof. If algorithm accepts, it outputs TRUE ; otherwise, FALSE .

d)   Update Phase

Update(m′,sk,pk)→(σ′,L′) . The algorithm of Update is the complement of SigGen , for deleting or adapting data blocks. Data owner invokes this algorithm to upload modified signature σ′ and ring list L′ to CSP.

e)   Revocation Phase

ReSig(sk,pk,L,σ)→(L′,σ′) . Before exiting group, the user to be revoked invoke this algorithm to re-sign its data blocks which need to be kept in the group. Each signature σ with ring list L will be recomputed to new one (L′,σ′) .

UsrRevo(pk)→(TRUE,FALSE) . After resigning the blocks, user call this algorithm to inform TPA of formal revocation. TPA checks whether there are omitted blocks not resigned yet, and decides to accept or reject the application.

4.2 Concrete Construction

Different from previous works [22], we use linkable ring signature instead of group signature, in order to obtain anonymous auditing. That is to say, TPA cannot infer the owner identity of challenged blocks, thus our proposed scheme is privacy-preserving.

KeyGen. When initializing a group, choose two be multiplicative cyclic groups of prime order q, denoted as G1 and G2 . Let g1,g2 be their generators respectively, and e:G1×G2→GT be bilinear map. Choose two collision-resistant cryptographic hash functions H1:(0,1)∗→Zq and H2:(0,1)∗→G1 . Pick a random element π←Zq as the private key of group users, then compute common public key ρ=g2π . At this point, the shared keys and public parameter of group have been established.

When a user ui joins group, it should set its own private and public keys as follows:

1)   Pick random element xi←Zq as private key.

2)   Compute yi=g1xi as public key.

SigGen. Consider a data owner uj and its data block m to be uploaded. Denote the total number of current members in group as d, and uj extracts n out of d users, generating a ring L=(y1,y2,…,yn),1≤j≤n , where yi is the public key of user ui registered in blockchain network before. A ring signature of block m is generated in the following way:

1)   Compute

h=H2(L)

y~=hxj

2)   Choose random element λ←Zq , then compute

cj+1=H1(L,y~,g1λ,hλ)

3)   For other ui,i≠j in ring L, pick random element si←Zq and compute

ci+1=H1(L,y~,g1siyici,hsiy~ci),j<i<n

c1=H1(L,y~,g1siyici,hsiy~ci),i=n

ci+1=H1(L,y~,g1siyici,hsiy~ci),i<j

4)   Compute

sj=λ−xici

t=(c1g1m)π

Finally, the ring signature for data block m is σ=(c1,s1,…,sn,y~,t) .

ChalGen. In data auditing scheme, there are two cases when choosing block to check. One case is that user wants to check some certain blocks and learn their status. The other is randomly selecting a few blocks for inspection. No matter which case, user choose K blocks with indices (idx1,idx2,…,idxK),K≥1 to be challenged. The procedures follow the steps below:

1)   Pick K random elements γk←Zq,1≤k≤K for each block. Assemble a challenge chal={(idxk,γk)}1≤k≤K .

2)   Send chal to blockchain network.

ProofGen. When receive challenge request from blockchain network, CSP generates an aggregated zero-knowledge proof as follows:

1)   Pick random element r←Zq and compute R=g2r , in order to masking blocks.

2)   Aggregate the blocks as

μ=r+∑k=1K⁡γk⋅midxk

Then send (μ,R) to blockchain network as integrity proof.

ProofVerify. Once receiving proof, TPA check the integrity in the following way:

1)   For each data block midxk , refer to its record in distributed ledger and extract corresponding ring Lk={yi,k}1≤k≤K .

2)   Then reconstruct the ring signatures:

for 1≤i≤n−1 , compute

zi,k′=g1si,kyi,kc~i,k

zi,k′′=hsi,ky~c~i,k

c~i+1,k=H1(Lk,y~,zi,k′,zi,k′′)

After that, compute

c~1,k=H1(Lk,y~,zn,k′,zn,k′′)

3)   Finally, check the equation

e(g1μ⋅∏k=1K⁡c~1,kγidxk,ρ)=e(R⋅∏k=1K⁡tidxkγidxk,g2) (1)

If it holds, accept the proof; otherwise, reject.

Update. In our scheme, the identity of data owner for each block is confidential. So when a user tries to update a block, it must prove itself as the legal owner of targeted block. Our method provides good support for such operation. Considering two valid data tags with blocks (σ,m) and (σ′,m′) , it is easy to construct F1 as judgement of whether σ=(c1,s1,…,sn,y~,t),σ′=(c′1,s1′,…,s′n,y~′,t′) holds y~=y~′ . Since σ,σ′ share the same ring L, y~=y~′=[H2(L)]xj generated by the same user uj must holds.

•   Modifying. Procedure of modifying a block can be seen as uploading a new block m′ to replace the original m. To prove ownership of original block m, data owner only needs to offer the new tag σ′ for checking whether y~=y~′ holds. In this way, we ensure data sovereignty of owners without adding heavy computation and communication overhead.

•   Deleting. There is no new block to be uploaded in the case of deleting. Therefore, data owner needs to generate a temporary signature to prove its ownership. Data owner should choose a random message m′ and generate σ′ following the method in SigGen. If y~=y~ holds and σ′ is a valid tag, the deleting request can be identified as coming from the real data owner.

ReSig. Considering a block m of user u1 with private key x1 and public y1 , when u1 need to quit from group, it has two choices to dispose m : deleting or re-signing. The deleting case can be classified as that of Update, so here we just introduce the part of re-signing. The process of re-signing is as below:

1)   User u1 -negotiates with user u2 and u2 agrees to take over block m.

2)    u1 sends a request (y~′,u2) to blockchain network, proving that it is the original owner of m and u2 will be the new one.

3)   TPA checks y~ and agrees with the re-signing request, informing u2 to compute new signature.

4)    u2 choose a new ring L′ and compute (c′1,s1′,…,s′n,y~′′) following the method in SigGen. Then compute

C=(c1′c1)π

t′=tC

5)    u2 sends (c′1,s1′,…,s′n,y~′′,t′) as the new signature to blockchain network and receives the verification from TPA, just as that of SigGen.

UsrRevo. After disposing all its blocks, the user to be revoked sends a request to inform the blockchain network. TPA checks its ledger for whether there are still blocks to be dealt with. If all blocks are re-signed or deleted, TPA accepts the revocation. Otherwise, reject.

4.3 Smart Contract Construction

In order to obtain non-repudiation and collusion-resistant group auditing, we need to wrap the algorithms above into chaincodes to be executed in blockchain network. Due to the mechanism of smart contract endorsement, each phase should be divided into two parts: on-chain transaction and off-chain operation. The on-chain transaction is similar to generating a new blockchain transaction. User or cloud service, acting as client, sends requests to blockchain network. And TPA plays the role of endorsement node, checking the validity of those requests and making decision for whether to accept transactions or not. The off-chain operation, just as it namely implies, is performed by entities locally at their own storage and computing resource, such as generating secret keys, signatures and integrity proofs. The reason for such division is that the operations about random element picking cannot be simulated in endorsement computation, and computing using private key should be secret.

a)   Setup Phase

KeyGen. User firstly execute the off-chain operation to generate its own private and public keys. Then it signs a message as the proof of public key and send transaction to blockchain network. TPA checks the validity of public key following method in smart contracts. If the key passes verification, TPA accepts the user to join in the group; otherwise, reject. In this way, we protect the secret of private key for user and make sure that each public key is valid when joining the group. The whole process is shown in Fig. 2.

Figure 2: On-chain transaction and off-chain operation of setup phase

b)   Preprocessing Phase

SigGen. Before uploading data blocks to cloud, data owner executes off-chain operation to generate signatures with private key and ring list. Then the owner sends request to TPA to register these signatures, meanwhile transferring data blocks to cloud storage. The CSP, once receiving the blocks, generates an integrity proof and sends to the blockchain network to check the validity of block signatures. If the proof can pass verification by TPA, CSP and TPA both agree that these signatures are valid and data blocks are intact. Otherwise, they refuse to accept the result and contact data owner for further dealing. The whole process is shown in Fig. 3.

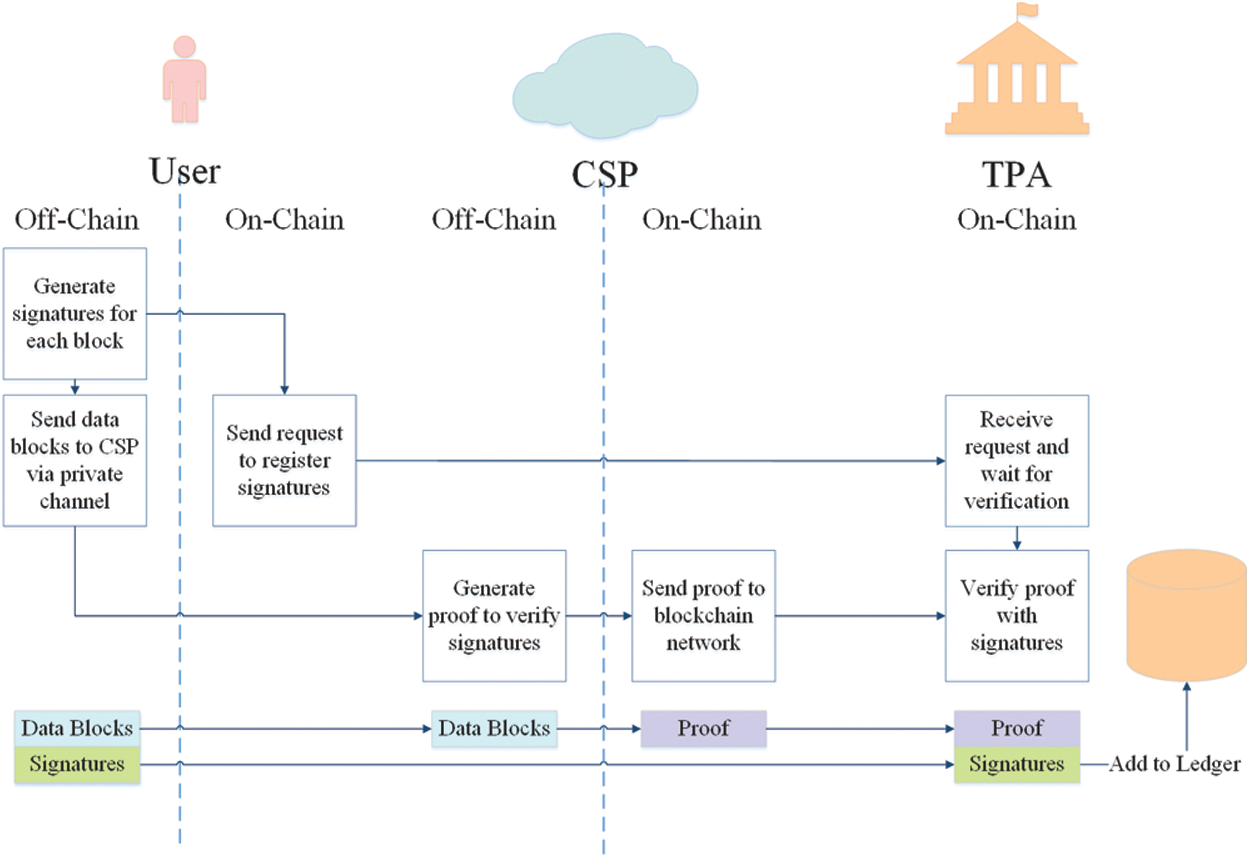
Figure 3: On-chain transaction and off-chain operation of preprocessing phase

c)   Verification Phase

ChalGen. Group user decides challenged block indices and chooses random elements to generate challenge request in off-chain operation. Then it sends the request to blockchain network via on-chain transaction. TPA, working as endorsement node, checks whether the request is from valid user.

ProofGen. Once receiving challenge request, CSP extracts data blocks from its storage and computes integrity proof as off-chain operation. In this way, content of data blocks can avoid to be exposed to TPA in blockchain network. And in on-chain transaction, it sends the proof to blockchain network.

ProofVerify. This algorithm is a full on-chain transaction. TPA verifies the proof and gives result in form of endorsement. The whole process of this phase is shown in Fig. 4.

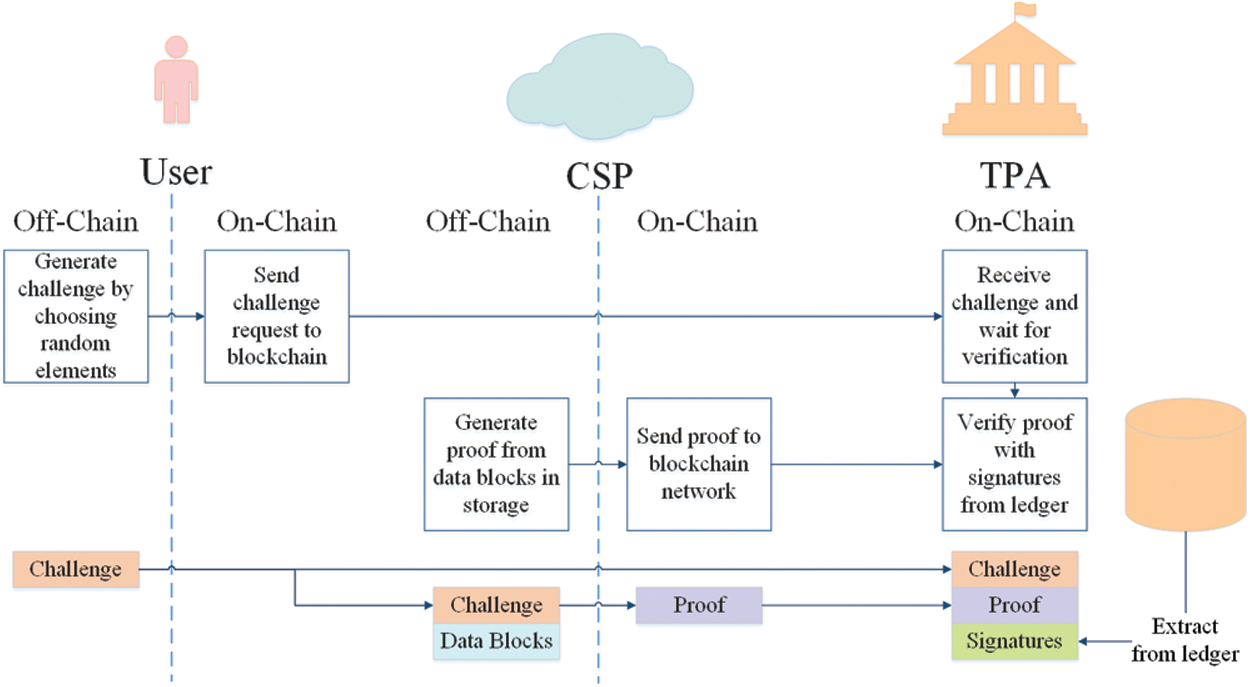
Figure 4: On-chain transaction and off-chain operation of verification phase

d)   Update Phase

Update. The off-chain operation of this phase is similar to that of Preprocessing. User firstly computes new signature and proof of ownership in the off-chain part, and then sends the information to blockchain network in on-chain part. TPA will check the ownership proof, making sure the validity of updating and accept new signature. The whole process is shown in Fig. 5.

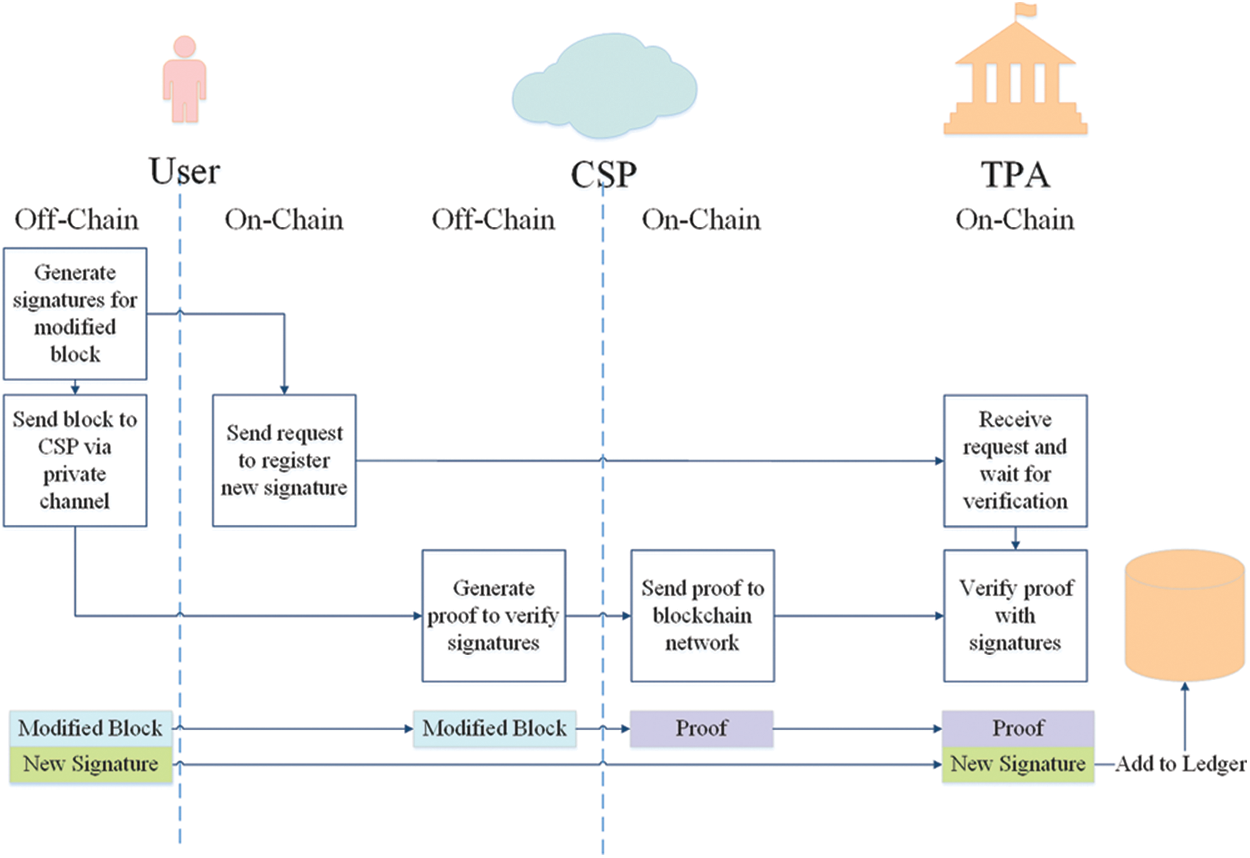
Figure 5: On-chain transaction and off-chain operation of update phase

e)   Revocation Phase

ReSig. User generates re-signed signatures in the off-chain part, and then sends the request to blockchain network via on-chain transaction. TPA checks validity of re-signing signatures in the endorsement process. Finally, the re-signed signatures will be written into distributed ledger.

UsrRevo. User sends the revocation request as on-chain transaction, and TPA checks its validity according to whether all the signatures of user has been processed. If the user has finished the disposition of its signatures, TPA will accept its revocation and remove its public key from user key list. The whole process of this phase is shown in Fig. 6.

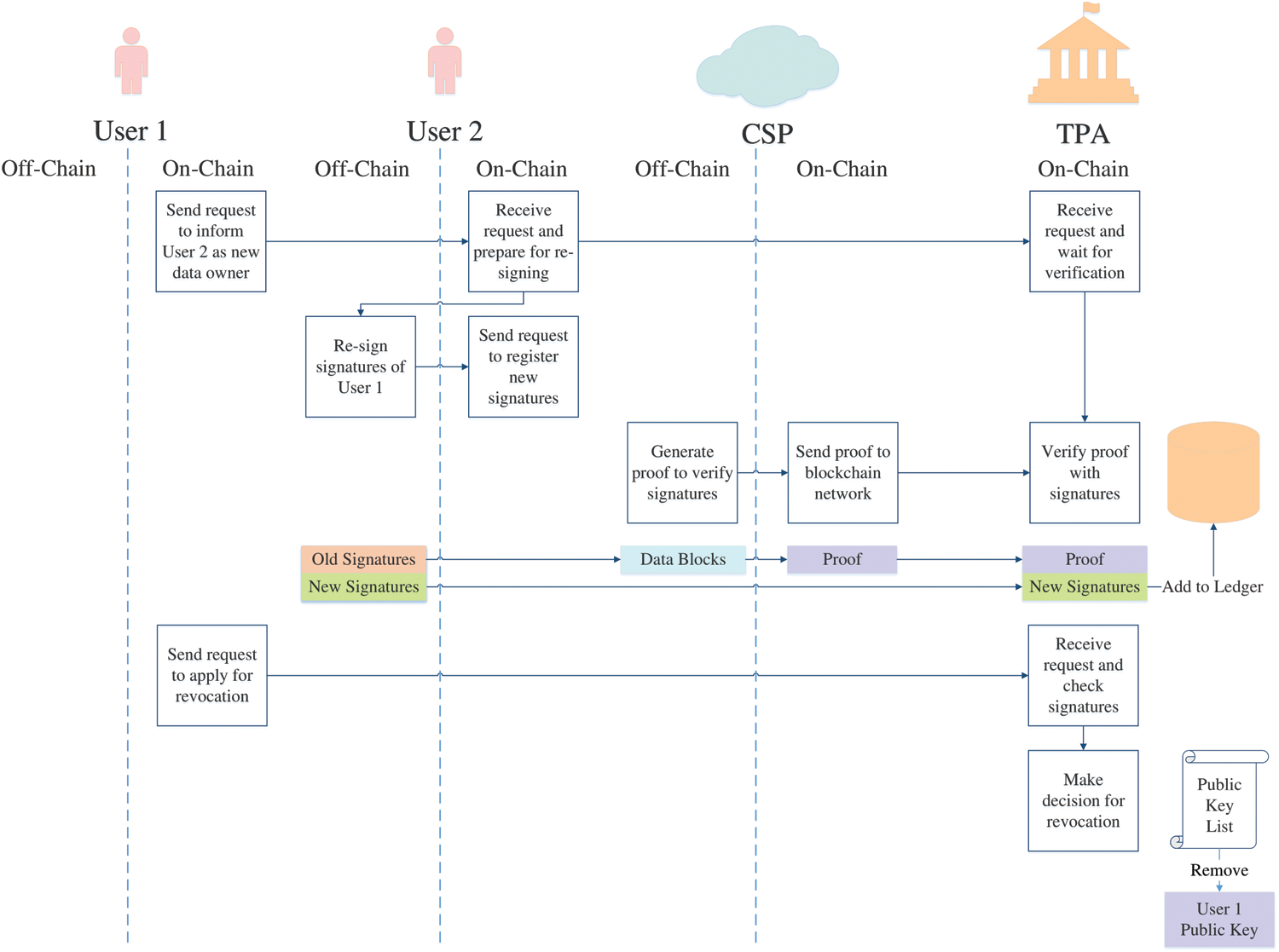
Figure 6: On-chain transaction and off-chain operation of revocation phase

5  Security and Performance Analysis

5.1 Security Analysis

In this part, we will discuss the security properties of our blockchain-based PDP scheme, including correctness, non-repudiation, unforeability and privacy preserving.

Theorem 1. (Correctness) If when most TPAs in blockchain network are honest, an integrity proof from CSP cannot pass the integrity verification unless the cloud holds correct data, we say that the proposed scheme has the property of correctness.

Proof. First of all, as the basis of whole scheme, we will prove that Eq. (1) of ProofVerify holds. With preliminary knowledge introduced before, we deduce the left-hand side of (1) as follows:

e(R⋅∏k=1K⁡tidxkγk,g2)=e(g1r⋅∏k=1K⁡(c1,k⋅g1midxk)π⋅γk,g2)

=e(∏k=1K⁡c1,kγk⋅g1midxk⋅γk+r,g2π)

=e(g1μ⋅∏k=1K⁡c1,kγk,ρ)

=e(g1μ⋅∏k=1K⁡c~1,kγk,ρ)

The last step of deduction holds if and only if c~1,k=c1,k,k=1,…,K also holds.

Therefore, we can say that if an integrity proof pass checking in ProofVerify, both the ownership (contained in c1,k ) and content (contained in midxk ) are ensured to be correct.

Theorem 2. (Non-repudiation) If most TPAs in blockchain network are honest, any malicious adversary cannot control the result of integrity verification by in collusion with CSP or data owner.

Proof. We have already proved the correctness of our integrity auditing scheme. Therefore, we can say that if a TPA is honest, it will always give honest decision for proof checking. On the other hand, the extraction of signatures for verification is based on distributed ledger of blockchain network. So even CSP or data owner in collusion with any dishonest adversary, they cannot tamper signatures used for verification. An honest TPA can always draw correct result. Also, blockchain network is believed to resist history attack, so we can say that our scheme can resist attacking from minor malicious adversary.

Theorem 3. (Unforgeability) For any user or CSP, forging signature of another member is infeasible in polynomial time if and only if the DL assumption holds.

Proof. Let L=(y1,y2,…,yn) be a given ring of n group users. Assume a PPT adversary A , able to make at most qH times of queries to hash functions H1 and H2 as well as qS times to RSO , can forge ring signature σ with non-negligible probability as

Pr[A(L)→(m,σ):V(L,m,σ)=1]>1Q(k)

where Q is polynomial and k is the security parameter. RSO is a ring signature oracle which returns valid LHARS signatures upon queries of A .

Now we assume that A constructs a PPT simulator M to generate forged signature. Since π←Zq,ρ=g2π are the common keys shared by group members, we suppose that M holds (π,ρ) and simplify the problem as follows.

Ring Signing Oracle: Given any data block m, any public key list L=(y1,y2,…,yn) , the ring signing oracle RSO generate a signature. M simulates RSO to generate a signature without holding any secret keys of individual group members.

Without loss of generality, we assume that M randomly picks r←Zq and queries hash function to get h=H2(L) . Then compute y~=hr and chooses c1,…,cn,s1,…,sn . Back patch to

ci+1=H1(L,y~,g1siyici,hsiy~ci),1≠i≠n,n+1→1

Eventually A successfully forges (c1,…,cn,s1,…,sn,y~) and M performs rewind-simulation to generate (c′1,s1′,…,s′n,y~) . Denote the forgery signer of A is $j$, then M can obtain xj as follows:

cj+1=H1(L,y~,g1sjyjcj,hsjy~cj)

c′j+1=H1(L,y~,g1sj′yjcj′yjcj′,hsj′y~cj′)

Remember y~=hr , then

sj+cjxj=sj′+cj′xj

sj+cjr=sj′+cj′r

Solve and obtain

xj=sj−sj′cj−cj′

According to [27], the probability of M to achieve a solution is at least (1/[n(qH+nqS)Q(k)])2 , which is non-negligible. Therefore, once A is able to forge signature with an advantage of 1/Q(k) , M is able to solve Co-CDH problem with an advantage of (1/[n(qH+nqS)Q(k)])2 . Desired contradiction. Theorem is proved.

Theorem 4. (Privacy Preserving) If and only if DDHP (Decisional Diffie-Hellman Problem) is hard, in the random oracle model, the probability of distinguishing signer of an LHARS signature is at most 1/n , where n is the size of ring list L.

Proof. For any g1,h∈G1 , and 1≤j≤n , the distribution of (c1,…,cn,s1,…,sn) is identical. Therefore, the probability of a PPT adversary A to distinguish cj,sj from (c1,…,cn,s1,…,sn) , in order to point out the signer uj , is at most 1/n . Reference [27] gives further detailed explanation.

5.2 Performance Analysis

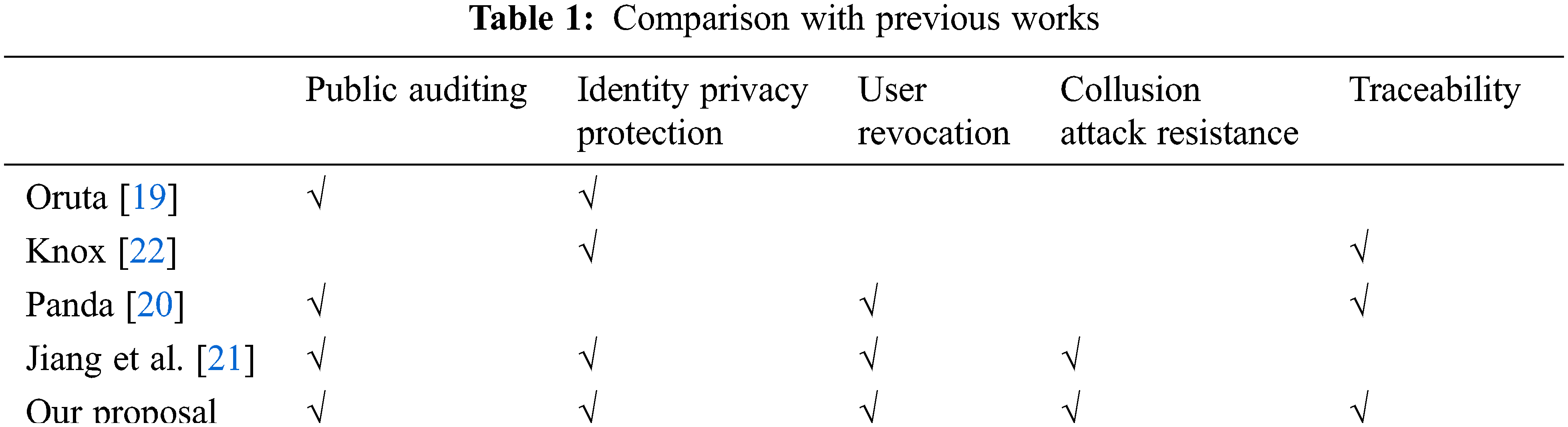
Our proposal is a comprehensive solution for group data integrity auditing, including improvement on both security and efficiency. First of all, we compare the security features of our proposal with other comparable solutions, shown in Tab. 1.

To evaluate the practical performance of our scheme, we deploy an instance of our proposed scheme on virtual private server (VPS), which has 1 CPU, 2GB memory and 2TB bandwidth. The server has installed the open source blockchain platform Hyperledger Fabric and we implemented chaincode for our scheme based on Fabric SDK for JAVA. Fabric offers necessary membership services, certificate authority management, consensus plugin and customizable endorsement policies, thus we can focus on implementing our scheme itself.

In our instance, the on-chain operations are wrapped as smart contracts, while off-chain algorithms are implemented in the form of local scripts, both written in Node.js. Entities in our scheme execute their local scripts to complete the off-chain computation and invoke smart contracts to finished the on-chain parts. In this way, we realize the separation of on-chain and off-chain parts.

Choosing a secure length of 1024 bit, time for the off-chain part of generating signature is shown in Fig. 7. We deploy two patterns of our proposal--original and simplified ones. For one file divided into blocks, an intuitive way to reduce computational overhead and storage cost is using the same ring for all the blocks, which will not compromise the security, called ‘’simplified’’. We also implement a few comparable works under the same security length, in order to present efficiency of our proposal.

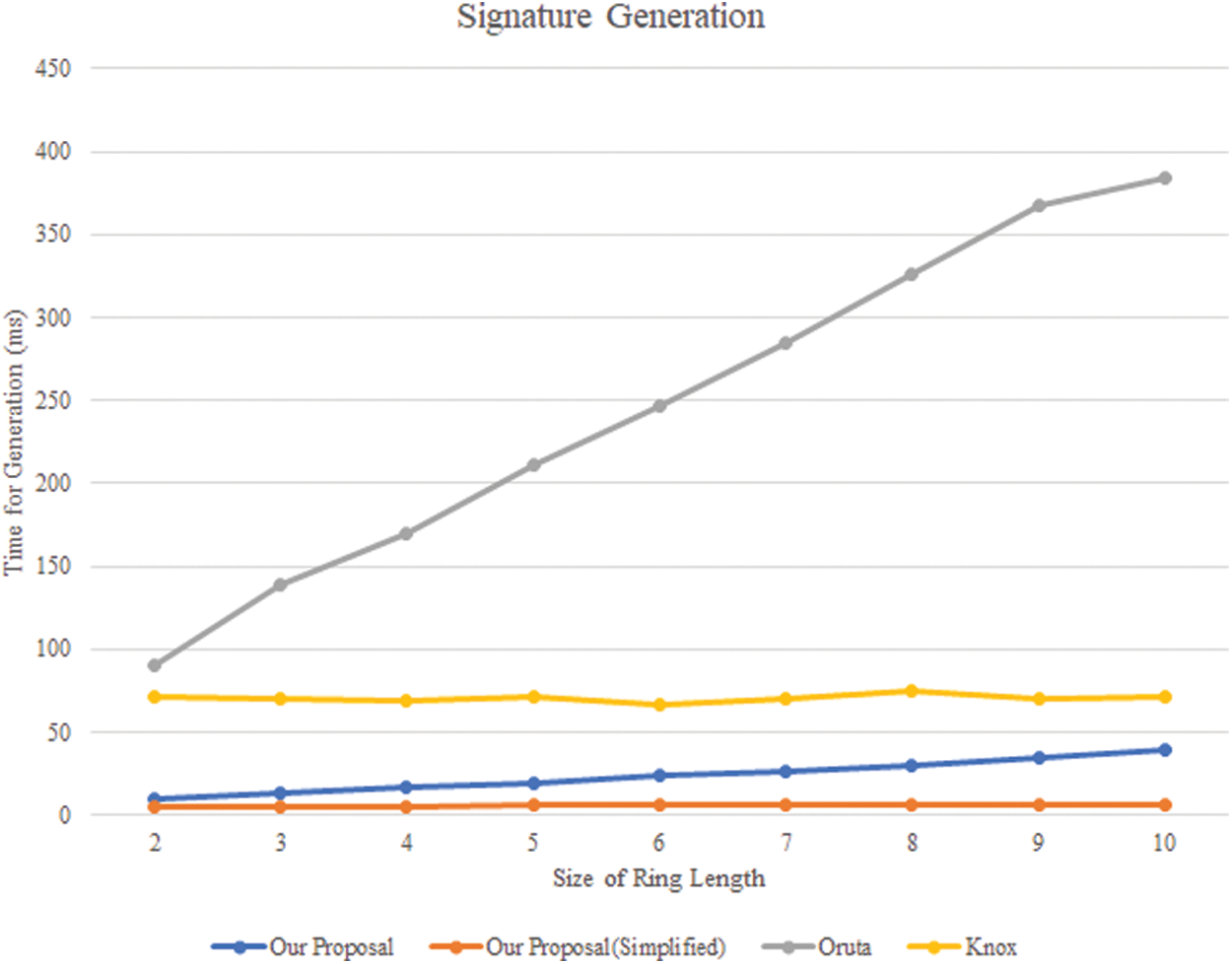
Figure 7: Time for signature generation

As the size of ring length grows, time of generating signature for data owner increases from 10.07 ms per block to 39.36 ms for our original proposal, as well as from 5.39 to 6.16 ms for simplified mode. However, previous works cost much more time to generate signatures. The main reason is that Knox needs to compute more modular exponential operations and Oruta has complex progress of group signature computation. Work of Jiang et al. [21] has the same signing algorithms with those of Knox, and will undoubtedly suffer from the heavy overhead of modular exponentiation. The result also suggests that choosing a reasonable size of ring, computation overhead of our proposal for data owner is very low.

Under the same secure length mentioned above, we also measure the time cost of re-signing signature for the new data owner, as shown in Fig. 8. The time cost varies from 0.19 to 0.84 ms per block along with the increasing of ring length. Comparing to generating signature, the computation overhead of re-signing is relatively much lower, which also shows the efficiency of our scheme.

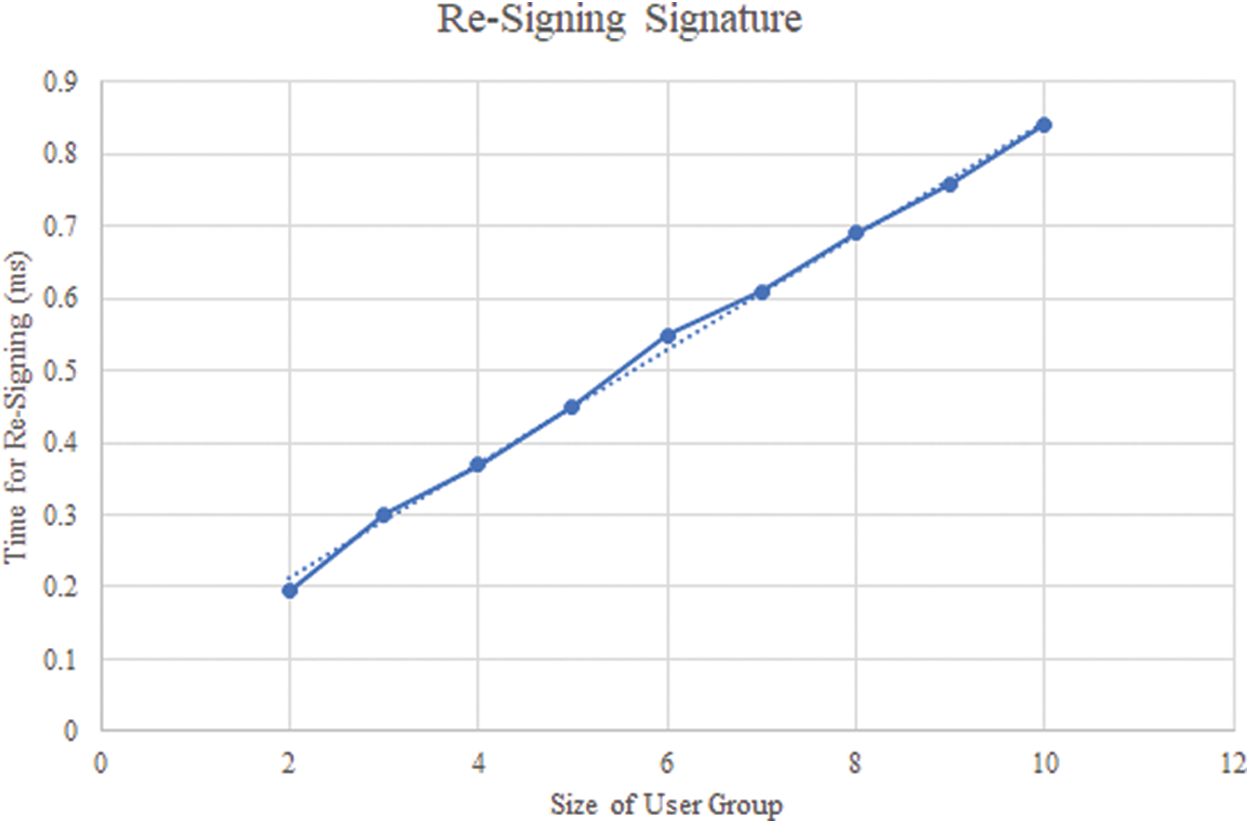
Figure 8: Time for re-signing signature

To evaluate the performance of on-chain operations in blockchain network, we also perform smart contracts in VPS. We employ the benchmark test tool Hyperledger Caliper, which enables users to write the test and network configuration, launching an instance and executing required smart contracts defined in given chaincode automatically. We execute 7 rounds of test, 100 times per round. Each round the proportion of challenged blocks varies from 1%, 10%, 20%, 40% to 100%. Since the verification is the most expensive part for endorsement peer (TPA), we choose it as the test chaincode. Fig. 9 shows the indicators of efficiency for each round. The figure suggests that each round does not show a huge difference in verification. The possible reason is that we use an aggregated proof, thus the main cost of such verification lies in the computation of bilinear mapping. It also proves that our scheme has a relatively smooth performance in on-chain operation.

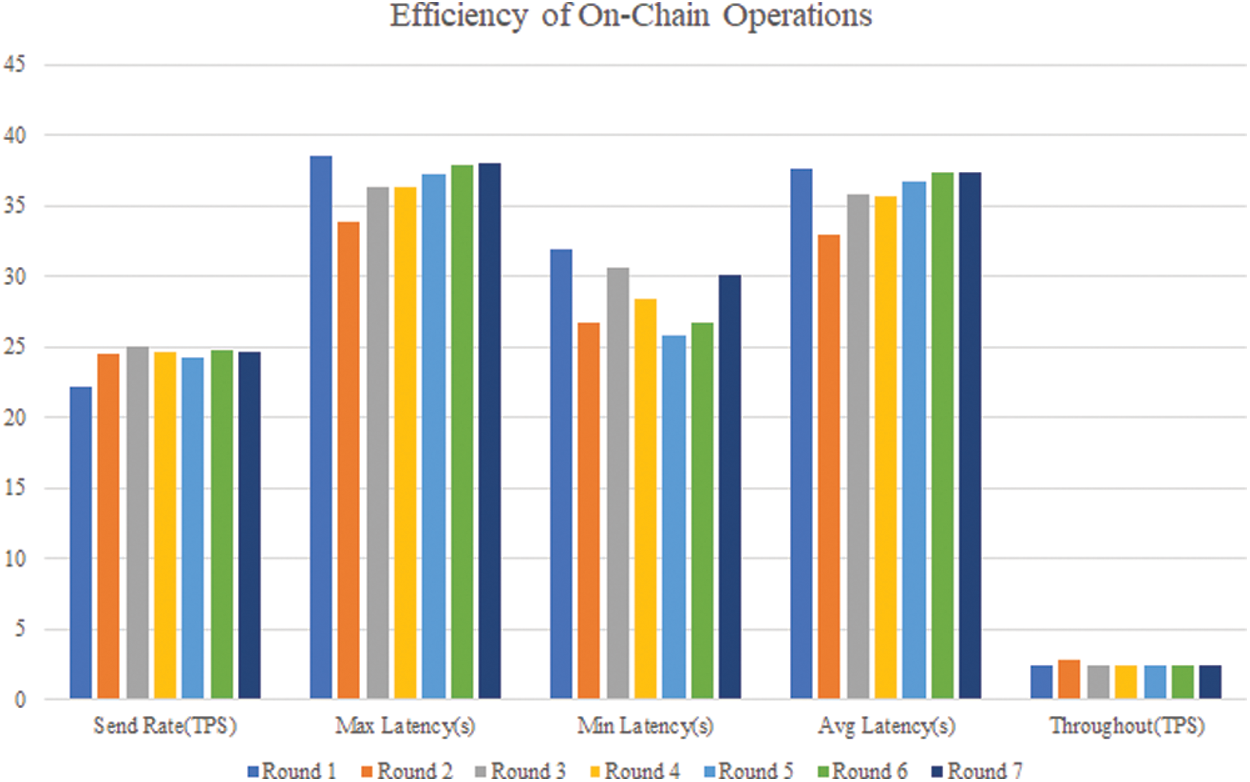
Figure 9: 7-round test for on-chain verification

6  Conclusion

This paper focuses on exploring a public PDP scheme for shared data with secure group user revocation. We find that previous works failed to obtain both security and identity privacy for group users. We design a re-signing method for public PDP scheme to hide the identity of data owner in a n-member ring. On the other hand, we also try to build a non-repudiation scheme which can resist collusion between CSP, TPA and users. Blockchain network and smart contracts offer reliable properties to solve such problem. Blending the two points above, we design a novel blockchain-based PDP scheme with group user revocation. Security analysis and performance evaluation prove that our scheme is both secure and efficient.

Funding Statement: The work is supported by the National Key Research and Development Program of China (No. 2018YFC1604002) and the National Natural Science Foundation of China (No. U1836204, No. U1936208, No. U1936216, No. 62002197).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Rudniy, “Data warehouse design for big data in academia,” Computers, Materials & Continua, vol. 71, no. 1, pp. 979–992, 2022. [Google Scholar]

 2.  A. Berguiga and A. Harchay, “An IoT-based intrusion detection system approach for tcp syn attacks,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3839–3851, 2022. [Google Scholar]

 3.  R. Jia, Y. Xin, B. Liu and Q. Qin, “Dynamic encryption and secure transmission of terminal data files,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1221–1232, 2022. [Google Scholar]

 4.  J. Almutairi and M. Aldossary, “Exploring and modelling IoT offloading policies in edge cloud environments,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 611–624, 2022. [Google Scholar]

 5.  L. Jiang and Z. Fu, “Privacy-preserving genetic algorithm outsourcing in cloud computing,” Journal of Cyber Security, vol. 2, no. 1, pp. 49–61, 2020. [Google Scholar]

 6.  M. Naor and G. N. Rothblum, “The complexity of online memory checking,” Journal of the ACM, vol. 56, no. 1, pp. 1–46, 2009. [Google Scholar]

 7.  A. Oprea, M. K. Reiter and K. Yang, “Space-efficient block storage integrity,” in Proc. of 12th Annual Network and Distributed System Security Symp. (NDSS), San Diego, California, USA, 2005. [Google Scholar]

 8.  G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. of 14th ACM Conf. Computer and Communication Security (CCS ‘07), Alexandria, Virginia, USA, pp. 598–609, 2007. [Google Scholar]

 9.  Q. Wang, C. Wang, K. Ren, W. Lou and J. Li, “Enabling public auditability and data dynamics for storage security in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 22, no. 5, pp. 847–859, 2011. [Google Scholar]

10. X. Tang, Y. Qi and Y. Huang, “Reputation audit in multi-cloud storage through integrity verification and data dynamics,” in Proc. of 2016 IEEE 9th Int. Conf. on Cloud Computing (CLOUD), San Francisco, California, USA, pp. 624–631, 2016. [Google Scholar]

11. Z. Mo, Y. A. Zhou, S. G. Chen and C. Z. Xu, “Enabling non-repudiable data possession verification in cloud storage systems,” in Proc. of 2014 IEEE 7th Int. Conf. on Cloud Computing (CLOUD), Anchorage, Alaska, USA, pp. 232–239, 2014. [Google Scholar]

12. H. Jin, H. Jiang and K. Zhou, “Dynamic and public auditing with fair arbitration for cloud data,” IEEE Transactions on Cloud Computing, vol. 6, no. 3, pp. 680–693, 2018. [Google Scholar]

13. C. Liu, R. Ranjan, C. Yang, X. Zhang, L. Wang et al., “MuR-DPA: Top-down levelled multi-replica merkle hash tree based secure public auditing for dynamic big data storage on cloud,” IEEE Transactions on Computers, vol. 64, no. 9, pp. 2609–2622, 2015. [Google Scholar]

14. Z. Mo, Y. A. Zhou and S. Chen, “A dynamic proof of retrievability (POR) scheme with O(log n) complexity,” in Proc. of 2012 IEEE Int. Conf. on Communications (ICC), Ottawa, Canada, pp. 912–916, 2012. [Google Scholar]

15. Y. Zhu, H. Wang, Z. Hu, G. J. Ahn, H. Hu et al., “Dynamic audit services for integrity verification of outsourced storages in clouds,” in Proc. of ACM Symp. on Applied Computing (SAC ‘11), TaiChung, Taiwan, pp. 1550–1557, 2011. [Google Scholar]

16. Y. Zhu, H. Hu, G. J. Ahn and M. Yu, “Cooperative provable data possession for integrity verification in multi-cloud storage,” IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 12, pp. 2231–2244, 2012. [Google Scholar]

17. K. Yang and X. Jia, “An efficient and secure dynamic auditing protocol for data storage in cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 9, pp. 1717-1726, 2013. [Google Scholar]

18. H. Tian, Y. Chen, C. C. Chang, H. Jiang, Y. Huang et al., “Dynamic-hash-table based public auditing for secure cloud storage,” IEEE Transactions on Services Computing, vol. 10, no. 5, pp. 701–714, 2017. [Google Scholar]

19. B. Wang, B. Li and H. Li, “Oruta: Privacy-preserving public auditing for shared data in the cloud,” IEEE Transactions on Cloud Computing, vol. 2, no. 1, pp. 43–56, 2014. [Google Scholar]

20. B. Wang, B. Li, and H. Li. “Panda: Public auditing for shared data with efficient user revocation in the cloud,” IEEE Transactions on Services Computing, vol. 8, no. 1, pp. 92–106, 2013. [Google Scholar]

21. T. Jiang, X. Chen and J. Ma, “Public integrity auditing for shared dynamic cloud data with group user revocation,” IEEE Transactions on Computers, vol. 65, no. 8, pp. 2363–2373, 2015. [Google Scholar]

22. B. Wang, B. Li and H. Li, “Knox: Privacy-preserving auditing for shared data with large groups in the cloud,” in Proc. of Int. Conf. on Applied Cryptography and Network Security, Berlin, Heidelberg, Springer, 2012. [Google Scholar]

23. H. Wang, “Proxy provable data possession in public clouds,” IEEE Transactions on Services Computing, vol. 6, no. 4, pp. 551–559, 2013. [Google Scholar]

24. J. Yuan and S. Yu, “Efficient public integrity checking for cloud data sharing with multi-user modification,” in Proc. of 2014 IEEE Int. Conf. on Computer Communications (INFOCOM), Toronto, Canada, pp. 2121–2129, 2014. [Google Scholar]

25. Y. Zhang, C. Xu, X. Lin and X. S. Shen, “Blockchain-based public integrity verification for cloud storage against procrastinating auditors,” IEEE Transactions on Cloud Computing, vol. 9, no. 3, pp. 923–937, 2021. [Google Scholar]

26. P. C. Wei, D. Wang, Y. Zhao, S. K. S. Tyagi and N. Kumar, “Blockchain data-based cloud data integrity protection mechanism,” Future Generation Computer Systems, vol. 102, pp. 902–911, 2020. [Google Scholar]

27. J. K. Liu, V. K. Wei and D. S. Wong, “Linkable spontaneous anonymous group signature for ad hoc groups,” in Proc. of Australasian Conf. on Information Security and Privacy, Sydney, Australia, pp. 325–335, 2004. [Google Scholar]