Hybrid Bacterial Foraging Optimization with Sparse Autoencoder for Energy Systems

1  Introduction

Internet of Things (IoT) represents the network-oriented interrelationship of daily used structures. It refers to the self-organizing wireless connection of devices focused on the interrelationship of day to day objects [1]. The IoT mechanism aids to attain intercommunication among an individual and machine or machine to machine [2]. The amalgamation of grid tools in utility network systems will definitely influence amazing conversion in grid administration and electrical power usage in forthcoming years [3]. The systematic modifications in load regulation, accompanied by boosted dispersal of unconventional power sources, recommends a new array of challenges in balancing expenses and production [4]. With this rising implementation of unconventional power sources and increase in familiarity with plugin hybrid electric vehicles (PHEVs) and every electric vehicle (EV), the demand is more effective electric infrastructures [5]. Fig. 1 illustrates the process of energy management system.

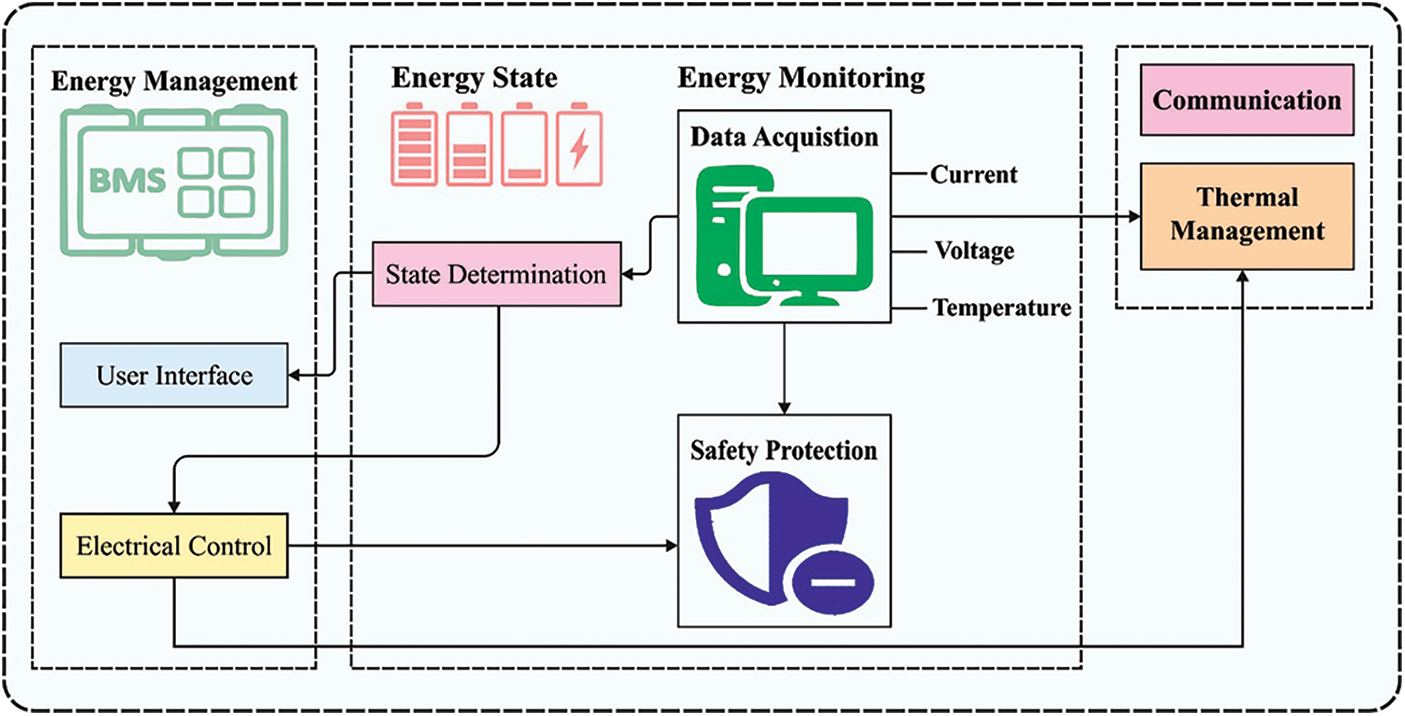
Figure 1: Process of energy management systems

The state of charge (SOC) is referred to as a critical criterion to represent the present and existing charge of batteries [6]. But, it is very hard to forecast SOC of the battery because of the battery’s nonlinear features and complex electrochemical reaction. For example, ampere-hour technique use present integration for forecasting SOC which is considered to be a simple methodology and could be applied with relatively lower energy consumption [7,8]. The electrochemical model depends on the external policies that use lots and lots of parameters with incomplete differential equations to estimate the battery SOC. but, a massive computational load highly raises the execution difficulty in practical use. In recent times, modeling batteries through neural networks (NNs) is also been broadly executed. The application zones of NNs deliver significant accessibility to the modeling procedure [9]. It could not necessary to evaluate the model parameter independently at various SOC points. The implemented method explains the interrelation among SOC and its influential elements with mathematical formulas [10].

Liu et al. [11] focus on developing an IoT-based energy management scheme based on edge computing structure through deep reinforcement learning. Firstly, a summary of IoT-based energy handling is defined. Next, the software and framework of an IoT-based scheme using edge computing are presented. In [12], IoT energy management has a tendency to accomplish green energy response and transmission from demand and supply. Consequently, smart industrial preparation should be capable of using energy productively to resolve related problems.

Safara et al. [13] focus on energy utilization, in which the priority oriented routing (PriNergy) technique is presented. The technique is depending upon the routing method for low-power and lossy networks (RPL) that defines routing via content. Every network slot employs timing pattern while transmitting information to the termination when taking network traffic, image, and audio information into account. In [14], a new method is presented for handling energy consumption in a smart grids platform using profound penetration of renewable resources. The presented method compares some predictive methods for precise predicting of energy using day ahead and hourly preparation. Particle swarm optimization (PSO) based support vector machine (SVM) regression technique outperformed by various other predictive methods in terms of efficiency.

Utama et al. [15] recommended SOC approximation with an artificial neural network (ANN) to decrease the approximation error because of physical parameters and decrease computational cost by means of an IoT-assisted embedded scheme. Asaad et al. [16] suggest a Battery Monitoring System (BMS) with coulomb counting technique for SoC approximation and message based MQ Telemetry Transport (MQTT) as the transmission method. The presented method is executed on hardware framework with the environment, suitable sensing technique, central processor, and interfacing devices.

This paper offers a new Hybridization of Bacterial foraging optimization with Sparse Autoencoder (HBFOA-SAE) model for IoT Enabled energy systems. The proposed HBFOA-SAE model majorly employs SAE model for proper determination of the SOC values in the energy systems. Next, for improving the performance of the SOC estimation process, the HBFOA is employed. In addition, the HBFOA technique is derived by the integration of the hill climbing (HC) concepts with the BFOA to improve the overall efficiency. For ensuring better outcomes for the HBFOA-SAE model, a comprehensive group of simulations are executed and the outcomes are inspected under several aspects.

2  The Proposed Model

In this study, a new HBFOA-SAE model has been developed for proper determination of the SOC values in the energy systems. Next, for improving the performance of the SOC estimation process, the HBFOA is employed. In addition, the HBFOA technique is derived by the integration of the HC concepts with the BFOA to improve the overall efficiency.

The study has established an HBFOA-SAE method for precise SOC estimates in HEV. Initially, the input as well as output of presented method are defined. According to the concept of NN, the sampling procedure of the SOC occur in step k, SOC(k) is taken into account as the input as it signifies the existing situation of the battery. As the direct variable current I(k) is taken into account as the input, as well as the battery voltage V(k) is denoted by the output. v(k−1) indicates the situation of the battery in the last phase and it means the previous operational status.

V(k)=OCV(SOC(k))+RsI(k)+URC(k) (1)

whereas Rs indicates the battery internal resistance, URC shows the RC circuit voltage associated with URC(k−1) through the 1st order differential formula. To generate the input directly evaluated parameters, URC(k−1) is taken into account as V(k−1) . Consequently, V(k−1) holds a direct link with V(k) . It can be expressed in the following

V(k)=f(V(k−1),I(k),SOC(k)), (2)

It undergoes estimates through the learning method. The input and output vectors of the presented technique have been determined by p(k)=[V(k−1)ISOC(k)]T and V(k) .

F(p(k))=V(k) (3)

The input and output sample of {p(k)∼V(k)} is acquired previous to model training. Assume p(k)=xj and V(k)=tj. The trained subset is denoted as {(xj,tj)|xj∈Rn,tj∈Rm,j=1,…,N} .

2.1 Process Involved in SOC Estimation

Primarily, the proposed HBFOA-SAE model employs SAE model for proper determination of the SOC values in the energy systems. Auto encoder (AE) is an unsupervised 3-layer NN containing input, hidden, and output layers (also mentioned that reconstruction layer). The AE is slowly transformed into particular feature vectors as abstract feature vectors that are well realizing the non-linear transformation in higher to lower dimensional data spaces [17]. The work flow procedure of the automatic encoding is separated as to 2 phases such as encoder and decoder and these 2 stages are demonstrated as:

The encoder procedure in the input to hidden layers:

H=gθ1(X)=σ(WijX+φ1) (4)

The decoder method in the hidden to reconstruction layers:

Y=gθ2(H)=σ(WjkH+φ2) (5)

Here, Wij∈Rm×n signifies the weighted linked matrix amongst input as well as hidden layers. Wjk∈Rn×m denotes the weighted connection matrix amongst hidden as well as output layers. For reconstructing the input data as correctly as feasible but decreasing the resource utilization under the method trained, Wjk=WijT commonly exist from the experiment. φ1∈Rn×1 and φ2∈Rm×1 are the bias vectors of input as well as hidden layer correspondingly. gθ1(⋅) and gθ2(⋅) represents the activation function of hidden as well as output layer neurons correspondingly that role is for mapping the network summation outcome to zero and one. It can be utilized sigmoid function as activation function as:

gθ1(⋅)=gθ2(⋅)=11+e−x (6)

With changing the parameters of encoding as well as decoding, the error amongst the output reconstructed data and original data are minimized representing AE reconstructing the original data with trained. The reconstruction error function JE (W,φ) amongst H and Y utilizes the mean squared-error function as illustrated in Eq. (7), whereas N refers the amount of input instances.

JE(W,φ)=12N∑r=1N⁡‖Y(r)−X(r)‖2 (7)

The concept of sparse coding was initially presented for simulating the computation learning of the receptive field of cells in mammalian primary visual cortex. We assume that the average activation ρ^j methods a constant ρ that is closer to zero.

KL(ρ‖ρ^)=ρlogρρ^j+(1−ρ)log1−ρ1−ρ^j (8)

Now, the error function of the sparse AE comprises: regularization term and mean square error term. It is given in the following:

Jsparse(W,b)=J(W,b)+μ∑j=1m⁡KL(ρ‖ρ^j) (9)

Jsparse(W,b)=JE(W,b)+μ∑j=1m⁡KL(ρ‖ρ^j)+λ2∑r=13⁡∑i=1m⁡∑j=1m+1⁡(wijr)2 (10)

2.2 HBFOA Based Parameter Optimization

At this stage, the HBFOA technique is derived by the integration of the HC concepts with the BFOA to improve the overall efficiency. The original BFOA is theorized as swarming, chemotaxis, elimination-dispersal, and reproduction. Generally, the swarming process has adverse impact on the BFOA accuracy [18].

Chemotaxis process: The bacteria movement can be inspired by the chemotaxis process. Here, tumbling and swimming are the two major activities of bacteria. Xi(j,k,l) characterizes the ith bacterium at jth chemotaxis, kth reproduction, lth elimination-dispersal; c(i) indicates the chemotaxis step length; and Δ(i) represents a random direction vector within (−1, 1).

xi(j+1,k,l)=xi(j,k,l)+C(i)Δ(i)Δ(i)TΔ(i) (11)

Reproduction operation: Here, the survival capacity of bacteria is measured according to the fitness value. A small fitness value implies the bacterium has a high capacity to achieve nutrition for surviving, then the bacteria are assumed healthier. The healthy half of the bacteria depends on the fitness value is carefully chosen as parent to generate offspring in a similar place. The bacteria reproduction is shown in the following, whereas ji(j,k,l) denotes the fitness value of ith bacterium at jth chemotaxis, kth reproduction, lth elimination-dispersal.

Jhealth=∑j=1Nc⁡ji(j,k,l). (12)

Elimination-dispersal process: Once the evolutionary environment deteriorates, the bacteria migrates to a novel location to avoid trapping into local optimal and the process is given below. Fig. 2 demonstrates the flowchart of BFOA.

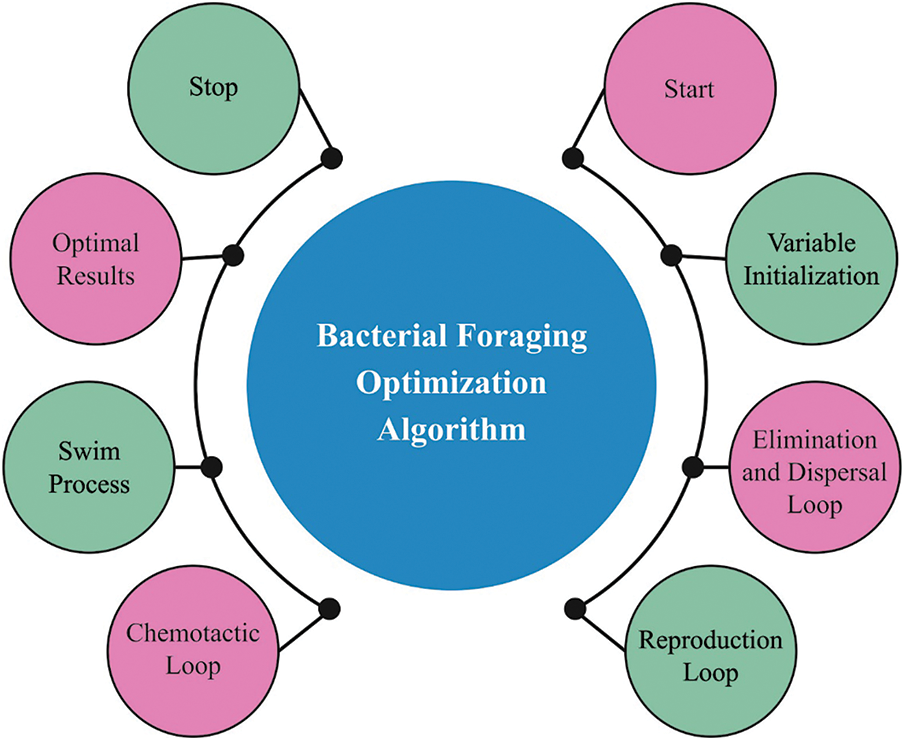
Figure 2: Flowchart of BFOA

For every bacterium

if rand < Ped

xi = VarMin + rand * (VarMax − Varmin)

end

end

For boosting the technique’s exploitation capability and quality of final solutions, AβHC is combined as to the fundamental BFOA to support searching the neighborhoods for optimum solutions during this case [19]. And the explanation of AβHC was signified mathematical as follows. In order to provide existing solution Xi=(xi,1,xi,2,…,xi,D), AβHC is iteratively created an improved solution Xi″=(xi,1″,xi,2″,…,xi,D″) on the fundamental of 2 control operators: N and β operators. The N operator primary transfers Xi to a novel neighborhood solution. Xi′=(xi,1′,xi,2′,…,xi,D′) that is determined in Eqs. (13) and (14) as:

xij′=xij±U(0,1)×N,j=1,2,…,D (13)

N(t)=1−t1KMaxiter1K (14)

whereas U(O,1) signifies the arbitrary number from the interval of zero and one , xij refers the value of decision variable from the jth dimensional, t stands for the existing iteration, Maxiter signifies the maximal amount of iterations, N denotes the bandwidth distance amongst existing solution and their neighbor, D signifies the spatial dimensional, and the parameter K is a constant.

3  Performance Validation

In this section, the experimental validation of the HBFOA-SAE model is tested using three datasets namely BJDST (Dataset-1), US06 (Dataset-2), and FUDS (Dataset-3). Tabs. 1–3 offer a detailed SOC estimation outcomes of the HBFOA-SAE model under distinct number of hidden units (HUs).

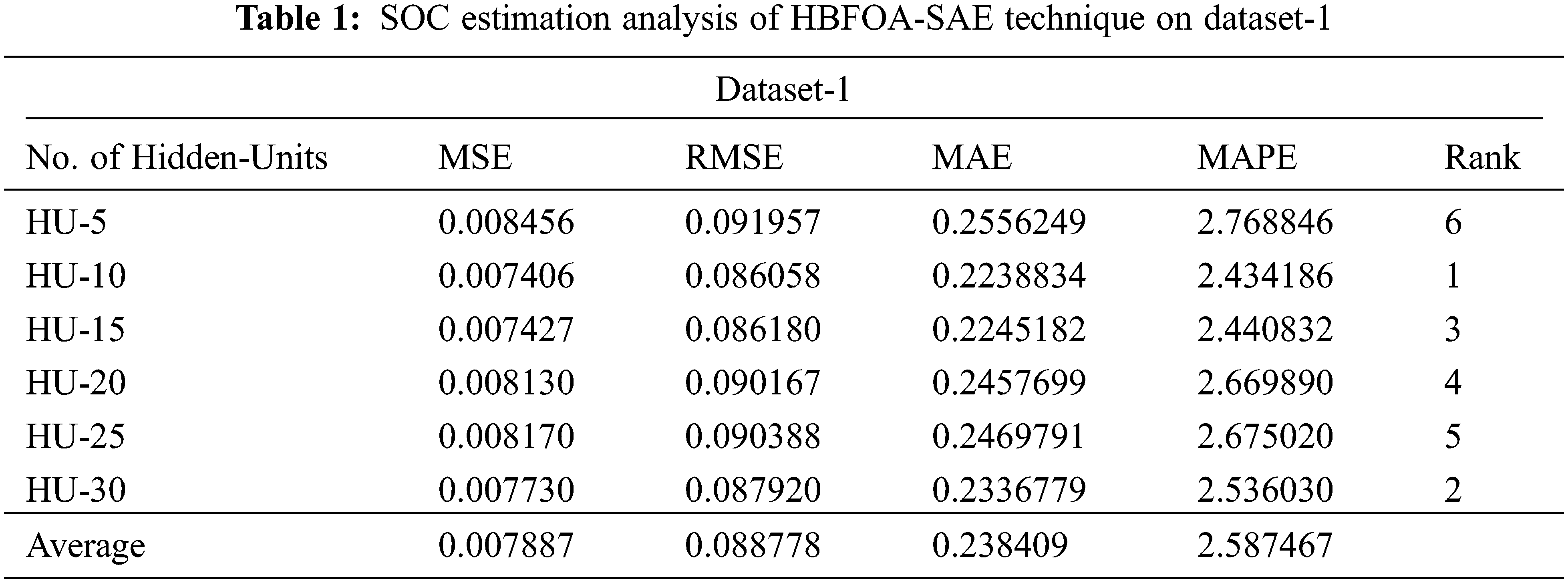
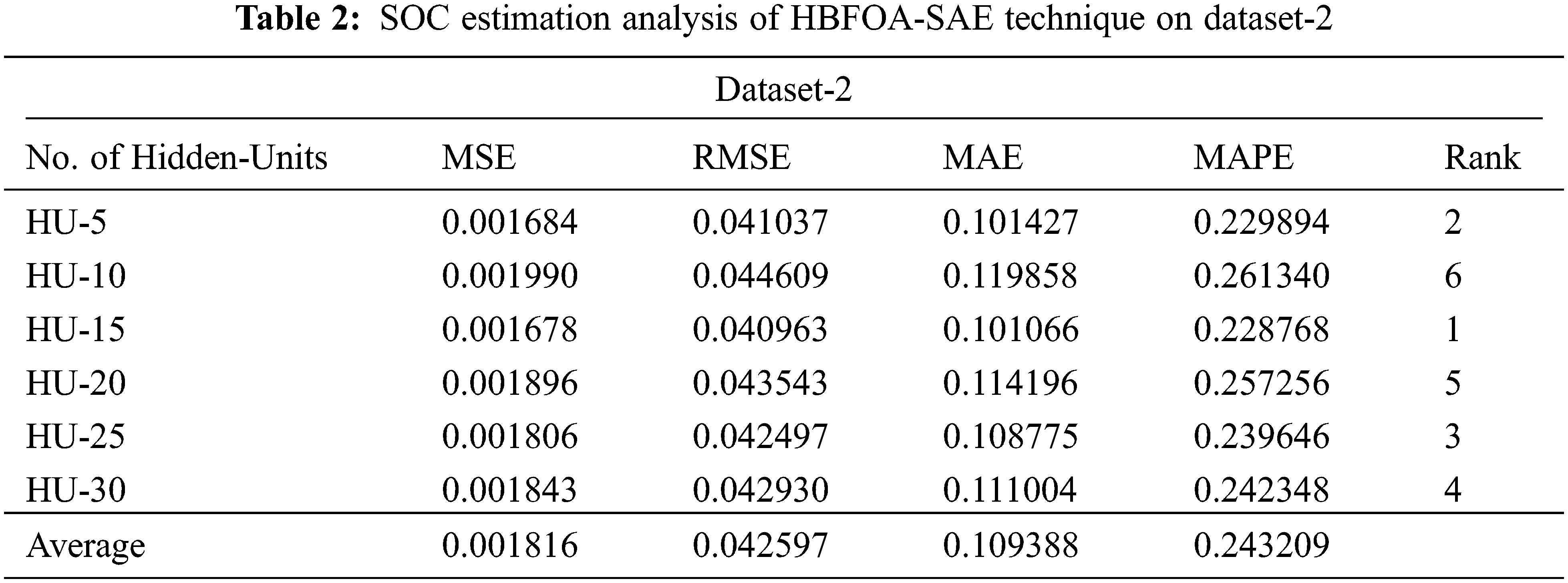
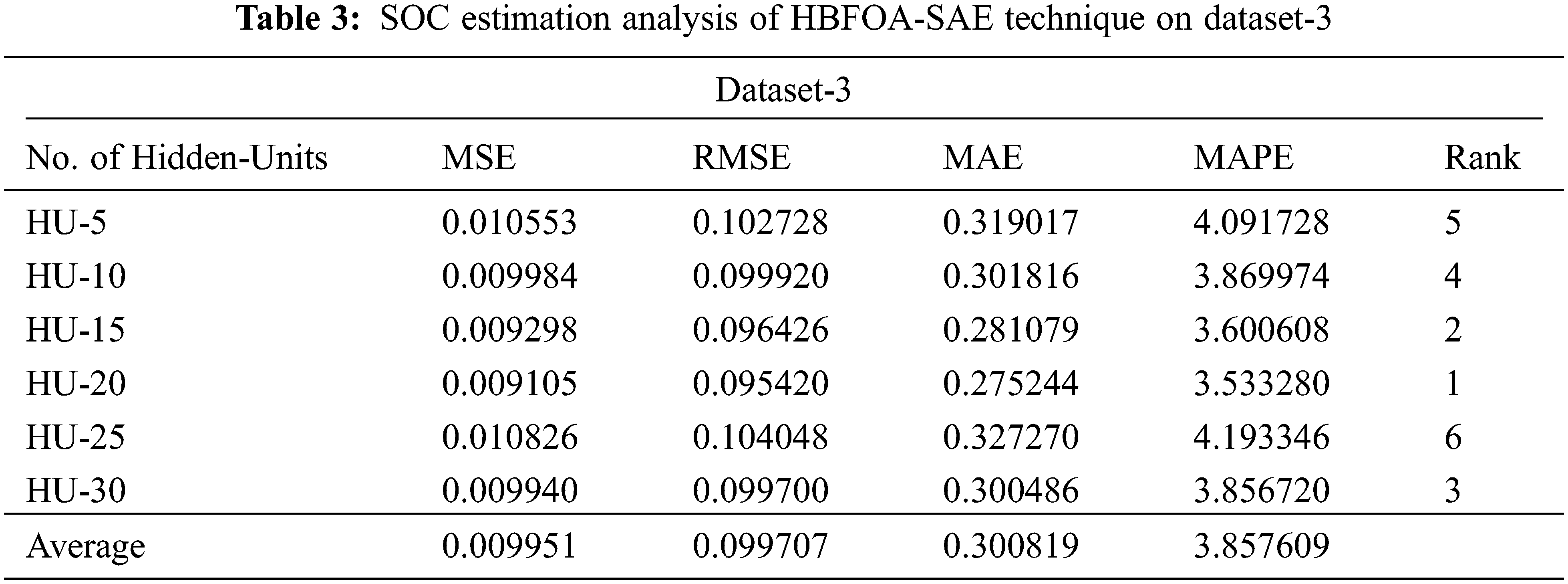
Fig. 3 reports a detailed mean square error (MSE) examination of the HBFOA-SAE model under distinct HUs and datasets. On dataset-1 and HU-5, the HBFOA-SAE model has provided a MSE of 0.008456. Besides, on dataset-1 and HU-30, the HBFOA-SAE model has offered a MSE of 0.007730. In addition, on dataset-2 and HU-5, the HBFOA-SAE model has gained a MSE of 0.001990. Besides, on dataset-2 and HU-30, the HBFOA-SAE model has reached a MSE of 0.001843. Moreover, on dataset-3 and HU-5, the HBFOA-SAE model has resulted to a MSE of 0.010553. Furthermore, on dataset-3 and HU-30, the HBFOA-SAE model has provided a MSE of 0.009940.

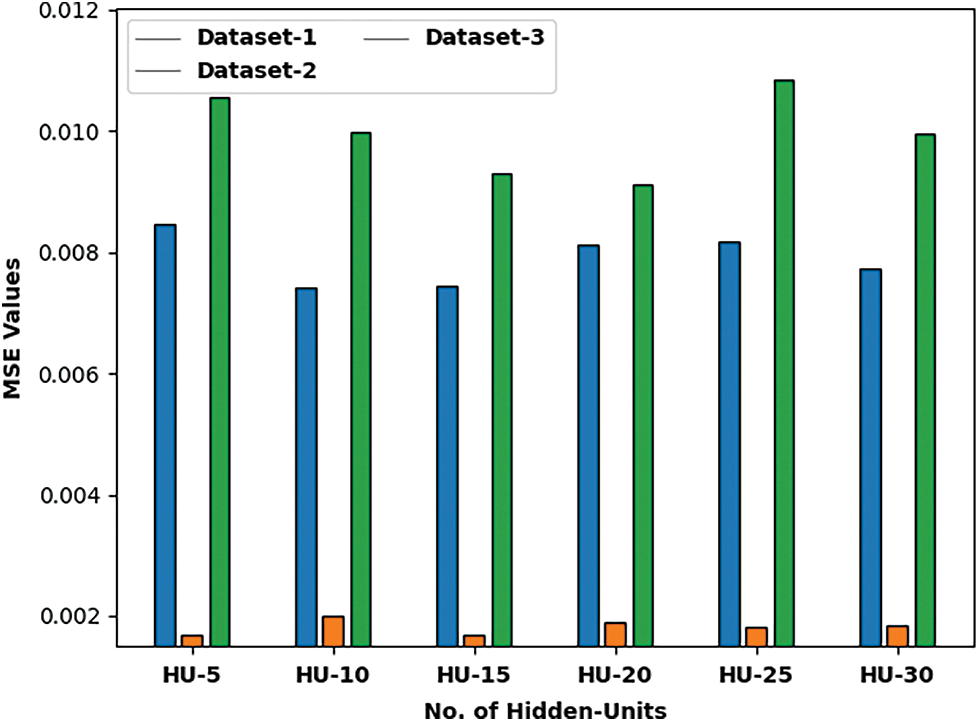
Figure 3: MSE analysis of HBFOA-SAE technique under three datasets

Fig. 4 defines a detailed root mean square error (RMSE) examination of the HBFOA-SAE model under distinct HUs and datasets. On dataset-1 and HU-5, the HBFOA-SAE model has provided a RMSE of 0.091957. Besides, on dataset-1 and HU-30, the HBFOA-SAE model has offered a RMSE of 0.087920. Furthermore, on dataset-2 and HU-5, the HBFOA-SAE model has gained a RMSE of 0.041037. Moreover, on dataset-2 and HU-30, the HBFOA-SAE model has reached a RMSE of 0.042930. Additionally, on dataset-3 and HU-5, the HBFOA-SAE model has resulted to a RMSE of 0.102728. Also, on dataset-3 and HU-30, the HBFOA-SAE model has provided a RMSE of 0.099700.

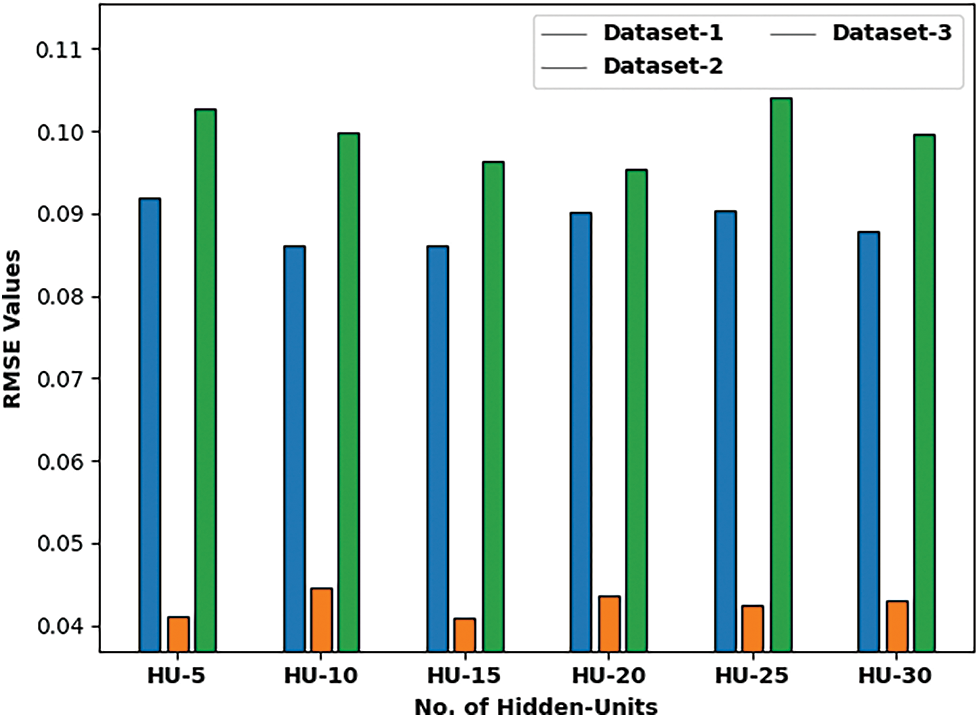
Figure 4: RMSE analysis of HBFOA-SAE technique under three datasets

Fig. 5 reports a detailed mean absolute percentage error (MAPE) examination of the HBFOA-SAE model under distinct HUs and datasets. On dataset-1 and HU-5, the HBFOA-SAE model has provided a MAPE of 2.768846. Followed by dataset-1 and HU-30, the HBFOA-SAE model has offered a MAPE of 2.536030. Likewise, on dataset-2 and HU-5, the HBFOA-SAE model has gained a MAPE of 0.229894. Along with that, on dataset-2 and HU-30, the HBFOA-SAE model has reached a MAPE of 0.242348. At the same time, on dataset-3 and HU-5, the HBFOA-SAE model has resulted in a MAPE of 4.091728. Lastly, on dataset-3 and HU-30, the HBFOA-SAE model has provided a MAPE of 3.856720.

Figure 5: MSPE analysis of HBFOA-SAE technique under three datasets

In order to further assure the enhanced performance of the HBFOA-SAE model, a comparative examination with the deep learning based SOC (DLSOC) and optimal extreme learning machine (ELM) models takes place under distinct measures as shown in Tab. 4 [20,21].

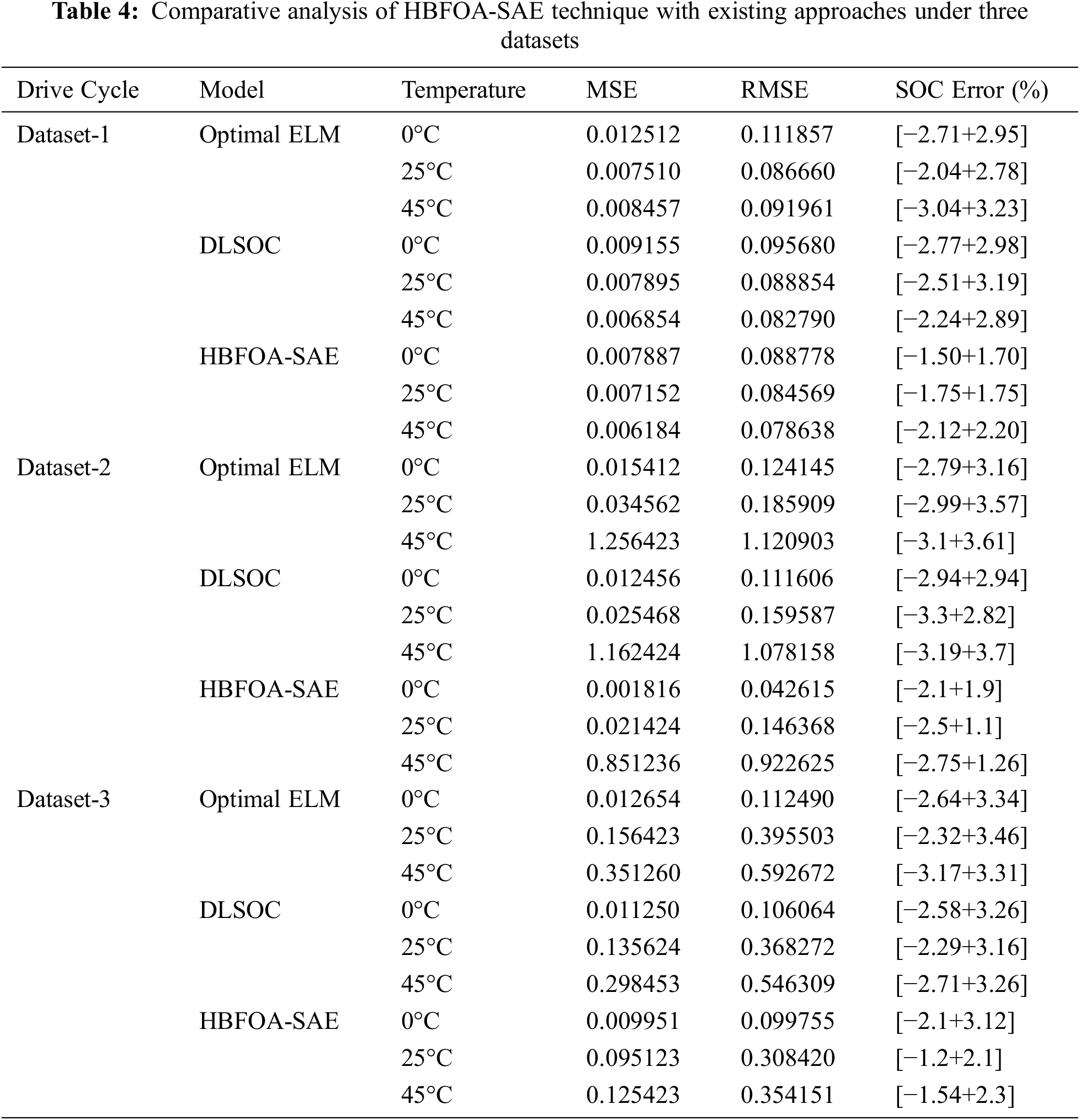
Fig. 6 demonstrates the MSE, RMSE, and SOC error values of the HBFOA-SAE model with existing DLSOC and optimal ELM approaches under distinct temperatures on dataset-1. The experimental results implied that the HBFOA-SAE model has shown effectual outcomes with minimal values of MSE, RMSE, and SOC error. For instance, with 0°C, the HBFOA-SAE model has offered MSE, RMSE, and SOC errors of 0.007887, 0.088778, and [−1.50+1.70] respectively. Similarly, with 25°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.007152, 0.084569, and [−1.75+1.75] respectively. Similarly, with 45°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.006184, 0.078638, and [−2.12+2.20] respectively.

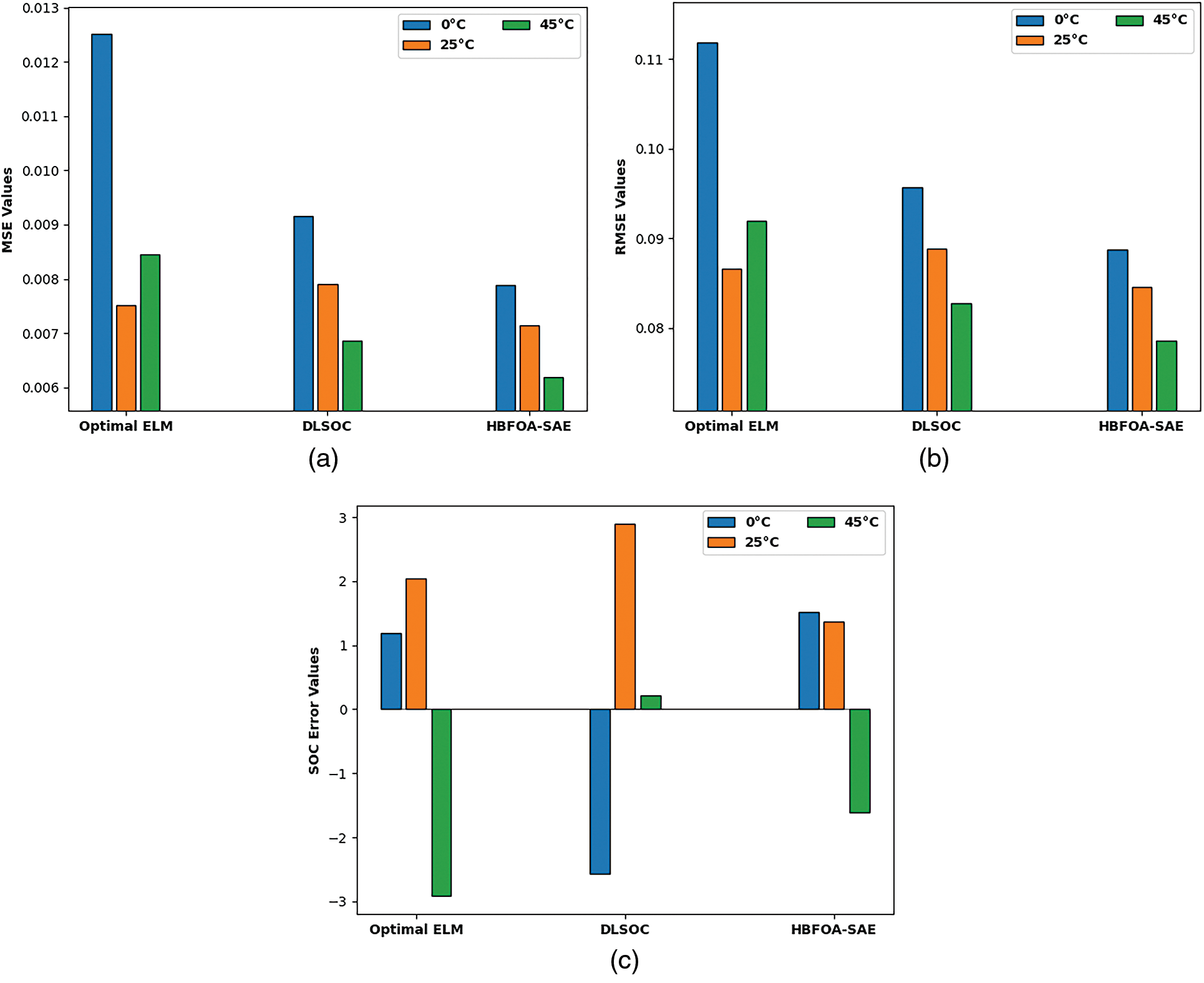
Figure 6: Comparative analysis of HBFOA-SAE technique with existing approaches on Dataset-1

Fig. 7 exhibits the MSE, RMSE, and SOC error values of the HBFOA-SAE model with existing DLSOC and optimal ELM approaches under distinct temperatures on dataset-2. The experimental results implied that the HBFOA-SAE model has shown effectual outcomes with minimal values of MSE, RMSE, and SOC error. For instance, with 0°C, the HBFOA-SAE model has offered MSE, RMSE, and SOC errors of 0.001816, 0.042615, and [−2.1+1.9] respectively. In the same way, with 25°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.021424, 0.146368, and [−2.5+1.1] respectively. At last, with 45°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.851236, 0.922625, and [−2.75+1.26] respectively.

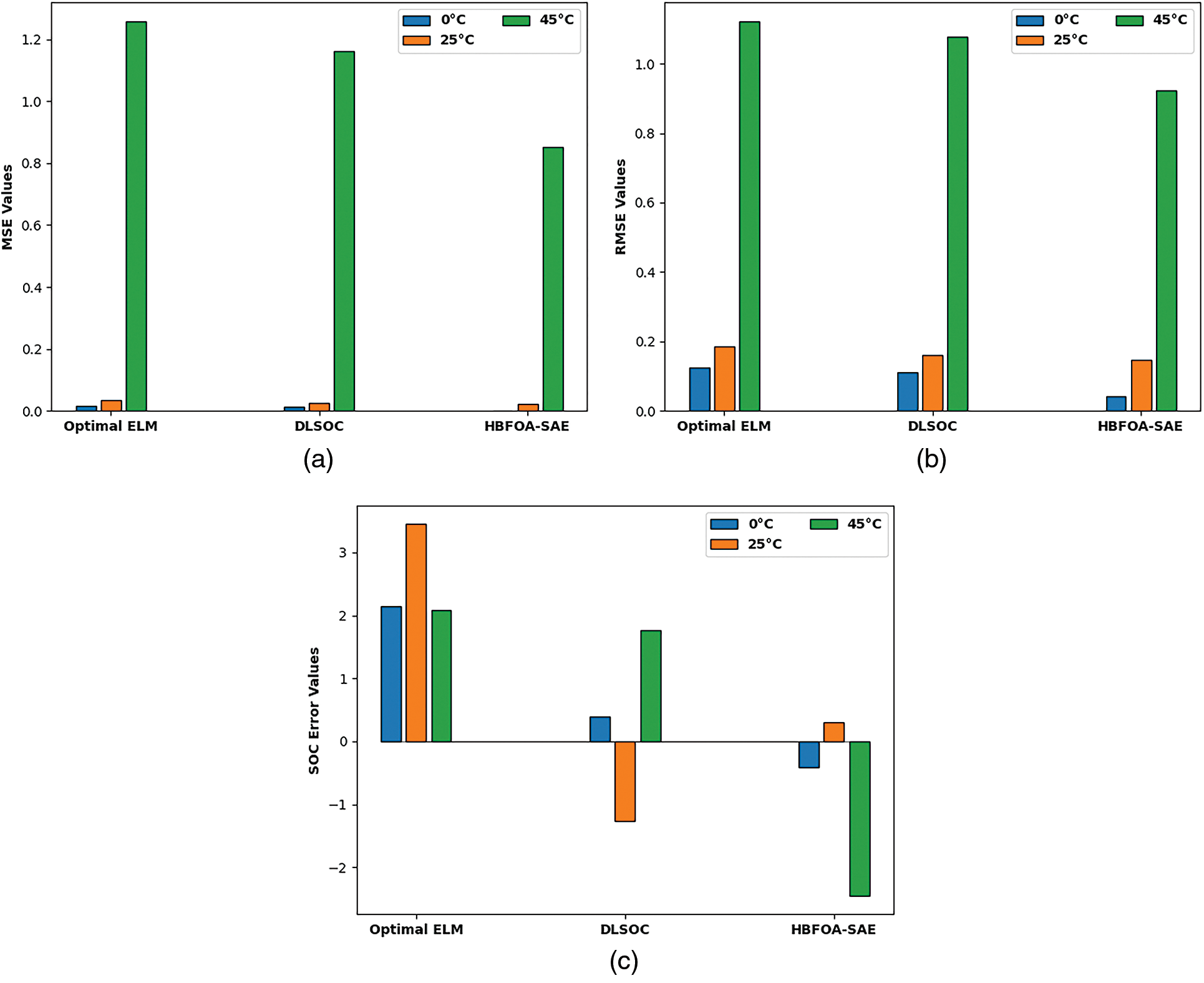
Figure 7: Comparative analysis of HBFOA-SAE technique with existing approaches on Dataset-2

Fig. 8 establishes the MSE, RMSE, and SOC error values of the HBFOA-SAE model with existing DLSOC and optimal ELM approaches under distinct temperatures on dataset-3. The experimental results implied that the HBFOA-SAE model has shown effectual outcomes with minimal values of MSE, RMSE, and SOC error. For instance, with 0°C, the HBFOA-SAE model has offered MSE, RMSE, and SOC errors of 0.009951, 0.099755, and [−2.1+3.12] respectively. Likewise, with 25°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.095123, 0.308420, and [−1.2+2.1] correspondingly. Also, with 45°C, the HBFOA-SAE model has provided MSE, RMSE, and SOC errors of 0.125423, 0.354151, and [−1.54+2.3] respectively.

Figure 8: Comparative analysis of HBFOA-SAE technique with existing approaches on Dataset-3

After examining the results and discussion, it is confirmed that the HBFOA-SAE model has shown effective SOC estimation outcomes.

4  Conclusion

In this study, a new HBFOA-SAE model has been developed for proper determination of the SOC values in the energy systems. The proposed HBFOA-SAE model majorly employs SAE model for proper determination of the SOC values in the energy systems. Next, for improving the performance of the SOC estimation process, the HBFOA is employed. In addition, the HBFOA technique is derived by the integration of the HC concepts with the BFOA to improve the overall efficiency. For ensuring the better outcomes for the HBFOA-SAE model, a comprehensive set of simulations were performed and the outcomes are examined under several aspects. The experimental results reported the supremacy of the HBFOA-SAE model over the recent state of art approaches. In future, hybrid DL models can be included to improve the prediction outcomes.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Shakerighadi, A. A. Moghaddam, J. Vasquez and J. Guerrero, “Internet of things for modern energy systems: State-of-the-art, challenges, and open issues,” Energies, vol. 11, no. 5, p. 1252, 2018. [Google Scholar]

 2.  P. K. Khatua, V. K. Ramachandaramurthy, P. Kasinathan, J. Y. Yong, J. Pasupuleti et al., “Application and assessment of internet of things toward the sustainability of energy systems: Challenges and issues,” Sustainable Cities and Society, vol. 53, no. 400, p. 101957, 2020. [Google Scholar]

 3.  G. Bedi, G. K. Venayagamoorthy, R. Singh, R. R. Brooks and K. C. Wang, “Review of Internet of Things (IoT) in electric power and energy systems,” IEEE Internet of Things Journal, vol. 5, no. 2, pp. 847–870, 2018. [Google Scholar]

 4.  R. Samuel and S. Devi Priya, “Contribution of BFO in grid scheduling,” in 2012 IEEE Int. Conf. on Computational Intelligence and Computing Research, Piscataway, IEEE, 2012. [Google Scholar]

 5.  R. Samuel and V. Vasudevan, “Smart bacterial foraging optimization algorithm for scheduling in grid,” European Journal of Scientific Research, vol. 94, no. 2, pp. 253–260, 2013. [Google Scholar]

 6.  W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]

 7.  W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

 8.  M. Asaad, F. Ahmad, M. S. Alam and Y. Rafat, “IoT enabled monitoring of an optimized electric vehicle’s battery system,” Mobile Networks and Applications, vol. 23, no. 4, pp. 994–1005, 2018. [Google Scholar]

 9.  A. Elmouatamid, Y. Naitmalek, R. Ouladsine, M. Bakhouya, N. El kamoun et al., “A microgrid system infrastructure implementing IoT/big-data technologies for efficient energy management in buildings,” in Advanced Technologies for Solar Photovoltaics Energy Systems, Green Energy and Technology Book Series, Springer, Cham, pp. 571–600, 2021. [Google Scholar]

10. A. Elmouatamid, Y. NaitMalek, M. Bakhouya, R. Ouladsine, N. Elkamoun et al., “An energy management platform for micro-grid systems using Internet of Things and big-data technologies,” Proceedings of the Institution of Mechanical Engineers, Part I, vol. 233, no. 7, pp. 904–917, 2019. [Google Scholar]

11. Y. Liu, C. Yang, L. Jiang, S. Xie and Y. Zhang, “Intelligent edge computing for IoT-based energy management in smart cities,” IEEE Network, vol. 33, no. 2, pp. 111–117, 2019. [Google Scholar]

12. A. H. Bagdadee, L. Zhang and S. H. Remus, “A brief review of the IoT-based energy management system in the smart industry,” in Artificial Intelligence and Evolutionary Computations in Engineering Systems, Advances in Intelligent Systems and Computing book Series, vol. 1056, Singapore: Springer, pp. 443–459, 2020. [Google Scholar]

13. F. Safara, A. Souri, T. Baker, I. Al Ridhawi and M. Aloqaily, “PriNergy: A priority-based energy-efficient routing method for IoT systems,” The Journal of Supercomputing, vol. 76, no. 11, pp. 8609–8626, 2020. [Google Scholar]

14. P. Pawar, M. TarunKumar and K. P. Vittal, “An IoT based Intelligent smart energy management system with accurate forecasting and load strategy for renewable generation,” Measurement, vol. 152, no. 4, p. 107187, 2020. [Google Scholar]

15. P. H. K. Utama, H. H. Husniyyah, I. N. Haq, J. Pradipta and E. Leksono, “State of charge (SOC) estimation of battery energy storage system (BESS) using artificial neural network (ANN) based on IoT- enabled embedded system,” in 2021 Int. Conf. on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, pp. 77–82, 2021. [Google Scholar]

16. M. Asaad, F. Ahmad, M. S. Alam and Y. Rafat, “IoT enabled electric vehicle’s battery monitoring system,” in 1st EAI Int. Conf. on Smart Grid Assisted Internet of Things, Sault Ste. Marie, Ontario, Canada, pp. 1–10, 2017. [Google Scholar]

17. B. Yan and G. Han, “Effective feature extraction via stacked sparse autoencoder to improve intrusion detection system,” IEEE Access, vol. 6, pp. 41238–41248, 2018. [Google Scholar]

18. C. Guo, H. Tang and B. Niu, “Evolutionary state-based novel multi-objective periodic bacterial foraging optimization algorithm for data clustering,” Expert Systems, vol. 39, no. 1, pp. e12812, 2022. [Google Scholar]

19. H. Wang, D. Wang and S. Yang, “A memetic algorithm with adaptive hill climbing strategy for dynamic optimization problems,” Soft Computing, vol. 13, no. 8–9, pp. 763–780, 2009. [Google Scholar]

20. M. S. H. Lipu, M. A. Hannan, A. Hussain, M. H. Saad, A. Ayob et al., “Extreme learning machine model for state-of-charge estimation of lithium-ion battery using gravitational search algorithm,” IEEE Transactions on Industry Applications, vol. 55, no. 4, pp. 4225–4234, 2019. [Google Scholar]

21. M. Vellingiri, I. Mehedi and T. Palaniswamy, “A novel deep learning-based state-of-charge estimation for renewable energy management system in hybrid electric vehicles,” Mathematics, vol. 10, no. 2, pp. 260, 2022. [Google Scholar]