Oppositional Red Fox Optimization Based Task Scheduling Scheme for Cloud Environment

1  Introduction

Internet of Things (IoT) is the vital technique to form smart city because it enables objects or entities to deliver data and service to users by communicating and collaborating with others [1]. There has been a rapid progression that the multiple devices get interconnected to the system with the tremendous growth of the IoT. Once the device requests resource service from the cloud datacentre simultaneously, it would take a massive network bandwidth, as well as information access and data transmission would be slow [2]. Furthermore, when some -sensitive requests namely emergency and medical are uploaded to the remote cloud to process, the delay created by bandwidth constraint and resource bottleneck of the cloud datacentre affects the quality of service (QoS). In the meantime, cloud computing (CC), a novel computing structure, was extensively employed in the last few decades. CC is a technique which focuses on providing a flexible heterogeneous source pool via the system, and users rent distinct resources on demand [3,4]. User procures and releases computing resource that is generally virtual machine (VM) with distinct provisions, based on the particular requirements within a limited period. Since these techniques are highly dependent on the Internet, the CC and IoT are strongly associated with the role. The IoT digitalizes various information and wisely manages equipment, and CC is utilized by a carrier for higher-speed information utilization, processing, and storage. CC provides the advantage of security, speed, and convenience that the lacks IoT, and the technique that makes intelligent analysis and the realtime dynamic management of the IoT consistent [5,6].

Even though implementation of IoT applications in CC has different benefits, many problems continue a challenge. Firstly, scheduling of tasks is considered an NP-hard problem [7]. Especially, scheduling of tasks represents the task assignment to virtual resources based on sequential implementation. Next, once a computing resource (VM) is released or leased, an appropriate handoff takes time [8]. Indeed, there are distinct kinds for the skilled data traffic in IoT paradigm and it requires distinct QoS limitations which should be resolved when increasing the offered Cloud resource usage [9]. Consequently, it can be important to present a proper scheduling approach for offering optimal queue management for multiple class data traffic to guarantee the likely usage of the IoT resource allocation amongst the heterogeneous schemes of personal devices and servers. There could be case where scheduling algorithm in CC model could not fulfil the QoS constraint. Also, this ineffective scheduling might result in low network throughput and undesirable lengthy delay [10].

This article focuses on the design of an oppositional red fox optimization based task scheduling scheme (ORFO-TSS) for IoT enabled cloud environment. The presented ORFO-TSS model resolves the challenge of allocating resources from the IoT based cloud platform. It realizes the makespan by performing task scheduling (TS) procedures with various aspects of incoming tasks. The designing of ORFO-TSS approach includes the idea of oppositional based learning (OBL) as to traditional RFO technique in enhancing its efficiency. A wide-ranging experimental analysis was applied on the CloudSim platform.

The rest of the paper is organized as follows. Section 2 offers a brief related works and Section 3 provides the proposed model. Next, Section 4 gives performance validation and Section 5 draws conclusions.

2  Related Works

In [11], the authors proposed a Hybrid ant genetic approach for scheduling tasks. The presented technique adopts features of genetic algorithm (GA) and ant colony optimization (ACO) and splits virtual machines and tasks into small groups. Afterward task allocation, pheromone is included in VMs. Bezdan et al. [12] present a method that is capable of finding an estimated (near-optimum) solution for multiobjective TS issues in cloud platforms and simultaneously reduces the searching time. Then proposed a hybridized bat algorithm, a swarm intelligence (SI) based approach, for multiobjective TS. In [13], integrates security effective using TS in CC with a hybrid ML (RATS-HM) method is projected for overcoming the problem. The presented method is described in the following: Firstly, an enhanced cuckoo search optimization (CSO) approach-based shorter scheduler for TS (ICS-TS) maximizes throughput and diminishes the makespan time. Next, a group optimization-based DNN (GO-DNN) for effectual RA with distinct limitations including resource load and bandwidth.

Fu et al. [14] investigated the procedure of cloud TS and projected a particle swarm optimization (PSO) genetic hybrid approach-based phagocytosis PSO_PGA. Initially, generation of PSO is separated, in addition, the location of particles in the sub-population has been altered by crossover mutation of genetic algorithm and phagocytosis for expanding the searching space of the solution. In [15], an effectual hybridized scheduling method that imitates food gathering habits of the crow bird and the parasitic action of the cuckoo, called Cuckoo Crow Search approach (CCSA) was introduced to enhance the scheduling task. They often stares at its neighbour to search for an improved food source. In certain circumstance, the crow goes a further step and steal the neighbor's food. Amer et al. [16] introduce an adapted Harris hawk’s optimizer (HHO), named elite learning HHO (ELHHO), for multiobjective scheduling issues. The modification is performed by utilizing a smart technology named elite OBL for enhancing the superiority of exploration stage of the typical HHO approach.

3  The Proposed Model

In this article, a novel ORFO-TSS algorithm has been developed to resolve the problem of allocating resources from the IoT based cloud platform. It accomplishes the makespan by performing optimal TS procedures with various aspects of incoming task. The designing of ORFO-TSS technique includes the idea of OBL as to typical RFO algorithm in enhancing its efficiency. Fig. 1 depicts the overall procedure of ORFO-TSS approach.

Figure 1: Overall process of proposed technology

3.1 Process Involved in ORFO Algorithm

According to hunting procedure of red foxes, a novel meta-heuristic technique is determined that is named as RFO technique. During the RFO approach, the red foxes search for food from territory. During the next stage, then moving on the territories for obtaining nearer sufficient to prey before attack. This technique begins with constant amount of arbitrary candidates as foxes whereas, all of them determined a point such that x¯=(x0,x1,…,xn−1) and n defines co-ordinates. For discriminating all foxes x¯i in iteration t , whereas i refers the fox number from the population, it can be present notation (x¯ji)t , whereas i demonstrates the co-ordinate as specified by the solution space dimensional. With assuming f∈Rn as the condition function of n variables dependent upon the dimensional of searching space, and with assuming the notation (x¯)(i)=[(x¯0)(i),(x¯1)(i),(x¯n−1)(i)] refers the point from the space [a,b]n whereas a,b∈R . At that moment, (x¯)(i) is an optimum solution when the value of function f((x¯)(i)) is global optimal on [a,b] . The outcomes of the estimated function by candidates were initially sorted dependent upon the fitness criteria, and for (x¯best)t , the square of Euclidean distance was measured for the candidates as [17]:

D(((x¯)(i))t,((x¯)best )t)=‖((x¯)(i))t−((x¯)best )t‖ (1)

and the candidate moves nearby an optimum population as follows:

((x¯)(i))t=((x¯)(i))t+α×sgn((((x¯)best)t−(x¯)(i))t) (2)

whereas, α defines the arbitrary integer whereas α∈(0,D((x¯)best)c, ((x¯)best)t) .

During the RFO technique, the observation and movement for delude prey but hunting as to local searching phase. For simulating a fox possibility modeling nearby prey, an arbitrary value γ∈[0,1] set from the iteration to every candidate.

{movedoserifγ>3/4stayandhileiγ≤3/4 (3)

whereas, γ∈[0,1].

One other terms under the simulation is radius. The radius contains: a as an arbitrary value amongst and 0.2 and φ0 refers the arbitrary value amongst and . It is demonstrated in the subsequent formula [18]:

r={a×sin⁡(φ0)/φ0ifφ0≠0βifφ0=0 (4)

In which, β refers the arbitrary value from the range zero and one. It is formulated in the following:

{χ0New=a×r×cos⁡(φ1)+X0actualx1New=a×r×sin⁡(φ1)+a×r×cos⁡(φ2)+x1actualx1New=a×r×sin⁡(φ1)+a×r×sin⁡(φ2)+a×r×cos⁡(φ3)+x2actual⋮xn−1New=a×r×∑k=1n−2sin(φ1)+a×Y×cos⁡(φn−1)+Xn−2actualxn−1Neω=a×r×sin⁡(φ1)+a×r×sin⁡(φ2)+…+a×r×sin⁡(φn−1)+a×r×sin⁡(φn−1)+Xn−aactual (5)

In 5 percent of worse-case candidates are extracted and some upgraded candidates are then exchanged. Similarly, two of optimum individuals are attained as (X(1))t and (X(2))t as an alpha couple from iteration t . It can be mathematical as under:

Hct=12(X(1))t−(X(2))t (6)

And the diameter of habitat utilizing Euclidean distance is attained as:

Hdt=(‖(X(1))t−(X(2))t‖)12 (7)

An arbitrary value, θ , is also regarded as:

{Newnomadiccandidateifθ>0.45Reproductionofthealphacoupleifθ≤045 (8)

where, θ∈[0,1].

Afterward, a novel candidate is reached by the alpha couple as follows:

(Xrep)t=θ2(X(1))t−(X(2))t (9)

Even though the RFO approach provides better achievement to resolve the optimization problem, in some cases, it could not get make it to attain the optimal achievement due to the local optimum points trapping, lower consistency, and premature convergence. One amendment is to apply the oppositional based learning (OBL) method. This method determines that possible location from the solution space comprises an opposite position. It could be an appropriate improvement to enhance the exploration process. Therefore, it produces the opposite position of all the solutions, a comparison with its opposite is performed for selecting an optimal one as the novel solutions. By considering Xi as a solution among Xi∈X_i,Xi¯ and its opposite value Xˇij , the equation can be modelled by the following. Fig. 2 illustrates the steps involved in RFO.

((x¯)(i))opt=((x¯)(i))lt+((x¯)(i))ut−((x¯)(i))t (10)

whereas, ((x¯)(i))t , ((x¯)(i))opt∈Ri .

Figure 2: Steps involved in RFO

3.2 Steps Involved in ORFO-TSS Algorithm

The presented model fulfills the makespan by performing optimal TS procedures with various aspects of incoming tasks. In this approach, the cloud application was considered as collected of user jobs (UJs) that implement complex computing tasks employing cloud resources [19]. Let UserJob=(U1,U2,U3…UN) represents the batch of user applications obtained at particular time. Every UJ (Ui) is represented as duplet <ai,di> . In which aj stands for the arrival time of UJ (Ui) and di stands for the purpose of UJs (Ui) . During the scheduling approach, the UJ was allocated for the available DCs (D1,D2,D3…DM) , whereas N≤M . All DCs (Di) has linked to duplet <Ci, mj>.ci , the price per unit time charged as DC to implement UJ, mi demonstrates the count of available Processing Elements (PEs) to apply UJs. Each DC has a set of PEs {PE1,PE2…PEm} to compute allocated UJs. Every PE is linked to duplet <s,p> . ′s′ and ′p′ represent the executed speed and power consumption of all PEs correspondingly. The set of nodes V={T1…Tn} represents the tasks, and the set of arcs demonstrates the control or data dependency among tasks. Optimal scheduling of UJs to accessible PEs from cloud in different DC is a vital objective of this work.

Considering the UJs Ui has assigned to DC (Dj) . Tk implies the set of tasks of the UJs (Ui) was given to PE (Pj) . Once the time need that applying Tk employ Pj is signified as Gj . The termination time of Tj is expressed as:

Finish(Tk)=start(Tk)+Γj (11)

Therefore, the whole time vital to complete the UJ as Dj is demoted as Makespanj and defined as:

Makespanj=max{Finish(Tk)} (12)

whereas T(k=1…n) the tasks are assigned to Dj . The energy consumption for calculating the UJs (Ui) by DC Dj has measured as:

Ei=∑k=1n(Γk×pk) (13)

In which pk denotes the power consumption per unit time through PEs (Pj) for procedure offered task (Tk) . The cost of processing the UJ as DC Dj is calculated as:

Cj=cj×Makespanj (14)

whereas cj denotes the price per unit time charged by DC Dj to applied the UJs.

The consumption (Uj) of DCs (Dj) is estimated as:

Uj=Makespanjmax{Makespank},k=1…M (15)

An objective function of this projected approach are expressed as:

MinimizeMakespanj j=1..M (16)

MinimizeEjj=1..M (17)

Minimize{∑j=1MCj} (18)

MaximizeUjj=1..M (19)

Subjected to:

•   The UJ requirement end before deadline (di)

•   Every UJ is allocated to only one DC.

The count of UJs is reduced to the count of present DC at a particular time.

4  Performance Validation

The performance validation of the ORFO-TSS approach is carried out using distinct types of tasks based on the number of sizes namely extra-large (EL), large (LAR), medium (MED), and small (SMA). Tab. 1 provides a brief average response time (ART) and average turnaround time (ATAT) of the ORFO-TSS model with recent methods.

Fig. 3 inspects a detailed ATAT examination of the ORFO-TSS model with existing models. The figure indicated that the round robin (RR) model has gained poor outcomes with higher ATAT of 0.196 s. Followed by, the first come first serve (FCFS) and shortest job first (SJF) models have resulted in slightly enhanced performance with ATAT of 0.172 s and 0.169 s respectively. Along with that, the Firefly and FIMPSO-TS models have reached reasonable ATAT of 0.158 s and 0.142 s respectively. However, the ORFO-TSS model has outperformed the other methods with maximum ATAT of 0.085.

Figure 3: ATAT analysis of ORFO-TSS technique with recent algorithms

Fig. 4 examines a detailed ART examination of the ORFO-TSS model with existing models. The figure indicated that the RR approach has gained poor outcomes with maximum ART of 0.144 s. Afterward, the FCFS and SJF models have resulted in somewhat enhanced performance with ART of 0.120 s and 0.119 s respectively. Likewise, the Firefly and FIMPSO-TS models have reached reasonable ART of 0.115 s and 0.108 s correspondingly. Eventually, the ORFO-TSS technique has outperformed the other methods with maximal ART of 0.074.

Figure 4: ART analysis of ORFO-TSS technique with recent algorithms

Tab. 2 and Fig. 5 illustrate a brief CPU utilization (CPUU) investigation of the ORFO-TSS model with other models on distinct types of tasks [20,21]. The results indicated that the ORFO-TSS model has reached effectual outcomes with higher CPUU. For instance, with small tasks, the ORFO-TSS model has obtained higher CPUU of 77.78% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS models have reached lower CPUU of 58.01%, 65.91%, 67.64%, 71.17%, and 75.68% respectively. Moreover, with large tasks, the ORFO-TSS methodology has obtained superior CPUU of 98.33% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS algorithms have reached to lower CPUU of 78.50%, 86.67%, 86.66%, 91.59%, and 96.18% correspondingly.

Figure 5: CPUU analysis ORFO-TSS technique interms of various measures

Tab. 3 and Fig. 6 depict a brief memory utilization (MU) investigation of the ORFO-TSS model with other models on distinct types of tasks. The results designated that the ORFO-TSS model has achieved effectual outcomes with higher MU. For sample, with small tasks, the ORFO-TSS model has obtained higher MU of 75.95% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS methods have reached to lower MU of 53.83%, 57.54%, 57.65%, 60.98%, and 68.73% respectively. Additionally, with large tasks, the ORFO-TSS model has obtained higher MU of 95.64% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS approaches have reached minimal MU of 70.89%, 79.49%, 84.23%, 83.64%, and 90.77% correspondingly.

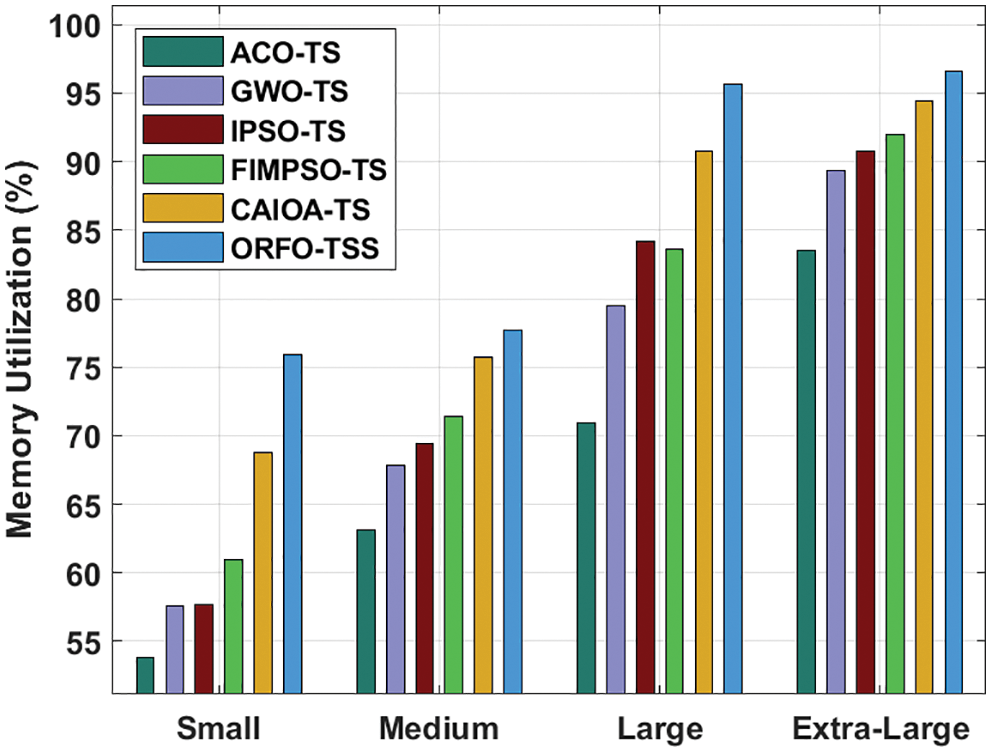
Figure 6: MU analysis ORFO-TSS technique interms of various measures

A detailed makespan examination of the ORFO-TSS approach with other existing models is compared in Tab. 4 and Fig. 7. The experimental results indicated that the ORFO-TSS model has accomplished effectual outcomes with minimal makespan. For instance, with small tasks, the ORFO-TSS model has provided minimal makespan of 38.69 s whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS models have obtained maximum makespan of 51.12 s, 48.47 s, 47.15 s, 45.52 s, and 43.93 s respectively. In line with, with large tasks, the ORFO-TSS approach has provided minimal makespan of 135.26 s whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS models have obtained maximal makespan of 181.34 s, 154.31 s, 151.13 s, 150.22 s, and 144.44 s correspondingly.

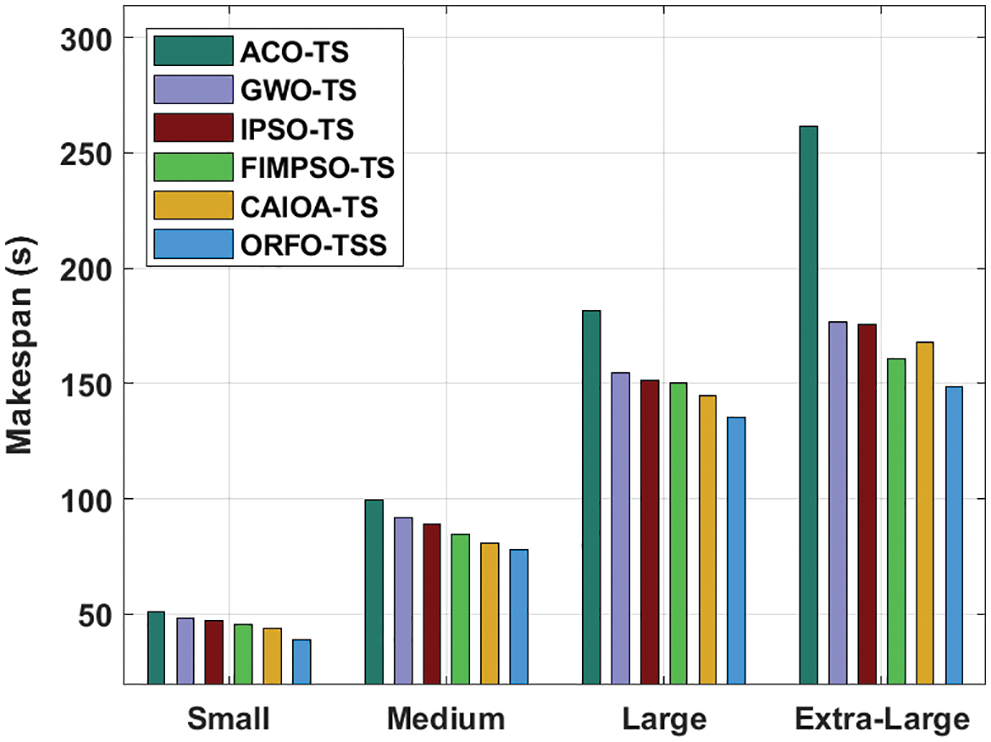
Figure 7: Makespan analysis of ORFO-TSS technique with existing algorithms

Tab. 5 and Fig. 8 demonstrate a brief average throughput (ATHPT) analysis of the ORFO-TSS technique with other techniques. The results indicated that the ORFO-TSS model has reached effectual outcomes with higher ATHPT. For instance, with small tasks, the ORFO-TSS approach has attained higher ATHPT of 99.78% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS models have reached lower ATHPT of 89.42%, 95.27%, 99.23%, 99.70%, and 98.73% correspondingly. Furthermore, with large tasks, the ORFO-TSS technique has obtained higher ATHPT of 92.10% whereas the ACO-TS, GWO-TS, IPSO-TS, FIMPSO-TS, and CAIOA-TS techniques have reached to minimal ATHPT of 63.01%, 73.13%, 71.91%, 75.16%, and 86.91% correspondingly.

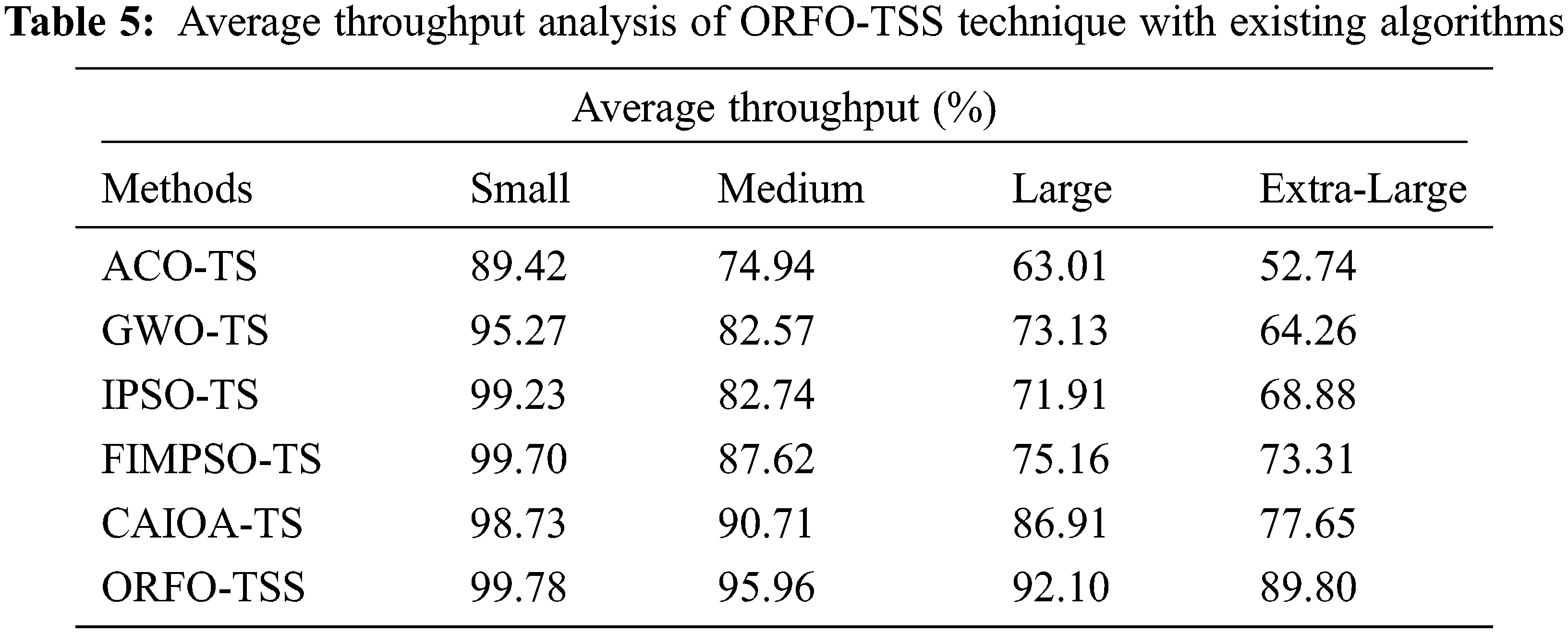
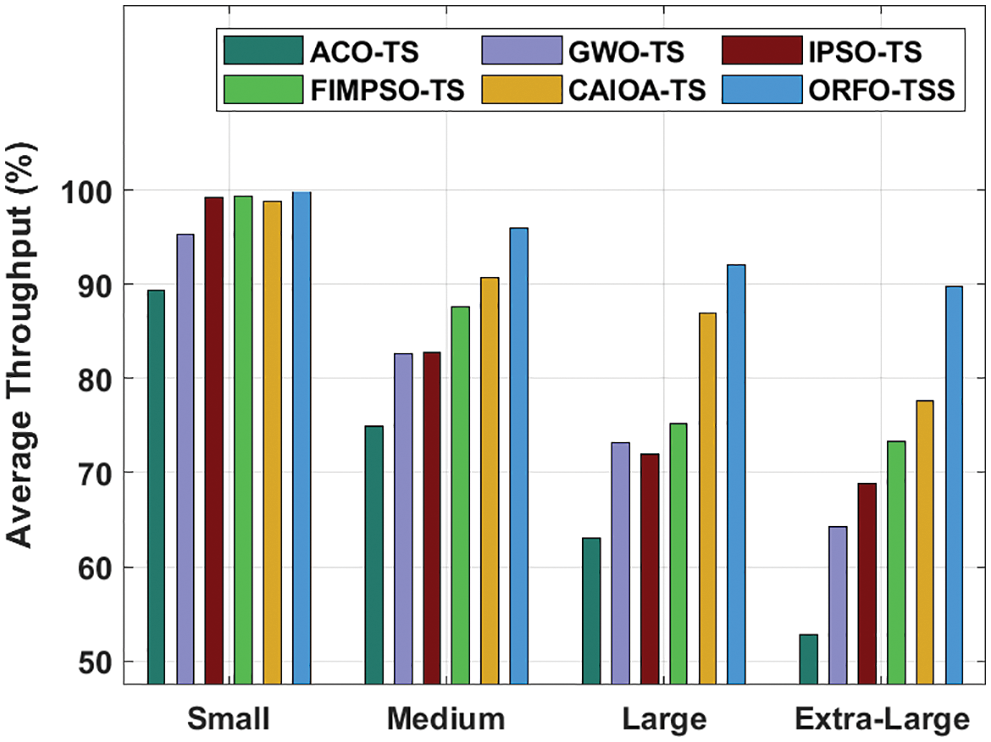
Figure 8: Average throughput analysis of ORFO-TSS technique with existing algorithms

After examining the above mentioned tables and discussion, it is evident that the ORFO-TSS model has accomplished maximum scheduling efficiency over the other models.

5  Conclusion

In this article, a novel ORFO-TSS algorithm has been developed to resolve the problem of allocating resources from the IoT based cloud platform. It fulfils the makespan by performing optimum TS procedures with various aspects of incoming tasks. The designing of ORFO-TSS method includes the idea of OBL as to typical RFO algorithm in enhancing its efficiency. A wide-ranging experimental analysis was applied on the CloudSim platform. The experimental outcome highlighted the efficacy of the ORFO-TSS technique over existing approaches. Thus, the ORFO-TSS technique can be exploited for optimizing the efficacy of the IoT enabled cloud environment. In future, hybrid deep learning models can be employed to schedule the sources that exist in the IoT enabled cloud environment.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. H. Houssein, A. G. Gad, Y. M. Wazery and P. N. Suganthan, “Task scheduling in cloud computing based on meta-heuristics: Review, taxonomy, open challenges, and future trends,” Swarm and Evolutionary Computation, vol. 62, no. 3, pp. 100841, 2021. [Google Scholar]

 2.  S. E. Shukri, R. A. Sayyed, A. Hudaib and S. Mirjalili, “Enhanced multi-verse optimizer for task scheduling in cloud computing environments,” Expert Systems with Applications, vol. 168, no. 4, pp. 114230, 2021. [Google Scholar]

 3.  S. Velliangiri, P. Karthikeyan, V. M. A. Xavier and D. Baswaraj, “Hybrid electro search with genetic algorithm for task scheduling in cloud computing,” Ain Shams Engineering Journal, vol. 12, no. 1, pp. 631–639, 2021. [Google Scholar]

 4.  M. A. Elaziz and I. Attiya, “An improved Henry gas solubility optimization algorithm for task scheduling in cloud computing,” Artificial Intelligence Review, vol. 54, no. 5, pp. 3599–3637, 2021. [Google Scholar]

 5.  K. Karthikeyan, R. Sunder, K. Shankar, S. K. Lakshmanaprabu, V. Vijayakumar et al., “Energy consumption analysis of virtual machine migration in cloud using hybrid swarm optimization (ABC-BA),” Journal of Supercomputing, vol. 76, no. 5, pp. 3374–3390, 2020. [Google Scholar]

 6.  P. Bal, S. Mohapatra, T. Das, K. Srinivasan and Y. Hu, “A joint resource allocation, security with efficient task scheduling in cloud computing using hybrid machine learning techniques,” Sensors, vol. 22, no. 3, pp. 1242, 2022. [Google Scholar]

 7.  W. Jing, C. Zhao, Q. Miao, H. Song and G. Chen, “QoS-DPSO: QoS-aware task scheduling for cloud computing system,” Journal of Network and Systems Management, vol. 29, no. 1, pp. 5, 2021. [Google Scholar]

 8.  M. S. Sanaj and P. M. J. Prathap, “An efficient approach to the map-reduce framework and genetic algorithm based whale optimization algorithm for task scheduling in cloud computing environment,” Materials Today: Proceedings, vol. 37, pp. 3199–3208, 2021. [Google Scholar]

 9.  H. B. Alla, S. B. Alla, A. Ezzati and A. Touhafi, “A novel multiclass priority algorithm for task scheduling in cloud computing,” Journal of Supercomputing, vol. 77, no. 10, pp. 11514–11555, 2021. [Google Scholar]

10. R. Masadeh, N. Alsharman, A. Sharieh, B. A. Mahafzah and A. Abdulrahman, “Task scheduling on cloud computing based on sea lion optimization algorithm,” International Journal of Web Information Systems, vol. 17, no. 2, pp. 99–116, 2021. [Google Scholar]

11. M. S. Ajmal, Z. Iqbal, F. Z. Khan, M. Ahmad, I. Ahmad et al., “Hybrid ant genetic algorithm for efficient task scheduling in cloud data centers,” Computers & Electrical Engineering, vol. 95, no. 3, pp. 107419, 2021. [Google Scholar]

12. T. Bezdan, M. Zivkovic, N. Bacanin, I. Strumberger, E. Tuba et al., “Multi-objective task scheduling in cloud computing environment by hybridized bat algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 42, no. 1, pp. 411–423, 2021. [Google Scholar]

13. P. Bal, S. Mohapatra, T. Das, K. Srinivasan and Y. Hu, “A joint resource allocation, security with efficient task scheduling in cloud computing using hybrid machine learning techniques,” Sensors, vol. 22, no. 3, pp. 1242, 2022. [Google Scholar]

14. X. Fu, Y. Sun, H. Wang and H. Li, “Task scheduling of cloud computing based on hybrid particle swarm algorithm and genetic algorithm,” Cluster Computing, vol. 51, no. 7, pp. 9, 2021. [Google Scholar]

15. P. Krishnadoss, “CCSA: Hybrid cuckoo crow search algorithm for task scheduling in cloud computing,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 4, pp. 241–250, 2021. [Google Scholar]

16. D. A. Amer, G. Attiya, I. Zeidan and A. A. Nasr, “Elite learning Harris hawks optimizer for multi-objective task scheduling in cloud computing,” Journal of Supercomputing, vol. 78, no. 2, pp. 2793–2818, 2022. [Google Scholar]

17. E. Khorami, F. M. Babaei and A. Azadeh, “Optimal diagnosis of COVID-19 based on convolutional neural network and red fox optimization algorithm,” Computational Intelligence and Neuroscience, vol. 2021, no. 3, pp. 1–11, 2021. [Google Scholar]

18. M. Zhang, Z. Xu, X. Lu, Y. Liu, Q. Xiao et al., “An optimal model identification for solid oxide fuel cell based on extreme learning machines optimized by improved red fox optimization algorithm,” International Journal of Hydrogen Energy, vol. 46, no. 55, pp. 28270–28281, 2021. [Google Scholar]

19. R. Raj, M. Varalatchoumy, V. L. Josephine, A. Jegatheesan, S. Kadry et al., “Evolutionary algorithm based task scheduling in IOT enabled cloud environment,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1095–1109, 2022. [Google Scholar]

20. A. Devaraj, M. Elhoseny, S. Dhanasekaran, E. Lydia and K. Shankar, “Hybridization of firefly and improved multi-objective particle swarm optimization algorithm for energy efficient load balancing in Cloud computing environments,” Journal of Parallel and Distributed Computing, vol. 142, no. 4, pp. 36–45, 2020. [Google Scholar]

21. M. Golchi, S. Saraeian and M. Heydari, “A hybrid of firefly and improved particle swarm optimization algorithms for load balancing in cloud environments: Performance evaluation,” Computer Networks, vol. 162, no. 6, pp. 106860, 2019. [Google Scholar]