Learning-Based Metaheuristic Approach for Home Healthcare Optimization Problem

1  Introduction

During the last decades, many studies have focused on healthcare management [1–4], etc. The main objective of these works is to provide new models and approaches to increase the productivity and the efficiency of healthcare system, which is considered as a very expensive sector. In recent years, Home Health Care (HHC) is gaining more importance within the European healthcare system. It offers an alternative to traditional hospitalization. HHC can be considered as a way to reduce healthcare system expenditure, while ensuring better quality of service [5].

Home Health Care (HHC) is defined as a set of workers serving the patients at their homes by providing the required services (e.g., nursing, cleaning, drug delivery, etc.). The major challenge for HHC companies is to improve the quality of services offered to patients, in particular the quality of care, the competence of the medical staff, the management of intervention and punctuality, etc. The main objectives of HHC Companies are to minimize costs and maximize patient satisfaction. This alternative is complex due to the integration of the patient’s home in the supply chain of care and the uncertainties related to the care process (i.e., demand, durations of care and travel time). HHC decision-makers are making complex decisions that include optimization of staff travel and assignment of patients to workers by considering several constraints, such as, workload balancing, arriving on time and patient preferences, etc. The constraints may vary depending on the type of service to be performed or the pathology to be treated. These optimization problems are known in the literature as routing and scheduling problems. Transportation cost is the biggest operating cost for the HHC companies. Thus, it is very important to optimize traveling routes for the medical staff. The main resource that influences operating costs is workforce. Therefore, a good staff management strategy should be implemented (Ben Houria et al., 2016). In HHC, a new caregiver is usually going through a learning phase. The learning process can vary from a couple of weeks to several months. The beginner caregiver will eventually obtain all the skills necessary for independent performance. This approach is named in literature, “Learning curves” (LC) or Experience Curves. Human learning is considered as one of the most important factors that affect workforce capacity. The impacts of employee learning on the scheduling problem has becoming very recently a research topic. Several researches have applied the learning curve strategy to the industrial field and more precisely to scheduling problems [6–10]. Learning curve theory is applied to cost and time prediction of a future task, assuming repetitive work with the same working conditions [11]. Assuming that a set of caregivers daily visit a set of patients at their homes and perform the same tasks over a given horizon. When the caregiver repeats the same task, he becomes more experienced and so more productive [12]. The increase in productivity is often referred to ‘‘learning”. Therefore, it influences the operating time [13]. Assuming also, that each caregiver has a known LC which determines the worker’s productivity. The main objective of this paper is to take advantage of the learning curve that can influence the service time. In this context, a new mixed-integer programming model (MIP) is proposed to deal with the HHC routing and scheduling problem (HHCRSP). This class of problem has a lot of similarities with the multiple Travelling Salesman Problem (mTSP) that is met several industrial fields such as transportation, logistics, delivery and many others social applications [14]. Solving a mTSP consists of finding the shortest path to travel through a given number of cities [15]. The proposed MIP model aims to minimize the overall service times for all caregivers over a given time horizon. The problem is considered as NP-Hard. However, exact approaches cannot solve the problem in reasonable run-time due to the problem complexity and input data size. Thus, approximate solutions using heuristic and metaheuristic methods are proposed to find good solutions to the problem. The genetic algorithm (GA) is one of the most popular and suitable algorithms for scheduling problems [16–18]. In healthcare, several works prove the efficiency of GA for scheduling problem such as [16–23]. In this paper, a new learning genetic algorithm for mTSP (LGA-mTSP) approach is proposed to solve the HHCRSP when a long term planning horizon is considered. The solution approach is composed of a new genetic algorithm, designed for mTSP (GA-mTSP) combined with the LC approach.

This work is organized as follows: Section 2 summarizes the recent works related to HHC routing and scheduling problems and describes briefly the learning curves theory. The elaborated mathematical model and the proposed solution approach are presented in Section 3 and Section 4 respectively. Experimental results are presented and discussed in Section 5, conclusion is given in Section 6.

2  Literature Review

During this decade, the healthcare sector is becoming one of the largest economic sectors in Europe and North America. Due to the problem of increasing global aging, the HHC industry is developing very rapidly [24]. HHC companies aim to reduce travel and service costs and satisfy their patients by improving the quality of services. The HHC’s problematic arouse the curiosity of several researchers in the field of industrial engineering and operation research [25]. These problematics involve assigning workers (e.g., nurses, doctors, etc.) to the patients’ homes and finding the shortest route for those workers. In the literature, these problems are called, Home Health Care Routing and Scheduling Problems (HHCRSPs). [24] described the HHCRSP as a set of patients who need care services which should be provided by care workers. [25,26] defined the HHCRSP as two sub-problems which are the personnel scheduling and the routing problem, and they consider it as an extension of well-known problem: Vehicle Routing Problem (VRP). The VRP can be defined as a problem of finding the optimal routes for deliveries, who travel with their vehicles from one or several depots to a number of cities or customers, while satisfying some constraints and giving minimal total cost [27]. VRP was proposed by Dantzig and Ramser in 1959, it is described as a generalized problem of TSP. [28–30] have defined the TSP as a set of cities to be visited by a salesman, it aims to find the optimal path of visiting all the cities and returning to the starting point and minimize the travel cost (or travel distance). The TSP is classified as symmetric Travelling Salesman Problem (sTSP), when the Euclidean distance between two nodes a,b is the same in the two ways ( dab=dba ); otherwise, it is called asymmetric Travelling Salesman Problem (aTSP). It is also called multi Travelling Salesman Problem (mTSP), when it consists of finding the shortest routes for m salesmen (m>1); and mTSP with Time Windows (mTSPTW), when some nodes have to be visited in a particular time periods. The mTSP can be considered as a relaxation of the VRP, without vehicle capacity restrictions [29]. Many types of personnel scheduling problems have been tackled in the literature. Examples of these types include nurse visiting patients at home and technician carrying out repairs at customers’ locations, etc. [31]. Various optimization criteria are considered in the HHCRSP literature. The most of them focused on minimization problems, especially on minimizing travel and service time (TST). Other optimization criteria were considered such as workload balancing (e.g., number of assigned patients, total travelled distance, etc.), and waiting time referring to late arrival at patients’ homes (e.g., delay due to road traffic, weather conditions, etc.). Among the maximization problems, there are many works which focused on patients satisfactions, such as [32,33]. They maximize the quality of service (e.g., arrive on time, visit time preference, etc.). Several constraints are considered such as maximal workload (Cmax) that defines the workload to not be exceeded (e.g., maximal number of assigned patients, maximal number of working days, maximal working time, etc.). Time Window is one of the most considered constraints, which defines an interval of time to be respected (e.g., arrive at the patient’s home within a specific time, etc.) and other specific constraints such as the break lunch. [12–31] and [34–36] refer to the staff scheduling and routing problems as Workforce Scheduling and Routing Problems (WSRP). The majority of works related to HHCRSP focused on nurse scheduling. [37] propose a linear model for nurse scheduling that aims to minimize the travel cost and maximize the satisfaction of patients. The treated problem is an extension of mTSP, solved by Cplex1. [33] design the nursing routing problem by a mixed integer linear model (MILP) aiming to maximize the number of visits. [38] propose a MILP model to optimize the travel time for a HHC staff, solved by Cplex solver. [34] propose a VRP model with time window (VRPTW) for the HHCRSP where travel and service times uncertainties are considered. [39] propose also an uncertainty approach to optimize service time for HHCRSP. They solve their model by the General Algebraic Modeling System (GAMS)2. [31] suggest a new extension of integer programming model for the WSRP. They solved it by Gurobi Solver3. Scheduling problem becomes NP-hard since the number of tasks is more than the normal number that can be processed by exact algorithms. In this case, efficient optimization algorithms are needed. Metaheuristic methods aim to solve difficult optimization problems by providing approximate solutions in a reasonable run-time. In recent years, many metaheuristic algorithms are used to solve scheduling problems in various real-world applications [40,41], especially, in manufacturing, healthcare, aeronautic, transport, etc. Metaheuristics have been proposed by several studies to solve the healthcare scheduling problems including operation room scheduling problem, patients’ admission scheduling problem, personnel scheduling problem and surgery scheduling problem, etc. This paper focuses on personnel scheduling problem that is well studied in the literature and solved by a lot of metaheuristic algorithms such GA [17] [20–22], Ant Colony Optimization (ACO) [42–45], Particle Swarm Optimization (PSO) [46–48], etc. and hybrid metaheuristic algorithms that combine two or more algorithms to take advantage of each of them and make some improvements in term of performance criteria such as accuracy or run-time. [49] proposed a hybridization algorithm for cloud computing resource scheduling based on ACO and PSO. [50–53] proposed hybrid GA to solve scheduling problems. The main objective of these works is to minimize the makespan for scheduling problems. This work proposes a new formulation for the HHCRSP aiming to minimize the travel and service time (TST). The considered problem is an extension of mTSP. Therefore, a hybridization method is also proposed to solve it, combining a GA designed for mTSP with a learning approach.

The definition of learning in operation and production management is the improvement in performance when an individual is involved in a repetitive task [9]. More the workers learn, more they become productive and gain experience. In the literature, “learning” means the impact of experience on service times. The improvement in service times is represented by mathematical representations. These representations are often called Learning Curves “LC” [12]. The LC is a correlation between the learner’s performance on a task and the time required to complete the task. The LC has proven to be an efficient tool to estimate costs and to assign workers to tasks based on their performance [54]. The first application of LC was reported by [13]. The use of this concept began to gain importance during the world war II, when an accurate prediction of the time and the cost of producing military ships and combat aircraft was needed. Since that, an extensive number of research studies have reported the use of LC in many applications. [55] have applied the LC theory in production planning. [35] have used LC approach in the field of manpower assignment and [12] have applied the theory of LC in Healthcare. In this work, the LC theory is applied for the first time in a HHC domain. There are three known models of LC in the literature, which are: the log-linear, exponential and hyperbolic models. [54] provide a literature review of learning curve models and their applications. According to [55–58], the log-linear model is the most used compared to other LC models for predicting production rate in repetitive tasks while his mathematical formulation is not complex. The original formulation of the learning curve, referred to the Wright’s Log model [13]. Many works recommended the Wright’s model and considered it as the best suitable model to handle repetitive work [59,60]. This model is applied in several domains, such as project scheduling [61,62]. Inspired by these works, the wright’s log linear model is considered in this paper as the most adequate one to the considered problem.

3  Problem Description and Mathematical Formulation

This section addresses a HHCRSP and presents the proposed mathematical formulation. The considered problem is an extension of mTSP that can be defined as follows. Given a directed graph G = (P, A) with a set of nodes P = {0, 1, …, n} and a set of arcs A = {(i, j) |i, j ∈ P, i ≠ j}. Node 0 represents the depot and nodes P = {1, 2, …, n} represent the patients. Each arc (i, j) ∈ A is associated with a travel time dij , measured in minutes. For each HHC company, there are a set of caregivers C = {1, …, m} available each day to perform specific tasks in patients’ homes. Let H = {1, …, T) be a set of working days and T the planning horizon. Each caregiver visits a set of patients and each patient can be assigned to exactly one caregiver during a given horizon. The caregivers have the same daily workload (e.g., 5 working hours, from 8:00 am to 1:00 pm) and the same volume of work Vct  that represents the maximum number of patients to be visited per day. Each patient i ∈ P/{0} is associated with a service duration Sci and each caregiver has a daily lunch break, denotes kc .

3.1 Decision Variable

Xijct={1  if caregiver c visits successively nodes i and j in day t0   otherwise

3.2 Mathematical Formulation

Min Z=∑i=0n⁡∑j=0n⁡∑c=1m⁡∑t=1T⁡(dij+Sci+kc).Xijct (1)

Subject to

∑j=1n⁡∑c=1m⁡X0jct=m, ∀t=1..T (2)

∑i=1n⁡∑c=1m⁡Xi0ct=m,∀ t=1..T (3)

∑j=1n⁡∑c=1m⁡∑t=1T⁡Xijct =1, ∀  i=1,..., n (4)

∑i=1n⁡∑j=1n⁡Xijct≤Vct−1,∀ i≠j,∀ c=1..m, ∀ t=1..T (5)

∑i,jϵn,i≠j⁡ (dij+Sci+ kc).Xijct≤Q , ∀ c=1..m, ∀ t=1..T (6)

fijct≤(|P|−1)⋅Xijct ∀i,j ∈ P, i≠j,∀c∈C,∀t∈T (7a)

fijct≥fkict+1−(| P |−1)⋅(1−Xijct) ∀k,i,j∈P, k≠ i, i≠j,∀c∈C,∀t∈T (7b)

Xijct∈{0,1},i≠j (8)

Sci>0 (9)

dij>0 (10)

The objective function (1) aims to minimize the overall service times, including travel times, operating times and lunch break for all caregivers during a given horizon. Constraints (2) and (3) guarantee that all caregivers daily start and finish their services at the HHC company. Constraint (4) ensures that each patient is assigned to only one caregiver during the horizon and each caregiver crosses a path exactly once over the horizon. Constraint (5) forces each caregiver to visit a fixed number of sub-paths. Constraint (6) guarantees that each caregiver does not exceed its maximum daily workload. Constraint (7) removes the sub-tours. Constraint (8) indicates that the decision variable Xijct is binary. Constraint (9) and Constraint (10) indicate that the service and travel times must be positive.

3.3 Learning Curve Model and Mathematical Reformulation

In this sub-section, a LC model is integrated to the proposed MIP model in order to calculate the appropriate service time for each caregiver and prove the influence of experience on caregiver’s productivity. It is inspired by the Wright’s Log Linear [13] and presented by the following mathematical function:

Scn=Ec.nlc (11)

where Scn is the time required, for the caregiver c, to complete the nth task during a given horizon T,  Ec  represents the time spent by the caregiver c to complete the first task, n corresponds to the number of repeated task and lc is the learning rate of the caregiver c. The learning rate is calculated as following:

lc=ln⁡(rc)/ln⁡(2),  −1≤lc≤0 (12)

The learning percentage is represented by rc and calculated as following:

rc=elcln⁡2 (13)

Resuming the above MIP model, we add the following equations in order to calculate service times

Sci=Ec.ilc,∀ c=1..m, ∀ t=1..T (14)

Ec≥Sci≥ScVct,∀ c=1..m,∀ i=1..Vct, ∀ t=1..T (15)

−1< lw< 0 (16)

Constraints (14) and (15) calculate the service time for each caregiver. Constraint (16) indicates that the learning rate should be between −1 and 0.

4  A New Learning Genetic Algorithm Approach (LGA-mTSP)

This section presents the solution approach for the HHCRSP, called Learning Genetic Algorithm for mTSP (LGA-mTSP). The proposed solution approach is carried out in two stages. It is composed of a learning approach combined with a genetic algorithm for mTSP.

4.1 Learning Process

The learning process, proposed in this study, allows to generate learning curves for a given set of caregivers. Let’s take the example a set of beginner caregivers (c: 1,…, m) who start a new task T and have to repeat it n times. The service time records, performed by these caregivers, are saved in the database. Each caregiver has a fixed number of tasks to perform, generated by the solver. The learning process consists of extracting the learning rates lc  from the database and predicting the future service times. Fig. 1 illustrates the learning process.

–   The extraction model is based on the following equation:

lc= [ln⁡(Tn)/ln⁡(n)]−[ln⁡(T1)/ln⁡(n)]           (17)

–   Predictive model:

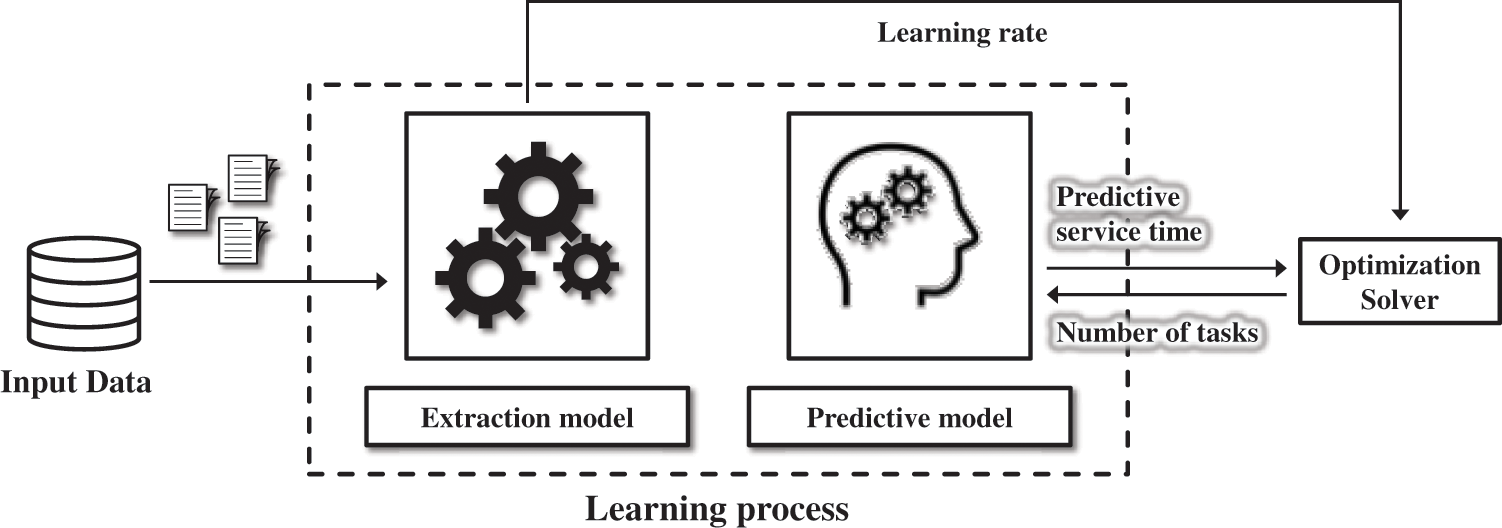
Figure 1: Proposed learning process

The predictive model is based on Eq. (11). It provides service times for each caregiver, according to the number of tasks to perform.

–   The optimization solver:

The solver consists of equitably assigning patients to caregivers, founding the shortest path for all caregivers and providing the optimal solution that is the minimized overall service times.

4.2 Genetic Algorithm for mTSP

The execution-time increases with the problem instance size, and often only small or medium-sized instances can be solved with exact solver. Therefore, a metaheuristic method is proposed to solve the problem in order to find the best solution in accepted simulation time. Genetic algorithms is a good example of stochastic algorithms. The considered problem is an extension of mTSP that receive a big attention in the last years. mTSP is a NP-Hard that various approaches have been proposed to solve it, especially the Genetic Algorithms (GAs). They are successfully implemented to solve TSP and mTSP such as in [63–66]. GA was first proposed by John H. Holland in the 1960 s. It is an iterative procedure that starts with a constant population size and generates new individuals called chromosomes by the genetic operators. The algorithm finishes when the stop criteria is satisfied [63]. The proposed genetic algorithm, called GA-mTSP, starts with different types of input data, such as GA’ parameters (population size, number of generations, mutation and crossover rates, etc.), chromosome representation that is generated from the problem description (number of workers, number of patients, etc.) and the learning rates which are generated from the learning process (the learning rate of each worker).

4.2.1 Chromosome Representation

The chromosome is a numeric vector. Each number inside the chromosome is called a gene. In the case of mTSP, each gene represents a city. There are many ways to represent the chromosome for the mTSP. In this work, chromosomes are represented by the multi-chromosome technique [63]. Fig. 2 illustrates an example of the chromosome representation for mTSP. Each salesman must start and finish its route at the depot. In this chromosome representation, the depot is not presented but it is taken into account when calculating the travel time. According to Fig. 2, the chromosome is composed of 45 genes, which represents the number of cities to be visited by salesmen during the horizon (3 days). Due to the constraint of workload balancing, imposed by the proposed MIP model, the total number of cities must be fairly divided between salesmen. First, the chromosome is divided into H fairly parts, where H is the number of days. After that, the number of cities assigned to each day is equally divided between salesmen. The sequencing of cities is called route. Each salesman travels daily a single route (number of salesmen = number of routes = 3). Due to the problem constraints, each gene must appear in the chromosome only once to ensure that each city is visited only once during the horizon.

Figure 2: Chromosome representation

4.2.2 Fitness Evaluation

After the random generation of the initial population, each individual is evaluated according to the fitness function. In this work, the fitness value is the overall service times performed by all workers. The considered problem is a minimization problem; thus, the smallest value is the best. The fitness function is calculated as following:

f=∑i,j=0,i≠jn⁡∑c=1m⁡∑t=1T⁡(dij+Sci+kc).Xijct (18)

where dij is the travel time between two nodes i and j . Sci is the operating time performed by caregiver c at node i in day t. kc represents the daily lunch break of caregiver c and Xijct is a binary variable that has 1 as value, when the nodes i and j are assigned to the same caregiver c on day t. Otherwise, Xijct = 0.

4.2.3 Genetic Operators

The genetic operators consist of evolving the chromosomes. They influence the search ability and convergence speed. There are two basic types of operators, which are the crossover and the mutation operators [63]:

–   Crossover operator: generates new solutions (offspring) by exchanging genes of two previous solutions (parents). The crossover rate is the probability that crossover reproduction will be performed. Various crossover methods are available, including single point and multi-point crossover, etc. In this work, a three-point crossover method is adopted. This method refers to using 3 randomly points in order to determine the order and the distance between the genes. Fig. 3 illustrates an example of 3-point crossover. The three points are randomly chosen with the following constraints: P2−P1>0, P3−P2>0 and P1, P2, P3<Chromosome size.

–   Mutation operator: changes one or more gene values in a chromosome from its original state. There are several mutation methods available in the literature. A two-stage mutation operator is used in this paper. This method combines two mutation operators, which are the random swap and the reverse swap operators. First, two genes are exchanged basing on two randomly selected points ( P1  and P2 ). After that, two other points  P3 and P4  are randomly chosen ( P4>P3 and P3, P4<chromosome size) to define a segment in the obtained chromosome. The genes inside the segment are reversed. An illustrative example is shown in Fig. 4.

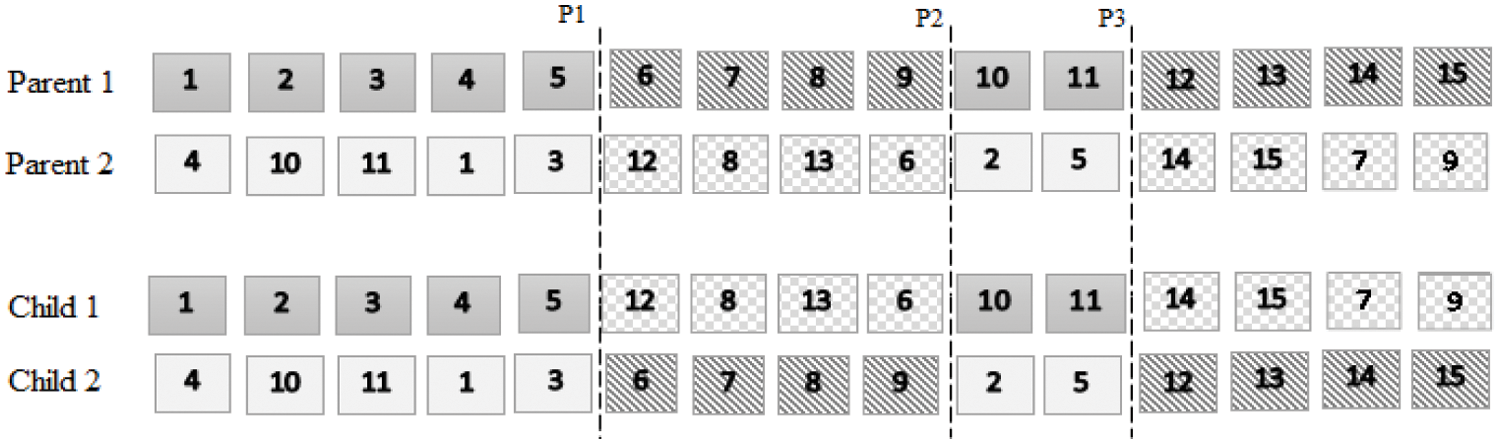
Figure 3: Three-point crossover operator

Figure 4: Mutation operator

4.2.4 Iterative Process

The iterative process is composed of four phases (evaluation, selection, reproduction and replacement). The best individuals are selected according to their fitness values and memorized in “the mating pool”. These individuals are called parents. The mating pool is a concept used in evolutionary computation that consists of expecting to get a better-quality offspring (children) than its parents. The mating pool and the population have the same size. The original solution is replaced by a new solution if its rank is worse than the rank of the new solution. The stop criteria is satisfied when the maximum number of generations and the maximum execution time are reached or no improvement is made compared to previous generations.

5  Experimentations

The proposed LGA-mTSP is implemented in Java language with the Integrated Development Environment Eclipse IDE4, version 2020–03. The algorithm is executed on a 2.50-GHz Intel(R) Core(TM) i5–7200 CPU computer under Windows 10 with 8 GB of RAM. The proposed MIP model is testing on illustrative example of a HHC company with 3 caregivers who have to perform medical services at patients’ homes. To our knowledge there is no standard benchmark in the literature for the considered problem. Therefore, based on the benchmark data of the Single-Depot Multiple Traveling Salesman Problem (multiple-TSP)5, several instances are generated and reported in Tab. 1.

The benchmark is generated from TSPLIB6 library. It contains 4 TSP instances: eil517, berlin528, eil769 and rat9910. The model is tested with instances of one and multiple working days, (see Tab. 1: times are given in minute), in order to evaluate the influence of caregiver’s experience over time. This experience is traduced by some learning parameters which are given in Tab. 2.

The proposed GA-mTSP is implemented with fixed parameters, presented in Tab. 3, to validate the MIP model and define reliable results.

5.1 Computational Results

This section describes computational experiments carried out to investigate the performance of the proposed solution approach LGA-mTSP.

5.1.1 Results of One Working Day

The results of one working day instances are shown in Tab. 4. In fact, the table presents for each caregiver in each instance, the assigned route, the travelled time, the number of repeated tasks (corresponding to the number of patients visited by the caregiver), the total operating times, the service time (including the total operating time, the total travelled time and the break lunch), the operating time at the last task (corresponds to the required time to perform the last task), and the learning GAP which refers to the percentage of reduced time between the operating time at the first and the last task. The reduced time between the first and the last task is calculated as following:

δ=Tn− T1 (19)

where Tn is the operating time at the last task and T1 is to the operating time at the first task. The learning state of each caregiver is defined according to the learning GAP. Times are given in minute.

Route assignment is based on both: the shortest path routing strategy and the workload balancing between caregivers which is defined by the number of patients assigned to caregivers.

5.1.2 Results of Multiple Working Days

The instances of multiple working days are inspired from those of one working day. The travelled path of each instance is repeated during a given horizon. For example, the horizon of “Modified Eil51-m3” corresponds to five days. So, the travelled path of “Eil51-m3” is repeated five times. Tab. 5 presents the obtained results for each caregiver: travelled time, number of repeated tasks, operating and service times, learning GAP and learning state.

According to Tabs. 5 and 6 it is worth noting that more the task is repeated, more the caregiver get experience and more the service time decreases until a minimum threshold is reached. A statistical test has been done. Through this the impact of learning on the operating time can be shown. Let μ0 is the average operating time at the first task and μ1 is the average operating time at the last task. there are two hypotheses H0 and H1 . the first one represents the case where there is no learning, in this case μ0 =  μ1 . while H1 represents the case where learning is considered. the impact of learning is demonstrated by the fact that μ0≠ μ1 . For all instances, it is observed that the average operating time without learning (in the case of H0 ) is the same from the first task to the last task and from the first working day to the 60 working days. In this case μ0=μ1 . E.g. for Berlin 52-m3: μ0=μ1=25  min. Also, it is shown that the average operating time with learning (in the case of H1 ) is different. E.g. for Berlin 52-m3: μ0≠μ1 . Therefore, we are allowed to say that learning has a notable impact on operating time.

5.2 Discussion

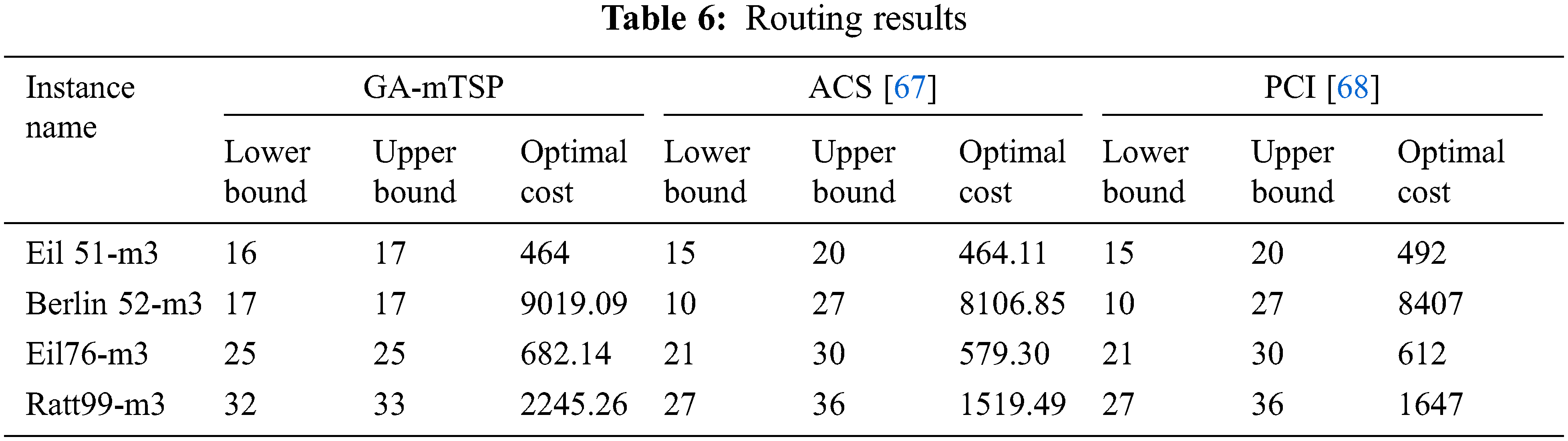
In this sub-section, a comparative study is provided in order to evaluate the effectiveness of GA-mTSP as well as the robustness of the elaborated MIP model. First, a comparative table is given by Tab. 6 in term of routing results. This paper proposes a new mathematical formulation for HHCRSP extended of mTSP. Thus, the authors cannot compare directly the proposed solution with another work in the literature. In order to evaluate the performance of GA-mTSP, the authors remove the constraints related to the considered problem in expectation of returning to the basic formulation of mTSP. After that, they solve it by GA-mTSP with instances taken from the benchmark data of multiple-TSP. Finally, they compare the obtained results with two similar works from the literature. Tab. 6 shows the obtained results of GA-mTSP. Ant Colony System (ACS) taken from [67] and PCI-algorithm taken from [68] in terms of lower and upper bounds (the minimum and the maximum number of cities that a salesman must visit on his tour) and the optimal costs.

Both works [67,68] aim to balance workloads between salesmen. It is observed that the optimal costs obtained by [67] are better than those of GA-mTSP and PCI [68]. Meanwhile. the best workload balancing is given by GA-mTSP that shares fairly the workloads between salesmen compared to the other works.

In order to evaluate the influence of caregiver’s experience (human learning) on caregiver’s productivity (service time). a performance study is given below. Fig. 5 shows the influence of learning on the caregiver’s productivity during a period of time.

Figure 5: Learning curves

When the learning rate tends to 50%. the caregiver gets more experience and become faster. Therefore. operating time decreases considerably during a given period. This phenomena is called “learning phase”. When the operating time becomes stable. this phase is called “steady state phase” i.e., “no learning” and so. the caregiver become expert. Regarding to Figs. 5a and 5b. caregiver 1 is faster than others. He is the first one who reaches the steady state phase. In Figs. 5b and 5c. caregiver 2 has not reached the steady state phase. thus. he needs more time to reach it. In Fig. 5d. all caregivers reach the steady phase but not at the same time. Caregiver 2 learns faster than others. The average difference (Average GAP) between the pre-fixed operating time and the effective operating time for one-working-day instances is about 41% while the average GAP for the multiple-working-days instances is 44%. According to Tab. 7 and Fig. 5. it is clearly shown that there is a significant decrease in operating time for all instances. Service time is thus impacted by the same phenomenon.

Regarding to Fig. 6 it is important to note that the run-time (CPU) increases with the instance size and then with the problem complexity. For all the considered instances, the solving time is reasonable. It did not exceed 13 min and the average run-time for all instances is around 5 min (5274 ms exactly). Computational results show the effectiveness of the LGA-mTSP approach in term of execution time and good quality solutions. Thus, LGA-mTSP is able to minimize service costs. maximize productivity and balance workload depending on workers’ experiences. simultaneously.

Figure 6: Run-time of all instances

6  Conclusion

This paper presents a new mixed-integer programming (MIP) model for a HHCRSP problem. The proposed MIP model aims to minimize the overall service time for a set of caregivers, visiting a set of patients in their homes, in order to perform medical tasks, during a given time horizon. This model was used to solve small size instances. Nevertheless, due to the NP hardness of this class of problems and in order to solve large size instances, a Learning Genetic Algorithm approach (LGA-mTSP) is proposed. This approach combines a genetic algorithm, designed for mTSP, with a learning approach, called learning curves approach. The obtained results prove the effectiveness of the LGA-mTSP in term of run-time and reliability of learning curves approach to minimize service times. Moreover, the proposed solution approach proves its ability to reduce service costs and balance the workload between caregivers using their experiences. In future works, it would be interesting to consider uncertainty in task time duration as in [69].

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1Cplex Solver: https://www.ibm.com/fr-fr/analytics/cplex-optimizer

2GAMS Solver: https://www.gams.com/optimization-solvers/

3GUROBI Solver: https://www.gurobi.com/

4Eclipse IDE : https://www.eclipse.org/

5https://profs.info.uaic.ro/~mtsplib/

6http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/index.html

7https://profs.info.uaic.ro/~mtsplib/TSPLIB/eil51.tsp

8https://profs.info.uaic.ro/~mtsplib/TSPLIB/berlin52.tsp

9https://profs.info.uaic.ro/~mtsplib/TSPLIB/eil76.tsp

10https://profs.info.uaic.ro/~mtsplib/TSPLIB/rat99.tsp

References

 1.  Y. Xue, B. Onzo, R. F. Mansour and S. Su, “Deep convolutional neural network approach for COVID-19 detection,” Computer Systems Science and Engineering, vol. 42, no. 1, pp. 201–211, 2022. [Google Scholar]

 2.  K. Muthumayil, M. Buvana, K. R. Sekar, A. El-Amraoui, I. Nouaouri et al., “Optimized convolutional neural network for automatic detection of COVID-19,” CMC-Computers. Materials & Continua, vol. 70, no. 1, pp. 1159–1175, 2021. [Google Scholar]

 3.  Z. Ben Houria, M. Masmoudi, A. Al Hanbali, I. Khatrouch and F. Masmoudi, “Quantitative techniques for medical equipment maintenance management,” European Journal of Industrial Engineering, vol. 10, no. 6, pp. 703–723, 2016. [Google Scholar]

 4.  B. Armagan and C. Xi, “Optimising teams and the outcomes of surgery,” European Journal of Industrial Engineering, vol. 14, no. 1,. pp. 127–145, 2020. [Google Scholar]

 5.  C. Fikar and P. Hirsch, “Home health care routing and scheduling: A review,” Computers & Operations Research, vol. 77, pp. 86–95, 2017. [Google Scholar]

 6.  C. C. Wu, Y. Yin, W. H. Wu and S. R. Cheng, “Some polyno-mial solvable single-machine scheduling problems with a trun-cation sum-of-processing-times based learning effect,” European Journal of Industrial Engineering, vol. 6, no. 4, pp. 441–453, 2012. [Google Scholar]

 7.  S. C. Liu, W. L. Hung and C. C. Wu, “Note on a single-machine scheduling problem with Sum of processing times based learning and ready times,” Mathematical Problems in Engineering, vol. 2015,. pp. 9, 2015. [Google Scholar]

 8.  A. Azzouz, M. Ennigrou and L. B. Said, “Scheduling problems under learning effects: Classification and cartography,” Proceedings of the International Journal of Production Research, vol. 56, no. 4, pp. 1642–1661. 2017. [Google Scholar]

 9.  Y. Wang, X. Li and R. Ruiz, “An exact algorithm for the shortest path problem with position-based learning effects,” IEEE Transactions on Systems. Man and Cybernetics: Systems, vol. 47, no. 11, pp. 3037–3049, 2017. [Google Scholar]

10. C. C. Wu, J. Chen, W. C. Lin, K. Lai, S. Liu et al., “A Two-stage three-machine assembly flow shop scheduling with learning consideration to minimize the flowtime by six hybrids of particle swarm optimization,” Swarm and Evolutionary Computation, vol. 24, pp. 1–18, 2018. [Google Scholar]

11. L. Mályusz and A. Varga, “An estimation of the learning curve effect on project scheduling with working days calculation,” Periodica Polytechnica Architecture, vol. 47, pp. 104–109, 2016. [Google Scholar]

12. H. Jin, B. W. Thomas and M. Hewit, “Integer programming techniques for makespan minimizing workforce assignment models that recognize human learning,” Computers & Industrial Engineering, vol. 97, pp. 202–211, 2016. [Google Scholar]

13. T. P. Wright, “Factors affecting the cost of airplanes,” Journal of Aeronautical Sciences, vol. 3, no. 4, pp. 122–128, 1936. [Google Scholar]

14. K. Jayamoorthi, D. Karunanidy, A. Jayavel and S. Ramalingam, “A survey on multi-objective travelling salesmen problem,” Institute of Integrative Omics and Applied Biotechnology, vol. 8, no. 2, pp. 223–233, 2017. [Google Scholar]

15. I. A. Hameed, “Multi-objective solution of traveling salesman problem with time,” Advances in Intelligent Systems and Computing, vol. 921,. pp. 121–132, 2020. [Google Scholar]

16. A. Ala, F. E. Alsaadi, M. Ahmadi and S. Mirjalili, “Optimization of an appointment scheduling problem for healthcare systems based on the quality of fairness service using whale optimization algorithm and NSGA-II,” Scientific Reports, vol. 11, no. 1, pp. 1–19, 2021. [Google Scholar]

17. M. Mutingi and C. Mbohwa, “Home healthcare worker scheduling: A group genetic algorithm approach,” Proceedings of the World Congress on Engineering, vol. 1, pp. 3–5, 2013. [Google Scholar]

18. M. Squires, X. Tao, S. Elangovan, R. Gururajan, X. Zhou et al., “A novel genetic algorithm based system for the scheduling of medical treatments,” Expert Systems with Applications, vol. 195, pp. 116464, ISSN 0957–4174, 2022. [Google Scholar]

19. X. Zhang, S. Ma and S. Chen, “Healthcare service configuration based on project scheduling,” Advanced Engineering Informatics, vol. 43, pp. 101039, 2020. [Google Scholar]

20. R. Borchani, M. Masmoudi and B. Jarboui, “Hybrid genetic algorithm for home healthcare routing and scheduling problem,” in 6th Int. Conf. on Control. Decision and Information Technologies (CoDIT), IEEE, Saint Julian’s, Malta, pp. 1900–1904, 2019. [Google Scholar]

21. F. Alves, A. I. Pereira, A. Fernandes and P. Leitão, “Optimization of home care visits schedule by genetic algorithm,” in Int. Conf. on Bioinspired Methods and Their Applications, Springer. Cham, Paris, France, pp. 1–12, 2018. [Google Scholar]

22. Ş Inanç and A. E. Şenaras, “Solving nurse scheduling problem via genetic algorithm in home healthcare,” Transportation, Logistics and Supply Chain Management in Home Healthcare: Emerging Research and Opportunities, edited by Jalel Euchi, IGI Global, pp. 20–28, 2020. https://doi.org/10.4018/978-1-7998-0268-6.ch002. [Google Scholar]

23. T. Sinthamrongruk, K. Dahal, O. Satiya, T. Vudhironarit and P. Yodmongkol, “Healthcare staff routing problem using adaptive genetic algorithms with adaptive local search and immigrant scheme,” in Int. Conf. on Digital Arts. Media and Technology (ICDAMT), Chiang Mai, Thailand, pp. 120–125, 2017. [Google Scholar]

24. Y. Shi, T. Boudouh and O. Grunder, “A robust optimization for a home health care routing and scheduling problem with consideration of uncertain travel and service times,” Transportation Research Part E: Logistics and Transportation Review, vol. 128, pp. 52–95, 2019. [Google Scholar]

25. M. E. Cisse, S. Kergosien, Y. Sahin, E. Lenté, C. Yalcindag et al., “OR problems related to home health care: A review of relevant routing and scheduling problems,” Operations Research for Health Care, vol. 13–14, pp. 1–22, 2017. [Google Scholar]

26. R. Liu, B. Yuan and Z. Jiang, “Mathematical model and exact algorithm for the home care worker scheduling and routing problem with lunch break requirements,” International Journal of Production Research, vol. 55, no. 2, pp. 558–575, 2017. [Google Scholar]

27. C. Y. Liong, W. Ismail, K. Omar and M. Zirour, “Vehicle routing problem: Models and solutions,” Journal of Quality Measurement and Analysis, vol. 4, no. 1, pp. 205–218, 2008. [Google Scholar]

28. R. Matai, S. P. Singh and M. L. Mittal, “Traveling salesman problem: An overview of applications, formulations, and solution approaches,” Traveling Salesman Problem, Theory and Applications, vol. 1, pp. 1–24, 2010. [Google Scholar]

29. T. Bektas, “The multiple traveling salesman problem: An overview of formulations and solution procedures,” Omega-international Journal of Management Science, vol. 34, pp. 209–219, 2006. [Google Scholar]

30. L. Tang, J. Liu, A. Rong and Z. Yang, “A multiple traveling salesman problem model for hot rolling scheduling in shanghai baoshan iron and steel complex,” European Journal of Operational Research, vol. 124, pp. 267–282, 2000. [Google Scholar]

31. J. A. Castillo-Salazar, D. Landa-Silva and R. Qu, “Workforce scheduling and routing problems: Literature survey and computational study,” Annual Operations Research, vol. 239, no. 1, pp. 39–67, 2016. [Google Scholar]

32. J. Decerle, O. Grunder, A. Hajjam El Hassani and O. Barakat, “A memetic algorithm for multi-objective optimization of the home health care problem,” Swarm and Evolutionary Computation, vol. 44, pp. 712–727, 2019. [Google Scholar]

33. B. Issaoui, I. Zidi, E. Marcon and K. Ghédira, “New multi-objective approach for the home care service problem based on scheduling algorithms and variable neighborhood descent,” Electron. Notes in Discrete Mathematics, vol. 47, pp. 181–188, 2015. [Google Scholar]

34. D. L. Pereira, J. Alves and M. C. Moreira, “A multiperiod workforce scheduling and routing problem with dependent tasks,” Computers and Operations Research, vol. 118, pp. 104930, 2020. [Google Scholar]

35. E. Attia, P. Duquenne and J. M. Le Lann, “Considering skills evolutions in multi-skilled workforce allocation with flexible working hours,” International Journal of Production Research, vol. 52, pp. 4548–4573, 2014. [Google Scholar]

36. G. Guastaroba, J. F. Côté and L. C. Coelho, “The multiperiod workforce scheduling and routing problem,” Omega, vol. 102, p.102302, 2021. [Google Scholar]

37. F. Gayraud, L. Deroussi, N. Grangeon and S. Norre, “A new mathematical formulation for the home health care problem,” Procedia Technology, vol. 9, pp. 1041–1047, 2013. [Google Scholar]

38. D. Aiane, A. El-Amraoui and K. Mesghouni, “A new optimization approach for a home health care problem,” in Int. Conf. on Industrial Engineering and Systems Management (IESM), Seville, Spain, pp. 285–290, 2015. [Google Scholar]

39. M. Issabakhsh, S. Hosseini-Motlagh, M. Pishvaee and M. Saghafi Nia, “A vehicle routing problem for modeling home healthcare: A case study,” International Journal of Transportation Engineering, vol. 5, no. 3, pp. 211–228, 2018. [Google Scholar]

40. X. S. Yang and L. Press, in Nature-inspired Metaheuristic Algorithms Second Edition, Luniver Press, Frome, United Kingdom, p.160, 2010. [Google Scholar]

41. M. I. Restrepo, L. Rousseau and J. Vallée, “Home healthcare integrated staffing and scheduling,” Omega-international Journal of Management Science, vol. 95, pp. 102057, 2020. [Google Scholar]

42. J. Yin and W. Xiang, “Ant Colony Algorithm for Surgery Scheduling Problem,” in Advances in Swarm Intelligence. Lecture Notes in Computer Science, Springer, Shenzhen, China, vol. 7331, pp. 198–205, 2012. [Google Scholar]

43. H. Jin, W. Wang, M. Cai, G. Wang and C. Yun, “Ant colony optimization model with characterization-based speed and multi-driver for the refilling system in hospital,” Advances in Mechanical Engineering, vol. 9, no. 8, pp. 1–18, 2020. [Google Scholar]

44. E. Martin, A. Cervantes, Y. Saez and P. Isasi, “IACS-HCSP: Improved ant colony optimization for large-scale home care scheduling problems,” Expert Systems with Applications, vol. 142, pp. 112994, 2020. [Google Scholar]

45. A. A. Obiniyi, “Multi-agent based patient scheduling using ant colony optimization,” African Journal of Computing and ICT, vol. 8, no. 8, pp. 91–96, 2015. [Google Scholar]

46. E. G. M. Kanaga and M. L. Valarmathi,“Multi-agent based patient scheduling using particle swarm optimization,” Procedia Engineering, vol. 30, pp. 386–393, 2012. [Google Scholar]

47. C. Lo and T. H. Lin, “A particle swarm optimization approach for physician scheduling in a hospital emergency department,” in Seventh Int. Conf. on Natural Computation, IEEE, Shanghai, China, vol. 4. pp. 1929–1933, 2011. [Google Scholar]

48. S. C. Gao and C. W. Lin, “Particle swarm optimization based nurses’ shift scheduling,” in Proc. of the Institute of Industrial Engineers Asian Conf., Springer. Singapore, pp. 775–782, 2013. [Google Scholar]

49. H. Yang, “Improved ant colony algorithm based on PSO and its application on cloud computing resource scheduling,” Advanced Materials Research, Trans Tech Publications Ltd, vol. 989, pp. 2192–2195, 2014. [Google Scholar]

50. A. M. Manasrah and H. Ba Ali, “Workflow scheduling using hybrid GA-PSO algorithm in cloud computing,” Wireless Communications and Mobile Computing, vol. 2018,. pp. 16, 2018. [Google Scholar]

51. X. Li and L. Gao, “An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem,” International Journal of Production Economics, vol. 174, pp. 93–110, 2016. [Google Scholar]

52. X. Li, L. Gao, Q. Pan, L. Wan and K. M. Chao, “An effective hybrid genetic algorithm and variable neighborhood search for integrated process planning and scheduling in a packaging machine Workshop,” in IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 10, pp. 1933–1945, 2018. [Google Scholar]

53. N. Kundakci and O. Kulak, “Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem,” Computers and Industrial Engineering, vol. 96, pp. 31–51, 2016. [Google Scholar]

54. M. Anzanello and F. S. Fogliatto, “Learning curve models and applications: Literature review and research directions,” International Journal of Industrial Ergonomics, vol. 41, pp. 573–583, 2011. [Google Scholar]

55. R. S. Blancett, “Learning from productivity learning curves,” Research-Technology Management, vol. 43, no.3, pp. 54–58, 2002. [Google Scholar]

56. S. Globerson and D. Gold, “Statistical attributes of the power learning curve model,” International Journal of Production Research, vol. 35, no no. 3, pp. 699–711, 2010. [Google Scholar]

57. S. Globerson and N. Levin, “Incorporating forgetting into learning curves,” International Journal of Production Management, vol. 7, no. 4, pp. 80–94, 1987. [Google Scholar]

58. J. Vits and L. Gelders, “Performance improvement theory,” International Journal of Production Economics, Elsevier, vol. 77, no. 3, pp. 285–298, 2002. [Google Scholar]

59. C. H. Glock, M. Jaber and S. Zolfaghari, “Production planning for a ramp-up process with learning in production and growth in demand,” International Journal of Production Research, vol. 50, pp. 5707–5718, 2012. [Google Scholar]

60. S. Shanks, “Wright’s competency model and quality and safety competencies,”Walden Dissertations and Doctoral Studies Collection, Ph.D. dissertation, Walden University, 2019. [Google Scholar]

61. M. Eslam, A. Elyamany and A. El Hakeem, “Learning curve effect in scheduling repetitive projects,” Al-Azhar University Civil Engineering Research Magazine (CERM), vol. 40, no. 4, pp. 8, 2018. [Google Scholar]

62. K. Zahran, M. Nour and O. Hosny, “The effect of learning on line of balance scheduling: Obstacles and potentials,” International Journal of Engineering Science and Computing, vol. 6, no. 4, pp. 3831–3841, 2016. [Google Scholar]

63. K. M. Lo, W. Y. Yi, P. K. Wong, K. S. Leung, Y. Leung et al., “A genetic algorithm with new local operators for multiple traveling salesman problems,” International Journal of Computational Intelligence Systems, vol. 11, no. 1, pp. 692–705, 2018. [Google Scholar]

64. A. Hussain, Y. Muhammad, M. Sajid, I. Hussain, A. M. Shoukry et al., “Genetic algorithm for traveling salesman problem with modified cycle crossover operator,” Computational Intelligence and Neuroscience, vol. 2017, pp. 7, 2017. [Google Scholar]

65. A. Király and J. Abonyi, “Optimization of multiple traveling salesmen problem by a novel representation based genetic algorithm,” Intelligent Computational Optimization in Engineering, vol. 366, pp. 241–269, 2011. [Google Scholar]

66. E. N. Kencana, I. Harini and K. Mayuliana, “The performance of ant system in solving multi traveling salesmen problem,” Procedia Computer Science, vol. 124, pp. 46–52, 2017. [Google Scholar]

67. R. Necula, M. Breaban and M. Raschip, “Performance evaluation of ant colony systems for the single-depot multiple traveling salesman problem,” in 10th Int. Conf. on Hybrid Artificial Intelligence Systems, Springer, Cham, Bilbao, Spain, pp. 257–268, 22nd-24th June, 2015. [Google Scholar]

68. V. Pacheco-Valencia, N. Vakhania, J. A. Hernández and J. C. Hernández-Gómez, “A fast algorithm for Euclidean bounded single-depot multiple traveling salesman problem,”Algorithms, vol. 1, no. 0, pp. 8, 2021. [Google Scholar]

69. A. El Amraoui, S. Harbi and A. N. Sidi Moh, “Home health care scheduling problem under uncertainty: Robust optimization approaches,” Computing and Informatics, vol. 41, no. 1, pp. 288–308, 2022. [Google Scholar]