TG-SMR: A Text Summarization Algorithm Based on Topic and Graph Models

1  Introduction

In the field of automatic text summarization, most of the computing methods used in real systems are based on graph models, which are characterized by their simplicity and stability. First of all, the graph model does not require pre-training, and can directly calculate the weight coefficients of text sentences, which effectively avoids the disadvantage of relatively lack of training samples in the field of text summarization. Secondly, the weight contribution strategy of the graph model makes the selected abstract sentences not particularly remote, even if the extracted sentence is not the target abstract sentence. It also expresses relevant content without extracting sentences that are completely unrelated to the topic of the article.

In many areas, graph-based ranking methods such as Kleinberg’s HITS (Hyperlink-Induced Topic Search) and Google’s Pagerank algorithms have had considerable success. A graph model is a concept produced by abstraction of the real-world. Based on graph theory, the modeling process of a graph model is a series of abstract expressions of concrete things. Nodes are abstraction of specific things and can have some inherent properties. Edges represent the relationship between nodes and usually an edge has a weight representing the distance between two nodes. The computation of node weights based on relationships is an important feature of graph models.

In the field of text summarization, various methods have been proposed in the literature. For example, TextRank [1,2], HyperSum [3] and LexRank [4] have achieved good results.

In this context, this paper improves the TextRank algorithm by using the Latent Dirichlet Analysis (LDA) model [5], the thematic features of sentences on the semantic level, and analyzing the relationship among words and topics.

The rest of the paper is structured as follows. Section 2, presents the state of the art in automatic text summarization. Section 3 gives an overview of the TextRank algorithm. An improved graph model-based summarization algorithm is proposed in Section 4. The experimental results are presented in Section 5. Finally, Section 6 summarizes this paper.

2  Literature Review

The rise of statistics in the 1950 s inspired the emergence of text summarization techniques. Lunh [6] stated that word frequencies are related to document’s topic. Therefore, word weights can be determined based on their frequency in the document, and sentence weights can be calculated based on word weights. As the document’s abstract, choose sentences with higher weights. This concept has been a cornerstone of text summarization technology development. Despite the fact that the theory appears simple, the achieved results using this method have high accuracy, outperforming many later, more complicated techniques. Later, Baxendale [7] suggested that some particular words should be given more weight because they convey the document’s topic. Edmundson [8] weighted sentences based on three factors: keywords, clue words and location, and selected the ones with the most weight as summaries. Several integer linear programming-based methods [9–11] and approaches for maximizing sub-modular functions [12,13] have been developed to deal for sentence redundancy in the sentence selection process.

With the growth of the Internet in the 1990 s, the volume of documents grew at an exponential rate. Simultaneously, advances in machine learning have helped natural language processing, providing additional impetus to text summarization technologies. Kupiec et al. [14] proposed a method based on a Naive Bayes classification algorithm to choose document summary phrases. Conroy and O’leary [15] proposed a hidden Markov-based model to calculate the correlation between words. To find the most significant information in the analyzed texts, Goularte [16] utilized a linear regression model with some fuzzy rules. Svore et al. [17] used a neural network-based summarization technique for assessing the relevance of each sentence in the document by extracting a collection of features from each sentence. Summarization is represented as a classification problem based on neural network architectures in some recent work, and it is solved by constructing sentence representations [18–22]. Using document-level attributes, Zhong et al. [23] ranked extractive abstracts.

With the development of graph model theory, text summarization methods based on graph model appears. TextRank [1], HyperSum [3] and LexRank [4] are widely used as mainstream graph model-based algorithms. By exploiting semantic information of sentences, Han et al. [24] proposed a semantic graph model. El-Kassas et al. [25] proposed a graph-based framework by combining many extractive methods.

Recently, Widyassari et al. [26] provided a complete and consistent review of text summarization techniques. Several in-depth research and analysis on automated text summarizing algorithms have been conducted by [27–29].

3  TextRank Algorithm

The main idea of TextRank comes from the famous page ranking model PageRank algorithm developed by Lary Page, the co-founders of Google. PageRank algorithm believes that the importance of a web page depends on the number and the quality of sites linked to it. Suppose there is a set of n web pages, one of which is Pi. Each web page has links to other web pages, and the collection of web pages linked to Pi is IN(Pi). The collection of other pages linked from Pi is OUT(Pi). The importance of a web page Pi is given as follows:

I(Pi)=1∑j∈IN(Pi)⁡|OUT(Pj)|I(Pj) (1)

There is an n-dimensional vector, and each dimension represents the importance of a web page, and there is an n × n matrix H, then:

I=HI (2)

H is the link matrix generated by all connected web pages, and the value of each element is:

Hij={1|OUT(Pj)|;ifPj∈IN(Pi)0;Otherwise (3)

I is called the stationary vector of H, that is, the eigenvector of H whose eigenvalue is 1. The method used to calculate I is the power method: Select an initial vector I, then Ik+1 = HIk (k = {0, 1, 2, …, n}) , eventually converges to a stationary vector I. But in practice, there will be some special cases. Some web pages, called endpoints, do not point to any other web pages. The corresponding columns in matrix H are all 0 s, or some subsets of web pages form rings. In this case, the power method described above does not apply. Therefore, all calculations need to adjust H to get a new matrix G = a(H + A) + (1 − d) J, where a is a damping factor between 0 and 1. This factor represents that in the graph composed of web pages, the probability of selecting the next web page according to the link relationship in the graph is a, and the probability of randomly selecting the next web page is 1 − a. The value of a used in this paper is 0.85.

Let the set of endpoints be T, the values of the columns corresponding to each point in T in matrix A are all 1/n, and the values of the columns corresponding to all non-terminal points in A are all 0. In matrix J, all elements are 1/n. After the above matrix adjustments, the calculation process of the stationary vector I becomes as follows:

Ik+1=GIk=aHIk+aAIk+(1−a)JIk;k={0,1,2,…,n} (4)

Until convergence or the maximum number of iterations n is reached, the final I is obtained.

The basic idea of the PageRank algorithm can be summarized as follows. Treat each web page as a node in a graph, and each web page will have an initial weight. The relationships between web pages are based on hyperlinks to other web pages. If some web pages are endpoints, the damping factor method will be adopted to give the web page an estimated value of 0.85 for linking to other ones. After the graph model is established, each web page will distribute its own weight equally to all the web pages it wants to link to. Finally, a mutual equilibrium is reached. After each iteration of weight sharing, if the weight decreases below a certain threshold, and the algorithm converges, the final weight of each web page can be determined. This can effectively increase the importance of quality web pages.

TextRank algorithm is an important method similar to PageRank algorithm for text summarization or keyword extraction. A very important improvement is that the graph model constructed by the PageRank algorithm is a directed graph, and the edges in the graph have no weights. Mihalcea and Tarau [1] verified by experiments the number of iterations when the model converges when the sentence weight is considered or not. Experiments show that undirected edges with weights converge faster, so the edges of the TextRank algorithm are undirected edges with weights calculated according to the association between sentences. The change of the model means that the calculation method has also been adjusted.

After the PageRank algorithm obtains the stationary vector S(Vi), the iterative algorithm calculates the weight of each node as follows.

S(Vi)=(1−a)+a1∑j∈IN(Vi)⁡|OUT(Vj)|S(Vj) (5)

The weight at each iteration of the TextRank algorithm is calculated as Eq. (6).

S(Vi)=(1−a)+a∑j∈IN(Vi)Wji∑k∈OUT(Vj)⁡WjkS(Vj) (6)

One difference between Eqs. (5) and (6) is that TextRank algorithm not only considers the out-degree of nodes, but also considers the influence of connected edges Wji when calculating the weight contribution.

This similarity of sentence A relative to sentence B is measured using the BM25 (Best Matching-25) algorithm [30]. First, sentence B is decomposed into a single meaningful word, and the correlation score for each word and sentence A is calculated. Then, these scores are summed to obtain the relevance score between sentences A and B, thereby describing the similarity of the two sentences.

In the graph model constructed by the TextRank algorithm, text summaries are calculated as follows. The nodes select the shortest sentences separated by commas, periods, semicolons and exclamation marks. The relationship between two nodes is established based on whether the sentences represented by the two nodes have the same word. If the same word appears, an edge is established, and the weight of the edge is calculated. A matrix of edge-to-edge relationships is calculated using the BM25 algorithm, and then iteratively calculated using Eq. (6), until the algorithm converges.

The above mainly introduces the basic idea of the sorting algorithm based on the graph model, the construction process of the nodes and edges in the graph model, the introduction of the weight calculation method of the undirected edge, and the iterative contribution weight of the graph model. The general approach when using a graph model for text summarization is given in Algorithm 1.

3.1 TextRank Algorithm Flaws

3.1.1 Establishment of Nodes Relationship

Usually, the smallest unit that can be analyzed is selected as the node in the graph model. In text summarization, the smallest unit that can be analyzed is a complete sentence, so the node in the constructed graph model is the abstraction of each sentence.

TextRank algorithm compares whether two sentences contain the same word as a basis to establish relationship between nodes. In order to reduce the interference of words that have no actual meaning, such as conjunctions, words such as function words, conjunctions, and modal particles. These words cannot represent the stem of the sentence and are usually removed. But in practice, this still has many drawbacks.

All languages in the world have polysemy. Often a word has a different meaning in one usage context than in another usage context. This leads to the fact that although the word is the same word from the participle level, they have different meanings in different sentences. Therefore, it is obviously not advisable to create systemically an edge between two nodes containing the same word like in TextRank algorithm.

Also due to the diversity of languages, the phenomenon of synonyms and polysemous words is also very common. Basically, synonyms mean the same thing, but use different words. Usually, in order to read fluently and highlight the writing level of the writer, if an article needs to express a meaning repeatedly, different words are usually used to describe the same meaning, that is, the use of synonyms in the article. Rules for edge building, like in TextRank algorithm, cannot recognize that two sentences are related and need to build edges in this case. If an edge is not created for this kind of word, the two nodes of the connection are disconnected.

3.1.2 Edge Weight Calculation

The weight of an edge is a measure of the distance between two nodes. Mihalcea and Tarau [1] verified that a graph model with edge weights converges faster than without weights. In TextRank algorithm, the weight calculation of the edge can be calculated by BM25 algorithm. If there are n sentences, an n × n matrix will be generated. The matrix is not diagonally symmetric, which means that every two edge-connected nodes are connected by two directional edges, that is, a directed weighted graph. Therefore, for two nodes A and B connected by an edge, the weight of the edge from A to B is different from the weight of the edge from B to A.

However, the method of establishing an edge between two nodes is simply based on the appearance of the same word between two sentences and ignores the semantic-level attributes of the word. An improved method is proposed in this paper and will be described in Section 4. Since, BM25 algorithm is a word-based sentence correlation calculation method, so it is no longer applicable to the improved algorithm model.

4  Improved Summarization Algorithm

4.1 Redefining Edge Relations

Since the method of judging whether the corresponding two nodes in the graph model should establish an edge based on whether the two sentences contain the same keyword has the disadvantage of only considering the application of the word and ignoring the specific meaning of the word. This paper hopes that a new evaluation method can perfectly solve the phenomenon of synonyms and polysemy. Based on these considerations, a text summarization method based on an LDA-based topic model is proposed.

The LDA (Latent Dirichlet Analysis) [5] model is a bag-of-words model, which means that the words in an article have nothing to do with its location. An article is regarded as a collection of words, and then the association between words and topics is extracted. The advantage of this is to take into account the co-occurrence of certain words to express a certain theme. The probability distribution of words and topics is produced by the LDA model, allowing us to determine which subjects are mostly expressed by a given sentence.

It can be seen that, understanding sentences from the topic level, seeing sentences as composed of topics. Therefore, it is judged whether two sentences are related according to whether they contain the same topic, and the relationship between the two sentences is revealed from the semantic level. In this way, it not only finds interrelated sentences by using words as association judgment objects, but also reveals deeper semantic associations.

4.2 Edge Weight Calculation Method

The establishment of the edge relationship is based on whether the two sentences contain the same topic. If the weight of the edge is still calculated based on the words on the sentence, it is equivalent to finding a path from sentence A to sentence B. But it is measured by the length of the other path, which is obviously wrong. It is necessary to find a method that can describe the approximation of the topics expressed on the sentences. The relative entropy is used to obtain the degree of similarity of two sentences.

The rationale for this is that each sentence uses its topic probability distribution as a benchmark to measure how similar other sentences are to its own topic probability distribution. You can also use another strategy to find a topic probability distribution that can be used as a benchmark in the full text, calculate the distance from each sentence to this benchmark, and then calculate the distance between the two sentences. Doing so becomes computationally more complex and it is relatively difficult to find a baseline for comparison. Using this asymmetric feature, not only leads to simpler calculation, but also the difference between other sentences and the current sentence can be reflected.

4.3 Relative Entropy Definition

The difference between two probability distributions P and Q is measured by relative entropy, also known as KLD (Kullback–Leibler Divergence). It can be stated in the form of DKL(P||Q), where Q is the probability distribution of simulated data, which serves as a measurement standard, and P is the probability distribution of real data, which serves as the estimate object. When fitting the probability distribution P with the probability distribution Q, DKL(P||Q) reflects the loss, or difference. Asymmetry (DKL(P||Q) ≠ DKL(Q||P)) is the most prominent aspect of relative entropy.

According to Shannon’s theory, if the character set’s probability distribution is known, a method for encoding the character set with the fewest number of bits may be devised using this probability distribution. Let a character set X, and P(x) the probability of a character x ∈ X, then the entropy of the character set is equal to the average number of ideally encoded bits of character x as follows.

H(x)=∑x∈X⁡P(x)log(1P(x)) (7)

In order to encode characters corresponding to the probability distribution Q(x) on the same character set, we used the optimum encoding based on P(x). The number of required bits for encoding will be larger due to the change in probability distribution. The idea of relative entropy, which assesses the average amount of bits utilized to encode each character, is introduced in this context. The distance between two probability distributions P and Q is calculated using this relationship.

DKL(P||Q)=∑x∈X⁡P(x)log(1Q(x))−∑x∈X⁡P(x)log(1P(x))=∑x∈X⁡P(x)log(P(x)Q(x)) (8)

If the two probability distributions are the same, relative entropy a value of 0, else it is greater than zero. It can be deduced from Eq. (8) that if P and Q are discrete random variables, the relative entropy calculation is as follows.

DKL(P||Q)=∑x∈X⁡P(x)ln(P(x)Q(x)) (9)

4.4 Distance Metrics and Relative Entropy

Because relative entropy is dependent on the difference between the test and reference distributions, it cannot be used as an absolute distance measurement technique because it lacks symmetry and transitivity.

It is often assumed that the ideas presented in a sentence can more fully contain the document’s subject if the distribution of the topic on this sentence is similar to the distribution on the document than other sentences. We need to calculate the relative entropy of a sentence to the document, without calculating the relative entropy of the document to a sentence. As a result, relative entropy’s asymmetric nature will have no influence on the information that require attention.

Based on the abovementioned, the document’s topic distribution is viewed as a hypothetical probability distribution, while the sentence’s probability distribution is treated as the actual probability distribution. Then, a method is developed for determining sentence similarity and sentence weight, using relative entropy.

The probability distribution of a topic on the sentence Si and the document D are comparable in the following way:

DKL(P(T|Si)||P(T|D))=∑k=1K⁡P(Tk|Si)log⁡(P(Tk|Si)P(Tk|D)) (10)

The similarity of two sentences Si and Sj can be obtained as follows.

DKL(P(T|Si)||P(T|Sj))=P(T|Si)log⁡(P(T|Si)P(T|Sj)) (11)

4.5 Sentence Initial Weight Computation

Before the graph model iterative contribution weight calculation, each sentence Si needs to have an initial weight, and the acquisition of the initial weight can accumulate the sum of the probabilities of the topics on the sentence. Statistics can also be used to measure sentences based on the basic characteristics of words. According to [31,32], and other researches on text summarization methods based on statistics, TF-IDF (Term Frequency–Inverse Document Frequency), sentence length and sentence position are used as factors to measure the initial weight of sentences, as follows.

1.    TF-IDF: This feature value reflects the particularity of a word in a document. Words that appear more frequently in many documents and appear less frequently in other documents are relatively important, and their weights are larger. The calculation method is as follows:

TFIDF(Si)=Dw,i∑w∈Si,k⁡Dw,k⋅log(DwDset) (12)

2.   Sentence position: Baxendale [7] shows that there is an 85% probability that the first sentence of a paragraph is talking about the main subject of the paragraph. Based on this theory, each sentence of a paragraph is regarded as a sequence, and the influence factor of its corresponding position is calculated as in Eq. (13).

Pos(Si)=n+1−in (13)

where n is the number of sentences and i is the position of sentence Si in the paragraph.

3.   Sentence length: Word-based calculations are all affected by the sentence length. The longer the sentence, the more words it contains, the more weight it will get. It will influence the result if it is too long or too short. The sentence length is calculated according to the Gaussian distribution function as follows:

Li=1σ2π⋅e−(x−μ)22σ2 (14)

Based on the above three characteristics, a method for synthesizing all weights is given in Eq. (15).

Score(Si)=αTFIDF(Si)+βPos(Si)+γLi;α,β,γ∈[0,1] (15)

4.6 Description of the Improved Summarization Method

The basic unit of computation of the proposed improved method has changed from observable word features to topic features hidden behind words. There are new methods for the establishment of the corresponding edge and the calculation of the weight of the edge, and the iterative contribution method for the transformed model is similar to the TextRank algorithm. An overview of the text summarization method after improving the graphical model is presented in Algorithm 2.

In the above algorithm, the step of calculating the edge weight can be calculated in the sixth step, but it is listed separately in order to highlight the importance of this step. The size of d in the iterative formula in the step of the graph model iterative contribution weight is usually 0.75. The understanding of the formula is that each time the weight of a node Vi is calculated, first find all the node sets IN(Vi) that point to it. For each node Vj in it, find the weight Wedge[j][i] that points to Vi, and calculate the sum of all out-degrees of node Vj. The ratio of the two is multiplied by the current weight of Vj, which is the weight contributed to Vi, and the weight contributed by Vi to all nodes pointing to it is the weight after this iteration. The algorithm exits when it converges or the maximum number of iterations is reached.

5  Experimental Results

In order to verify the performance of our proposed algorithm, this paper uses the public dataset of the DUC (Document Understanding Conference) conference for verification, and uses the automatic evaluation metric ROUGE [33] to evaluate the experimental results.

5.1 Experimental Datasets

The DUC is currently one of the most influential evaluation conferences in the field of text summarization. DUC has a large-scale text summary dataset, which is considered to be the most authoritative datasets that can be compared. At the same time, it uses the objective evaluation criterion ROUGE (Recall-Oriented Understudy for Gisting Evaluation). The purpose is to enable all participants to evaluate on these public open corpora, not only to promote text summarization datasets to become more standard and unified, but also to promote more research scholars to engage in text summarization research.

This paper selects DUC2004 and DUC2006 datasets for experiments (see Tab. 1). The DUC2004 dataset has five tasks, and the second task is considered in this paper. The data sources are TDT (Topic Detection and Tracking) dataset and TREC (Text REtrieval Conference) dataset.

5.2 Experiments and Results Analysis

In the modeling and training process of the LDA model, the number of implicit topics T is usually set manually, and the number of topics has a direct effect on the quality of the LDA model after training. There is no way to know the number of topics for, so first a way to determine the number of topics in a document set is needed.

In this paper, a Bayesian statistical standard method is used to obtain the number of topics T. We can obtain the approximate value of P(W|T) by the Gibbs sampling method. It is simpler and effective to solve the LDA model.

In this paper, on the DUC2004 and DUC2006 datasets respectively, the number of topics T with different values at intervals of 20, ln(P(W|T)) is proportional to P(W|T), and it can be seen from Fig. 1 that, as the number of topics increases, the value of P(W|T) first decreases and then increases. P(W|T) takes the minimum value when the number of topics on the DUC2004 and DUC2006 datasets is 80 and 120, respectively. Therefore, the LDA model is trained on the DUC2004 and DUC2006 datasets with the number of topics as 80 and 120, respectively.

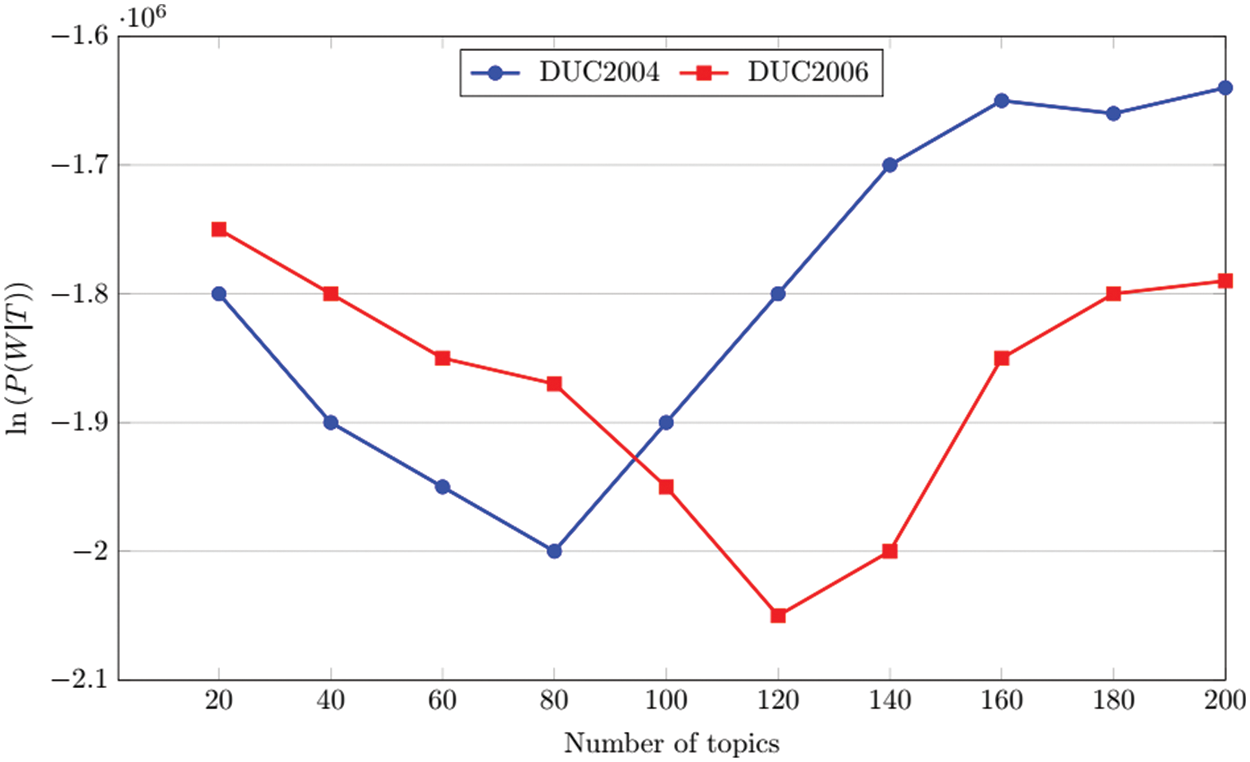
Figure 1: Relationship between ln(P(W|T)) and the number of topics

After setting the experimental parameters, this paper uses the improved algorithm proposed in this paper, that is, based on the LDA topic model and relative entropy to improve the edge establishment conditions of the graph model and the edge weight calculation method, to perform automatic text summarization on the DUC2004 and DUC2006 datasets.

In order to compare the performance of our proposed method, this paper uses four text summarization algorithms for comparison in terms of ROUGE-1, ROUGE-2, ROUGE-3, ROUGE-L, and ROUGE-SU.

■   TextRank: A graph model-based high-quality text summarization algorithm, described in detail in Section 3. It’s widely used in practical project applications.

■   TeamBest: The best performing computational model among competing algorithms on the datasets.

■   Doc-LDA: Sort by topic probability, then select topics from large to small, and then select sentences with a relatively high probability of expressing the topic as summary sentences according to the topic.

■   KL-Based: Use KL divergence to measure the importance of sentences in the way that sentences are thematically similar to articles.

Tabs. 2 and 3 show the experimental results on ROUGE metrics in DUC2004 and DUC2006 datasets, respectively. It can be seen from the results that our proposed method TG-SMR has great improvement compared to the other methods, which verifies the effectiveness of our algorithm.

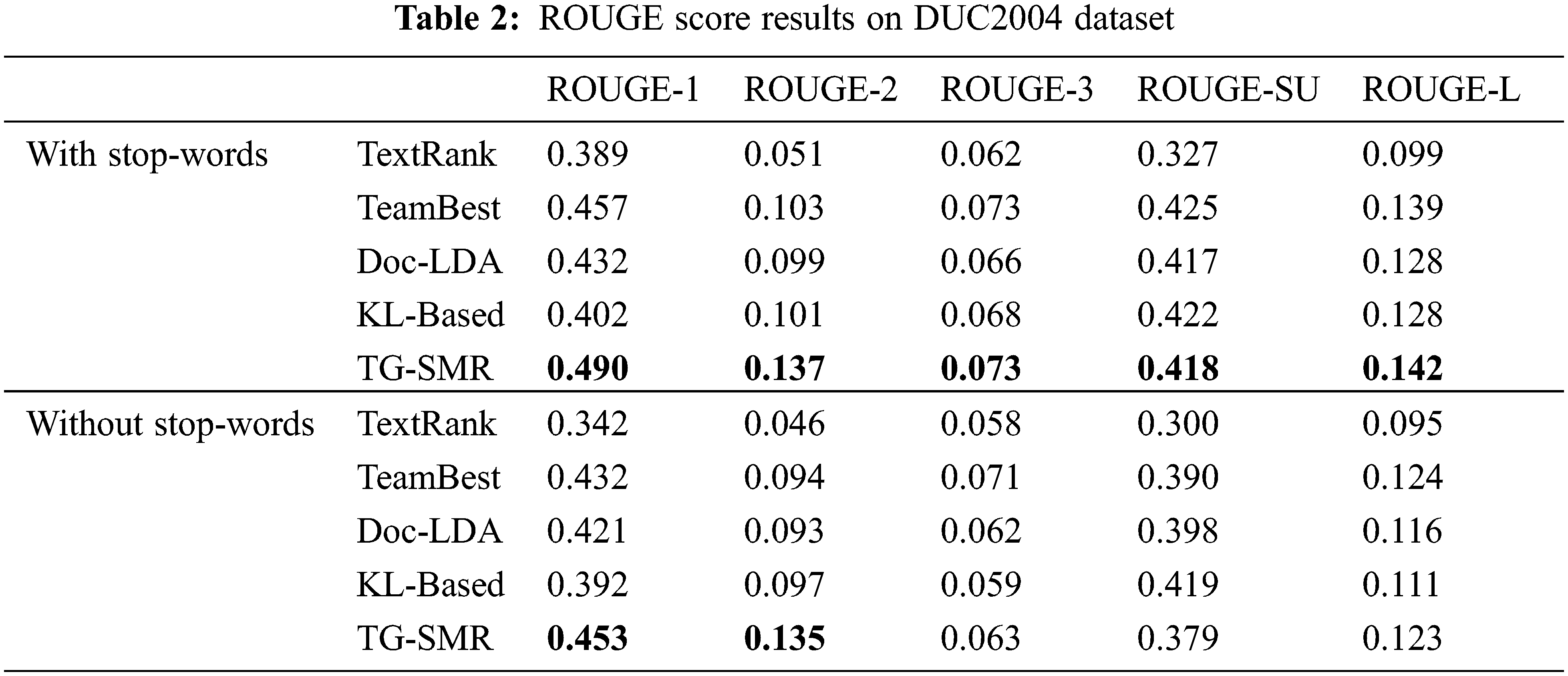
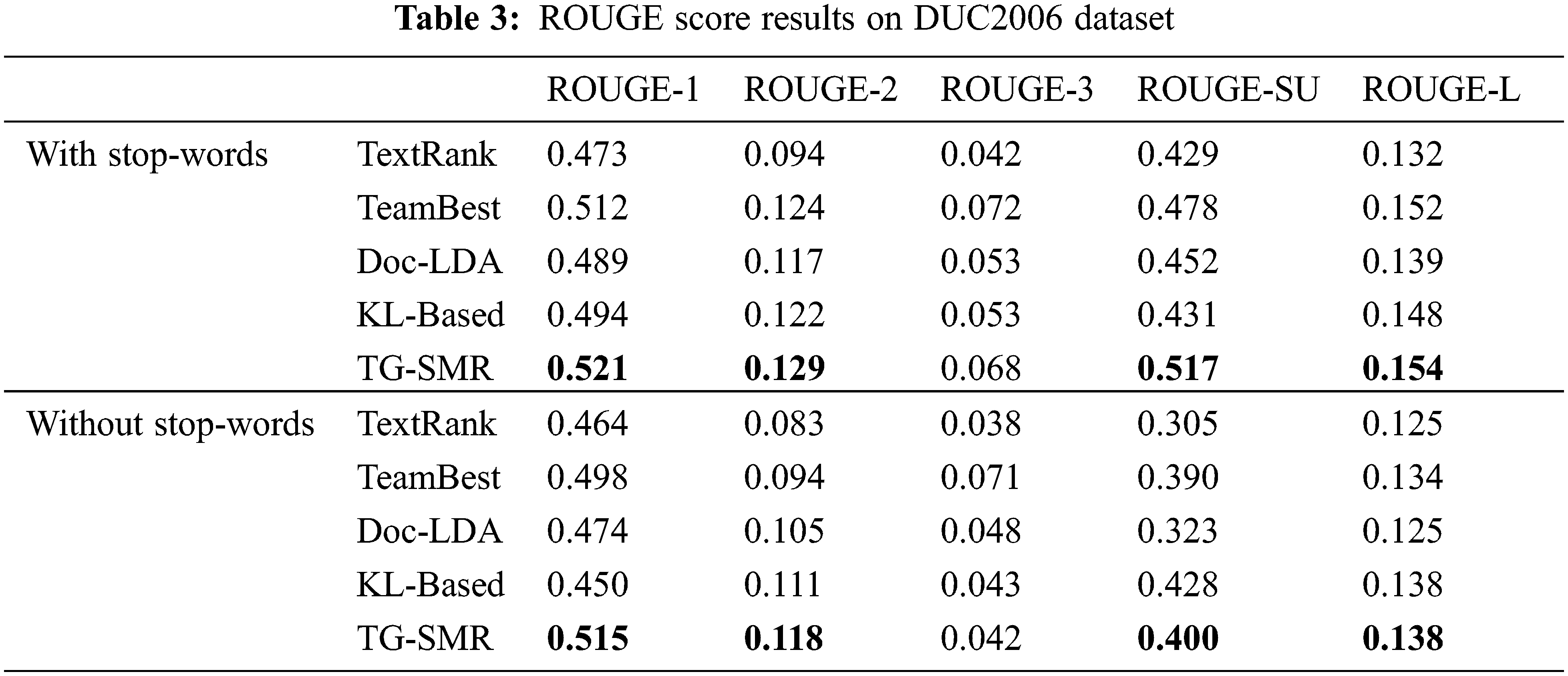
From Tabs. 2 and 3, we remark that for all algorithms on the two datasets have the same phenomenon. The scores with stop-words are higher than the scores without stop-words. This is determined by the ROUGE evaluation criterion, the more occurrences of the same words, the higher the score.

The ROUGE indicator has a value range of 0 to 1. The automated abstract becomes closer to the expert abstract as it gets closer to 1. On the DUC2004 dataset, the scores of the algorithms ROUGE-1 and ROUGE-2 proposed in this paper are higher than that of TeamBest. On the set, the algorithm proposed in this paper is higher than the scores of TeamBest on ROUGE-1, ROUGE-2, ROUGE-L, and ROUGE-SU. In other cases, our proposed algorithm TG-SMR is not much different from TeamBest. Compared with the other three algorithms, ROUGE scores of TG-SMR have been improved, especially compared to the TextRank algorithm. ROUGE-1 indicates the degree of similarity between automatic and expert summarizing, whereas ROUGE-2 denotes the smoothness of summarization. The scores of TG-SMR algorithm on ROUGE-1 and ROUGE-2 are higher than those of the other four algorithms, reflecting the superiority of text summarization based on semantic level and the effectiveness of TG-SMR algorithm.

6  Conclusion

After introducing the basic idea and calculation model of the TextRank algorithm, this paper points out its defects in the scenarios of synonyms and polysemy. An improved method is proposed, which relies on the semantic level association to reconstruct the graph model, thus fundamentally solving the defects of the TextRank algorithm in multi-semantic scenarios. Finally, through experiments on the DUC2004 and DUC2006 datasets, our proposed improved graph model algorithm TG-SMR is compared to other text summarization systems. The experimental results prove that our algorithm has the best performance on the majority of ROUGE evaluation indicators.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Mihalcea and P. Tarau, “TextRank: Bringing order into texts,” in Proc. 2004 Conf. on Empirical Methods in Natural Language Processing, Barcelona, Spain, vol. 85, pp. 404–411, 2004. [Google Scholar]

 2.  C. Mallick, A. K. Das, M. Dutta, A. K. Das and A. Sarkar, “Graph-based text summarization using modified TextRank,” Advances in Intelligent Systems and Computing, vol. 758, pp. 137–146, 2018. [Google Scholar]

 3.  W. Wang, F. Wei, W. Li and S. Li, “HyperSum: Hypergraph based semi-supervised sentence ranking for query-oriented summarization,” in Proc. Int. Conf. on Information and Knowledge Management, Hong Kong, pp. 1855–1858, 2009. [Google Scholar]

 4.  G. Erkan and D. R. Radev, “LexRank: Graph-based lexical centrality as salience in text summarization,” Journal of Artificial Intelligence Research, vol. 22, pp. 457–479, 2004. [Google Scholar]

 5.  D. M. Blei, A. Y. Ng and M. I. Jordan, “Latent dirichlet allocation,” Journal of Machine Learning Research, vol. 3, no. 4–5, pp. 993–1022, 2003. [Google Scholar]

 6.  H. P. Lunh, “The automatic creation of literature abstracts,” IBM Journal of Research Development, vol. 2, no. 2, pp. 159–165, 1958. [Google Scholar]

 7.  P. B. Baxendale, “Machine-made index for technical literature-An experiment,” IBM Journal of Research and Development, vol. 2, no. 4, pp. 354–361, 1958. [Google Scholar]

 8.  H. P. Edmundson, “New methods in automatic extracting,” Journal of the ACM, vol. 16, no. 2, pp. 264–285, 1969. [Google Scholar]

 9.  R. McDonald, “A study of global inference algorithms in multi-document summarization,” In: G. Amati, C. Carpineto and G. Romano (Eds.Advances in Information Retrieval, ECIR 2007, Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, vol. 4425, pp. 557–564, 2007. [Google Scholar]

10. D. Gillick and B. Favre, “A scalable global model for summarization,” in Proc. of the NAACL HLT Workshop on Integer Linear Programming for Natural Language Processing, Boulder, Colorado, pp. 10–18, 2009. [Google Scholar]

11. C. Li, X. Qian and Y. Liu, “Using supervised bigram-based ILP for extractive summarization,” in Proc. ACL 2013-51st Annual Meeting of the Association for Computational Linguistics, Sofia, Bulgaria, vol. 1, pp. 1004–1013, 2013. [Google Scholar]

12. H. Lin and J. Bilmes, “Multi-document summarization via budgeted maximization of submodular functions,” in Proc. NAACL HLT 2010-Human Language Technologies: The 2010 Annual Conf. of the North American Chapter of the Association for Computational Linguistics, Los Angeles, USA, pp. 912–920, 2010. [Google Scholar]

13. H. Lin and J. Bilmes, “A class of submodular functions for document summarization,” in Proc. ACL-HLT 2011-49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, USA, vol. 1, pp. 510–520, 2011. [Google Scholar]

14. J. Kupiec, J. Pedersen and F. Chen, “Trainable document summarizer,” in Proc. of the 18th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Seattle, USA, pp. 68–73, 1995. [Google Scholar]

15. J. M. Conroy and D. P. O’leary, “Text summarization via hidden markov models,” in Proc. of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, New Orleans, USA, pp. 406–407, 2001. [Google Scholar]

16. F. B. Goularte, S. M. Nassar, R. Fileto and H. Saggion, “A text summarization method based on fuzzy rules and applicable to automated assessment,” Expert Systems with Applications, vol. 115, pp. 264–275, 2019. [Google Scholar]

17. K. M. Svore, L. Vanderwende and C. J. C. Burges, “Enhancing single-document summarization by combining RankNet and third-party sources,” in Proc. 2007 Joint Conf. on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Prague, Czech Republic, pp. 448–457, 2007. [Google Scholar]

18. J. Cheng and M. Lapata, “Neural summarization by extracting sentences and words,” in Proc. ACL 2016-54th Annual Meeting of the Association for Computational Linguistics, Berlin, Germany, vol. 1, pp. 484–494, 2016. [Google Scholar]

19. R. Nallapati, B. Zhou, C. dos Santos, C. Gulcehre and B. Xiang, “Abstractive text summarization using sequence-to-sequence RNNs and beyond,” in Proc. CoNLL 2016-20th SIGNLL Conf. on Computational Natural Language Learning, Berlin, Germany, pp. 280–290, 2016. [Google Scholar]

20. R. Nallapati, F. Zhai and B. Zhou, “SummaRuNNer: A recurrent neural network based sequence model for extractive summarization of documents,” in Proc. Thirty-First AAAI Conf. on Artificial Intelligence, San Francisco, USA, pp. 3075–3081, 2017. [Google Scholar]

21. J. Xu and G. Durrett, “Neural extractive text summarization with syntactic compression,” in Proc. 9th Int. Conf. on Natural Language Processing, Zurich, Switzerland, pp. 3292–3303, 2020. [Google Scholar]

22. D. Anand and R. Wagh, “Effective deep learning approaches for summarization of legal texts,” Journal of King Saud University-Computer and Information Sciences, In Press, 2019. [Google Scholar]

23. M. Zhong, P. Liu, Y. Chen, D. Wang, X. Qiu et al., “Extractive summarization as text matching,” in Proc. 58th Annual Meeting of the Association for Computational Linguistics, Online, pp. 6197–6208, 2020. [Google Scholar]

24. X. Han, T. Lv, Z. Hu, X. Wang and C. Wang, “Text summarization using framenet-based semantic graph model,” Scientific Programming, vol. 2016, no. 3, pp. 1–10, 2016. [Google Scholar]

25. W. S. El-Kassas, C. R. Salama, A. A. Rafea and H. K. Mohamed, “EdgeSumm: Graph-based framework for automatic text summarization,” Information Processing and Management, vol. 57, no. 6, pp. 102264, 2020. [Google Scholar]

26. A. P. Widyassari, S. Rustad, G. F. Shidik, E. Noersasongko, A. Syukur et al., “Review of automatic text summarization techniques & methods,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 4, pp. 1029–1046, 2022. [Google Scholar]

27. M. Gambhir and V. Gupta, “Recent automatic text summarization techniques: A survey,” Artificial Intelligence Review, vol. 47, no. 1, pp. 1–66, 2017. [Google Scholar]

28. J. Li, C. Zhang, X. Chen, Y. Hu and P. Liao, “Survey on automatic text summarization,” Computer Research and Development, vol. 58, no. 1, pp. 1–21, 2021. [Google Scholar]

29. W. S. El-Kassas, C. R. Salama, A. A. Rafea and H. K. Mohamed, “Automatic text summarization: A comprehensive survey,” Expert Systems with Applications, vol. 165, pp. 113679, 2021. [Google Scholar]

30. S. Robertson and H. Zaragoza, “The probabilistic relevance framework: BM25 and beyond,” Foundations and Trends in Information Retrieval, vol. 3, no. 4, pp. 333–389, 2009. [Google Scholar]

31. M. Liu, S. Li and K. Jin, “Feature combination optimization in automatic multi-document summarization,” Computer System Applications, vol. 17, no. 8, pp. 59–63, 2008. [Google Scholar]

32. C. Sun and L. Li, “Research and implementation of knowledge-based text summarization system,” Computer Research and Development, vol. 37, no. 7, pp. 874–881, 2000. [Google Scholar]

33. C. Y. Lin, “Rouge: A package for automatic evaluation of summaries,” in Proc. WAS 2004 Workshop on Text Summarization Branches Out, Barcelona, Spain, no. 1, pp. 25–26, 2004. [Google Scholar]