A Double Threshold Energy Detection-Based Neural Network for Cognitive Radio Networks

1  Introduction

Cognitive radio (CR) comes as an intelligent solution to get over spectrum scarcity and inefficient spectrum usage issues. Cognitive users can use the licensed spectrum when such spectrum usage does not result in harmful interference with the license users. This spectrum usage form leads to new challenges such as spectrum sensing. Being aware of the primary licensed user activities is the first step performed by the cognitive radio system. Many spectrum-sensing techniques have been proposed in the literature in [1].

Through these sensing methods, the most commonly used technique is energy detection; because it is low cost and simple implementation [2]. The performance of energy detection is deteriorating due to the impact of noise uncertainty, especially in low signal-to-noise ratio SNR environments, in this case, to get a reliable detection the gathered samples for the energy detection test must be large enough [3,4]. A large sample size takes extra time for sensing and this may decrease the network capacity [5]. Thus, the sample size is an important optimization problem.

The conventional energy detector maximizes the generalized likelihood function, this is may not maximize the detection probability or minimize the false alarm/missed detection probability. Chen, replace the squaring operation of the conventional energy detector with arbitrary positive power, a new energy detector “improved energy detector” with better detection performance can be derived [6]. In addition, when the double threshold technique is applied to the improved energy detection scheme; a more reliable detection technique with trade-offs between sensing efficiency, computational complexity, can be achieved.

In this paper, local and cooperative spectrum sensing performance has been optimized based improved double threshold energy detection scheme by finding the optimum sample size, which minimizes the total error rate. The rest of this paper is organized as follows: Section 2 review the background and motivations. In Section 3, the machine and learning approach in cognitive radio is presented. The concept of sample size effect on the performance metrics reviewed in Section 4. In Section 5, the methodologies of study illustrated show the theoretical and mathematical calculations related to optimum sample size. In Section 6, results and discussion are presented, and the paper is concluded in Section 7.

2  Background and Motivations

Learning techniques for spectrum sensing are known as tools in solving complex classification problems. These techniques are used to efficiently manage the spectrum in wireless communication, in addition to managing the resource power to obtain high quality of service (QoS) to mobile users. In the CR domain, one of the objectives of using learning techniques is to enhance the performance of spectrum sensing.

In general, learning mechanisms in CR are divided into two types. namely learning and prediction, so that the data is provided in a format that is related to the learning stage of the primary user (PU) features and secondary user (SU) sensor parameters such as test statistics, signal to noise ratio (SNR), geographical location, etc., while the prediction stage can be related to with the result of the sensor, energy efficiency, and the operating model to be adopted [7].

In normal spectrum sensing, SU has to determine the threshold for the test statistic before deciding on the PU presence. This threshold may be calculated based on target false alarm and detection rates. Thus, many statistical parameters related to noise, channel, and PU signal must be known in advance. The majority of work focuses on tuning learning methods with numerical statistics of two hypotheses: H0, where PU is assumed absent, and H1, where PU is assumed active.

Learning methods help to determine the optimum threshold value for the minimum error that appears on the spectrum sensing, which can lead to interference between the transmission from primary and secondary users, or the secondary user misses the transmission opportunity caused by using the available spectrum bands, see Fig. 1. This usually occurs when a constant change in the environment such as a change in background noise, movements of users or transmitters, and interference alters the sensing spectrum parameters such as the detection threshold [7].

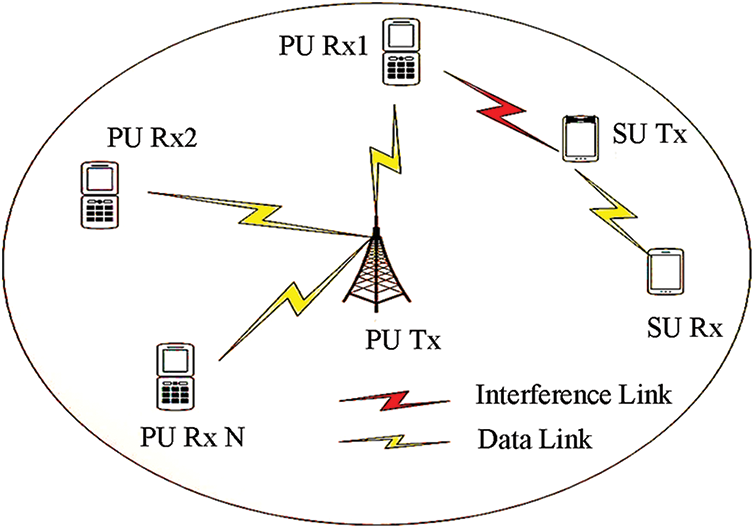
Figure 1: A cognitive radio network (CRN) with a primary base station, primary users (Pus), and secondary users (SU) interference

According to what has been presented, the motivation of this paper is to present a method based on the use of machine learning to improve spectrum sensing based on the analysis and evaluation of an optimized error minimization model. The scope of the study is a case for integrating double threshold energy detection and machine learning into perceptual radio systems to optimize the error minimization method. In short, the contributions of this paper can be summarized as follows:

•   Reviews the effects of sample size on detection and false alarm probabilities in spectrum sensing technique.

•   Review the mathematical calculations related to spectrum sensing and double threshold energy detection.

•   Develop an optimization model for minimizing error probability based on machine learning and optimum sample size.

•   Analysis of the developed model in performance compared with local spectrum sensing and optimum sample size.

3  Machine Learning in Cognitive Radio Network

Learning can enable performance improvement for the cognitive radio network by using stored information both of its actions and the results of these actions and the actions of other users to aid the decision-making process. Intelligence, as the main ingredient of cognitive radio technology, can be employed in every stage of the cognition cycle [8]. Learning is defined as the modification of behavior through practice, training, or experience [9]. According to [10], learning ability is an indispensable component of intelligent behavior. A practical definition for the term learning was given in [11] to be the ability to create knowledge from the information acquired about the environment and the internal states.

Based on this definition, learning is related to the ability to synthesize the acquired knowledge to improve the future behavior of the learning agent. This makes knowledge a fundamental component of the learning process and relates to the term cognition, which is defined as the act or process of knowing or perception [9]. Fig. 2, shows the relations among intelligence, learning, and cognitive radio, and illustrates the concept of knowledge as a common feature of both learning and detection threshold.

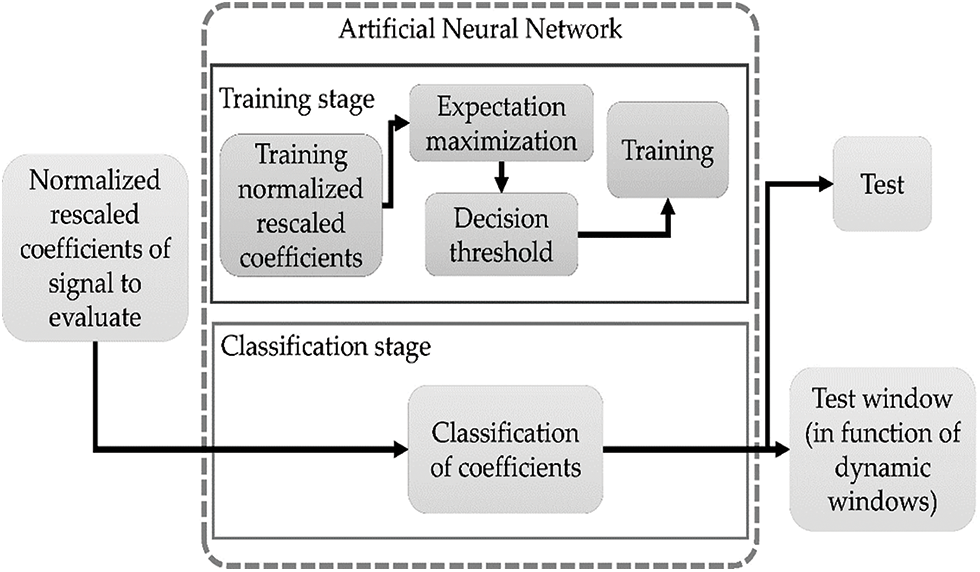
Figure 2: Machine learning approach in cognitive radio spectrum sensing

Artificial neural networks (ANN), shown as classifiers, often employ supervised learning where the information is processed to achieve a predefined target output [12]. This approach, indeed, can be considered as an optimization problem whose objective function is to minimize the total error resulting from the difference between the target and the actual outputs [13]. Working on ANN is based on the human brain, which computes responses rather differently from the way conventional computers work. A neural network is defined to be a massively parallel-distributed processor made up of simple processing units, which has a natural propensity for storing experiential knowledge and making it available for use [14]. Thus, it can be concluded that an ANN and the human brain have the following similarities.

•   The network obtains knowledge from its environment through a learning process.

•   The strengths of interneuron connection, commonly called synaptic weights, are used for storing the gained knowledge. ANN has some capabilities such as nonlinearity fitness to underlying physical mechanisms. In addition, adaptive to minor changes in the surrounding environment.

To the classification of the pattern, the ANN provides information about which particular pattern to choose, besides the confidence in making the suitable decision. The main features of ANN are; their ability to learn complex nonlinear input/output relationships. Usage of sequential training procedures and adapting themselves to the data. These features qualified ANN to be a significant tool for classification, which is needed frequently in decision–making assignments of human activities [15]. In cognitive radio, neural networks help to optimize the sample size, which will lead to minimizing the error probability depending on spectrum-sensing parameters such as the targeted detection, false alarm probabilities, and SNR.

4  Sample Size Effects on Cooperative Spectrum Sensing

In cognitive spectrum sensing sample size can affect performance metrics because the sample size N must be large enough to achieve the requirements on detection and false alarm probabilities (i.e., IEEE standard Pf ≤ 0.1 and Pd ≥ 0.9,). When the number of the sample (N), is large the sensing time becomes longer which leads to high detection probability. Sensing time depends on and increases with the sample size (N). The decrease in false alarm probability and the increase in detection probability with the sensing time increasing it supposed to increase the network throughput [16]. However, it found that increasing the sensing time does not result in a monotonic increase of the throughput of the CR users’ networks.

The achievable throughput of cooperative spectrum sensing can be defined as the average amount of the successfully delivered transmitted bits. Considering the sampling time as (t), sensing time is derived as in Eq. (1),

τ =tN (1)

Let P (H0) and P (H1) be the probabilities that hypothesis H0 and H1 are true respectively. Let γs represent the signal-to-noise ratio of the secondary point-to-point link and γp represents the signal-to-noise ratio of the primary user at the secondary receiver [17]. The achievable throughput of the secondary network is given by the following equations.

φ = T−τT[C0(1−Pf)P(H0)+C1(1−Pd)P(H1)] (2)

C0=log2(1+γs) (3)

C1=log2(1+(γs1+γp)) (4)

where, Co is the capacity of the secondary network in the absence of the primary user, and C1 is the capacity of the secondary network in the presence of the primary user.

5  The Methodologies

This paper aims to develop two new methods to calculate optimum sample size, which minimizes the total error probability; based on an improved double threshold energy detector depending on network requirement. In the first method, the optimization problem, which minimizes total error rate probability, is solved mathematically. In the second method, the neural network has been used as an intelligent way to find the optimum sample size that minimizes error probability when the inputs are the targeted detection, false alarm probabilities, and SNR is known. These methods are shown as follows.

5.1 Local Spectrum Sensing

The local spectrum-sensing problem can be formulated as follows;

y(n)={u(n):H0s(n)+u(n):H1 (5)

where, s(n), and u(n) represent the primary user’s signal and the noise, where they are assumed to be an independent and identically distributed (i.i.d) random process with mean zero and variance σs2. The test statistic of the improved energy detector is given by Eq. (6).

Y=∑n=1N|y(n)σw2|pH1≻≺H0T (6)

For any p, |y(n)σw2|p , are independent and identically distributed random variables. The mean and variance of |y(n)σw2|p given by the following equations.

μ0 = 2p/2πΓ(P+12) (7)

σ02=2pπ[Γ(2P+12)−1πΓ2(P+12)] (8)

μ1=2p/2(1+γ)p/2πΓ(P+12) (9)

σ12=2p(1+γ)pπ[Γ(2P+12)−1πΓ2(P+12)] (10)

where, Γ (.) is a gamma function, (µ0, µ 1) and (σ02, σ12), are the means and variance under H0 and H1.

As |y(n)σw2|p are Gaussian random variables, the sum of such N random variables is also Gaussian distributed. Thus, the test statistic (Y) is Gaussian distributed. Now, if the number of samples N is large enough, we can invoke the central limit theorem. Then (Y) is Gaussian distributed with the following Eq. (11).

Means:E(y)={μ0H0μ1H1andvariance:var(Y)={σ02/NH0σ12/NH1 (11)

The performance of the energy detector is characterized by using the following metrics, which have been introduced based on the test statistic under the binary hypothesis as follows;

Pf=Q(T−μ0σ0/N) (12)

Pd=Q(T−μ1σ1/N) (13)

Pm=1−Pd (14)

where, Pf, Pd, and Pm, are false alarm, detection, and miss detection probabilities. T is the threshold.

A good sensing technique must have a high Pd for (PU protection) and a low Pf (for SU protection). Pm is proportional to the interference induced from each SU on the PU, which must be as low as possible. Now the total error probability Pr is given by:

Pr=(1−p)Pf+p(Pm) (15)

Pr=(1−p)Q(T−μ0σ0/N)+p(1−Q(T−μ1σ1/N)) (16)

5.2 Improved Double Threshold Energy Detection

For improved double threshold energy detector, the optimization problem when K, L = 1, 2… K, and SNR are known, can be defined by the Eqs. (12), (13), (17), and (18).

Pa=1−Q(T1−μ0σ0/N) (17)

Pm=1−Q(T1−μ1σ1/N) (18)

where, Pa=1−Pf−Δ0 , Pm=1−Pd−Δ1,andΔ0 probability of uncertainty under H0 and Δ1 probability of uncertainty under H1

5.3 Optimum Sample Size

We can get the optimum sample size (N∗) which minimizes total error probability for local improved energy detector by solving Eq. (15) as follows;

N∗=argmin(N⁡Pr);∂Pr∂N|N=N∗=0 (19)

For improved double threshold energy detector, the optimal (N*), that minimizes the total error probability for improved double threshold energy detector [16]:

N∗argmin(N⁡Qr);∂Qr∂N|N=N∗=0 (20)

Qr=Qf+Qm (21)

The optimal N ( N∗ ), can be found by the Eq. (22) as follows;

∂Qr∂N=∂Qf∂N+∂Qm∂N=0 (22)

where, Qr represents the total error probability. Qf is an overall false alarm probability, and Qm represents the overall miss detection probability.

5.4 Neural Network for Number of Sample Optimization

In Section 5.3, the optimal sample size was calculated which enables minimization of the error probability to zero. In some cases, the optimal sample size might be too large. This is the main disadvantage in spectrum sensing at a low SNR environment because of the limitation on the maximal allowable sensing time and this may lead to inefficient spectrum utilization as is mentioned earlier in this subsection [18]. The sample size here can be modified by using a neural network through feeding it as a targeted output and predefined another network requirement like SNR and detection, false alarm, probabilities as a targeted input to calculate the optimum sample size [19].

The neural networks, shown as classifiers, often employ supervised learning where the information is processed to achieve a predefined target output. This approach can be considered as an optimization problem whose objective function is to minimize the total error resulting from the difference between the target and the actual outputs [20–22]. The following are the steps followed for the proposed methodology. Tab. 1 shows the NN and the cognitive radio network parameters used in the proposed study.

•   Step1: Designing neural network based on, input-output parameters, network type, network parameters, in addition to database length.

•   Step2: Analyze the results.

•   Step3: Redesign the network

In the study, the performance metrics like total error rate (Qr), throughput, and error probability are used to evaluate the NN method compared with fixed N samples and optimum N methodologies. The total error rate (Qr) can be calculated based on the overall probabilities of false alarm ( Qf ) and detection ( Qd ) and Missed-detection ( Qm ) for double threshold energy detection technique.

The false alarm ( Qf ) and detection ( Qd ) can be calculated by the following equations.

Qf=∑l=kM(Ml)∑k=lM(M−lk−l)Pak−lPflΔ1M−k (23)

Qd=∑l=kM(Ml)∑k=lM(M−lk−l)Pmk−lPdlΔ2M−k (24)

From the Eqs. (23) and (24), the Qd and Qf can be formulated by Eqs. (25) and (26), then Qm is equal to 1−Qd .

Qd=∑l=kM(Ml)Pmk−lPdl(1−Δ2)M (25)

Qf=∑l=kM(Ml)Pak−lPfl(1−Δ1)M (26)

According to Eq. (26) and the Qm value, the total error rate (Qr) can be calculated as follows,

Qr=Qf+Qm (27)

where M is the total number of secondary users, and k is the number of secondary users chosen for cooperation.

The throughput against sensing time calculations, the cooperative spectrum-sensing throughput is given by the average amount of the successfully delivered transmitted bits. It depends on the correct identification of the spectrum hole. The sensing time optimization problem can be mathematically formulated as,

minPf,γτ=tγ2(Q−1(Pf)−Q−1(Pd)2γ+1)2;s.t.{Pc≤Pc¯Rn≥R¯n (28)

where, R¯n is target-normalized throughput of SUs and Pc¯ is the maximum allowable probability of collision between samples of SUs.

6  Results and Discussion

All simulations in this paper are executed on MATLAB (version R2020a). The Monte Carlo (MC) method, which is a stochastic technique, based on the use of random numbers forms the basis of these simulations [23]. Receiver operating characteristics (ROC) curves are used to compare different scenarios described in the previous sections.

For simulation, additive white Gaussian noise (AWGN) channel is considered with signal-to-noise ratio SNR range is taken from −20 dB to 0 dB. For cooperation k-out-of-M fusion rule is used with M = 5, 10, 20,150. M is the total number of SUs participating in cooperation. The number of samples during the detection period (N) is from 10 to 1000 calculated by the proposed methods. Pf varies from 0 to 1. Noise power is assumed to be known σn2 = 1.

Before we evaluate the optimized error minimization-based machine learning method, we analyze the fixed N and optimum N methods as calculated in Sections 5.1 and 5.3 in terms of throughput and power operation. The optimum power operation value that minimizes the total error rate is found (p = 2.4) as shown in Fig. 3.

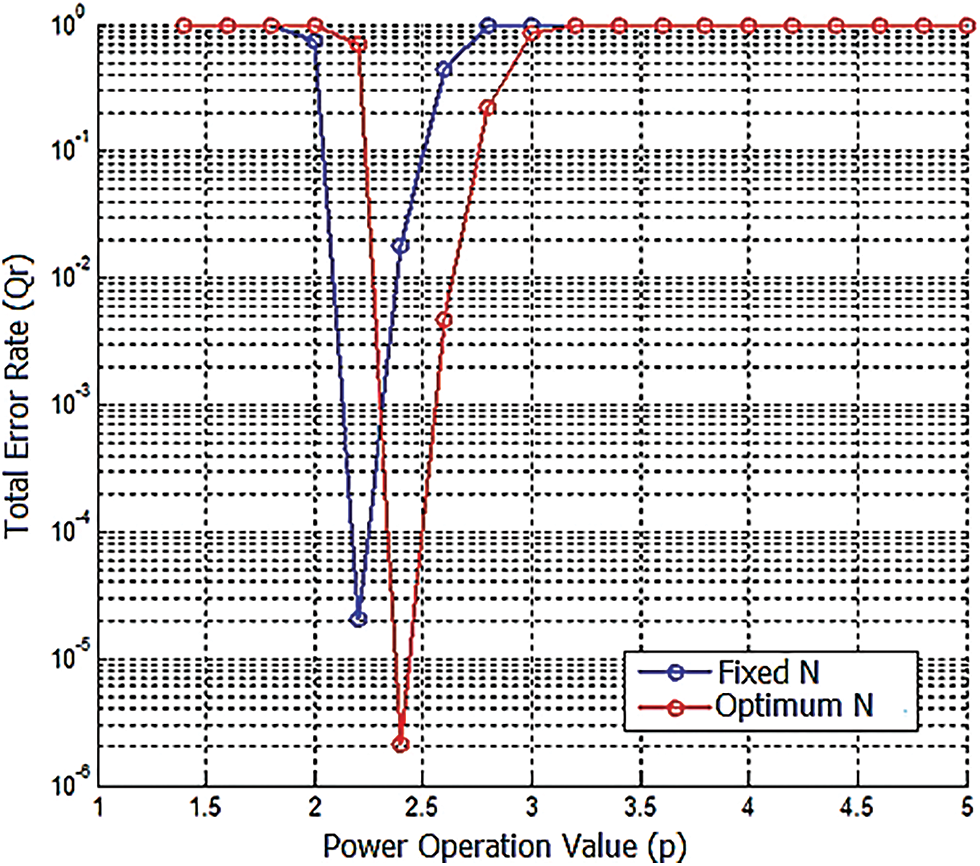
Figure 3: Power operation value vs. total error rate

The evaluation of throughput in Fig. 4 shows that the optimum N method will increase the network throughput by 5% compared with Fixed N. The sensing time increased with sample size increasing, in this case, we found optimal sensing time = 2.55 ms compared with the previous method sensing time = 2.5 ms. This is a very low increase so the agility will not affect while the throughput enhanced.

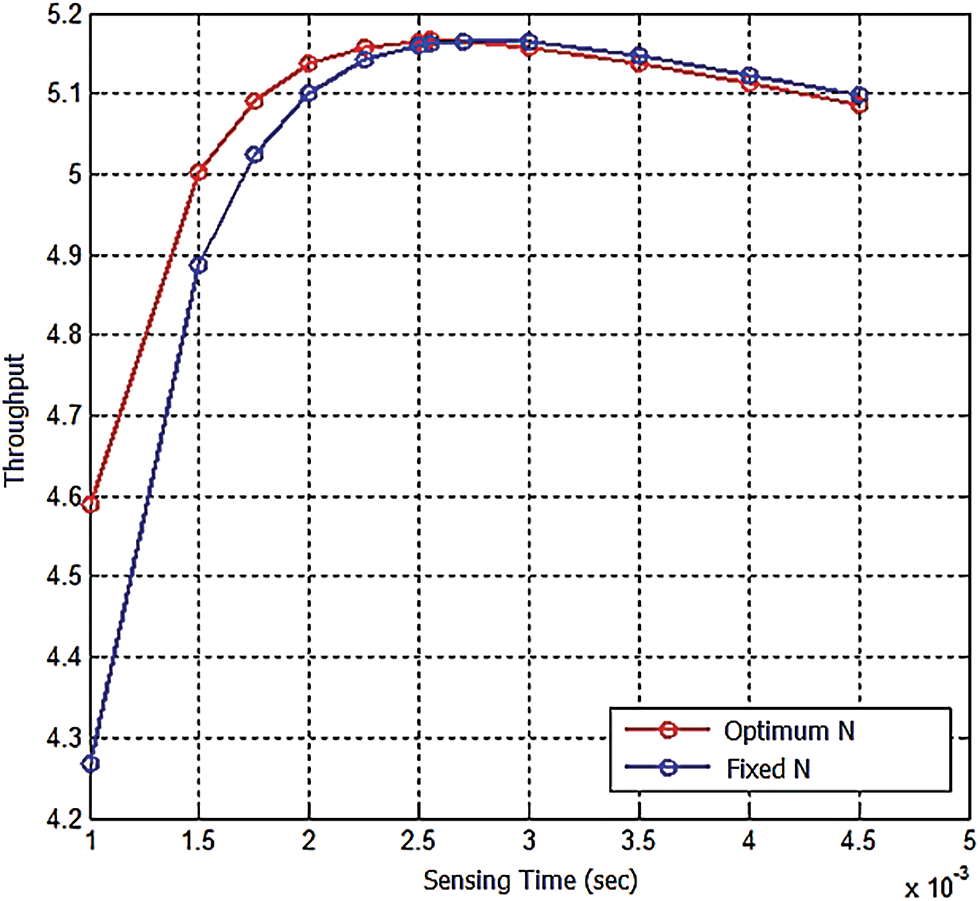
Figure 4: Throughput vs. sensing time

According to the last evaluation outputs, we analyze the optimized error minimization-based machine learning method compared with fixed N and optimum N methods in terms of error probability, detection, and miss detection probabilities, and optimal fusion rule in the following sections [24].

6.1 Error Probability

Using the above-mentioned methods to find optimum sample size, compression between the two methods and a constant N selection are shown in terms of error probability [25–27]. Fig. 5 shows the signal-to-noise ratio versus error probability, SNR = −5 dB, N = 500; N2 = 610; N3 = 756; it is clear that the error probability decreases as the sample size increase. The optimum N method outperforms the other methods in terms of total error rate minimization.

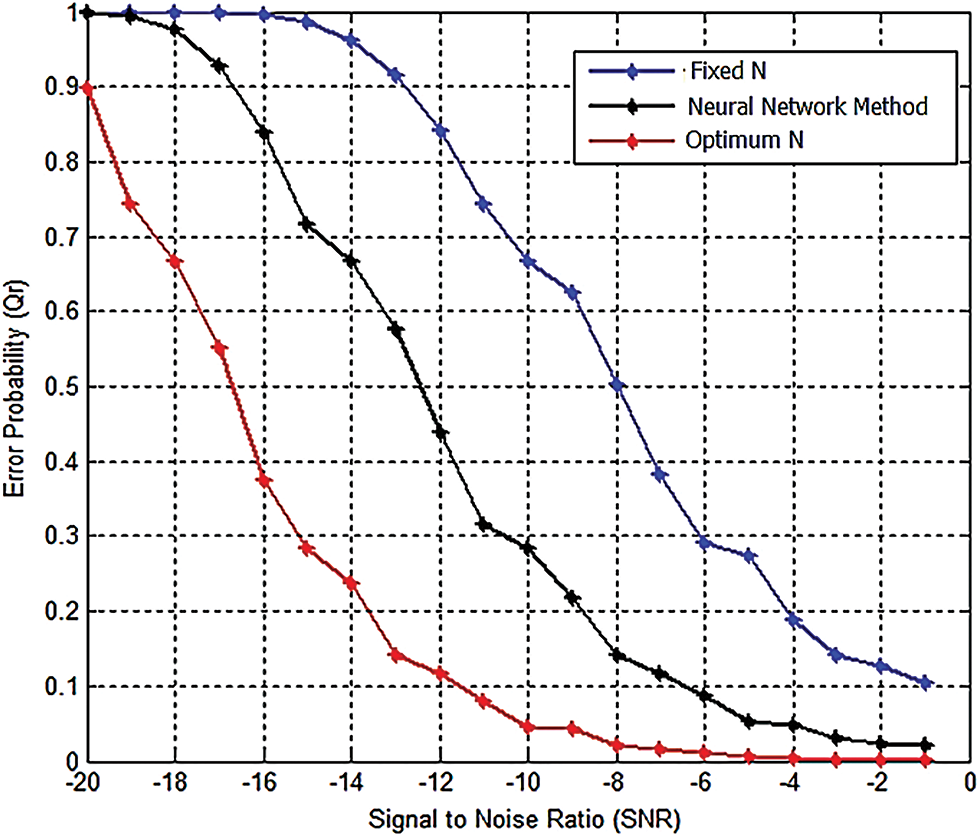
Figure 5: SNR vs. error probability, SNR = −5 dB

6.2 Detection and Miss Detection Probabilities

In terms of detection probability from simulation, it is clear that when the optimum number of sample methods are used; better detection can be achieved as shown in Fig. 6. In addition, the collision (missed detection) probability has been minimized when the proposed methods were used as shown in Fig. 7.

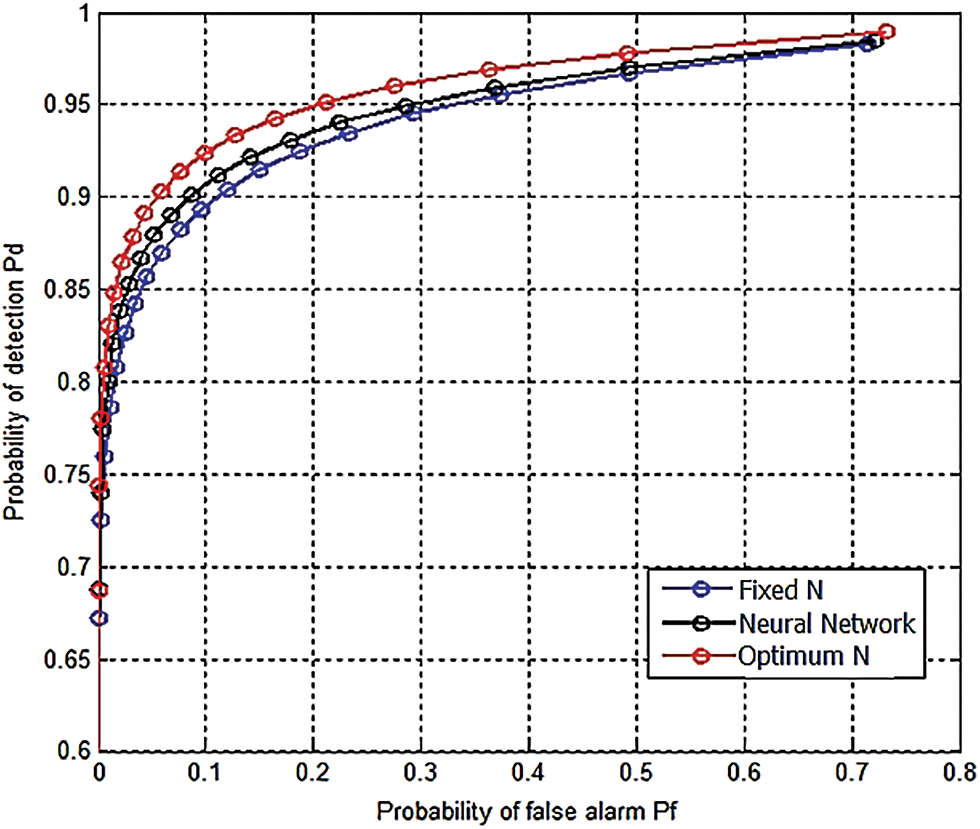
Figure 6: Probability of false alarm vs. probability of detection

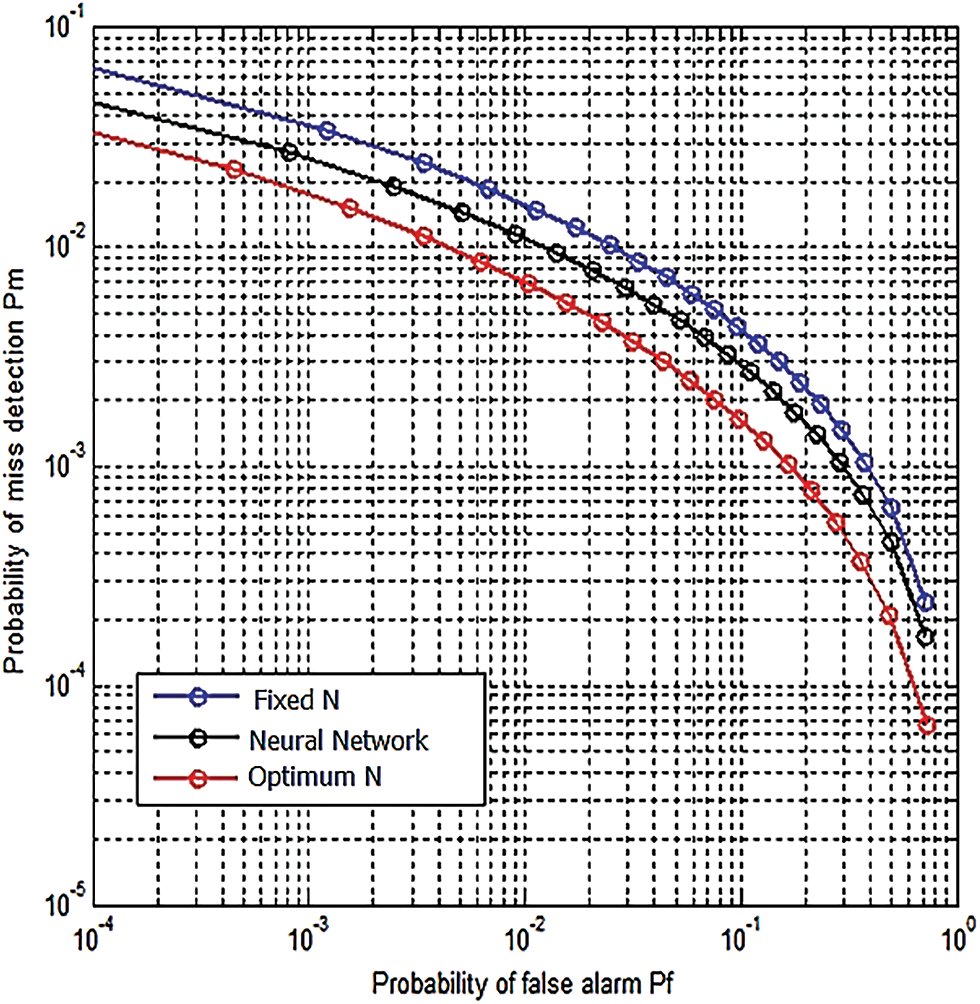
Figure 7: False alarm vs. detection probabilities, SNR = −5 dB, p = 2.8

6.3 Optimal Fusion Rule

The optimum fusion rule is the rule, which minimizes error probability [28,29]. Using the two proposed methods to calculate the optimum number of the sample that minimizes the error probability we found that the optimum fusion rule is the majority rule. Fig. 8 shows several users versus error probability, SNR = −5 dB, p = 2.8, N = 500; N2 = 610; N3 = 756; it is clear that the error probability decreases as the sample size increase. In addition, the optimum fusion rule is not affected when all users have the same SNR and the sample sizes are closed to each other [30].

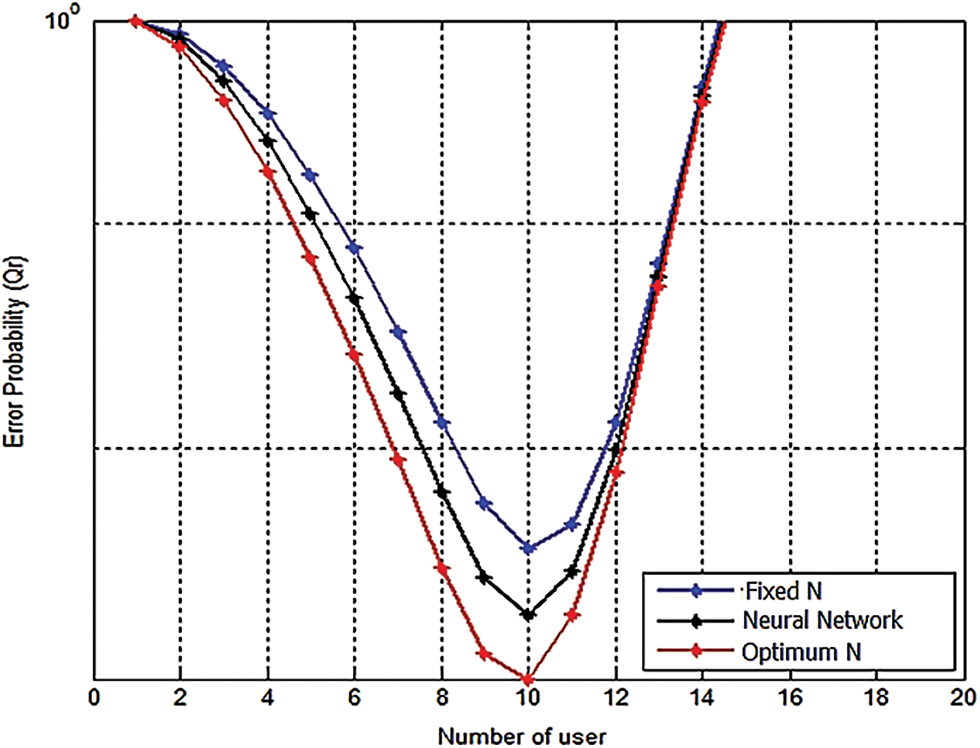
Figure 8: SNR vs. error probability, SNR = −5 dB, p = 2.8, N = 500; N2 = 610; N3 = 756

Since sample size affects the local sensing performance at each cognitive user, this will affect the optimal fusion rule when all users cooperate. The optimal fusion rule changed with the total number of cooperative users changing. In addition, deference in SNR at each cognitive user might affect the optimal fusion rule as shown in Fig. 9.

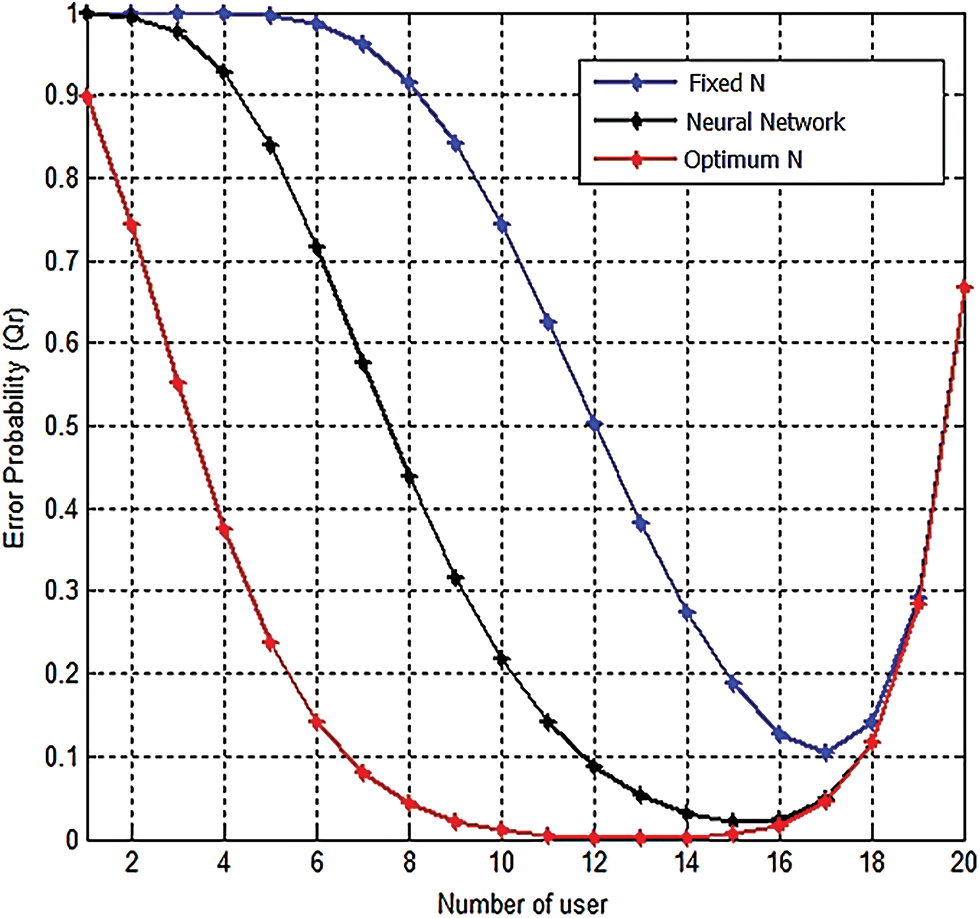
Figure 9: Various fusion rules under different SNR at each user

7  Conclusion

In this paper, the effects of sample size in performance metrics are discussed and shown that the sample size is an important optimization problem, especially in the low signal-to-noise ratio region. Two new methods to calculate the optimum number of samples are proposed in this paper. These methods outperform the traditional sample size selection in terms of the total error rate, detection probability, and throughput. The optimum power operation which minimizes the total error rate is found (p = 2.4). We found that optimum fusion is the majority rule when all user has the same SNR, otherwise closed to the majority fusion rule. In addition, it found that when sensing time is increased; the throughput of the CR network is enhanced. It increases with sensing time and reaches a maximum, thereafter the throughput decreases.

Acknowledgement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R97), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R97), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

 1.  A. G. A. Elrahim and N. M. Elfatih, “A survey for cognitive radio networks,” Computer Science and Telecommunications, vol. 5, no. 11, pp. 1–6, 2014. [Google Scholar]

 2.  G. Mahendru, A. K. Shukla and L. M. Patnaik, “An optimal and adaptive double threshold-based approach to minimize error probability for spectrum sensing at low SNR regime,” Ambient Intelligence and Humanized Computing, vol. 60, no. 8, pp. 1–10, 2021. [Google Scholar]

 3.  R. Wan, L. Ding, N. Xiong, W. Shu and Li Yang, “Dynamic dual threshold cooperative spectrum sensing for cognitive radio under noise power uncertainty,” Human-Centric Computing and Information Sciences, vol. 9, no. 22, pp. 1–21, 2019. [Google Scholar]

 4.  Y. Liu, J. Liang, N. Xiao, X. Yuan, Z. Zhang et al., “Adaptive double threshold energy detection based on Markov model for cognitive radio,” PLOS ONE, vol. 12, no. 5, pp. 1–18, 2017. [Google Scholar]

 5.  Y. Tingting, W. Yucheng, L. Liang, X. Weiyang and T. Weiqiang, “A two-step cooperative energy detection algorithm robust to noise uncertainty,” Wireless Communications and Mobile Computing, vol. 2019, pp. 1–10, 2019. [Google Scholar]

 6.  Y. Chen, “Improved energy detector for random signals in gaussian noise,” IEEE Transactions on Wireless Communications, vol. 9, no. 2, pp. 558–563, 2010. [Google Scholar]

 7.  J. Lorincz, I. Ramljak and D. Begusic, “Algorithm for evaluating energy detection spectrum sensing performance of cognitive radio MIMO-OFDM systems,” Sensors (Basel), vol. 21, no. 20, pp. 1–22, 2021. [Google Scholar]

 8.  D. Giral, C. Hernández and C. Salgado, “Spectral decision for cognitive radio networks in a multi-user environment,” Heliyon, vol. 7, no. 5, pp. e07132, 2021. [Google Scholar]

 9.  K. A. Yau, G. Poh, S. F. Chien and H. A. Al-Rawi, “Application of reinforcement learning in cognitive radio networks: Models and algorithms,” The Scientific World, vol. 2014, no. 6, pp. 1–23, 2014. [Google Scholar]

10. E. S. Ali, M. K. Hasan, R. Hassan, R. A. Saeed, M. B. Hassan et al., “Machine learning technologies for secure vehicular communication in internet of vehicles: Recent advances and applications,” Security and Communication Networks, vol. 2021, no. 3, pp. 1–23, 2021. [Google Scholar]

11. K. kockaya and I. Develi, “Spectrum sensing in cognitive radio networks: Threshold optimization and analysis,” Wireless Communications and Networking, vol. 255, no. 1, pp. 1–19, 2020. [Google Scholar]

12. Y. E. Morabit, F. Mrabti and E. H. Abarkan, “Survey of artificial intelligence approaches in cognitive radio networks,” Information and Communication Convergence Engineering, vol. 17, no. 1, pp. 1–20, 2019. [Google Scholar]

13. L. Alzubaidi, J. Zhang, A. J. Humaidi, A. Al-Dujail, Ye Duan et al., “Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions,” Journal of Big Data, vol. 8, no. 1, 1–74, 2021. [Google Scholar]

14. S. Davidson and S. Furber, “Comparison of artificial and spiking neural networks on digital hardware,” Frontiers in Neuroscience, vol. 15, pp. 1–7, 2021. [Google Scholar]

15. M. G. M. Abdolrasol, S. M. S. Hussain, T. S. Ustun, M. R. Sarker, M. A. Hannan et al., “Artificial neural networks based optimization techniques: A review,” Electronics, vol. 10, no. 21, pp. 1–43, 2021. [Google Scholar]

16. D. T. Dagne, K. A. Fante and G. A. Desta, “Compressive sensing-based maximum-minimum subband energy detection for cognitive radios,” Heliyon, vol. 6, no. 9, pp. e04906, 2020. [Google Scholar]

17. E. Axell, G. Leus, E. G. Larsson and H. V. Poor, “Spectrum sensing for cognitive radio state-of-the-art and recent advances,” IEEE Signal Processing Magazine, vol. 29, no. 3, pp. 101–116, 2012. [Google Scholar]

18. M. Xu, Z. Yin, Y. Zhao and Z. Wu, “Cooperative spectrum sensing based on multi-features combination network in cognitive radio network,” Entropy, vol. 24, no. 1, pp. 1–15, 2022. [Google Scholar]

19. A. Ivanov, K. Tonchev, V. Poulkov and A. Manolova, “Probabilistic spectrum sensing based on feature detection for 6g cognitive radio: A survey,” IEEE Access, vol. 9, pp. 116994–117026, 2021. [Google Scholar]

20. N. Nurelmadina, M. K. Hasan, I. Mamon, R. A. Saeed, K. Akram et al., “A systematic review on cognitive radio in low power wide area network for industrial iot applications,” Sustainability, vol. 13, no. 1, pp. 1–20, 2021. [Google Scholar]

21. R. Mokhtar, R. A. Saeed, R. Alsaqour and Y. Abdallah, “Study on energy detection-based cooperative sensing in cognitive radio networks,” Networks, vol. 8, no. 6, pp. 1255–1261, 2013. [Google Scholar]

22. R. A. Mokhtar, R. A. Saeed and R. A. Alsaqour, “Modeling of distributed sensing framework in spectrum aware cognitive radio networks,” in Proc. IRECOS, Italy, 7, pp. 25–31, 2012. [Google Scholar]

23. R. A. Saeed, R. Mokhtar and S. Khatun, “Spectrum sensing and sharing for cognitive radio and advanced spectrum management,” in Proc. ICGST, Barlin, Germany, 9, pp. 87–97, 2009. [Google Scholar]

24. R. A. Saeed, TV white space spectrum technologies: Regulations, standards, and applications, First Edition ed., New York, USA: The CRC Press, 2011. [Google Scholar]

25. R. A. Saeed, A. Ismail, M. K. Hasan, R. Mokhtar, S. K. Salih et al., “Throughput enhancement for WLAN TV white space in coexistence of IEEE 802.22,” Indian Journal of Science and Technology, vol. 8, no. 11, pp. 1–7, 2015. [Google Scholar]

26. T. Baykas, M. Kasslin, M. Cummings, H. Kang, J. Kwak et al., “Developing a standard for tv white space coexistence: technical challenges and solution approaches,” IEEE Wireless Communication Magazine, vol. 19, no. 2, pp. 10–22, 2012. [Google Scholar]

27. M. A. Elmubark, R. A. Saeed, M. A. Elshaikh and R. A. Mokhtar, “Fast and secure generating and exchanging a symmetric-keys with different key size in TVWS,” in Proc. ICCNEEE, Khartoum, Sudan, pp. 114–117, 2015. [Google Scholar]

28. M. A. Elmubark, R. A. Saeed, R. A. Mokhtar, H. Mohamad and H. Elshafie, “Design a new confidant protocol for master mode TV band devices,” in Proc. ISTT, Kuala Lumpur, KL, Malaysia, pp. 192–197, 2012. [Google Scholar]

29. R. A. Saeed, R. A. Mokhtar, J. Chebil and A. H. Abdallah, “TVBDs coexistence by leverage sensing and geo-location database,” in Proc. ICCCE, Kuala Lumpur, KL, Malaysia, pp. 33–39, 2012. [Google Scholar]

30. R. A. Saeed and R. A. Mokhtar, “TV white spaces spectrum sensing: Recent developments, opportunities and challenges,” in Proc. SETIT, Tunisia, Tunisia, pp. 634–638, 2012. [Google Scholar]