Modified Elliptic Curve Cryptography Multi-Signature Scheme to Enhance Security in Cryptocurrency

1  Introduction

Internet of Things (IoT) with blockchain technology is an emerging technology in the concerns of security and privacy issues. In IoT, the message transformation is done through central server. But it leads to the security and privacy issues including spoofing the wireless devices, less trustworthiness, false identification, and difficult to prevent the system from vulnerabilities. As well as protecting large amount of data is difficult [1,2]. To address these issues, blockchain technology can be introduced with IoT by removing the central authority [3]. Because it has special characteristics including decentralized and distributed network, immutable and auditable records, easily traceable, transparent transaction, enhanced security.

In blockchain, the blocks are linked together to form chain by the process of mining. Each block has header and body with validated and authenticated transaction details. The first block of chain is known as genesis block. Each block in blockchain consists of version, timestamp, nonce, previous block hash, root hash, and target hash [4]. The completed transactions are stored in block. When block is finished, it can be connected to the next block through cryptography hash function to ensure the security. It can be used in wide areas including supply chain management, healthcare, financial industries, energy trading and identity management, smart grid, voting system, education sector, insurance, asset tracking, digital ledgers, cyber security system, law and enforcement [5].

In supply chain management, it is used to enhance the transparency, traceability to prevent the transaction from attacks. In healthcare, blockchain technology is used to secure the clinical and unified patient information. It is used to trace the drugs and patient’s information without intermediaries. In financial industries, it offers the authentication and economic benefits. In retail services, it reduces the paperwork to rapid settlement procedure. In smart grid, it can be used to secure transactions of energy retailing and purchasing by increasing the resiliency. The blockchain based voting system provides distributed ledger with fast counting. In insurance field, it provides fast transaction between clients, policyholders and companies. In identity management, it eliminates the identity and password theft without central authority [6]. But still, it needs more concentration on research areas including scalability, interoperability, privacy, selfish mining and secure cryptography hash algorithm.

The cryptography algorithm is the important reason to increase the security in cryptocurrency and it can be divided into symmetric, asymmetric, and hash algorithms. The prime numbers have been chosen to generate the private and public key. In cryptocurrency, hash functions and asymmetric cryptography algorithms are mainly used to validate and secure the transaction [7]. Because the symmetry cryptography algorithm like Advanced Encryption Standard (AES), Rivest Shamir Adleman (RSA) generate only one key at a time and it allows maximum of 32-bit key size only. So, it can be easily tracked by hackers and lead to prime number loss. In digital signature algorithm, the private key and public key can be linked by using mathematical function for secure transaction.

The digital information can be signed with private key by sender. Then the signed message is validated by the receiver with the help of public key. But it allows only one transaction at a time and less transaction speed. So, the proposed method uses the elliptic curve cryptography digital signature algorithm for multiple node transaction with multi signature. When the node gets attacked by hackers, the proposed algorithm finds the nearest path to transfer the information to prevent the data from corruption. The multi signature function can be divided into three process including generation of key pair, signing phase, and verification phase. In generation phase, the private key and public key can be generated by choosing the prime numbers, and elliptic curve parameters. In signing phase, the data are encoded and signed many times by authority to avoid the data outflow. In verification phase, the signed message with private key can be validated with the help of public key. It uses all hash functions (Secure Hashing Algorithms (SHA) such as SHA1, SHA2, and SHA3 generations) to generate the message digest and it can be extended key size of 512 bits. It is not easily tracked by attackers.

The main objectives of this work are as follows:

     i)  To provide the overview of blockchain technology and its IoT applications,

    ii)  To analyze different cryptography hash algorithms, signature schemes and its drawbacks in cryptocurrency,

   iii)  To propose the Modified Elliptic Curve Cryptography Multi Signature Scheme (MECC-MSS) which can be extended up to 512 bytes of input key size for multiple transactions,

    iv)  To investigate the performances of our proposed algorithm with other cryptography hash algorithms in terms of input key size, accuracy, time complexity and hash output with multi signature,

     v)  To analyze the statistical performances of mean accuracy and mean time for the MECC-MSS with other cryptography hash algorithms by one-way ANalysis Of VAriance (ANOVA) test.

This paper is organized as follows. Section 2 is discussed the existing signature schemes in blockchain technology. Section 3 explains the different cryptography hash algorithms with digital signature. The proposed MECC-MSS system is explained in Section 4. In Section 5, the results and the statistical analysis of the MECC-MSS with different hash algorithms are discussed. Finally, Section 6 concludes the paper.

2  Related Works

Blockchain technology uses the hash functions and asymmetric key algorithm with digital signature to enhance the security, integrity and reliability [8]. Hash algorithms are used to convert the known plaintext input to fixed unchangeable output. It has a special characteristic of collision resistance. Cryptocurrency uses the hash functions including Message Digest (MD5), SHA224, SHA256, SHA384, SHA512, SHA3-224, SHA3-256, SHA3-384, SHA3-512 to avoid the stealing of data and key from attackers. Modifications of any information will change the hash value in the block. It can be used to achieve the immutable and secure data transmission. But sometimes it leads to generate the false root hash. Similarly, digital signature algorithm with elliptic curve can be used to achieve the secure and trustworthy transactions due to its rapid process [9]. In elliptic curve digital signature algorithm, the private key is used to sign the transactions with digital hash value. The public key is used to verify the signature for authenticated transactions. If the signature is verified, the transaction is forwarded to all other nodes. If the signature is not valid, the transaction will be discarded [10]. It can be used to perform blockchain technology in effective manner. But it leads to more computational performance due to the requirement of identical signature for various transactions. So, the multiple signatures can be used to verify the transaction with the usage of multiple keys. It allows multiple node accessibility to enhance the security.

A blockchain technology for controlling and managing IoT devices is discussed in [11]. It uses RSA public key for receiving information and private key for transferring information. Hash is generated to enhance secure transaction. A blockchain based transactions with combination of IoT applications is discussed in [12]. But it is not suitable to combine mobile device due to low internet connectivity. A blockchain technology is introduced in [13] in vehicular networks. It uses the Bayesian inference model to verify the neighbouring vehicles messages. Road side unit can be used to collect validated blocks from vehicles. The uses of blockchain technology in improving transaction security of IoT applications are discussed in [14]. It mainly discusses on issues and challenges of IoT applications with blockchain technology. A software defined blockchain technology to configure dynamic IoT systems is discussed in [15]. It is for mainly protecting IoT device from distributed denial of service attack. Though blockchain technology is suffering from security and privacy issues, it has high potential in many recent research areas. The security vulnerabilities including 51% attack, double spending attack, private key attack, transaction data leakage in blockchain technology are discussed in [16]. The decentralized energy trading system using multiple signature schemes with enhanced security and privacy is discussed in [17]. It provides the complications in understanding of blockchain technology and double compensation. But it does not give required solution for decentralized architecture.

A multi-signature scheme for mining in consortium blockchain technology is discussed in [18] with signing scheme for verification. It gives high transparency but it leads to tampering attack. A key-derived certificate less signature algorithm to secure public key is described in [19]. It improves the block generation and transaction speed without digital signature. But it is not suitable to combine with traditional consortium blockchain. A multi signature scheme with RSA is discussed in [20] which differentiate the active nodes and the inactive nodes. It ensures that the node obtained enough authorization before encryption. But it limits the data transfer in blockchain and length of signature is larger in RSA based schemes. A signature scheme to combine multiple signatures from many nodes into single signature for hiding the transaction amount is discussed in [21]. It can be implemented for transaction on big data in blockchain technology. However, it is vulnerable in ring signature scheme. The identity based homomorphic signature to avoid identity attacks in blockchain technology is discussed in [22]. It can be implemented to provide data authentication. A ring signature for peer-to-peer network to provide privacy protection is discussed in [23]. It can be constructed by elliptic curve cryptography. Also, it verifies the legality of new node, then if it is validated the new block will be added to the network. A signature scheme based on attributes for decentralized application is discussed in [24]. The nodes cannot trace other’s identity and its information. A group signature in edge computing is discussed in [25] to validate each block in order to add them in the blockchain network. But it does provide constant size hash value. Tab. 1 shows the summary of the existing systems with our major inclusion.

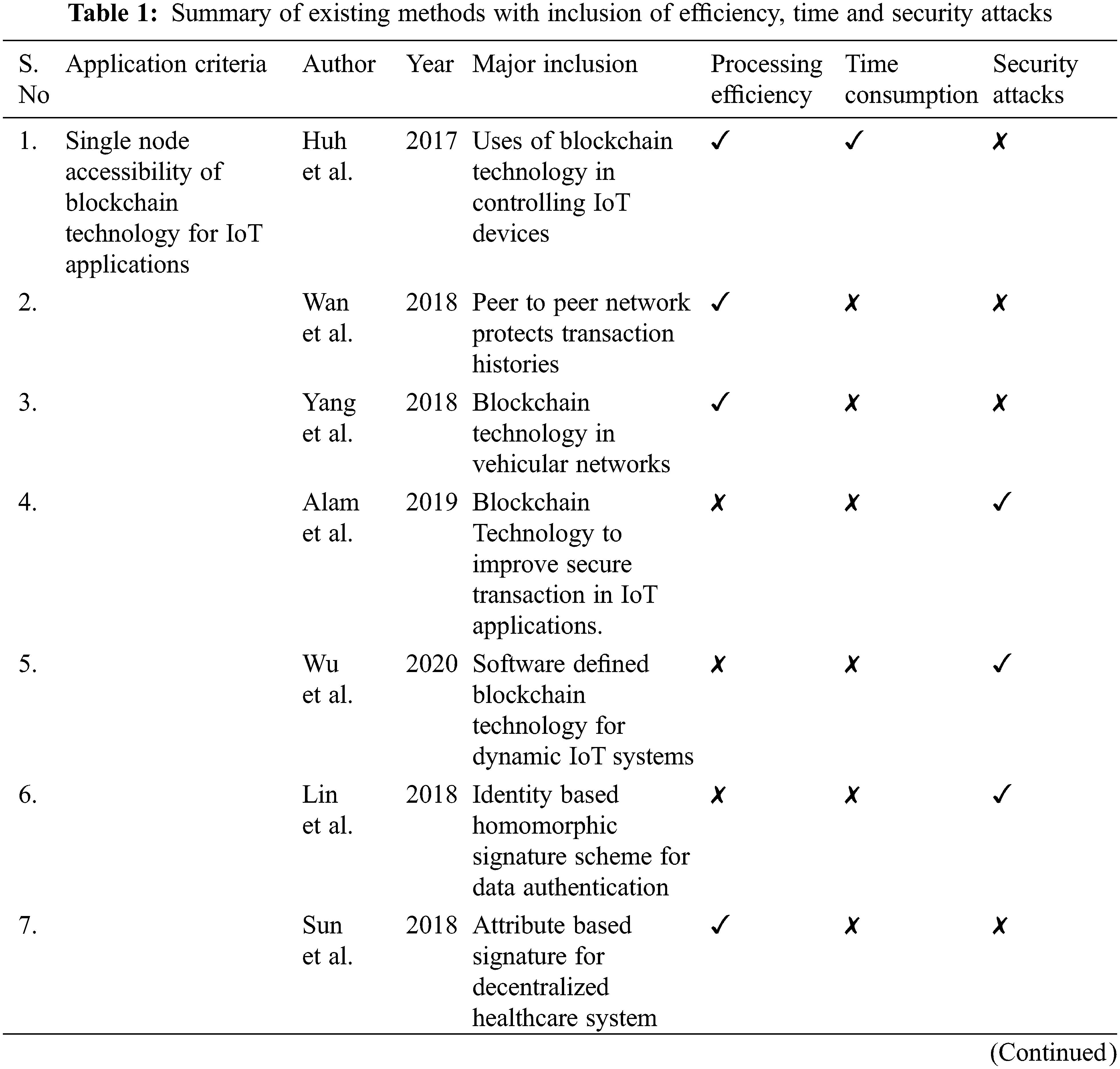
In AES and RSA cryptography algorithm, only one key can be generated at a time for the transaction and prime numbers are used to create the secret key. But it has drawbacks like loss of prime number and easily tracked by user. In existing blockchain technology, digital signature algorithm provides only one transaction at a time and it is not secured. So, it leads to less speed transaction. Existing solutions in cryptocurrency has issues like single node accessibility and accessed up to 128 bytes of key size only. If attacker tries to hack the key, it leads to cancel the transaction. As well as, it is easily attacked by brute force attack and sybil attack. To overcome these issues, multiple node accessibility using the proposed MECC-MSS is proposed to find the nearest path for transferring the information in this work. It generates the hash value by multiplying the private key, the public key, the message key and the address bytes. It can be extended up to 512 bytes of key size to increase security. The MECC-MSS scheme has the following advantages. Firstly, the key size can be extended up to 512 input bytes. Secondly, it avoids single node accessibility by finding another path to transfer the data. Thirdly, the transaction cannot be modified by anyone due to digital signature in the signing phase. Finally, it removes the security attacks like brute force attack and sybil attack.

3  Cryptography Hash Algorithms

3.1 MD5 and SHA

Message digest is a reduced representation of large input keys. It gives maximum of 32 bytes hash output. Mainly it can be used for single digital signature. But it does not give efficient results in multi signature purposes. It is vulnerable to collisions of bits and analytical attack. So, it is not giving proper results in signature verification [24]. In this function, input bytes are converted into hash bytes by splitting into four parts.

Each part contains 4 bytes of input. It can be written by, A1 = 0x67452301, A2 = 0xefcdab89, A3 = 0x98badcfe, and A4 = 0x10325376. Message digest 5 can be achieved by four rounds of functions by the operations of addition, left rotation etc., these four rounds can be obtained as, Hash1(A1, A3, A4) = (A2&A4) ǁ (! A2&A4), Hash2(A2, A3, A4) = (A2&A4) ǁ (A3&! A4), Hash3(A2, A3, A4) = A2 ^ A3 ^ A4 and Hash4(A2, A3, A4) = A3 ^ (A2ǁ! A4).

Multi signature with MD5 generates 32 bytes of hash value. It is easily identified by hacker due to less byte. It does not give efficient result for security attacks. SHA has the family members of SHA-0, SHA-1, SHA-2, and SHA-3. Cryptography hash algorithms have the features including pre-image resistance, second pre image resistance and collision resistance. Pre image resistance represents the irreversible of hash functions. This feature enhances the security by reducing the opportunity to guess the hash value. Second pre image resistance represents the different hash values for same input. It is very hard to find different input with same hash output. Collision resistance can be representing the quality of hash value to avoid hacking of keys from security vulnerabilities. From this feature, it can be decided that hash of one input is not equal to hash of another input. SHA-224 is similar to MD5 by producing 32 bytes of hash value [25]. But compared to MD5, it has 512 bits of block size. The hash values are generated by 64 rounds of operations including addition, XOR, AND, OR and rotation. It has less collision resistance due to less hash value generation but it is vulnerable to password hacking. Generally, SHA-256 can be used in existing decentralized network by utilizing 64 rounds to create hash value. It generates 64 bytes of hash value. But it accepts only 128 bits of input key size. SHA-384 and SHA-512 produces 64 bytes of hash output by 80 rounds of operation. It has 1024 bits of block size. SHA-2 family versions cannot be affected by vulnerable attacks easily. SHA-3 family is working based on keccak. SHA3-224 and SHA3-256 is responsible for 128 bits of security level [26]. SHA3-224 produces 64 bytes of hash output and SHA3-256 produces 96 bytes of hash output. SHA3-384 and SHA3-512 is accessed 256 bits for security level using sponge construction concept. SHA3-512 is similar to elliptic curve digital signature algorithm to produce 128 bytes of constant hash value. But SHA3-512 accepts only up to 128 bytes of input key. The below steps are followed in SHAs.

3.1.1 Multiple Keys Generation Phases

All group Ki(1 ≤ i ≤ N), generate the keys as follows,

1.    Select the number of integers (npr1,npr2,npr3) and specify the pair {npr1, npr2, npr3, …} as private keys.

2.    Select the number of integers (npb1,npb2,npb3) and specify the pair {npb1, npb2, npb3, …} as public keys.

3.    Select the number of integers (nmsg1,nmsg2,nmsg3) and specify the pair {nmsg1, nmsg2, nmsg3, …} as message.

4.    Select the number of integers (addr1,addr2,addr3) and specify the pair {addr1, addr2, addr3, …} as address keys.

5.    Select the brute force attack keys and specify as bf1.

6.    Select the sybil attack keys and specify as sb1.

3.1.2 Multi Signature Generation Phase

To generate the multi signature, each signature in the groups Si(1 ≤ i ≤ N) performs the following steps.

1.    Compute the encryption bytes of public keys with message

shak1=∑i=1n∑j=1mpbn∗msgn (1)

2.   Compute the encryption bytes of private keys with message

shak2=∑i=1p∑j=1qprn∗msgn (2)

where prn-private keys.

3.   Compute the different hash function of message with private keys

H=sha=h(msgn,prn) (3)

4.   Calculate the accuracy measurement of different hash function with private keys

pracc=round(f1s1∗100)−1 (4)

where pracc-private key accuracy and S1 = sum(f1)

5.   Compute the time measurement of different hash function with private keys

V1=f1∗np.log⁡2(i)/100r (5)

6.   Combine the attacks of private keys with message bytes

bfak1=bfn1+bf1 (6)

sybak1=sybn1+sybn (7)

where bfn1-length of brute force attack, bf1 (or) sybn-private key bytes for different hash function and sybn1-length of sybil attack.

7.   Compute the recovery of attacks in private keys with message measurement

bfaks=bfs1−bfn1 (8)

sybaks=sybn1−sybn (9)

where bfs1-brute force attack password with private key, syb1–sybil attack with private key.

3.1.3 Multi Signature Verification Phase

1.    Compute the address with different hash function values of public keys

vhad=vhad1+vhak (10)

2.    Compute the different hash function values of public keys with message measurements

vhad=vh+vhp (11)

3.   Compute the different hash function with public keys and message

s2=vhs=h(msg,vsd) (12)

where msg–message bytes, vsd–encoded bytes of different hash values with private keys and message.

4.   Compute the accuracy and time complexity of public keys.

5.   Compute the different hash function values with address data

vsh=h(vaddr,vhd) (13)

4  MECC-MSS Scheme

In this section, the MECC-MSS scheme that can be extended up to 512 input bytes for improving security is discussed. Blockchain technology performance depends on the selection of hash functions. It is divided into multiple keys generation, private key validation, recovering keys from attacks, public key verification. In this work, three levels of comparisons are being carried out based on hash output, accuracy, and time complexity. These results can be analyzed with various hash algorithms MD5, SHA 224, SHA 256, SHA 384, SHA 512, SHA3-224, SHA3–256, SHA3-384, and SHA3-512.

Digital signature scheme has private key for signature generation, and public key for signature verification. The transaction can be divided into two phases. These are signer phase and verifier phase. In signer phase, the multi digital signature is generated to initiate the transaction. In verifier phase, the multi signature is validated with usage of signer’s public key. Before signature generation, the private keys can be multiplied with message bytes to produce hash bytes. Then it will generate multi signature (r, s) by utilizing private keys with message hash bytes. In verification phase, the generated hash bytes can be multiplied with public key for validating the key. If it is validated, then the message bytes are transferred into different address based on its requirement. Sometimes, the changes in length of hash bytes denote that hacker is trying to guess the private keys. The person who does not know private key, they cannot able to generate correct digital signature. It increases the difficulty of attacker. If the attacker node is continuously trying to identify the private key, the hash bytes can be changed. The MECC-MSS scheme signature generation and verification steps are shown in Fig. 1.

Figure 1: MECC-MSS signature generation and verification steps

Multi signature scheme can be performed for multiple transactions at a time. It generates multiple keys to sign the transactions and not tracked by attackers. It removes single point failure. Every signature scheme has key pairs (private key, public key), address, and message. MECC-MS scheme is proposed by changing the curve parameters to choose the number of elliptic curves over finite field Fp. It can be proposed by avoiding backdoors in curve secp521r1. This elliptic curve accepts the input strength up to 512 bytes and specified by T = (p, Aj, Bj, G, n, H) over finite field Fp. If n number of elliptic curves is created, then curve equation can be written as ECj over finite prime numbers. It can be written as,

Y2=X3+AiX+BjandP=2251−1 (14)

The elliptic curve domain parameters can be specified by T = (m, f(X) Aj, Bj, G, n, H) over finite field F2m

f(X)=X571+X10+X5+X2+1andm=251 (15)

The elliptic curve ECj is given by,

Y2+XY=X3+AjX2+Bjwherej=1,2,3,4…..n (16)

This work is divided into 5 steps. These are

1.    Multiple keys generation: Multiple numbers of private keys, public keys, message keys and address keys are generated for multiple transactions. Private keys can be multiplied with message key to produce hash output.

2.    Validation of private keys and signature generation: The hash output of private key with message is encrypted for initiating the transaction. Digital signature can be added using modified ECC multi signature scheme after validation of private keys.

3.    Discovering Attacks: If any hackers tried to attack the key, the hash output changes abnormally. From these abnormal changes, we can find the vulnerabilities. In multi signature algorithm, following two attacks are possible.

Brute force attack: An attacker tries to guess the key or crack the password continuously. Our proposed algorithm reduces the possibility of vulnerabilities by increasing input key bytes up to 512 bytes.

Sybil attack: An attacker tries to create vulnerable identity for hacking the transaction. The attackers try to identify the password through these vulnerable identities.

4.   Recovering keys from attacks: From the changes in hash output, this work discovers the attack present in keys. The vulnerable password can be removed from original keys by filtering.

5.   Verification of multi signature with public key: The destination node verifies the public key with multi signature and address. If the keys are validated, messages are transmitted to multiple nodes. Fig. 2 shows the flow chart for four signature MECC-MSS.

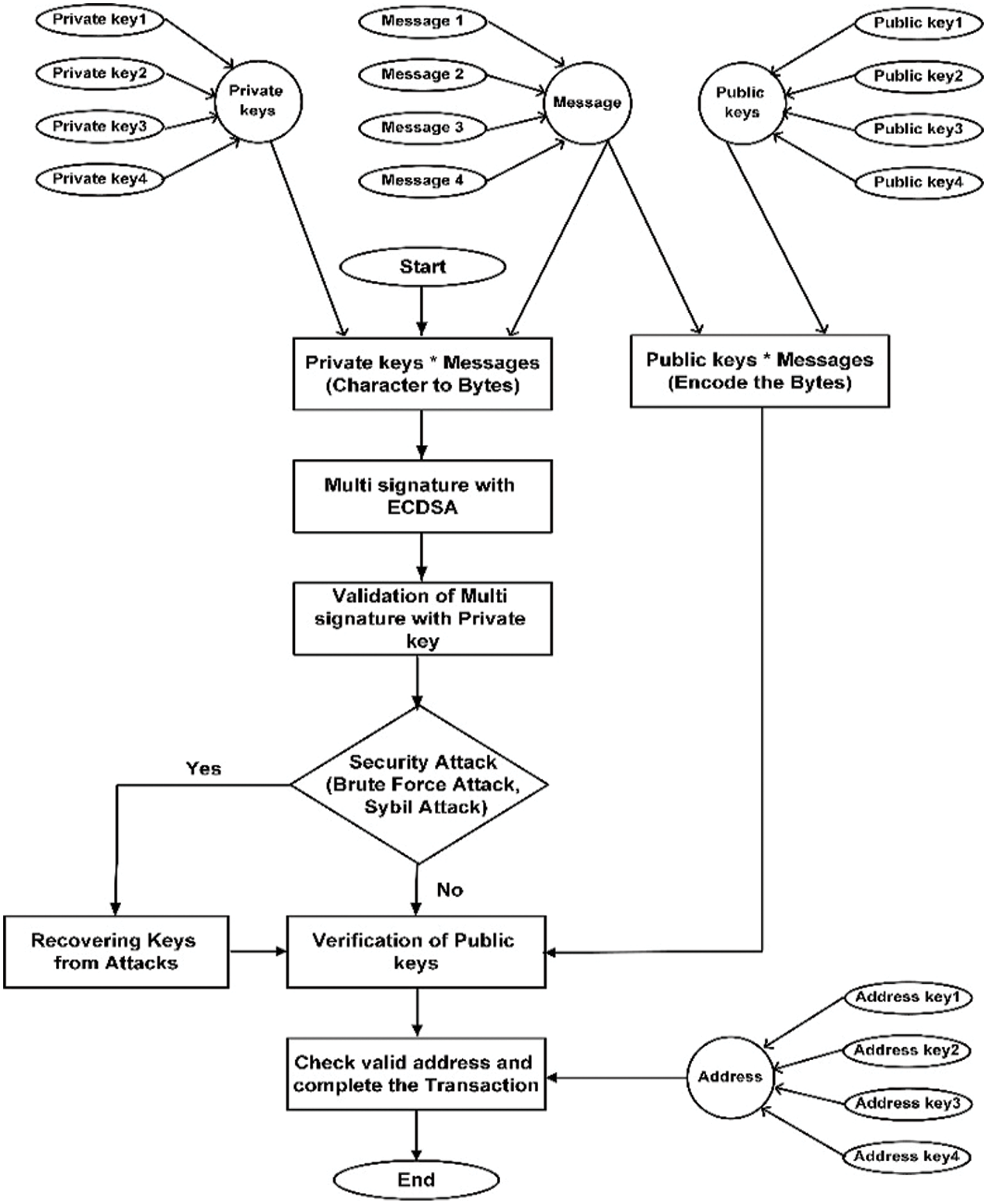
Figure 2: Flow chart for 4 signatures MECC-MSS

The below steps are implemented to achieve the MECC-MSS for multiple node transactions.

4.1 Modified ECC Multi Signature Generation Phase

General form of elliptic curve digital signature equation gives a curve with finite numbers of valid point on its N.

1.    Compute the valid points of elliptic curve in private keys with message

G=prk×msgn (17)

2.   Calculate the point of reference of elliptic curve in public keys with message

G=vh×vhp (18)

3.   Send the individual private keys to other signers in the group of points Gi to the equation

G=∑i=1NGi (19)

4.   Compute the hash functions of the MECC-MSS

sha=h(msgn,prn,G) (20)

where msgn–message values, prn–private keys and G–individual signer with group of points.

5.   Calculate the accuracy measurement of MECC with private keys

pracc=(f1s2∗100)−1 (21)

where pracc–private key accuracy, S2 = sum(f1)

6.   Calculate the time measurement of MECC with private keys

V2=f1×log⁡2(f1)×100 (22)

where f1–hash values of MECC.

7.   Combine the attacks of private keys with message bytes

bfak1=bfn1+bf1 (23)

sybak1=sybn1+sybn (24)

where bfn1-length of brute force attack, bf1 (or) sybn-private key bytes for different hash function and sybn1-length of sybil attack.

8.   Compute the recovery of attacks in private keys with message measurement

bfaks=bfs1−bfn1 (25)

sybaks=sybn1−sybn (26)

where bfs1-brute force attack password with private key, syb1–sybil attack with private key.

4.2 Modified ECC Multi Signature Verification Phase

1.    Compute the address with the MECC-MSS values of public keys

vhad=vhad1+vhak

2.    Calculate the reference points of the MECC-MS scheme values of public keys with message measurements

vhad=vh×vhp×G (27)

3.   Compute the accuracy measurement of MECC function public key and message

z=(ms4×100)−1 (28)

where m–MECC values, S4 = sum(fad).

5.   Calculate the time measurement of MECC function with public key and address

V=fad×log⁡(fad)/100 (29)

6.   Compute the different hash function values with address data

vsh=h(vaddr,vhd) (30)

5  Results and Discussions

5.1 MECC-MSS Results

The MECC-MSS can be used to create multiple numbers of private keys for multiple transactions. Multiple keys can be used to secure information or funds on multiple nodes. It improves the security and safeguards the funds from security attacks. It is not possible to identify all keys. If hacker tries to identify the key, it increases the output hash. Tab. 2 shows the example hash output for cryptography hash algorithms. Tab. 3 represents the input bytes including private key for signature generation, public key for signature verification, message bytes to nodes, and address bytes for transaction. As well as it gives brute force attack and sybil attack bytes which is tried by hacker to track private keys.

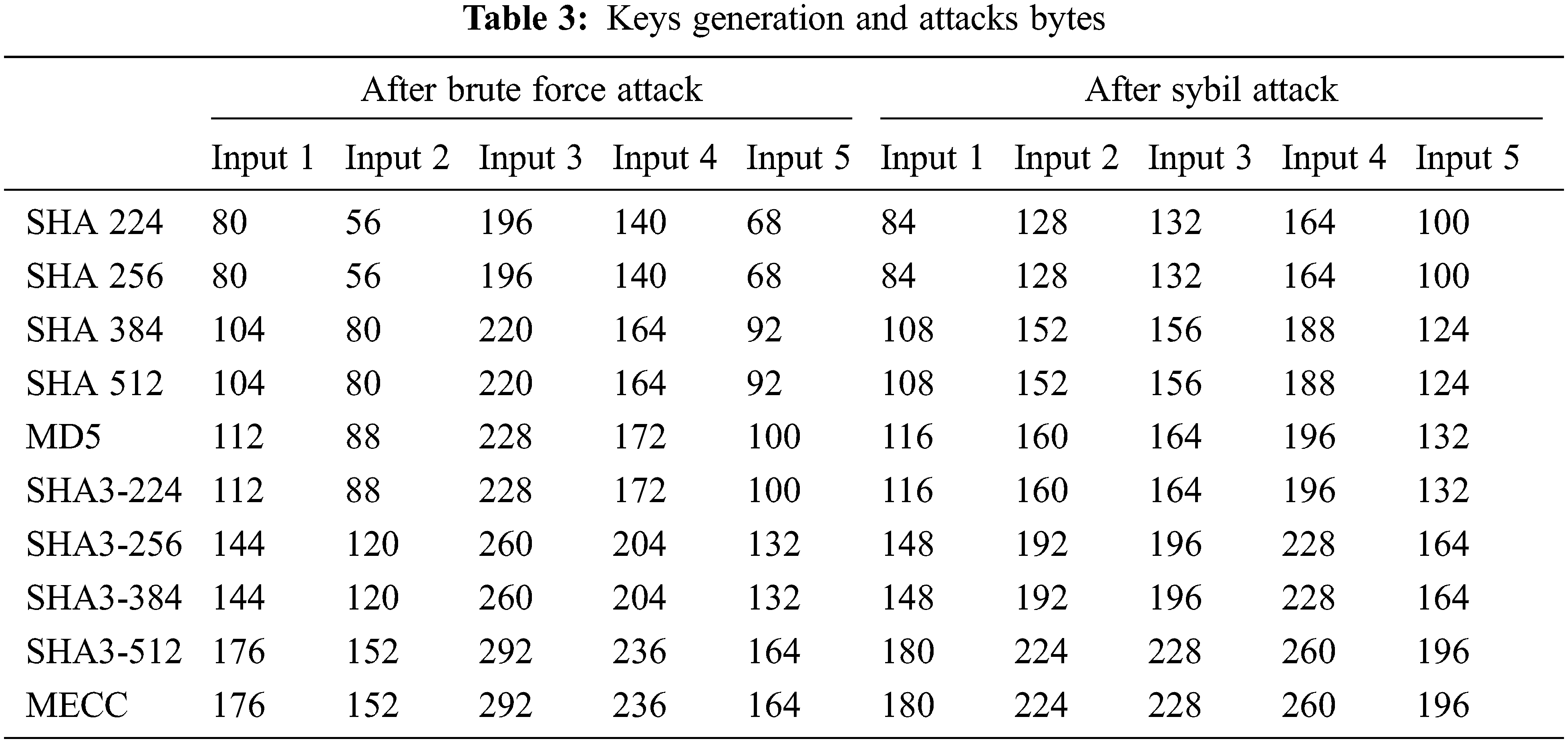
The input key size can be extended up to 512 bytes in our proposed algorithm. Tab. 4 shows changed hash bytes during attacker tries to identify the private keys. It gives brute force attack key in bytes by continuously trying to guess the key and changed hash bytes after sybil attack. The hacker creates the vulnerable identity to hack the transaction. In existing methodologies, sybil attack leads to single node failure. If one node gets attacked, the whole transaction can be cancelled. But in our proposed algorithm, multiple node accessibility finds another nearest path to transact the message securely. After identifying the vulnerable node, it changes the root without corrupting the data due to multiple node accessibility.

Fig. 3 shows the generated output hash for private key and message with multi signature for different hash algorithms, the verification of Hash output for public keys with multi signature, and the verification of Hash output for multi signature with decoding address.

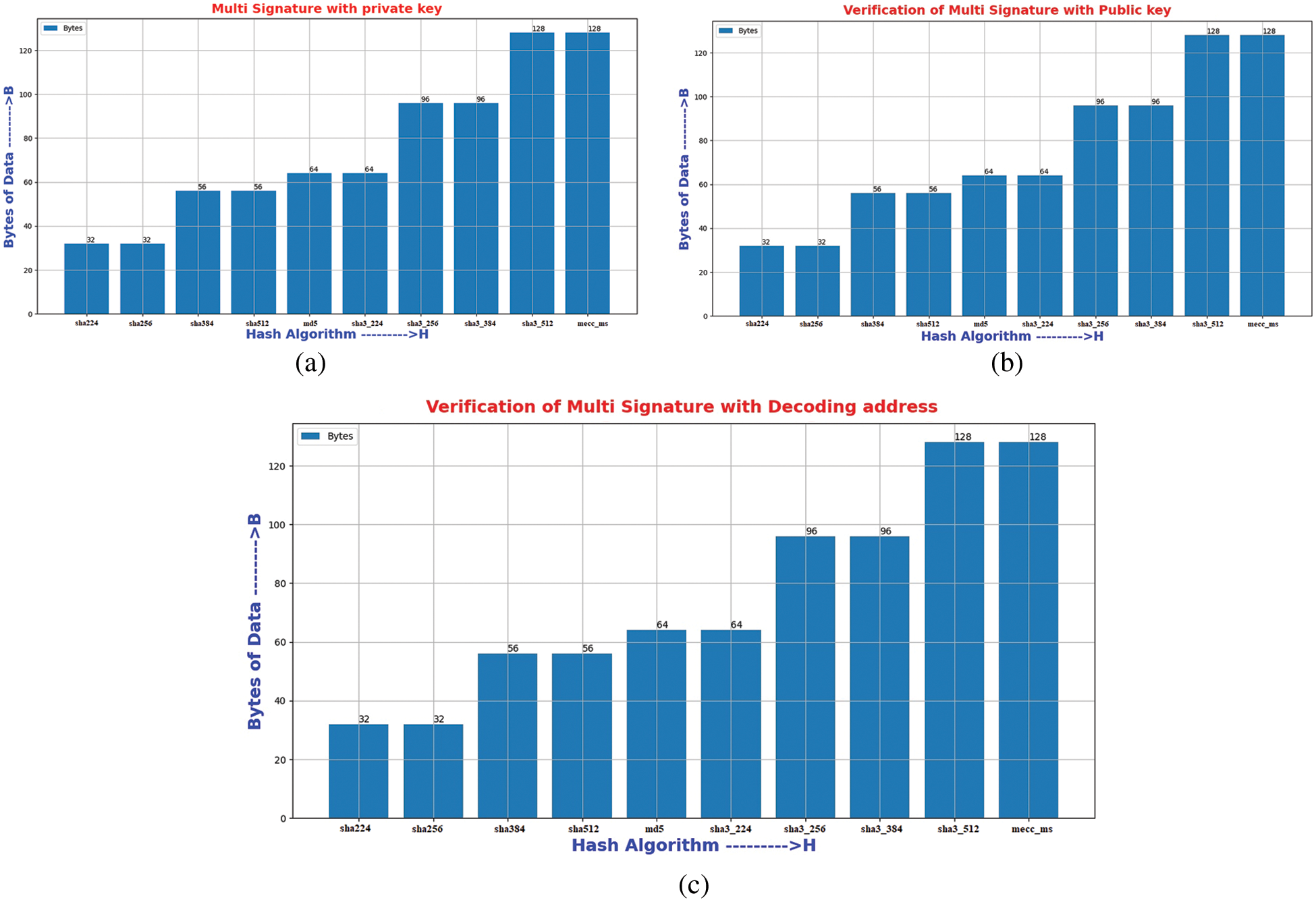
Figure 3: (a) Hash output for private keys with multi signature (b) Verification of Hash output for public keys with multi signature (c) Verification of Hash output for multi signature with decoding address

The hash bytes in Fig. 3a can be generated by multiplying message keys and private keys individually. SHA 224 and SHA 256 produces 32 bytes small hash output. So, the keys are easily identified by attacker. SHA 384 and SHA 512 generate 56 bytes of hash value. Message digest algorithm produces hash output of 64 bytes which is similar to SHA3-224. SHA3-256 and SHA3-384 produces 96 bytes of hash output for private key with multi signature. SHA3-512 and elliptic curve cryptography algorithm produces 128 bytes of hash output. But it accepts up to 256 bytes input key only.

These cryptography hash functions produce hash output up to 128 bytes of input key. The MECC-MSS algorithm generates hash output up to 512 bytes of input key. Fig. 3b shows validation of multi signature with public key in verification phase. Public key bytes can be multiplied with hash bytes of private key. If attacker tries to identify the private key, it changes the hash output of private key. Private keys can be recovered from vulnerabilities by filtering attack bytes. Fig. 3c shows verification of multi signature with decoding address. After confirmation in verification phase, the message bytes are transformed into different addresses. In this phase, the encoded address and message bytes are decoded to check valid address. Both generation and verification of signature produces constant size hash value even if it is multiple transactions. Tab. 5 represents an accuracy and time complexity analysis for different cryptography hash algorithms. It approximately gives similar accuracy values when the hacker tries to identify the private key.

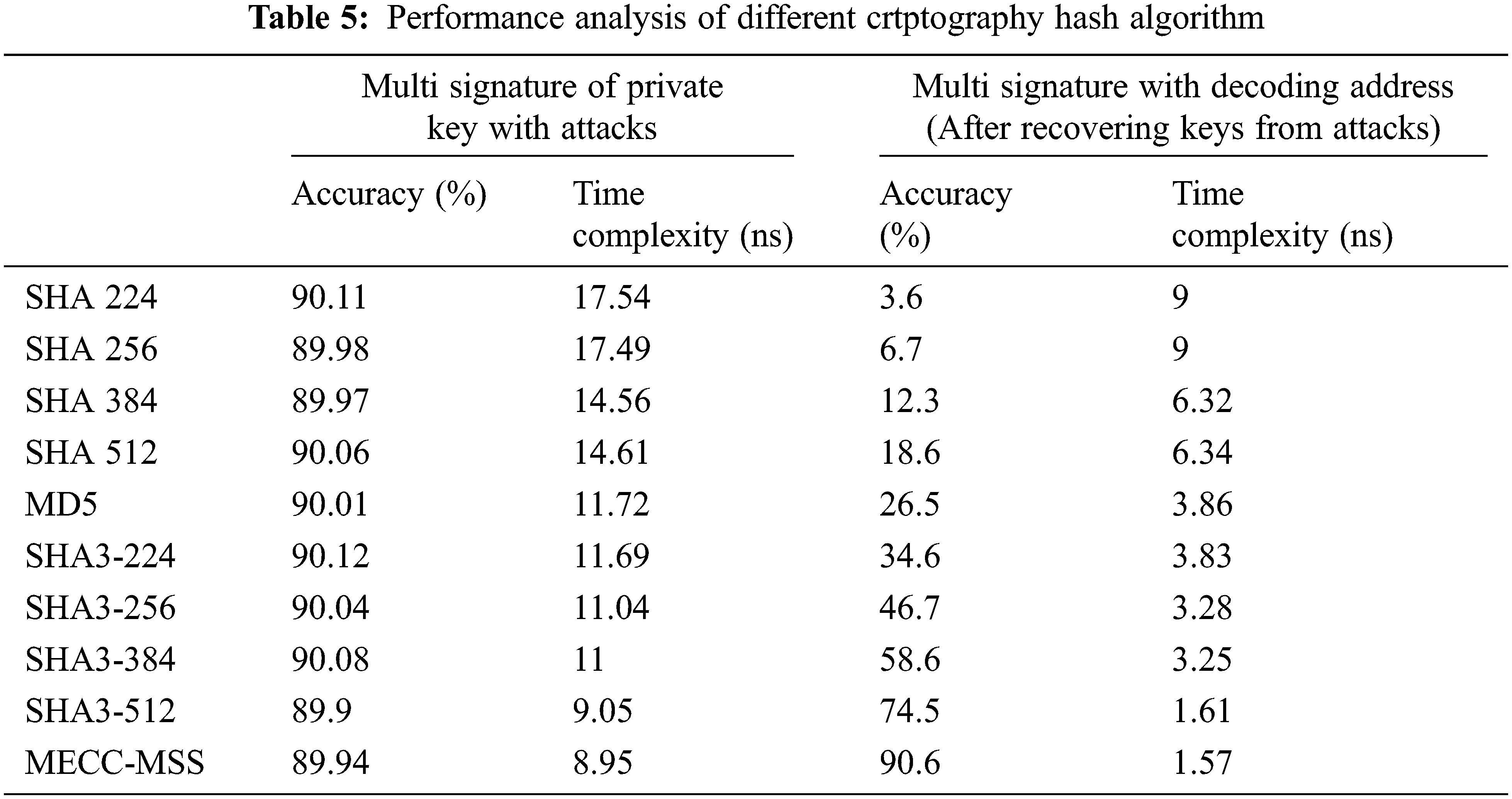
If the attacker tries to guess the password or creating the vulnerable identity to hack the transaction all cryptography hash algorithms gives an accuracy 89%∼90%. An accuracy represents the quality of the hash output that can be calculated by number of predicted values divided by total number of values. Number of predicted values denotes true positive and negative values and total number of values denotes true and false, positive and negative values. The hash algorithm is not secure when the hash bytes of key is easily identified by attacker. If hacker can not be able to guess the hash bytes, it enhances the security and accuracy.

Fig. 4a shows the accuracy analysis for different hash algorithms with multi signatures. From this analysis, the MECC-MSS generates good quality hash bytes with accuracy of 90.6% compared to other cryptography algorithms. The MECC-MSS accpets upto 512 bytes of input key size to produce unchangable hash bytes. Time complexity analysis of different cryptography hash algorithms is shown in Fig. 4b. It represents the time taken to generate hash value and complete the transaction. It includes the time for genearting the multi signature and validating the multi signature. It takes more time to validate the signature when attacker tries to hack the key. From this analysis, multi signature with elliptic curve cryptographic algorithm verifies the signature with time of 1.57 nano seconds. It is significantly less time compared to other cryptography hash algorithms.

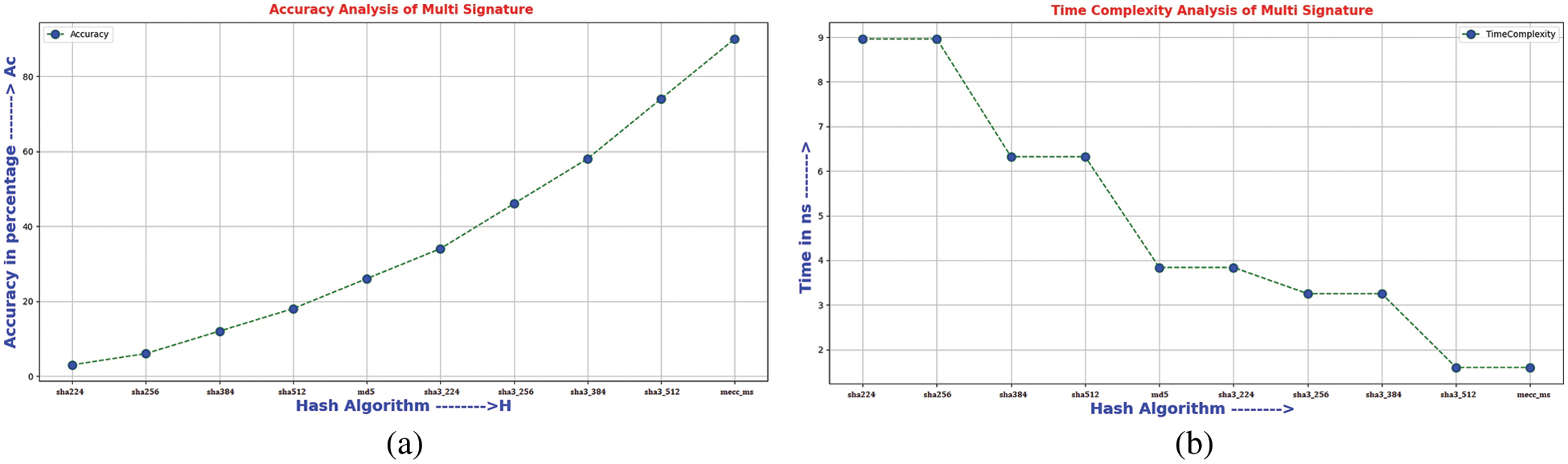
Figure 4: (a) Accuracy analysis of multi signature (b) Time complexity analysis of multi signature

5.2 Statistical Analysis

In this work, statistical analysis can be done by SPSS software [27]. Totally 10 groups and five samples per group was taken for analysis. One way ANOVA test can be used to calculate significance, sum of squares, mean square and F-score. Group 1 to 10 using SHA 224, SHA 256, SHA 384, SHA 512, MD5, SHA3-224, SHA3-256, SHA3-384, SHA3-512 and MECC-MSS respectively. The sample size computation was performed using G-power of 80% and alpha 0.05 with a confidence interval at 95%. Tab. 6 represents the one way ANOVA test for accuracy and time complexity analysis of proposed algorithm with other cryptography hash algorithms.

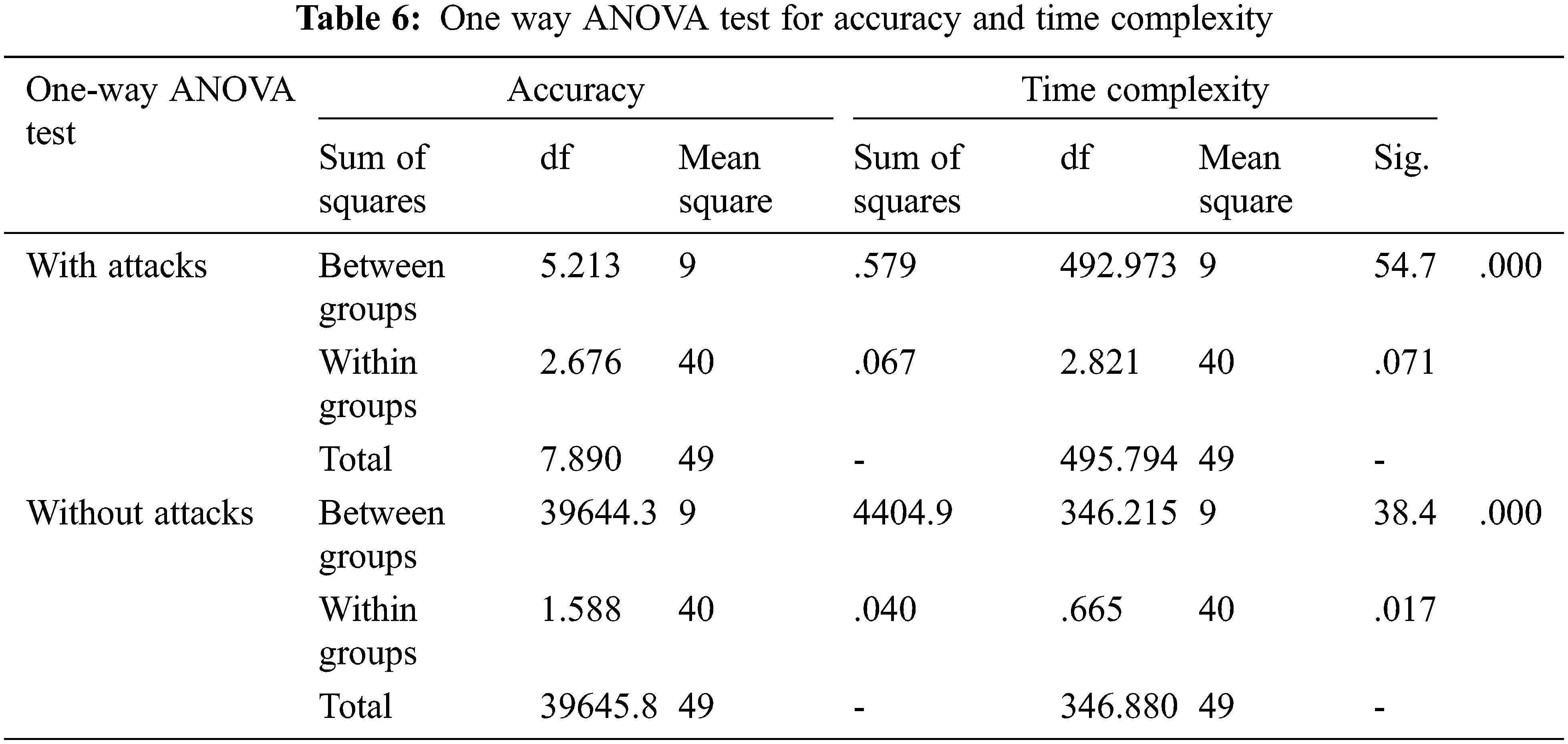
Accuracy 1 represents the changed accuracy value, when the keys are hacked by attackers. The sum of squares obtained for accuracy 1 is 7.89 and accuracy 2 is 39645.89. Obtained significance value is 0.00 (p < 0.05). The F-score obtained for time complexity 1 is 776.704 and time complexity 2 is 2313.328. It has a significance 0.00 (p < 0.05) with confidence interval 95%.

Fig. 5a shows the bar graph for accuracy analysis with and without attacks. SHA224 has a mean accuracy of 90.17% in the presence of attack and 3.74% accuracy after recovering keys from attacks. SHA256 and SHA384 have a mean accuracy of 6.8% and 12.47% respectively. SHA512 and MD5 produce a mean accuracy of 18.64% and 26.70% respectively. Similarly, SHA3-224 and SHA3-256 has a mean accuracy of 3.7% and 46.63% in an ANOVA test. SHA3-384, SHA3-512 and proposed algorithm have an accuracy of 58.66%, 74.34% and 90.85% respectively. From this analysis, the proposed MECC-MSS achieves better accuracy when compared to other cryptography algorithms. Fig. 5b shows the bar graph for time complexity analysis with and without attacks which has +/- 1 standard deviation and 95% confidence interval.

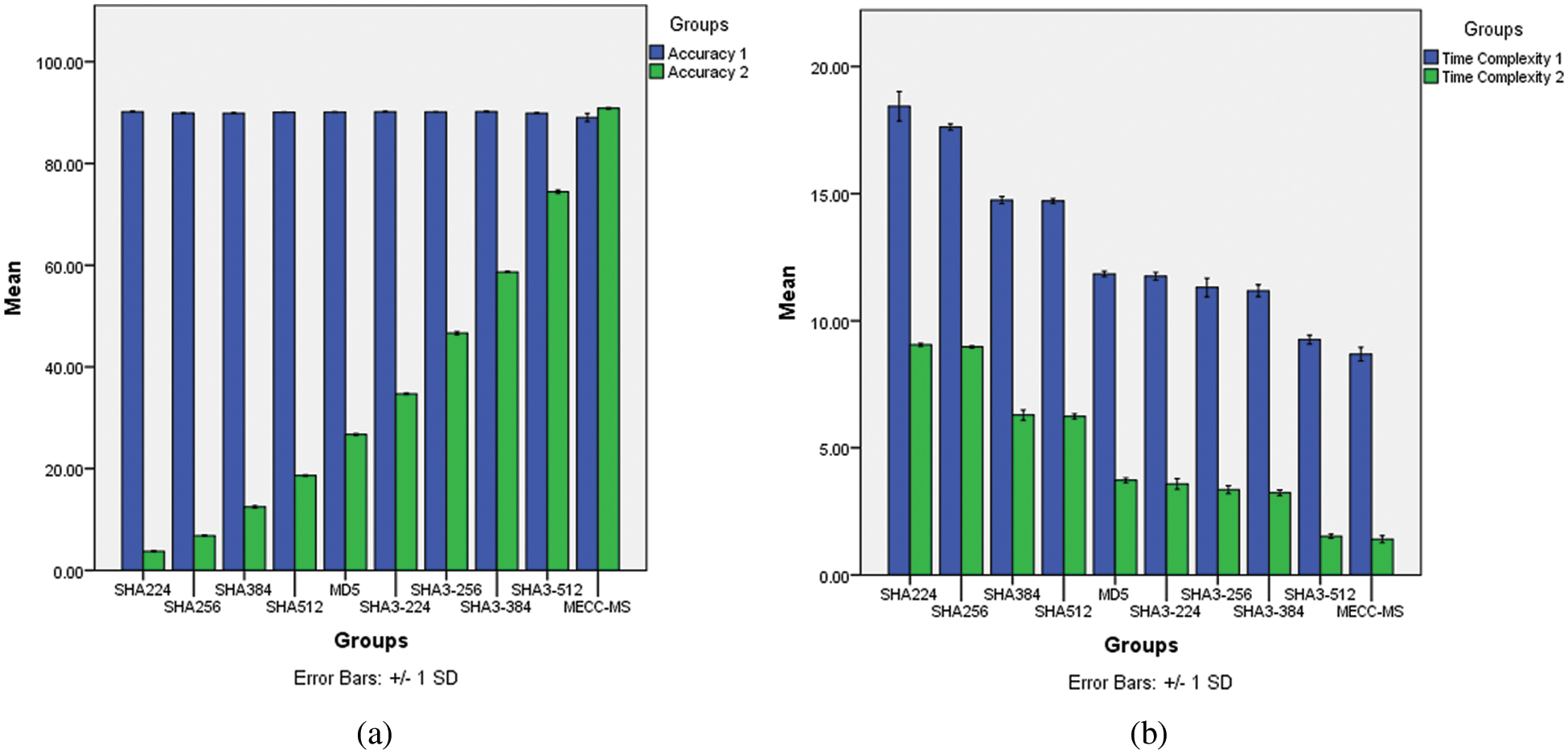
Figure 5: Bar graph in ANOVA test (a) Accuracy analysis (b) Time complexity analysis

The HA224 has a mean time of 18.43 ns in the presence of attack and 9.05 ns after recovering keys from attacks. SHA256 and SHA384 have a mean time of 8.97 and 6.29 ns respectively. SHA512 and MD5 produce a mean time of 6.23 and 3.73 ns respectively. Similarly, SHA3-224 and SHA3-256 has a mean time of 3.58 and 3.36 ns in an ANOVA test. SHA3-384, SHA3-512 and proposed algorithm have mean time of 3.23, 1.52 and 1.4 ns respectively. From this analysis, the proposed MECC-MSS completes the transaction with less time when compared to other cryptography algorithms.

6  Conclusion

Blockchain technology is a growing technology to enhance the security in many IoT applications with the help of cryptography hash algorithms. The proposed MECC-MSS finds the shortest path between nodes for multiple node accessibility. It allows multiple transactions using multiple keys and input key size can be extended up to 512 bytes. The performance of the proposed algorithm is analyzed with different SHAs like SHA224, SHA256, SHA384, SHA512, MD5, SHA3-224, SHA3-256, SHA3-384, and SHA3-512. The statistical performance can be done by one-way ANOVA test for analyzing the accuracy and time complexity. MECC-MS scheme achieves an accuracy of 90.85% and time complexity of 1.4 nano-seconds with significance less than 0.05. From the statistical analysis, the proposed algorithm achieves significantly better accuracy with less time complexity when compared with other cryptography hash algorithms. In future, this work can be focused on the usage of images as keys instead of string bytes to enhance the secure transaction in the health care applications.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 2.  X. Zhang, X. Sun, X. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 3.  G. Uganya, B. Radhika and N. Vijayaraj, “A survey on internet of things: Applications, recent issues, attacks, and security mechanisms,” Journal of Circuits, Systems and Computers, vol. 30, no. 5, pp. 2130006, 2021. [Google Scholar]

 4.  S. Nakamoto, “A Peer-to-peer electronic cash system,” Bitcoin.–URL: https://bitcoin.org/bitcoin.pdf, 4, 2008. [Google Scholar]

 5.  A. A. Monrat, O. Schelén and K. Andersson, “A survey of blockchain from the perspectives of applications, challenges, and opportunities,” IEEE Access, vol. 7, pp. 117134–117151, 2019. [Google Scholar]

 6.  D. D. F. Maesa and P. Mori, “Blockchain 3.0 applications survey,” Journal of Parallel and Distributed Computing, vol. 138, pp. 99–114, 2020. [Google Scholar]

 7.  Z. Zheng, S. Xie, H. N. Dai, X. Chen and H. Wang, “Blockchain challenges and opportunities: A survey,” International Journal of Web and Grid Services, vol. 14, no. 4, pp. 352–375, 2018. [Google Scholar]

 8.  Q. Feng, D. He, S. Zeadally, M. K. Khan and N. Kumar, “A survey on privacy protection in blockchain system,” Journal of Network and Computer Applications, vol. 126, pp. 45–58, 2019. [Google Scholar]

 9.  D. Johnson, A. Menezes and S. Vanstone, “The elliptic curve digital signature algorithm,” International Journal of Information Security, vol. 1, no. 1, pp. 36–63, 2001. [Google Scholar]

10. D. He, Y. Zhang, D. Wang and K. K. R. Choo, “Secure and efficient two-party signing protocol for the identity-based signature scheme in the IEEE p1363 standard for public key cryptography,” IEEE Transactions on Dependable and Secure Computing, vol. 17, no. 5, pp. 1124–1132, 2018. [Google Scholar]

11. S. Huh, S. Cho, and S. Kim, “Managing IoT devices using blockchain platform,” in 19th Int. Conf. on Advanced Communication Technology, PyeongChang, Korea (Southpp. 464–467, 2017. [Google Scholar]

12. L. Wan, D. Eyers and H. Zhang, “Evaluating the impact of network latency on the safety of blockchain transactions,” in IEEE Int. Conf. on Blockchain (Blockchain), Atlanta, GA, USA, pp. 194–201, 2019. [Google Scholar]

13. Z. Yang, K. Yang, L. Lei, K. Zheng and V. C. Leung, “Blockchain-based decentralized trust management in vehicular networks,” IEEE Internet of Things Journal, vol. 6, no. 2, pp. 1495–1505, 2018. [Google Scholar]

14. T. Alam, “Blockchain and its role in the internet of things (IoT),” International Journal of Scientific Research in Computer Science, Engineering and Information Technology, vol. 5, no. 1, pp. 151–157, 2019. [Google Scholar]

15. J. Wu, M. Dong, K. Ota, J. Li and W. Yang, “Application-aware consensus management for software-defined intelligent blockchain in IoT,” IEEE Network, vol. 34, no. 1, pp. 69–75, 2020. [Google Scholar]

16. X. Li, P. Jiang, T. Chen, X. Luo and Q. Wen, “A survey on the security of blockchain systems,” Future Generation Computer Systems, vol. 107, pp. 841–853, 2020. [Google Scholar]

17. N. Z. Aitzhan and D. Svetinovic, “Security and privacy in decentralized energy trading through multi-signatures, blockchain and anonymous messaging streams,” IEEE Transactions on Dependable and Secure Computing, vol. 15, no. 5, pp. 840–852, 2016. [Google Scholar]

18. T. Meng, Y. Zhao, K. Wolter and C. Z. Xu, “On consortium blockchain consistency: A queueing network model approach,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 6, pp. 1369–1382, 2021. [Google Scholar]

19. X. Guo, Q. Guo, M. Liu, Y. Wang, Y. Ma et al., “A certificateless consortium blockchain for IoTs,” in IEEE 40th Int. Conf. on Distributed Computing Systems, Singapore, pp. 496–506, 2020. [Google Scholar]

20. M. Yu, J. Zhang, J. Wang, J. Gao, T. Xu et al., “Internet of things security and privacy-preserving method through nodes differentiation, concrete cluster centers, multi-signature, and blockchain,” International Journal of Distributed Sensor Networks, vol. 14, no. 12, pp. 1–15, 2018. [Google Scholar]

21. C. Yuan, M. X. Xu, and X. M. Si, “Research on a new signature scheme on blockchain,” Security and Communication Networks, vol. 2017, pp. 50–58, 2017. [Google Scholar]

22. Q. Lin, H. Yan, Z. Huang, W. Chen, J. Shen et al., “An ID-based linearly homomorphic signature scheme and its application in blockchain,” IEEE Access, vol. 6, pp. 20632–20640, 2018. [Google Scholar]

23. X. Li, Y. Mei, J. Gong, F. Xiang and Z. Sun, “A blockchain privacy protection scheme based on ring signature,” IEEE Access, vol. 8, pp. 76765–76772, 2020. [Google Scholar]

24. Y. Sun, R. Zhang, X. Wang, K. Gao and L. Liu, “A decentralizing attribute-based signature for healthcare blockchain,” in 27th Int. Conf. on Computer Communication and Networks, Hangzhou, China, pp. 1–9, 2018. [Google Scholar]

25. S. Zhang and J. H. Lee, “A group signature and authentication scheme for blockchain-based mobile-edge computing,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4557–4565, 2019. [Google Scholar]

26. R. N. A. Sosu, K. Quist-Aphetsi and L. Nana, “A decentralized cryptographic blockchain approach for health information system,” in Int. Conf. on Computing, Computational Modelling and Applications, Cape Coast, Ghana, pp. 120–1204, 2019. [Google Scholar]

27. C. Holzer, and M. Precht, “Multiple comparison procedures for normally distributed ANOVA models in SAS, SPSS, BMDP, and MINITAB,” Computational Statistics & Data Analysis, vol. 13, no. 3, pp. 351–358, 1992. [Google Scholar]