DOI:10.32604/csse.2023.029074

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.029074 |  |
| Article |
Hybrid Approach for Privacy Enhancement in Data Mining Using Arbitrariness and Perturbation
1Department of Computer Science and Engineering, Velammal Engineering College, Chennai, 600066, India
2Department of Information Technology, Velammal Institute of Technology, Chennai, 601204, India
*Corresponding Author: B. Murugeshwari. Email: niyansreemurugeshwari@gmail.com
Received: 24 February 2022; Accepted: 30 March 2022
Abstract: Imagine numerous clients, each with personal data; individual inputs are severely corrupt, and a server only concerns the collective, statistically essential facets of this data. In several data mining methods, privacy has become highly critical. As a result, various privacy-preserving data analysis technologies have emerged. Hence, we use the randomization process to reconstruct composite data attributes accurately. Also, we use privacy measures to estimate how much deception is required to guarantee privacy. There are several viable privacy protections; however, determining which one is the best is still a work in progress. This paper discusses the difficulty of measuring privacy while also offering numerous random sampling procedures and statistical and categorized data results. Furthermore, this paper investigates the use of arbitrary nature with perturbations in privacy preservation. According to the research, arbitrary objects (most notably random matrices) have "predicted" frequency patterns. It shows how to recover crucial information from a sample damaged by a random number using an arbitrary lattice spectral selection strategy. This filtration system's conceptual framework posits, and extensive practical findings indicate that sparse data distortions preserve relatively modest privacy protection in various situations. As a result, the research framework is efficient and effective in maintaining data privacy and security.
Keywords: Data mining; data privacy; arbitrariness; data security; perturbation
Assume a corporation needs to create an accumulated representation of its customers’ personal information. For instance, a chain outlet needs to find the date born and earnings of its shoppers who are far more willing to buy Stereos or hill mountaineering gear. A film recommendation engine demands to learn viewers’ film desires to focus on ad campaigns. Finally, an internet store organizes its web content based on an accumulated framework of its online users. There is a centrally located server and many customers in any of these scenarios, each with its own set of data. The web-server gathers this data and uses it to create an accumulated model, such as a classification model or an approach for association rules. Often, the resultant model incorporates just statistics across vast groups of customers and no identifying information. The most common way to solve this issue described previously is to communicate their individual information to the computer. On the other hand, many individuals are becoming ever more extremely protective of their personal information.
Many data mining tools deal with information that is vulnerable to privacy. Some examples are cash payments, patient records, and internetwork traffic. Data analysis in such sensitive areas is causing increasing worry. As a result, we must design data mining methods attentive to privacy rights. It has created a category of mining algorithms that attempt to extract patterns despite obtaining the actual data, ensuring that the feature extraction does not obtain enough knowledge to rebuild the essential information. This research looks at a set of strategies for privacy-preserving data mining that involves arbitrarily perturbing the information to maintain the fundamental probability-based features. In addition, it investigates the random value perturbation-based method [1], a well-known method for masking data with random noise [2]. This method attempts to protect data privacy by introducing randomness while ensuring that the random noise retains the information’s “signal” to predict reliable patterns.
The pseudo-random number perturbation-based strategy’s effectiveness in maintaining anonymity is a big question in this research [3]. It demonstrates that, in many circumstances, using a spectral filter that utilizes some theoretical aspects of the random matrix, the source data (also referred to as “signal” in this study) may be reliably reconstructed from the disturbing data. It lays out the basic concepts and backs them up with experimental evidence. They want to keep their personal information to a minimum to conduct business with the company. Suppose the organization requires the aggregate model, a method that minimizes the exposure of private information while still enabling the webserver to construct the model. One idea is that each customer perturbs its information and transmits it to remove some truthful information and add some fake stuff. Random selection is the term for this method.
Another option is to reduce data precision by normalizing, concealing some values, changing values with ranges, or substituting discrete values with much more broad types higher up the taxonomic classification structure, as described in [4] In the form of statistical datasets, the use of randomness for privacy preservation has been thoroughly studied [5]. In that situation, the server has a piece of complete and precise information, including input from its users. It must make a standard edition of this dataset available for anyone to use. Population data is a good example: a nation’s leadership obtains personal data about its citizens and transforms that knowledge into a tool for study and budget allocation. Private information of any specific person, on the other hand, is considered not to be disclosed or traceable from what reveal.
For instance, a corporation must not link items in an available online dataset with detailed comparison in its internal client list. However, the collection shuffles once it explores extensively in preserving data. It differs from our problem, and the randomness technique is carried out on the client’s behalf and therefore must agree upon prior to collecting data. We use a statistical document’s randomness to retain or transform boundary aggregate properties (estimates and covariance for numeric values or total margin values in cross-tabulation for categorical attributes) [6]. Other privacy-preserving operations, including sample selection and swapping data among entries, are utilized in addition to randomness [7].
In [8], they used the randomness approach to distort data. The probability density function is reliant on this strategy. Data tampering in studies has a significant impact on privacy. Imagine a server that has a large number of users. Every user has that volume of data. The server gets all the data and uses data mining to create the pooled data model. In the randomness approach [9], users may arbitrarily interrupt their data and transmit it to the server by removing essential attributes and generating noise. The aggregation related to information extraction retrieves by utilizing statistical estimates to the measurement noise; possible values are compounded or appended to genuine items or can be accomplished by removing some actual values and inserting incorrect values in the entries [10] induce noise. It is crucial to assess the collective model with high accuracy to use the correct amount of randomness and the right approach. The notion of privacy in characterizing randomness analyze in the conventional privacy architecture, disclosure risk, and destruction metrics in data handling [11]; however, it describes in current designs [12].
The information miner’s skill simulates to reflect a probabilistic model to cope with randomized ambiguity. The main benefit is that studying the randomized method is required to ensure privacy, with no need to understand data mining activities. However, the criteria are imprecise in that a massive proportion of random input is required to provide highly significant outcomes [13]. In-anonymous approaches, they utilize methods like suppressing and generalization to minimize quasi granularity expression. The objective of generality is to reduce the complexity of expression inside a range by entirely generalizing data points.
Age, for example, will be used to generalize birth dates to lessen the danger of detection. The suppressing technique eliminates the value of characteristics. Using public documents can lessen the risk of identifying, but it lowers the application efficiency of modified data. Sensitive information is suppressed prior to calculation or dissemination to protect privacy. If the data suppressions are reliant on a relationship between suppressed and exposed data, this suppressing process becomes challenging. If data mining tools necessitate complete access to sensitive information, suppressing will be impossible to achieve. Specific statistical characteristics protect against discovery by using suppression. It reduces the effects of all other distortions on data analysis. The majority of optimization techniques are numerically insoluble [14,15].
There is a developing amount of research on data mining sensitive to privacy. These technologies categorize into numerous categories. A distributed framework is one method. This method facilitates the development of machine learning algorithms and the derivation of “patterns” at a given point by communicating only the bare minimum of data among involved parties and avoiding the transmission of original data. A few instances are privacy-preserving cluster analysis mining using homogeneity [16] and heterogeneity distributed information sets. The following method relies on data-switching [17], which involves changing data values inside the same characteristic. There is also a method involving introducing noisy data so that single data values are corrupt while preserving the implemented features at a macroscopic scale. This category of algorithms operates by first perturbing the input with randomized procedures. The pattern and extract frameworks from the modified data [18] exemplify this approach by the random value distortion method for training tree structure and cluster analysis learning.
Other research on randomized data masking might be found here [19]. It points out in most circumstances, the noise distinguishes from the perturbed data by analyzing the information’s spectral features, putting the data’s privacy at risk. The strategy in [20] was also studied and developing a rotating perturbation algorithm for recreating the dispersion of the source data from perturbed observations. They also propose theoretic data measurements (mutual data) to evaluate how much privacy a randomized strategy provides. Remark in [21] that the method proposed does not compensate for the dispersion of the source data. [22], on the other hand, it does not provide an explicit process for reconstructing the actual data values. [23–25] have looked at the concept in the framework of mining techniques and made it appropriate for minimizing privacy violations. Our significant contribution is to present a straightforward filtering approach based on privacy enhancement in data mining using arbitrariness and perturbation for estimating the actual data values.
As mentioned in the previous section, randomness uses increasingly to hide the facts in many privacy-preserving data collection techniques. While randomization is a valuable tool, it must operate with consideration in a privacy-sensitive application. Randomness does not always imply unpredictability. Frequently, We investigate distortions and their attributes using probabilistic models. There is a vast range of scientific concepts, principles, and practices in statistics, randomness technology, and related fields. It is dependent on the probabilistic model of unpredictability, which typically works well. For example, there are several filters for reducing white noise [26]. These are usually helpful at eliminating information distortion. In addition, the properties of randomly generated structures like graphs captivate me [27]. Randomness seems to have a “pattern,” If we are not careful, we can leverage this pattern to compromise privacy. The following section depicts this problem using a well-known privacy-preserving approach. Randomized additive noise is used in this work.
Data mining technologies extract relevant data from large data sets and consider many clusters. Data warehousing is a technique that allows a central authority to compile data from several sources. This method has the potential to increase privacy breaches. Due to privacy concerns, users are cautious about publishing publicly on the internet. In this platform, we will apply privacy-preserving techniques to protect that information as shown in Fig. 1.
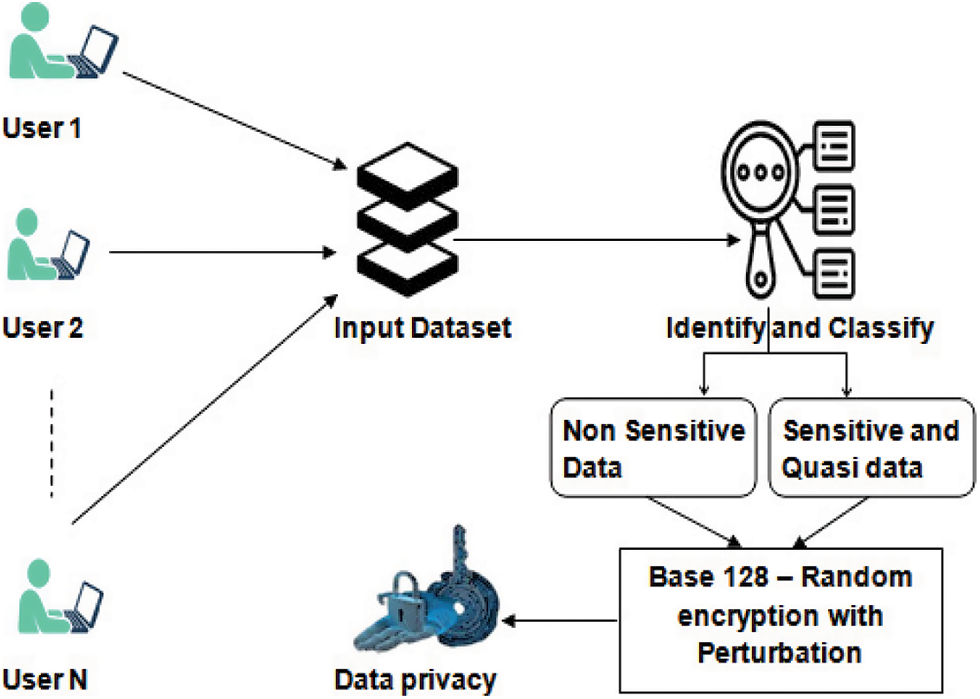
Figure 1: Hybrid architecture of proposed system
As mentioned in the previous section, randomness uses increasingly to hide the facts in many privacy-preserving data collection techniques. While randomization is a valuable tool, it must operate with consideration in a privacy-sensitive application. Randomness does not always imply unpredictability. Frequently, We investigate distortions and their attributes using probabilistic models. There is a vast range of scientific concepts, principles, and practices in statistics, randomness technology, and related fields. It is dependent on the probabilistic model of unpredictability, which typically works well. For example, several filters reduce white noise. These are usually helpful at eliminating information distortion. In addition, the properties of randomly generated structures like graphs captivate me [28–30]. Randomness seems to have a “pattern,” If we are not careful, we can leverage this pattern to compromise privacy.
To prevent multiple data calculation, we employed an arbitrariness encoding approach to alter the n numbers of customers kept in a central authority into some other form in our suggested work. It incorporates multiple database randomness, which aids in achieving both user and multiple database privacy. Randomization’s primary goal is to sever the link among records, lowering the danger of leaked private information. As a result, it determines that encoded provides user privacy while randomness guarantees information privacy.
This study investigates a data transformation strategy based on Base 128 encoding with randomness to safeguard and retain sensitive and confidential data against unauthorized use. The Base 128 encryption and decryption procedure is not a stand-alone method; instead, we use the perturbation technique to make it more resistant and safe in protecting the privacy of the cloud environment. According to the experiment results, confidential data may retain and safeguarded from illegal disclosure of personal information, resulting in no data leakage. Furthermore, it states that the document might be decrypted and precisely rebuilt without any key interaction. Consequently, disclose the private data without fear of losing it. Furthermore, compared to the anonymization strategy employed for ensuring privacy over both stages, the suggested technique operates well and efficiently in aspects of privacy-preserving and data quality. The encoding method converts the information into a different format. At the same time, randomness utilizes to minimize limitations imposed by data generality and reduction and preserve higher data usefulness. In addition, the suggested methodology has an advantage over one-way anonymization due to its reversible characteristic.
We consider arbitrariness to classify data, in the perspective of association rules. Assume that each User ui has a records ri, which is a subset of a given finite set of sample data D, |D| = n. For any subset S ⊂ D, In Eq. (1) its support in the dataset of Records
Dataset, S is frequent if its hold is at least a minimum threshold supmin. An association rule S ⇒ V is a couple of disjoint datasets S and V; and support is the S ∪ V support, and In Eq. (2) confidence is the fraction of records enclose S that also enclose V:
R fulfills classification rules if support is minimum supmin and confidence is minimum conmin; that is another criterion. Apriori, an inexpensive technique for association rules that apply to a particular dataset, was proposed in past research. The concept behind Apriori is to take advantage of the counter homogeneity characteristic.
In terms of competence, it detects frequent 1-item datasets initially, following tests the supports of all 2-item datasets with frequent 1-subsets, subsequently examines all 3-item datasets with frequent 2-subsets, and so on. It comes to a standstill if no candidate’s datasets (with many subgroups) can be generated. Then, discovering frequent patterns can be simplified to locating standard datasets as in Eq. (3).
Delete existing data and replacing it with new data is a logical technique to arbitrarily a collection of elements. Paper [11] looks into the choose-a-size group of arbitrariness algorithms. A choose-a-size arbitrariness operator is constructed for a fixed record size |r| = n and has three conditions: a arbitrariness level 0< ρ < 1 and a distribution function (d [0], d [1],.., d[n]) over the dataset {0, 1, . . . , n}. The operator creates a arbitrarily selected record r’ from tuples of length n in the following way:
1. To make D [k is chosen] = d[k], the function chooses a value k at arbitrary out from dataset 0,1,…, n.
2. It arbitrarily chooses k elements from r. Those objects are stored in r’, along with no more elements from r.
3. It flips a coin with a chance of “heads” and one of “tails” for every piece of data. r’ is multiplied by all things whereby the coin faces “heads.”
If different customers have variable size records, choose-a-size attributes for each record size must be selected. As a result, the (non-arbitrariness) size must send to the host with the arbitrarily selected record. The randomness mechanism used in has no such flaw; it has one variable, 0 < p < 1, that sets the chance of every object to not be “rolled” (thrown away if existent, or entered if missing) in the record for each data separately. This function is a particular instance of choose-a-size for any fixed record size n, with ρ = 1 − p and
Datasets have the support that is significantly distinct from their values in the non-arbitrariness data-set D in the set D’ of arbitrariness record-sets accessible to the server. As a result, we devise strategies for estimating native support from arbitrariness supports. It is worth noting that the arbitrariness support of a dataset S is a random number determined by the original support of all subgroups of this dataset. Similarly, a record containing everything than one data of S has a much lower chance of containing S after randomness than one containing nil data. So, In Eq. (4) each (k + 1)-vector of its incomplete supports
In Eqs. (5) and (6) the anticipation and covariance matrices of the vector
for (n + 1) (n + 1) matrices U as well as V [0], V [1],…, V[n] that are dependent on the arbitrariness operator’s variables. The definition of Matrix U as in Eq. (7),
In Eqs. (8) and (9) R stands for the arbitrariness operator. The unbiased estimate
In Eqs. (10) and (11) It allows us to estimate the non-arbitrariness supports of S as well as its variance:
The support estimator equation employed within the Apriori method for extracting frequent record sets allows the system to cope with arbitrary data. However, it violates the anti homogeneity requirement since the estimate is random. It could result in a deleted dataset even though its projected and actual support levels are over the limit. This impact can mitigate by decreasing the limit by a factor equivalent to an estimator’s variance.
The random value perturbation approach aims to protect data by arbitrarily altering sensitive values. The proprietor of a collection returns a value of sl + t, where sl is the actual data and t is an arbitrary number selected from a distribution. The most widely utilized distributions are the homogeneous distribution across a range [−∞,∞] and the Distribution function with means µ = 0 and standard deviation σ. The n actual dataset entries s0,s1,…,sn regards as realizations of n independently dispersed random variables Sl, l = 0, 1,2,…,n. Each has the same distribution as a random number S. n different samples t0,t1,…,tn are selected from a T distribution to disrupt the data. The data holder provides the perturbed numbers s0 + t0,s1 + t1,…,sn + tn, and the cumulative probability function dt(x) of T. The restoration challenge entails estimating the actual data’s distribution ds(y) from perturbed data.
5.3 Base 128 bits Encryption over Arbitrary Data after Perturbation
A bit n is created from s for encrypting and decrypting by choosing one of several 128 elements methodically, then permuting the values in s.
Method for Key Planning:
Generates a transient Record V from the items of s, which are datasets with entries that vary from 0 to 127 in increasing order.
If the key n has a size of 128 bits, it allocates to V. Instead, the primary n-len components of V are duplicated from N, and then N is replicated as many times as it takes to fill V for a key of size(n-len) bits. The following is an illustration of the concept:
for
l ranges from 0 to 127.
s[l] = I
N[l mod n-len] = V[l];
V is used to generate the first permutation of s. Beginning with s0 to s127, exchange with another bit of data in s as per a strategy suggested by V[l] for each s[l] method, although s would still include numbers from 0 to 127:
m = 0;
for
do l = 0 to 127
{
(m + s[l] + V[l])mod 127;
Swap(s[l], s[m]);
}
Method for pseudo-random generating (Stream Formation):
The inputting key will not be used until the Record S has been setup. Exchange each bit in s with some other bit in s as per a pattern required by the modern incarnation of s in this phase. After hitting s [127], the pattern repeats itself, beginning at s [0].
l = 0; m = 0;
in the meantime (true)
(l + 1)mod 127;
(m + s[l])mod 127;
swap(s[l], s[m]);
(s[l] + s[m])mod 127;
s[v] = n;
5.3.2 Detailed Algorithm for Encryption and Decryption Process
Step 1 - Begin
Step 2 - Fetching dataset
Step 3 - Loading dataset in to Server
Step 4 - Data Cleansing Operation
Step 5 – S[0,1…..n]
Step 6 - Want to perform data privacy and preservation?, Goto 12
Step 7 - Transform data in to respective ASCII value, Replicate the steps until l=no. of rows, m=no. of columns
Step 7(a) - Celldata
Step 7(b) - Transform Celldata’s value in to their respective ASCII values
Step 7(c) - rowdata
Step 8 - Perform Perturbation (Append Noise to the Data), Replicate the steps until l=no. of rows, m=no. of columns
Step 8(a) - size
Step 8(b) - DataValue
Step 8(c) - TempValue
Step 8(d) - UpdatedValue
Step 8(e) - S[l][m]
Step 9 - Encrypt the Data (BASE-128 Algorithm), Replicate the steps until l=no. of rows, m=no. of columns
Step 9(a) - PlainTextij
Step 9(b) - CipherText
Step 9(c) - S[l][m] = CipherText
Step 10 - More records are there, Goto 17
Step 11 - Goto 7
Step 12 – Decrypt the Data (BASE-128 Algorithm), Replicate the steps until l=no. of rows, m=no. of columns
Step 12(a) - cipherextij
Step 12(b) - PlainText
Step 12(c) - S[l][m] = PlainText
Step 13 - Perform Perturbation (Clear Noise from the Dataset), Replicate the steps until l=no. of rows, m=no. of columns
Step 13(a) - size
Step 13(b) - DataValue
Step 13(c) - TempValue
Step 13(d) - ActualValue
Step 13(e) - S[l][m]
Step 14 - Transform ASCII values in to respective data or values, Replicate the steps until l=no. of rows, m=no. of columns
Step 14(a) - tempdata
Step 14(b) - S[l][m]
Step 15 - More records are there, Goto 17
Step 16 - Goto 12
Step 17 - Stop
6 Performance of Proposed Work
We use the datasets from the UCI machine learning repository. The content in each dataset was either numerical or alphanumerical. Furthermore, the volume of each collection is variable. We employed a serial configuration to evaluate the hybrid-privacy concept due to the limited number of Computer systems. The dispersed approach works on a single computer well with the following specifications: i3 processor, 8Gb Of ram, and an x86 operating system. We used Python to code the techniques and produced reliable findings over Python 3.7. We used a more popular performance metric, accuracy, to assess the hybrid-privacy model. In addition, the Naive Bayes classifier and our algorithm were evaluated in this study to see how effective the hybrid-privacy model is. On the effectiveness of performance measure-accuracy, we evaluate the performance of the proposed model.
This chapter examines the efficiency, quality of data, utility, information loss, and scalability of implementing the appropriate 128-encoding strategies before and after arbitrariness and perturbation of data classification. The following is a representation of the findings.
The suggested technique encrypts quantitative and alphanumerical values of high sensitivity and semi-sensitive, preventing the qualities from being revealed to unauthorized users. The benefit of implementing Base 128 Encryption in our technique is that there is no data loss, as demonstrated in Tab. 1 and Fig. 2, during information transfer to the cloud, ensuring perfect privacy.
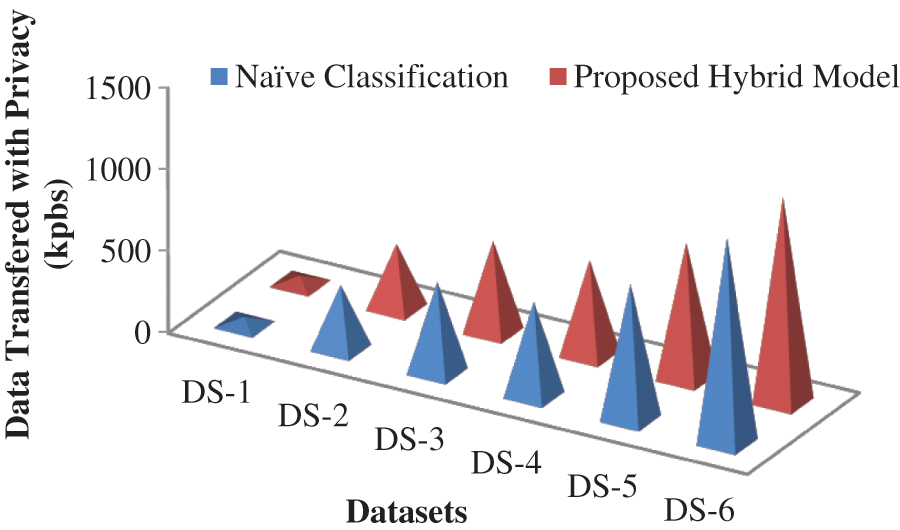
Figure 2: Comparative analysis of Naive vs Hybrid Model without data loss
When contrasting the suggested strategy to existing privacy-preserving strategies such as the naive base approach, it was discovered that the approach has a 92 percent data loss, as shown in Tab. 2 and Fig. 3 following.
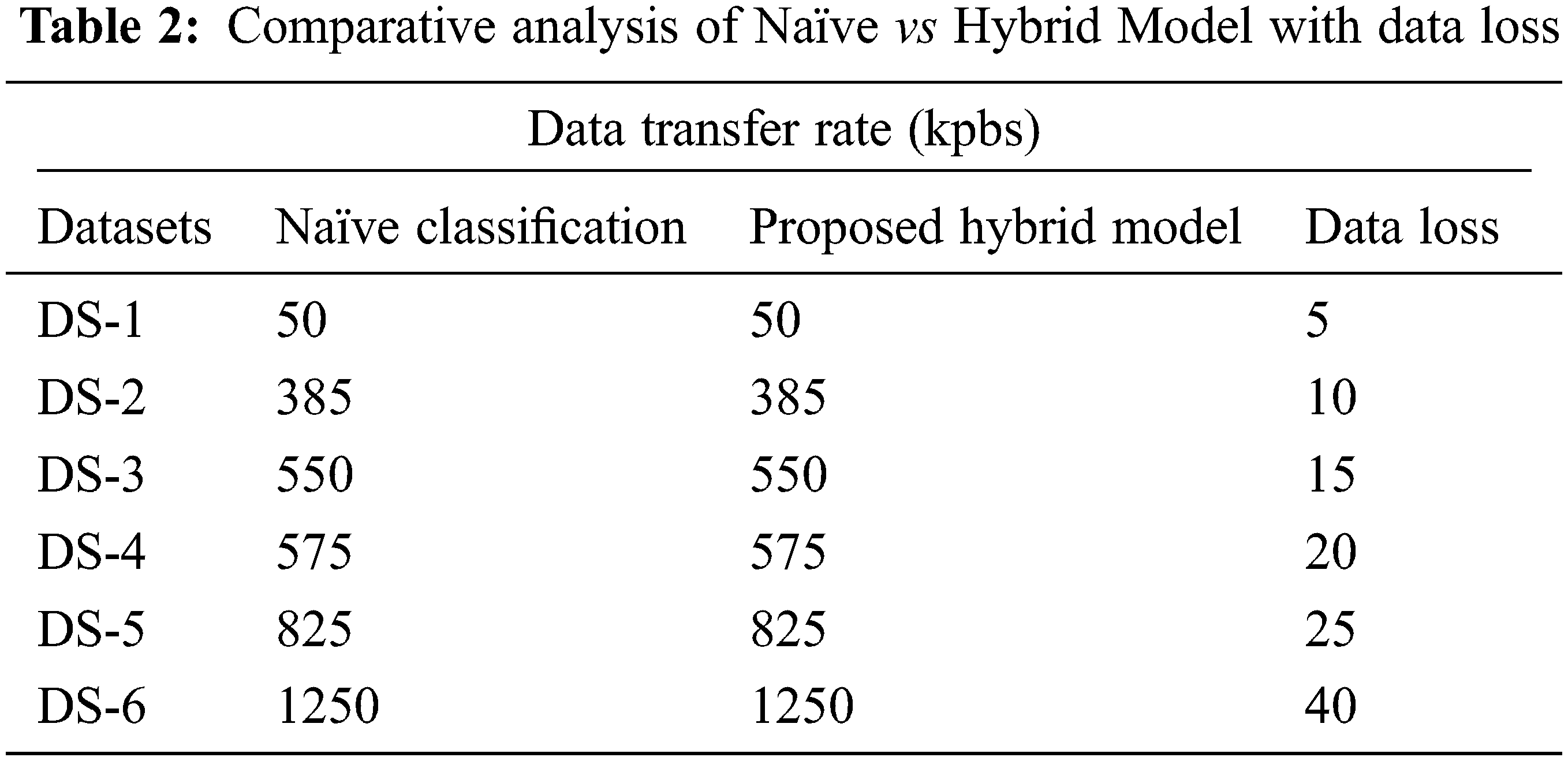
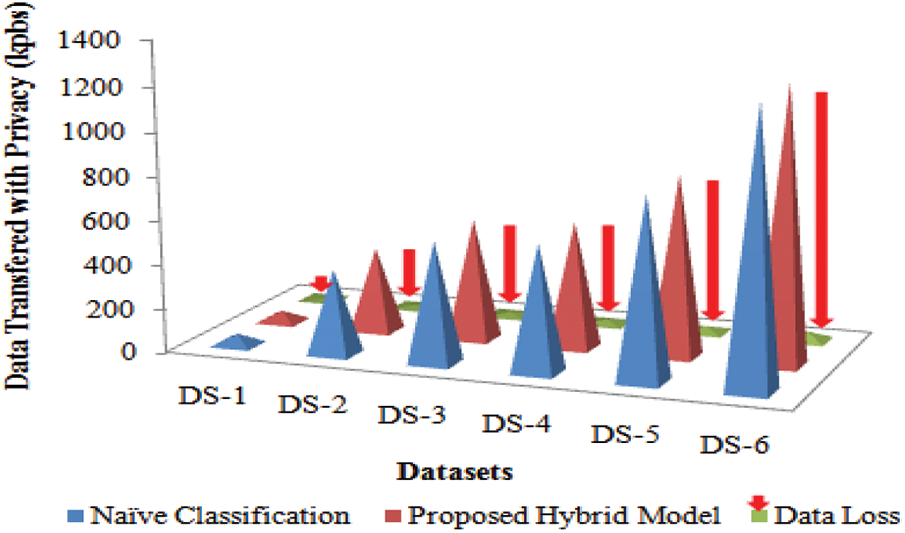
Figure 3: Comparative analysis of Naïve vs Hybrid Model with data loss
As illustrated in Tab. 3 and Fig. 4, the data value and quality of data published remain stable and suitable for mining purposes while sensitive data’s privacy is protected.
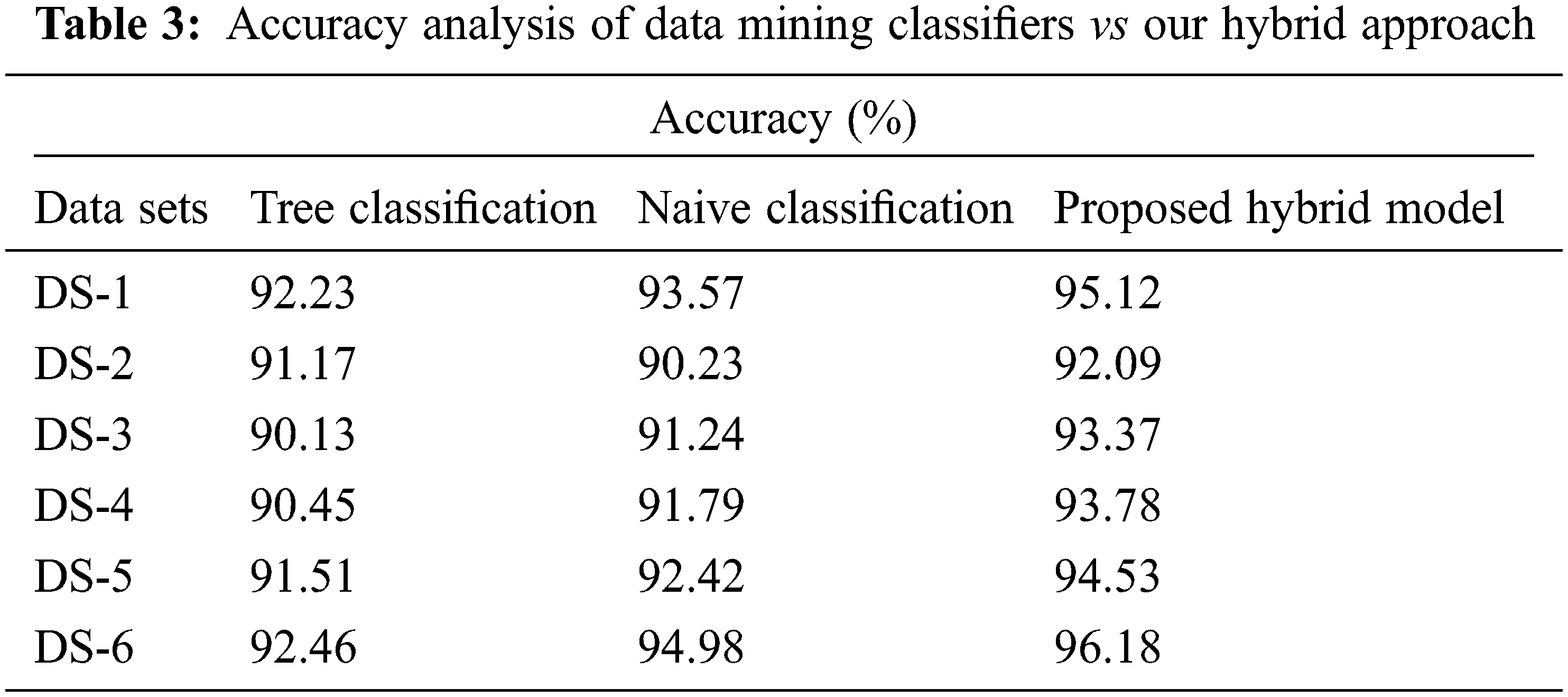
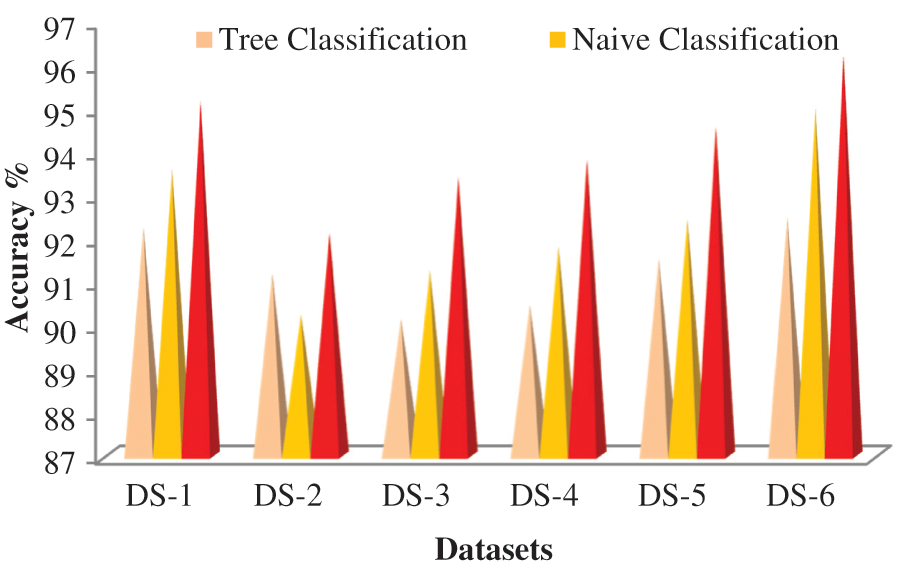
Figure 4: Accuracy analysis of data mining classifiers vs our hybrid approach
With our hybrid approach, we examine the data usage in terms of accuracy through data mining classifiers like classification Tree and Naive Bayes.
6.3.1 Computational Efficiency
We evaluate the suggested system’s efficiency using both temporal and spatial as in Tab. 4. The Base 128 encoding and decoding operations have a total time complexity of O(N).
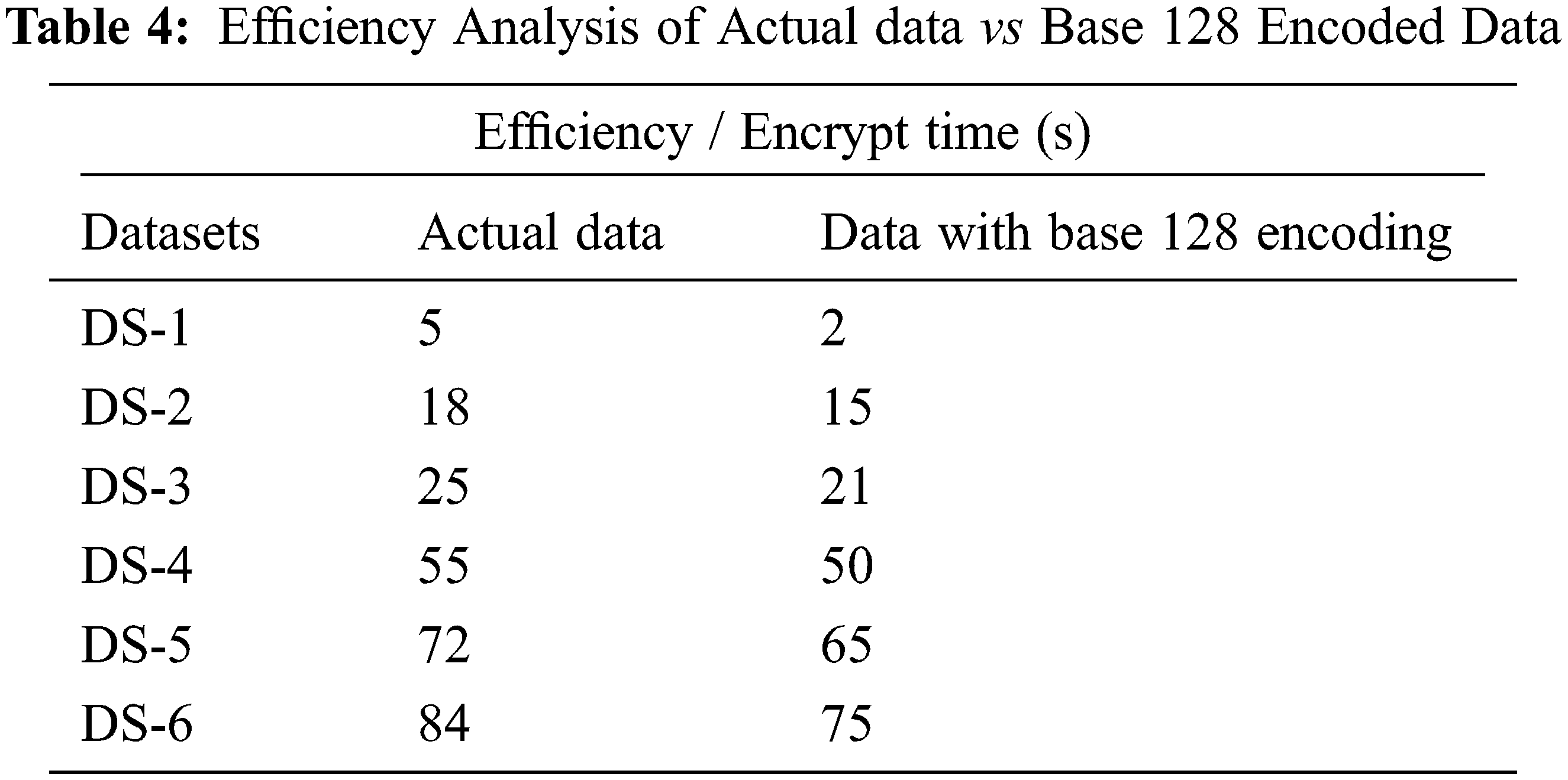
Categorizing characteristics is perhaps the most essential step in achieving the encode computation efficiency. The time required to send encrypted messages prior to categorizing data items is contrasted to the time required to decrypt data post categorization of data items in Fig. 5.
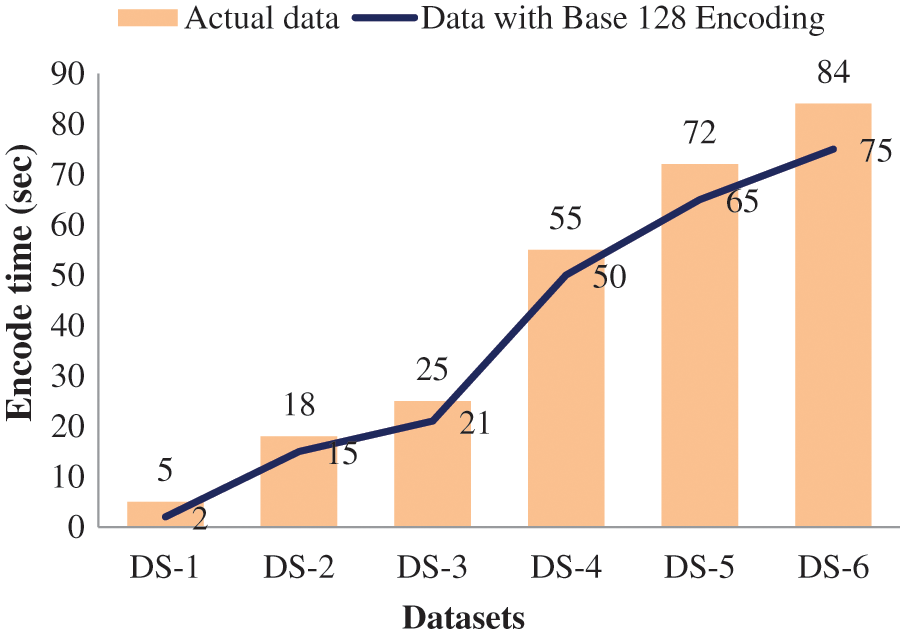
Figure 5: Efficiency Analysis of Actual data vs Base 128 Encoded Data
6.3.2 Computational Scalability
Various data quantities were used in our research, as shown in Tab. 1, to assess the Scalability of our suggested technique before and after dataset arbitrariness with perturbation. Fig. 6. shows The influence of the suggested technique on the amount of the raw data before and after dataset arbitrariness with perturbation.
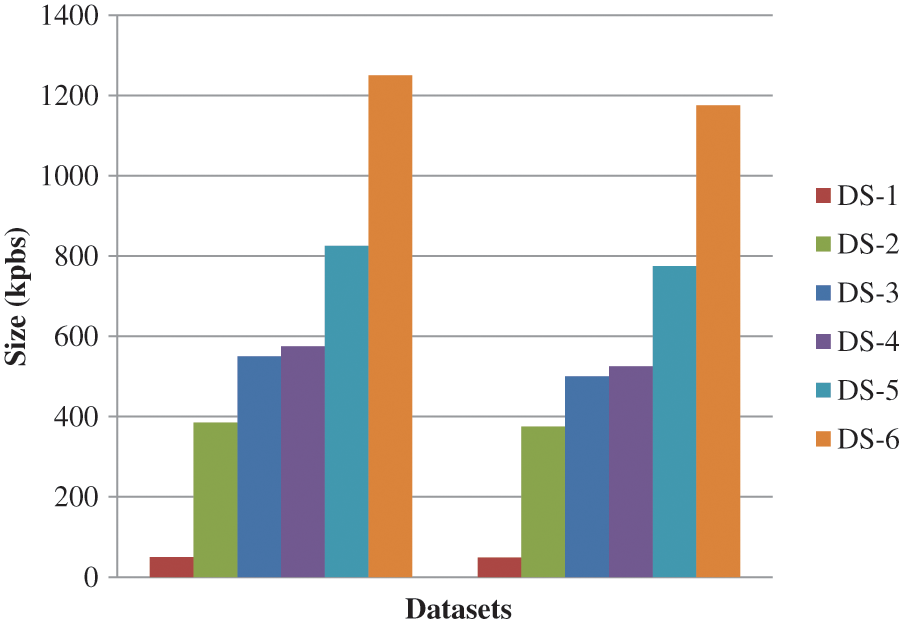
Figure 6: Amount of the raw data before and after dataset arbitrariness with perturbation
The size enhancement between the raw and encrypted data is owing to categorization depicted in Fig. 7. For example, encoding expanded the given dataset-1 by around 26% prior categorization. However, this increase in the volume of given dataset-1 decreased to 6% post categorization.
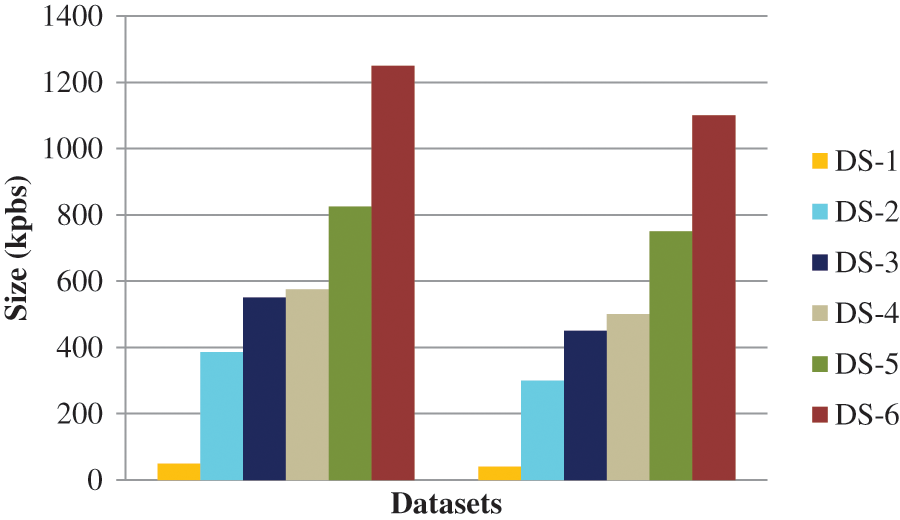
Figure 7: Amount of the Base 128 encoded data before and after dataset arbitrariness with perturbation
In many situations, maintaining privacy in data mining operations is critical. In this area, randomization-based strategies anticipate predominating. On the other hand, this research demonstrates a few of the difficulties these strategies encounter in maintaining data protection. It demonstrated that using perturbation-based techniques is reasonably possible to overcome the privacy protections afforded by arbitrariness under exceptional circumstances. Furthermore, it gave detailed experimental findings with various kinds of data, demonstrating that it is a serious issue to be addressed. Aside from raising an issue, the research also proposes a Base 128 encoding technique that could be useful in establishing a new approach to building more robust privacy-preserving algorithms. We have improved the Base 128 encoding technique in this research by adding arbitrariness with perturbation to modify the data to preserve the individuals’ personal and sensitive data. It’s been tested on UPI datasets with both continuous and categorical input variables to show that the suggested method is fast and stable in retaining critical categorized private information and difficult to obtain the actual information. The changed data acquired by mixing encrypted and quasi data, on the other hand, allows for significant data mining while preserving data integrity and efficiency. As a result, the proposed methodology was proven efficient and successful in preserving data privacy and quality. Data perturbation is a prominent strategy for safeguarding privacy in data mining, which comprises, along with other things, purchase behavior, criminal convictions, patient history, and credit documents. On the one side, such information is crucial to governments and companies for both judgment and social benefits, including medical science, reducing crime, and global security, among others.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. Kousika and K. Premalatha, “An improved privacy-preserving data mining technique using singular value decomposition with three-dimensional rotation data perturbation,” The Journal of Supercomputing, vol. 77, no. 9, pp. 10003–10011, 2021. [Google Scholar]
2. P. Mahit Kumar and Md Islam, “Enhancing the performance of 3d rotation perturbation in privacy preserving data mining using correlation based feature selection,” in Proc. of the Int. Conf. on Big Data, IoT, and Machine Learning, Singapore, Springer, pp. 205–215, 2022. [Google Scholar]
3. W. Haoxiang and S. Smys, “Big data analysis and perturbation using data mining algorithm,” Journal of Soft Computing Paradigm, vol. 3, no. 1, pp. 19–28, 2021. [Google Scholar]
4. D. Jayanti and A. Singh, “A machine learning approach in data perturbation for privacy-preserving data mining,” in Smart Computing Techniques and Applications. Singapore: Springer, pp. 645–654, 2021. [Google Scholar]
5. S. Mariammal, “An additive rotational perturbation technique for privacy preserving data mining,” Turkish Journal of Computer and Mathematics Education, vol. 12, no. 9, pp. 2675–2681, 2021. [Google Scholar]
6. S. Singaravelan, P. Gopalsamy and S. Balaganesh, “Accumulation of data perturbation techniques for privacy preserving data classification,” Asian Journal of Current Research, vol. 6, no. 1, pp. 38–49, 2021. [Google Scholar]
7. W. Ouyang, “Privacy preserving mining sequential pattern based on random data perturbation,” in 2021 7th Int. Conf. on Systems and Informatics, China, IEEE, pp. 1–6, 2021. [Google Scholar]
8. E. Zorarpacı and S. A. Özel, “Privacy preserving classification over differentially private data,” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 11, no. 3, pp. 1–20, 2021. [Google Scholar]
9. A. Aminifar, F. Rabbi, K. I. Pun and Y. Lamo, “Privacy preserving distributed extremely randomized trees,” in Proc. of the 36th Annual ACM Symp. on Applied Computing. Association for Computing Machinery, New York, NY, USA, pp. 1102–1105, 2021. [Google Scholar]
10. V. Sharma, D. Soni, D. Srivastava and P. Kumar, “A novel hybrid approach of suppression and randomization for privacy preserving data mining,” Elementary Education Online, vol. 20, no. 5, pp. 2451–2457, 2021. [Google Scholar]
11. A. Aminifar, M. Shokri, F. Rabbi, V. K. I. Pun and Y. Lamo, “Extremely randomized trees with privacy preservation for distributed structured health data,” IEEE Access, vol. 10, pp. 6010–6027, 2022. [Google Scholar]
12. A. K. Sahoo, C. Pradhan, B. K. Mishra and B. S. P. Mishra, “An Extensive study of privacy preserving recommendation system using collaborative filtering,” in Deep Learning in Data Analytics. Studies in Big Data. Vol. 91. Cham: Springer, pp. 171–190, 2022. [Google Scholar]
13. X. Jiang, Z. Xuebing and J. Grossklags, “Privacy-preserving high-dimensional data collection with federated generative autoencoder,” Proceedings on Privacy Enhancing Technologies, vol. 2022, no. 1, pp. 481–500, 2022. [Google Scholar]
14. P. Kalia, D. Bansal and S. Sofat, “Privacy preservation in cloud computing using randomized encoding,” Wireless Personal Communications, vol. 120, no. 4, pp. 2847–2859, 2021. [Google Scholar]
15. S. A. Abdelhameed, S. M. Moussa, N. L. Badr and M. Essam Khalifa, “The generic framework of privacy preserving data mining phases: Challenges & future directions,” in 2021 Tenth Int. Conf. on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, pp. 341–347, 2021. [Google Scholar]
16. M. Shivashankar and S. A. Mary, “Privacy preservation of data using modified rider optimization algorithm: Optimal data sanitization and restoration model,” Expert Systems, vol. 38, no. 3, pp. e12663, 2021. [Google Scholar]
17. M. A. P. Chamikara, P. Bertok, I. Khalil, D. Liu and S. Camtepe, “PPaaS: Privacy preservation as a service,” Computer Communications, vol. 173, no. 16, pp. 192–205, 2021. [Google Scholar]
18. T. Kanwal, A. Anjum and A. Khan, “Privacy preservation in e-health cloud: Taxonomy, privacy requirements, feasibility analysis, and opportunities,” Cluster Computing, vol. 24, no. 1, pp. 293–317, 2021. [Google Scholar]
19. M. Keshk, B. Turnbull, E. Sitnikova, D. Vatsalan and N. Moustafa, “Privacy-preserving schemes for safeguarding heterogeneous data sources in cyber-physical systems,” IEEE Access, vol. 9, pp. 55077–55097, 2021. [Google Scholar]
20. C. Ma, L. Yuan, L. Han, M. Ding, R. Bhaskar et al., “Data level privacy preserving: A stochastic perturbation approach based on differential privacy,” IEEE Transactions on Knowledge & Data Engineering, 2021. [Google Scholar]
21. K. Macwan and S. Patel, “Privacy preservation approaches for social network data publishing,” in Artificial Intelligence for Cyber Security: Methods, Issues and Possible Horizons or Opportunities. Studies in Computational Intelligence, In: S. Misra, A. Kumar Tyagi (Eds.vol. 972. Cham: Springer, pp. 213–233, 2021. [Google Scholar]
22. P. Kalia, D. Bansal and S. Sofat, “A hybrid approach for preserving privacy for real estate data,” International Journal of Information and Computer Security, vol. 15, no. 4, pp. 400–410, 2021. [Google Scholar]
23. P. R. M. Rao, S. M. Krishna and A. S. Kumar, “Novel algorithm for efficient privacy preservation in data analytics,” Indian Journal of Science and Technology, vol. 14, no. 6, pp. 519–526, 2021. [Google Scholar]
24. S. Madan and P. Goswami, “Hybrid privacy preservation model for big data publishing on cloud,” International Journal of Advanced Intelligence Paradigms, vol. 20, no. 3/4, pp. 343–355, 2021. [Google Scholar]
25. S. Mewada, “Data mining-based privacy preservation technique for medical dataset over horizontal partitioned,” International Journal of E-Health and Medical Communications, vol. 12, no. 5, pp. 50–66, 2021. [Google Scholar]
26. N. Partheeban, K. Sudharson and P. J. Sathish Kumar, “SPEC- serial property based encryption for cloud,” International Journal of Pharmacy & Technology, vol. 8, no. 4, pp. 23702–23710, 2016. [Google Scholar]
27. K. Sudharson, A. Mudassar Ali and N. Partheeban, “Natural user interface technique foremulating computer hardware,” International Journal of Pharmacy & Technology, vol. 8, no. 4, pp. 23598–23606, 2016. [Google Scholar]
28. J. Aruna Jasmine, V. Nisha Jenipher, J. S. Richard Jimreeves, K. Ravindran and D. Dhinakaran, “A traceability set up using digitalization of data and accessibility,” in 3rd Int. Conf. on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, pp. 907–910, 20202020 [Google Scholar]
29. D. Dhinakaran and P. M. Joe Prathap, “Ensuring privacy of data and mined results of data possessor in collaborative ARM,” in Pervasive Computing and Social Networking. Lecture Notes in Networks and Systems. Vol. 317. Singapore: Springer, pp. 431–444, 2022. [Google Scholar]
30. Z. Suxia, W. Lei and S. Guanglu, “A perturbation mechanism for classified transformation satisfying local differential privacy,” Journal of Computer Research and Development, vol. 59, no. 2, pp. 430–439, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |