Computer Systems Science & Engineering DOI:10.32604/csse.2023.027129
Article

Cat and Mouse Optimizer with Artificial Intelligence Enabled Biomedical Data Classification

B. Kalpana1, S. Dhanasekaran2, T. Abirami3, Ashit Kumar Dutta4, Marwa Obayya5, Jaber S. Alzahrani6 and Manar Ahmed Hamza7,*

1Department of Information Technology, RMD Engineering College, Chennai, 601206, India
2Department of Information Technology, Kalasalingam Academy of Research and Education, Srivilliputtur, 626126, India
3Department of Information Technology, Kongu Engineering College, Erode, 638060, India
4Department of Computer Science and Information Systems, College of Applied Sciences, AlMaarefa University, Ad Diriyah, Riyadh, 13713, Kingdom of Saudi Arabia
5Department of Biomedical Engineering, College of Engineering, Princess Nourah bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
6Department of Industrial Engineering, College of Engineering at Alqunfudah, Umm Al-Qura University, Saudi Arabia
7Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 11 January 2022; Accepted: 11 March 2022

Abstract: Biomedical data classification has become a hot research topic in recent years, thanks to the latest technological advancements made in healthcare. Biomedical data is usually examined by physicians for decision making process in patient treatment. Since manual diagnosis is a tedious and time consuming task, numerous automated models, using Artificial Intelligence (AI) techniques, have been presented so far. With this motivation, the current research work presents a novel Biomedical Data Classification using Cat and Mouse Based Optimizer with AI (BDC-CMBOAI) technique. The aim of the proposed BDC-CMBOAI technique is to determine the occurrence of diseases using biomedical data. Besides, the proposed BDC-CMBOAI technique involves the design of Cat and Mouse Optimizer-based Feature Selection (CMBO-FS) technique to derive a useful subset of features. In addition, Ridge Regression (RR) model is also utilized as a classifier to identify the existence of disease. The novelty of the current work is its designing of CMBO-FS model for data classification. Moreover, CMBO-FS technique is used to get rid of unwanted features and boosts the classification accuracy. The results of the experimental analysis accomplished by BDC-CMBOAI technique on benchmark medical dataset established the supremacy of the proposed technique under different evaluation measures.

Keywords: Artificial intelligence; biomedical data; feature selection; cat and mouse optimizer; ridge regression

1  Introduction

Information and Communication Technology (ICT) has evolved tremendously in the recent years which made it possible to save huge volumes of information from different fields of engineering and medical applications. This information should be provided mandatorily, in terms of objects (patterns) and massive number of features so that all the aspects of the domain get characterized [1]. However, there is a complexity exits i.e., it could often result in the inclusion of several irrelevant or redundant characteristics. This may lead to poor results when utilizing Data Mining (DM) or Machine Learning (ML) methods for knowledge discovery. Dimensionality reduction [2] is a type of reduction technique in knowledge discovery procedure when handling massive set of information. There are two major methods used in this study towards reduction problems such as selection- and transformation-based methods. Selection-based method is otherwise called as feature extraction which encodes or transforms the fundamental meaning of the feature [3]. Transformation-based method reduces the original feature space without conversion owing to which the original feature is maintained. Here, cogent interpretation is feasible, and is commonly called as Feature Selection (FS) [4]. When conducting a survey, FS models can be categorized as two types in which the former FS method returns a set of features whereas in latter, the FS method returns the ranking order of each feature (according to the importance of the feature) [5]. Likewise, based on the relationships of FS method with learning models (classification), FS method is generally categorized in addition to other two distinct methods such as classification-dependent (embedded and wrapper), and classification-independent (filter). The last few years have experienced the predominant application of numerous FS models in the fields of E-commerce, medical, and healthcare which are designed by different mainstream study communities on different metrics such as probability, data theory, correlation, and so on [6]. Fig. 1 illustrates the processes involved in biomedical data classification.

Figure 1: Biomedical data classification process

Traditionally, FS method includes four fundamental stages such as subset evaluation, subset generation, result validation, and stopping criterion [7]. Amongst the four phases, subset evaluation and subset generation are the two leading factors in the creation of FS algorithm. Subset generation is assumed to be a searching issue that focuses on identifying the optimal subset from each feasible feature subset. Various searching approaches like heuristic search, greedy search, and exhaustive search are mainly utilized and explored by the authors to recognize the optimal or sub-optimal feature subset [8]. On the other hand, exhaustive approach devises every feasible combination of the feature and its ‘combinatory explosion’ results in computation load that exponentially gets improved with several features. Heuristic search strategy utilizes metaheuristic approaches like Grey Wolf Optimizer (GWO), Simulated Annealing (SA), Genetic Algorithm (GA), and many other optimization methods to resolve FS issues [9]. In spite of the developments achieved in the abovementioned search methods, it remains unfeasible since the methods are computationally impractical or the methods achieved a solution apart from the optimal one [10]. The advanced methods report that wrapper or filter FS methods can be applied, when the consequence of hybrid FS is not considered. Due to the established fact that no single method can assure optimum outcomes regarding prediction efficiency, the efficacy of the ‘hybrid’ method using the advantages of filter and wrapper models is examined mainly in the study.

The current research work presents a novel Biomedical Data Classification using Cat and Mouse Based Optimizer with AI (BDC-CMBOAI) technique. The proposed BDC-CMBOAI technique involves the design of Cat and Mouse Optimizer-Based Feature Selection (CMBO-FS) technique to derive a useful subset of features. In addition, Ridge Regression (RR) model is utilized as a classifier to diagnose the disease. Moreover, the utilization of CMBO-FS technique helps in removing the unwanted features and boosts the classification accuracy. The experimental results of the analysis accomplished by BDC-CMBOAI technique on benchmark medical dataset was investigated under different dimensions and the technique’s supremacy is established.

2  Related Works

Khademi et al. [11] established a novel scheme to diagnose diabetes. In this study, an ensemble classifier was utilized in applying SVM, KNN, and WOA. WOA is responsible for the creation of weight for all the classifiers to improve the accuracy of diabetes classifiers. The diabetes dataset was collected from Medical centers located in Iran and the empirical analysis was conducted. In literature [12], the authors proposed a novel FS technique to improve the classification accuracy. Differential Evolution optimization algorithm was utilized to find the optimum subset attained by Filter-based FS technique. The performance of the presented FS was evaluated using classifiers as RF, Gradient Boosting Tree, ANN, and SVM.

Abdar et al. [13] presented a novel, easy, and effectual fusion technique with uncertainty-aware component to medicinal image classifier which is named as Binary Residual Feature fusion (BARF). Monte Carlo (MC) dropout was executed to manage the uncertainties and to obtain the mean and Standard Deviation (SD) of forecasts. The presented technique utilized four distinct medical image dataset and tested the same using two important approaches such as direct and cross-validation. The authors in the literature [14] proposed an effectual method to diagnose diabetes using a hybrid-optimized SVM. The presented hybrid optimized approach is a combination of Crow Search algorithm (CSA) and Binary Grey Wolf Optimizer (BGWO). This approach is used to exploit the complete potential of SVM to diagnose the disease. In [15], a novel technique named FR–KDE was proposed. This technique is a combination of FR and Kernel Density Estimation (KDE) from Dempster–Shafer theory. The evidence model was presented to manage the classification issue. When the outcomes of both FR and KDE were fused together using Dempster combination rule, it decreased the uncertainty of FR and attained the optimum accuracy.

3  The Proposed Model

In this study, a novel BDC-CMBOAI technique is presented to determine the occurrence of diseases using biomedical data. The proposed BDC-CMBOAI technique involves different processes namely, pre-processing, feature subset selection using CMBO-FS technique, and RR-based classification. Moreover, the utilization of CMBO-FS technique helps in getting rid of unwanted features and boosts the classification accuracy.

3.1 Algorithmic Design of CMBO-FS Technique

CMBO is a population-based technique simulated by the natural phenomena in which the cat attacks the mouse while mouse gets away from haven. The search agent, from the presented technique, is separated into two sets of cats and mice which scan the problem search spaces in an arbitrary movement. The presented technique upgrades the members of the population through two stages. In primary stage, the progress of cats near mice is demonstrated while in secondary stage, the mice running away to haven so as to save their life is modeled. From a mathematical viewpoint, all the members of the population denote the presented solutions to the problem. In general, the member of the populations contribute certain values to the problem variables based on their place from search spaces. Therefore, all the members of the population have vector whose value defines the variable of the problem. The population of this technique is defined with the help of a matrix name called population matrix as shown in Eq. (1).

X=[X1XiXN]N×m=[X1,1⋯X1,d⋯X1,m⋮⋱⋮⋰⋮Xi,1⋯Xi,d⋯Xi,m⋮⋰⋮⋱⋮XN,1⋯XN,d⋯XN,m]N×m (1)

where X refers to the population matrix of CMBO, Xi implies the ith search agent, xi,d signifies the value of dth problem variable attained by ith search agent, N signifies the number of population members, and m stands for amount of problem variables. As noted, all the members of the population define the presented values to problem variables [16]. So, the value is identified to the main function for all the population members. The values attained to the main function, are represented through a vector given in Eq. (2).

F=[F1⋮Fi⋮FN]N×1 (2)

where F denotes the vector of main purpose value and Fi indicates the main purpose value to the ith search agent. According to the values attained for the main purpose, the member of populations is classified as the optimum member with a minimal value of main function to worse member of populations with maximum value of main function. The arranged population matrix and arranged main function are defined in Eqs. (3) and (4).

XS=[X1S⋮XiS⋮XNS]=[X1,1S⋯X1,dS⋯X1,mS⋮⋱⋮⋰⋮Xi,1S⋯Xi,dS⋯Xi,mS⋮⋰⋮⋱⋮XN,1S⋯XN,dS⋯XN,mS]N×m (3)

FS=[F1Smin(F)⋮⋮FNSmax(F)]N×1 (4)

where XS refers to the sort population matrix which depends upon main function value, XiS signifies the ith member of sorting population matrix, xi,ds represents the value to dth problem variable attained by ith search agent of sorting population matrix, and FS stands for sorted vector of the main function. In CMBO, it can be considered that half of the population members offered optimum values to the main function so as to create the population of mice whereas the other half of the population members offered lesser values to the main function which constitutes the population of cats. According to this method, the population of mice and cats are defined through the Eqs. (5) and (6), correspondingly

M=[M1=X1S⋮Mi=XiS⋮MNm=XNmS]Nm×m=[X1,1S⋯X1,dS⋯X1,mS⋮⋱⋮⋰⋮Xi,1S⋯Xi,dS⋯Xi,mS⋮⋰⋮⋱⋮XNm,1S⋯XNm,dS⋯XNm,mS]N×m, (5)

C=[C1=X1S⋮Cj=XiS⋮CNc=XNm+NcS]Nc×m=[XNm+1,1S⋯XNm+1,dS⋯XNm+1,mS⋮⋱⋮⋰⋮XNm+j,1S⋯XNm+j,dS⋯XNm+j,mS⋮⋰⋮⋱⋮XNm+Nc,1S⋯XNm+Nc,dS⋯XNm+Nc,mS]Nc×m, (6)

where M refers to the population matrix of mice, Nm signifies the number of mice, Mi implies the jth mouse, C stands for population matrix of cats, Nc defines the number of cats, and Cj determines the ith cat. To update the search factor, a primary stage i.e., the the place of the cats is altered according to the natural performance of cats and progress near mice. This upgradation stage of the presented CMBO is mathematical modeled with the help of the Eqs. (7)–(9).

Cjnew:cj,dnew=cj,d+r×(mk,d−I×cj,d)&j=1:Nc′d=1:m,k∈1:Nm′ (7)

I=round(1+rand), (8)

Cj={Cjnew,|Fjc,new<FjC,Cj,|else (9)

At this point, Cjnew denotes the novel condition of jth cat, cj,dnew indicates the novel value to dth problem variable attained by jth cat, r implies the arbitrary number in the interval of 0 and1 , mk,d means the dth dimensional of kth mouse, Fjc,new stands for the main function value which is dependent upon the novel condition of jth cat. In secondary stage of the presented CMBO, the run-away of the mice to haven is demonstrated. The place of haven, from the search space, is arbitrarily generated based on how the places of distinct members of the technique are modelled. This upgradation stage of the place of mice is mathematically processed through the Eqs. (10)–(12).

Hi:hi,d=xl,d&i=1:Nm,d=1:m,l∈1:N, (10)

Minew:mi,dnew=mi,d+r×(hi,d−I×mi,d)×sign(Fim−FiH)&i=1:Nm,d=1:m, (11)

Mi={Minew,|Fim,new<FimMi′|else (12)

At this point, Hi defines the haven to ith mouse and FiH represents their main function value. Minew signifies the novel condition of ith mouse and Fim,new denotes the main function value. Then, each member of this population is upgraded and this technique enters the next iteration based on the Eqs. (5)–(12). The technique is applied iteratively until the termination criteria is obtained. This start-to-end optimization technique denote the specific amount of iterations to determine the acceptable error between the attained solutions and consecutive iteration. Fig. 2 demonstrates the flow process of CMO technique.

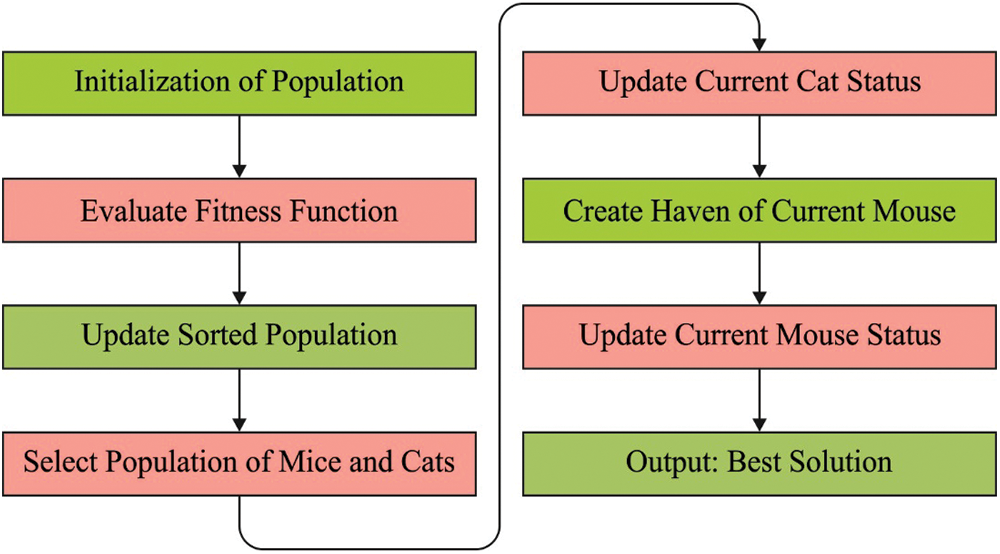
Figure 2: Process in CMO

Transfer function manner refers to the chances of different place vector elements in terms of zero to one, conversely a further simplified ad efficiency model. When exploring the ab optimum group of features, the transfer function significantly controls the resultant of FS approach than it avoids the local optimum problems and preserves the trade-off between exploration and exploitation methods. Based on the above-mentioned scenario, FF provides a solution in this condition to obtain a balance between the purposes as follows.

fitness=αΔR(D)+β|Y||T| (13)

ΔR(D) signifies the classifier error rate. |Y| implies the size of subsets that this technique selects and |T| refers to the whole count of features contained in the presented dataset. α demonstrates the parameter ∈[0,1] compared with the weight of error rate of classification correspondingly. However β=1−α stands for the importance of reducing feature.

3.2 Process Involved in RR-Based Classification

At the time of classification, RR model is applied to derive a meaningful subset of features. RR [17], a type of SLFN in which the weight between the input as well as hidden layers are selected following an arbitrary method. So, the weights between the hidden and resultant layers require the learning whereas, in RR, a least square-based learning technique is utilized to tackle binary- and multi-class classifier issues. RR is computationally-free in iterations which generate the results rapidly, by considerably decreasing the computational time required for training the SLFN. SLFN technique frequently needs a maximum amount of hidden neurons since it creates optimum solution. The resultant function of the SLFN with L hidden node is demonstrated through the formulas given below.

fL(x)=∑i=1Lβigix=∑i=1LβiG(ai,bi,x),x∈Rd,βi∈Rm (14)

To additive nodes with activation function g, g is demonstrated as follows

gi=G(ai,bi,x)=g(aix+bi),ai∈Rd,bi∈R (15)

∑i=1LβiG(ai,bi,x)=tj,j=1,…,N (16)

The above formula is revised as follows.

Hβ=T (17)

At this point,

H(w1⋯wL,b1⋯bL,x1⋯xN)

=(g(w1⋅x1+b1)⋯g(wL⋅x1+bL)⋮⋱⋮g(w1⋅xN+b1)⋯g(wL⋅xN+bL)) (18)

β=[β1T⋮βNT] (19)

T=[t1T⋮tNT] (20)

H implies the hidden layer resultant matrix of NN. SLFN is trained to resolve a linear system optimized problem with the help of subsequent formulas:

||Hβ^−T||=minβ||Hβ−T|| (21)

At this point, β^ is represented as:

β^=H†T=(HTH)−1HTT (22)

is the lowest norm least square solution of wi=T and HT signifies the Moore Penrose generalization inverse of H .

The process of RR is outlined in the subsequent steps.

Step1 Select the input weight wi and hidden layer bias bi arbitrarily.

Step2 Calculate the hidden layer resultant matrix H.

Step3 Achieve the resultant weight β^ utilizing the formula β^=H†T

4  Experimental Validation

The performance validation of the proposed BDC-CMBOAI technique was conducted using three benchmark medical datasets [18]. The results were inspected under varying runs of execution on each dataset. The details related to the dataset are given in Tab. 1.

Tab. 2 demonstrates the results of the analysis, accomplished by BDC-CMBOAI technique against other methods on Wisconsin breast cancer dataset, in terms of accuracy and Computation Time (CT) [19].

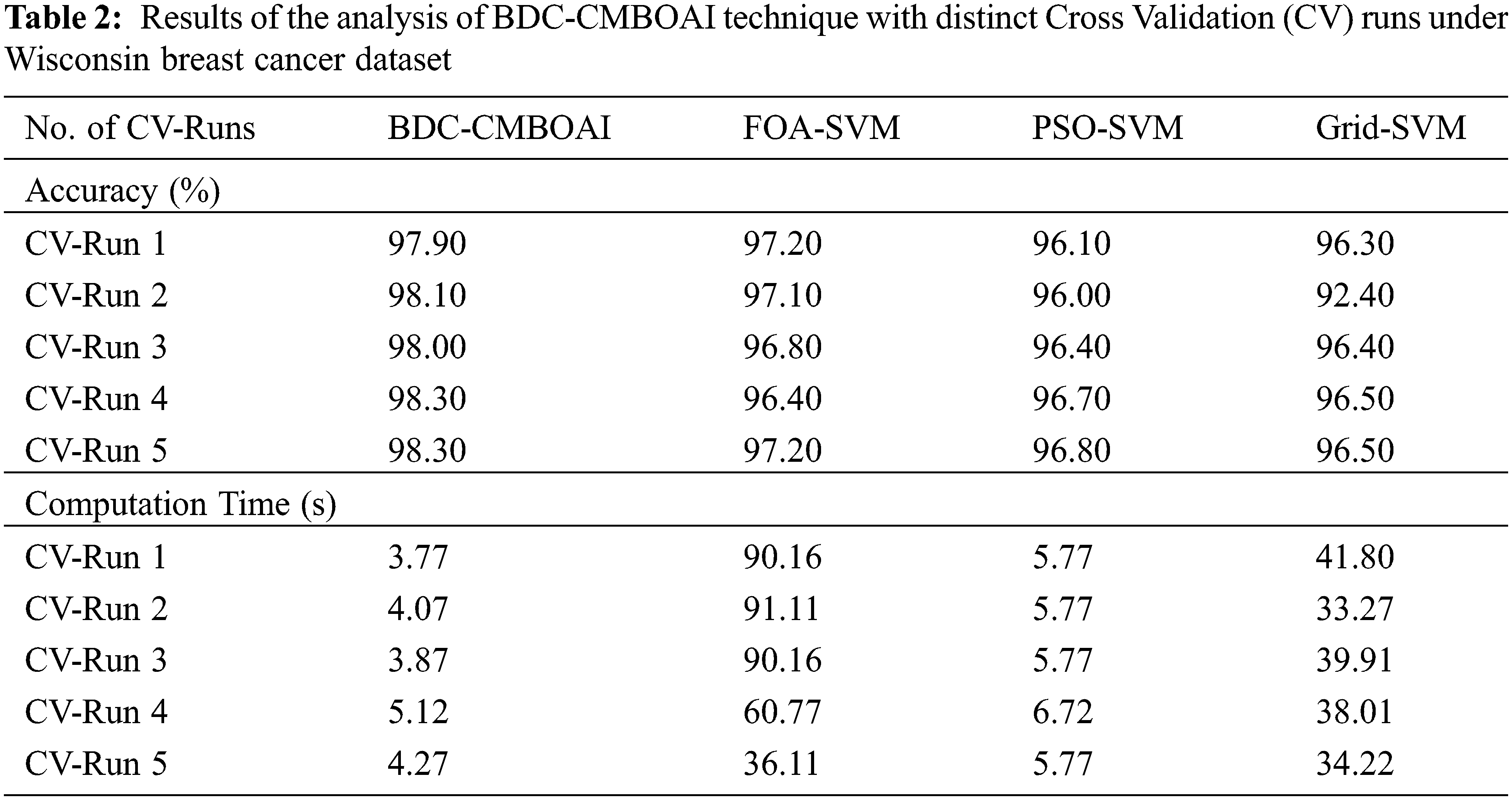
Fig. 3 provides the results for comparative accuracy analysis, achieved by BDC-CMBOAI technique against recent methods under different Cross Validation (CV) runs. The results indicate that the proposed BDC-CMBOAI technique obtained a high accuracy under all CV runs. For instance, with CV run-1, BDC-CMBOAI technique achieved an increased accuracy of 97.90%, whereas FOA-SVM, PSO-SVM, and Grid SVM techniques achieved the least accuracy values such as 97.20%, 96.10%, and 96.10% respectively. Along with that, under CV-run 5, the proposed BDC-CMBOAI technique offered a maximum accuracy of 98.30%, whereas FOA-SVM, PSO-SVM, and Grid SVM techniques reached minimum accuracy values namely, 97.20%, 96.80%, and 96.50% respectively.

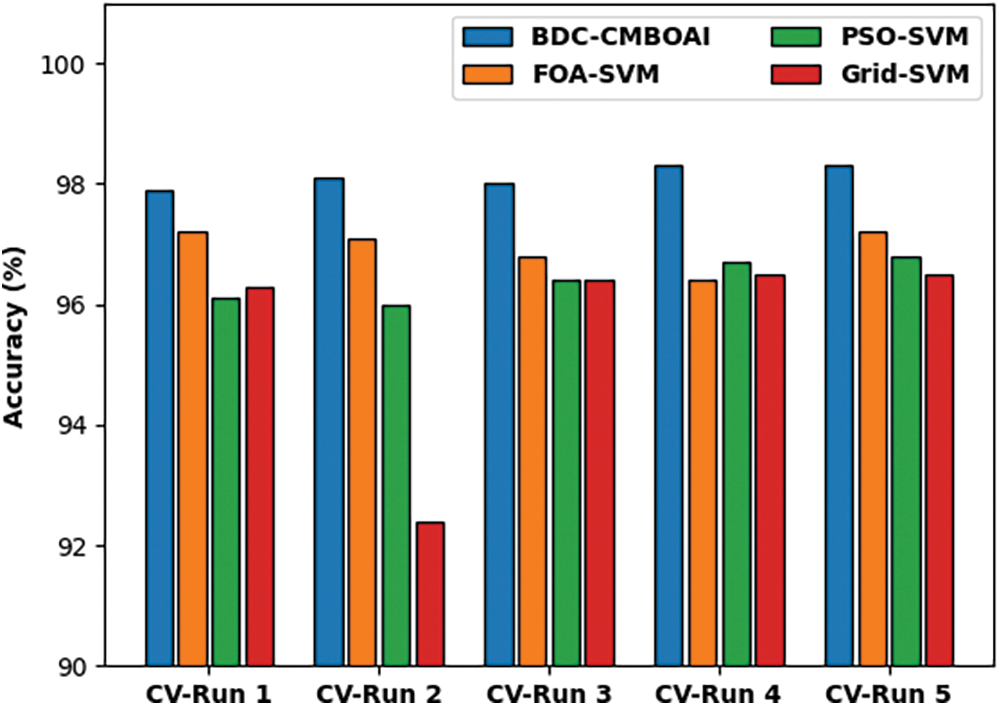
Figure 3: Accuracy analysis of BDC-CMBOAI technique under Wisconsin breast cancer dataset

A detailed CT analysis results accomplished by BDC-CMBOAI technique against existing techniques is shown in Fig. 4. The results infer that BDC-CMBOAI technique achieved better outcomes with least values of CT. For instance, with CV-run 1, BDC-CMBOAI technique required a low CT of 4.27s, whereas other techniques such as FOA-SVM, PSO-SVM, and Grid-SVM reached high CT values such as 90.16, 5.77 and 41.80s respectively. Likewise, with CV-run 5, the presented BDC-CMBOAI technique attained a low CT of 3.77s, whereas FOA-SVM, PSO-SVM, and Grid-SVM techniques demanded more CT values such as 36.11, 5.77 and 34.22s respectively.

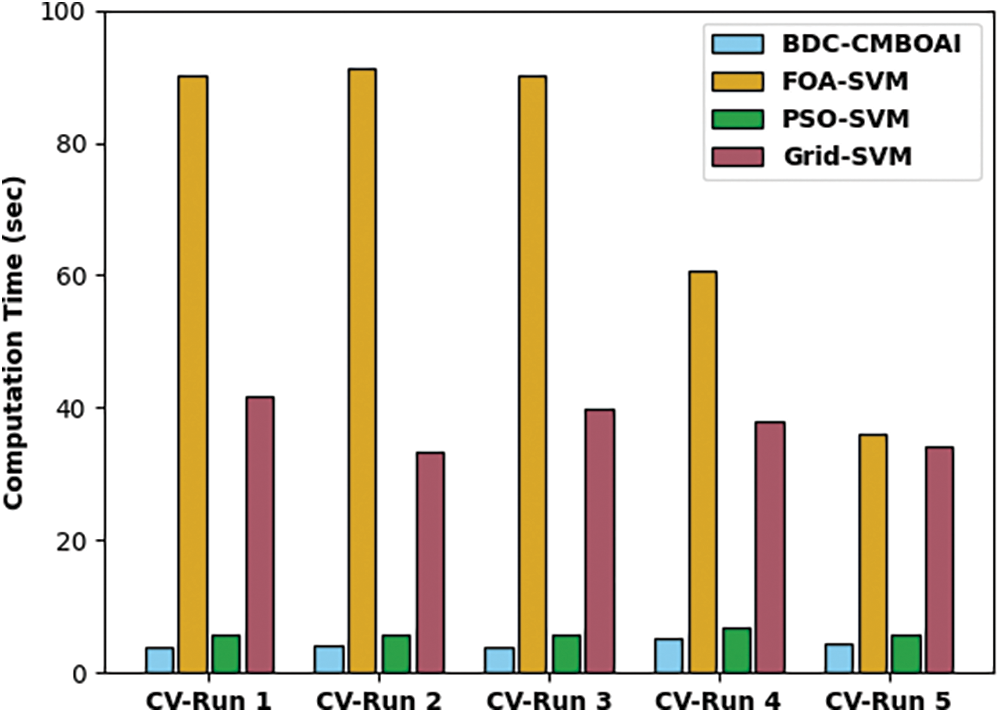
Figure 4: CT analysis of BDC-CMBOAI technique under Wisconsin breast cancer dataset

Fig. 5 demonstrates the ROC analysis results generated by IDTL-MPDC technique on test dataset. The figure exposes that IAOA-DLFD technique reached an enhanced outcome with a minimum ROC of 99.8792.

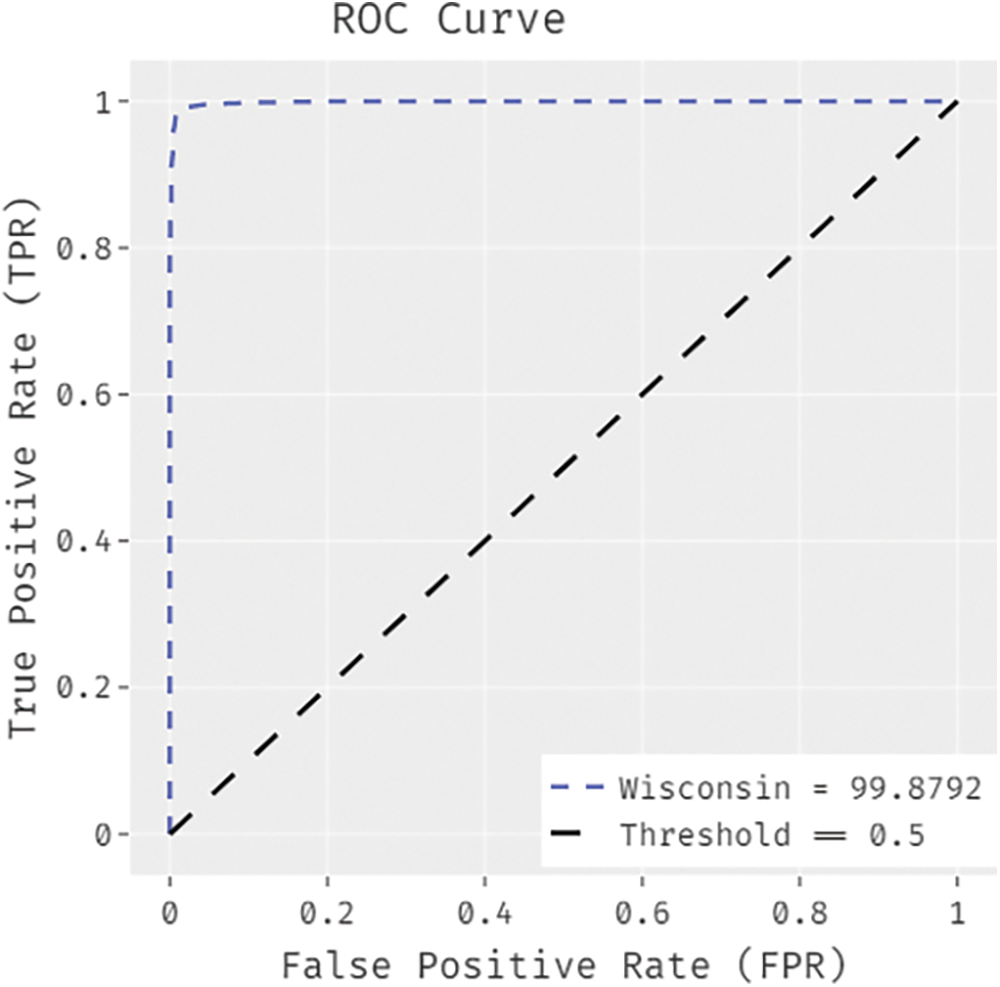
Figure 5: ROC analysis results of BDC-CMBOAI technique under Wisconsin breast cancer dataset

Tab. 3 illustrates the analytical results achieved by BDC-CMBOAI approach against other techniques on Pima Indians diabetes dataset in terms of accuracy and CT.

Fig. 6 shows the results of comparative accuracy analysis achieved by BDC-CMBOAI methodology against recent techniques under distinct CV runs. The results infer that the proposed BDC-CMBOAI technique obtained a high accuracy under all CV runs. For instance, with CV run-1, BDC-CMBOAI technique achieved a high accuracy of 78.12%, whereas FOA-SVM, PSO-SVM, and Grid SVM methods achieved less accuracy values such as 77.40%, 76.73%, and 75.92% respectively. Besides, under CV-run 5, the BDC-CMBOAI approach offered a maximum accuracy of 78.75%, whereas FOA-SVM, PSO-SVM, and Grid SVM systems gained the least accuracy values such as 77.60%, 76.49%, and 76.11% correspondingly.

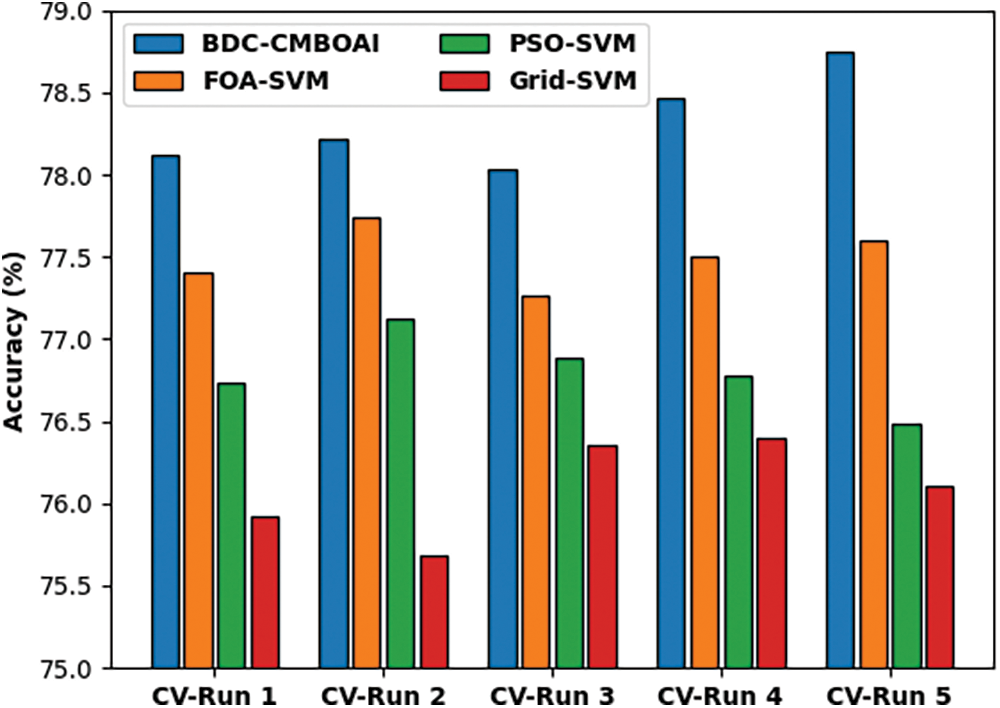
Figure 6: Accuracy analysis results of BDC-CMBOAI technique under Pima Indians diabetes dataset

A brief CT analysis was conducted between BDC-CMBOAI technique and existing techniques and the results are shown in Fig. 7. The outcomes demonstrate the supremacy of the proposed BDC-CMBOAI approach with minimal CT values. For sample, with CV-run 1, the presented BDC-CMBOAI technique decreased the CT value to 66.87s whereas FOA-SVM, PSO-SVM, and Grid-SVM systems reached high CT values such as 79.67, 313.11 and 183.42s respectively. Eventually, with CV-run 5, the proposed BDC-CMBOAI approach attained a reduced CT of 159.22s, whereas FOA-SVM, PSO-SVM, and Grid-SVM methodologies needed high CT values such as 183.42, 364.99 and 209.36s respectively.

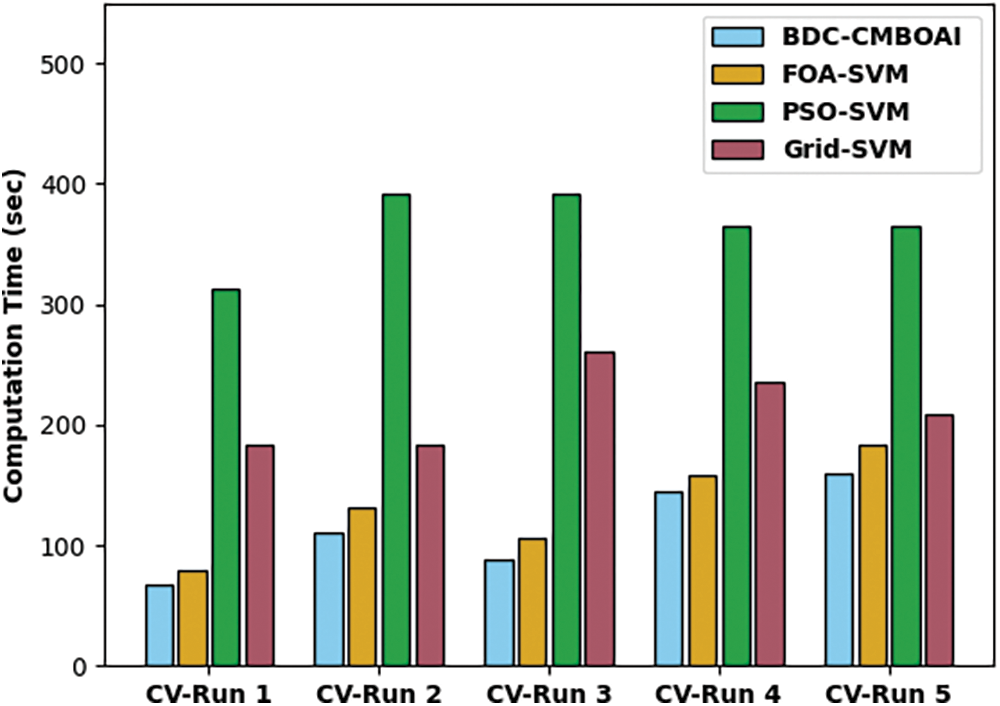
Figure 7: CT analysis of BDC-CMBOAI technique under Pima Indians diabetes dataset

Fig. 8 illustrates the ROC analysis results achieved by IDTL-MPDC method on Pima Indians diabetes dataset. The figure shows that IAOA-DLFD approach obtained superior increased outcomes with a minimal ROC of 95.6760.

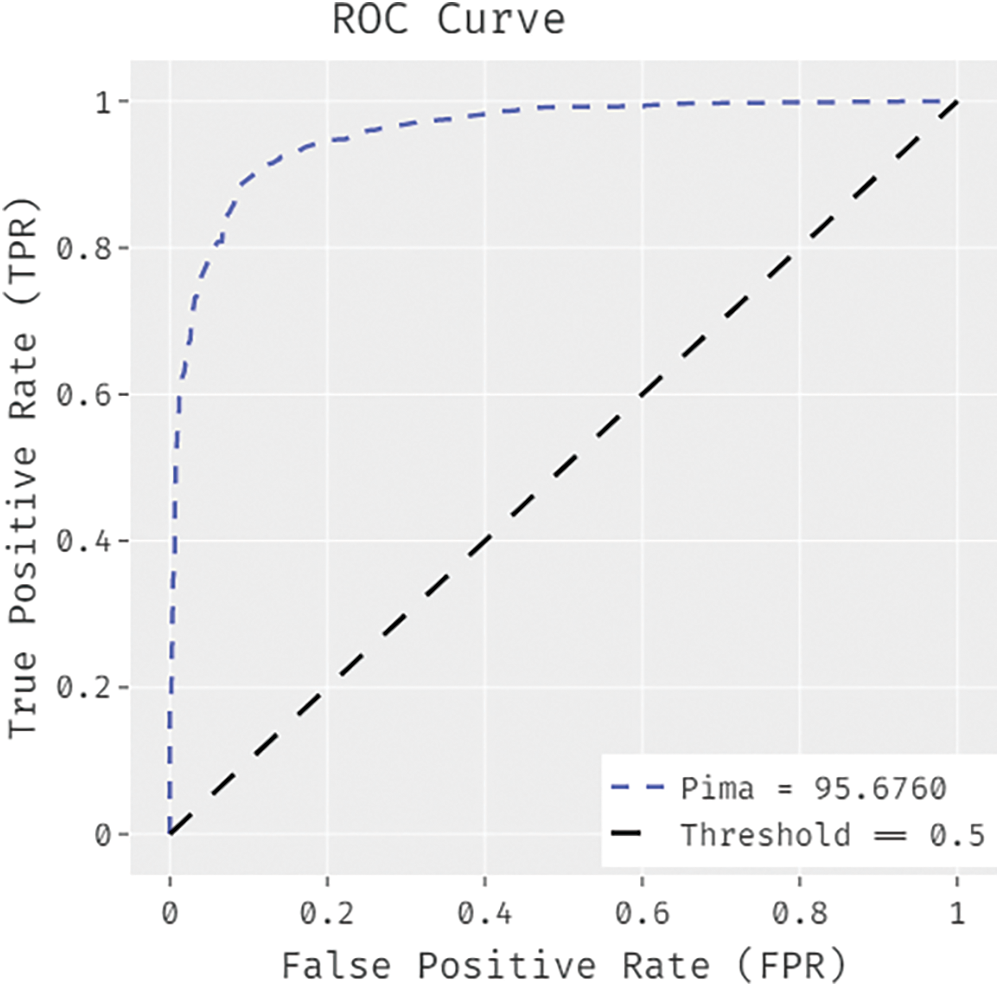
Figure 8: ROC analysis results of BDC-CMBOAI technique under Pima Indians diabetes dataset

Tab. 4 depicts the analytical results accomplished by BDC-CMBOAI method against other techniques on Thyroid dataset with respect to accuracy and CT.

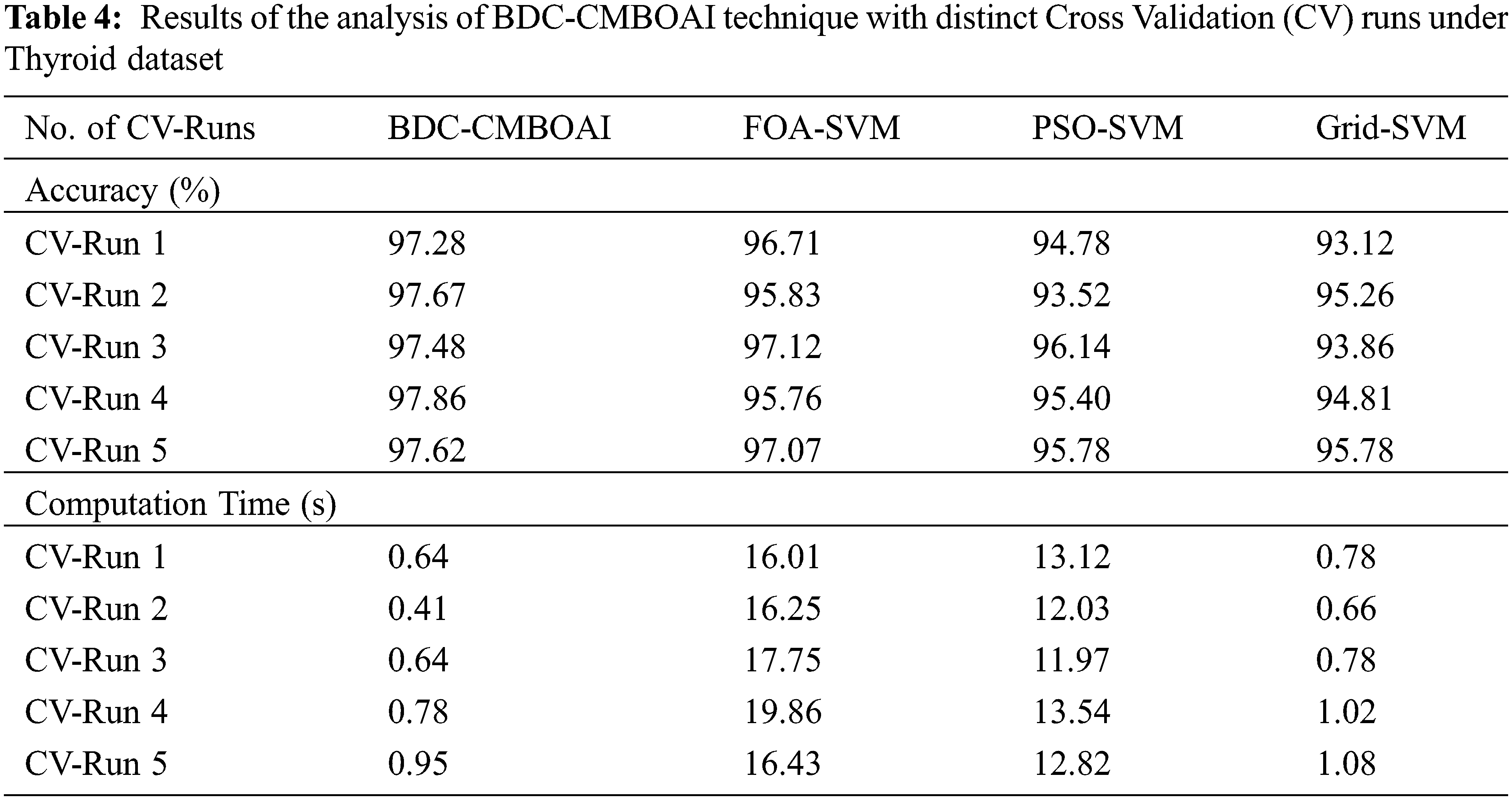
Fig. 9 shows the comparative accuracy analysis results accomplished by BDC-CMBOAI approach with recent techniques in terms of varying CV runs. The results reveal that the proposed BDC-CMBOAI technique gained a superior accuracy under all CV runs. For instance, with CV run-1, the presented BDC-CMBOAI system achieved an enhanced accuracy of 97.28% whereas FOA-SVM, PSO-SVM, and Grid SVM techniques achieved less accuracy values namely, 96.71%, 94.78%, and 93.12% correspondingly. In addition, under CV-run 5, BDC-CMBOAI methodology offered an increased accuracy of 97.62%, whereas FOA-SVM, PSO-SVM, and Grid SVM techniques achieved less accuracy values namely, 97.07%, 95.78%, and 95.78% correspondingly.

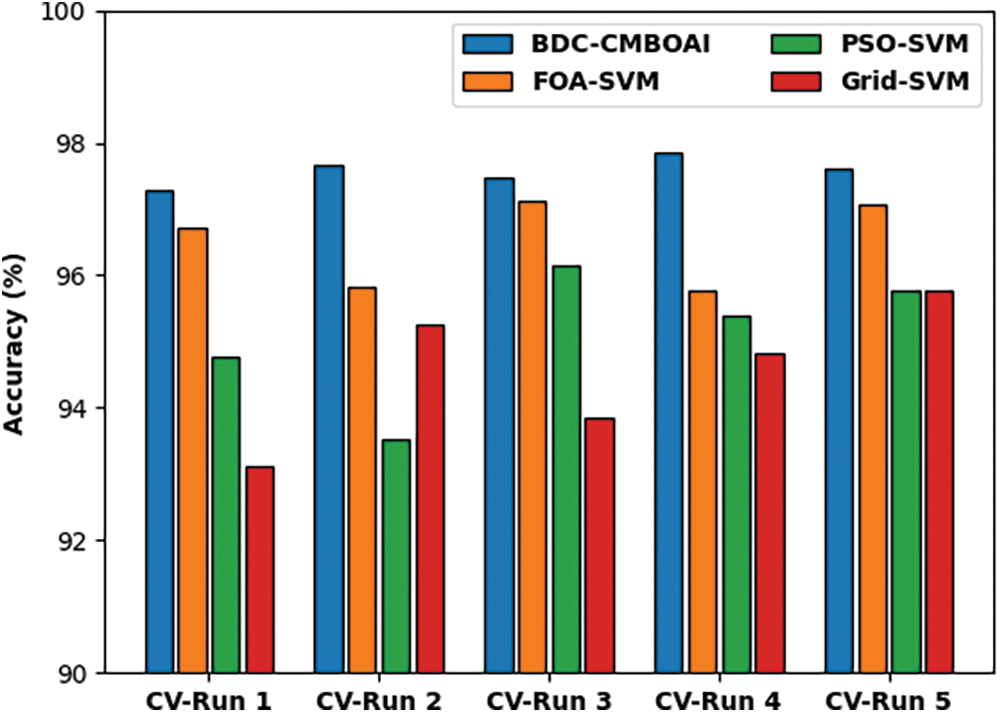
Figure 9: Accuracy analysis of BDC-CMBOAI technique under Thyroid dataset

A detailed CT analysis was conducted between BDC-CMBOAI method against existing methods and the results are shown in Fig. 10. The outcomes show that the presented BDC-CMBOAI approach achieved minimal CT values and outperformed other methods. For sample, with CV-run 1, the BDC-CMBOAI technique required a low CT of 064s, whereas other techniques such as FOA-SVM, PSO-SVM, and Grid-SVM methods gained high CT values such as 16.01, 13.12 and 0.78s correspondingly. In addition, with CV-run 5, BDC-CMBOAI system obtained a low CT of 0.95s, whereas FOA-SVM, PSO-SVM, and Grid-SVM methodologies demanded high CT values such as 16.43, 12.82 and 1.08s correspondingly.

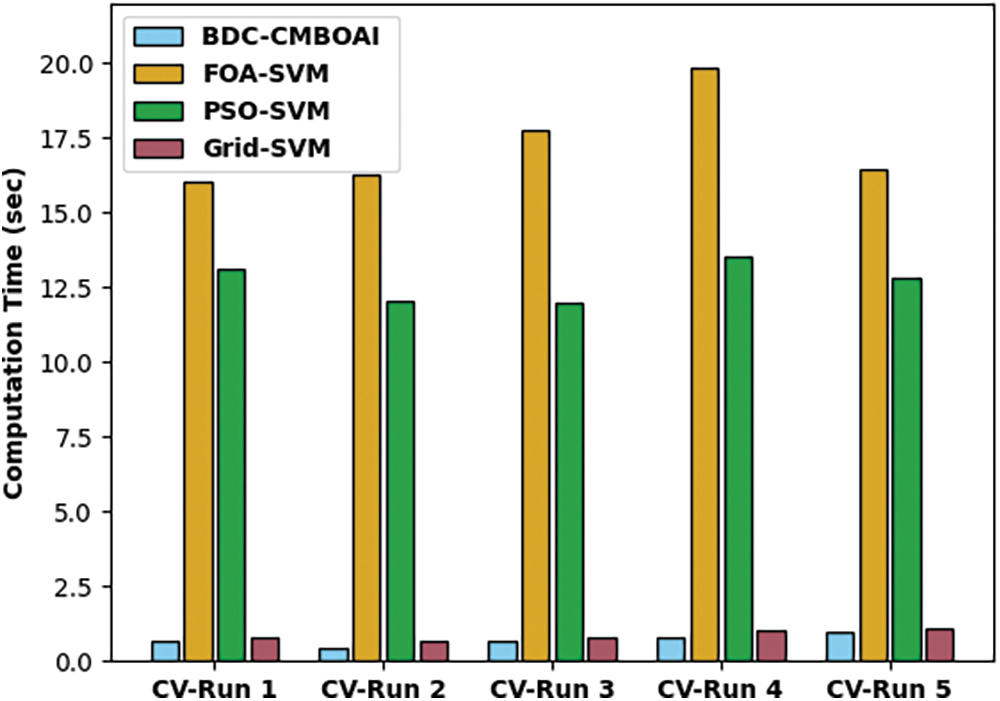
Figure 10: CT analysis of BDC-CMBOAI technique under Thyroid dataset

Fig. 11 illustrates the ROC analysis results achieved by IDTL-MPDC methodology on Thyroid dataset. The figure demonstrates that IAOA-DLFD approach achieved an increased outcome with a low ROC of 99.8176. By looking into the above mentioned tables and figures, it is obvious that the proposed BDC-CMBOAI technique has the ability to attain the maximum medical data classification accuracy.

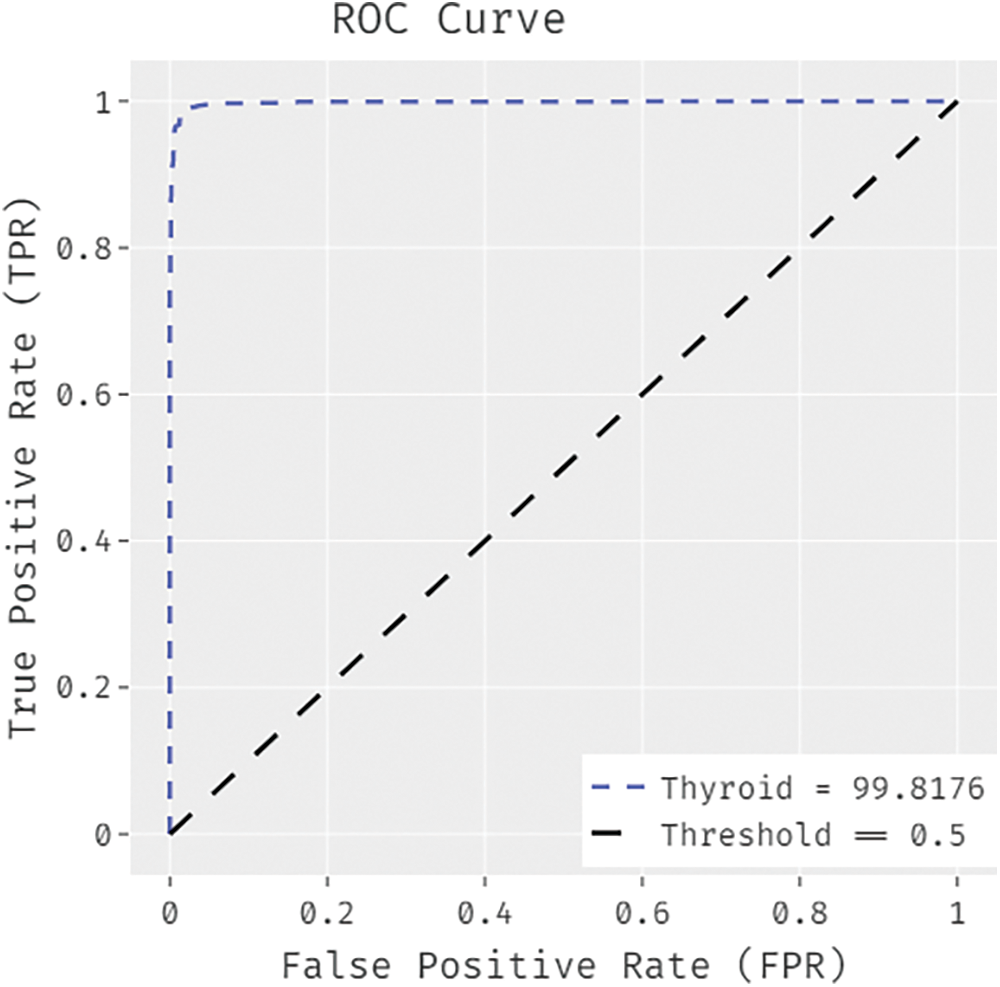
Figure 11: ROC analysis results of BDC-CMBOAI technique under Thyroid dataset

5  Conclusion

In this study, a novel BDC-CMBOAI technique is presented to determine the occurrence of diseases using biomedical data. The proposed BDC-CMBOAI technique involves different processes namely pre-processing, feature subset selection using CMBO-FS technique, and RR-based classification. Moreover, the utilization of CMBO-FS technique helps in removing unwanted features and boosts the classification accuracy. The experimental analysis results of BDC-CMBOAI technique on benchmark medical dataset were investigated under several aspects. The extensive comparative results established the enhanced outcomes of BDC-CMBOAI technique under different evaluation measures. Therefore, BDC-CMBOAI technique can be recognized as a novel approach for biomedical data classification. In future, outlier detection approaches can be utilized to design effective biomedical data classification processes.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R203), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4340237DSR03.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Boyapati, S. R. Swarna, V. Dutt and N. Vyas, “Big data approach for medical data classification: A review study,” in 2020 3rd Int. Conf. on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, pp. 762–766, 2020. [Google Scholar]

 2.  S. Yang, J. Z. Guo and J. W. Jin, “An improved Id3 algorithm for medical data classification,” Computers & Electrical Engineering, vol. 65, no. 4, pp. 474–487, 2018. [Google Scholar]

 3.  B. Sahmadi, D. Boughaci, R. Rahmani and N. Sissani, “A modified firefly algorithm with support vector machine for medical data classification,” in IFIP Int. Conf. on Computational Intelligence and its Applications, Oran, Algeria, pp. 232–243, 2018. [Google Scholar]

 4.  W. Xing and Y. Bei, “Medical health big data classification based on knn classification algorithm,” IEEE Access, vol. 8, pp. 28808–28819, 2020. [Google Scholar]

 5.  X. Gu, C. Zhang and T. Ni, “Feature selection and rule generation integrated learning for takagi-sugeno-kang fuzzy system and its application in medical data classification,” IEEE Access, vol. 7, pp. 169029–169037, 2019. [Google Scholar]

 6.  A. Kalantari, A. Kamsin, S. Shamshirband, A. Gani, H. A. Rokny et al., “Computational intelligence approaches for classification of medical data: State-of-the-art, future challenges and research directions,” Neurocomputing, vol. 276, no. 2, pp. 2–22, 2018. [Google Scholar]

 7.  R. Tang and X. Zhang, “CART Decision tree combined with boruta feature selection for medical data classification,” in 2020 5th IEEE Int.Conf. on Big Data Analytics (ICBDA), Xiamen, China, pp. 80–84, 2020. [Google Scholar]

 8.  M. M. Kodabagi and A. Tikotikar, “Clustering-based approach for medical data classification, concurrency and computation,” Practice and Experience, vol. 31, no. 14, 2019. [Google Scholar]

 9.  V. J. Kadam and S. M. Jadhav, “Optimal weighted feature vector and deep belief network for medical data classification,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 2, pp. 2050006, 2020. [Google Scholar]

10. R. Bania and A. Halder, “R-Ensembler: A greedy rough set based ensemble attribute selection algorithm with kNN imputation for classification of medical data,” Computer Methods and Programs in Biomedicine, vol. 184, no. 4, pp. 105122, 2020. [Google Scholar]

11. F. Khademi, M. Rabbani, H. Motameni and E. Akbari, “A weighted ensemble classifier based on WOA for classification of diabetes,” Neural Computing and Applications, vol. 25, pp. 3892–3913, 2021. [Google Scholar]

12. C. S. Kumar and P. Thangaraju, “Optimal feature subset selection method for improving classification accuracy of medical datasets,” Annals of the Romanian Society for Cell Biology, vol. 25, no. 2, pp. 3892–3913, 2021. [Google Scholar]

13. M. Abdar, M. A. Fahami, S. Chakrabarti, A. Khosravi, P. Pławiak et al., “BARF: A new direct and cross-based binary residual feature fusion with uncertainty-aware module for medical image classification,” Information Sciences, vol. 577, no. 11, pp. 353–378, 2021. [Google Scholar]

14. C. Mallika and S. Selvamuthukumaran, “A hybrid crow search and grey wolf optimization technique for enhanced medical data classification in diabetes diagnosis system,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 157, 2021. [Google Scholar]

15. X. Song, B. Qin and F. Xiao, “FR-KDE: A hybrid fuzzy rule-based information fusion method with its application in biomedical classification,” International Journal of Fuzzy Systems, vol. 23, no. 2, pp. 392–404, 2021. [Google Scholar]

16. M. Dehghani, S. Hubálovský and P. Trojovský, “Cat and mouse based optimizer: A new nature-inspired optimization algorithm,” Sensors, vol. 21, no. 15, pp. 5214, 2021. [Google Scholar]

17. P. Mohapatra, S. Chakravarty and P. K. Dash, “Microarray medical data classification using kernel ridge regression and modified cat swarm optimization based gene selection system,” Swarm and Evolutionary Computation, vol. 28, no. Suppl. 8, pp. 144–160, 2016. [Google Scholar]

18. https://archive.ics.uci.edu/ml/datasets.php. [Google Scholar]

19. L. Shen, H. Chen, Z. Yu, W. Kang, B. Zhang et al., “Evolving support vector machines using fruit fly optimization for medical data classification,” Knowledge-Based Systems, vol. 96, no. 3, pp. 61–75, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.