Computer Systems Science & Engineering DOI:10.32604/csse.2023.026254
Article

Multi-attribute Group Decision-making Based on Hesitant Bipolar-valued Fuzzy Information and Social Network

Dhanalakshmi R1, Sovan Samanta2, Arun Kumar Sivaraman3, Jeong Gon Lee4,*, Balasundaram A5, Sanamdikar Sanjay Tanaji6 and Priya Ravindran7

1Department of Computer Science and Engineering, KCG College of Technology, Chennai, 600097, Tamil Nadu, India
2Department of Mathematics, Tamralipta Mahavidyalaya, West Bengal, 721636, India
3School of Computer Science and Engineering, Vellore Institute of Technology, Chennai, 600127, Tamil Nadu, India
4Division of Applied Mathematics, Wonkwang University, Iksan-Si, Jeonbuk, 54538, Korea
5School of Computer Science and Engineering, Center for Cyber Physical Systems, Vellore Institute of Technology, Chennai, 600127, Tamil Nadu, India
6Department of Instrumentation Engineering, PDEAs College of Engineering, Manjari, 412307, Pune, India
7Engineering and Research Services, HCL Technologies, Chennai, 600119, India
*Corresponding Author: Jeong Gon Lee. Email: jukolee@wku.ac.kr
Received: 20 December 2021; Accepted: 27 February 2022

Abstract: Fuzzy sets have undergone several expansions and generalisations in the literature, including Atanasov’s intuitionistic fuzzy sets, type 2 fuzzy sets, and fuzzy multisets, to name a few. They can be regarded as fuzzy multisets from a formal standpoint; nevertheless, their interpretation differs from the two other approaches to fuzzy multisets that are currently available. Hesitating fuzzy sets (HFS) are very useful if consultants have hesitation in dealing with group decision-making problems between several possible memberships. However, these possible memberships can be not only crisp values in [0,1], but also interval values during a practical evaluation process. Hesitant bipolar valued fuzzy set (HBVFS) is a generalization of HFS. This paper aims to introduce a general framework of multi-attribute group decision-making using social network. We propose two types of decision-making processes: Type-1 decision-making process and Type-2 decision-making process. In the Type-1 decision-making process, the experts’ original opinion is proces for the final ranking of alternatives. In Type-2 decision making processs, there are two major aspects we consider. First, consistency tests and checking of consensus models are given for detecting that the judgments are logically rational. Otherwise, the framework demands (partial) decision-makers to review their assessments. Second, the coherence and consensus of several HBVFSs are established for final ranking of alternatives. The proposed framework is clarified by an example of software packages selection of a university.

Keywords: Group decision-making; aggregation operators; hesitant bipolar-valued fuzzy set

1  Introduction

After introducing fuzzy set theory, the number of generalizations is proposed. Hesitant fuzzy set (HFS) demonstrates a number of advantages over the classic fuzzy set and its numerous expansions, particularly when used in group decision making under the condition of anonymity. The HFS has drawn the interest of a large number of academics. Actual multi-criteria decision-making (MCDM) approaches currently in use produce potentially problematic and untrustworthy outcomes. These methods frequently overlook the issues of uncertainty and the rank reversal paradox, which are fundamental and essential barriers to using MCDM techniques. The Characteristic Objects Method (COMET) was created in response to these difficulties. Despite the fact that it is immune to the rank reversal paradox, classical COMET is not intended for use in uncertain, decisional situations. In this research, we propose to use hesitant fuzzy set (HFS) theory to extend COMET’s capabilities. Hesitant fuzzy set theory is a powerful tool for expressing uncertainty from an expert comparing characteristic objects and identifying membership functions for each criterion domain. It is a powerful tool for expressing uncertainty from an expert comparing characteristic objects and identifying membership functions for each criterion domain. Researchers [1–5] introduced the notion of HFS and established the concepts of complement, union, and intersection of HFSs for the first time. To further elaborate on this point, the authors offered an extension concept that allowed the current operations on fuzzy sets to be generalised to HFSs and a description of how this new type of set was applied in the context of decision-making. HFS is a set of membership values in [0,1] . That is considered positive information. In [3–7], authors pointed out that any opinion may be considered two parts; one is their positive part, and other is the negative part. But it does not necessarily mean the negative part strictly complements the positive part. Bipolar fuzzy sets are an extension of fuzzy sets. The concept that underpins such a description has to do with the existence of “bipolar information” (for example, positive and negative information) regarding the provided set of data. When it comes to information, positive information reflects what is acknowledged as possible, while negative information represents what is acknowledged as impossible. It is actually true that human decision-making is founded on double-sided or bipolar judgemental thinking, which can be both positive and negative in nature. Examples of such opposing viewpoints include: collaboration and competition, friendliness and animosity, common interests and conflict of interests, effect and side effect, likelihood and unlikelihood, feedforward and feedback, and so on. The terms “yin” and “yang” are used to describe the two opposing sides of traditional Chinese medicine (TCM). The feminine or negative side of a system is represented by yin, and the masculine or positive side of a system is represented by ying. For the mental and physical health of an individual as well as for the stability and prosperity of a social system, it is believed that coexistence, equilibrium, and harmony between the two sides are essential.

As a result, bipolar fuzzy sets can have significant implications in a wide range of fields, including artificial intelligence, computer science, information science, cognitive science, decision science, management science, economics, neural science, quantum computing, and medical and social science. In recent years, bipolar fuzzy sets appear to have been explored and implemented with a certain amount of enthusiasm and increasing frequency. For that reason, authors [8–11] introduced a bipolar-valued fuzzy set (BVFS), where the positive part is considered in [0,1] , and the negative part is considered in [−1,0] . In [12], the authors proposed a hesitant bipolar-valued fuzzy set (HBVFS), which is a generalization of HFS and BVFS. In this paper, we carry out the work by proposing two types of multi-attribute decision-making approaches. Type-1 multi-attribute decision-making approach discussed in the algorithm with a numerical example. Selection of a software package of a university is discussed in this type of decision-making. In Type-2 decision-making, we propose a general framework with a figure. Readers can look in for recent papers [13–16].

This text is remembered in the following way: Section 2 provides fundamental HBVFS principles. Section 3 offers an example of the Type-1 decision-making mechanism with multiple attributes. Section 4 outlines the general context for Type-2 decision-making. Section 5 provides deference between Type-1 and Type-2 decision-making process. The conclusion is given in Section 5.

2  Literature Review

Definition 1. A HBVFS H on a reference set X is defined as

H={⟨x,hH(x)=(hHP(x),hHN(x))⟩|x∈X}, (1)

where hHP(x)∈[0,1] and hHP(x)∈[−1,0] are called hesitant fuzzy positive and negative elements (HFPE) to the set H , respectively. hH(x)=(hHP(x),hHN(x))∈[0,1]×[−1,0] is called the hesitant bipolar-valued fuzzy element (HBVFE) to the set H . In this paper, we use h=(hP,hN) instead of hH(x)=(hHP(x),hHN(x)) .

Definition 2. Let hi=(hiP,hiN) , (i=1,2) be the HBVFEs, then

(1) Complement: h1c=(⋃αP∈hP{1−αP},⋃αN∈hN{−1−αN}) .

(2) Union: h1∪ h2=(⋃α1P∈h1P,α2P∈h2Pmax{α1,α2},⋃α1N∈h1N,α2N∈h2Nmin{α1,α2}) .

(3) Intersection: h1 ∩ h2=(⋃α1P∈h1P,α2P∈h2Pmin{α1,α2},⋃α1N∈h1N,α2N∈h2Nmax{α1,α2}) .

(4) Algebraic sum:

h1⊕h2=(⋃α1P∈h1P,α2P∈h2P{α1+α2−α1α2},⋃α1N∈h1N,α2N∈h2N{α1+α2+α1α2}).

(5) Algebraic product:

h1⊗h2=(⋃α1P∈h1P,α2P∈h2P{α1α2},⋃α1N∈h1N,α2N∈h2N{−α1α2}).

Definition 3. The score of a HBVFE h=(hP,hN) is denoted by s(h) and defined as follows:

s(h)=12(1lhP∑αP∈ hPαP− 1lhN∑αN∈ hNαN)(2)

where lhP and lhN are the cardinality of hP and hN , respectively.

Let h1 and h2 be the HBVFEs. Then, h1<h2 , if s(h1)<s(h2) and h1=h2 , if s(h1)=s(h2) .

Definition 4. Let w=(w1,w2,⋯,wn)T be the corresponding weight vector of the collection of HBVFEs hj=(hjP,hjN)(j=1,2,⋯,n) such that wj∈[0,1] , ∑j=1nwj=1 and λ>0 . Then the two aggregation operators named hesitant bipolar-valued fuzzy weighted averaging and geometric operators denoted by GHBVFWA and GHBVFWG is defined in the following way:

(1) GHBVFWA:Hn↦H , where

GHBVFWAλ(h1,h2,⋯,hn)=⊕j=1n(wjhjλ)1λ

=(⋃α1P∈h1P,α2P∈h2P,⋯,αnP∈hnP{(1−∏j=1n(1−(αjP)λ)wj)1λ},⋃α1N∈h1N,α2N∈h2N,⋯,αnN∈hnN{(−1+∏j=1n(1+(αjN)λ)wj)1λ}).

(2) GHBVFWG:Hn↦H , where

GHBVFWGλ(h1,h2,⋯,hn)=1λ(⊗j=1n(λhj)wj)

=(⋃α1P∈h1P,α2P∈h2P,⋯,αnP∈hnP{1−(∏j=1n(1−(1−αjP)λ)wj)1λ},⋃α1N∈h1N,α2N∈h2N,⋯,αnN∈hnN{−1+(1−∏j=1n(1−(1+αjN)λ)wj)1λ}).

3  Type-1: HBVFSs Based Group Decision-making

Throughout this section, we offer an algorithm for decision-making multi-attributes community based on HBVFS and social networks. In the following first, we describe the problem and then list the steps how to solve this problem.

Problem Description: Let X={x1,x2,⋯,xm} and C={c1,c2,⋯,cn} be the set of alternatives and the set of criteria/attribute. We assume that the set of experts denoted by E={e1,e2,⋯,ek} , are invited for evaluation of the alternatives with respect to the corresponding criteria set.

The steps are listed in the following:

Step 1: Each experts or decision makers interacting each others using social network and then provide their performance with respect to either bipolar-valued fuzzy value [17–20] or fuzzy value [21].

Step 2: After interacting experts through social network, they decide the wight of the attributes. Let us assume that w=(w1,w2,⋯,wm)T be the weight of attribute such that ∑j=1nwj=1 .

Step 3: After receiving the evaluation of all experts we now perform the resultant evaluation hesitant bipolar-valued fuzzy matrix by the union of positive and negative information. For example, suppose experts e1 and e2 given the judgement x1 with respect to c1 are {0.6} and ({0.3},{−0.2}) , respectively. Then the HBVFEs x1 with respect to c1 is ({0.6,0.3},{−0.2}) . Let D=(hij)m×n be the construct hesitant bipolar-valued decision matrix, where hij=(hijP,hijN) (i=1,2,⋯,m;j=1,2,⋯,n) .

Step 4: Using the aggregation operators defined in Definition 4 to obtain the HBVFEs hi=(hiP,hiN) for the alternative xi (i=1,2,⋯,m) . For example if we use GHBVFWA operator, then

hi=GHBVFWAλ(hi1,hi2,⋯,hin)=⊕j=1n(wjhijλ)1λ

=(⋃αi1P∈hi1P,αi2P∈hi2P,⋯,αinP∈hinP{(1−∏j=1n(1−(αijP)λ)wj)1λ},⋃αi1N∈hi1N,αi2N∈hi2N,⋯,αnN∈hinN{(−1+∏j=1n(1+(αijN)λ)wj)1λ}),

where i=1,2,⋯,n .

Step 5: Using Definition 3, obtain the score values of hi , i.e., s(hi) (i=1,2,⋯,m) .

Step 6: Comparing the priority of options hi by ranking s(hi) (i=1,2,⋯,m) .

The general process of Type-1 decision making is display in Fig. 1.

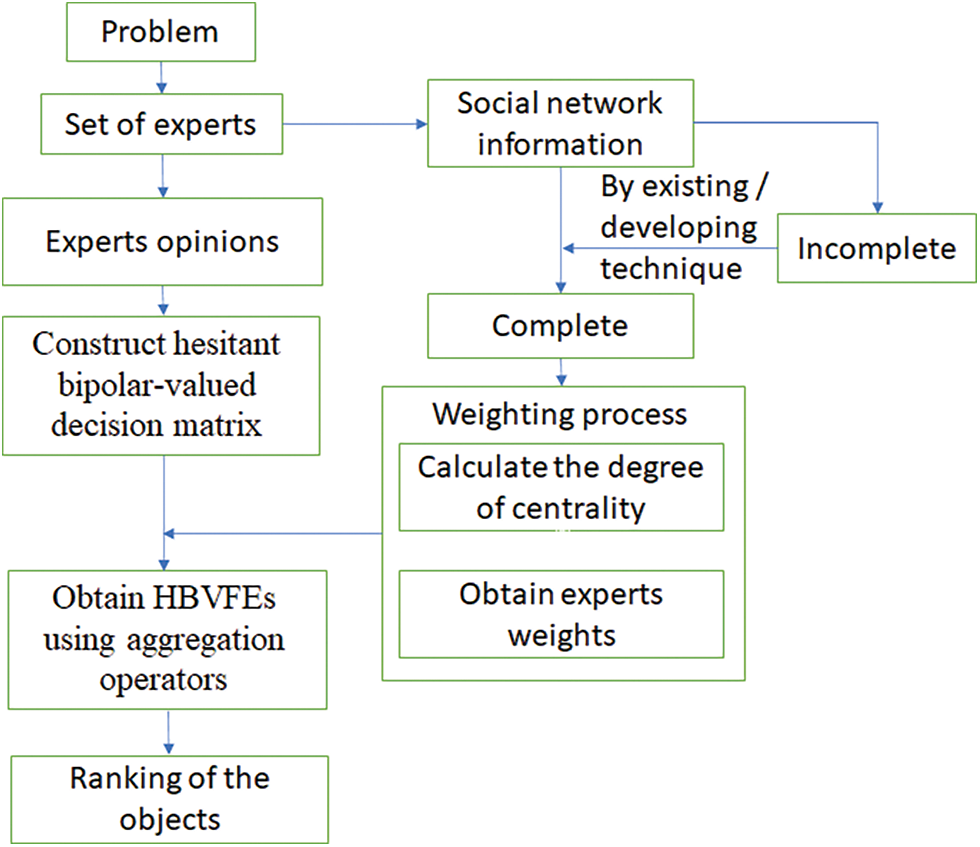
Figure 1: Type-1 decision-making process

By a realistic example discussed in [22–29], we further explain the possible application of the generation in this report.

Example 1. A university data center prepares a new information system to be chosen and purchased to increase its work efficiency. Software packages to be chosen are the alternatives here. The four characteristics under consideration are the following criteria: (1) budget cost savings (c1) ; (2) organizational output contribution (c2) ; (3) efforts to move from existing structures (c3) ; and (4) developer product reliability outsourcing (c4) . Four alternatives xj (j=1,2,3,4) remain in the applicant list after the preliminary screening. Four experts ek (j=1,2,3,4) , each with the same weight is entitled to serve as decision-makers and assess four attributes choices. Each experts interact through social network shown in Fig. 2. and then decided the weight of the attribute and the assessment of alternatives.

Figure 2: The experts interaction network

The attribute weights are w=(w1=0.35,w2=0.15,w3=0.2,w4=0.3) and the assessment of alternative is shown in Tabs. 1–4 as bipolar fuzzy sets or fuzzy sets.

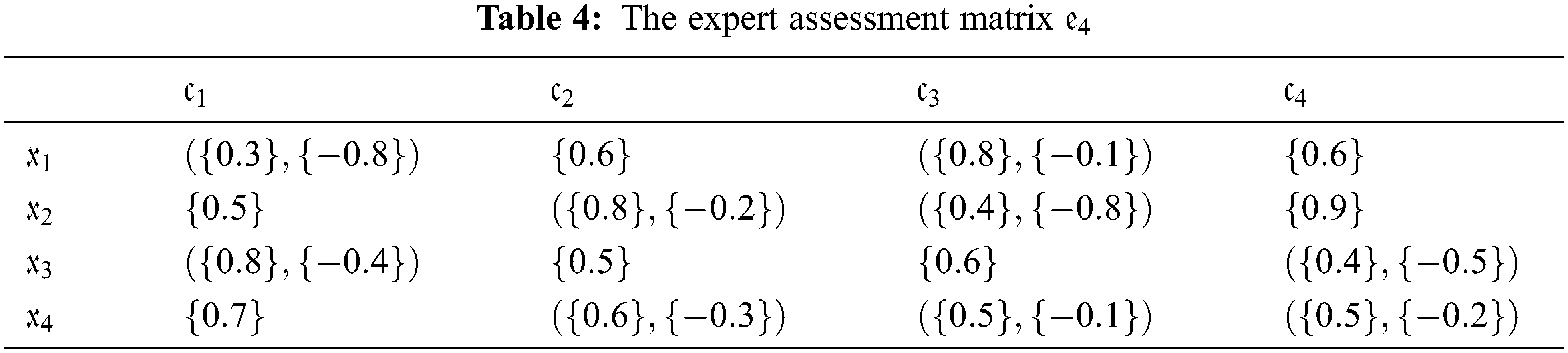
From Tabs. 1–4, we construct hesitant bipolar-valued decision matrix is shown in Tab. 5.

Using GHBVFA operator to calculate the GHBVFEs hi (i=1,2,3,4) for the alternatives xi (i=1,2,3,4) . For example we only display the calculation of x3 and λ=1 , then we have

h3=HBVFWA(h31,h32,h33,h34)=⊕j=14(wjh3j)

=(⋃α31P∈h31P,α32P∈h32P,α33P∈h33P,α34P∈h34P{1−∏j=14(1−α3jP)wj},⋃α31N∈h31N,α32N∈h32N,α33N∈h33N,α34N∈h34N{−1+∏j=14(1+α3jN)wj})

=(⋃α31P∈{0.8,0.9,0.7},α32P∈{0.7,0.5,0.6},α33P∈{0.4,0.5,0.6},α34P∈{0.4,0.6}{1−∏j=14(1−α3jP)wj},⋃α31N∈{−0.4−0.2},α32N∈{−0.2,−0.1},α33N∈{−0.4,−0.6},α34N∈{−0.2,−0.5}{−1+∏j=14(1+α3jN)wj})

=({0.6740,0.6319,0.6857,0.6450,0.6994,0.6605,0.6481,0.6026,0.6607,0.6168,0.6755,0.6335,0.6597,0.6156,0.6718,0.6294,0.6862,0.6456,0.7442,0.7112,0.7534,0.7215,0.7642,0.7337,0.7239,0.6882,0.7338,0.6993,0.7454,0.7125,0.7330,0.6984,0.7425,0.7092,0.7538,0.7219,0.6243,0.5757,0.6378,0.5909,0.6536,0.6088,0.5944,0.5419,0.6089,0.5584,0.6260,0.5776,0.6078,0.5570,0.6218,0.5729,0.6383,0.5915},{−0.3171,−0.4069,−0.3703,−0.4531,−0.3049,−0.3963,−0.3590,−0.4433,−0.2447,−0.3441,−0.3036,−0.3951,−0.2313,−0.3324,−0.2911,−0.3844)}.

With the changes in the parameter λ we can get various results for individual alternatives. obtain the score values s(hi) (i=1,2,3,4) by Definition 3. Tab. 6 displays the score values for the choices.

The ranking of the alternatives established by the values of s(hi (i=1,2,3,4) are shown in Tab. 6 for various λ . When we use GHBVFWG operator to add option values instead of GHBVFWA operator, the score values with alternatives rankings are shown in Tab. 7.

It should be noted that if the parameter λ changes, the rating of the alternatives will change. However, the preference choice x3 is by evaluating Tabs. 6 and 7. Here, we can only determine the outcome and judge which one is more acceptable in relation to what is given as possible and what is considered impossible under the given attributes. Since one key parameter is included in our proposed process, we successively examine the parameter’s effect in this example, which is shown in Fig. 3.

Figure 3: Comparison of score values of the alternatives with different λ obtained by the GHBVFWA and GHBVFWG operators

The Fig. 3. we are discussing five cases of λ . Given the values of λ , there can be found a growing pattern of score values achieved by GHBVFWA operators in regard to the alternatives xi (i=1,2,3,4) , and an increase of λ . Where the GHBVFWG operator score values can be found in relation to alternatives, xi xi (i=1,2,3,4) continues to deteriorate with the rise of λ .

The approach discussed in [30–35] is only considered a set of positive information. But our approach is considered positive information as well as at the same time negative information.

4  Type-2: Decision Making Based on HBVFS

The estimation of decision-making is nuanced in the complexity of the real-life problem and increases in line with the number of alternatives and parameters. Therefore, the measurement process involves decision-making. The framework incorporates the specifics of theoretical models. Decision-making [36] is a class of information-based systems which support decision-making, among other systems. Many studies concentrate on developing decision-making for various ideas, methods or implementations. To improve the group’s overall satisfaction level and overcome confusion during the decision. Researchers [37–39] have built a flippant, multi-criteria decision making and established their respective decisions as solutions to multi-criteria decision-making problems. With the exception of approaches based on fuzzy set theories and many other techniques such as fuzzy measures can also be used to construct decision-making, such as technique of information management, game theory, and artificial intelligence techniques.

Similarly, we suggest a decision-making process in this section to demonstrate how the HBVFS will help community decision making. As seen in Fig. 4. decision-makers communicate with the decision-making mechanism through the Social Network Platform in a community or many groups. The Knowledge Base is used by HBVFSs or their special cases to enable decision-makers to perform their assessments. Any valuable information is retained through Social Network Platform, such as comparable previous instances, the corresponding membership degree of linguistic speech. HBVFSs represent the decision table of a final result is also generated by the system when evaluations are ready. There are two major aspects to the roles of the Model Base. First, consistency tests and checking of consensus models are given for detecting that the judgments are logically rational. Otherwise, the framework demands (partial) decision-makers to review their assessments. Since the latter study established the coherence and consensus of several HBVFSs, we omitted this interaction in Fig. 4.

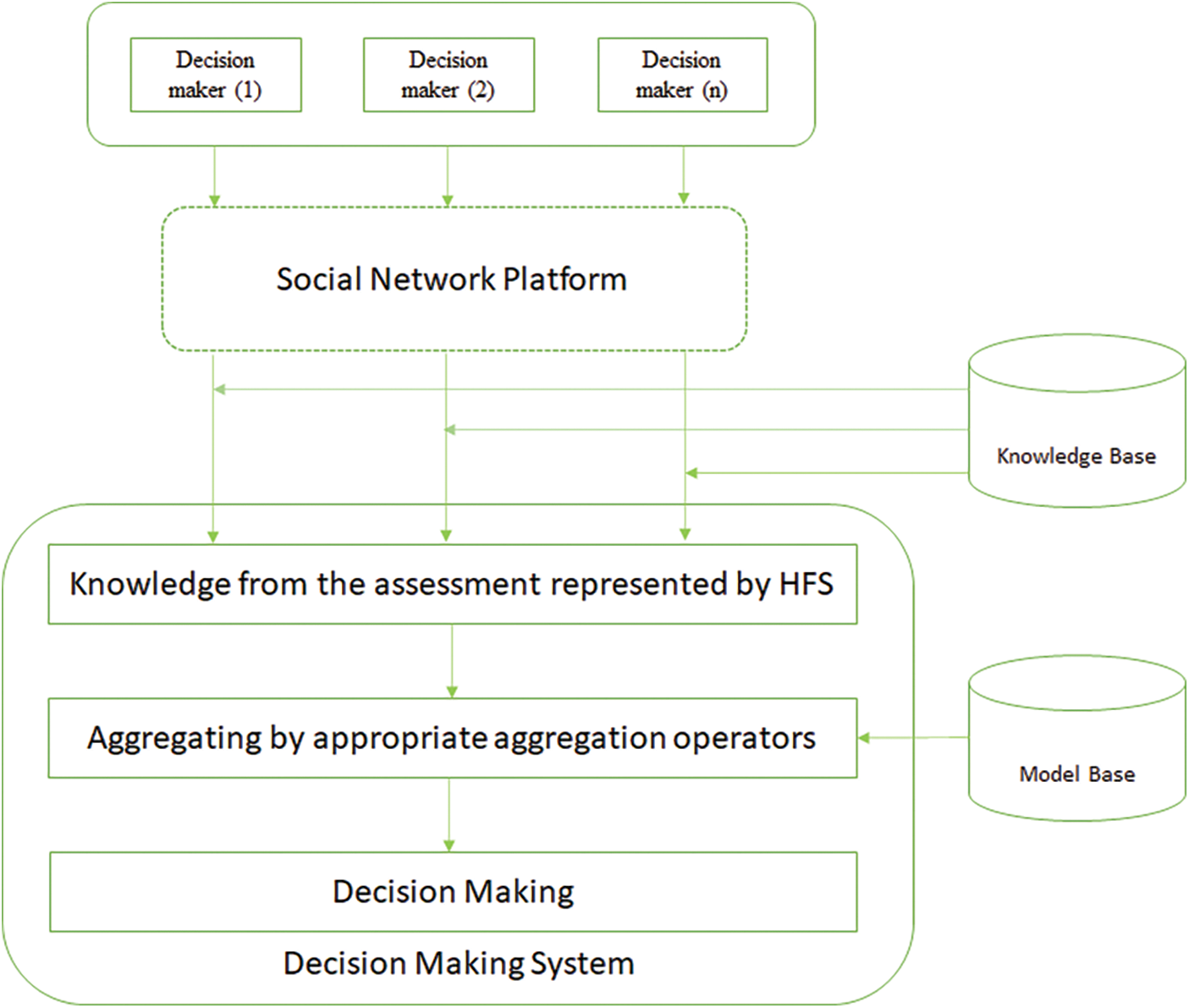
Figure 4: Type-2 decision-making process

The system will add up the assessment according to the expansion principle by selecting individual model HBVFS aggregates according to the choice of decision-makers. Finally, the overall acceptable levels of the alternatives are determined. Then the priority is obtained, and the comparison law provided in Definition 3 will make the final decision. What decision-makers need to do in this framework is to provide fair and reasonable judgments. The framework uses HBVFSs to quantify the assessment’s uncertainties and produce the final decision.

5  Relation and Difference between Type-1 and Type-2 Decision-making

In the Type-1 decision-making process, the experts’ original opinion’s is proces for final ranking of alternatives. In Type-2 decision-making processs, first checking consistency of experts original opinion’s. If the experts’ opinions are consistent, then we process their opinions—otherwise, we advise the experts to change their opinions according to advised rule. The consistency tests and checking of all experts’ opinions are complete, then process their opinions for final ranking of alternatives.

6  Conclusion

We suggested in this paper two forms of HBVFS decision-making. It has the desired characteristics and its advantages and seems to be a more versatile approach to be evaluated according to realistic requirements than current generalizations of HFSs and takes far more data (not only taking into account positive information, but negative information) from decision-making. The approach can be reduced to some established approaches. In this sense, decision-makers should state their values in respect to what is granted and those decision-makers should give their values in relation to the options given in the attributes concerned which are considered impossible. Two types of decision making process is propoesed. Type-1 decision making is considered without consistency of experts opinion’s and Type-2 decision-making process consider with the consistency of experts opinion’s. In future the theories can be developed to implement large scale data to solve real network problems.

Acknowledgement: The authors wish to express their thanks to one and all who supported them during this work.

Funding Statement: This paper was supported by Wonkwang University in 2022.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Mandal and A. S. Ranadive, “Hesitant bipolar-valued fuzzy sets and bipolar-valued hesitant fuzzy sets and their applications in multi-attribute group decision making,” Granular Computing, vol. 4, no. 3, pp. 559–586, 2018. [Google Scholar]

 2.  S. Samanta, V. K. Dubey and B. Sarkar, “Measure of in uences in social networks,” Applied Soft Computing, vol. 99, no. 1, pp. 106858–106875, 2021. [Google Scholar]

 3.  M. Akram, A. Bashir and S. Samanta, “Complex pythagorean fuzzy planar graphs,” International Journal of Applied and Computational Mathematics, vol. 6, no. 3, pp. 1–27, 2020. [Google Scholar]

 4.  K. Das, S. Samanta and K. De, “Generalized neutrosophic competition graphs,” Neutrosophic Sets and Systems, vol. 31, pp. 156–171, 2020. [Google Scholar]

 5.  R. Gayathri, R. Vincent, M. Rajesh, A. K. Sivaraman and A. Muralidhar, “Web-acl based dos mitigation solution for cloud,” Advances in Mathematics: Scientific Journal, vol. 9, no. 7, pp. 5105–5113, 2020. [Google Scholar]

 6.  M. Akram, A. Sattar, F. Karaaslan and S. Samanta, “Extension of competition graphs under complex fuzzy environment,” Complex & Intelligent Systems, vol. 7, no. 1, pp. 539–558, 2021. [Google Scholar]

 7.  S. Samanta and B. Sarkar, “A study on generalized fuzzy graphs,” Journal of Intelligent & Fuzzy Systems, vol. 35, no. 3, pp. 3405–3412, 2018. [Google Scholar]

 8.  B. Sarkar and S. Samanta, “Generalized fuzzy trees,” International Journal of Computational Intelligence Systems, vol. 10, no. 1, pp. 711–720, 2017. [Google Scholar]

 9.  A. Shashank, R. Vincent, A. K. Sivaraman, A. Balasundaram, M. Rajesh et al., “Power analysis of household appliances using IoT,” in Int. Conf. on System, Computation, Automation and Networking (ICSCANIEEE Xplore, Puducherry, India, pp. 1–5, 2021. [Google Scholar]

10. S. Samanta and B. Sarkar, “Isomorphism on generalized fuzzy graphs and image visualizations,” Soft Computing, vol. 24, no. 19, pp. 14401–14409, 2020. [Google Scholar]

11. S. Samanta and B. Sarkar, “Generalized fuzzy euler graphs and generalized fuzzy hamiltonian graphs,” Journal of Intelligent & Fuzzy Systems, vol. 35, no. 3, pp. 3413–3419, 2018. [Google Scholar]

12. M. Ganga, N. Janakiraman, A. K. Sivaraman, A. Balasundaram, R. Vincent et al., “Survey of texture based image processing and analysis with differential fractional calculus methods,” in Int. Conf. on System, Computation, Automation and Networking (ICSCANIEEE Xplore, Puducherry, India, pp. 1–6, 2021. [Google Scholar]

13. D. Kothandaraman, A. Balasundaram, R. Dhanalakshmi, A. K. Sivaraman, S. Ashokkumar et al., “Energy and bandwidth based link stability routing algorithm for IoT,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3875–3890, 2021. [Google Scholar]

14. R. Sornalatha, N. Janakiraman, K. Balamurugan, A. K. Sivaraman, R. Vincent et al., “FPGA implementation of protected compact AES S-box using CQCG for embedded applications,” in Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology), vol. 38, Amsterdam: IOS Press, pp. 396–401, 2021. [Google Scholar]

15. M. Ganga, N. Janakiraman, A. K. Sivaraman, R. Vincent, A. Muralidhar et al., “An effective denoising and enhancement strategy for medical image using Rl-Gl-caputo method,” in Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology), vol. 38, Amsterdam: IOS Press, pp. 402–408, 2021. [Google Scholar]

16. K. Kalpana, B. Paulchamy, R. Priyadharsini, A. K. Sivaraman, R. Vincent et al., “Design and performance analysis of low power high speed adder and multiplier using MTCMOS in 90nm, 70nm, 25nm and 18nm regime,” in Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology), vol. 38, Amsterdam: IOS Press, pp. 409–416, 2021. [Google Scholar]

17. P. Mandal, S. Samanta and M. Pal, “Multiplicative consistency analysis of linguistic preference relation with self-confidence level and self-doubting level and its application in a group decision making,” International Journal of Intelligent Systems, vol. 36, no. 10, pp. 5389–5418, 2021. [Google Scholar]

18. P. Mandal, S. Samanta and M. Pal, “Large-scale group decision-making based on pythagorean linguistic preference relations using experts clustering and consensus measure with non-cooperative behavior analysis of clusters,” Complex & Intelligent Systems, vol. 16, no. 3, pp. 273–289, 2021. [Google Scholar]

19. R. Priya, S. Jayanthi, A. K. Sivaraman, R. Dhanalakshmi, A. Muralidhar et al., “Proficient mining of informative gene from microarray gene expression dataset using machine intelligence,” in Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology), vol. 38, Amsterdam: IOS Press, pp. 417–422, 2021. [Google Scholar]

20. P. Mandal, S. Samanta, M. Pal and A. S. Ranadive, “Pythagorean linguistic preference relations and their applications to group decision making using group recommendations based on consistency matrices and feedback mechanism,” International Journal of Intelligent Systems, vol. 35, no. 5, pp. 826–849, 2020. [Google Scholar]

21. A. Karpatne, G. Atluri, J. H. Faghmous, M. Steinbach, A. Banerjee et al., “Theory-guided data science: A new paradigm for scientific discovery from data,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 10, pp. 2318–2331, 2017. [Google Scholar]

22. P. Arunachalam, N. Janakiraman, A. K. Sivaraman, A. Balasundaram, R. Vincent et al., “Synovial sarcoma classification technique using support vector machine and structure features,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1241–1259, 2021. [Google Scholar]

23. E. J. Kieling, F. C. Rodrigues, A. Filippetto and J. Barbosa, “Smartalloc: A model based on machine learning for human resource allocation in projects,” in Proc. of the 25th Brazillian Symp. on Multimedia and the Web, Rio de Janeiro, Brazil, pp. 365–368, 2019. [Google Scholar]

24. A. Balasundaram, G. Dilip, M. Manickam, A. K. Sivaraman, K. Gurunathan et al., “Abnormality identification in video surveillance system using DCT,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 693–704, 2021. [Google Scholar]

25. R. Gayathri, A. Magesh, A. Karmel, R. Vincent and A. K. Sivaraman, “Low cost automatic irrigation system with intelligent performance tracking,” Journal of Green Engineering, vol. 10, no. 12, pp. 13224–13233, 2020. [Google Scholar]

26. P. M. Tagade, S. P. Adiga, S. Pandian, M. S. Park, K. S. Hariharan et al., “Attribute driven inverse materials design using deep learning Bayesian framework,” Computational Materials, vol. 5, no. 1, pp. 1–14, 2019. [Google Scholar]

27. A. Q. Md, D. Agrawal, M. Mehta, A. K. Sivaraman and K. F. Tee, “Time optimization of unmanned aerial vehicles using an augmented path,” Future Internet, MDPI, vol. 13, no. 12, pp. 1–13, 2021. [Google Scholar]

28. T. Wang, C. Rudin, F. Doshi-Velez, Y. Liu, E. Klampfl et al., “A bayesian framework for learning rule sets for interpretable classification,” The Journal of Machine Learning Research, vol. 18, no. 1, pp. 2357–2393, 2017. [Google Scholar]

29. L. Yang, X. Meng and G. E. Karniadakis, “B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data,” Journal of Computational Physics, vol. 425, pp. 232–246, 2021. [Google Scholar]

30. B. Hu, P. Ning, Y. Li, C. Xu and G. Christakos, “Space-time disease mapping by combining bayesian maximum entropy and kalman filter: The BME-kalman approach,” International Journal of Geographical Information Science, vol. 35, no. 3, pp. 466–489, 2021. [Google Scholar]

31. R. Vincent, P. Bhatia, M. Rajesh, A. K. Sivaraman and M. S. S. Al Bahri, “Indian currency recognition and verification using transfer learning,” International Journal of Mathematics and Computer Science, vol. 15, no. 4, pp. 1279–1284, 2020. [Google Scholar]

32. R. Bantan, A. S. Hassan, E. Almetwally, M. Elgarhy and F. Jamal, “Bayesian analysis in partially accelerated life tests for weighted lomax distribution,” Computers, Materials & Continua, vol. 68, no. 3, pp. 2859–2875, 2021. [Google Scholar]

33. S. Samanta, G. Muhiuddin, A. M. Alanazi and K. Das, “A mathematical approach on representation of competitions: Competition cluster hypergraphs,” Mathematical Problems in Engineering, vol. 16, no. 7, pp. 1–10, 2020. [Google Scholar]

34. A. Balasundaram, M. Naveen Kumar, A. K. Sivaraman, R. Vincent and M. Rajesh, “Mask detection in crowded environment using machine learning,” in Int. Conf. on Smart Electronics and Communication (ICOSEC), IEEE Xplore, Trichy, India, pp. 1202–1206, 2021. [Google Scholar]

35. A. Maity, K. Das, S. Samanta, S. Mondal and V. Dubey, “A study of cluster hypergraphs and its properties,” Social Network Analysis and Mining, vol. 11, no. 1, pp. 1–14, 2021. [Google Scholar]

36. S. Samanta, V. K. Dubey and B. Sarkar, “Measure of influences in social networks,” Applied Soft Computing, vol. 99, no. 5, pp. 106858, 2021. [Google Scholar]

37. Z. Ali, T. Mahmood, K. Ullah and Q. Khan, “Einstein geometric aggregation operators using a novel complex interval-valued pythagorean fuzzy setting with application in green supplier chain management,” Reports in Mechanical Engineering, vol. 2, no. 1, pp. 105–134, 2021. [Google Scholar]

38. M. Riaz, N. Cagman, N. Wali and A. Mushtaq, “Certain properties of soft multi-set topology with applications in multi-criteria decision making,” Decision Making: Applications in Management and Engineering, vol. 3, no. 2, pp. 70–96, 2020. [Google Scholar]

39. R. Sahu, S. R. Dash and S. Das, “Career selection of students using hybridized distance measure based on picture fuzzy set and rough set theory,” Decision Making: Applications in Management and Engineering, vol. 4, no. 1, pp. 104–126, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.