DOI:10.32604/csse.2023.028083

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.028083 |  |
| Article |
An Ordinal Multi-Dimensional Classification (OMDC) for Predictive Maintenance
Izmir Bakircay University, Department of Computer Engineering, Izmir, 35665, Turkey
*Corresponding Author: Pelin Yildirim Taser. Email: pelin.taser@bakircay.edu.tr
Received: 02 February 2022; Accepted: 04 March 2022
Abstract: Predictive Maintenance is a type of condition-based maintenance that assesses the equipment's states and estimates its failure probability and when maintenance should be performed. Although machine learning techniques have been frequently implemented in this area, the existing studies disregard to the natural order between the target attribute values of the historical sensor data. Thus, these methods cause losing the inherent order of the data that positively affects the prediction performances. To deal with this problem, a novel approach, named Ordinal Multi-dimensional Classification (OMDC), is proposed for estimating the conditions of a hydraulic system's four components by taking into the natural order of class values. To demonstrate the prediction ability of the proposed approach, eleven different multi-dimensional classification algorithms (traditional Binary Relevance (BR), Classifier Chain (CC), Bayesian Classifier Chain (BCC), Monte Carlo Classifier Chain (MCC), Probabilistic Classifier Chain (PCC), Classifier Dependency Network (CDN), Classifier Trellis (CT), Classifier Dependency Trellis (CDT), Label Powerset (LP), Pruned Sets (PS), and Random k-Labelsets (RAKEL)) were implemented using the Ordinal Class Classifier (OCC) algorithm. Besides, seven different classification algorithms (Multilayer Perceptron (MLP), Support Vector Machine (SVM), k-Nearest Neighbour (kNN), Decision Tree (C4.5), Bagging, Random Forest (RF), and Adaptive Boosting (AdaBoost)) were chosen as base learners for the OCC algorithm. The experimental results present that the proposed OMDC approach using binary relevance multi-dimensional classification methods predicts the conditions of a hydraulic system's multiple components with high accuracy. Also, it is clearly seen from the results that the OMDC models that utilize ensemble-based classification algorithms give more reliable prediction performances with an average Hamming score of 0.853 than the others that use traditional algorithms as base learners.
Keywords: Machine learning; multi-dimensional classification; ordinal classification; predictive maintenance
In industrial systems, equipment maintenance dramatically influences an equipment's operation time and efficiency [1]. Predictive Maintenance (PdM), which is one of the maintenance management strategies, monitors the equipment's performance and condition to reduce the probability of failure using predictive tools. The main aim of the PdM is to monitor equipment's condition and estimate the potential equipment failure based on historical data. Thus, it provides preventing equipment failure with regularly scheduled and corrective maintenance.
Machine learning (ML) techniques have been preferred as a powerful predictive tool for maintaining industrial environments in recent years [2]. It discovers hidden patterns within complex and multivariate data where the traditional methods (e.g., statistical inference methods) remain inadequate. In most of the ML-based PdM approaches, Multilayer Perceptron (MLP) [3,4], Convolutional Neural Network (CNN) [5–7], Long Short-term Memory Network (LSTM) [8–10], Support Vector Machine (SVM) [11,12], k-Nearest Neighbour (kNN) [13], Random Forest (RF) [14–17], and Decision Tree [18] were used. For example, Kiangala et al. [5] proposed a novel PdM framework that combines time-series imaging and CNN models to detect a conveyor system's impairments and reduce the risk of incorrect faults. According to the experimental results, the proposed method outperforms the traditional classification approaches. In another study [18], a novel decision support system based on decision trees (DTs) were developed for determining under what circumstances a machine learning-based PdM strategy is economically viable, with the goal of assisting practitioners in making sound decisions.
In addition to these single label predictive maintenance approaches, a few ML-based approaches classify multi-target attributes [19,20]. For example, Last et al. [19] developed a multi-target probability estimation model (M-IFN) to estimate the probability and timing of a failure in each subsystem in a car. In another study [20], a multi-label recurrent neural network model was presented for predicting faults of multi-dimensional time-series data. The proposed approaches in both of these studies give more accurate prediction performances than the conventional solutions. In this study, eleven different multi-dimensional classification (MDC) algorithms (BR, CC, BCC, PCC, MCC, CDN, CT, CDT, LP, PS, and RAKEL algorithms) are preferred for estimating the conditions of a hydraulic system's four components.
In the existing ML-based PdM approaches, it is assumed that there is no inherent natural order between the class values in the experimental data. However, in most real-world scenarios, the experimental datasets' class values have an order relation among them. As shown in the previous studies [21,22], the ordinal classification strategy often outperforms the nominal classification for the datasets consisting of class labels having ordered information. Considering this motivation, a novel approach, named Ordinal Multi-dimensional Classification (OMDC), is proposed for predicting multi-dimensional attributes by taking into the natural order of class values. This approach combines MDC and ordinal classification (OC) paradigms to improve prediction performance. The OMDC is a general approach that can be used for a prediction task in various fields. It was utilized to predict the conditions of a hydraulic system's four components as a case study. In the experiments, the proposed OMDC approach was applied to a well-known and real-world hydraulic system's condition dataset used in many ML-based studies [23–25].
The novelty and main contributions of this article are as follows: (i) This study gives a brief survey of MDC and OC, (ii) It is the first attempt to implement the OC method for predictive maintenance, (iii) It proposes a novel approach, named OMDC, that combines MDC and OC paradigms to improve prediction performance, (iv) This study is also original in that it implements the OMDC approach to classify the conditions of the hydraulic system's four components by considering the relationships between the class values of components, (v) This is also the first study that classifies multiple components of the hydraulic systems, (vi) It implements eleven different MDC algorithms using MLP, SVM, kNN, C4.5, Bagging, RF, and AdaBoost classification algorithms as base learners and compared with each other in terms of Hamming Score, Exact Match, Hamming Loss, and ZeroOne Loss metrics.
ML techniques are generally grouped under two main types: supervised learning and unsupervised learning. Classification, a commonly applied supervised learning method, assigns unlabeled data to predefined classes using an accurate model. The multi-class classification process is divided into two categories: nominal classification and ordinal classification. The nominal classification method assumes that there is no order between the target attribute's class labels. However, in most real-world scenarios, the datasets' class labels can have a natural order. For example, the internal pump leakage of hydraulic systems can be classified as “no leakage”, “weak leakage”, and “severe leakage”. The order among these class labels is stated as “severe leakage” > “weak leakage” > “no leakage”. To deal with this problem, an ordinal classification (OC) paradigm was proposed.
In the OC technique, a new sample's ordinal target value is predicted by considering the predefined classes' ordering relation [26]. The ordinal dataset
The traditional nominal classification algorithms can be used to solve OC problems by ignoring the existing inherent order among the class labels. However, this approach causes losing the natural order of the data that gets more accurate classification performance. To handle this problem, in this study, the Ordinal Class Classifier (OCC) algorithm [27] that converts the OC problem to multiple binary classification problems was preferred for predicting the conditions of four hydraulic components (cooler, valve, internal pump leakage, and hydraulic accumulator). This algorithm converts k different ordinal class labels C1, C2, …, Ck of the ordinal dataset D to binary values regarding their natural order C1 < C2 < ⋅ ⋅ ⋅ < Ck. According to this approach, first, the C1 classes are labeled as 0, and the classes with higher ranking order than
The OCC algorithm requires a base learner for predicting the ordinal-valued target attribute. In this study, MLP, SVM, kNN, C4.5, Bagging, RF, and AdaBoost classification algorithms were preferred as base learners for the OCC algorithm to classify multiple attributes of the experimental dataset.
• MLP: The MLP is a feedforward artificial neural network algorithm that consists of multiple interconnected layers of nodes in a weighted directed graph [28]. There are three types of layers in this algorithm: input layer, output layer, and hidden layer. The sample data is taken from the input layer, processed in the hidden layers as the computational engine, and then classified with a proper label by the output layer.
• SVM: In the SVM algorithm, each instance in the dataset is placed as a point in n-dimensional space, where n is the attribute number [29]. After that, a hyperplane that separates two different classes is constructed to perform the instances' classification. The key point of this approach's success is choosing the hyperplane with maximum margin to avoid overfitting and reducing misclassification results.
• kNN: The kNN classifier is non-parametric and instance-based learning that classifies a new sample with a majority vote of its k nearest neighbors with specific class labels [30]. To determine k nearest neighbors of a new sample, well-known distance metrics in the literature are used, such as Euclidean, Manhattan, Minkowski, etc.
• C4.5: C4.5 is the most commonly preferred decision tree algorithm that is grown using the depth-first strategy with the conjunction of rules [31]. The decision tree includes internal nodes, branches, and leaf nodes representing attributes, attribute values, and classes, respectively. Information gain and entropy metrics are used for the construction of the decision tree in this algorithm.
• Bagging: Bagging is an ensemble learning technique that generates multiple classification models from the multiple training sets created by choosing random and repeatable instances from the original dataset [32]. To classify a new sample using the Bagging method, each model produces an output, and then, these outputs obtained from each model are aggregated to get the single final decision.
• RF: The RF, a bagging-based ensemble classifier, creates a forest consisting of multiple decision trees constructed using a random feature subset selection method [33]. In this approach, the classification process of a new sample is performed by selecting a majority vote of all trees' predictions in the forest.
• AdaBoost: In the AdaBoost algorithm, the classification models are trained consecutively to convert weak learners to strong ones [34]. The algorithm increases the misclassified samples' weight values and decreases the correctly classified ones in each iteration.
2.2 Multi-Dimensional Classification
The traditional classification process, one of the most well-established machine learning paradigms, assumed that a learning task has only one objective (single-label). However, in real-world classification problems, there can be several multiple target attributes (multi-dimensional) that need to be classified. For example, predicting multiple diagnoses of a given patient, text categorization, analysis of nonverbal expressions in speech, etc. These target attributes can be related, semi-related or unrelated to each other. The conventional classification algorithms are not coping well with the multi-dimensional decision-making problems. Therefore, a multi-dimensional classification (MDC) paradigm has emerged as a solution for this problem.
MDC is a subfield of supervised learning that simultaneously predicts multiple target attributes of a given single new sample. Let D =
MDC is a particular case of multi-label classification, where each label contains only binary values representing relevance or not, as opposed to having multiple values. MDC methods are closely related to multi-label classification approaches. Several multi-label classification algorithms in the literature, which apply the problem transformation approach, proposed a solution for MDC problems. In the problem transformation method, multi-dimensional problems are divided into multiple traditional single-label problems. The problem transformation approach is implemented using two standard methods: binary relevance and label powerset.
Binary relevance, one of the widespread methods of the problem transformation approach, trains several multi-class classifiers using a one-against-all strategy. In other words, the MDC problem is converted into multiple multi-class problems. In this study, the traditional BR method (BR) was implemented on the experimental dataset.
• BR: The BR algorithm transforms the MDC problem into several well-established multi-class classification problems [35]. In this method, conventional multiple multi-class classifiers are trained on the dataset independently for predicting each target attribute value. The BR algorithm is commonly preferred in MDC problems because of its simplicity and having linear complexity. However, it is unable to capture the relationships among the target attributes.
The learning system's generalization performance is decreased because of the BR method's ignorance of the correlations between the target attributes. To overcome this problem, the implementation of the BR method with chaining structure is proposed. The target attribute information is passed between classifiers linked in a chain to consider label correlations in the chaining strategy. In this study, the conventional CC algorithm, its different improved versions such as BCC, MCC, PCC, and CDN were used.
• CC: The CC method links multiple multi-class classifiers along with a chaining order where each classifier deals with the binary relevance problem [36]. According to this approach, a multi-class classifier is constructed for each target attribute depending on the predictions of preceding classification models in the chain.
• BCC: The BCC algorithm implements the CC method using Bayesian networks that present the class values' dependency relations [37]. It also uses a maximum spanning tree depending on marginal label dependence to improve the classification performance.
• PCC: The PCC algorithm applies the CC method in the training phase of the multi-dimensional classification process [38]. However, in the testing phase, it uses Bayes-optimal inference by discovering all possible chain paths.
• MCC: The MCC method, which is proposed for obtaining a good chain sequence, uses a Monte Carlo optimization technique to search the space of possible chain sequences [39]. Besides the efficient inference performance it provides, the MCC algorithm also handles high-dimensional training sets.
• CDN: The CDN algorithms construct a cyclic directed graphical model that gives a non-rational presentation of correlations between the target attributes [40]. It predicts the input data labels using a Gibbs sampling inference.
The existing classifier chain algorithms in the literature show accurate classification performances, but they have scalability limitations on the large volume of datasets when constructing a fully cascaded chain. A classifier trellis method was proposed as a scalable solution for MDC problems to solve this high computational bottleneck. This study implements the traditional CT and CDT algorithms.
• CT: The CT algorithm generates a structure in which the target attributes are placed in an ordered method consistent with simply computable mutual information metrics [41]. The main advantage of this method is that it scales up to the vast number of target attributes.
• CDT: The CDT is an improved version of the CDN algorithm that uses a cyclic directed graphical model with a trellis structure instead of a fully connected network [42].
Label powerset transforms MDC problems into multi-class classification problems by combining all unique class labels in the training set as a new single label [43]. As a result of this process, each instance in the training set has only one target attribute with one class label. In this study, the traditional LP, PS, and RAKEL algorithms were utilized for the MDC problem.
• LP: The LP algorithm converts multi-dimensional data labels to an atomic label representing a distinct multi-class subset [44]. After that, the conventional multi-class classification algorithms are applied to this transformed dataset. Therefore, correlations between the target attributes are considered in this approach. The main drawback of this method is that it presents high time complexity in the worst case.
• PS: The PS method prunes infrequently occurring label sets to exploit the most significant correlations among the multi-dimensional dataset [45]. This approach reduces time complexity and improves classification accuracy with minimal information loss.
• RAKEL: The RAKEL method iteratively generates a k size ensemble combination of a small random subset of labels [46]. After that, it aggregated the obtained class outputs from each classifier to get the final class value.
3 Ordinal Multi-Dimensional Classification (OMDC)
The proposed approach, named Ordinal Multi-Dimensional Classification (OMDC), predicts the conditions of a hydraulic system's four components (cooler, valve, internal pump leakage, and hydraulic accumulator) by considering the natural order of class labels. In this approach, well-known MDC algorithms, which apply binary relevance and label powerset methods, are used for classifying multi-target attributes of an experimental dataset. Furthermore, the conventional OCC algorithm is applied for each target attribute's class values that have an inherent order. Finally, four different traditional classification algorithms (MLP, SVM, kNN, and C.5) and three different ensemble-based classification algorithms (Bagging, RF, and AdaBoost) are preferred as base learners for the OCC algorithm in this study.
Definition (OMDC). The OMDC aims to construct a classification model to predict multiple target attributes of a dataset without losing inherent order between the class values.
Let D =
In this method, the multi-dimensional classification problem is transformed into the conventional multi-class classification problem using binary relevance and label powerset methods. In the binary relevance method, each target attribute value of the dataset is estimated by conventional multi-class classifiers independently. The label powerset method combines all class values of the multiple target attributes in the multi-dimensional dataset as a new single label. To implement these methods, BR, CC, BCC, PCC, MCC, CDN, CT, CDT, LP, PS, and RAKEL algorithms are preferred in this approach.
After the problem transformation phase, the OCC algorithm is applied to convert ordinal multiple-class values to binary datasets by considering the order relationship among the labels. To give a clear example, consider the hydraulic system's condition dataset used in this study. It includes the measured process values of a hydraulic test rig with its condition properties (cooler, valve, internal pump leakage, and hydraulic accumulator) that will be predicted. The values of four different target attributes of this dataset have an inherent order. For example, the cooler condition attribute has three values with a linear order relation “full efficiency” > “reduced efficiency” > “close to total failure”. First, “close to total failure” class values are labeled as 0, and the rest are set as 1. In the next iteration, “full efficiency” class value, which has higher ranking order than “reduced efficiency” and “close to total failure”, is set as 1, and the others (“reduced efficiency” and “close to total failure”) are labeled as 0. Then, the same processes are implemented on all class labels of each target attributes in the dataset.
In this OMDC method, seven different classification algorithms (MLP, CVM, kNN, C.5, Bagging, RF, and AdaBoost) are used as base learners for the OCC algorithm. Let Mi indicates the model created for the ith binary problem for i = 1, 2, …, m − 1. Given an instance x, the class label obtained from Mi(x) is regarded as an estimation of the probability P(L > Ci|x), where L is the class label associated with x. In this algorithm, the probabilities for each k class of each n target attributes in the dataset are computed as follows:
where j = {2, 3, …, k}.
The probabilities for the first and final classes are predicted using a single model. The probability that an example belongs to the first class
The general overview of the proposed OMDC approach is given in Fig. 1. In the first step (data acquisition), various measured process values from multiple sensors (pressure, motor power, volume flows, temperature, vibration, cooling efficiency, and efficiency factor) and the conditions of the hydraulic system (cooler, valve, internal pump leakage, and hydraulic accumulator) are obtained from a hydraulic test rig. In the training step, first, the problem transformation process is applied to the raw experimental dataset. In this phase, binary relevance (BR, CC, BCC, PCC, MCC, CDN, CT, and CDT) and label powerset algorithms (LP, PS, and RAKEL) are applied for converting MDC problem into a multi-class classification problem. Then, the OCC algorithm is selected as a base learner for each binary relevance and label powerset algorithm using MLP, SVM, kNN, C4.5, Bagging, RF, and AdaBoost algorithms. Thus, the classification process is performed by preserving the inherent order between the class values. In the next step, each model's performance of the hydraulic test rig's condition estimations is evaluated using the n-fold cross-validation technique selecting n as 10. In the prediction step, a new sample's conditions are predicted using the OMDC approach. Finally, Hamming Score, Exact Match, Hamming Loss, and ZeroOne Loss results of each OMDC model are presented in the last step.
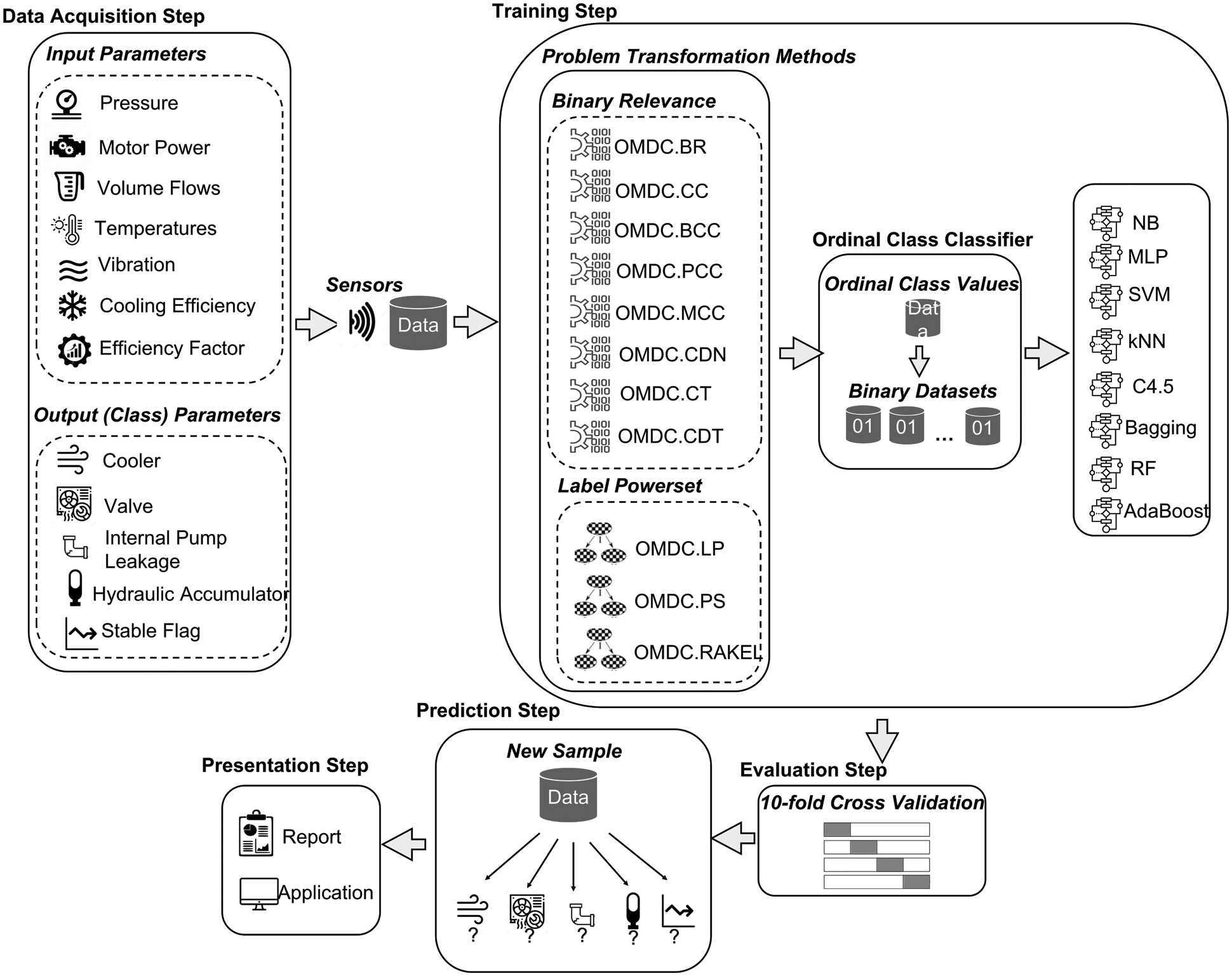
Figure 1: The general overview of the proposed OMDC approach
Algorithm 1 presents the pseudocode of the proposed OMDC approach. First, the base learner of the OCC algorithm is selected from seven different classification algorithms. Then, the multi-dimensional dataset D =

In the experimental studies, the proposed OMDC approach was implemented on a real-world hydraulic system's condition dataset to demonstrate its classification performance. The proposed application was developed using the MEKA open-source multi-label classification framework based on the WEKA library [47] in the Java programming language. In this approach, eleven different MDC algorithms were implemented on the experimental dataset using the OCC. Furthermore, seven different classification algorithms were chosen as base learners for the OCC algorithm independently. The k value of the kNN algorithm was set as 3. Also, the number of iteration parameter values of AdaBoost and Bagging algorithms were selected as 100. The implemented OMDC models with different MDC algorithms were compared to each other using the n-fold cross-validation technique selecting n as 10. The classification performances of each model were evaluated using Hamming Score, Exact Match, Hamming Loss, and ZeroOne Loss metrics.
• Hamming Score: It evaluates the average across the ratio of the correctly classified labels to the total number of labels.
• Exact Match: It gives the percentage of instances with all labels correctly classified.
• Hamming Loss: It presents the ratio of incorrectly classified labels to the total number of labels.
• ZeroOne Loss: It gives the ratio of instances whose actual value is not equal to the predicted value.
These evaluation metrics (Hamming Score, Exact Match, Hamming Loss, and ZeroOne Loss) are evaluated as shown in Eqs. (2)–(5), respectively.
where I refers indicator function, p is predicted value, y represents actual value, |N| is the number of instances, and |L| is the number of target attributes.
This paper introduces a new concept called OMDC and demonstrates its efficiency on a real-world hydraulic system's condition dataset [48]. It is constructed by a hydraulic test rig's measured process values from multiple sensors (pressure, motor power, volume flows, temperature, vibration, cooling efficiency, and efficiency factor) and the conditions (cooler, valve, internal pump leakage, and hydraulic accumulator). It consists of 2205 instances with seventeen input and four target attributes. Tabs. 1 and 2 present the basic characteristics of the experimental dataset's input and target attributes, respectively.


The proposed OMDC is a general approach that can be applied to any field using any experimental dataset. Although the used dataset in this study is publicly available, the OMDC methodology can also be applied to private datasets by safeguarding them using some coverless information hiding techniques [49,50].
In the experiments of this study, the proposed OMDC approach was executed on the hydraulic system's condition dataset to demonstrate its high accurate classification performance. The MDC algorithms were applied in the OMDC approach using the OCC algorithm with seven different classification algorithms as a base learner. The generated MDC models were compared with each other in terms of some evaluation metrics (Hamming Score, Exact Match, Hamming Loss, and ZeroOne Loss).
Tabs. 3 and 4 represent the Hamming Score and Exact Match results of the implemented OMDC models using the traditional and ensemble-based classification algorithms as base learners on the experimental dataset, respectively. The Hamming Score and Exact Match metrics give a degree ranging from 0 to 1 to present the success of the proposed algorithm. The fact that these values are close to 1 indicates that the model offers a classification ability with high accuracy. Furthermore, the evaluated Hamming Loss and ZeroOne Loss results of the same OMDC models are presented in Tabs. 5 and 6. Unlike Hamming Score and Exact Match, there is an inverse ratio between the classification ability of the model, and the Hamming Loss and ZeroOne Loss values. It means that the classification models having lower Hamming Loss and ZeroOne Loss values provide higher prediction performances than the others. According to the results obtained from these tables, it is clearly seen that OMDC.PCC model using AdaBoost algorithm as a base learner presents the highest Hamming Score and Exact Match values among the other OMDC models with 0.989 and 0.959, respectively. Also, it is observed that OMDC.CC, OMDC.BCC, OMDC.MCC, OMDC.CDN, and OMDC.CT algorithms using AdaBoost and RF base learners reached high classification abilities quite close to Hamming Score and Exact Match values of OMDC.PCC. Furthermore, when the obtained results are considered in general, it is possible to say that the OMDC models with binary relevance algorithms are more successful than the label powerset algorithms for predicting the hydraulic system's multiple conditions.




The average of the Hamming score values obtained by each OMDC model using seven different classification algorithms was evaluated, and the results are illustrated in the graph given in Fig. 2. The comparative results in this graph state that the OMDC.PCC model achieved the best hydraulic components' condition prediction performance with an average Hamming Score of 0.922. It can also be concluded that the OMDC models using binary relevance algorithms, except BR, outperform the label powerset algorithms. Thus, it can be said that the OMDC models using binary relevance algorithms can successfully predict the conditions of a hydraulic system's four components by considering the natural order of class labels.
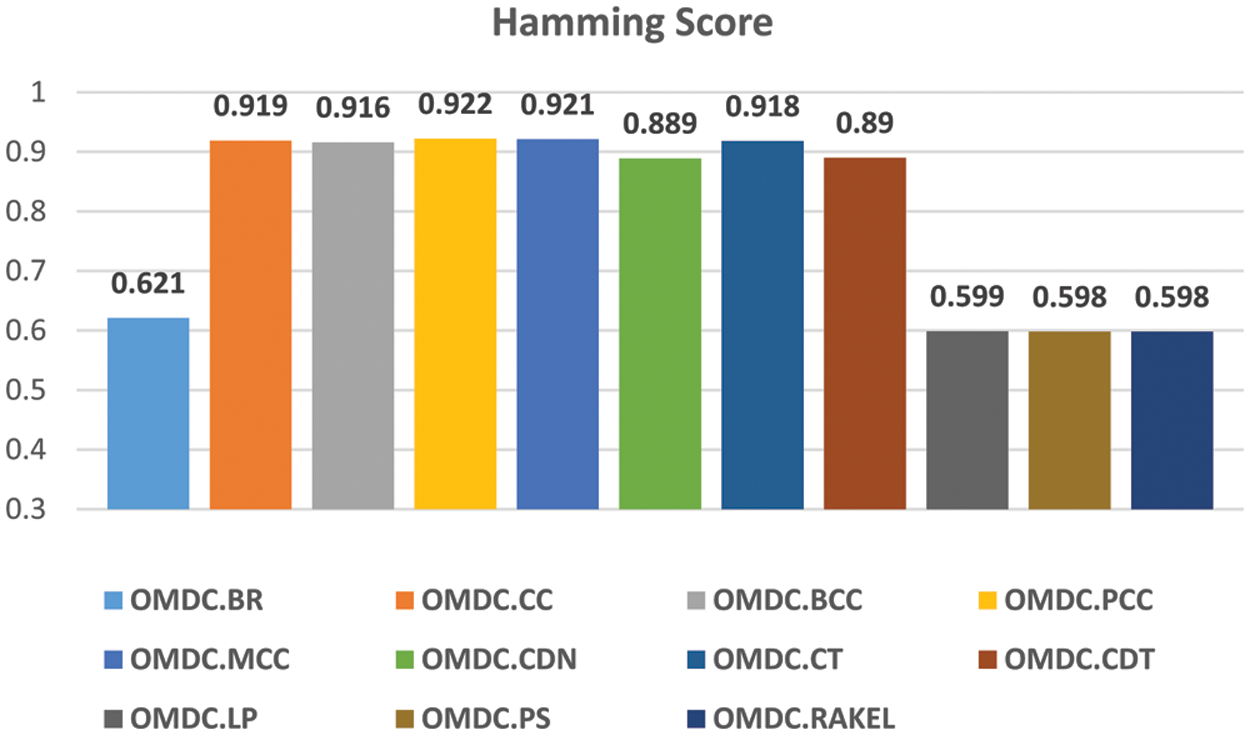
Figure 2: The average hamming score values of OMDC models
In addition to these results, the Hamming loss values of seven different base learners of the OMDC models were presented in Fig. 3. This graph demonstrates that the SVM algorithm presents the worst performance among the other base learners in each OMDC model with the high Hamming loss values. It is also understood from this figure that the AdaBoost algorithm has the lowest Hamming loss value, so this means that the AdaBoost outperforms the other base learners for each OMDC model. This is because of the fact that the AdaBoost is an ensemble learning algorithm and ensemble learners succeed more than traditional individual learners.
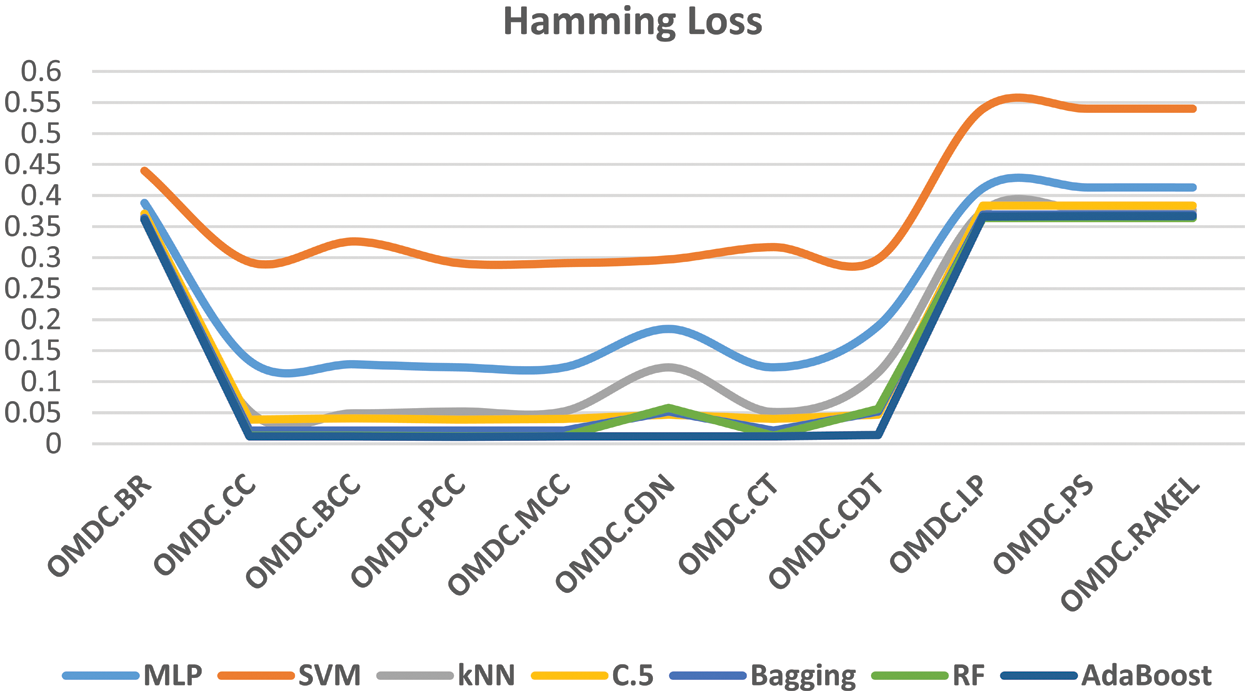
Figure 3: The average hamming loss values of base learners of the OMDC models
Finally, the average Hamming score values of the OMDC models using traditional and ensemble-based classification algorithms were calculated to show the effect of these algorithms on the prediction performances. The obtained values are presented in Fig. 4. When the results are considered in general, it is seen that the OMDC models that apply ensemble-based classification algorithms give more reliable prediction performances than the others that use traditional algorithms as base learners.
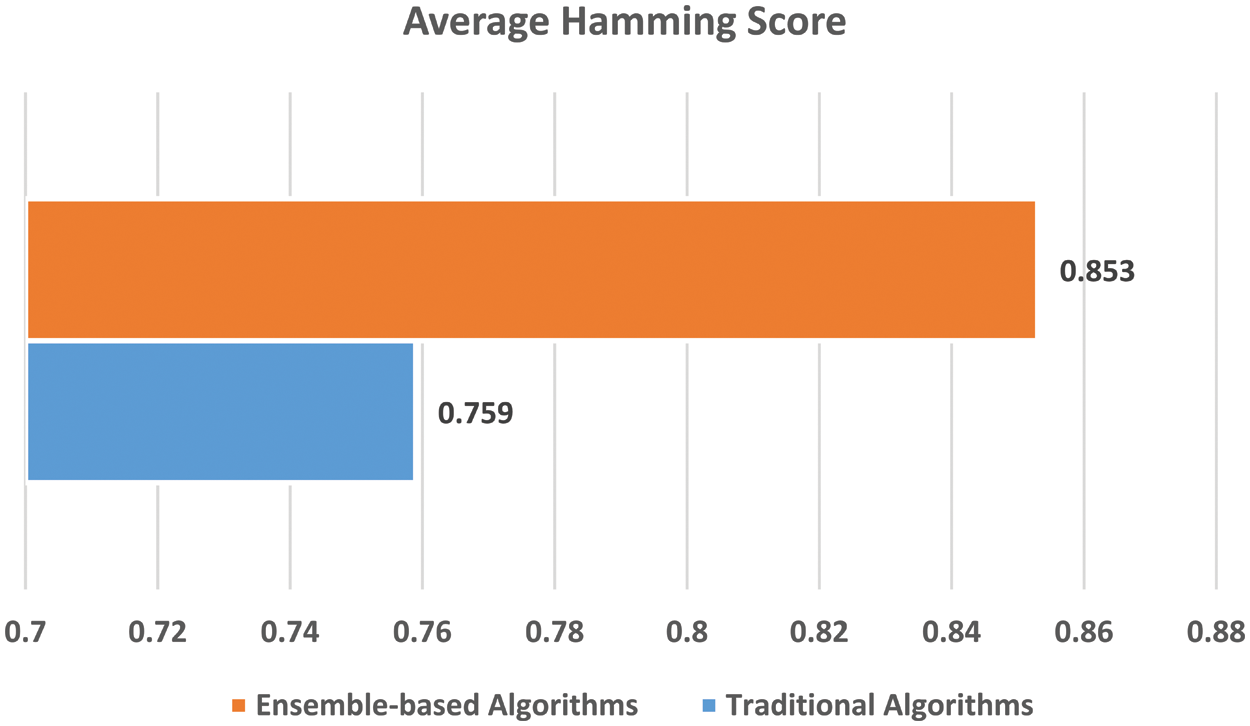
Figure 4: The average hamming score values of OMDC models using traditional and ensemble-based classification algorithms
PdM plays a vital role in maximizing productivity, product quality, and production agility of the manufacturing ecosystem. In recent years, machine learning methods have been preferred as an effective predictive method for maintaining industrial environments. The existing machine learning-based PdM studies ignore the inherent order relation between the target attribute values of the historical sensor data. To bridge the gap, this paper proposes an OMDC approach to predict the conditions of a hydraulic system's four components by combining MDC and OC paradigms to improve prediction performance. In the experiments, the OMDC approach was executed on a real-world dataset using the eleven different MDC algorithms with seven different base learners. The generated OMDC approaches were compared in terms of performance metrics. The results show that OMDC.PCC model using AdaBoost algorithm as a base learner provides the highest Hamming Score (0.989) and Exact Match (0.959) values among the other OMDC models. Also, it is clearly seen from the experimental results that the OMDC models using binary relevance algorithms present more accurate prediction performance than the others. Furthermore, the results indicate that the OMDC models that apply ensemble-based classification algorithms have higher prediction performances with an average Hamming score of 0.853 than those that use traditional algorithms as base learners. As a future study, the OMDC approach can be implemented using adaptive MDC algorithms on the same hydraulic system's condition dataset. In addition, a novel ordinal clustering method can be developed for clustering ordinal sensor data with the purpose of predictive maintenance.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author has no conflicts of interest to report regarding the present study.
1. T. Carvalho, F. Soares, R. Vita, R. Francisco, J. Basto et al., “A systematic literature review of machine learning methods applied to predictive maintenance,” Computers & Industrial Engineering, vol. 137, pp. 106024, 2019. [Google Scholar]
2. M. Becherer, M. Zipperle and A. Karduck, “Intelligent choice of machine learning methods for predictive maintenance of intelligent machines,” Computer Systems Science and Engineering, vol. 35, no. 2, pp. 81–89, 2020. [Google Scholar]
3. A. Massaro, S. Selicato and A. Galiano, “Predictive maintenance of bus fleet by intelligent smart electronic board implementing artificial intelligence,” IoT, vol. 1, no. 2, pp. 180–197, 2020. [Google Scholar]
4. A. Buabeng, A. Simons, N. K. Frempong and Y. Y. Ziggah, “A novel hybrid predictive maintenance model based on clustering, smote and multi-layer perceptron neural network optimised with grey wolf algorithm,” SN Applied Sciences, vol. 3, no. 593, pp. 1–24, 2021. [Google Scholar]
5. K. Kiangala and Z. Wang, “An effective predictive maintenance framework for conveyor motors using dual time-series imaging and convolutional neural network in an industry 4.0 environment,” IEEE Access, vol. 8, pp. 121033–121049, 2020. [Google Scholar]
6. W. Silva and M. Capretz, “Assets predictive maintenance using convolutional neural networks,” in Proc. SNPD, Toyama, Japan, pp. 59–66, 2019. [Google Scholar]
7. Q. Wang and G. Wu, “Effective latent representation for prediction of remaining useful life,” Computer Systems Science and Engineering, vol. 36, no. 1, pp. 225–237, 2021. [Google Scholar]
8. N. Kolokas, T. Vafeiadis, D. Ioannidis and D. Tzovaras, “Forecasting faults of industrial equipment using machine learning classifiers,” in Proc. INISTA, Sinaia, Romania, pp. 1–6, 2018. [Google Scholar]
9. F. Vita and D. Bruneo, “On the use of LSTM networks for predictive maintenance in smart industries,” in Proc. SMARTCOMP, Washington, DC, USA, pp. 241–248, 2019. [Google Scholar]
10. Q. Wang, S. Bu and Z. He, “Achieving predictive and proactive maintenance for high-speed railway power equipment with LSTM-RNN,” IEEE Transactions on Industrial Informatics, vol. 16, no. 10, pp. 6509–6517, 2020. [Google Scholar]
11. T. Praveenkumar, M. Saimurugan, P. Krishnakumar and K. I. Ramachandran, “Fault diagnosis of automobile gearbox based on machine learning techniques,” in Proc. GCMM, Vellore, India, pp. 2092–2098, 2014. [Google Scholar]
12. G. A. Susto, S. McLoone, A. Schirru and S. Pampuri, “Prediction of integral type failures in semiconductor manufacturing through classification methods,” in Proc. ETFA, Cagliari, Italy, pp. 1–4, 2013. [Google Scholar]
13. H. Wang, Z. Yu and L. Guo, “Real-time online fault diagnosis of rolling bearings based on KNN algorithm,” Journal of Physics: Conference Series, vol. 1486, no. 3, pp. 032019, 2020. [Google Scholar]
14. M. Canizo, E. Onieva, A. Conde, S. Charramendieta and S. Trujillo, “Real-time predictive maintenance for wind turbines using big data frameworks,” in Proc. ICPHM, Dallas, TX, USA, pp. 1–8, 2017. [Google Scholar]
15. A. Kusiak and Z. Zhang, “Optimization of power and its variability with an artificial immune network algorithm,” in Proc. PSCE, Phoenix, AZ, USA, pp. 1–8, 2011. [Google Scholar]
16. R. Prytz, S. Nowaczyk, T. Rögnvaldsson and S. Byttner, “Predicting the need for vehicle compressor repairs using maintenance records and logged vehicle data,” Engineering Applications of Artificial Intelligence, vol. 41, pp. 139–150, 2015. [Google Scholar]
17. S. Ayvaz and K. Alpay, “Predictive maintenance system for production lines in manufacturing: A machine learning approach using IoT data in real-time,” Expert Systems with Applications, vol. 173, no. 114598, pp. 1–10, 2021. [Google Scholar]
18. S. Arena, E. Florian, I. Zennaro, P. F. Orrù and F. Sgarbossa, “A novel decision support system for managing predictive maintenance strategies based on machine learning approaches,” Safety Science, vol. 146, no. 105529, pp. 1–19, 2022. [Google Scholar]
19. M. Last, A. Sinaiski and H. S. Subramania, “Predictive maintenance with multi-target classification models,” in Proc. ACIIDS, Hue City, Vietnam, pp. 368–377, 2010. [Google Scholar]
20. W. Zhang, D. K. Jha, E. Laftchiev and D. Nikovski, “Multi-label prediction in time series data using deep neural networks,” International Journal of Prognostics and Health Management, vol. 10, no. 4, pp. 1–14, 2020. [Google Scholar]
21. P. Campoy-Muñoz, P. Gutiérrez and C. Hervás-Martínez, “Addressing remitting behavior using an ordinal classification approach,” Expert Systems with Applications, vol. 41, no. 10, pp. 4752–4761, 2014. [Google Scholar]
22. B. Nguyen, C. Morell and B. De Baets, “Distance metric learning for ordinal classification based on triplet constraints,” Knowledge-Based Systems, vol. 142, pp. 17–28, 2018. [Google Scholar]
23. T. Berghout, M. Benbouzid, S. M. Muyeen, T. Bentrcia and L. H. Mouss, “Auto-NAHL: A neural network approach for condition-based maintenance of complex industrial systems,” IEEE Access, vol. 9, pp. 152829–152840, 2021. [Google Scholar]
24. A. Mallak and M. Fathi, “Sensor and component fault detection and diagnosis for hydraulic machinery integrating lstm autoencoder detector and diagnostic classifiers,” Sensors, vol. 21, no. 2, pp. 433–455, 2021. [Google Scholar]
25. Y. Yoo, “Data-driven fault detection process using correlation based clustering,” Computers in Industry, vol. 122, no. 103279, pp. 1–21, 2020. [Google Scholar]
26. P. Yıldırım, U. Birant and D. Birant, “EBOC: Ensemble-based ordinal classification in transportation,” Journal of Advanced Transportation, vol. 2019, pp. 1–17, 2019. [Google Scholar]
27. E. Frank and M. Hall, “A simple approach to ordinal classification,” in Proc. ECML, Freiburg, Germany, pp. 145–156, 2001. [Google Scholar]
28. S. Raghu and N. Sriraam, “Optimal configuration of multilayer perceptron neural network classifier for recognition of intracranial epileptic seizures,” Expert Systems with Applications, vol. 89, pp. 205–221, 2017. [Google Scholar]
29. H. Wang, B. Zheng, S. Yoon and H. Ko, “A support vector machine-based ensemble algorithm for breast cancer diagnosis,” European Journal of Operational Research, vol. 267, no. 2, pp. 687–699, 2018. [Google Scholar]
30. S. Zhang, “Cost-sensitive KNN classification,” Neurocomputing, vol. 391, pp. 234–242, 2020. [Google Scholar]
31. X. Meng, P. Zhang, Y. Xu and H. Xie, “Construction of decision tree based on C4.5 algorithm for online voltage stability assessment,” International Journal of Electrical Power & Energy Systems, vol. 118, pp. 105793, 2020. [Google Scholar]
32. P. Yildirim and D. Birant, “Comparative analysis of ensemble learning methods for signal classification,” in Proc. SIU, Izmir, Turkey, pp. 1–4, 2018. [Google Scholar]
33. P. Yildirim and D. Birant, “The relative performance of deep learning and ensemble learning for textile object classification,” in Proc. UBMK, Sarajevo, Bosnia and Herzegovina, pp. 22–26, 2018. [Google Scholar]
34. Y. Wu, Y. Ke, Z. Chen, S. Liang, H. Zhao et al., “Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping,” CATENA, vol. 187, pp. 104396, 2020. [Google Scholar]
35. B. Jia and M. Zhang, “Multi-dimensional classification via KNN feature augmentation,” in Proc. AAAI, Honolulu, Hawaii, USA, pp. 3975–3982, 2019. [Google Scholar]
36. J. Read, B. Pfahringer, G. Holmes and E. Frank, “Classifier chains for multi-label classification,” in Proc. ECML PKDD, Bled, Slovenia, pp. 5782, 2009. [Google Scholar]
37. J. Zaragoza, L. E. Sucar, E. F. Morales, C. Bielza and P. Larranaga, “Bayesian chain classifiers for multidimensional classification,” in Proc. IJCAI, Barcelona, Spain, pp. 2192–2197, 2011. [Google Scholar]
38. K. Dembczyinski, W. Cheng and E. Hüllermeier, “Bayes optimal multilabel classification via probabilistic classifier chains,” in Proc. ICML, Haifa, Israel, pp. 1–8, 2010. [Google Scholar]
39. J. Read, L. Martino and D. Luengo, “Efficient monte carlo optimization for multi-label classifier chains,” in Proc. ICASSP, Vancouver, BC, Canada, pp. 3457–3461, 2013. [Google Scholar]
40. Y. Guo and S. Gu, “Multi-label classification using conditional dependency networks,” in Proc. IJCAI, Barcelona, Spain, pp. 1300–1305, 2011. [Google Scholar]
41. J. Read, L. Martino, P. Olmos and D. Luengo, “Scalable multi-output label prediction: From classifier chains to classifier trellises,” Pattern Recognition, vol. 48, no. 6, pp. 2096–2109, 2015. [Google Scholar]
42. J. Read, B. Pfahringer, G. Holmes and E. Frank, “Classifier chains: A review and perspectives,” Journal of Artificial Intelligence Research, vol. 70, pp. 683–718, 2021. [Google Scholar]
43. C. Kosemen and D. Birant, “Multi-label classification of line chart images using convolutional neural networks,” SN Applied Sciences, vol. 2, no. 1250, pp. 1–20, 2020. [Google Scholar]
44. E. Cherman, M. Monard and J. Metz, “Multi-label problem transformation methods: A case study,” CLEI Electronic Journal, vol. 14, no. 1, pp. 1–10, 2011. [Google Scholar]
45. J. Read, B. Pfahringer and G. Holmes, “Multi-label classification using ensembles of pruned sets,” in Proc. ICDM, Pisa, Italy, pp. 1–6, 2008. [Google Scholar]
46. G. Tsoumakas and I. Vlahavas, “Random k-labelsets: An ensemble method for multilabel classification,” in Proc. ECML, Warsaw, Poland, pp. 406–417, 2007. [Google Scholar]
47. R. Read, P. Reutemann, B. Pfahringer and G. Holmes, “Meka: A multi-label/multi-target extension to Weka,” Journal of Machine Learning Research, vol. 17, no. 21, pp. 1–5, 2016. [Google Scholar]
48. N. Helwig, E. Pignalelli and A. Schütze, “Condition monitoring of a complex hydraulic system using multivariate statistics,” in Proc. I2MTC, Pisa, Italy, pp. 1–6, 2015. [Google Scholar]
49. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
50. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |