Computer Systems Science & Engineering DOI:10.32604/csse.2023.026294
Article

Improved Dual-image Quality with Reversible Data Hiding Using Translocation and Switching Strategy

Chin-Feng Lee and Kuo-Chung Chan*

Department of Information Management, Chaoyang University of Technology, Taichung, 41349, Taiwan
*Corresponding Author: Kuo-Chung Chan. Email: s10914902@gm.cyut.edu.tw
Received: 21 December 2021; Accepted: 18 February 2022

Abstract: Dual-image reversible data hiding (RDH) is a technique for hiding important messages. This technology can be used to safely deliver secret messages to the recipient through dual images in an open network without being easily noticed. The recipient of the image must receive the two stego-images before the secret message can be completely retrieved. Imperceptibility is one of the main advantages of data hiding technology; to increase the imperceptibility, the quality requirements of the stego-images are relatively important. A dual steganographic image RDH method, called a DS-CF scheme that can achieve a better steganographic image quality using the center folding (CF) strategy. In this paper, we developed a translocation and switching strategy (TaS) to shorten the distances between the stego-pixel coordinates and the cover pixel coordinates after information being hidden. Compared with the DS-CF scheme, our proposed DS-TaS scheme can effectively improve the quality of the steganographic images at the same level of embedding capability. The experimental results show that the PSNR of our DS-TaS scheme at k = 1 was 55.66 dB, which is an increase of 1.5 dB, and is 51.43 dB for k = 2, 46.66 dB for k = 3, and 40.91 dB for k = 4. In addition, the PSNR values of the stego images was increased by 1.5, 0.29, 0.29, and 0.19 dB, respectively. This shows that our proposed dual-image RDH method can optimize the visual quality of the stego-images and is better than many other dual-image RDH techniques.

Keywords: Information hiding; reversible data hiding (RDH); dual-image RDH; center folding (CF) strategy

1  Introduction

With the advances in information technology, the Internet has become an indispensable tool in human life; in particular, the Internet of Things along with 5G networks will produce a higher speed and greater data transmission on the network. Many transactions in a virtual environment can be easily, quickly, effectively, and conveniently conducted. However, data in these transactions may be illegally stolen, monitored, tampered, copied, and/or damaged during the transfer process. Therefore, security is a prerequisite in the virtual environment, and convenient functions in a secure environment have been in high demand.

To protect digital data and privacy from being infringed, encryption technology has been more commonly used. The sending parties use a key to generate the cipher text of the digital data and transmit the cipher text to the receiving parties. The data party uses the same key to restore the digital data; therefore, even if it is stolen during the transmission process, the original data cannot be known without the key. However, because the data during the transmission process are unintelligible cipher text, although it is impossible to know the original data, it is easy for the person of interest to know whether the data are cipher text, and if so, tamper with or destroy them. Even if the receiving party has the key, the data of the original sender cannot be smoothly obtained. Therefore, if privacy and important data are hidden in the transmitted media, such as pictures, images, sounds, texts, and other digital data, and not easily detected, they can be safely transmitted to the recipient without being detected or tampered with. To achieve the goal of information security, hiding plays an extremely important role in data transmission in a virtual environment.

Information hiding technology can be divided into non-reversible [1–4] and reversible [5–8] data hiding technology, depending on whether the cover image can be restored. Information hiding technology means that when the cover image is embedded with confidential information, it cannot be restored without distortion after the confidential information is retrieved. Extraction is a reversible information-hiding technology. A reversible dual image method can restore the original image that was first generated after removing the secret messages, and thus it can be used in military information transmission and medical applications that do not allow an image distortion.

The dual-image reversible data hiding (RDH) method uses the original image to generate two identical images, and then uses these two generated images to hide the secret message. This method is similar to the secret sharing method in cryptography, which involves splitting the secret in an appropriate manner. Each share after splitting is managed by a different participant, and secret information cannot be recovered by a single participant. Secret information can only be obtained through cooperation among these players.

This study proposes a translocation and switching (TaS) strategy that uses translocation and switching operations to effectively shorten the distance between the cover pixel coordinates and the stego-pixel coordinates. We use the TaS strategy to hide information on dual images, which is called the DS-TaS scheme. The DS-TaS scheme improves the image quality of the DS-CF scheme under the same payload, and can achieve almost the same quality of the dual images.

The contributions of this research are as follows:

1.    We developed a translocation and switching strategy, referred to as the TaS strategy, to shorten the distances between the stego-pixel coordinates and the cover pixel coordinates after information hiding.

2.    To effectively improve the image quality, we proposed a dual steganographic image reversible data hiding method called the DS-TaS scheme based on the TaS strategy.

3.    The DS-TaS scheme carries out (2, 2) secret sharing through a simple information hiding process, preventing over-concentration of secrets and providing efficient dispersal of information for security and load balancing.

2  Related Work

In 2007, Chang et al. proposed an exploiting modification direction (EMD) method based on dual-image reversible information hiding [9], hereinafter referred to as a DS-EMD scheme. For 8-bit gray images, pixel values are integers that range from 0 (black) to 255 (white). Therefore, the DS-EMD scheme creates a 256 × 256 reference matrix ( M) of numbers by exploiting a modulus function (mod 5), where each number in the matrix ranges from 0 to 4. Suppose the embedder extracts a pair of cover pixels in the original image each time as ( p1,p2 ), which is mapped into position (x, y) of the Cartesian coordinate system, such as x=p1 and y=p2,∀x,y ∈ {0, 1, 2, …, 255}. It then finds two sets of data L1andL2 along the two diagonals of the reference matrix (M), each containing five candidate values (candidate elements ) and intersecting at the coordinate point (x, y), where L1= { M ( x−2,y−2 ), M ( x−1,y−1 ), M ( x,y ), M ( x+1,y+1 ), M ( x+2,y+2 )} and L2= { M ( x−2,y+2 ), M ( x−1,y+1 ), M ( x,y ), M ( x+1,y−1 ) ,M ( x+2,y−2 )}. The embedder first converts 4-bit secret data into two hexadecimal values s1,s2 ∈ {0, 1, 2, 3, 4} in order, and then finds s1=M(q11,q12) in L1 , and s2=M(q21,q22) in L2 . At this time, the coordinates of the secret data s1ands2 in M correspond to the pixel values of the grayscale image, and two camouflaged pixel pairs (q11,q12)and(q21,q22) can be obtained.

In 2009, Lee et al. proposed a two-image reversible information hiding method based on the position and direction [10]. This technology uses two stego-pixels to match the four directions of the cross pattern to generate stego-pixels into a double image; thus, we abbreviate this method as the DS-Cross scheme. The DS-EMD scheme defines two sets of 2-bit data in four combinations in the upper, lower, left, and right directions of the center of the cross coordinates. Therefore, when embedding confidential information, two stego-pixel pairs can be generated based on a combination of the information in the cross coordinates. In 2013, Lee and Huang proposed a dual-image reversible information hiding method based on the orientation [11], which is referred to as the DS-OD scheme. The DS-OD scheme defines 25 rules for embedding information and controls the camouflage and original pixel pairs. The range of variation of the pixel pair improves the information load of both the DS-EMD and DS-Cross schemes. In 2014, Chang et al. proposed a two-image reversible information hiding method based on a tortoise shell [12], hereinafter referred to as the DS-TS scheme. The embedding method of the DS-TS scheme is similar to that of the DS-EMD scheme, and the main key technology is to develop a reference matrix with hexagonal turtle shells that are continuously and closely adjacent to each other. Each tortoise shell contains eight different numbers, ranging from 0 to 7.

In 2015, Lu et al. proposed a two-image reversible information hiding method with a central fold strategy [13], referred to as the DS-CF scheme. The center-folding strategy converts all k -bit secret data into a decimal value di ∈ {0, 1, 2, …., 2k−1} and encoded value di tod¯i according to the central folding strategy using Eq. (1), where the decimal value d¯i ∈ { −2k−1,−2k−1+1, …, − 1, 0, 1, …, 2k−1−2,2k−1−1} . As an example, in Fig. 2, the center folding strategy is shown as a schematic diagram of secret information folding. In the schematic diagram, when k = 3, the re-encoded value of decimal di ∈ {0, 1, 2, …, 7} is d¯i ∈ { − 4, − 3, − 2, − 1, 0, 1, 2, 3}.

d¯i=−2k−1+di (1)

The DS-CF scheme uses the concept of the averaging method to hide d¯ equally in two images. The hiding equation is as follows:

q1i=pi+⌊d¯i/2⌋,q2i=pi−⌈d¯i/2⌉, (2)

where pi, q1i , and q2i represent the original pixel and the first and second stego-pixels, respectively.

The DS-CF scheme of the central fold strategy recodes the secret values to reduce the difference between the stego-pixel and the original pixel, thereby improving the stego-image quality. The hiding process is as shown in Fig. 1.

Figure 1: Schematic diagram of the hiding process of the central folding strategy

Figure 2: Schematic diagram of k = 3, d is converted to d¯

In 2017, Yao et al. proposed using the selection strategy of shiftable pixels [14] (DS-SP scheme) to improve the collection of DS-CF schemes. The DS-SP scheme of Yao et al. finds more space to hide information through the central folding strategy. As key technology, if k is the number of bits that can be hidden at a time, when the value of the confidential information is equal to the maximum value (2 k−1 ), one more bit can be hidden.

3  Research Method

In this section, Section 3.1 elaborates on the viewpoints of this research method and describes how to use the translocation and switching strategy (TaS strategy) to optimize the quality of the stego-image. Section 3.2 proposes a reversible dual image information hiding method based on the TaS strategy.

3.1 Views of Research Method

The DS-CF scheme method takes one cover pixel pi from the original image each time and projects it to the 45-degree diagonal position ( pi,pi ) in reference matrix M . The DS-CF scheme re-encodes the binary secret data of length k to obtain d¯i , and splits d¯i in half and hides both halves into two stego pixels ( q1i,q2i ). In Fig. 3, we can observe the stego-pixel coordinates ( q1i,q2i ) and the original coordinates ( pi,pi ) after hiding the message data d¯i when k = 2 and k = 3. Fig. 3a shows the change in position of the stego-pixel after the hidden message relative to the cover pixel ( pi,pi ) when k = 2, where ( q1i , q2i ) ∈ {( pi,pi ), ( pi,pi−1 ), ( pi−1,pi ), ( pi−1,pi+1 )}, and the hidden rule is − 2 = M ( pi−1,pi+1 ), − 1 = M ( pi−1,pi ), 0 = M ( pi,pi ), 1 = M ( pi,pi−1 ). Fig. 3b shows that when k = 3, after hiding the message data d¯i , we obtain the stego-pixel pair ( q1i , q2i ) ∈ {( pi−2,pi+2 ), ( pi−2,pi+1 ), ( pi−1,pi+1 ), ( pi−1,pi ), ( pi,pi ), ( pi,pi−1 ), ( pi+1,pi−1 ), ( pi+1,pi−2 )} and the hidden rules are − 4 = M ( pi−2,pi+2 ), − 3 = M ( pi−2,pi+1 ), − 2 = M ( pi−1,pi+1 ), − 1 = M ( pi−1,pi ), 0 = M ( pi,pi ), 1 = M ( pi,pi−1 ), 2 = M ( pi+1,pi−1 ) , 3 = M ( pi+1,pi−2 ). In Figs. 3a and 3b, the symbol “*” represents the position of the shielding pixel ( pi,pi ).

It is worth noting that the position of the red frame in Fig. 3 is the coordinates of the stego-pixel pair d¯i = 2 k− 1, and the central folding strategy does not use this position for message embedding. However, if the symbol “*” in Fig. 3 is used as the center point, 2k−1 and −2k−1 will have the same distance characteristics as the “*” position (which can be observed based on the distance of a city block).

This research proposes a translocation and switching (TaS) strategy, which uses translocation and switching operations to effectively shorten the distance between the cover pixel coordinates and stego-pixel coordinates. The TaS strategy can make full use of (2k−1 , −2k−1 ) symmetrical to 0 (marked by the feature of symbol “*” in Fig. 3) and improve the quality of the image under the condition that the hidden capacity remains unchanged. Moreover, the information hiding technique that exploits the TaS strategy on dual images is called the DS-TaS scheme. From the original image, each time two original pixels pi and pi+1 are extracted, they generate two pairs of shielding pixels ( p1i,p2i) and (p1(i+1),p2(i+1)) . Two stego-pixel pairs (q1i,q2i) and (q1(i+1),q2(i+1)) are generated using the TaS strategy. The TaS strategy uses a translocation manipulation and switching manipulation to adjust the position of (q1i,q2i) or (q1(i+1),q2(i+1)) hidden in the reference matrix. Applying this TaS strategy to dual-image information hiding can reduce the offset between the stego-pixel pair and the mask pixel pair, and thus optimize the image quality.

Figure 3: The relative positions of the stego-pixels ( q1i,q2i ) and the original pixels ( pi,pi ) in the reference matrix (a) k = 2 and (b) k = 3

The proposed TaS strategy defines two manipulation functions: translocation () and switching ().

The translocation function is d′ = translocation(d)=d−(sgn(d)×2k−1) ), where sgn (.) is a function that returns 1 for numbers greater than 0, and −1 for negative numbers. The translocation () function applied is to move data D1= { d1 | d1 < ( −2k−1/2 )} in the collection to the location of the D1′ collection, or data D2={d2|d2⟩ ( 2k−1/2) } in the collection to the location of D2′ .

Through the translocation () operation, the value of d1 or d2 that is farther from the middle can be moved to a position closer to the middle, such as d1′ or d2′ . Assuming k = 4, the simple example in Fig. 4 is used to illustrate the translocation manipulation of the TaS strategy.

Taking d1=−6=M(v−3,v+3) as an example, using d1′ = translocation(−6)=d−(sgn(d1)×2k−1)=−6−(−1×24−1) ) = 2 = M(v+1,v−1) , which indicates that the −6 originally located at the coordinates ( v − 3, v + 3), as shown in Fig. 4a, will be shifted to ( v + 1, v − 1) through the translocation manipulation coordinates, and changed into a value of 2, as shown in Fig. 4b.

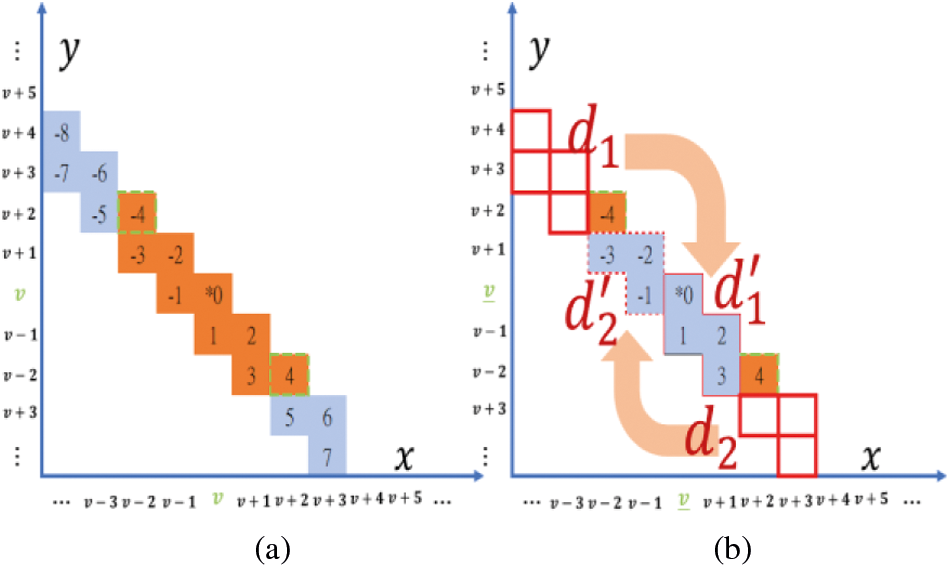
Figure 4: TaS strategy (translocation manipulation)

Again, taking d2=7=M(v+3,v−4) as an example, as shown in Fig. 4a, through translocation manipulation, d2′ = translocation(7)=d−(sgn(d2)×2k−1)=7−(1×24−1) ) = − 1 = M(v−1,v) , as shown in Fig. 4b.

For the switching manipulation, when d=−2k−1 , after applying the switching function, we can obtain the value d′=switching(d)=−d=2k−1 , where the positions of d and d′ are (v−4 , v +4 ) and ( v+4 , v−4 ), respectively. The switching () function will switch a value d to its additive inverse d′ and in the meantime, the offsets (distances) of d and d′ to the center are the same.

Assuming k = 4, we also use Fig. 5 to illustrate the switching manipulation of the TaS strategy. When d=−8=M(v−4,v+4) , then d′=switching(−8)=8=M(v+4,v−4) . This means that the coordinates ( v+4,v−4 ), as shown in Fig. 5a, will be shifted to (v+4,v−4) through a switching manipulation, and changed into a value of 8, as shown in Fig. 5b.

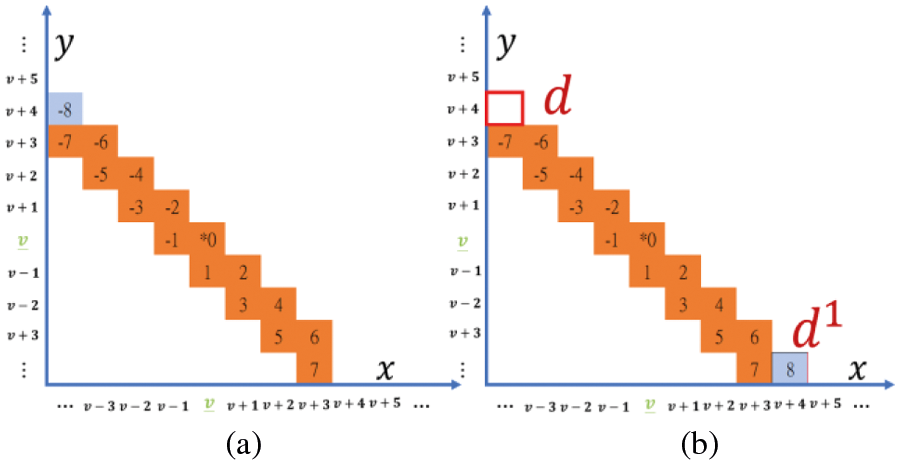
Figure 5: TaS strategy (switching function)

3.2 Proposed Dual Stegano Image Method

Using the TaS strategy, we propose a dual stegano image RDH method, referred to as the DS-TaS scheme. In contrast to the DS-CF scheme, our DS-TaS scheme takes out two secret messages di and di+1 each time, and the re-encoded values are d¯i and d¯i+1 . Finally, through the translocation manipulation or switching manipulation of the TaS strategy, the information that was originally to be hidden is transformed into d¯i′ and d¯i+1′ . At the same time, because of the shift effect, after the information is hidden, the fluctuation range of the pixel value is reduced, and thus our DS-TaS scheme can optimize the image quality under the condition that the embedding capacity remains unchanged. The following steps describe the process of hiding secret messages.

Input: An original image I and secret bits

Output: Two stego-images I′ and I′′

Step 1: For i = 1 to (H×W) /2, a set of pixel pairs is taken out each time as ( pi , pi+1 ). If the pixel value of the original image is between 0 and 2k−2 − 1 or 254 −2k−2 to 255, no secret data are hidden, and the stego-pixels are obtained from the original pixels; therefore, the value of the stego-pixel pair is directly set to ( q1i , q1(i+1) ) = ( pi , pi+1 ) and ( q2i , q2(i+1) ) = ( pi , pi+1 ); skip to step 6.

Step 2: Extract two sets of secret bytes each time, namely, ( s1,s2, …, sk) and ( sk+1,s2, …, s2k ), and then convert them into two decimal values d1 and d2 , respectively.

Step 3: Use the center-folding strategy to convert di and di+1 into d¯i and d¯i+1 , respectively.

Step 4: If the condition (d¯i=−2k−1 and |d¯i+1|>2k−1/2) or (d¯i+1=−2k−1 and |d¯i|>2k−1/2) is not satisfied, use Eq. (1) to calculate the two pairs of pixel values { q11 , q21 }, { q12 , q22 }.

Step 5: If the conditions of Step 4 are true, use the TaS strategy to calculate the two pairs of stego-pixels ( q1i , q2i ), ( q1(i+1) , q2(i+1) ). The three cases are as follows:

Case 1: if d¯i=−2k−1 and d¯i+1=−2k−1

d¯i+1′ = translocation(d¯i+1)=d¯i+1−(sgn(d¯i+1)×2k−1) = 0, q1(i+1)=pi+1−⌈d¯i+1′/2⌉ , q2(i+1)=pi+1+⌊d¯i+1′/2⌋,d¯i′=switching(d¯i)=−d¯i = 2k−1 , q1i=pi−⌈d¯i′/2⌉ , q2i=pi+|d¯i′/2|

Case 2: i f d¯i=−2k−1

d¯i′=switching(d¯i)=−d¯i = 2k−1 , q1i=pi−⌈d¯i′/2⌉ , q2i=pi+|d¯i′/2| ,

d¯i+1′ = translocation(d¯i+1)=d¯i+1−(sgn(d¯i+1)×2k−1 , q1(i+1)=pi+1−⌈d¯i+1′/2⌉ , q2(i+1)=pi+1+|d¯i+1′/2|

Case 3: if d¯i+1=−2k−1

d¯i′ = translocation(d¯i)=d¯i−(sgn(d¯i)×2k−1) , q1i=pi−⌈d¯i′/2⌉ , q2i=pi+⌊d¯i′/2⌋ , d¯i+1′=switching(d¯i+1)=−d¯i+1 = 2k−1 , q1(i+1)=pi+1−⌈d¯i+1′/2⌉ , q2(i+1)=pi+1+|d¯i+1′/2|

Step 6: Let i=i+2 , and after Steps 2–5, until all the pixels are processed, two stego-images I′ and I′′ can be obtained.

The following sections describe the process of using the TaS strategy to embed information. Let k=3 and assume that the two original pixels ( pi,pi+1 ) = (2, 88), then the following three cases may occur during the hiding process of the DS-TaS scheme:

Case 1: When d¯i=−2k−1 and d¯i+1=−2k−1 , the TaS strategy is used; when d¯i′ = 4, a switching manipulation is used; in addition, when d¯i+1′ = 0, a translocation manipulation is used. This process is illustrated in Fig. 6.

For the black part shown in Figs. 6a1 and 6a2, d¯i=−4=M(0,8) and d¯i+1 = − 4 = M (86, 90). Through the switching manipulation calculation using the TaS strategy, it converts d¯i+1′ = translocation(−4)=0 , as shown in the black part of Fig. 6b1. Then, through the translocation manipulation by the TaS strategy, d¯i+1′=translocation(−4)=0 is calculated, as shown in the black part of Fig. 6b2. The message hidden by the DS-TaS scheme is (4, 0), and the two pairs of stego-pixels generated are

(q1i,q2i)=(pi+⌊d¯i′/2⌋,pi−⌈d¯i′/2⌉)=(2+2,2−2)=(4,0),(q1(i+1),q2(i+1)))=(pi+1+⌊d¯i+1′/2⌋,pi+1−⌈d¯i+1′/2⌉)=(88+0,88−0)=(88,88).

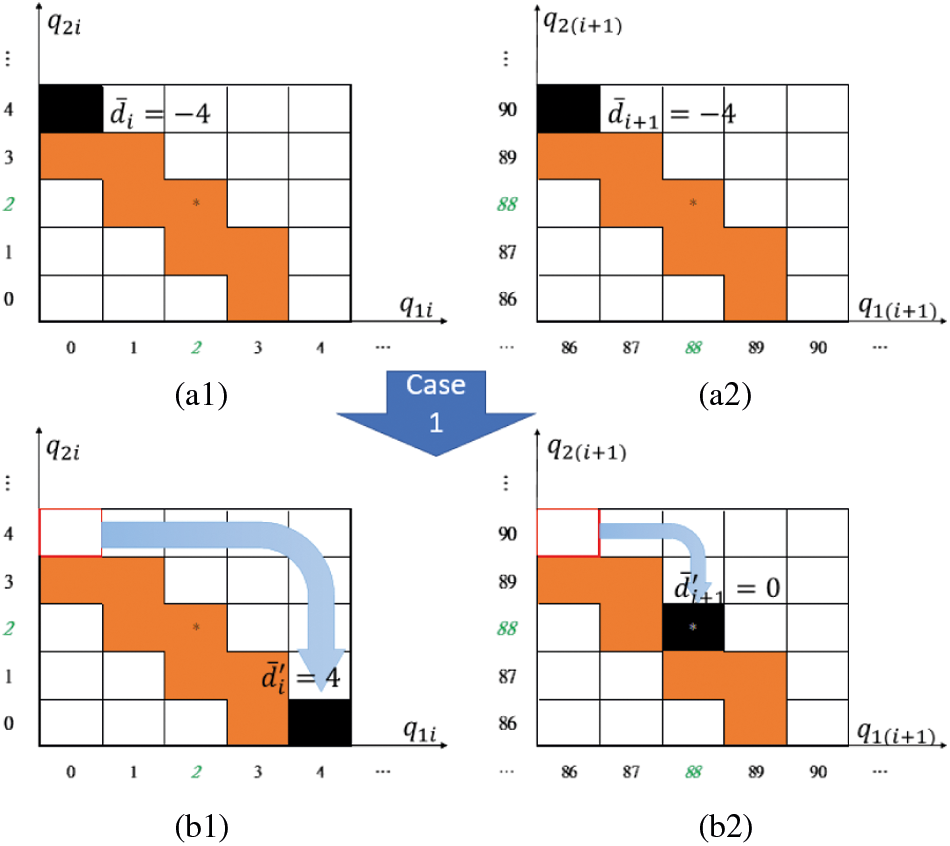
Figure 6: Case1: switching ( d¯i ) and translocation ( d¯i+1 )

The probability of occurrence of the condition is observed as follows, where the image size is H × W. For a grayscale image with a size of 512 × 512, where the 3-bit data are to be hidden into a pair of cover pixels, the image will be modified into 2048 pixels.

(H×W2)×(12k×12k)2=(512×5122)×(18×18)2=2048(pixels).

Case 2: When d¯i=−2k−1 , that is, d¯i=−4=M(0,4) , as shown in the black part of Fig. 7a1, and when | d¯i+1 | > 23–1/2 and | d¯i+1 | < 23−1 , d¯i+1∈{−3=M(86,89),3=M(89,86)} , such as the black part of Fig. 7a2. A switching manipulated through the ToS strategy converts d¯i′=switching(−4)=4=M(4,0) , as shown in the black part of Fig. 7b1. Then, through the translocation manipulation of the ToS strategy, d¯i+1′ = translocation(d¯i+1)=d¯i+1−(sgn(d¯i+1)×2k−1) is calculated as shown in the black part of Fig. 7b2. Therefore, in our DS-TaS scheme, the message d¯i=−4 , which was intended to be hidden in M(0, 4), was changed into the value d¯i′=4 hidden in M(4, 0) through a transposition operation. Another secret message d¯i+1∈{−3,3} , which was originally intended to be hidden, was changed into the value d¯i+1′∈ { − 1, 1} through a translocation operation. The two pairs of hidden stego-pixels are

ifd¯i+1′=1then(q1i,q2i)=(pi+⌊d¯i′/2⌋,pi−⌈d¯i′/2⌉)=(2+2,2−2)=(4,0),

(q1(i+1),q2(i+1))=(pi+1+⌊d¯i+1′/2⌋,pi+1−⌈d¯i+1′/2⌉)=(88+(0),88−1)=(88,87).

ifd¯i+1′=−1then(q1i,q2i)=(pi+⌊d¯i′/2⌋,pi−⌈d¯i′/2⌉)=(2+2,2−2)=(4,0),

(q1(i+1),q2(i+1))=(pi+1+⌊d¯i+1′/2⌋,pi+1−⌈d¯i+1′/2⌉)=(88+(−1),88−0)=(87,88).

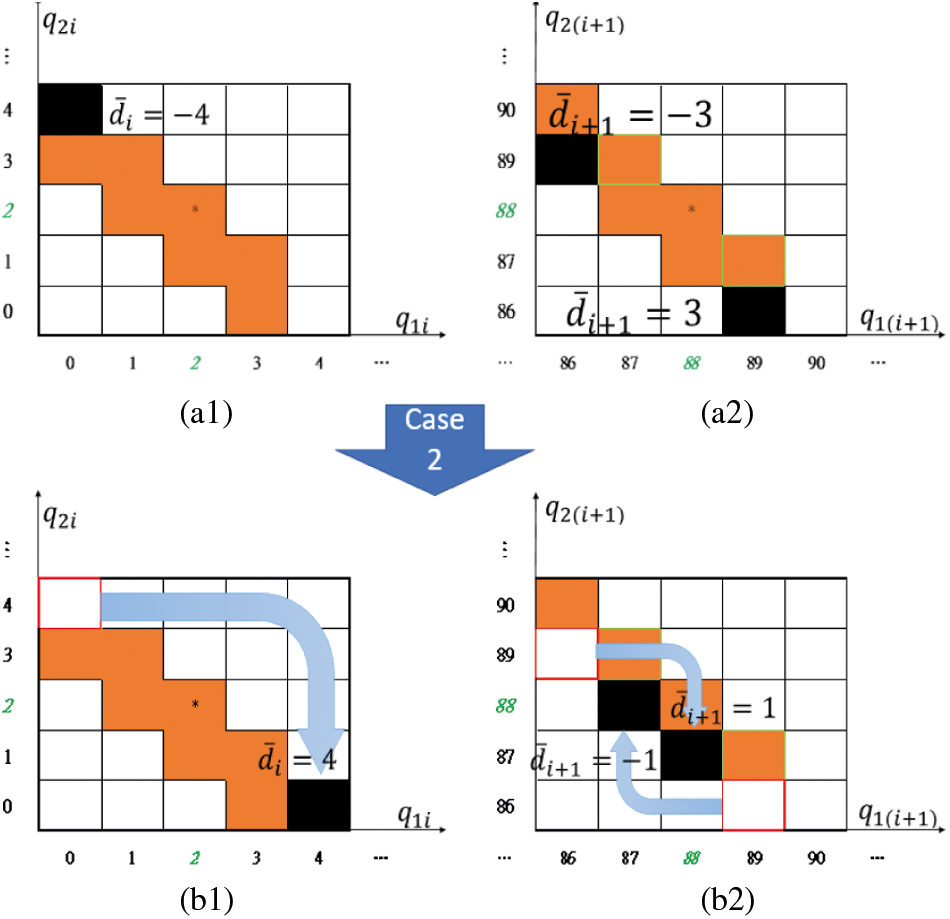
Figure 7: Case2: switching ( d¯i) and translocation ( d¯i+1 )

The number of pixels that the image will be modified into is shown below.

(H×W2)×(12k×12k)2=(512×5122)×(18×28)2=4096(pixels).

Case 3: When d¯i+1=−2k−1 , that is, d¯+1=−4=M(86,90) , as shown in the black part of Fig. 8a2, and when | d¯i | > 23–1/2 and | d¯i+1 | < 23−1 , d¯i∈{−3=M(0,3),3=M(3,0)} , as shown in the black part of Fig. 8a1. The switching manipulation calculation using the ToS strategy converts d¯i+1 into d¯i+1′=switching(−4)=4 = M(90,86) , as shown in the black part of Fig. 8b2. Then, through the translocation manipulation of the ToS strategy, d¯i′ = translocation(d¯i)=d¯i−(sgn(d¯i)×2k−1) is calculated to obtain d¯i′∈ {−1, 1}, as shown in the black part of Fig. 8a2. Therefore, in our DS-TaS scheme, the message d¯i=−4 , which was intended to be hidden in M(86,90) , is changed into the value d¯i′=4 and hidden in M(90,86) through a transposition operation. Another secret message d¯i+1∈{−3,3} , which was originally intended to be hidden, was changed into the value d¯i+1′∈ { − 1, 1} through a translocation operation.

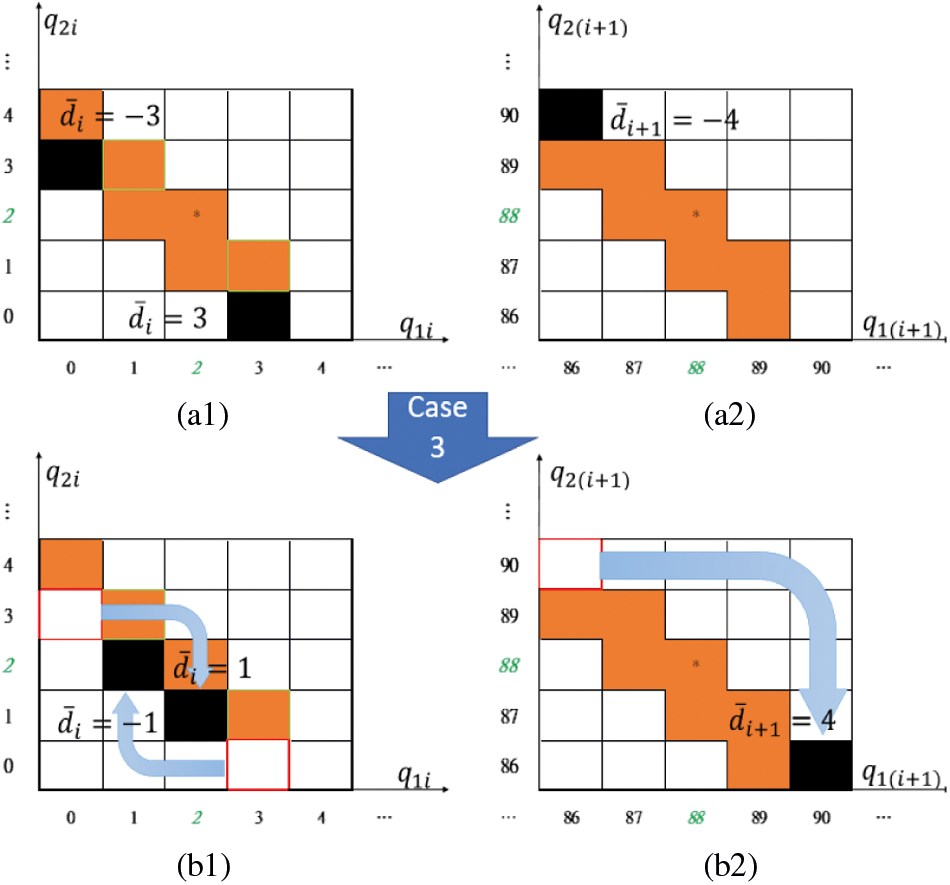
Figure 8: Case3: switching ( d¯i ) and translocation ( d¯i+1 )

The two pairs of stego-pixels hidden are as follows:

ifd¯i′=1then(q1i,q2i)=(pi+⌊d¯i′/2⌋,pi−⌈d¯i′/2⌉)=(2+(0),2−1)=(2,1),

(q1(i+1),q2(i+1))=(pi+1+⌊d¯i+1′/2⌋,pi+1−⌈d¯i+1′/2⌉)=(88+2,88−2)=(90,86).

ifd¯i′=−1then(q1i,q2i)=(pi+⌊d¯i′/2⌋,pi−⌈d¯i′/2⌉)=(2+(−1),2−0)=(1,2),

(q1(i+1),q2(i+1))=(pi+1+⌊d¯i+1′/2⌋,pi+1−⌈d¯i+1′/2⌉)=(88+2,88−2)=(90,86).

The number of pixels that the image will be modified into is the same as in Case 2.

3.3 Data Extraction and Image Recovery Procedure

Input data: Stego-image I′ , Stego-image I′′ .

Output data: Cover image I , Secret bits

Step 1: First, take out two pairs of pixels { q1i , q2i }, { q1(i+1) , q2(i+1) } of two stego-images sequentially at a time.

Step 2: Restore the pixel pair { pi,pi+1 } of the original image, as follows:

pj=⌈q1j+q2j2⌉,j∈{i,i+1}.

Step 3: Calculate d¯i , d¯i=q1i− q2i , and d¯i+1=q1(i+1)−q2(i+1) , and judge whether the conditions of the following three modes are met; if they are met, modify d¯1 and d¯2 are modified according to the following equations:

Case 1: if d¯i=2k−1 and d¯i+1=0 , then d¯I=−2k−1 , d¯i+1=−2k−1

Case 2: if d¯i=2k−1 , then d¯i=−2k−1 , d¯i+1=(d¯i+1−(sgn(d¯i+1)×2K−1)

Case 3: if ifd¯i+1=2k−1 , then d¯i+1=−2k−1 , d¯i=(d¯i−(sgn(d¯i)×2K−1)

Step 4: By Eq. (4), d¯i and d¯i+1 are restored into di and di+1

Step 5: Convert d1 and d2 into binary data, complete the extraction of the two sets of secret information, and return to step 1 to extract the next pair of pixel data until each pixel has been extracted to obtain cover image I and secret bits.

4  Experiment Results

Section 4.1 describes the experiment environment and metrics evaluation. Section 4.2 presents the reduction in the number of shifted pixels through the proposed DS-Tas scheme. Finally, Section 4.3 shows the results and benefits of the DS-TaS scheme compared with other methods.

4.1 Experiment Environment and Metrics Evaluation

The experiment uses MATLAB R2017ab software to implement the proposed method and compare the results with those of other methods. We used six commonly applied standard grayscale images (size 512 × 512) as test images, i.e., Lena, Goldhill, Peppers, Baboon, Barbara, and Boat, as shown in Fig. 9.

Figure 9: Six standard grayscale images

The distortion in a stego-image can be measured based on the peak signal-to-noise ratio (PSNR), which can be computed using Eq. (3), where pij and qij are the respective pixel values at position ( i,j ) for the original and the stego-image, and MSE is the mean square error. A higher PSNR represents a lower distortion, and vice versa.

PSNR=10×log102552MSE,whereMSE=1H×W×∑i=1H⁡∑j=1W⁡(qij−pij)2 (3)

The bits per pixel (bpp) provide the average embedding capacity for each pixel. The higher the bpp value is, the greater the embedding capacity. The total embedding capacity must be divided by 2 to apply dual images to hide the secret information. Eq. (4) shows the calculation method used to express the capacity of each image to carry information.

bpp=12×=−b±b2−4ac2aLW×H,L={thetotalpayloadbits} (4)

We calculated the length of the secret information that can be carried by each pixel k∈{1,2,3,4,5} to compare the image quality and total embedding capacity in the proposed DS-TaS scheme under different lengths k of secret information. Among them, PSNR1 and PSNR2 represent the image quality of the first and second camouflage images, respectively; PSNR (Avg) is the average quality of the two stego-images; and bpp is the average number of secret bits that can be carried by each pixel.

Observing the various evaluation indicators in the Lena image, when k = 1, PSNR2 is as high as 57.17 dB, and when k = 2, k = 3, k = 4, and k = 5, the PSNR (Avg) reaches 51.43, 46.66, 40.92, and 34.91 dB, respectively. Even in the case of a high inventory of k = 5, the image quality PSNR (Avg) of the stego-image can be maintained at an average of 34.91 dB, which is still not easily noticeable by the naked eye. Fig. 10 shows the resulting visual quality of proposed scheme when k = 3 for the Lena image.

Figure 10: Visual quality results of proposed scheme when k = 3 on images “Lena”

4.2 Using DS-Tas Scheme to Reduce Shifted Pixels

The DS-TaS scheme is used to optimize the DS-CF scheme [13]; therefore, when observing all pixels of the two stego-images hidden using the DS-CF scheme, it is important that the sum of the pixels and the MSE be optimized by the DS-TaS scheme. The MSE is the square of the difference between the mask and stego-pixels. The larger the value is, the worse the displayed image quality, as shown in Eq. (3).

As shown in Tab. 1. this method is used to adjust the conditions of Case 1, Case 2, and Case 3 in a stego-image under k = 1, k = 2, and k = 3, respectively, to make the stego-pixels closer to the original pixels. In addition, the number of reductions in the MSE, where k≥3 , there will be Case 1 and the hiding mode of the case (please refer to the fourth step of data hiding process).

In Tab. 1, “the number of adjusted pixels” shows that our method reduces the number of pixel modifications compared to the DS-CF method under the same embedding capacity. In addition, “MSE reduction” represents the difference between the MSEs of the two methods. In the process of hiding the message, when k = 1 and k = 2, the DS-TaS method will use only Case 1; when k = 3, three cases, that is, Cases 1, 2, and 3 will be used in the TaS method. Note that when k = 1, the sum of the adjusted pixels is 32,954; when k = 2, the sum of the adjusted pixels is 8,291; and when k = 3, the sum of the adjusted pixels is 10,253. Therefore, when k = 1, our DS-TaS scheme can optimize the image quality to the highest degree. In addition, when k = 1, because one secret bit is removed at a time, and the value of d¯i is converted according to Eq. (1), it is either 0 or 1; therefore, the DS-CF scheme is inapplicable. In addition, our DS-TaS scheme can still hide secret information when k = 1, and thus the bpp of each image is 0.5, and PSNR(avg) = 55.66 dB for the Lena image, PSNR(avg) = 55.66 dB for the Goldhill image, PSNR(avg) = 55.66 dB for the Peppers image, and PSNR(avg) = 55.66 dB for the Boat image, which is extremely important when applied to produce high-quality stego-images.

4.3 Comparison of DS-TaS Scheme with Other Methods

Tab. 2 shows the DS-TaS scheme and other methods proposed in this paper, i.e., Lee et al. [10], Lee et al. [11], Lu et al. [15], Jafar et al. [16], and Lu et al. [13] for k = 2 and k = 3. PSNR1 and PSNR2 are the image quality of the first and second stego-images, PSNR (Avg) is the average PSNR of the two images, and Capacity (bit) is the total number of bits of the hidden data.

In the proposed DS-TaS scheme, when k = 2, PSNR(Avg) = 51.43 dB, and when k = 3, PSNR(Avg) = 46.66 dB, which outperforms the DS-CF scheme proposed by Lu et al. [13]. Compared with three methods, i.e., Lee et al. [10] (bpp = 0.75, PSNR(Avg) = 52.39 dB), Lee et al. [11], (bpp = 1.07, PSNR(Avg) = 49.63 dB), and Jafar et al. [8] (bpp = 1.24, PSNR(Avg) = 48.71 dB), when k = 2 or k = 3, this strategy achieves the same excellent performance as other dual-image RDH methods in terms of the bpp and PSNR (Avg). Looking at the method adopted in this study, the larger k is, the better the image quality that can be adjusted.

In Tab. 3, the DS-TaS method (when k=3) provides the average SSIM [21], VIF [22], and PCC [23] values for each steganographic image of eight test images (Lena, Goldhill, Peppers, Boat, Baboon, and Barbara). We can also calculate the average value of each indicator in all test images. The average SSIM value of all eight images is greater than 0.9984, the average VIF value is greater than 0.9728, and the average PCC value is also greater than 0.9997. It can be seen from the results of these image evaluation indicators that the DS-TaS method is extremely effective in terms of the steganographic image quality.

5  Conclusion

In this study, a translocation and switching strategy (TaS strategy) is proposed that uses switching and transposition functions to calculate a “re-encoding substitute” of a confidential message such that the changes from the original pixels are significantly reduced, thus effectively improving the image quality. The results show that when the hiding capacity is the same, the quality of the stego-image of the proposed DS-TaS scheme is better than that of the other methods. Compared with the DS-CF scheme proposed, the proposed DS-TaS scheme can effectively improve the quality of stenographic images. Not only does our method achieve a better performance in terms of the image quality, it also has more options than the DS-CF method in terms of the embedding capacity for each stego-pixel. It can hide 0.5 bits for each stego-pixel and can be applied to produce higher-quality stego-images.

Our proposed DS-TaS RDH scheme produces high image quality, and the quality of the 2 images is similar, so an attacker cannot suspect that the image carries a secret message. In addition, because of the spirit of (2, 2) secret sharing, a legal person with two secret images can fully extract the secret information. Therefore, this dual-image-based technology can avoid excessive concentration of information, thereby achieving risk dispersion and load balancing.

In the future, the method will be strengthened by combining it with other reversible dual-image approaches to improve the quality of information hiding images and increase imperceptibility requirements.

Acknowledgement: We are grateful to all authors who participated in this research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. K. Chan and L. Cheng, “Hiding data in images by simple LSB substitution,” Pattern Recognition, vol. 37, no. 3, pp. 469–474, 2004. [Google Scholar]

 2.  J. Mielikainen, “LSB matching revisited,” IEEE Signal Processing Letters, vol. 13, no. 5, pp. 285–287, 2006. [Google Scholar]

 3.  R. Z. Wang, C. F. Lin and J. C. Lin, “Image hiding by optimal LSB substitution and genetic algorithm,” Pattern Recognition, vol. 34, no. 3, pp. 671–683, 2001. [Google Scholar]

 4.  X. Zhang and S. Wang, “Efficient steganographic embedding by exploiting modification direction,” IEEE Communications Letters, vol. 10, no. 11, pp. 781–783, 2006. [Google Scholar]

 5.  Z. Ni, Y. Shi, N. Ansari and W. Su, “Reversible data hiding,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 16, no. 3, pp. 354–362, 2006. [Google Scholar]

 6.  J. Tian, “Reversible data embedding using a difference expansion,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 13, no. 8, pp. 890–896, 2003. [Google Scholar]

 7.  C. C. Chang, K. T. Duc and Y. C. Chou, “Reversible data hiding scheme using two steganographic images,” in Proc. of TENCON 2007, Taipei, Taiwan, pp. 1–4, 2007. [Google Scholar]

 8.  C. F. Lee, K. H. Wang, C. C. Chang and Y. L. Huang, “A reversible data hiding scheme based on dual steganographic images,” in Proc. of the Third Int. Conf. on Ubiquitous Information, New York, NY, USA, pp. 228–237, 2009. [Google Scholar]

 9.  C. C. Chang, T. D. Kieu and Y. C. Chou, “Reversible data hiding scheme using two stenographic images,” in Proc. of IEEE Region Tenth Int. Conf. (TENCON), Taipei, Taiwan, pp. 1–4, 2007. [Google Scholar]

10. C. F. Lee, K. H. Wang, C. C. Chang and Y. L. Huang, “A reversible data hiding scheme based on dual steganographic images,” in Proc. of the Third Int. Conf. on Ubiquitous Information Management and Communication, New York, NY, USA, pp. 228–237, 2009. [Google Scholar]

11. C. F. Lee and Y. L. Huang, “Reversible data hiding scheme based on dual stegano images using orientation combinations,” Telecommunication Systems, vol. 52, no. 4, pp. 2237–2247, 2011. [Google Scholar]

12. C. C. Chang, Y. J. Liu and T. S. Nguyen, “A novel turtle shell based scheme for data hiding,” in Proc. of the Tenth Int. Conf. on Intelligent Information Hiding and Multimedia Signal Processing Conf. IIH-MSP, Kitakyushu, Japan, pp. 89–93, 2014. [Google Scholar]

13. T. C. Lu, J. H. Wu and C. C. Huang, “Dual-image based reversible data hiding method using center folding strategy,” Signal Processing, vol. 115, no. 4, pp. 195–213, 2015. [Google Scholar]

14. H. Yao, C. Qin, Z. J. Tang and Y. Tian, “Improved dual-image reversible data hiding method using the selection strategy of shiftable pixels’ coordinates with minimum distortion,” Signal Processing, vol. 135, no. 8, pp. 26–35, 2017. [Google Scholar]

15. T. C. Lu, C. Y. Tseng and J. Wu, “Dual imaging-based reversible hiding technique using LSB matching,” Signal Processing, vol. 108, no. 4, pp. 77–89, 2015. [Google Scholar]

16. I. F. Jafar, K. A. Darabkh, R. T. Al-Zubi and R. R. Saifan, “An efficient reversible data hiding algorithm using two steganographic images,” Signal Processing, vol. 128, no. 2, pp. 98–109, 2016. [Google Scholar]