DOI:10.32604/csse.2023.025999

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.025999 |  |
| Article |
Secured ECG Signal Transmission Using Optimized EGC with Chaotic Neural Network in WBSN
1Department of ECE, New Horizon College of Engineering, Bengaluru, 560103, India
2CMR Institute of Technology, Bengaluru, 560037, India
3SRM University, Chennai, 603203, India
*Corresponding Author: Ishani Mishra. Email: mishra.ishani@gmail.com
Received: 12 December 2021; Accepted: 24 January 2022
Abstract: In wireless body sensor network (WBSN), the set of electrocardiogram (ECG) data which is collected from sensor nodes and transmitted to the server remotely supports the experts to monitor the health of a patient. While transmitting these collected data some adversaries may capture and misuse it due to the compromise of security. So, the major aim of this work is to enhance secure transmission of ECG signal in WBSN. To attain this goal, we present Pity Beetle Swarm Optimization Algorithm (PBOA) based Elliptic Galois Cryptography (EGC) with Chaotic Neural Network. To optimize the key generation process in Elliptic Curve Cryptography (ECC) over Galois field or EGC, private key is chosen optimally using PBOA algorithm. Then the encryption process is enhanced by presenting chaotic neural network which is used to generate chaotic sequences or cipher data. Results of this work show that the proposed cryptography algorithm attains better encryption time, decryption time, throughput and SNR than the conventional cryptography algorithms.
Keywords: Wireless body sensor network; ECG; pity beetle swarm optimization algorithm; elliptic galois cryptography and chaotic neural network
WBSN alludes to networking technology that interconnects many sensor nodes in or on the human body. It very well may be utilized in the use of medical care for persistent monitoring of patients [1–3]. Information is gathered from a few sensor nodes, either embedded or surface mounted on the human body and is forwarded to smart gadgets like cell phones or tabs. Information gathered at the smart gadget from sensors can be remotely communicated to specialists or doctors in any side of the world through the Internet, who can screen, analyze, or send messages to the patient distantly. The wearable sensors move with the patients. In this way, WBSN gives mobile monitoring of patients, where patients need not be at or close to clinics for their ceaseless health observing.
WBSN can sense numerous physiological signals like electromyogram (EMG), electroencephalogram (EEG), electrocardiogram (ECG), internal heat level, pulse and surprisingly breathing or movement of the patients. Among all, ECG is essential as a result of its capacity to analyze cardiovascular illnesses that is the significant reason for deaths according to the report of WHO [4]. Given the significance of ECG signal examination from the health point of view, this work concentrates just around ECG signals [5,6]. Probably the greatest challenge in WBSN is to send the sensed ECG data safely to the medical server because any progressions of this delicate data may cause wrong diagnosis and wrong treatment of the patient. As the ECG data collected from the sensors will forward to the base stations through a network coordinator, an hacker can without much of a stretch catch the information from the remote channels and adjust that. So, the major challenge we focus in this approach is secure data transmission [7]. Recent years cryptographic computations are profoundly impervious to attacks, however insecure movement of keys is the main disadvantage. While dividing the secret key among communicating parties in the WBSNs in the regular strategy like through telephone or email, the attackers will get the private key. Along these lines, in this paper, we investigate basic security threats: secure key generation as well as encryption.
To attain this goal, the following contributions are presented in this paper.
• In this approach, the sensed ECG signals are transmitted securely with the proposed optimized elliptic Galois cryptography with chaotic neural network.
• For public key generation, Elliptic Curve Cryptography (ECC) over Galois field is presented, where prime numbers are considered as private key. For optimal private key selection, pity beetle swarm optimization algorithm (PBSOA) is presented.
• With the generated public key, encrypted data is created using chaotic neural network.
• The performance of the proposed scheme is analyzed in terms of encryption time, decryption time, throughput and network lifetime.
Upcoming sections of the manuscript are sorted as follows. Some recent literatures which focused research on secured ECG signal transmission in WBSN are survived in Section 2. Section 3 presents PBOA algorithm based EGC with chaotic neural network for secure ECG data transmission in WBSN. Results of the proposed method are analyzed in Section 4. Finally, the conclusion of the research work is discussed in Section 5.
Some recent articles which focused research on secured ECG signal transmission in WBSN are reviewed in this section. Qiu et al. [8] had the goal to reduce the time and energy consumption of body sensors while applying the standard encryption methods on the health data. As the lightweight Selective Encryption methods achieve the efficient encryption by decreasing the volume of data, the authors had re-defined the Selective Encryption methods for transmitting ECG signal in the body sensor network environment. They had designed the Selective Encryption depend on the disease classification using machine learning model. By presenting this proposed scheme, they had protected ECG data against unauthorized classification. Pandey et al. [9] had proposed confidential data patient hiding method in ECG signal and secure transmission. In the approach, the authors had embedded the confidential data of patient in ECG signal with the use of chaotic map and the sample value difference scheme. The sample value difference scheme hided the confidential data of patient at the predefined locations of EGC sample. The remote transmission of this embedded ECG signal was analysed based on the Orthogonal Frequency Division Multiplexing system. Because of the proposed scheme, the authors attained better peak signal to noise ratio and Percentage Root-meansquare Difference.
Karthikeyan et al. [10] had proposed a secret key generation method based on ECG signal abbreviated as ESKG. In the proposed scheme, from the ECG signal of patient the secret key was generated. This secret key was utilized for the data encryption in the sensor node. Besides, 64 bit secret key was made at receiver end. Also, the authors never used additional algorithm for distribution of key, refreshment of key and retrieving. Due to the proposed scheme, the authors had achieved the resource constrained secure ECG transmission. Algarni et al. [11] had presented three cryptosystems for encryption of ECG signal. The first one was performed based on using random projection on ECG signals’ DWT coefficients. The second one was performed utilizing salting algorithm. The third one was performed depend the following steps that are fusion, substitution and chaotic permutation. In the approach, the ECG signal was fusion with the speech signals. The permutation was achieved by applying 2-D chaotic Baker map. The fusion and chaotic encryption was used and verified in the transform and spatial domains. Simulation results of the article showed that, the proposed scheme achieved high level of security.
Sanivarapu et al. [12] had aimed to solve the problem of ECG watermarking as due to failure of ECG signal to extract the information of patient. So, the authors had presented a watermarking method based on wavelet. Using this proposed method, they hided the information of patient as QR image in the ECG signal. At first, using Pan–Tompkins algorithm, they had converted the 1D-ECG signal to 2D-ECG image. Wavelet method extracted the ECG information. Besides, the embedded data was decomposed using QR decomposition. By presenting this proposed scheme, the authors had achieved better peak signal to noise ratio and Percent root mean square difference. Xu [13] had proposed IoT based ECG monitoring system with secure data transmission for continuous monitoring of cardiovascular. Also, for automatic classification, lightweight ECG Signal Strength Analysis was proposed besides the author had presented Lightweight Access Control and Lightweight Secure IoT for secure transmission of data. They had implemented the proposed scheme in real time using android phones, ECG sensors, Bluetooth, arduino and cloud servers. Because of the proposed scheme, the authors had achieved better reliability and security as well as energy consumption was reduced. Tan et al. [14] had presented a secure certificateless biometric authentication and group key management for wireless body area network. In the proposed approach, the authors had designed the smartphone of user as the personal controller. In the authentication process, the collected ECG feature records were used as the biometric parameter. Then authentication was enabled in every sensor nodes. Besides, effective group key management was applied to all validated sensors. The performance analysis of the proposed scheme achieved targeted properties of security as well as it provided resistance to different attacks.
3 Optimized EGC with Chaotic Neural Network for Secure ECG Data Transmission
Fig. 1 shows the workflow diagram of the proposed scheme. As depicted in the figure, the body sensors collect the ECG data from the human body and the collected data is wirelessly transmitted to the medical server. For secure data transmission, optimized EGC with chaotic neural network is presented. To reduce the computation time and round of error in ECC, Galois field is used in this approach. In the phase of key generation in EGC, the private key is chosen optimally using PBOA algorithm. Using the optimal private key, secret key or public key is generated. Then the key generation phase is followed by the phase of encryption. In this work, encryption is done with the chaotic neural network where chaotic sequences or cipher text is generated. Finally at the receiver or medical server, the cipher text is deciphered in the phase of decryption.
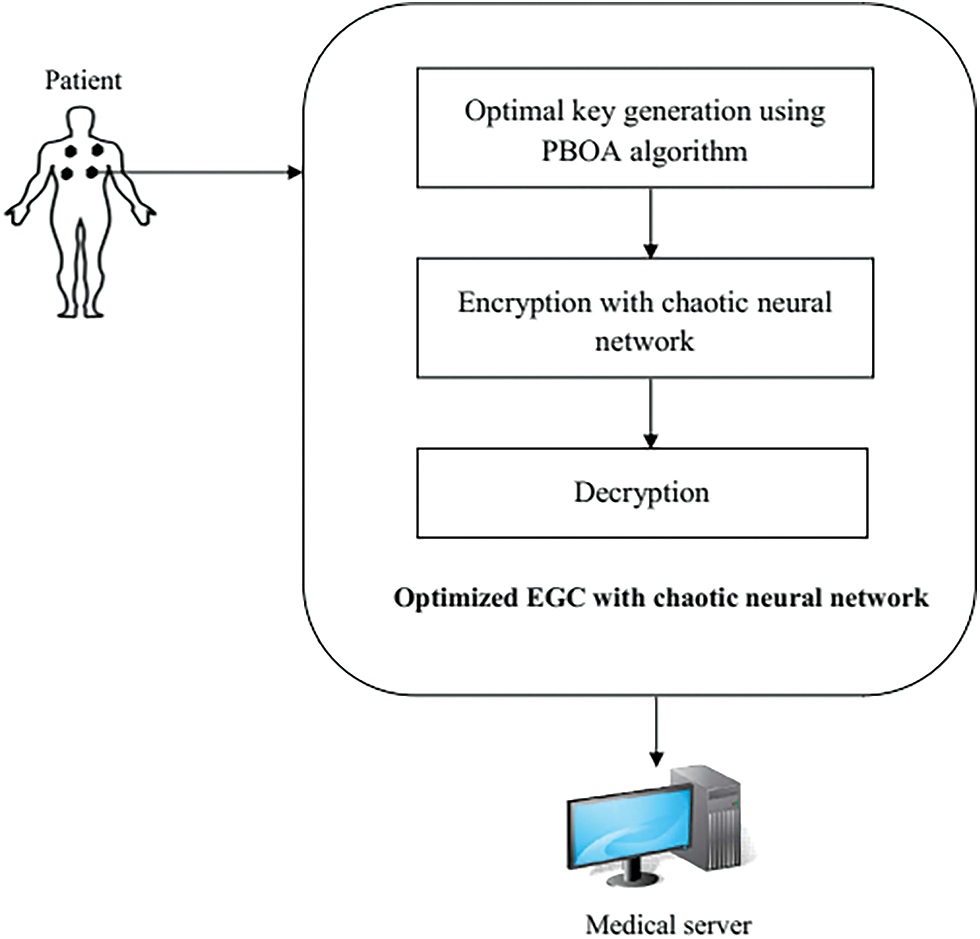
Figure 1: The workflow diagram
For this work, MIT-BIH Normal Sinus Rhythm dataset is used. This dataset incorporates 18 long haul ECG recordings of subjects alluded to the Arrhythmia Laboratory at Boston’s Beth Israel Hospital (presently the Beth Israel Deaconess Medical Center). Subjects added for this data set were found to have had no critical arrhythmias; they incorporate 5 men, matured 26 to 45, and 13 ladies, matured 20 to 50.
3.3 Elliptic Galois Cryptography (EGC)
The EGC algorithm is the extension of Elliptic Curve Cryptography (ECC) i.e., ECC over Galois field (GF). EGC is the public key cryptography where public key or secret key is generated for the user’s authentication. For authorization, public and private keys are more significant. In this approach, elliptic curve over Galois field (FG) is introduced to reduce the complexity of round of error and processing time.
For effective calculation, the value of Galois field is higher than one. Galois field consists of the infinite field range that defined as follows,
Galois field is defined as it is an infinite field with the number of integers as well as it is the integer with modulo prime field denoted as ‘p’ as shown in Fig. 2. In EGC, an elliptic curve over GF of characteristics is formed depend on the variable a and b with the range FG. Besides, the collective elements denoted as (x, y) confirms the elliptic curve equation as,
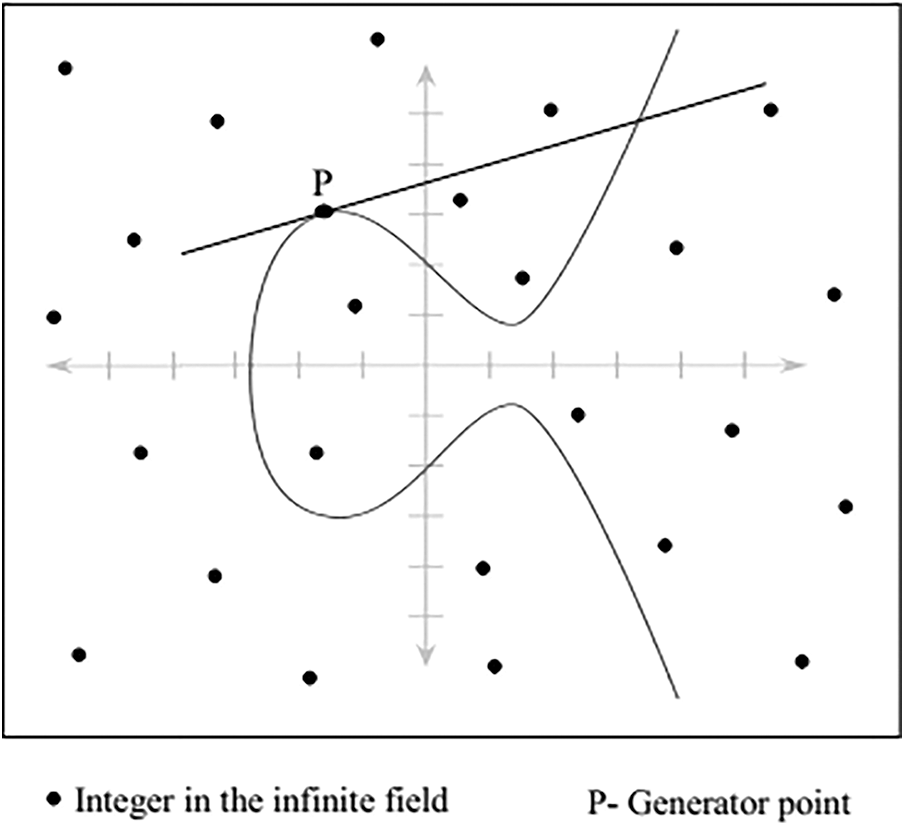
Figure 2: ECC over Galois field
According to the Eq. (1), the various elliptic curve points are generated depending on the various values of a and b. Also, in the elliptic curve point, x and y values lie within the range of GF
where, U denotes the public key, R denotes the private key and P denotes the generator point on the curve. Elliptic curve group is structured when
As the private key (R) is considered as random prime number for secret key generation in EGC, throughput of the algorithm may decrease. Thus, to enhance the performance of key generation in EGC, private key is selected optimally. For optimal private key selection, rain optimization algorithm (ROA) is presented in this paper. Following section explains the private key selection.
3.4 PBOA Based EGC for Optimal Private Key Selection
PBOA is presented for choosing the optimal private key or prime number. As this algorithm can search large areas of suitable solutions for the best global solution while solving local optima, it is chosen for selecting the private key optimally.
PBOA is executed reliant upon the behaviour of bark beetle. It shows the behaviour of polygamous mating, with the male mating with 3 to 6 females. The male beetles drill into the phloem of successfully incapacitated trees uncovering there a material chamber. While reinforcing, they change have terpenes into pheromones, pulling in females, with which they mate in the wedding chamber. From this chamber, in a star-like game-plan, females store 40–70 eggs in egg claims to fame. In this calculation, a populace contains males and females; a some of folks go about as pioneer particles that mission for the most sensible host. A numerical definition of this PBOA is depicted as follows.
Initialization: The candidate solutions or particles are initialized in the global search space which is equal to the hyper volume. In this work, prime numbers are considered as solutions. Initial population of pioneer particles is described as follows,
Here,
where, S denotes the private key or prime number.
Here, RST [] represents an acronym as random sampling method and is applied to solve the problem of premature convergence. Using this RST, the positions of search space are defined into Npop samples. U and L denote the global bounds.
SFitness: For each initialized solution, fitness or objective function is calculated to evaluate the solution. To select the optimal private key, the solution should satisfies the following fitness function,
where, Thr (i) denotes the throughput of the ith solution and it can be defined as follows,
According to Eq. (6), the optimal solution is obtained if it satisfies the maximum throughput. Otherwise, the solution is updated until finding the optimal solution. Through the following phases the solution is updated.
Selection pattern of new hyper volume: All recently initialized solutions will look into the search space searching for a superior solution so as to create their own population. As per the new hypervolume determination selection pattern is chosen, a hunting territory is created around the particles position. For every instance, the sense of this territory is computed using a chosen pattern factor (fp) and used as a parameter of PBOA. According to every example, Npop new pioneer particles are haphazardly situated into this inquiry territory by methods for RST:
where,
where, g denotes the generation step,
As the beetle’s behaviour depicted already, five kinds of new hypervolume determination examples are executed into the algorithm. These determination examples are depicted as pursues:
Neighboring search hypervolume: Some progeny produced in a new beetle brood will definitely search for a new brooding reasonable position. This is because of the way that some solid bugs can’t fly significant distances or the proper positions are excessively near birth position or the beetles have an enormous populace in short proximity which can prompt an assault towards the solid trees set inside. In this manner, a hunt region is made around the particles’ initial position as indicated by the neighboring search hypervolume. The neighboring factor (fne) that is utilized to characterize the region size is a parameter of the PBOA, the worth scope of fne is equivalent to [0.01, 0.20]. As indicated by this example, the new Npop pioneer particles are arbitrarily situated into this search space dependent on the declaration of Eq. (9) where fp is equivalent to fne.
These generated new Npop solutions are contrasted with one another to characterize the best pioneer particle. The best is then contrasted with the beginning position, and if the rest are better drawn in, new populations will be made as follows:
where,
Mid-scale search hypervolume: This search pattern example is empowered if the neighbouring search hypervolume has neglected to enhance the population contrasted with the beginning position. Like the neighboring search hypervolume, a search area is generated around the current best beginning situation of the particles. The mid-scale factor (fms) is used to characterize this search area size, the worth scope of fms is equivalent to [0.10, 1.00]. As per this example, the new Npop pioneer particles are haphazardly situated to this search space dependent on the outflow of Eq. (9) where fp is equivalent to fms.
Like the neighboring search hypervolume, these as of late portrayed Npop populations are appeared differently in relation to each other to describe the best pioneer particle. The best can compare the starting position, and it attracts others better and new people are generated.
Large-scale search hypervolume: Some new beetles, usually very strong beetles that have formed in a new brood, will fly farther away from their birth position in search of a suitable tree-a new brooding host. A third large-scale search hypervolume is used when the neighbouring search hypervolume fails to improve the solution compared to the initial position. Neighbouring search is built around the current ideal initial position of particles, similar to the hypervolumia search area. The large scale factor (fls) that is utilized to characterize the size of this territory, the worth scope of fls is equivalent to [1, 100]. As indicated by this example, the new Npop pioneer particles are haphazardly situated into this search space dependent on the outflow of Eq. (9) where fp is equivalent to fls.
Similar to the previous search hypervolume patterns these newly defined Npop solutions are compared with each other for defining the best pioneer particle.
Global-scale search hypervolume: This is implemented if a better solution cannot be found for a large number of functional estimates. Maximum unsuccessful function evaluations (FEun), which dictates the use of the global search hypervolume method, are defined with reference to the total function evaluations (FEtotal) using the algorithm’s multiplier factor (fFE). The worth scope of fFE is equivalent to [0.05, 0.25]. As indicated by this example, the new Npop pioneer particles are haphazardly situated inside this search space with the utilization of RST:
Memory consideration search hypervolume: In this search pattern, the optimal solutions determined by the PBOA so far are put away in memory (MEM) of size equivalent to Npop and are in this manner utilized as portrayed beneath.
For the situation that a superior position is distinguished, as per memory consideration search hypervolume design, a limited neighbourhood search is performed by a fine-tuning factor (ftn) utilized to characterize the size of this space. The worth scope of ftn is equivalent to [0.005, 0.05].
Update the population: Based on the above phases, hypervolume patterns are selected for the new populations. Collectively, the hypervolume patterns are selected in accordance with the following expression:
If k = 1,
Else
Else
(Mid-scale search hypervolume)
Else
End
Where, r represents the random number within the interval [0, 1].
Termination: The solution is terminated once it finds optimal solution or prime number. Else, the solution gets updated.

3.5 Chaotic Neural Network for Encryption
For encryption phase in EGC, chaotic neural network is presented. Chaotic neural network is used to enhance the security and performance of the algorithm. In this network, the plain text is converted into the cipher text using the ECC over GF secret key. Fig. 3 shows the general structure of the chaotic neural network. The input plain signal of the network is represented as
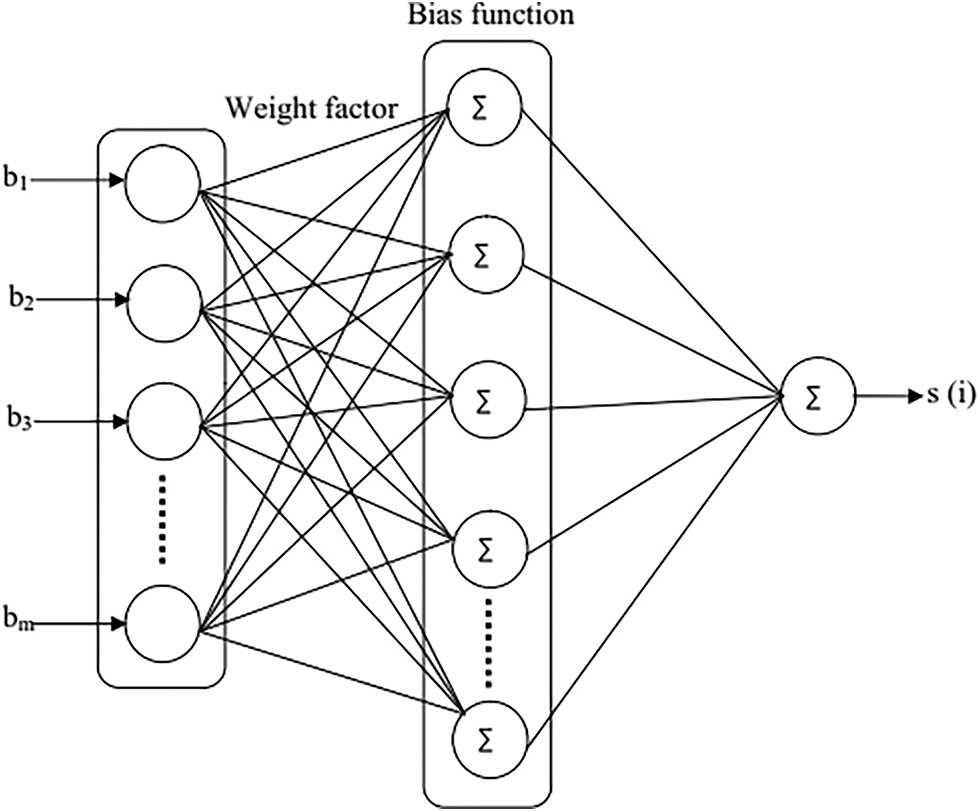
Figure 3: Chaotic neural network
Initially, the input plain signal
Here, m = 1, 2,…., m
Using this binary sequence, the function of weight factor is defined. This weight factor can be varied depend on the input functions. The generation of weight factor is defined as follows,
Here, j value is ranged between 0–7. As depicted in Eq. (16), weight factor is varied depend on the various inputs.
Third, weight factor generation is followed by the bias function generation. For each chaos, bias function is generated using the weight factor. This bias function solves the problem of singularity. It is defined as follows,
where,
At final, cipher signal is generated using the input function and weight factor. The generation of cipher is defined as follows,
where, the point
After the completion of encryption, decryption phase will be processed at the receiver. The following section describes the phase of decryption of input signal.

3.6 Decryption at the Receiver
The encrypted data will be decrypted at the receiver or medical server. In the phase of decryption, binary sequences are generated for the chaotic sequences and these binary sequences are given as input to the neural network. Also, the neural network generates the weight factor and bias function for the input function. Finally, decipher signal is generated with the ECC over GF secret key.
The proposed scheme is simulated in the platform of MATLAB with the system has the operating system of windows ‘10 with 64 bit and with 4GB main memory at 2 GHz dual-core PC. In this work, MIT-BIH Normal Sinus Rhythm dataset is used. For ECG signal compression, compressive sensing technique is used as well as Sparsity Adaptive Matching Pursuit algorithm (SAMP) is used for decompression. For secure transmission, PBOA based ECC over Galois field (EGC) with chaotic neural network (CNN) is presented.
The performance of the proposed EGC-PBOA-CNN is analysed in terms of encryption time, decryption time, energy consumption, throughput and network lifetime. Besides, the performance of the proposed scheme is compared with that of the EGC-CNN, EGC and ECC. The following sections describe the performance analysis of the different cryptography algorithms in terms of different metrics.
4.1 The Performance Analysis in Terms of Encryption Time
Encryption time is the total time to encrypt the ECG data. Fig. 4 shows the comparative analysis of the encryption time of different cryptography algorithms. As shown in the figure, the conventional ECC algorithm takes 10.5 ms to encrypt the ECG data. But, the encryption time of ECC is reduced to 8 ms when ECC is presented over Galois field. As the encryption process is performed using CNN, the encryption time of EGC-CNN is reduced to 6.2 ms than the EGC and ECC. However, the encryption time of EGC-CNN is further reduced to 3.4 ms as the private key of EGC is selected optimally using PBOA algorithm.
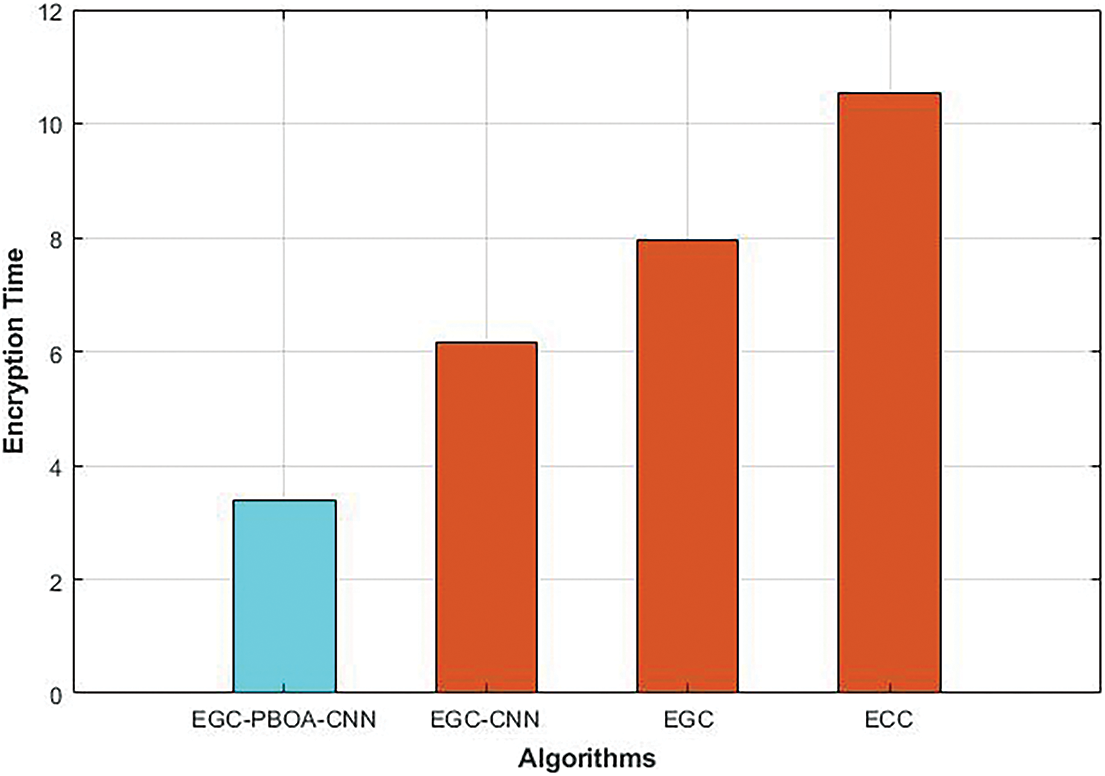
Figure 4: Encryption time of different cryptography algorithms
4.2 The Performance Analysis in Terms of Decryption Time
Decryption time is the total time to decrypt the encrypted ECG data. The comparison of decryption time of different cryptography algorithms is shown in Fig. 5. As shown in the figure, decryption time of EGC is reduced to 37% than that of the ECC. Compared to ECC and EGC, decryption time of EGC-CNN is reduced to 39% and 2% respectively. Like encryption process, CNN is used in the proposed scheme for decrypting the encrypted data. So, the decryption time of EGC-PBOA-CNN is reduced to 36%, 36.3% and 20% than that of EGC-CNN, EGC and ECC respectively.
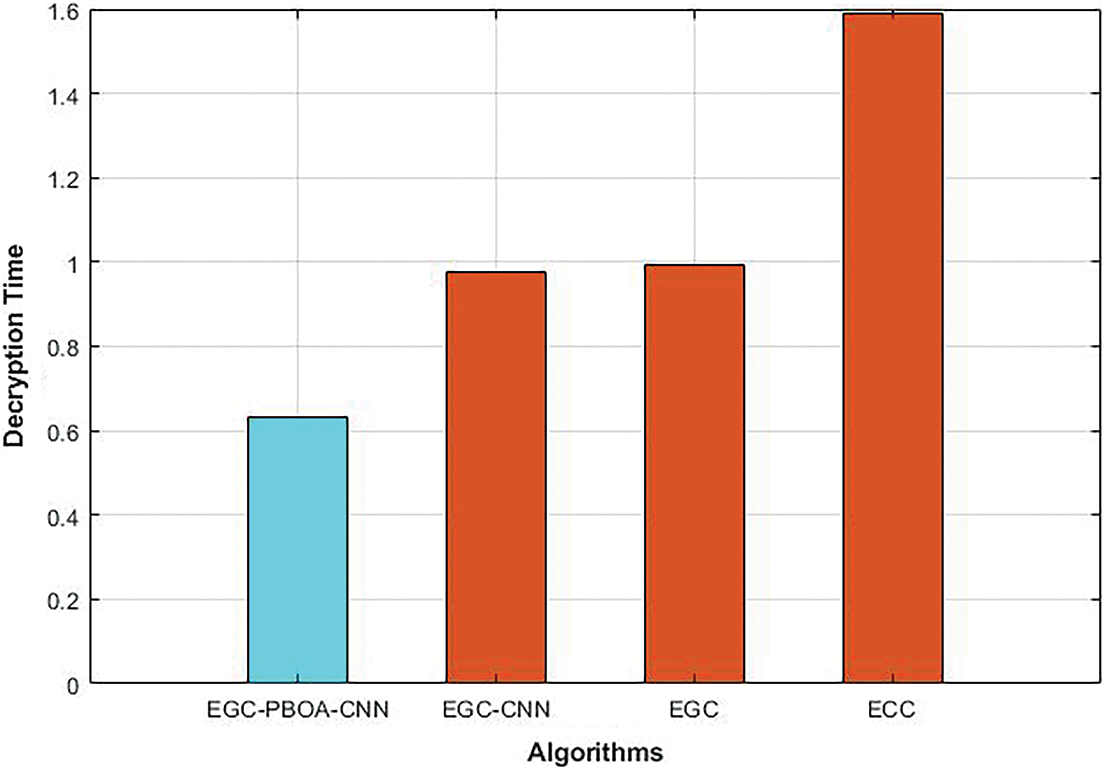
Figure 5: Decryption time of different cryptography algorithms
4.3 The Performance Analysis in Terms of Energy Consumption
Energy consumption defines that the total amount of energy consumed by the body sensors in the network. Fig. 6 shows the comparative analysis of the energy consumption of the different cryptography algorithms. As the ECC over Galois field reduces the processing time of ECC, energy consumption of EGC is reduced to 8% than that of the ECC. Compared to ECC and EGC, energy consumption of the EGC-CNN is reduced to 22% and 15% respectively as the encryption process of EGC is enhanced using CNN. Nevertheless, as the private key selection process is optimized using PBOA algorithm, energy consumption of EGC-PBOA-CNN is reduced to 10%, 24% and 30% than that of the EGC-CNN, EGC and ECC respectively.
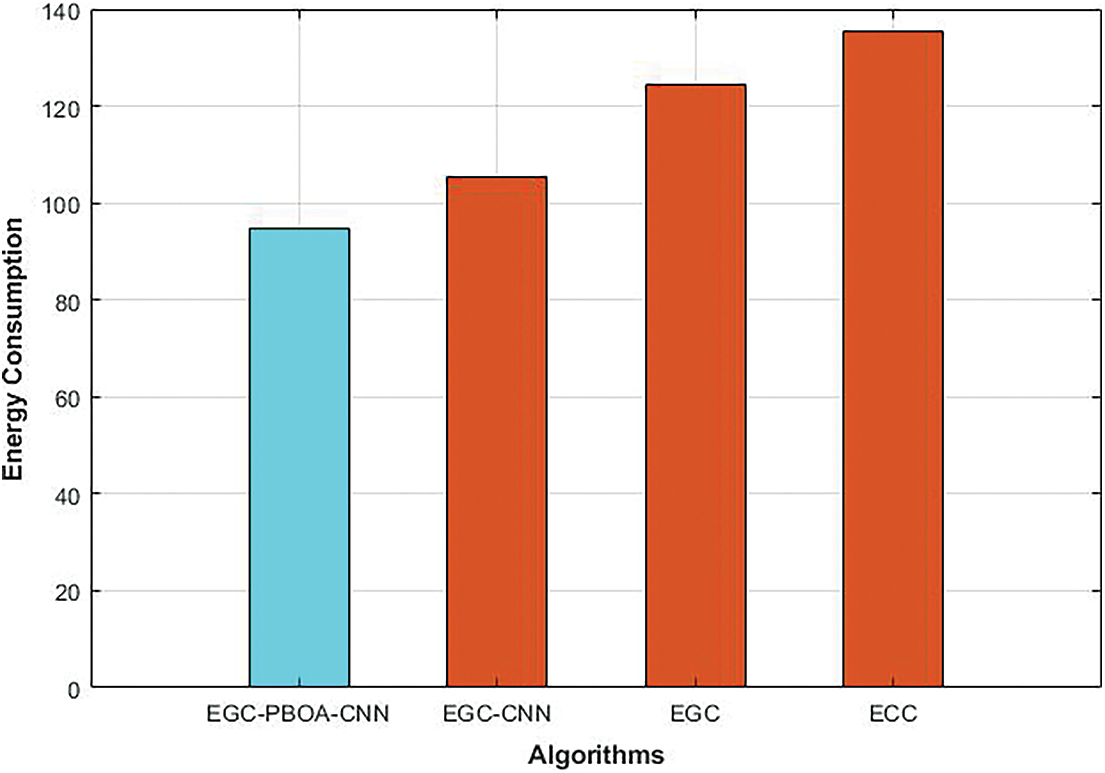
Figure 6: Energy consumption of different cryptography algorithms
4.4 The Performance Analysis in Terms of Throughput
Throughput defines that the number of ECG data received at the receiver to the delay of data transmission. The comparison of throughput of different cryptography algorithms is shown in Fig. 7. As shown in the figure, throughput of EGC is increased to 2.4% than that of the ECC. Compared to ECC and EGC, throughput of EGC-CNN is increased to 6.3% and 3.7% respectively. Throughput of EGC-PBOA-CNN is increased to 14%, 18% and 21% than that of EGC-CNN, EGC and ECC respectively.
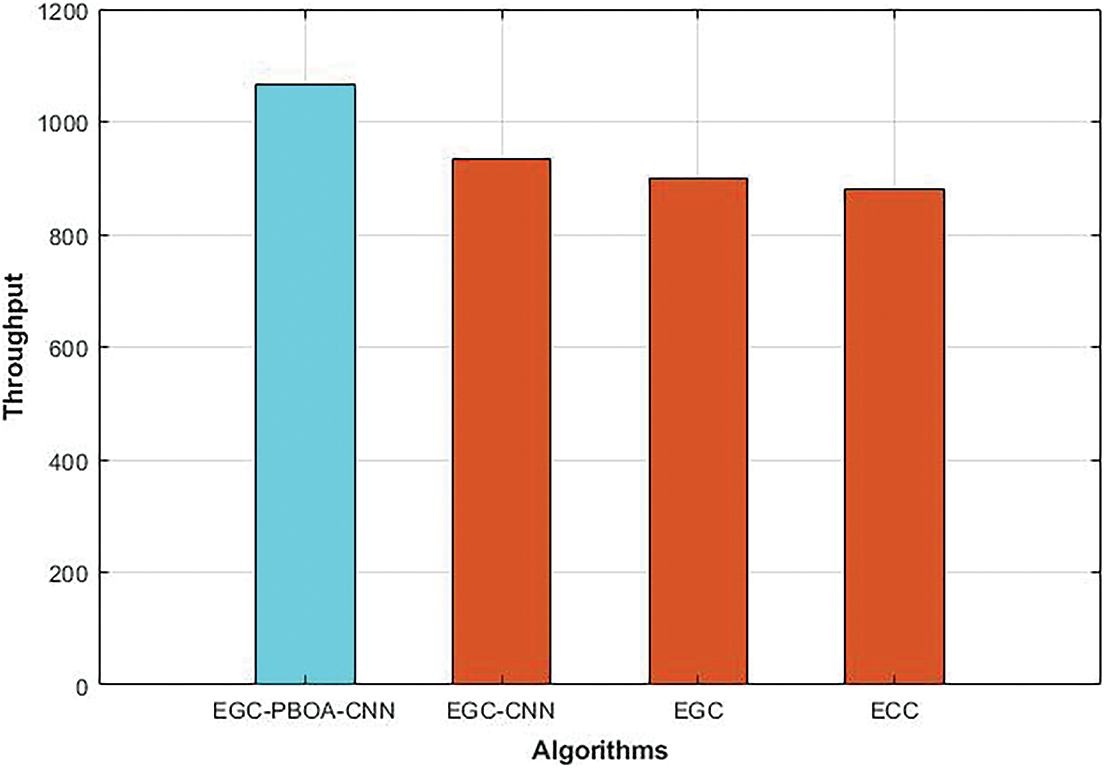
Figure 7: Throughput of different cryptography algorithms
4.5 The Performance Analysis in Terms MSE and SNR
Fig. 8 shows the comparative analysis of the MSE of the different cryptography algorithms. As shown in the figure, MSE of the EGC-PBOA-CNN is reduced to 68%, 71% and 89% than that of the EGC-CNN, EGC and ECC respectively. The comparison between SNR of the different cryptography algorithms is shown in Fig. 9. As illustrated in the figure, compared to EGC-CNN, EGC and ECC, the SNR of the EGC-PBOA-CNN is increased to 14%, 18% and 39% respectively.
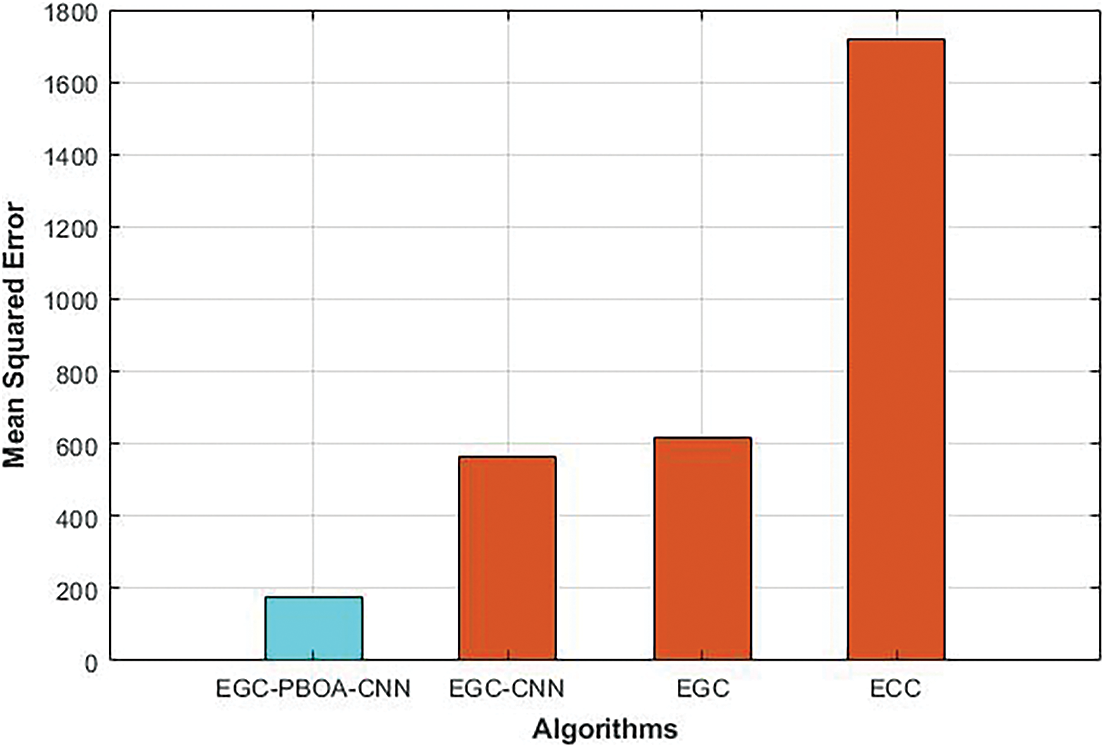
Figure 8: MSE of different cryptography algorithms
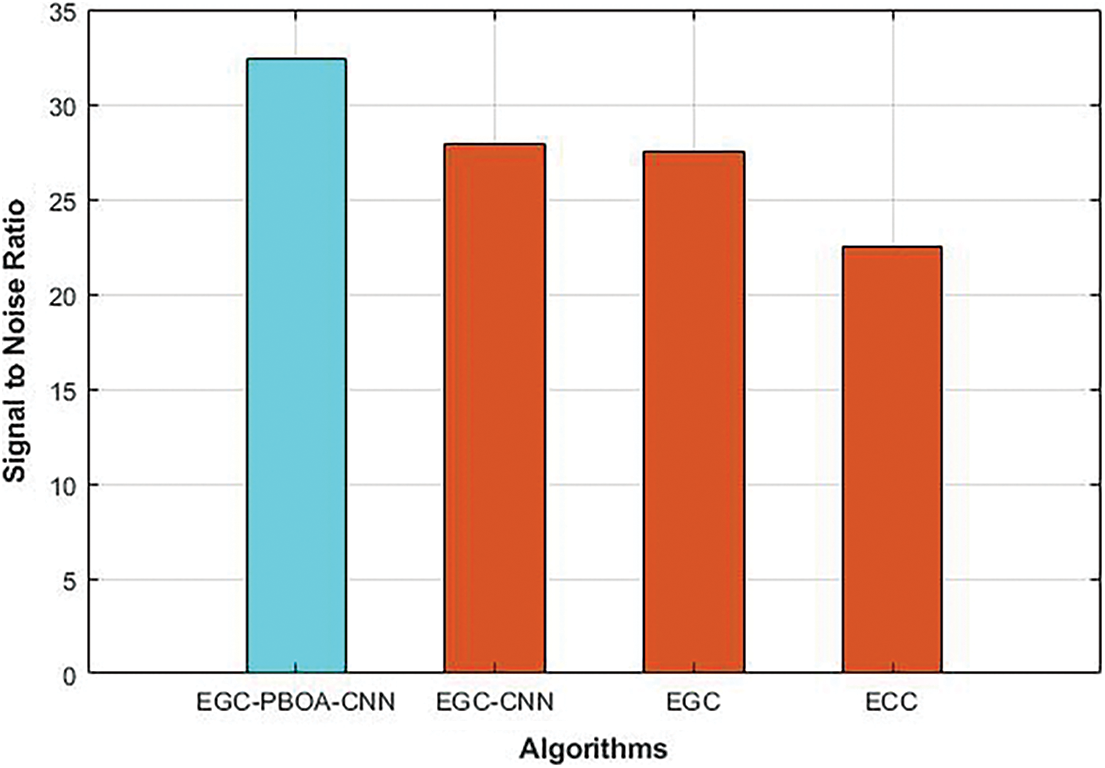
Figure 9: SNR of different cryptography algorithms
To solve the problem of transmission of ECG data against adversaries, an enhanced Elliptic Galois Cryptography (EGC) is presented in this paper. In the proposed EGC, private key has been selected optimally using PBOA algorithm. Using this optimal private key, public key has been generated. Then the encryption process of EGC has been done using chaotic neural network. As well as, the encrypted data has been decrypted using chaotic neural network. To evaluate the performance of the proposed cryptography algorithm, MIT-BIH Normal Sinus Rhythm dataset is used. The performance of the EGC-PBOA-CNN has been compared with that of the EGC-CNN, EGC and ECC. Simulation results showed that the proposed EGC-PBOA-CNN decreased the encryption time and decryption time as well as it increased the throughput of the network. In future, deep learning models will be presented for secure and efficient ECG signal transmission.
Acknowledgement: The author with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. U. H. Al Rasyid, D. Prasetyo, I. U. Nadhori and A. H. Alasiry. “Mobile monitoring of muscular strain sensor based on wireless body area network.” in 2015 Int. Electronics Symposium (IES), IEEE, pp. 284–287, 2015. [Google Scholar]
2. M. R. Yuce, “Recent wireless body sensors: Design and implementation.” in 2013 IEEE MTT-S Int. Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-BIO), IEEE, pp. 1–3, 2013. [Google Scholar]
3. S. Sharma, A. L. Vyas, B. Thakker, D. Mulvaney and S. Datta. “Wireless body area network for health monitoring.” in 4th Int. Conf. on Biomedical Engineering and Informatics (BMEI), IEEE, vol. 4, pp. 2183–2186, 2011. [Google Scholar]
4. K. Uemura, A. Kamiya, S. Shimizu, T. Shishido, M. Sugimachi and K. Sunagawa. “Comprehensive physiological cardiovascular model enables automatic correction of hemodynamic in patients with acute life-threatening heart failure.” in 2006 Int. Conf. of the IEEE Engineering in Medicine and Biology Society, IEEE, pp. 198–201, 2006. [Google Scholar]
5. N. Dey, A. S. Ashour, F. Shi, S. J. Fong and R. S. Sherratt. “Developing residential wireless sensor networks for ECG healthcare monitoring.” IEEE Transactions on Consumer Electronics, vol. 63, no. 4, pp. 442–449, 2017. [Google Scholar]
6. R. Shanthapriya and V. Vaithianathan. “ECG-Based secure healthcare monitoring system in body area networks.” in 2018 Fourth Int. Conf. on Biosignals, Images and Instrumentation (ICBSII), IEEE, pp. 206–212, 2018. [Google Scholar]
7. I. A. Sawaneh, I. Sankoh and D. K. Koroma. “A survey on security issues and wearable sensors in wireless body area network for healthcare system.” in 2017 14th Int. Computer Conf. on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), IEEE, pp. 304–308, 2017. [Google Scholar]
8. H. Qiu, M. Qiu and Z. Lu, “Selective encryption on ECG data in body sensor network based on supervised machine learning,” Information Fusion, vol. 55, pp. 59–67, 2020. [Google Scholar]
9. A. Pandey, B. Saini, B. Singh and N. Sood, “An integrated approach using chaotic map & sample value difference method for electrocardiogram steganography and OFDM based secured patient information transmission,” Journal of Medical Systems, vol. 41, no. 12, pp. 1–20, 2017. [Google Scholar]
10. M. Karthikeyan and J. Manickam, “ECG-Signal based secret key generation (ESKG) scheme for WBAN and hardware implementation,” Wireless Personal Communications, vol. 106, no. 4, pp. 2037–2052, 2018. [Google Scholar]
11. A. Algarni, N. Soliman, H. Abdallah and F. Abd El-Samie, “Encryption of ECG signals for telemedicine applications,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10679–10703, 2020. [Google Scholar]
12. P. Sanivarapu, K. Rajesh, N. Reddy and N. Reddy, “Patient data hiding into ECG signal using watermarking in transform domain,” Physical and Engineering Sciences in Medicine, vol. 43, no. 1, pp. 213–226, 2020. [Google Scholar]
13. G. Xu, “IoT-Assisted ECG monitoring framework with secure data transmission for health care applications,” IEEE Access, vol. 8, pp. 74586–74594, 2020. [Google Scholar]
14. H. Tan and I. Chung, “Secure authentication and group key distribution scheme for WBANs based on smartphone ECG sensor,” IEEE Access, vol. 7, pp. 151459–151474, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |