DOI:10.32604/csse.2023.025251

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.025251 |  |
| Article |
A Hybrid Regularization-Based Multi-Frame Super-Resolution Using Bayesian Framework
1Faculty of Information and Communication Technology, International Islamic University Malaysia, Kuala Lumpur, Malaysia
2College of Computer Science, King Khalid University, Abha, Saudi Arabia
3School of Theoretical & Applied Science, Ramapo College of New Jersey, Rampao Valley Road, Mahwah, USA
4Community College, King Khalid University, Abha, Saudi Arabia
*Corresponding Author: Mahmoud M. Khattab. Emails: mmkhattab2000@gmail.com, mktaab@kku.edu.sa
Received: 20 November 2021; Accepted: 20 December 2021
Abstract: The prime purpose for the image reconstruction of a multi-frame super-resolution is to reconstruct a higher-resolution image through incorporating the knowledge obtained from a series of relevant low-resolution images, which is useful in numerous fields. Nevertheless, super-resolution image reconstruction methods are usually damaged by undesirable restorative artifacts, which include blurring distortion, noises, and stair-casing effects. Consequently, it is always challenging to achieve balancing between image smoothness and preservation of the edges inside the image. In this research work, we seek to increase the effectiveness of multi-frame super-resolution image reconstruction by increasing the visual information and improving the automated machine perception, which improves human analysis and interpretation processes. Accordingly, we propose a new approach to the image reconstruction of multi-frame super-resolution, so that it is created through the use of the regularization framework. In the proposed approach, the bilateral edge preserving and bilateral total variation regularizations are employed to approximate a high-resolution image generated from a sequence of corresponding images with low-resolution to protect significant features of an image, including sharp image edges and texture details while preventing artifacts. The experimental results of the synthesized image demonstrate that the new proposed approach has improved efficacy both visually and numerically more than other approaches.
Keywords: Super-resolution; regularized framework; bilateral total variation; bilateral edge preserving
Over the last decade, there has been a tremendous advancement in software and hardware technology everywhere around the world. The resolution of an image has emerged to become one of the most important metrics for measuring the image quality in recent years. High-resolution (HR) images are often necessary and desirable for generating more extensive information within digital images. As a result, pictorial information and automatic machine perception are improved for human analysis and interpretation [1]. Nevertheless, the most effective use of image sensors and optical technology is typically a costly strategy that is also limited in its ability to improve the image resolution. As a result, the use of multi-frame super-resolution (SR) image reconstruction technology is a cheap and powerful way for generating an HR image from a series of low-resolution (LR) images [1].
HR images provide additional information to have a better visual perspective. HR images are also used widely in various imaging applications which include but are not limited to surveillance videos [2], medical imaging domain [3], forensics imaging field [4], and remotely sensed imagery [5]. Therefore, there seems to be a great demand for an HR image that recurrently exceeds the capabilities of current HR digital cameras [6,7]. Nevertheless, the contemporary imaging system generates LR images, which should be enhanced to produce HR images. The image resolution is reduced due to a variety of possible factors, which include physical limitations on the images, insufficient image detectors, a lower spatial sampled rate, and an inappropriate approach for acquiring images [8–11]. Recently, SR image reconstruction algorithms have emerged as a significant and economical strategy for improving the quality of captured LR images, which satisfies the increasing business market need for using HR images [12–14].
Tsai and Huang are the first to describe the SR problem for reconstructing the HR image, which is based on the idea of using frequency domain [15]. There have since been a number of different techniques to resolve the SR problem presented in the literature [8–11,16,17]. The regularization method's primary goal is to overcome the SR problem, which is difficult to handle because of its ill-conditional structure. Recent researches have been carried out with the goal of overcoming the SR difficulty by utilizing the regularization framework [8–11,18–25]. In the regularized multi-frames SR image reconstruction, the maximum a posteriori (MAP) approach is used to correspond a posteriori-distributed over an HR image accordingly to a data-fidelity term, whilst a regularization term can be employed as an image prior [10,26].
Without using any prior knowledge, the reconstruction of an SR image is often an inverse issue, which is extremely challenging to solve [8,9,13,27]. Therefore, in recent researches, several regularization-based SR algorithms have been presented, each of which incorporates prior knowledge to approximate an unidentified HR image. The Tikhonov prior-based SR technique suggests the use of the L2 norm, which has the advantage of being able to quickly reduce noise from images while also blurring the borders of images [28]. The bilateral total variation prior (BTV) is proposed by Farsiu et al. to penalize gradient magnitudes, and it is derived in accordance with the L1 norm [10,26,29]. BTV is utilized to maintain the edges effectively, although artifacts are generated in the smoothed regions when BTV is applied. The bilateral edge-preserving (BEP) prior is proposed to preserve sharp image edges, but ignore the local image features [16].
In this research, we propose a new SR approach to increase the effectiveness of multi-frame SR image reconstruction by increasing the visual information and improving the automated machine perception, which improves human analysis and interpretation processes. The proposed solution has been created by employing the regularization framework. Therefore, the main contribution is to develop an efficient approach which is derived from the hybrid of reconstruction models in the image reconstruction stage based on employing the adaptive norm and Lp norm in the data-fidelity term, beside adopting BEP and BTV prior models in the regularization term respectively. This new SR approach is used to protect image texture information while eliminating noise and improving the edges of the estimated image from a series of LR images. Extensive experiments have indeed been performed to explore the reliability and performance of the proposed SR approach.
The remainder of this research work is structured as follows: the image observation or degradation model explains the formulation of SR problem and Bayesian framework. Next, we illustrate the image SR reconstruction prior models in detail. Then, we present and discuss the proposed multi-frame SR approach, while the experimental results are illustrated. At last, the conclusion is provided.
2 Multi-Frame SR Problem Formulation
In this section, we formulate the multi-frame SR image reconstruction problem that needs to be resolved. Accordingly, this formulation is classified into an image observation model and also the Bayesian framework, which are described in the following subsections.
In SR image reconstruction, a suitable image model has to be established that can accurately represent the physical mechanism of image degradation. In the practical sampling process, there are certain degrading effects such as atmospherically imbalance, object movements, blurring effects, and down sampled devices. As a result, the image degrading model must first be developed from a mathematical perspective to study the issue of SR reconstruction through the model that links the LR images to the HR image [12]. As a result, the selection of an appropriate degradation model is the first step in reconstructing the SR image, as illustrated in Fig. 1, where it serves as the essential kernel of the whole image reconstruction processes [1].
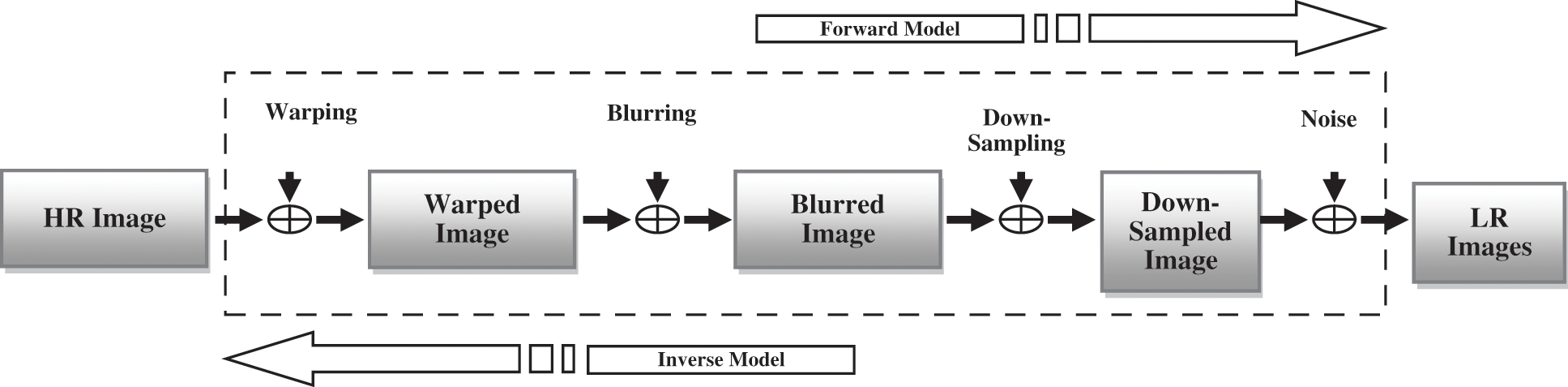
Figure 1: Sketch of degradation model
In this paper, the warping process is the movement from the image acquisition mechanism, where X presents the HR image, while Fk is the motion matrix that is utilized to create the motion degradation process of the kth LR image [8]. Initially, let's assume that Yk is a collection of LR images, where M is the number of images in this collection. For instance, Yk,1 is the first LR image to be processed and Yk,m is the mth LR image processed. Therefore, the sequence of LR images can be rewritten as:
Thereafter, let's assume that Hk is the blurred matrix that describes the point spread function (PSF) of the imaging system, and Dk defines the matrix of down-sampling which goes in both the movement and blurring matrices of the kth image. Finally, nk denotes the additive system noise. In this paper, we presume the use of global motion which is used in the warping process and also the use of White-Gaussian noise. As a result, the image degradation model that is used to emulate the entire processes may be expressed in Eq. (2) as follow [8,9,11,13]:
Keep in mind that, regardless of the fact that complicated movements in real sequences are widespread and cannot be described by a simple parametric form, global translational displacements throughout many frames, which serve as a basic issue, remain the goal of this study. In general, we suppose that the produced LR images are obtained in comparable conditions; hence, the following formula can be modeled as follow:
D and H are the identical motion and blurring matrices respectively, where Fig. 1 shows the image degradation model [1].
2.2 Bayesian Framework of Super-Resolution
Essentially, the Bayesian framework's primary task is to estimate the probability of an unpredictability issue depending on the available information or knowledge. This is accomplished by incorporating multiple priors into a mathematical form that is more effective than statistical inference in this situation. As a result, the uncertainty inference issue lies at the heart of SR technology used to predict an unknown HR image from a set of LR recorded images. In the other aspect, the measured LR images constitute proof of HR image inference, and the regularization which defines the image prior is constrained by the recovered result of SR [30].
For the Bayesian framework, one of the most widely used methods is the maximum a posteriori technique, which takes into account prior limitations on the image and accomplishes outcomes by maximizing the posterior probability objective functions. Furthermore, it is well-known for its adaptability in terms of edge preservation and the estimate of joint parameters. Generally, Bayesian estimation can be used when it is necessary to determine the posteriori probability distribution for uncertain parameters instead of utilizing the specified parameters [30]. The MAP estimator is widely used as follow:
where P(Yk|X) describes the conditional probability of the LR image (Yk) through searching for the HR image (X), and P (X) denotes the prior probability of the HR image.
The image degradation model in Eq. (3) outlines the process of creating LR images while also inversely estimating the unknown HR image. There are two terms in the core structure of multi-frame SR: a term for data-fidelity and another for regularization. In order to reduce the residual between both the expected HR image and the recorded LR images, M estimator is used for the data-fidelity term. In order to limit the minimization function to a steady state of the produced HR image [18], the regularization term is used. The following is a description of the classical multi-frame SR model:
where ρ(.), R(.), and λ describe the data-fidelity term, the regularization term, and the regularization parameter respectively.
In this section, we explain the multi-frame SR image reconstruction models, which they are required to generate the HR image. A short discussion of the Lp norm and adaptive norm is provided as the data-fidelity term, and also the BTV and BEP models are described as the regularization term in the next subsections.
3.1 Lp Norm and Bilateral Total Variation (BTV)
The L1 error norm is proposed by Farsiu et al. [29] to be utilized as a data-fidelity term, and the predicted HR image is resolved when p = 1 by:
Farsiu et al. [29] propose an appropriate model named BTV, which incorporates a bilateral filtering and total variation (TV) regularization to achieve the desired results. A huge number of neighbors is used to estimate the gradient at a particular pixel, and BTV regularization takes this into consideration. Furthermore, BTV has the advantage of preserving sharp edges in images with few distortions while still being computationally economical and simple to implement. The following is the definition of the primary formula of BTV prior:
where
A large variety of solutions are available and can be achieved in an unknown situation that's because SR is an ill-posed issue. Furthermore, a few levels of noise in observations result in huge variations in the final outcome, which is an unsteady solution. As a result, the techniques of utilizing regularization-based approaches for SR image reconstruction are a really beneficial approach to get a stable solution, remove distortions from the final outcome, and increase the rate of convergence. An extensive range of regularization approaches are available; one of them is employed to generate HR images with sharp-edged and simplicity of implementation. The primary advantage of employing the regularization term during the image reconstruction phase is that it allows for the compensation of lost data with many prior information, which can then be employed as a penalty function for the minimizing objective function [26]. Consequently, the objective function of the BTV regularization term [29] is denoted in Eq. (7) as follows:
In this study, we use the steepest descent method to obtain a close result in Eq. (8). The iteration of measurement that uses the steepest descent method is given below:
where β is a scalar which controls the step size in the gradient plane, the regularization parameter is denoted by λ,
3.2 Adaptive Norm and Bilateral Edge Preserving (BEP)
Charbonnier et al. [31] propose the BEP regularization model, then it is later modified by Zeng et al. [26]. The BEP regularization follows the same BTV concept, but with using an adaptive norm rather than the L1 norm as follows:
where a represents a positive number while e is the difference to be minimized. Initially, this norm proposes to protect edges and boundaries in the process of image regularization. Parameter a calculates the value of error in which the regularization changes the linear formula to constant. Also, the same definition of the adaptive norm is used in the case of SR problems [26]. ρ (e, a) function seems to be M-estimator as it matches the maximum likelihood (ML) estimator and its effect function is provided by:
Using the adaptive norm in Eq. (10), the data-fidelity term is
where ak represents the kth frame of the threshold parameter. A constant subtraction has really no effect on the minimization function and can be solved by the following:
An SR regularization framework for edge preservation is developed to restrict image gradients. Furthermore, it can protect large gradients that fit the edges appropriately, whereas smooth small gradients often have a noise effect. Therefore, the function ρ(e, a) in Eq. (10) follows the requirements for the preservation of the edges to propose a BEP regularization that looks like:
with α, q,
The cost function can be defined as:
where ek is the observation error which equals to (DHFkX − Yk). ak represents the threshold parameter of the kth LR image, which is determined using the average error of observation. In the estimation of the HR image process, the total number of pixels is represented by parameter N.
The objective function can be optimized with the steepest decent approach. Nevertheless, it normally performs faster with the optimization of the conjugate gradient (CG). CG algorithm's iterative function is defined as:
where the conjugate-gradient vector is represented by Pn at the nth iteration. Additionally, the gradient of C(
where
4 Proposed Multi-Frame SR Approach
As stated previously, the generated HR image (
A large number of multi-frame SR image reconstruction techniques have indeed been proposed in order to increase the quality of the predicted HR image, with different levels of success. Edges and noises cannot be distinguished using conventional regularization terms such as Tikhonov and TV. As a result, although noise is eliminated well, the texture data is distorted which decreases the efficiency of these strategies. BTV and BEP are extensively utilized prior functions in many situations. The BTV regularization method is efficient in recovering sharp-edged images because it incorporates the greater neighbors into the computation of the gradient at a given pixel. However, it fails when trying to retrieve images of flat surfaces that are sensitive to the staircase effects. The BEP method is useful for preserving edge features and reducing artifacts in areas of flat images. Nevertheless, it discards the image's primary properties. As a result, BTV and BEP are still affected by noise and blur.
In this paper, based on the strengths and weaknesses of the regularizations that are addressed above, a new approach is proposed for the image reconstruction of multi-frame SR, so that it is created on the regularization framework. This new SR approach is derived from employing the adaptive norm and Lp norm in the data-fidelity term, beside adopting BEP and BTV prior models in the regularization term respectively to measure the HR image through the use of the corresponding LR image series, where image noise suppression and edge preservation can be accomplished concurrently. One of the primary goals of the proposed method is to protect essential image features as much as possible including borders and boundaries, while also protecting the sharp image edges and avoiding artifacts. Additionally, the high-frequency portions of the proposed method are increased, degradations inside the image capture systems are eliminated, and a good balance between edge preservation and noise elimination is achieved.
The overall procedure flow of the proposed approach can be implemented via the following steps:
Step (1): Generate a series of LR images from the original HR image by using the above observation model in Eq. (3), so that it is used as an input to the proposed approach.
Step (2): Assign one of its LR images as the LR reference image to be used for initializing the HR image.
Step (3): Estimate the motion parameters by calculating both of the rotate dangle and the vertical and horizontal shift among the LR reference image and the next LR image to enhance the warp matrix Fk.
Step (4): Apply the bi-cubic interpolation on the LR reference image by using the magnification factor to measure the initial HR image (X0) which is used as an input to the image reconstruction stage.
Step (5): Input both of the initial estimation image (X0) and the LR images into an SR image reconstruction model that depend on the adaptive norm and BEP prior model according to Eq. (17) beside using shift and rotation angle parameters to reconstruct the intermediate HR image (Xi).
Step (6): Assign the intermediate HR image (Xi) that was extracted from Step (5) into the initial HR image (X0) in form X0 = Xi to be used as an input to the next step.
Step (7): Reconstruct the final HR image (Xf) through inputting both of the intermediate HR image (Xi) which is assigned to the initial HR image (X0) and the LR images into an SR image reconstruction model that depend on L2 norm and BTV prior model according to Eq. (9) beside using the motion parameters.
The schematic diagram of the whole procedure flow for SR image reconstruction approach based on BTV and BEP prior models is shown in the Fig. 2.
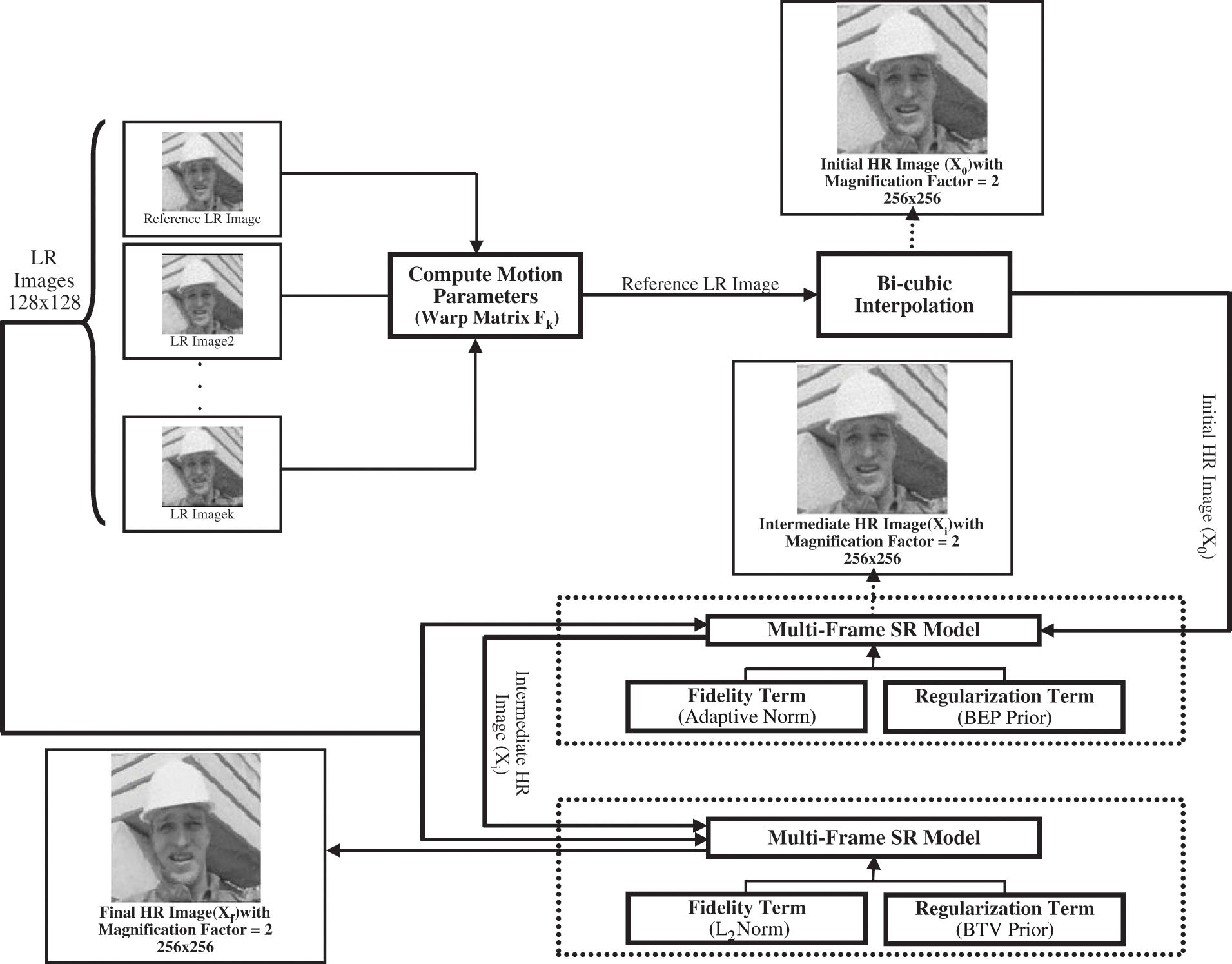
Figure 2: The flow illustration of the proposed multi-frame SR method
5 Experimental Results and Discussion
This section outlines the real performance assessment of the technique provided above, particularly when compared to numerous state-of-the-art methods described in literature. Numerous experiments are conducted in order to evaluate the performance of the proposed methodology. Section 5.1 discusses the experimental environment, and then describes the parameter settings. Section 5.2 illustrates the performance evaluation. A comparison of the four most popular SR techniques to our proposed SR method is offered in Section 5.3.
This sub-section presents a variety of simulated results to measure the effectiveness of the proposed SR methods. The proposed SR techniques are examined using a huge benchmark datasets available on the Web [32], which contains images of various scenes. According to Fig. 3, we chose six images from a benchmark collection that represented a variety of styles in order to produce our synthetic LR sequences. The original 120 × 120 pixel images for acen, cartap, foreman, text, and brain, as well as the 250 × 100 pixel license plate image are shown in Fig. 3. Furthermore, the primary factors for selecting these datasets are their contents, their accessibility for comparability, their realism, and the fact that they are regularly utilized by the most current works relevant to [3,33–35]. Also, these datasets differ in their complexity, irregularity, textural characteristics, gray level histogram, contrasts, and smoothness.

Figure 3: A set of original benchmark datasets (a) Acen (b) Cartap (c) Foreman (d) Text (e) Brain (f) License plate
In practice, it is extremely difficult to measure the performance of SR techniques mathematically because the ground truth of the HR images is still not available. The proposed technique is tested using simulated data in all experiments since the ground truth HR images for simulated LR images are already available. The proposed SR techniques are tested against the four state-of-the-art SR approaches in all experiments using the same information and parameter settings:
1. Patanavijit and Jitapunkul present an SR approach that incorporates the Lorentzian error norm for both data fidelity and regularization [36] (referred to as “LOR”).
2. Farsiu et al. present L1 and L2 norms using BTV prior [29] (referred to as “L1-BTV” and “L2-BTV”).
3. Zeng and Yang introduce an adaptive norm using BEP prior [26] (referred to as “BEP”).
The system configuration requirements for implementing the extensive experiment are described in Tab. 1. Tab. 2 highlights the parameter settings which are used to provide a fair assessment of all experiments.


To be able for evaluating and comparing the performance of the approximated HR image with respect to the original HR image, the structural similarity (SSIM) and the peak-signal-to-noise ratio (PSNR) indicators are computed [1,8,25,37,38]. As a result, the PSNR indicator is determined using the mean-square error (MSE). Accordingly, the MSE is the average error between the recovered SR and ground truth HR images. MSE and PSNR are explained by providing a recovered SR m x n image
Using SSIM measurement, we can determine the degree of similarities between the generated SR and original HR images. Additionally, the SSIM measurement takes into account the luminance, contrast, and structural differences among two images. The SSIM measurement can be expressed as follows:
where the means are denoted by μX and
There are two different kinds of evaluation criteria used in this research work. The first type is subjective or qualitative evaluation and the second type is objective or quantitative evaluation. One of the clearest and straightforward approaches is subjective evaluation. In order to begin analyzing the generated HR images, it is necessary for people to be familiar with a few key features of the rebuilt images. Therefore, it's important to use the human eye to determine which HR images have been most accurately reconstructed. On the other side, objective evaluation is a strategy aimed to estimate the outcomes by computing the correlation coefficient among the images. SR image reconstruction is often evaluated using PSNR and SSIM metrics. Generally, a better reconstruction effect can be achieved if PSNR and SSIM values are large.
In order to determine the efficacy of SR reconstruction technique, the experimental outcomes of the suggested SR technique on simulated data are shown in this subsection. Typically, it is essential to perform the image formation model in Eq. (3) for all techniques in order to ensure a fair direct comparison. In order to assess the performance of the suggested SR technique, comparisons are presented that are visually and quantitatively in nature. In Figs. 4–9, the recovered SR images for “Acen,” “Cartap,” “Foreman,” “Text,” “Brain,” and “License Plate” from Fig. 3 are shown in comparison with numerous existing state-of-the-art techniques. For each experiment, the results of reconstruction are shown in Figs. 4–9. The following are the descriptions of the meanings for these figures: (a) illustrates the original HR image, (b) represents a single estimated LR images, and (c-f) the reconstructed HR images using LOR, L1-BTV, BEP, and L2-BTV techniques are demonstrated, respectively. Finally, (g) specifies the generated SR image for the proposed approach. Moreover, reconstructed images are displayed in the lower right-hand corner of each image in order to provide a clear visual representation.

Figure 4: A visually comparison on the “Acen” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method

Figure 5: A visually comparison on the “Cartap” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method


Figure 6: A visually comparison on the “Foreman” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method

Figure 7: A visually comparison on the “Text” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method

Figure 8: A visually comparison on the “Brain” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method

Figure 9: A visually comparison on the “License Plate” image of the proposed method and several SR techniques. (a) Original HR image (b) Single LR image (c) LOR (d) L1-BTV (e) BEP (f) L2-BTV (g) Proposed method
Figs. 4–9 show the reconstruction results for HR images. For all of the simulated data, the additive white Gaussian noise and blurring are added to the generated sequence of LR images as previously described. Therefore, Figs. 4–9 show that the HR image reconstructed by LOR and L1-BTV have poor performance to suppress the additive white Gaussian noise, appear blurry, and lead to a staircase effect in the recovered HR images as shown in Figs. 4–9 (c)-(d). For example, the image of Acen in Figs. 4c and 4d shows the presence of a lot of noise and more distortion, which leads to the appearance of the numbers 500 and 600 to look bad and blurry. These distortions appear because both LOR and L1-BTV do not work well when the additive white Gaussian noise is used.
On the other side, the experiment shows that the results of BEP method are better than LOR and L1-BTV methods. In addition, the BEP method has satisfactory inhibitory performance on the staircase effect. This improvement is due to the BEP method uses an adaptive error norm in the fidelity term, which is capable to suppress the additive white Gaussian noise well. However, the BEP method still suffers from some noisy pixels exists in the local areas of the reconstructed image due to its simple initial estimation as shown in Figs. 4–9 (e). For example, the Cartap image in Fig. 5e demonstrates a little noise in the white blank region, which causes the final image to look fairly well.
In the contrary, the L2-BTV method provides better image reconstruction and leads to relatively smooth image reconstruction results for smooth image regions, because the use of L2 norm achieves the best result than Lorentzian norm or L1 norm when the additive white Gaussian noise is used. Moreover, the distributional characteristics of the additive white Gaussian noise and the L2 norm is a quadratic model which are similar to each other. However, some image edges are over-smoothed, because the image variations are reduced and the image is uniformly smoothed in all dimensions. It is possible to prevent the staircase effect by using the proposed BEP-BTV method, which is able to rebuild the image pixels with identical grayscale values in smooth areas of the image and preserve the image edges. Furthermore, the proposed approach shows more fine details, presents more information and displays more textures by suppressing the white Gaussian noise, preserving the image details, and estimating errors as shown in Figs. 4–9 (f)-(g). This improvement is due to the use of the advantages of both the adaptive error norm and the L2 error norm in the data fidelity term of the proposed approach which can well estimate errors and prevent the additive white Gaussian noise. Moreover, BTV prior takes into consideration the utilization of a high number of neighbors to estimate the gradient at each individual pixel, while BEP regularization penalizes the gradients of images in order to protect high gradients according to the edges and smooth tiny gradients which are typically noise effects. For example, the image of Foreman in Fig. 6g shows the suppression of noise, excellent image clarity, and no aliasing at the edges of the reconstructed image.
Finally, after presenting the reasons for improving the results in the previous discussion, it becomes clear that the proposed approach generates the reconstructed HR image with good visual quality compared to other SR approaches and gives the most visually pleasing results. Furthermore, it avoids the stair-casing effect and preserves the image details such as sharp edges while suppressing the noise. Moreover, the proposed approach achieves decent results in terms of the reconstruction of image structures while the other SR approaches prone to over-smoothing or residual noise. Therefore, the proposed approach is significantly cleaner and more vivid, which is closest to the ground truth image.
In order to support the visual appearance comparison, a computational analysis is necessary. As a result, PSNR and SSIM metrics are used to estimate the quantitative quality of produced HR images. PSNR and SSIM indexes are used to evaluate produced HR images; SSIM is a supplemental measure of image quality based on the identified characteristics of the human visual system, whilst PSNR is used to evaluate the quality of produced HR images. The PSNR and SSIM measurements for the six investigated images from Fig. 3 are shown in Tabs. 3 and 4, where the best PSNR and SSIM values are shown in bold numerals.

Tab. 3 summarizes the quantitative quality assessment results and shows that the proposed approach has the best PSNR values, indicating that it is successful in reducing blur and noise. Additionally, the SSIM data in Tab. 4 indicate that the image quality is excellent in terms of image preserving characteristics. In accordance with subjective evaluations, the proposed approach produces images with sharped and powerful edges, which enhances PSNR and SSIM values. Therefore, this quantitative quality evaluation validates the observation that the results are visually pleasing (Figs. 4–9). In particular, the proposed approach achieves higher PSNR and SSIM values, which has been shown to be correlated well with human perception of image SR. The following findings can be derived from the information presented in the previous tables (Tabs. 3 and 4):
1. The proposed approach in this paper is superior to other SR methods (LOR, L1-BTV, BEP, L2-BTV) for image reconstruction in terms of PSNR and SSIM. This demonstrates that the proposed approach performs well in terms of deblurring and noise removal, while preserving a higher degree of similarity between the recovered and original images.
2. In comparison to the BEP technique, the PSNR values obtained using the proposed approach are higher by 1.4535–5.2232 decibel (dB) for the six images. For example, the PSNR value of the proposed approach (29.9477 dB) is 5.2232 dB greater than that of the BEP technique (24.7245 dB) for the Cartap image, and the PSNR difference becomes 2.1296 dB for the image of the License Plate (32.6064 dB vs. 30.4768 dB).
3. Compared with the L2-BTV method, the proposed approach increases and improves the capability to describe image gradient sparsity. The proposed approach has PSNR values that are 0.0103–0.5475 dB higher than those of the L2-BTV method, when recovering the six images. For the Brain image, PSNR of the proposed approach (30.647 dB) is 0.1042 dB higher than that of the L2-BTV method (30.5428 dB).
4. Our average PSNR is at least 0.1426 dB higher than the average PSNRs of the four chosen state-of-art methods (LOR, L1-BTV, BEP, L2-BTV).

The visual examination from Figs. 4–9 shows that LOR, L1-BTV and BEP methods suffer greatly from the presence of noise because the L1 norm and the adaptive norm in Eqs. (6) and (13) respectively have some difficulties in dealing with an additive white Gaussian noise. While the solved result by the L2 norm is ideal, if the model error is a white Gaussian distribution. Therefore, the L2-BTV method clearly demonstrates its efficiency in the case of eliminating noise and protecting the edges inside the image, even though we notice that the noise is not completely removed and there is a small staircase artifact appears in some smooth regions. Certainly, the generated HR images from the proposed SR approach have a better quality visually as compared to the others. Moreover, it improves the ability to recover image information, preserve edges, eliminate noises in smooth regions and improve the brightness of the entire image. Tab. 3 summarizes the quantitative quality assessment results and shows that the proposed approach has the best PSNR values, indicating that it is successful in reducing the blur and noise. Additionally, the SSIM data in Tab. 4 indicate that the image quality is excellent in terms of image preserving characteristics. As a result, the proposed SR approach always has better results as compared to other methods which guarantee its efficiency. As a result, the proposed approach always has better results as compared to other methods (LOR, L1-BTV, BEP, L2-BTV) which guarantee its efficiency.
In this paper, we propose a new approach for multi-frame SR image reconstruction dependent on the hybrid of reconstruction models in the image reconstruction stage to measure the HR image through the use of the corresponding LR image series. This new SR approach is based on employing the adaptive norm and Lp norm in the data-fidelity term, beside adopting BEP and BTV prior models in the regularization term respectively. One of the primary goals of the proposed method is to protect essential image features as much as possible including borders and boundaries, while also protecting the sharp image edges and avoiding artifacts. Additionally, the high-frequency portions of the proposed method are increased, degradations inside the image capture systems are eliminated, and a good balance between edge preservation and noise elimination is achieved. The efficiency of the proposed SR approach is measured for synthetic image, and it can be compared with several related state-of-art approaches through both visual and quantitative comparison. The experimental results of the synthesized image demonstrate that the new proposed approach has improved efficacy both visually and numerically more than other approaches. Additionally, we demonstrate numerically that the suggested technique always provides the best PSNR and SSIM values.
Acknowledgement: The authors extend their appreciation to the Institute for Research and Consulting Studies at King Khalid University.
Funding Statement: The funding was provided by the Institute for Research and Consulting Studies at King Khalid University through Corona Research (Fast Track) [Grant Number 3-103S-2020].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. M. Khattab, A. M. Zeki, A. A. Alwan and A. S. Badawy, “Regularization-based multi-frame super-resolution: A systematic review,” Journal of King Saud University-Computer and Information Sciences, vol. 32, no. 7, pp. 755–762, 2020. [Google Scholar]
2. H. Seibel, S. Goldenstein and A. Rocha, “Eyes on the target: Super-resolution and license-plate recognition in low-quality surveillance videos,” IEEE Access, vol. 5, pp. 20020–20035, 2017. [Google Scholar]
3. T. Köhler, “Multi-frame super-resolution reconstruction with applications to medical imaging,” Ph.D. thesis, Friedrich-Alexander-Universität (FAU) Erlangen-Nürnberg, Bamberg, Deutschland, 2018. [Google Scholar]
4. J. Satiro, K. Nasrollahi, P. L. Correia and T. B. Moeslund, “Super-resolution of facial images in forensics scenarios,” in 2015 Int. Conf. on Image Processing Theory, Tools and Applications (IPTA), IEEE, Orleans, France, pp. 55–60, 2015. [Google Scholar]
5. W. Ma, Z. Pan, J. Guo and B. Lei, “Super-resolution of remote sensing images based on transferred generative adversarial network,” in IGARSS 2018-2018 IEEE Int. Geoscience and Remote Sensing Symp., Valencia, Spain, pp. 1148–1151, 2018. [Google Scholar]
6. S. C. Park, M. K. Park and M. G. Kang, “Super-resolution image reconstruction: A technical overview,” IEEE Signal Processing Magazine, vol. 20, pp. 21–36, 2003. [Google Scholar]
7. H. Hou, M. Wang and X. Wang, “RL-MS-L filter function for CT image reconstruction,” TELKOMNIKA (Telecommunication Computing Electronics and Control), vol. 14, pp. 195–202, 2016. [Google Scholar]
8. S. C. Mohan, “Adaptive super-resolution image reconstruction with lorentzian error norm,” Indian Journal of Science and Technology, vol. 10, no. 16, pp. 1–6, 2017. [Google Scholar]
9. S. Huang, J. Sun, Y. Yang, Y. Fang, P. Lin et al., “Robust single-image super-resolution based on adaptive edge-preserving smoothing regularization,” IEEE Transactions on Image Processing, vol. 27, no. 6, pp. 2650–2663, 2018. [Google Scholar]
10. X. Liu, L. Chen, W. Wang and J. Zhao, “Robust multi-frame super-resolution based on spatially weighted half-quadratic estimation and adaptive BTV regularization,” IEEE Transactions on Image Processing, vol. 27, no. 10, pp. 4971–4986, 2018. [Google Scholar]
11. A. Laghrib, A. Hadri, A. Hakim and S. Raghay, “A new multiframe super-resolution based on nonlinear registration and a spatially weighted regularization,” Information Sciences, vol. 493, pp. 34–56, 2019. [Google Scholar]
12. L. Wang, Z. Lin, X. Deng and W. An, “Multi-frame image super-resolution with fast upscaling technique,” Computer Vision and Pattern Recognition, pp. 1–11, 2017. [Google Scholar]
13. A. Laghrib, A. Ben-Loghfyry, A. Hadri and A. Hakim, “A nonconvex fractional order variational model for multi-frame image super-resolution,” Signal Processing: Image Communication, vol. 67, pp. 1–11, 2018. [Google Scholar]
14. M. Hakim, A. Ghazdali and A. Laghrib, “A Multi-frame super-resolution based on new variational data fidelity term,” Applied Mathematical Modelling, vol. 87, pp. 446–467, 2020. [Google Scholar]
15. R. Tsai and T. S. Huang, “Multiframe image restoration and registration,” Advances in Computer Vision and Image Processing, vol. 1, no. 2, pp. 317–339, 1984. [Google Scholar]
16. S. Zhao, R. Jin, X. Xu, E. Song and C. C. Hung, “A variational Bayesian superresolution approach using adaptive image prior model,” Mathematical Problems in Engineering, vol. 2015, pp. 1–13, 2015. [Google Scholar]
17. S. Zhao, H. Liang and M. Sarem, “A generalized detail-preserving super-resolution method,” Signal Processing, vol. 120, pp. 156–173, 2016. [Google Scholar]
18. Q. Yuan, L. Zhang and H. Shen, “Multiframe super-resolution employing a spatially weighted total variation model,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 22, no. 3, pp. 379–392, 2012. [Google Scholar]
19. H. Zhang, L. Zhang and H. Shen, “A Super-resolution reconstruction algorithm for hyperspectral images,” Signal Processing, vol. 92, no. 9, pp. 2082–2096, 2012. [Google Scholar]
20. D. Kim and H. Byun, “Regularization based super-resolution image processing algorithm using edge-adaptive non-local means filter,” in Proc. 7th Int. Conf. on Ubiquitous Information Management and Communication (ICUIMC2013), Kota Kinabalu, Malaysia, Article No: 78, pp. 1–5, 2013. [Google Scholar]
21. Z. Ren, C. He and Q. Zhang, “Fractional order total variation regularization for image super-resolution,” Signal Processing, vol. 93, no. 9, pp. 2408–2421, 2013. [Google Scholar]
22. W. Z. Shao, H. S. Deng and Z. H. Wei, “A posterior mean approach for MRF-based spatially adaptive multi-frame image super-resolution,” Signal, Image and Video Processing, vol. 9, no. 2, pp. 437–449, 2013. [Google Scholar]
23. R. M. Bahy, G. I. Salama and T. A. Mahmoud, “Adaptive regularization-based super resolution reconstruction technique for multi-focus low-resolution images,” Signal Processing, vol. 103, no. C, pp. 155–167, 2014. [Google Scholar]
24. B. J. Maiseli, O. A. Elisha and H. Gao, “A Multi-frame super-resolution method based on the variable-exponent nonlinear diffusion regularizer,” EURASIP Journal on Image and Video Processing, vol. 1, pp. 1–16, 2015. [Google Scholar]
25. T. Köhler, X. Huang, F. Schebesch, A. Aichert, A. Maier et al., “Robust multiframe super-resolution employing iteratively re-weighted minimization,” IEEE Transactions on Computational Imaging, vol. 2, no. 1, pp. 42–58, 2016. [Google Scholar]
26. X. Zeng and L. Yang, “A robust multiframe super-resolution algorithm based on half-quadratic estimation with modified BTV regularization,” Digital Signal Processing, vol. 23, no. 1, pp. 98–109, 2013. [Google Scholar]
27. V. K. Ghassab and N. Bouguila, “Light field super-resolution using edge-preserved graph-based regularization,” IEEE Transactions on Multimedia, vol. 22, no. 6, pp. 1447–1457, 2019. [Google Scholar]
28. X. Zhang, E. Y. Lam, E. X. Wu and K. K. Wong, “Application of Tikhonov regularization to super-resolution reconstruction of brain MRI images,” in Proc. the 2nd Int. Conf. on Medical Imaging and Informatics (MIMI2007), Beijing, China, pp. 51–56, 2007. [Google Scholar]
29. S. Farsiu, M. D. Robinson, M. Elad and P. Milanfar, “Fast and robust multiframe super resolution,” IEEE Transactions on Image Processing, vol. 13, no. 10, pp. 1327–1344, 2004. [Google Scholar]
30. Z. Wang, H. Yang, W. Li and Z. Yin, “Super-resolving IC images with an edge-preserving Bayesian framework,” IEEE Transactions on Semiconductor Manufacturing, vol. 27, no. 1, pp. 118–130, 2014. [Google Scholar]
31. P. Charbonnier, L. Blanc-Féraud, G. Aubert and M. Barlaud, “Deterministic edge-preserving regularization in computed imaging,” IEEE Transactions on Image Processing, vol. 6, no. 2, pp. 298–311, 1997. [Google Scholar]
32. K. Nasrollahi and T. B. Moeslund, “Super-resolution: A comprehensive survey,” Machine Vision & Applications, vol. 25, no. 6, pp. 1423–1468, 2014. [Google Scholar]
33. I. El Mourabit, M. El Rhabi, A. Hakim, A. Laghrib and E. Moreau, “A new denoising model for multi-frame super-resolution image reconstruction,” Signal Processing, vol. 132, pp. 51–65, 2017. [Google Scholar]
34. R. Nayak and D. Patra, “Super resolution image reconstruction using penalized-spline and phase congruency,” Computers & Electrical Engineering, vol. 62, no. C, pp. 232–248, 2016. [Google Scholar]
35. M. Kumar and M. Diwakar, “A new exponentially directional weighted function based CT image denoising using total variation,” Journal of King Saud University-Computer and Information Sciences, vol. 31, no. 1, pp. 113–124, 2016. [Google Scholar]
36. V. Patanavijit and S. Jitapunkul, “A lorentzian stochastic estimation for a robust iterative multiframe super-resolution reconstruction with lorentzian-tikhonov regularization,” EURASIP Journal on Advances in Signal Processing, vol. 2007, no. 2, pp. 1–21, 2007. [Google Scholar]
37. A. Laghrib, A. Ghazdali, A. Hakim and S. Raghay, “A Multi-frame super-resolution using diffusion registration and a nonlocal variational image restoration,” Computers & Mathematics with Applications, vol. 72, no. 9, pp. 2535–2548, 2016. [Google Scholar]
38. W. Long, Y. Lu, L. Shen and Y. Xu, “High-resolution image reconstruction: An envℓ1/TV model and a fixed-point proximity algorithm,” International Journal of Numerical Analysis & Modeling, vol. 14, no. 2, pp. 255–282, 2017. [Google Scholar]
39. M. M. Khattab, A. M. Zeki, A. A. Alwan, A. S. Badawy and L. S. Thota, “Multi-frame super-resolution: A survey,” in 2018 IEEE Int. Conf. on Computational Intelligence and Computing Research (ICCIC), Madurai, India, pp. 348–355, 2018. [Google Scholar]
40. M. M. Khattab, A. M. Zeki, A. A. Alwan, B. Bouallegue, S. S. Matter et al., “Regularized multiframe super-resolution image reconstruction using linear and nonlinear filters,” Journal of Electrical and Computer Engineering, vol. 2021, Article ID 8309910, pp. 1–16, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |