DOI:10.32604/csse.2023.024973

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.024973 |  |
| Article |
Metaheuristics Based Node Localization Approach for Real-Time Clustered Wireless Networks
1Department of Information Technology, PSNA College of Engineering and Technology, Dindigul, 624622, India
2Department of Computer Science and Engineering, MEA Engineering College, Mallapuram, 679325, Kerala, India
3Department of Electronics and Communication Engineering, Rajalakshmi Institute of Technology, Kuthambakkam, Chennai, 600124, India
4Department of Electronics and Communication Engineering, Sri Eshwar College of Engineering, Coimbatore, 641202, India
5Department of Computer Science and Engineering, Sejong University, Seoul, 05006, Korea
6Department of Software Convergence, Daegu Catholic University, Gyeongsan, 38430, Korea
*Corresponding Author: Woong Cho. Email: wcho@cu.ac.kr
Received: 06 November 2021; Accepted: 22 December 2021
Abstract: In recent times, real time wireless networks have found their applicability in several practical applications such as smart city, healthcare, surveillance, environmental monitoring, etc. At the same time, proper localization of nodes in real time wireless networks helps to improve the overall functioning of networks. This study presents an Improved Metaheuristics based Energy Efficient Clustering with Node Localization (IM-EECNL) approach for real-time wireless networks. The proposed IM-EECNL technique involves two major processes namely node localization and clustering. Firstly, Chaotic Water Strider Algorithm based Node Localization (CWSANL) technique to determine the unknown position of the nodes. Secondly, an Oppositional Archimedes Optimization Algorithm based Clustering (OAOAC) technique is applied to accomplish energy efficiency in the network. Besides, the OAOAC technique derives a fitness function comprising residual energy, distance to cluster heads (CHs), distance to base station (BS), and load. The performance validation of the IM-EECNL technique is carried out under several aspects such as localization and energy efficiency. A wide ranging comparative outcomes analysis highlighted the improved performance of the IM-EECNL approach on the recent approaches with the maximum packet delivery ratio (PDR) of 0.985.
Keywords: Wireless networks; real time applications; clustering; node localization; energy efficiency; metaheuristics
Since wireless node is powered generally by batteries and is anticipated to continue in operation for longer time period, how to save energy for extending network lifetime and node lifetime is a significant challenge in almost all wireless networks [1]. One-way of conserving energy is to function this node at low-powered as far as feasible. But this would considerably decrease their functionality [2]. Once “quality” is measured based on the latency, the tradeoff is in-between time and energy [3]. An example arises in wireless communication, in which transmitter trades off transmission speed to energy, and in real-world computing, in which processor trades-off processing rate to energy [4]. Once the energy of wireless nodes is mostly expended by the transmission task, scheduling an RF transmission effectively becomes very significant in preserving the energy of nodes. It can be familiar that there is an explicit connection among channel capacity and broadcast power [5]; broadcast power could be adapted by altering the rate of transmission, only if suitable coding systems are employed. This offers a choice to preserve the broadcast energy of wireless nodes with slowing down the rate of transmission. E.g., extreme delay might create buffer overflow that augments the packet dropping rate. The presence of these trade-offs among latency and energy stimulates Dynamic Transmission Control technology to design energy-effective wireless systems [6]. Fig. 1 illustrates the overview of node localization.

Figure 1: Overview of clustered wireless networks
Energized sensors in hostile environments need to survive for longer period of time, however, it is almost impossible or ambiguous to change or boost their battery [7], and this necessitates discovering novel energy-effective alternates to any advanced wireless network challenges that contian self-organization, intermediate access control, security, routing, and bandwidth distributions [8]. Certain factors to consider in extending network lifetime are using the gain of trade-offs like accuracy, power, and latency, combined with hierarchical (tiered) frameworks. The location of a localized unknown node was significant since it assists in solving big WSN challenges such as data aggregation and routing. For these reasons, it can be essential to focus on localization method in WSN work [9]. Clustering has a preferred methodology to attain competent and available overall performances in WSN [10]. The clustering node minimizes disputes and preserves power at the network because the node transmits its data to cluster head (CH) via decreased distances.
This study presents an Improved Metaheuristics based Energy Efficient Clustering with Node Localization (IM-EECNL) approach for real-time wireless networks. Firstly, Chaotic Water Strider Algorithm based Node Localization (CWSANL) technique to determine the unknown position of the nodes. Secondly, an Oppositional Archimedes Optimization Algorithm based Clustering (OAOAC) technique is applied to accomplish energy efficiency in the network. Besides, the OAOAC technique derives a fitness function (FF) comprising residual energy, distance to cluster heads (CHs), distance to base station (BS), and load. The performance validation of the IM-EECNL technique is carried out under several aspects such as localization and energy efficiency.
The rest of the paper is arranged as follows. Section 2 offers the literature survey, Section 3 elaborates the proposed model, Section 4 investigates the results, and Section 5 concludes the paper.
Ahmad et al. [11] projected a novel wireless localization method based on social network analysis (SNA), in order to explore the dissimilar properties of the network as graph. The node with maximum amount of CC is selected as a CH, then all the CHs could form its trilateration method for collecting information from its cluster. Khriji et al. [12], presented a localization-based RSSI technique to describe the node location. Next, a fuzzy-based unequal clustering method has been designed for balancing the power utilization amongst each sensor node. An actual application of energy aware routing method was performed on wireless sensors PanStamp NRG 2.0. In Sackey et al. [13], the standard GA method would be expanded by a clustering method that contributes to the increase in localization accuracy. The amount of clusters made in the network assist to enhance the performance. The election of the primary cluster centre is performed for reducing the intensity of distant points.
Tamtalini et al. [14] introduce a new method for localization in WSN. To forecast unknown node position, they choose top-3 anchor node with hybrid techniques such as CSO-ANFIS method. For making decision, fusion centre is utilized that discards the reported locational data when the distance among anchor and unknown nodes is beyond a threshold. To decrease the power utilization, they presented a secure cluster-based routing for data forwarding by validating all the nodes to sink nodes. Tamtalini et al. [15] suggest a new packet routing algorithm and grid based joint localization in WSN based beacon node for enhancing the accuracy from place prediction. Initially, system framework of Grid based WSN node localization has been created. Next, localization method of WSN is presented by utilizing Hybrid Algorithm named Type-2 Fuzzy Logic Filter and Particle Swarm Optimization. Then, form dynamic clusters with node energy. Next, accomplish packet routing with Enriched Ant Colony Optimization Algorithm (E-ACO).
Yu et al. [16] present a hybrid localization system to deep mine monitoring through WSN. The method is developed for optimum efficiency and accuracy. clustering based wheel graph theory is presented to decrease the difficulty of succeeding CSO and normalize the subnetwork quantity. Chen et al. [17] proposed energy-effective clustering and localization cantered on genetic algorithm (ECGAL), where the coverage connection, RE, and distance estimation are designed for procedure the FF. The presented method exhausts a smaller number of energy and expands the existence of wireless networks.
3 The Proposed IM-EECNL Technique
In this study, a novel IM-EECNL technique has been derived to accomplish effective energy efficiency and node localization performance. The proposed IM-EECNL technique involves two major processes namely CWSANL based node localization and OAOAC based clustering. Fig. 2 shows the brief workflow involved in the IM-EECNL technique and the detailed working of every stage is elaborated in the following sections.

Figure 2: Overall process of IM-EECNL model
3.1 Stage 1: Process Involved in CWSANL Technique
During the node localization process, the CWSANL approach is derived for determining the exact position of the sensors. In recent times, Kaveh et al. [18] presented a novel way of this metaheuristics, named the WSA to provide well-improved outcomes. This method resolves complex optimization problems dependent upon simulating territorial behavior of Water Strider bugs. The initial phase in WSA is the Birth phase. It can be arithmetically expressed by:
whereas r denotes an arbitrarily generated values among zero and one, n determines the quantity of individuals, Xi(0) indicates the primary location of ith individual, and Ub & Lb describes the up as well as down ranges, correspondingly. Then, the novel generation has been evaluated by estimating its objective value that defines the food accessibility for an individual. The next step is for simulating the model of founding territories. Next, the mating initiates. According to this beginning, a huge part of keystone utilizes subsequent searching the females and mating. It can be performed by transmitting certain signals in the keystone to female water strider. In this phase, 2 decisions could be found: when a female was fascinated by the signals, it would be react as transmitting a signal and mating would be initiated. or else, mating would be cancelled while keystone tries to forced mating, it isn’t going to happen because of the female strong shield on its body. It can be arithmetically expressed by:
whereas, Xi(t) represent the ith water strider position, R characterizes the distance among the keystone position (Xi(t)) and the female territory (XF(t)) the endpoint is attained by:
Later, the foraging phase initiates. It can be arithmetically expressed by:
Lastly, in the final phase (called death and succession), for keeping the solution from the determined boundary, when it can be outlandish water strider under the novel territory [19], the keystone provide a violent behavior to novel member to bring/kill him out. The arithmetical method can be expressed in the following equation:
In which, Ubj(t) and Lbj(t) denotes the maximal as well as minimal values of position of the water strider place from jth territory. Lastly, the process finishes while the end state has been achieved.
The CWSANL technique uses chaotic parameters with changeable nature rather than arbitrary parameters. It could be found in dynamic and non-convergent and non-linear methods are bounded, and non-periodic processes. It gives a higher convergence rate and simple searching when compared to arbitrary searching. This method assists the method to offer good exploration in the solution space i.e., due to thier dynamic nature of turbulence sequence. Different types of chaotic maps are applied in optimization methods which depend on different sequences, and primary conditions [20]. The current research exploits the sinusoidal chaotic map for improving the premature convergence and convergence speed of the AOA for considering the trade-offs among exploration and exploitation phases to provide better outcomes in the solution space therefore it doesn’t get trapped on the local optimum. For modifying the AOA with a chaos map, the chaos value is replaced by an arbitrary value,
whereas, P represent the control variables, ri & ri+1 represents the chaotic arbitrary number generated in the former and the current iteration, correspondingly. Now r0 = 0.7 and P = 2.3.
The CWSANL localization manner has been typically employed to evaluate the coordinate point of sensors from WSN. The purpose is for defining the coordinate point of target nodes with minimized main function. The developments contained from the CWSANL approach has been offered from the subsequent:
i) Initialize of N unidentified node and M anchor node arbitrarily from the sensing area with communication radius R. Each anchor node is determined to locate as well as send the coordinate point to neighboring nodes. In each iteration, the node that resolves down at the end has been recognized as location nodes and their role as anchor nodes from the successive iteration.
ii) The set of 3 or higher to 3 anchor nodes take place from the communication radius of node has been determined as localization nodes.
iii) The distance among the target as well as anchor nodes have been resolved and attains different utilizing additive Gaussian noises. The target nodes compute the distance with
iv)
v) where ni stands for the noise affects the determined distance in
vi) The target nodes have been named as localizable node when it comprises 3 anchor nodes in communication range of target nodes. Due to utilized trigonometric law of sine or cosine, the coordinate point of target nodes has been evaluated.
vii) The CWSANL manner has been working for resolving the coordinate points
viii)
ix) where N ≥ 3 indicates the anchor node count that communication range.
x) A better measure
xi) The whole localized error has been evaluated next for estimating of localizable target node NL. It could be validated measured as average square of distance in resolved node coordinate point
xii)
xiii) Steps 2–5 progress iterated until the position of target node has been recognized. The localization technique depends on maximal localization errors E1 and unlocalized node counts
3.2 Stage 2: Process Involved in OAOAC Technique
Once the nodes are localized, the next stage lies in the selection of CHs and constructing clusters using the OAOAC technique. As with other meta heuristic methods, the AOA initiates by a certain data of an arbitrary population of objects as a candidate (immersed object). In this phase, the object has been initiated by its arbitrary position. The primary location of all the objects is accomplished by:
In which, x(i) represent the ith object from the population with N object, and xl(i) & xu(i) denotes the lower as well as upper limits of solution space. Besides the location, the AOA initiates acceleration (A), volume (V), and density (D) for i object,
Afterward initialization, the cost value of candidate was estimated and kept as Abest, Vbest, and Dbest based early population. Next, the candidate has been upgraded by the model parameter. The upgrading of the object acceleration is depending on their collision conditions with another neighboring object. The recently upgraded location of an object can be defined by acceleration, volume, and density. The mathematical expression has been described in the following. In order to update the algorithm, the density, and volume of ith object for t + 1 iteration number was upgraded as:
In the equation,
In which, TF gradually step up in a period till attaining 1, t and tmax represents the iteration value and the maximal iteration count, correspondingly. Similarly, reducing factors of density (d) assist the model to offer global to local search. It can be expressed by:
Let, Dt+1 decreases with time that offers the capacity to converge. This term provides an appropriate tradeoff among exploitation and exploration phases. The exploration phase is inspired according to the collision between the objects [21]. It would take place when TF ≤ 0.5. In such cases, a random material (mr) is chosen for updating the acceleration of an object for t + 1 iteration:
While
Let, Abest be the optimal object acceleration. The following step is to standardize the acceleration for estimating the altering percentage by:
whereas, At+1(i) defines the percentage of step that all the agents would alter, l & u represents the standardization limit i.e., fixed to 0.9 and 0.1, correspondingly. In the following step, when TF ≤ 0.5, the location of an i object for the following iteration is accomplished:
In the equation, C1 indicates a constant equivalent to 2. Otherwise, when TF > 0.5, the location for an object was upgraded by:
In which, c2 defines a constant value. T rises with time in the interval [c3 × 0.3, 1] and take a percentage from an optimal location. This percentage gradually increases to reduce the differences among the present and optimal locations to offer an improved balance among exploitation and exploration. F describes the flag to change the direction of movement:
In which,
Eventually, the values of every object are estimated by the cost function and return the optimal solution when the end criteria condition is met.
The initial modification is to utilize opposition-based learning (OBL). Such modifications are employed for improving the variety of the early population. The OBL model is a common methodology to improve the efficacy of metaheuristics [22]. In optimization, the algorithm initiates by producing an arbitrarily distributed population. In this method, it is expected to be moving from the way of proper solution. Hence, when the arbitrarily created early population has a result closer to the optimum solution, the accurate solution would be accomplished. Optimization initiates by an arbitrary value farther in the optimum solution, or possibly in the opposite position of solution that increases the time to optimized. The OBL method provides an opposite position to the solution from early population:
In the equation,
Generally, there are 4 objective functions that include important factors needed for energy-efficient clustering such as identifying current energy ratio, preserving the energy by constraining overall number of CHs, mitigation of intracluster distance, balancing the load amongst CHs, reducing the distances between BS and CH, as well as enhanced intercluster distance from CH.
The recently proposed OAOAC method generates an optimum solution by obtaining a network load, FF with energy, distance to neighbor, and distance to BS. Thus, FF is defined in the recently deployed method as:
In which m1, m2, m3, and m4 indicates the weight constants defined by user, and FF implies the FF. In addition, y1, y2, y3, and y4, means the objective function.
The proposed method is employed for identifying the best solution-based FF. Now, result is attained using an agent. Therefore, the enhanced results for the abovementioned FF are made up of minimum number of clusters using maximal link < quality and vigorously determined CH with maximum residual energy (RE). The primary operation is regarded for preserving energy, and energy ratio is described in the following. When there are R clusters, M nodes, then the existing CH energy and ratio of nodes energy are represented in the following equation.
The following function defines the distance to neighbor, i.e., described as a Euclidean distance amongst the SNs.
The 3rd function decreases the distances among BS and CH. In this method, the region is regarded as A × A; the total clusters are R as follows
The final function is employed to handle the load from CH. Eq. (30) limits the higher load amongst CHs. |CNq| indicates the overall number of nodes in cluster q. Subsequently, the region is represented as A × A; overall clusters are R.
The performance validation of the IM-EECNL technique with existing ones takes place interms of different measures. In addition, the localization and energy efficient performance of the IM-EECNL technique is performed under varying anchor nodes [23,24].
Tab. 1 and Fig. 3 demonstrate the NLN analysis of the IM-EECNL technique with other ones under distinct anchors. The results pointed out that the IM-EECNL technique has gained proficient results with the maximum NLN.

Figure 3: NLN analysis of IM-EECNL model under varying anchors
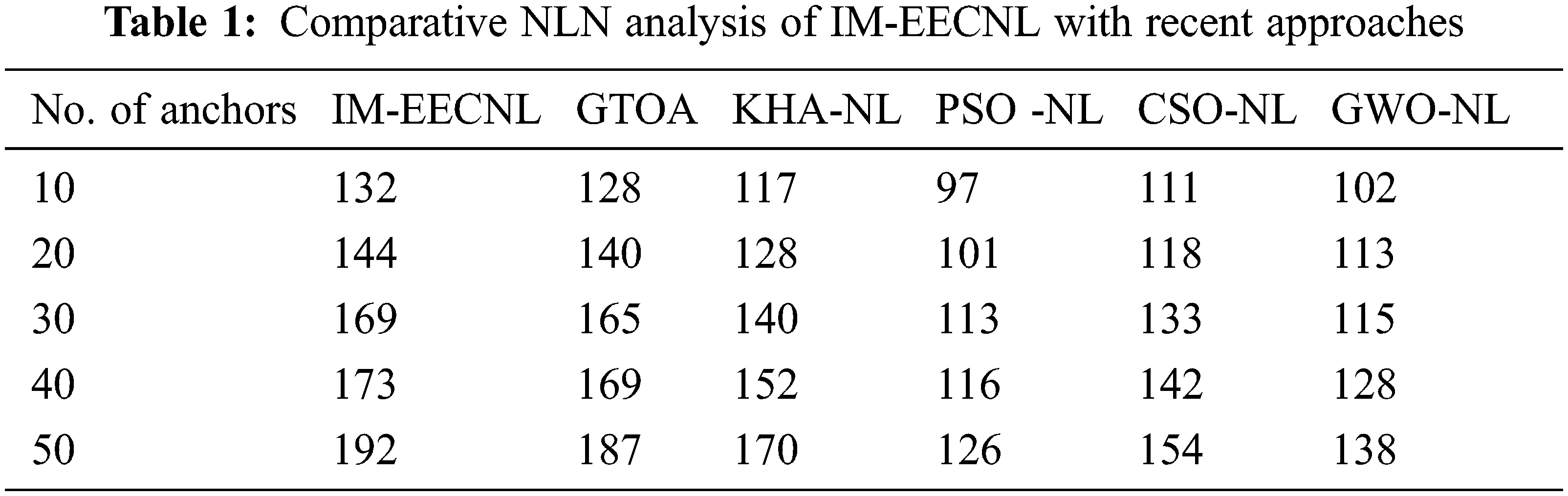
For instance, with 10 anchors, the IM-EECNL technique has offered an increased NLN of 132 nodes whereas the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL techniques have resulted to lower NLN of 128, 117, 97, 111, and 102 nodes respectively. In addition, with 50 anchors, the IM-EECNL manner has offered an increased NLN of 192 nodes whereas the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL methods have resulted to lesser NLN of 187, 170, 126, 154, and 138 nodes correspondingly.
Next, a detailed LE results analysis of the IM-EECNL technique with recent methods are performed in Fig. 4. The outcomes reported the supremacy of the IM-EECNL technique with the least LE. For instance, with 10 anchors, the IM-EECNL technique has gained a reduced LE of 0.36 while the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL systems have accomplished to higher LE of 0.44, 0.72, 0.54, 0.70, and 0.63 respectively. Followed by, with 50 anchors, the IM-EECNL approach has reached a lower LE of 0.16 but the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL methods have accomplished to superior LE of 0.30, 0.50, 0.39, 0.57, and 0.50 correspondingly.

Figure 4: Localization error analysis of IM-EECNL model
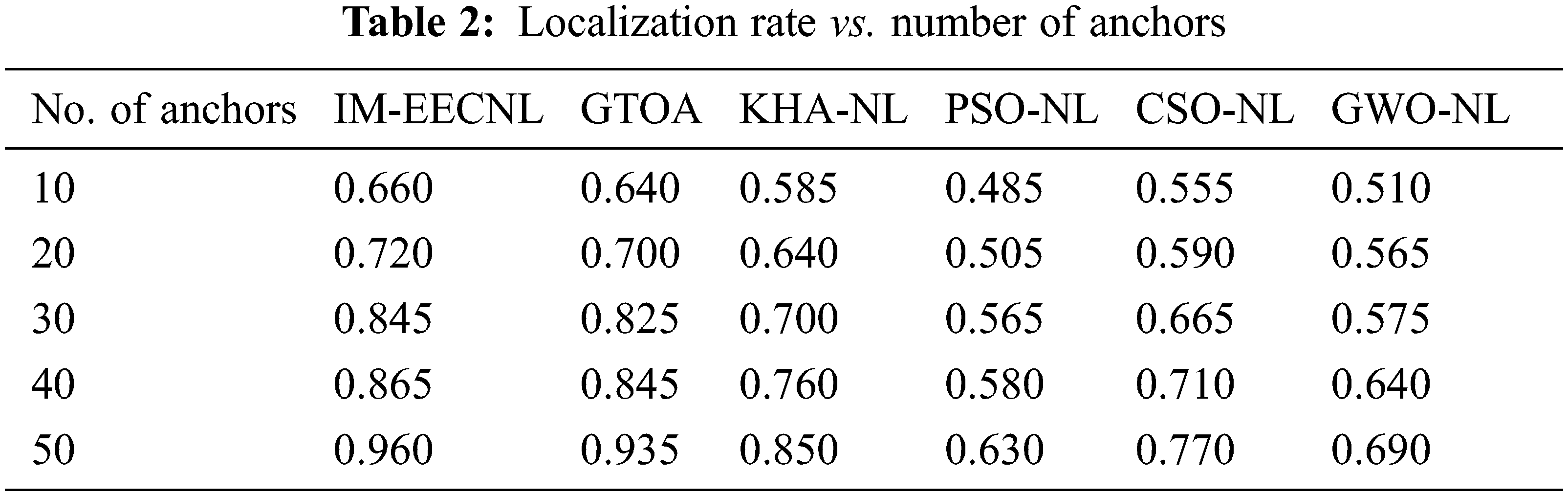
Tab. 2 and Fig. 5 showcases the LR analysis of the IM-EECNL manner with other ones under distinct anchors. The results pointed out that the IM-EECNL system has gained proficient results with the maximal LR. For instance, with 10 anchors, the IM-EECNL approach has offered a higher LR of 0.660 nodes whereas the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL methodologies have resulted in minimal LR of 0.640, 0.585, 0.485, 0.555, and 0.510 nodes correspondingly. Furthermore, with 50 anchors, the IM-EECNL system has obtainable a superior LR of 0.960 nodes whereas the GTOA, KHA-NL, PSO-NL, CSO-NL, and GWO-NL methodologies have resulted to lower LR of 0.935, 0.850, 0.630, 0.770, and 0.690 nodes correspondingly.

Figure 5: Localization rate analysis of IM-EECNL model
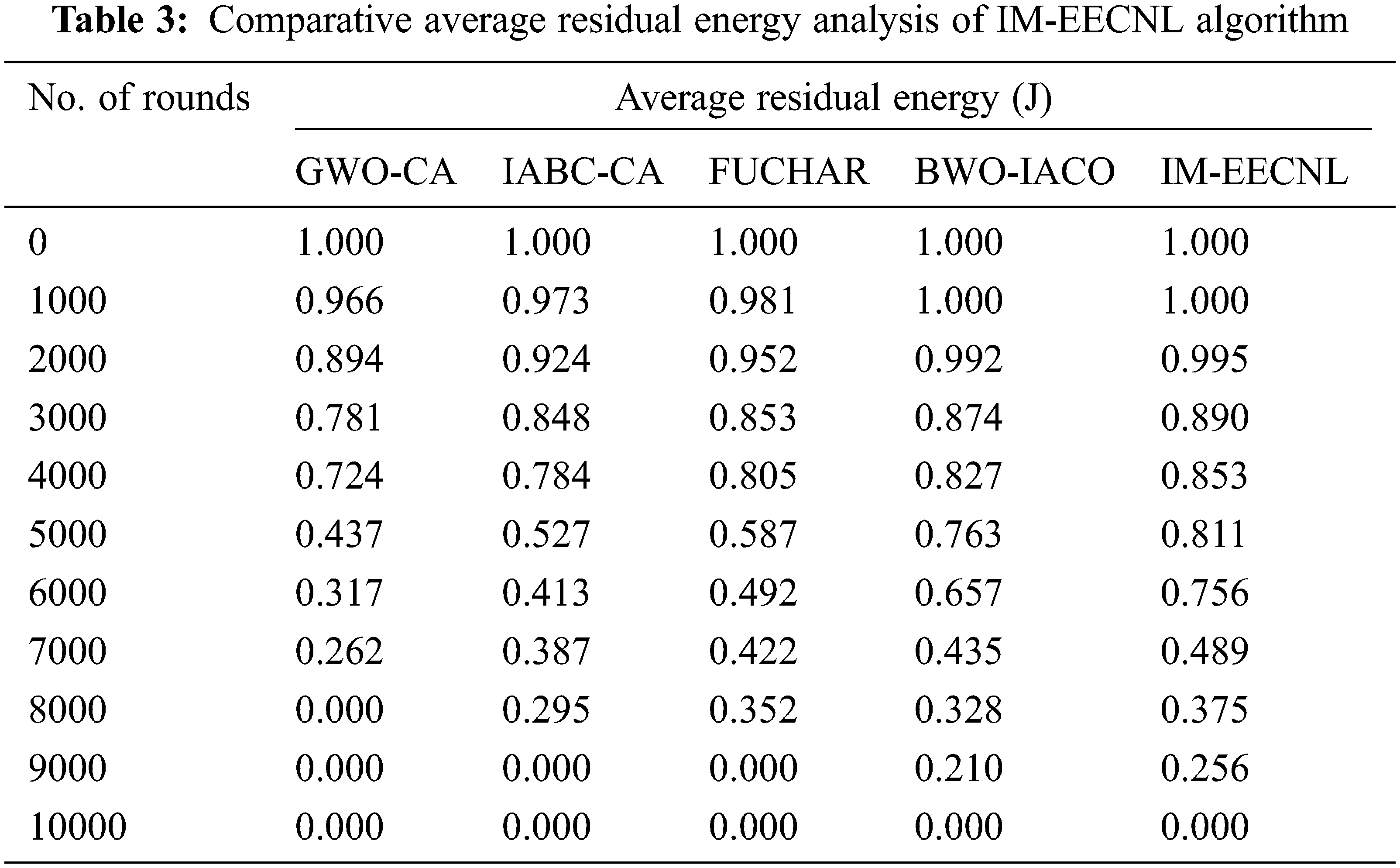
Afterward, a comparative PDR analysis of the IM-EECNL with recent techniques takes place in Tab. 3 and Fig. 6. The outcomes exhbited that the IM-EECNL technique has accomplished maximal PDR under different rounds. For instance, with 1000 rounds, the IM-EECNL technique has obtianed an increased PDR of 1.000 J but the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have reached decreased PDR of 0.966, 0.973, 0.981, and 1.000 J respectively. Besides, with 7000 rounds, the IM-EECNL manner has gained an enhanced PDR of 0.489 J while the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have reached reduced PDR of 0.262, 0.387, 0.422, and 0.435 J correspondingly.

Figure 6: Average residual energy analysis of IM-EECNL algorithm
An extensive ADE analysis of the IM-EECNL technique with other techniques takes place under different nodes in Tab. 4 and Fig. 7. The experimental values pointed out that the IM-EECNL technique has gained effective outcomes with the least ADE under distinct nodes. For instance, with 100 rounds, the IM-EECNL technique has gained lower ADE of 80 ms whereas the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have accomplished increased ADE of 123, 106, 93, and 86 ms respectively. In addition, with 1000 rounds, the IM-EECNL methodology has gained lower ADE of 134 ms whereas the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO methods have accomplished improved ADE of 211, 195, 161, and 154 ms correspondingly.

Figure 7: Average delay analysis of IM-EECNL algorithm

An extensive PLR analysis of the IM-EECNL approach with other techniques takes place under varying nodes in Tab. 5 and Fig. 8. The experimental values pointed out that the IM-EECNL system has achieved effective outcomes with the least PLR under distinct nodes. For instance, with 100 rounds, the IM-EECNL technique has reached minimal PLR of 0.015 whereas the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO approaches have accomplished increased PLR of 0.156, 0.140, 0.110, and 0.040 respectively. Moreover, with 1000 rounds, the IM-EECNL algorithm has gained lower PLR of 0.116 whereas the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have accomplished increased PLR of 0.360, 0.320, 0.230, and 0.160 correspondingly.
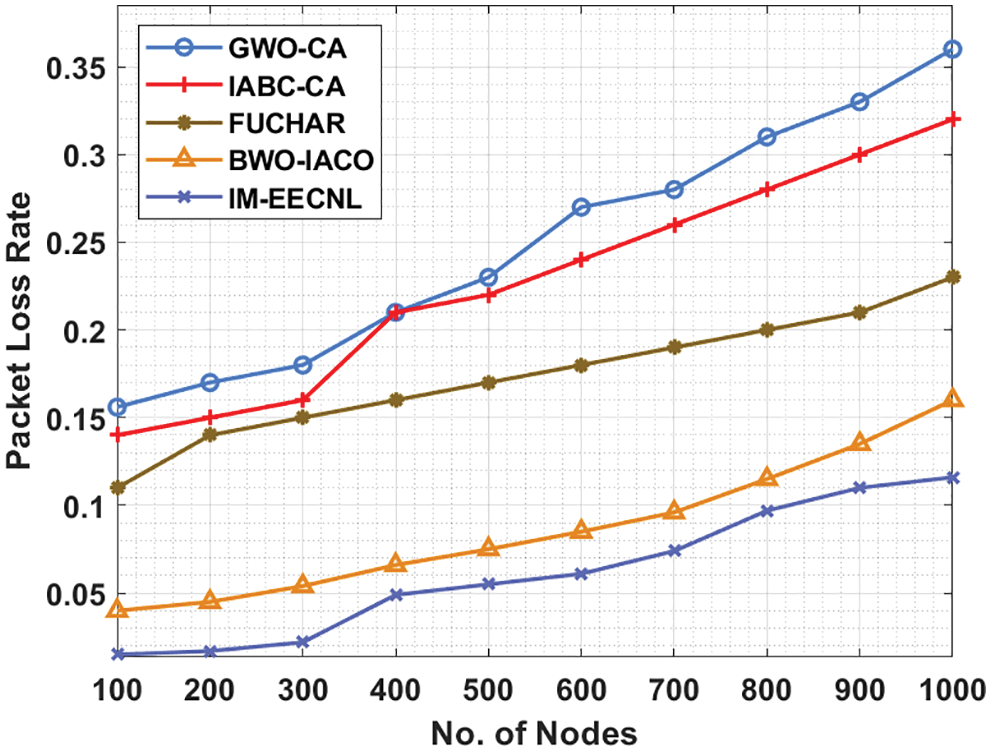
Figure 8: Packet loss rate analysis of IM-EECNL algorithm

Finally, a comparative PDR analysis of the IM-EECNL with recent approaches takes place in Tab. 6 and Fig. 9. The outcomes depicted that the IM-EECNL technique has accomplished maximum PDR under distinct nodes.
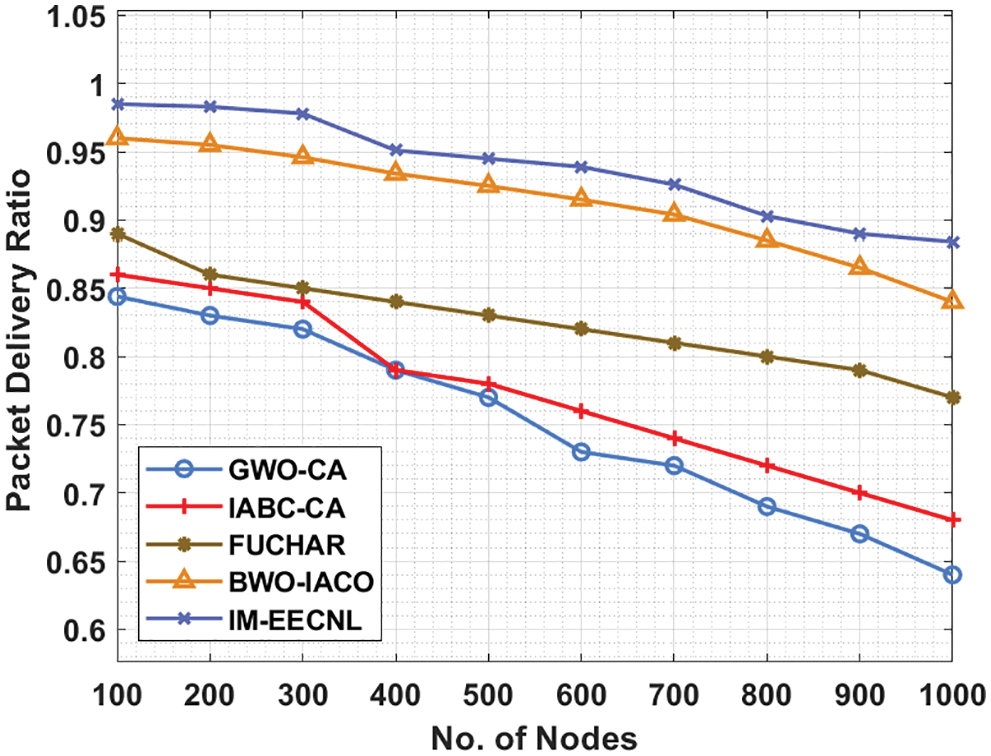
Figure 9: PDR analysis of IM-EECNL algorithm
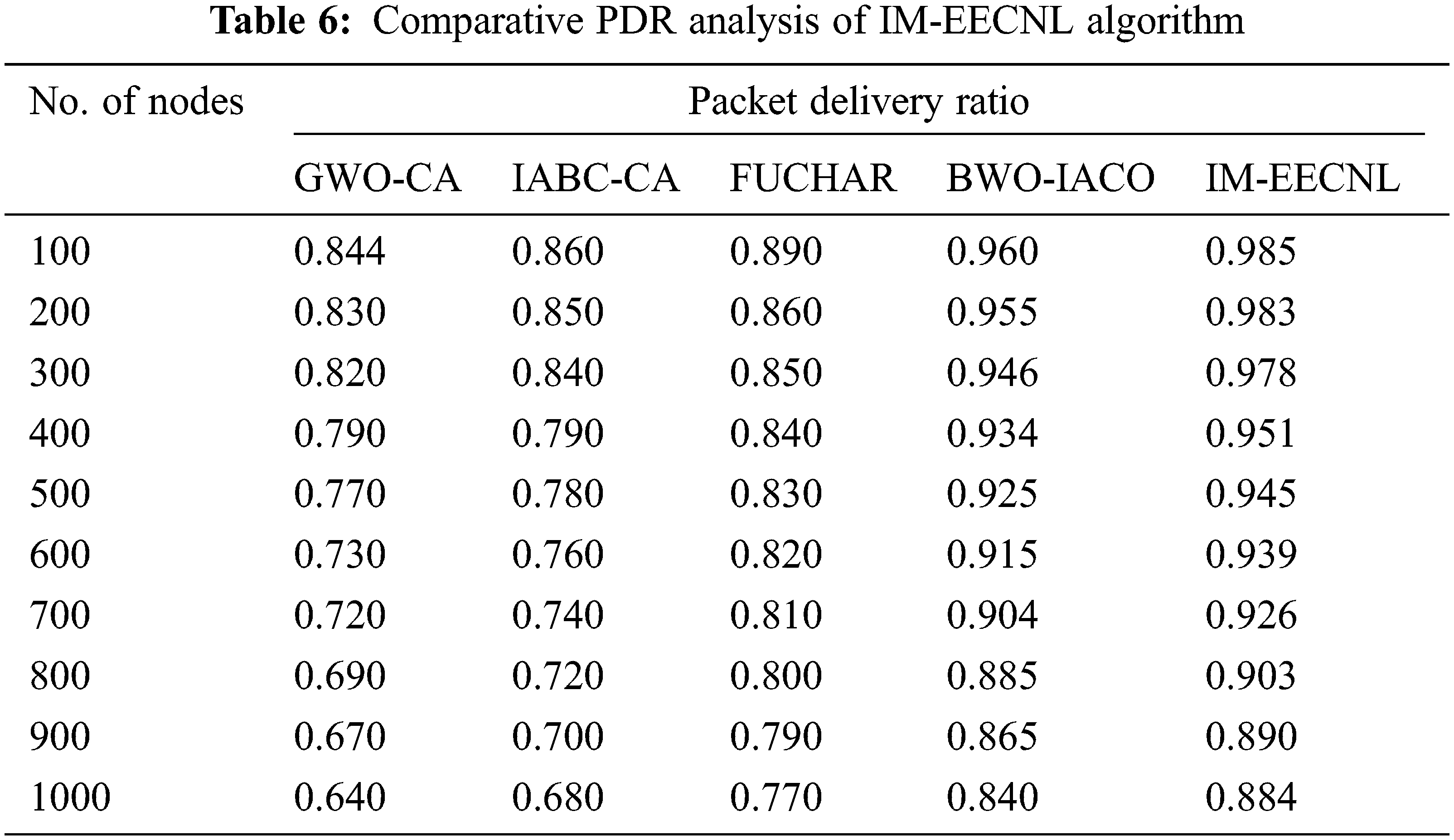
For instance, with 100 rounds, the IM-EECNL approach has reached a superior PDR of 0.985 but the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have reached reduced PDR of 0.844, 0.860, 0.890, and 0.960 respectively. Moreover, with 1000 nodes, the IM-EECNL system has obtained an enhanced PDR of 0.884 while the GWO-CA, IABC-CA, FUCHAR, and BWO-IACO techniques have reached reduced PDR of 0.640, 0.680, 0.770, and 0.840 respectively. By looking into the above mentioned tables and figures, it is evident that the proposed model is an effective tool for improving the performance of the wireless networks.
This study has been presented an IM-EECNL approach for real-time wireless networks. Firstly, CWSANL technique for determining the unknown place of nodes. Secondly, an OAOAC technique is applied to accomplish energy efficiency in the network. Besides, the OAOAC approach develops an FF comprising RE, distance to CHs, distance to BS, and load. Moreover, the design of CWSANL and OAOAC technique helps to optimally improve the overall network performance. The performance validation of the IM-EECNL technique is carried out under several aspects such as localization and energy efficiency. A wide-ranging comparative outcomes analysis highlighted the improved performance of the IM-EECNL approach on the recent approaches. Therefore, the IM-EECNL technique can be extended to the design of time synchronization techniques and sleep scheduling mechanisms. In future, data aggregation schemes can be designed to boost energy efficiency.
Funding Statement: This work was supported by Ulsan Metropolitan City-ETRI joint cooperation project [21AS1600, Development of intelligent technology for key industries and autonomous human-mobile-space autonomous collaboration intelligence technology].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. Miao, J. Mao and C. G. Cassandras, “Optimal energy-efficient downlink transmission scheduling for real-time wireless networks,” IEEE Transactions on Control of Network Systems, vol. 4, no. 4, pp. 692–706, 2016. [Google Scholar]
2. S. Arjunan and S. Pothula, “A survey on unequal clustering protocols in wireless sensor networks,” Journal of King Saud University-Computer and Information Sciences, vol. 31, no. 3, pp. 304–317, 2019. [Google Scholar]
3. S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]
4. S. Mao, N. Zhang, L. Liu, J. Wu, M. Dong et al., “Computation rate maximization for intelligent reflecting surface enhanced wireless powered mobile edge computing networks,” IEEE Transactions on Vehicular Technology, vol. 70, no. 10, pp. 10820–10831, 2021. [Google Scholar]
5. S. Mao, J. Wu, L. Liu, D. Lan and A. Taherkordi, “Energy-efficient cooperative communication and computation for wireless powered mobile-edge computing,” IEEE Systems Journal, pp. 1–12, 2020. http://dx.doi.org/10.1109/JSYST.2020.3020474. [Google Scholar]
6. S. M. Mazinani and M. Safari, “Secure localization approach in wireless sensor network,” International Journal of Machine Learning and Computing, vol. 5, no. 6, pp. 458–461, 2015. [Google Scholar]
7. P. Parwekar and R. Reddy, “An efficient fuzzy localization approach in wireless sensor networks,” in 2013 IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE), Hyderabad, India, pp. 1–6, 2013. [Google Scholar]
8. H. Wymeersch, J. Lien and M. Z. Win, “Cooperative localization in wireless networks,” Proceedings of the IEEE, vol. 97, no. 2, pp. 427–450, 2009. [Google Scholar]
9. S. El Khediri, W. Fakhet, T. Moulahi, R. Khan, A. Thaljaoui et al., “Improved node localization using K-means clustering for wireless sensor networks,” Computer Science Review, vol. 37, pp. 100284, 2020. [Google Scholar]
10. J. Li, M. Gao, J. S. Pan and S. C. Chu, “A parallel compact cat swarm optimization and its application in DV-hop node localization for wireless sensor network,” Wireless Networks, vol. 27, no. 3, pp. 2081–2101, 2021. [Google Scholar]
11. T. Ahmad, X. J. Li, B. C. Seet and J. C. Cano, “Social network analysis based localization technique with clustered closeness centrality for 3d wireless sensor networks,” Electronics, vol. 9, no. 5, pp. 738, 2020. [Google Scholar]
12. S. Khriji, D. E. Houssaini, I. Kammoun, K. Besbes and O. Kanoun, “Energy-efficient routing algorithm based on localization and clustering techniques for agricultural applications,” IEEE Aerospace and Electronic Systems Magazine, vol. 34, no. 3, pp. 56–66, 2019. [Google Scholar]
13. S. H. Sackey, J. Chen, A. J. Henry and X. Zhang, “A clustering approach based on genetic algorithm for wireless sensor network localization,” in 2019 15th Int. Conf. on Computational Intelligence and Security (CIS), Macao, Macao, pp. 54–58, 2019. [Google Scholar]
14. M. A. Tamtalini, A. E. B. E. Alaoui and A. E. Fergougui, “ESLC-WSN: A novel energy efficient security aware localization and clustering in wireless sensor networks,” in 2020 1st Int. Conf. on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, pp. 1–6, 2020. [Google Scholar]
15. M. A. Tamtalini, A. E. B. El Alaoui and A. El Fergougui, “A grid based joint localization and packet routing algorithm in wireless sensor networks,” in 2019 Int. Conf. on Systems of Collaboration Big Data, Internet of Things & Security (SysCoBIoTS), Casablanca, Morocco, pp. 1–6, 2019. [Google Scholar]
16. X. Yu, L. Zhou and X. Li, “A novel hybrid localization scheme for deep mine based on wheel graph and chicken swarm optimization,” Computer Networks, vol. 154, pp. 73–78, 2019. [Google Scholar]
17. J. Chen, S. H. Sackey, J. H. Anajemba, X. Zhang and Y. He, “Energy-efficient clustering and localization technique using genetic algorithm in wireless sensor networks,” Complexity, vol. 2021, pp. 1–12, 2021. [Google Scholar]
18. A. Kaveh and A. D. Eslamlou, “Water strider algorithm: A new metaheuristic and applications,” Structures, vol. 25, pp. 520–541, 2020. [Google Scholar]
19. L. Hu, Y. Zhang and N. Yousefi, “Nonlinear modeling of the polymer membrane fuel cells using deep belief networks and modified water strider algorithm,” Energy Reports, vol. 7, pp. 2460–2469, 2021. [Google Scholar]
20. M. Ramezani, D. Bahmanyar and N. Razmjooy, “A new optimal energy management strategy based on improved multi-objective antlion optimization algorithm: Applications in smart home,” SN Applied Sciences, vol. 2, no. 12, pp. 2075, 2020. [Google Scholar]
21. X. Sun, G. Wang, L. Xu, H. Yuan and N. Yousefi, “Optimal estimation of the PEM fuel cells applying deep belief network optimized by improved archimedes optimization algorithm,” Energy, vol. 237, pp. 121532, 2021. [Google Scholar]
22. H. R. Tizhoosh, “Opposition-based learning: A new scheme for machine intelligence,” in Int. Conf. on Computational Intelligence for Modelling, Control and Automation and Int. Conf. on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, vol. 1, pp. 695–701, 2005. [Google Scholar]
23. R. Punithavathi, C. Kurangi, S. P. Balamurugan, I. V. Pustokhina, D. A. Pustokhin et al., “Hybrid BWO-IACO algorithm for cluster based routing in wireless sensor networks,” Computers, Materials & Continua, vol. 69, no. 1, pp. 433–449, 2021. [Google Scholar]
24. P. Sekhar, E. L. Lydia, M. Elhoseny, M. A. Akaidi, M. M. Selim et al., “An effective metaheuristic based node localization technique for wireless sensor networks enabled indoor communication,” Physical Communication, vol. 48, pp. 101411, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |