DOI:10.32604/csse.2023.023920

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.023920 |  |
| Article |
Community Detection Using Jaacard Similarity with SIM-Edge Detection Techniques
Department of Computer Applications, Kongu Engineering College, Perundurai, 638060, India
*Corresponding Author: K. Chitra. Email: kchitrares21@outlook.com
Received: 26 September 2021; Accepted: 27 October 2021
Abstract: The structure and dynamic nature of real-world networks can be revealed by communities that help in promotion of recommendation systems. Social Media platforms were initially developed for effective communication, but now it is being used widely for extending and to obtain profit among business community. The numerous data generated through these platforms are utilized by many companies that make a huge profit out of it. A giant network of people in social media is grouped together based on their similar properties to form a community. Community detection is recent topic among the research community due to the increase usage of online social network. Community is one of a significant property of a network that may have many communities which have similarity among them. Community detection technique play a vital role to discover similarities among the nodes and keep them strongly connected. Similar nodes in a network are grouped together in a single community. Communities can be merged together to avoid lot of groups if there exist more edges between them. Machine Learning algorithms use community detection to identify groups with common properties and thus for recommendation systems, health care assistance systems and many more. Considering the above, this paper presents alternative method SimEdge-CD (Similarity and Edge between's based Community Detection) for community detection. The two stages of SimEdge-CD initially find the similarity among nodes and group them into one community. During the second stage, it identifies the exact affiliations of boundary nodes using edge betweenness to create well defined communities. Evaluation of proposed method on synthetic and real datasets proved to achieve a better accuracy-efficiency trade-of compared to other existing methods. Our proposed SimEdge-CD achieves ideal value of 1 which is higher than existing sim closure like LPA, Attractor, Leiden and walktrap techniques.
Keywords: Social media networks; community detection; divisive clustering; business community
With the emergence of social media, Information and communication technology has shown a drastic change and development over the past 20 years. Mobile technology is playing a vital role in shaping the impact of social media. This made people create network anywhere, at any time with their handheld devices. This led to very complex networks in the real world. Due to the advent of internet and social media usage, networks are now one of the most active research topic among the researchers. These networks create complex structures in which the basic components are nodes and links. One of a significant properties of networks is community structure that clearly pictures the interactions among the network components [1].
A community is defined as a group of nodes with similar characteristics and distinguishable affiliation to other community [2]. Structural and dynamic characteristics of a network can be extracted from the community detection and analysis [3]. Complex systems are characterised by community structure and its detection plays a vital role to study the complex networks. The main aim of detecting community is to find the group of nodes with similarities. The links to the nodes within the community is highly dense when compared to the links to the nodes outside the community [4–6]. Community detection implies a meaningful relation between objects of networks. Community Structure can be overlapping or non-overlapping [7]. This community detection method helps to understand the organizational network structures and extract a large amount of hidden information. It is commonly implemented in data organization, network changing prediction, recommendation system and others.
Many approaches have been developed in many aspects to approach the problem of community detection like statistical physics [8], optimization techniques [9,10], likelihood approaches [11–13]. The effectiveness of the community detection models is widely assessed by Lancichinetti–Fortunato–Radicchi (LFR) benchmark with the assumption of power law distributions and community sizes. LFR uses the mixing parameter, μ, to indicate the fraction of a node's links or edges that are external to its assigned cluster, i.e., the quality of the partition. This SimEdge-CD contributed an effective community detection method by using an iterative process and creates a well-defined community. It uses associated the boundary nodes to its respective communities where their similar neighbours are bounded too SimEdge-CD helps us to reveal the hidden relations among the nodes in the network.
Rest of the article is presented with 5 sections and organized as follows: Section 2 discusses related work of the proposed techniques. Third section describes the working principal and execution of proposed work. Section 4 evaluates the outcome of Section 3 and result is compared with existing system. Section 5 concludes the paper with future outcome.
Newman [14] proposed modularity to find the effectiveness of the community detection algorithms. Modularity is the difference between the actual number of linked edges in the community and number of expected edges. Higher the modularity better the community detection. Many works have been proposed to minimise its difficulties using various techniques [15,16]. Modularity function proposed by Newman in was redefined by adopting a spectral method to solve the problem of optimizing the target function [17]. Community structure obtained here is very less when compared to proposed methodology.
Sweeney et al., proposed a hedonic games in [18] for community detection. Modularity is used as a value function and the resolution problem is rectified by adding voting mechanism. Authors also demonstrated ratio cut and normalised cut approaches. Two new functions were proposed to overcome the resolution problem without additional voting mechanism. Gibbs sampling algorithm is used for local and global maxima search. This method proved to be effective for small networks.
Lancichinetti et al., [19] devised local optimization of a fitness function-based algorithm. The fitness function is the ratio of internal degree and the total degree of the sub graph. Further, a node which does not belong to any community is chosen at random and a sub graph from this node is created. The above process is iterated until all the nodes are assigned to one community. Fitness value will be decreased when a node is added or removed. Hierarchical community structure can be exposed by varying the fitness function's parameter.
A game theory-based framework is developed by Chen et al. [20] to detect community structure. Each node is considered as a rational and selfish game player. They have a gain function and a loss function. Joining a community can obtain benefits, however it takes time and energy for maintaining this community. According to these functions, they can choose from join, switch or leave a community. Another contribution of their work is that they proved when gain function and loss function is locally linear, the community formation game needs at most O(m2) steps to reach local equilibrium.
Tang et al., [21] improvised an algorithm for Surprise optimization by introducing three concepts namely: a pre-processing of topological structure based on local random walks (Pre_TS), a pre-processing of community partition (Pre_CS), and a post-processing of community partition (Post_CS). The authors proved that Pre_TS improves the resolution of surprise. Pre_CS and Post_CS can improve the optimization performance in different aspects and the combined effect of all the proposed strategies can enhance the ability of Surprise to detect communities in complex networks. Authors proved the effectiveness of the proposed algorithm with several real-world networks and disease analysis in computational biology.
An algorithm for overlapping community detection based on label propagation was proposed by Gregory [22]. Qiu et al., proposed a parallel multi-label propagation that discover communities based on map reduce model that takes new label updating strategy [23]. Guo et al., proposed a local community detection algorithm to discover communities accurately based on expanding the seeds by fitness function with internal force between nodes [24]. Liu et al., proposed a method to detect overlapping communities based coarsening strategy and local overlapping modularity [25].
Radicchi et al. [26] proposed the edge-clustering coefficient which is a local centrality index. Based on the edge-clustering coefficient, the proposed algorithm can remove multiple links from the network at each iteration. However, the result of the algorithm is a mass of trivial partitions. Finally it obtains a trade-of between accuracy and efficiency.
The literature studies states community detection and its outcome in various perspectives. Most of the existing studies obtain good result, however detection is complex when there is more than 1000 nodes. This motivates use to look for effective system to handle complex network.
3 Proposed SimEdge-CD Methodology
The proposed method takes care of three issues. Initial community formation, expanding community and finally reclassifying the wrongly classified boundary nodes. Sample social network architecture is shown in Fig. 1. It clearly depicts how people are interconnected with each other and it is also clearly visible how difficult it is to find the people with similarities. The proposed SimEdge-CD community detection method clearly groups the people into communities based on their similarities.

Figure 1: Social network architecture
The network considered in this work is undirected and unweighted graph. It is represented as G(V, E) where G represents a graph, V = {v1, v2, v3…vn} denotes a set of nodes and E = {e1, e2, e3…en} represents the edges.
3.1 Initial Community Formation
Initial community is formed by calculating the node similarities. For community detection, one of the commonly used similarity measure is Jaccard Similarity. Jaccard Similarity is a common proximity measurement used to compute the similarity between two nodes. The main drawback in Jaccard similarity is that the similarity measure is greater for the indirectly connected nodes compared to the directly connected nodes. To address this issue, a novel similarity measure is proposed by [p1.1] which proved to be effective than existing similarity measures. This paper improvises the similarity measure proposed by [1].
Jaccard Similarity:
where, τ(p) = {x|x ∈ V, (p, x) ∈ E}, is a set of neighbour nodes of p
Similarity measure proposed by [p1.1] is as follows
where au,v is the element of adjacency matrix. If (u, v) ∈ E, then au,v = 1 otherwise au,v = 0.

The above algorithm is iterated until all the nodes in the graph are processed. Thus, initial communities are obtained. The second step in this work is to find the community affiliation of the boundary nodes.
3.2 Boundary Node Community Affiliation
Initial community is created by using Algorithm 1 which seems to be great but, there might be situations when the boundary nodes between two communities are wrongly bound to communities. This issue is depicted in Fig. 2.
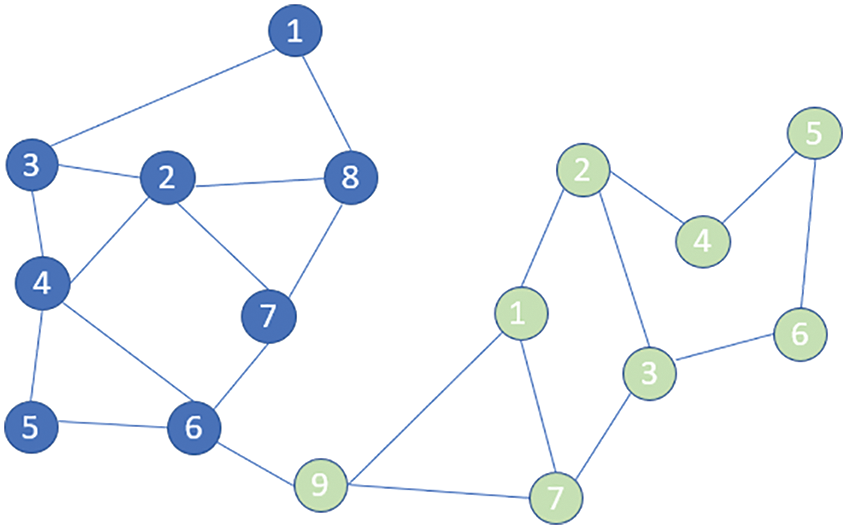
Figure 2: Initial community
From Fig. 2 it is observed that there are two communities one with blue nodes and another one with green nodes. The problem here is with 9th node of green community. It is intuitive that 9th node belongs to the blue community but it should be located in blue community as per the network topology. This issue should be handled by moving the 9th node to the community where its neighbours are. To resolve this, the proposed method uses the betweenness measure to identify the edges that connect the communities and then uses the similarity measure to find the similarity of the nodes to find the boundary node's affiliation. This concept is clearly depicted in Algorithm 2. This problem is resolved in two steps. First step involves the identification of boundary nodes using the betweenness of the edges [27]. In the second step, the similarity of the boundary nodes and its neighbours are calculated. Boundary nodes are associated with the community that has more similarity.
Edge betweenness is the fraction of shortest path between all pairs of vertices passing through that edge. Each and every path is given equal weight when there is more than one shortest path. When community groups contain very few intergroup edges, the shortest path between the communities must pass along one of the few edges. Such edges will have high betweenness.
Edge betweenness can be calculated using below
where σst is the total number of shortest paths from s to t and σst (v) is the number of paths that passes through v.

The above Algorithm 2 identifies well defined communities by moving the boundary nodes to its appropriate community. The flow diagram of the proposed SimEdge-CD is shown in Fig. 3.
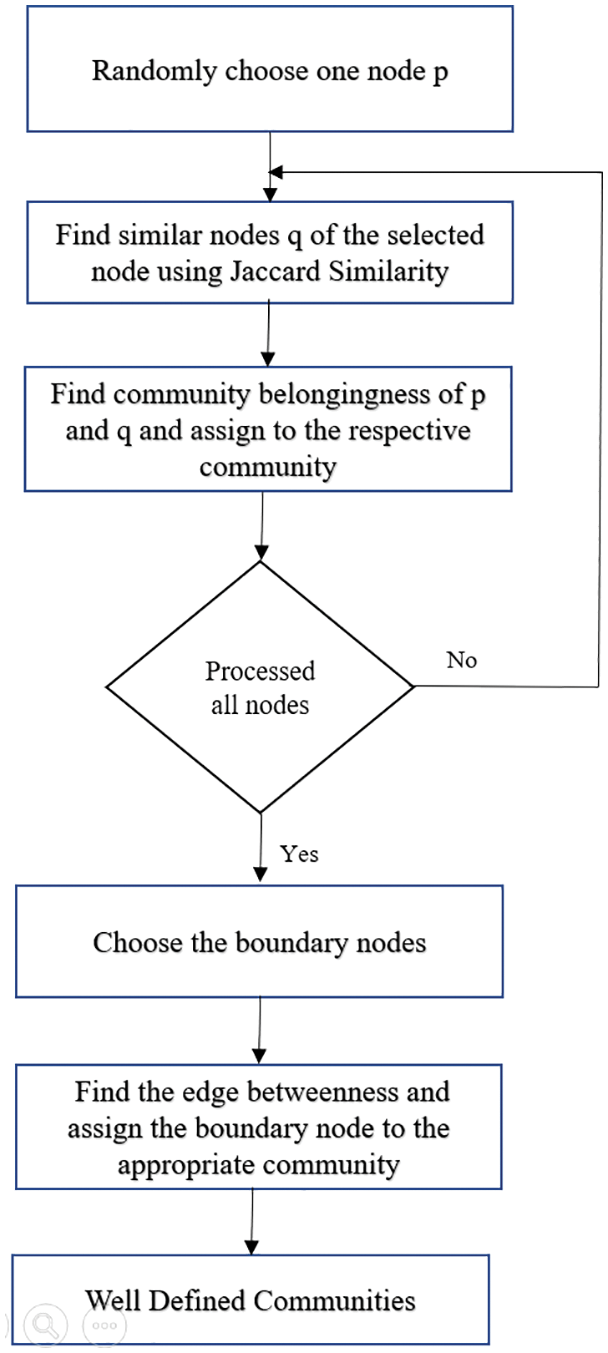
Figure 3: Flow diagram of SimEdgeCD
First, the node ‘p’ is randomly chosen from social network. Next node which is similar to ‘p’ is chosen as ‘q’ using jaccard similarity. The relationship between p and q is identified and their community is assigned respectively. Then the next node is checked for belongingness of this community. If they belong to respective community their edge are identified and boundary nodes are assigned to appropriate community. This Similarity based edge detection helps to identify the relatedness between the node and form the well defined community in the social media network.
This section describes the quality of the proposed community detection method using normalized mutual information (NMI) and modularity (R) for artificial networks. The experiments are carried out with Intel (R) core (TM) i5 processor, 2.42 GHz and 16 GB RAM. The below Tab. 1 depicts the parameter setting of Lancichinetti Fortunato Radicchi (LFR) generator to synthesize Artificial Networks.

The detected communities are embedded in 4 series network which are run in proposed method and other algorithms. The proposed method outperforms all artificial networks for mixing parameter μ ≤ 0.6, in the LFR500 and LFR1000 series of networks, μ ≤ 0.5, in LFR 5000 and μ ≤ 0.6 in LFR 10000. The detected NMI's are depicted in Fig. 4. It is observed that Sim closure is similar to the proposed method till μ < 0.3 and suddenly dropped at μ = 0.5 in LFR500 series. Leiden seemed to be good only at μ = 0.2 but then it declined for other values of μ in LFR 500. Sim closure equally performed well with the proposed method in all series except in LFR 5000 where it suddenly dropped at μ = 0.4. All the methods seem to be good in LFR 10000 in which Leiden was the least. This might be the reason that it cannot handle large scale networks. Attractor and walktrap performs fairly on all 4 series of networks. LPA seems to fluctuate in LFR500, LFR1000 and LFR 5000 but seems to be consistent in LFR 10000. Proposed method dropped suddenly in LFR1000 at μ = 0.7. The proposed method obtains high quality community structures and it is superior compared to other existing algorithms.
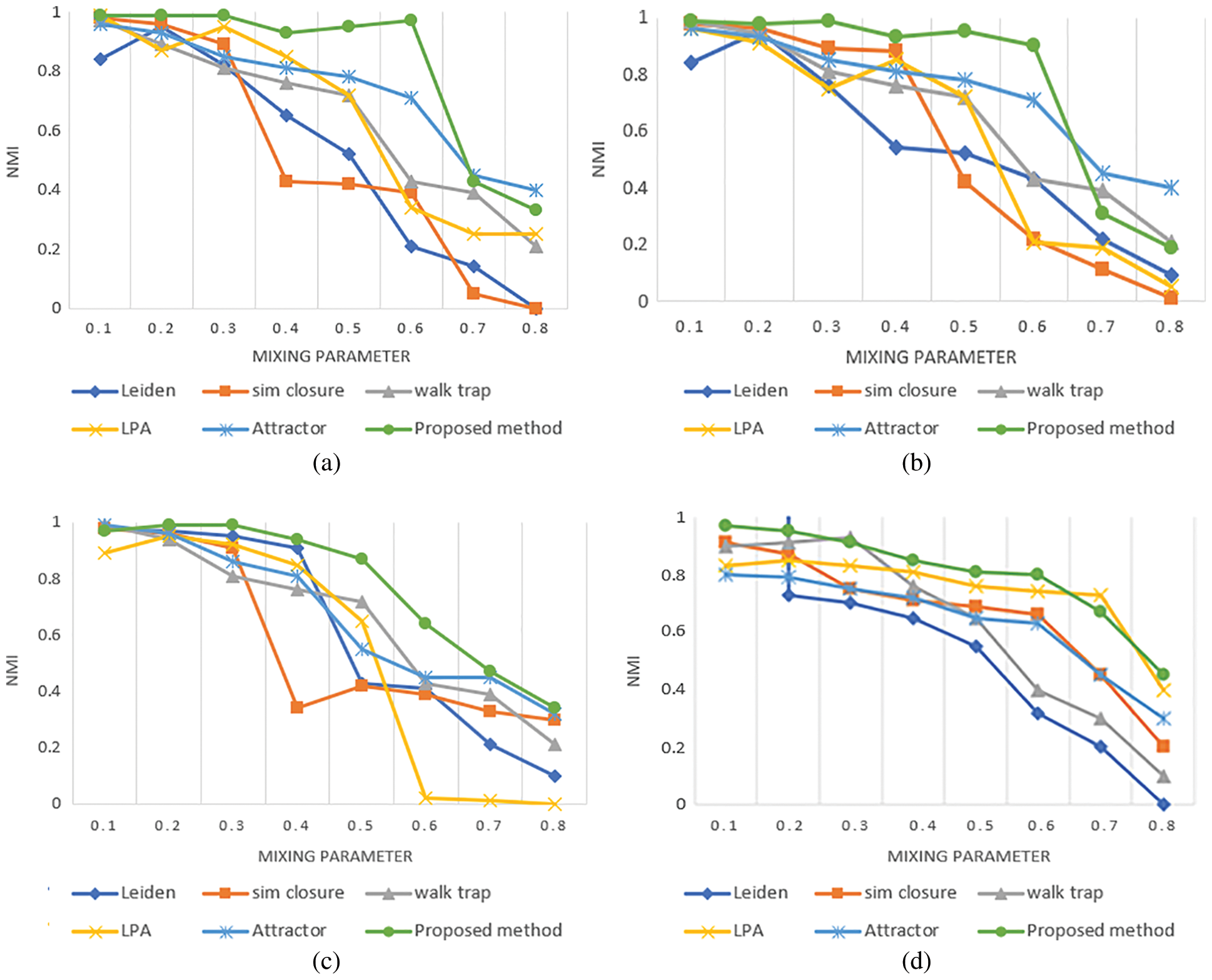
Figure 4: NMI from artificial networks (a) LFR 500 (b) LFR 1000 (c) LFR 5000 (d). LFR 10000
Comparison of detected results of proposed system and other algorithms in terms of R and the ratio between the detected number of communities and real number of communities are presented in Fig. 5. It is obvious from the result that the proposed method detects the accurate number of communities from all 4 series of networks. The R values seems to be ideal in all networks. In LFR500 and LFR10000, Leiden deviates from 1. Detection of the community in Sim Closure and the proposed method are almost closer. The number of communities detected in LFR1000 is not consistent.
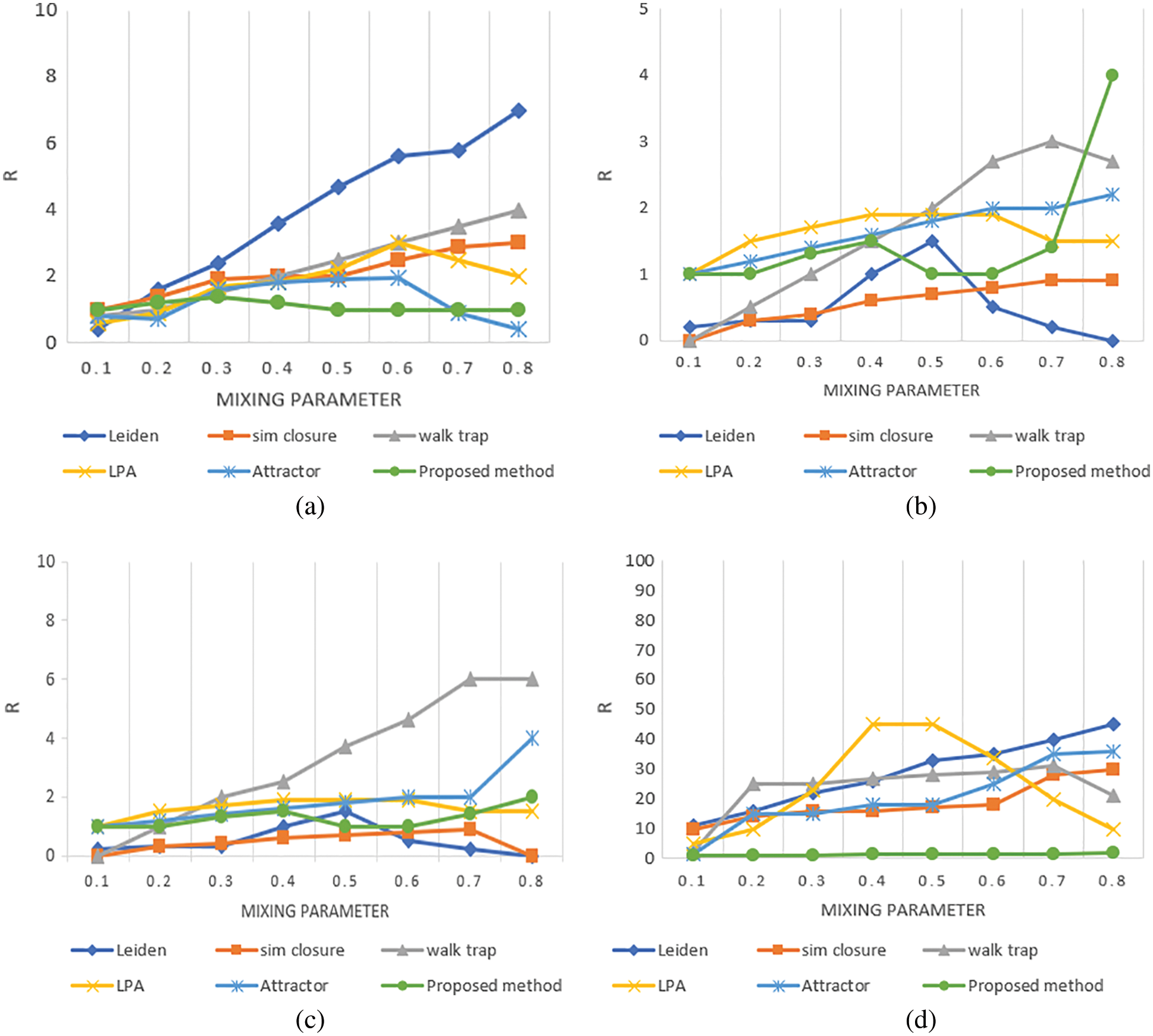
Figure 5: Ratio of detected communities and real communities in artificial networks (a) LFR 500 (b) LFR 1000 (c) LFR 5000 (d) LFR 10000
Experimental Results for Real Networks
This section overviews the results obtained in real world networks. Tab. 2 lists the ground truth communities of first four networks. Tab. 3 shows the ground truth communities. NMI and modularity (Q) are the measures to evaluate the quality of community structures detected by proposed and other existing methods. Tab. 3 shows the results of the comparison.


From the Tab. 3 it is observed that Leiden gains highest modularity for all 4 networks. The second highest modularity is attained by the proposed method for Karate, football game and Ecoli networks. SimEdge-CD modularity in Dolphin network was the third largest. The second largest modularity in Tab. 3 is highlighted with an underline. In terms of the metric NMI, the proposed method scored the largest NMI which is 1 for dolphin and football game schedule. Also, it proved to score the largest for karate and Ecoli. Results clearly show that sim_closure obtains 1 for dolphin network. Walkstrap gains 1 for Ecoli. It is clearly summarised from the result obtained that the proposed method outperforms the other existing methods and detects the high-quality community structures.
This work proposed SimEdge-CD for community detection and also finds the communities of the boundary nodes to define well defined communities. This method is evaluated on 4 series of synthetic networks and 4 real time networks. The results of the SimEdge-CD is compared with sim_closure, walktrap, LPA, Attractor and Leiden. SimEdge-CD scored the largest NMI 1 for dolphin and football game schedule. The proposed method considers the similarity of the nodes and uses this property to cluster the nodes in the network for achieving high quality community detection. The results of experiments demonstrates that the proposed SimEdge-CD provides superior community detection performance compared to the existing methods in terms of NMI indicator and modularity.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Yang, J. Cheng, Z. Yang, H. Zhang, W. Zhang et al., “A node similarity and community link strength based community discovery algorithm,” Complexity, vol. 2021, pp. 1–21, 2021. [Google Scholar]
2. B. Yang, D. Liu and J. Liu, “Discovering communities from social networks: Methodologies and applications,” in Handbook of social network technologies and applications, 1st edition, vol. 1, New York: Springer, pp. 331–346, 2010. [Google Scholar]
3. G. Michelle and M. E. Newman, “Community structure in social and biological networks,” in National Academy of Sciences, Proceedings of the National Academy of Sciences of the United States of America (PNASNew york, no. 12, pp. 7821–7826, 2002. [Google Scholar]
4. W. Liu, M. Pellegrini and X. Wang, “Detecting communities based on network topology,” Scientifc Reports, vol. 4, no. 5739, pp. 1–7, 2014. [Google Scholar]
5. X. Qi, W. Tang, Y. Wu, G. Guo, E. Fuller et al., “Optimal local community detection in social networks based on density drop of subgraphs,” Pattern Recognition Letters, vol. 36, pp. 46–53, 2014. [Google Scholar]
6. D. Rafailidis, E. Constantinou and Y. Manolopoulos, “Landmark selection for spectral clustering based on weighted pageRank,” Future Generation Computer Systems, vol. 68, pp. 465–472, 2017. [Google Scholar]
7. S. Fortunato, “Community detection in graphs,” Physics Reports, vol. 486, no. 5, pp. 75–174, 2010. [Google Scholar]
8. Y. R. Wang and P. J. Bickel, “Likelihood-based model selection for stochastic block models,” Annals of Statistics, vol. 45, no. 2, pp. 500–528, 2017. [Google Scholar]
9. A. Clauset, M. E. J. Newman and C. Moore, “Finding community structure in very large networks,” Physical Review, vol. 70, pp. 1–11, 2004. [Google Scholar]
10. A. Lancichinetti, F. Radicchi, J. Ramasco and S. Fortunato, “Finding statistically significant communities in networks,” PLoS ONE, vol. 6, no. 4, pp. e18961, 2011. [Google Scholar]
11. J. M. Hofman and C. H. Wiggins, “Bayesian approach to network modularity,” Physical Review Letters, vol. 100, no. 25, pp. 258701, 2008. [Google Scholar]
12. Y. Xiaoran, “Bayesian model selection of stochastic block models,” in Proc. ASONAM, Hague, Netherland, pp. 323–328, 2016. [Google Scholar]
13. J. J. Daudin, F. Picard and S. Robin, “A mixture model for random graphs,” Statistics and Computing, vol. 18, no. 2, pp. 173–183, 2008. [Google Scholar]
14. M. E. Newman, “Fast algorithm for detecting community structure in networks,” Physical Review, vol. 69, no. 6, pp. 1–17, 2004. [Google Scholar]
15. J. Jia, X. Xiao, B. Liu and L. Jiao, “Bagging-based spectral clustering ensemble selection,” Pattern Recognition Letters, vol. 32, no. 10, pp. 1456–1467, 2011. [Google Scholar]
16. R. Guimera and L. A. Nunes Amaral, “Functional cartography of complex metabolic networks,” Nature, vol. 433, pp. 895–900, 2005. [Google Scholar]
17. N. Mark and E. J. Newman, “Modularity and community structure in networks,” in Proc. NAS, Newyork, vol. 103, no. 23, pp. 8577–8582, 2006. [Google Scholar]
18. P. J. Sweeney and K. Mehrotra, “A game theoretic framework for community detection,” in Proc. ASONAM, Istanbul, Turkey, pp. 26–29, 2012. [Google Scholar]
19. A. Lancichinetti, S. Fortunato and J. Kert´esz, “Detecting the overlapping and hierarchical community structure in complex networks,” New Journal of Physics, vol. 11, no. 3, pp. 33015, 2009. [Google Scholar]
20. W. Chen, Z. Liu, X. Sun and Y. Wang, “A game-theoretic framework to identify overlapping communities in social networks,” Data Mining and Knowledge Discovery, vol. 21, no. 2, pp. 224–240, 2010. [Google Scholar]
21. Y. Tang, J. Xiang, Y. Gao, Z. Zhing Wang, H. Jia Li et al., “An effective algorithm for optimizing surprise in network community detection,” IEEE Access, vol. 7, pp. 148814–148827, 2019. [Google Scholar]
22. S. Gregory, “Finding overlapping communities in networks by label propagation,” New Journal of Physics, vol. 12, no. 10, pp. 1–17, 2010. [Google Scholar]
23. Q. Qiu, W. Guo, Y. Chen, K. Guo and R. Li, “Parallel multi-label propagation based on influence model and its application to overlapping community discovery,” International Journal on Artificial Intelligence Tools, vol. 26, no. 3, pp. 1–14, 2017. [Google Scholar]
24. K. Guo, L. He, Y. Chen, W. Guo and J. Zheng, “A local community detection algorithm based on internal force between nodes,” International Journal of Speech Technology, vol. 50, no. 2, pp. 328–340, 2020. [Google Scholar]
25. Z. Liu, B. Xiang, W. Guo, Y. Chen, K. Guo et al., “Overlapping community detection algorithm based on coarsening and local overlapping modularity,” IEEE Access, vol. 7, pp. 57943–57955, 2019. [Google Scholar]
26. F. Radicchi, C. Castellano, F. Cecconi, V. Loreto and D. Paris, “Defining and identifying communities in networks,” in Proc. National Academy of Sciences, US, vol. 101, no. 9, pp. 2658–2663, 2004. [Google Scholar]
27. M. Girvan and M. E. Newman, “Community structure in social and biological networks,” in Proc. National ACAD Sciences, USA, vol. 99, no. 12, pp. 7821–7826, 2002. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |