DOI:10.32604/csse.2022.030759

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.030759 |  |
| Article |
Lexicalized Dependency Paths Based Supervised Learning for Relation Extraction
New York University, New York, 10012, USA
*Corresponding Author: Huiyu Sun. Email: hs2879@nyu.edu
Received: 11 February 2022; Accepted: 16 April 2022
Abstract: Log-linear models and more recently neural network models used for supervised relation extraction requires substantial amounts of training data and time, limiting the portability to new relations and domains. To this end, we propose a training representation based on the dependency paths between entities in a dependency tree which we call lexicalized dependency paths (LDPs). We show that this representation is fast, efficient and transparent. We further propose representations utilizing entity types and its subtypes to refine our model and alleviate the data sparsity problem. We apply lexicalized dependency paths to supervised learning using the ACE corpus and show that it can achieve similar performance level to other state-of-the-art methods and even surpass them on several categories.
Keywords: Relation extraction; dependency paths; lexicalized dependency paths; supervised learning; rule-based models
There has been steady progress over the last fifteen years in relation extraction, primarily using supervised machine learning methods for training log-linear models [1–11], more recently neural network models [12–24] and joint models that combine several models in one [25–28]. This requires lots of training data and time, which limits the portability to new relations and domains. This has led in practice to the continued use of manually-curated rule-based systems, which are more inspectable and thus give the developer more control [29].
We believe that customization of extraction engines is ultimately a collaborative process, with system and developer both providing some guidance and both proposing and validating improvements to the model. This is possible only if the developer can grasp the current state of the model. This requires a rule-based representation that is (1) transparent and intuitive, so that rules can be easily understood, and (2) efficient, in the sense that, compared to other representations, a small set of rules yields satisfactory performance.
To achieve this desired goal, we propose the use of lexicalized dependency paths (LDP) with types and subtypes as the representation. Dependency paths have been widely used in relation extraction ([30–37]), so this seems a natural choice. However, adopting a constrained representation such as dependency paths will inevitably mean some loss of performance. Our main goal here is to gauge that loss. In the sections which follow we describe the proposed representation and compare its performance to published results using other types of models.
In dependency kernels, [38] proposed a tree kernel over shallow parse tree representations of sentences and [32] generalized the tree kernel and used dependency trees. [30] used the shortest-path between the two relation entities in the dependency graph as the kernel for relation extraction. Scoring on ACE 2004, they outperformed previous dependency tree kernels. Then [31] presented a new kernel based on generalization of subsequence kernels. [33] used dependency parse trees to extract relations in the biomedical domain. [11], [34–36], and [38] all utilized various modified, improved and augmented tree kernels to extract relations. [18] used augmented dependency paths composed of shortest dependency path as well as the subtrees attached to the path for relation classification. [20] tackled domain adaptation using word embeddings to generate semantic representations in tree kernels.
In terms of featured-based methods, [8] proposed a maximum entropy model combining lexical, syntactic and semantic features. [39] presented a feature-based system description for ACE 2005. [7] used various features including dependency parse tree representations. [6] and [10] exploited various knowledge information such as background knowledge in relation extraction. [1] proposed a feature-rich compositional embedding model of relation extraction. They handled arbitrary types of sentence annotations and utilized global information for composition. They outperformed previous compositional models as well as feature rich models on ACE 2005. In terms of neural network methods, [40] proposed a hybrid model that combines feature-based method with convolutional and recurrent neural networks to effectively extract relations from ACE 2005. [21–24] all proposed various neural networks for relation extraction.
3 Lexicalized Dependency Paths
Many previous works have utilized dependency paths ([30–37]) for relation extraction. A dependency path is essentially the path between two entities in a dependency graph, and it usually offers a condensed representation of the information needed to assess the relationship between the entities. We propose a lexicalized version of this path which we call lexicalized dependency path (LDP). A LDP has the following form:
arg1type–deptype:lex:deptype:lex:…:deptype–arg2type.
The arg1type and arg2type are entity types of the two arguments of a relation (e.g., PERSON, GPE), deptype specifies a type of dependency relation (e.g., nsubj, dobj), and lex is the base form of a lexical item (e.g. work, from). If an arc of type X in the dependency tree is traversed from governor to dependent, the path includes ‘X’; if the arc is traversed from dependent to governor, the path includes ‘X-1’, e.g., nsubj-1 or dobj-1.
Extending dependency path this way has several advantages over predecessors. First, it creates a rule-based system that is unified and easily understood and it allows a nature extension to other forms of learning such as active learning. Second, this representation also means we can dissect a sentence into a number of LDPs allowing for a supervised trainer to be used. A potential problem here is data sparsity and we propose a further representation based on type and subtypes LDPs to eliminate this problem which we describe in a following section.
3.2 Constructing a Lexicalized Dependency Path
To produce a set of LDPs for a sentence, we start with a dependency parse for the sentence (we use the dependency parser of [41]). Then several transformations are applied to the parse. These recognize various syntactic forms involving the same semantic relation, such as active, passive, relative, and reduced relative forms; these are all transformed to simple active clauses. By collapsing such forms, there will be fewer forms to learn and learning should be accelerated. A few of the transformations serve to restructure the tree so that crucial information will be included in the dependency path. One such transformation fuses a verb with a verbal particle.
We then generate a dependency path connecting every pair of entity mentions in the sentence using a shortest path algorithm. An entity mention is a name or noun phrase belonging to one of a specified set of semantic types. We reduce the conjunctions in the path: if the path includes a constituent conjoined with another entity, the conjoined constituent is eliminated. We then lemmatize the path: replacing each word in the path with the stem of the word, for example the word ‘sold’ becomes ‘sell’.
Finally, we generate an English phrase from each LDP. This is done in a rather straightforward way, combining the lexical items in the LDP with lexical realizations of some of the dependency relations (for example, the ’s for the possessive relation). In most cases the result is a word sequence containing a subset of the words between the two arguments in the original sentence, preserving their order. Internally the extraction customization uses LDPs, but interaction with the developer is in terms of these phrases.
We use ACE 2005 [42] to train and evaluate our model. ACE has approximately 600 documents with a total of 300,000 words, annotated for entities, relations, and events.
For ACE 2005, 6 relation classes are annotated: ORG-AFF (Organization-Affiliation), PART-WHOLE, PHYS (Physical), GEN-AFF (General-Affiliation), PER-SOC (Person-Social), and ART (Artifact). We also use the NR class to indicate ‘no relation’.
7 entity types are annotated in ACE 2005: PERSON, GPE (Geo-Political Entity), ORGANIZATION, LOCATION, FACILITY, WEA (Weapon), and VEH (Vehicle).
Take the example ACE 2005 ‘sentence’:
And here in Washington, Democratic senator Christopher Dodd of Connecticut.
This sentence contains three relation instances: ORG-AFF between Christopher Dodd (PERSON) and Democratic (ORGANIZATION), GEN-AFF between Christopher Dodd (PERSON) and Connecticut (GPE), and PHYS between Christopher Dodd (PERSON) and Washington (GPE).
The LDPs and associated English phrase of the three relation instances are respectively:
LDP: ORGANIZATION–amod-1:senator:nn-1–PERSON Phrase: Organization senator Person
LDP: PERSON–prep:of:pobj–GPE Phrase: Person of GPE
LDP: PERSON–pobj-1:here:prep:in:pobj–GPE Phrase: Person here in GPE
This same basic procedure is used for training and decoding. For training, each LDP taken from the corpus is tagged with its relation type or NR to indicate ‘no relation’. An extraction model is simply a set of LDPs with their tags. For decoding, each test LDP is compared with all the LDPs collected during training; if it matches one and that one is not labelled NR, we assign that test LDP with the label of the training LDP.
3.4 Type and Subtype Lexicalized Dependency Path
We counter the problem of data sparsity usually found in dependency-based models by using types and subtypes of entities. Entities in ACE assigned a type are also assigned a subtype, for example a PERSON entity can be classified into three subtypes: Individual, Group or Indeterminate, a GPE entity can be one of 7 subtypes: Continent, County-or-District, GPE-Cluster, Nation, Population-Center, Special, State-or-Province, and an ORGANIZATION entity can be one of 9 subtypes: Commercial, Educational, Entertainment, Government, Media, Medical-Science, Non-Governmental, Religious, or Sports.
To combine coarse and fine semantic classes, we differentiate LDPs formed between pairs of entity type arguments and all of its subtype arguments. Given a sentence with a pair of entity mentions, we can proceed in three ways: we can create a type LDP from the types of the entity mentions; we can create a subtype LDP from the subtypes of the entity mentions; or we can create both type and subtype LDPs. In the last case, a test LDP may have two matches against the model: one matching types, one matching subtypes. In that case the subtype match takes precedence. This makes it possible to have general rules and more specific exceptions.
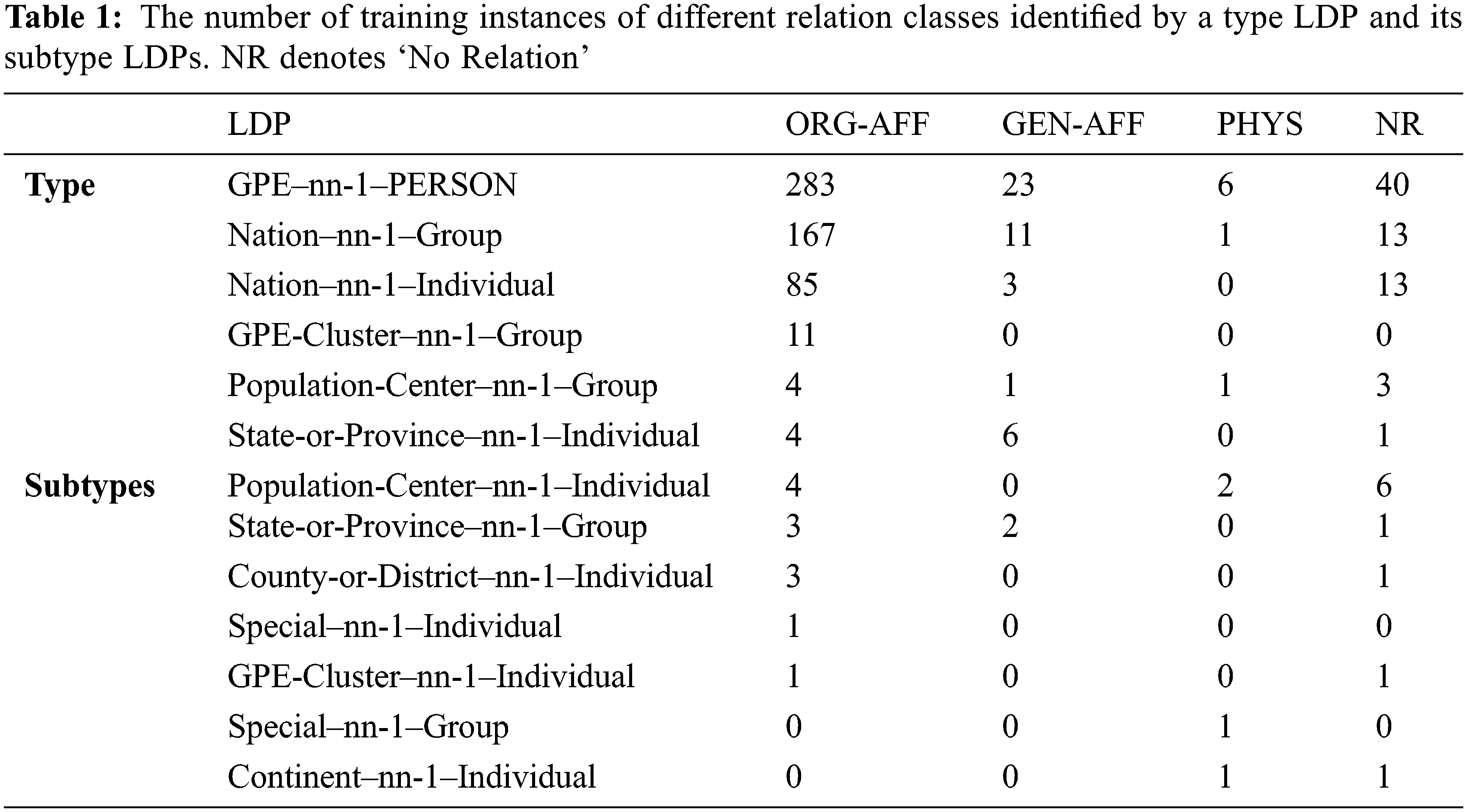
Training instances of each relation class identified by the type LDP GPE–nn-1–PERSON and its subtype LDPs are shown in Tab. 1. The type LDP is assigned ORG-AFF as that is the most common class with 283 instances. But some of its subtype LDPs get assigned a different class: State-or-Province–nn-1–Individual is assigned GEN-AFF, and Special–nn-1–Group and Continent–nn-1–Individual are assigned PHYS. This is a consequence of giving subtypes precedence over types.
4 Learning with Lexicalized Dependency Paths
We evaluate the performance under supervised learning with a substantial training corpus. We extract and score relations between all ACE entity mentions including named, nominal and pronominal mentions. On the ACE training split, we construct a LDP for every pair of entity mentions appearing within a single sentence. Following the general practice for the evaluation of relation extractors, we provide ‘perfect’ (hand-coded) entity mentions. To reduce the noise, only examples where the two arguments are separated by less than 5 entity mentions are kept. We count the number of relation instances of each relation label that a LDP identifies. If a LDP occurs with more than one relation label, e.g. PERSON–prep:of:pobj–GPE has four relation labels: ORG-AFF with 24 instances, NR with 13 instances, GEN-AFF with 11 instances, and PHYS with 1 instance, the most common relation label is assigned (ORG-AFF in this case). When deciding the most common type, the six ACE relation types all get an equal weight of 1.0, but the NR (no relation) type gets a weight of 0.5, as we found that assigning a lower weight to the NR class improves the F1 score on training, and the weight of 0.5 produced the best score. This is why the subtype LDP Population-Center–nn-1–Individual in Tab. 1 gets assigned the label ORG-AFF, not NR despite the latter having a higher count.
In terms of the kernel function, we compute the dot-product between two relations. If
where
We perform supervised training on both type and subtype LDPs. In the implementation of our system, we take the order of arguments in the text into account: ‘Fred is employed by IBM’ has the label ORG-AFF and ‘IBM hired Fred’ has a different label ORG-AFF-1 where ‘−1’ indicates the arguments of the relation are inverted. After the first pass through the training data producing type as well as subtype LDPs, we combine them together to form type + subtype LDPs: for each subtype LDP, if there are one or more training LDPs which match both arguments of the LDP at the subtype level, take the most common relation label at the subtype level (including no relation) among the training LDPs; otherwise if there are one or more training LDPs which match both arguments of the LDP at the type level, take the most common relation label at the type level (including no relation). This allows us to assign a type LDP and its subtype LDPs different relation labels based on the most common label at the subtype level.
To help resist overfitting, we can further exploit the dual formation to calculate the kernel. In this case, the kernel function is
There are six news sources (genres) in ACE: broadcast conversations (bc), broadcast news (bn), conversational telephone speech (cts), newswire (nw), usenet (un), and weblog (wl). Most earlier evaluations reported an aggregate score across these genres ( [5–7], [9–11]) but recently there have been several studies which assessed genre independence ( [1,34,40]). To provide an additional assessment of our LDP-based models, we have replicated this data split, using bn and nw as training data and testing on bc, cts, un and wl separately.
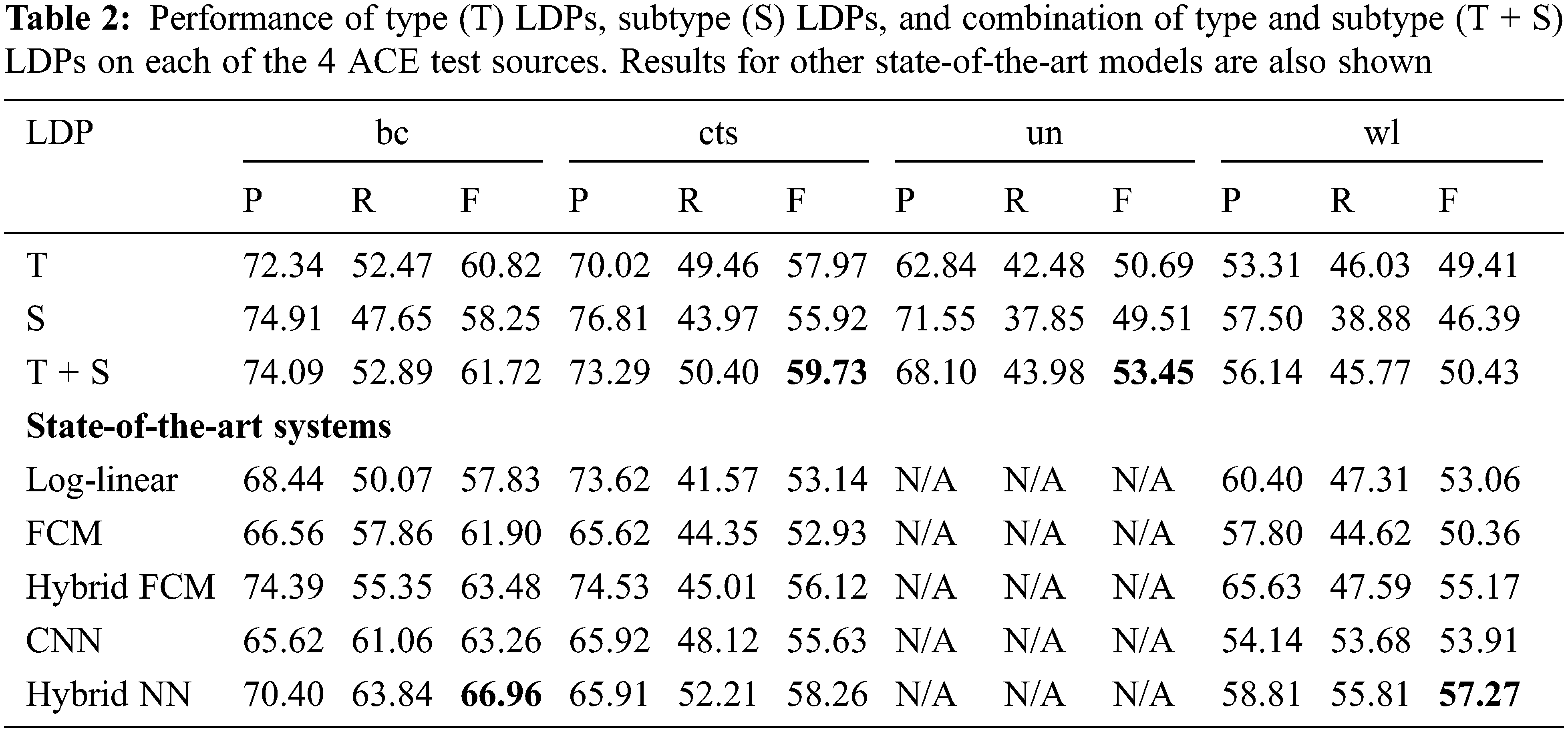
We train on nw and bn news sources of ACE, and test on bc, cts, un and wl separately. Type, subtype, and the combination of type and subtype (type + subtype) LDP scores on the test are shown in Tab. 2. Type + subtype LDPs produced the best result for each of the four test sources, and on the un genre, adding subtype LDPs on top of type LDPs achieved close to a 3% F1 increase compared to just type LDPs. This shows the advantage of combining coarse and fine semantic classes in type + subtype LDPs.
Performance comparisons between type and subtype LDPs are shown in Fig. 1. We see that using subtype LDP alone gets a worse performance compared to using type LDP. This is to be expected since utilizing entity subtype information is very limited and too fine-grained, giving a lot less recall score than typed LDP despite it producing better precision scores. Combining type and subtype outperforms both type and subtype LDPs on its own, showing its effectively in countering the data sparsity problem.
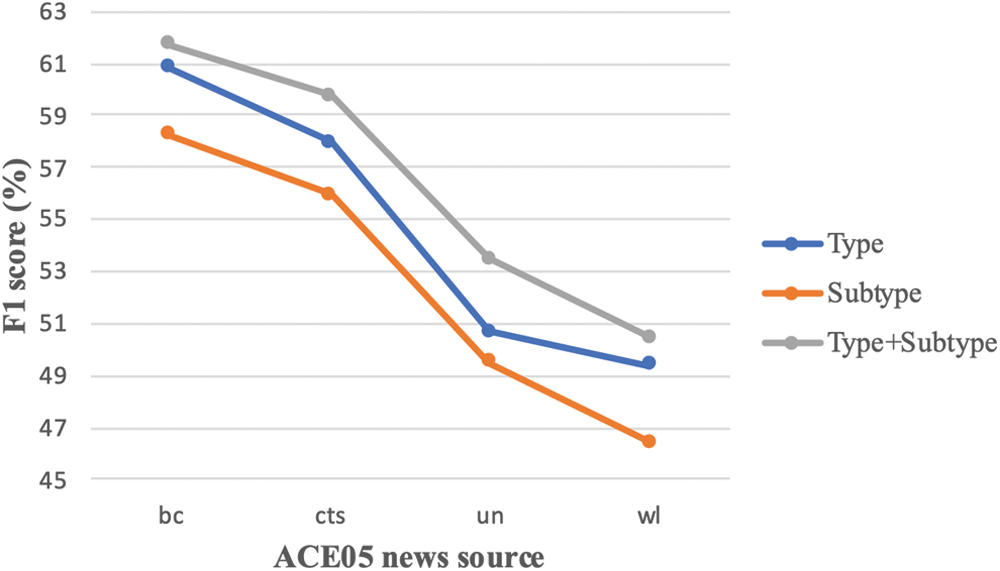
Figure 1: F1 scores of LDP representation with entity type, subtype and type + subtype comparisons across different ACE domains (bc, cts, un and wl)
Next, we compare our scores to state-of-the-art systems in Tab. 2. Precision (P), Recall (R), and F-score (F) are shown. The F score is the standard metric for comparing the overall performance of models. They can be calculated as follows:
As shown in the table, [1] proposed feature rich models FCM and Hybrid FCM, and our system outperforms their best system Hybrid FCM on the cts genre. Compared to log-linear models, we outperform on both bc and cts. Hybrid NNs were proposed in [40] and our system beats Hybrid NN and CNN on cts. Overall, the LDP model does exceptionally well on cts and does well on bc. These cross-domain results show that our rule-based LDP model can compete with feature-based models in the same as well as different domains, displaying the benefit of a transparent model and providing evidence that active learning using LDPs is very feasible.
5.2 Aggregate Performance and Variance
To evaluate the performance of the LDP model on ACE as a whole, we did 90%/10% splits on the train and test data, randomly selecting 10% of ACE as test, and the rest (90%) as training. We performed the random splits 20 times for type, subtype and type + subtype LDPs and recorded the scores on the test. The results of the 20 runs are separated in intervals ranging from the lowest score to the highest score with 1% as the increment. Distribution of the frequency of F1 scores on the test are shown in Fig. 2. There are certainly some fluctuations of scores obtained from different runs but we see that the variation in scores all somewhat conform to a normal distribution. The mean, standard deviation etc. of scores are shown in Tab. 3. Type + Subtype LDPs achieves the highest mean of 59.14 out of the three, a good indicator of the performance of the overall system. Type LDP achieved the second-best score, followed by just using subtype LDPs, which is to be expected. A comparable result given by [19] on the entire corpus using a convolutional neural net is 61.32, only slightly better than our score, while us having a much faster and transparent model.
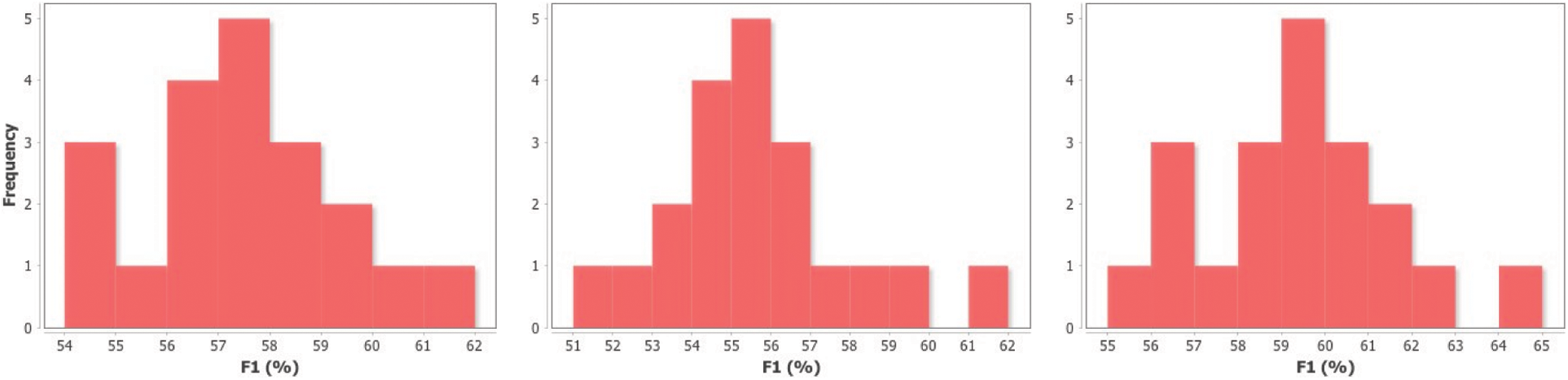
Figure 2: Frequency distributions of F1 scores after 20 random 90%/10% splits on train and test with type (left), subtype (middle) and type + subtype (right) LDPs

We expected LDP models to perform worse than log-linear and neural network models, particularly across domains. Log-linear models can be trained (and NN models can train themselves) to emphasize certain features of the input in ways that LDP models cannot. But our results show that this is not necessarily the case: our LDP-based models achieve a comparable performance to the best log-linear models. This can be attributed in part to the relatively local nature of most relations. More than half the relations are picked out by LDPs with length 1 and 3: either a direct dependency or a single word connecting the two arguments (for example GPE–nn-1–PERSON has length 1 and PERSON–prep:of:pobj–GPE has length 3). For these local relations, all the ‘features’ (words and dep. relations) are essential to the correct choice of label, and this exact match is just what you get with LDPs. There are lots of training examples for these small paths, so sparse data is not an issue. The performance of these local LDPs largely won’t be affected when switching between domains as local relations for different domains remain similar. On the other hand, long LDPs are responsible for picking out more distant relations. These LDPs more often include some sort of clause and so may benefit from the transformations which simplify clause structure.
Our future goal is to apply our Lexicalized Dependency Path (LDP) learner to simulated and real active learning of relations. We aim to experiment to see if we can achieve state-of-the-art results using a small number of annotations.
To remedy the inability of current supervised learning methods to examine the extraction model under development, we have presented a transparent and intuitive representation based on dependency path which we call lexicalized dependency path (LDP). We used entity types with specific subtypes to counter the effect of data sparsity inherent with such a dependency representation and it achieved a noticeable improvement over just dependency path representations. We applied our LDP model to supervised relation extraction and showed that supervised learning of LDPs achieved comparable performance to the state-of-the-art, with an average F1 of 59.14% on ACE 2005. This result allows us to extend LDP beyond supervised learning and makes the possibility of active learning feasible with this representation.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. R. Gormley, M. Yu and M. Dredze, “Improved relation extraction with feature-rich compositional embedding models,” in Proc. EMNLP, Lisbon, Portugal, pp. 1774–1784, 2015. [Google Scholar]
2. D. Can, H. Le, Q. Ha and N. Collier, “A richer-but-smarter shortest dependency path with attentive augmentation for relation extraction,” in Proc. NAACL, Minneapolis, Minnesota, USA, pp. 2902–2912, 2019. [Google Scholar]
3. C. Xie, J. Liang, J. Liu, C. Huang, W. Huang et al., “Revisiting the negative data of distantly supervised relation extraction,” in Proc. ACL, Bangkok, Thailand, pp. 3572–3581, 2021. [Google Scholar]
4. Z. Li, N. Ding, Z. Liu, H. Zheng and Y. Shen, “Chinese relation extraction with multi-grained information and external linguistic knowledge,” in Proc. ACL, Florence, Italy, pp. 4377–4386, 2019. [Google Scholar]
5. E. Boschee, R. Weischedel and A. Zamanian, “Automatic information extraction,” in Proc. the Int. Conf. on Intelligence Analysis, New York, NY, USA, vol. 71, 2005. [Google Scholar]
6. Y. S. Chan and D. Roth, “Exploiting background knowledge for relation extraction,” in Proc. Coling, Beijing, China, pp. 152–160, 2010. [Google Scholar]
7. J. Jiang and C. X. Zhai, “A systematic exploration of the feature space for relation extraction,” in Proc. NAACL, Rochester, New York, USA, pp. 113–120, 2007. [Google Scholar]
8. N. Kambhatla, “Combining lexical, syntactic, and semantic features with maximum entropy models for information extraction,” in Proc. ACL, New York, NY, USA, pp. 178–181, 2004. [Google Scholar]
9. A. Sun, R. Grishman and S. Sekine, “Semi-supervised relation extraction with large-scale word clustering,” in Proc. ACL, Portland, Oregon, USA, pp. 521–529, 2011. [Google Scholar]
10. G. Zhou, J. Su, J. Zhang and M. Zhang, “Exploring various knowledge in relation extraction,” in Proc. ACL, Ann Arbor, Michigan, USA, pp. 427–434, 2005. [Google Scholar]
11. G. Zhou, M. Zhang, D. Ji and Q. Zhu, “Tree kernel-based relation extraction with context-sensitive structured parse tree information,” in Proc. EMNLP-CoNLL, Prague, Czech Republic, pp. 728–736, 2007. [Google Scholar]
12. X. Hu, C. Zhang, Y. Yang, X. Li, L. Lin et al., “Gradient imitation reinforcement learning for low resource relation extraction,” in Proc. EMNLP, Punta Cana, Dominican Republic, pp. 2737–2746, 2021. [Google Scholar]
13. H. Wu and X. Shi, “Synchronous dual network with cross-type attention for joint entity and relation extraction,” in Proc. EMNLP, Punta Cana, Dominican Republic, pp. 2769–2779, 2021. [Google Scholar]
14. A. Veyseh, F. Dernoncourt, D. Dou and T. Nguyen, “Exploiting the syntax-model consistency for neural relation extraction,” in Proc. ACL, Seattle, Washington, USA, pp. 8021–8032, 2020. [Google Scholar]
15. I. Beltagy, K. Lo and W. Ammar, “Combining distant and direct supervision for neural relation extraction,” in Proc. NAACL, Minneapolis, Minnesota, USA, pp. 1858–1867, 2019. [Google Scholar]
16. N. Zhang, S. Deng, Z. Sun, X. Chen and W. Zhang, “Attention-based capsule networks with dynamic routing for relation extraction,” in Proc. EMNLP, Brussels, Belgium, pp. 986–992, 2018. [Google Scholar]
17. Y. Tian, G. Chen, Y. Song and X. Wan, “Dependency-driven relation extraction with attentive graph convolutional networks,” in Proc. ACL, Bangkok, Thailand, pp. 4458–4471, 2021. [Google Scholar]
18. Y. Liu, F. Wei, S. Li, H. Ji, M. Zhou et al., “A dependency-based neural network for relation classification,” in Proc. ACL-IJCNLP, Beijing, China, pp. 285–290, 2015. [Google Scholar]
19. T. H. Nguyen and R. Grishman, “Relation extraction: Perspective from convolutional neural networks,” in Proc. 1st Workshop on Vector Space Modeling for Natural Language Processing at NAACL, Denver, Colorado, USA, pp. 39–48, 2015b. [Google Scholar]
20. T. H. Nguyen, B. Plank and R. Grishman, “Semantic representations for domain adaptation: A case study on the tree kernel-based method for relation extraction,” in Proc. ACL-IJCNLP, Beijing, China, pp. 635–644, 2015. [Google Scholar]
21. C. D. Santos, B. Xiang and B. Zhou, “Classifying relations by ranking with convolutional neural networks,” in Proc. ACL-IJCNLP, Beijing, China, pp. 626–634, 2015. [Google Scholar]
22. Y. Xu, L. Mou, G. Li, Y. Chen, H. Peng et al., “Classifying relations via long short-term memory networks along shortest dependency paths,” in Proc. EMNLP, Lisbon, Portugal, pp. 1785–1794, 2015. [Google Scholar]
23. D. Zeng, K. Liu, S. Lai, G. Zhou and J. Zhao, “Relation classification via convolutional deep neural network,” in Proc. COLING, Dublin, Ireland, pp. 2335–2344, 2014. [Google Scholar]
24. S. Zheng, Y. Hao, D. Lu, H. Bao, J. Xu et al., “Joint entity and relation extraction based on a hybrid neural network,” Neurocomputing, vol. 257, no. 2017, pp. 59–66, 2017. [Google Scholar]
25. Y. Wang, C. Sun, Y. Wu, H. Zhou, L. Li et al., “UniRE: A unified label space for entity relation extraction,” in Proc. ACL, Bangkok, Thailand, pp. 220–231, 2021. [Google Scholar]
26. Z. Yan, C. Zhang, J. Fu, Q. Zhang and Z. Wei, “A partition filter network for joint entity and relation extraction,” in Proc. EMNLP, Punta Cana, Dominican Republic, pp. 185–197, 2021. [Google Scholar]
27. L. Cui, D. Yang, J. Yu, C. Hu, J. Cheng et al., “Refining sample embeddings with relation prototypes to enhance continual relation extraction,” in Proc. ACL, Bangkok, Thailand, pp. 232–243, 2021. [Google Scholar]
28. X. Li, F. Yin, Z. Sun, X. Li, A. Yuan et al., “Entity-relation extraction as multi-turn question answering,” in Proc. ACL, Florence, Italy, pp. 1340–1350, 2019. [Google Scholar]
29. L. Chiticariu, Y. Li and F. Reiss, “Rule-based information extraction is dead! long live rule-based information extraction systems!,” in Proc. EMNLP, Seattle, Washington, USA, pp. 827–832, 2013. [Google Scholar]
30. R. C. Bunescu and R. J. Mooney, “A shortest path dependency kernel for relation extraction,” in Proc. the Human Language Technology Conf. and EMNLP, Vancouver, British Columbia, Canada, pp. 724–731, 2005. [Google Scholar]
31. R. C. Bunescu and R. J. Mooney, “Subsequence kernels for relation extraction,” in Proc. NIPS, Cambridge, MA, USA, pp. 171–178, 2006. [Google Scholar]
32. A. Culotta and J. Sorensen, “Dependency tree kernels for relation extraction,” in Proc. ACL, Barcelona, Spain, pp. 423–429, 2004. [Google Scholar]
33. K. Fundel, R. Kuffner and R. Zimmer, “RelEx-relation extraction using dependency parse trees,” Bioinformatics, vol. 23, no. 3, pp. 365–371, 2006. [Google Scholar]
34. B. Plank and A. Moschitti, “Embedding semantic similarity in tree kernels for domain adaptation of relation extraction,” in Proc. ACL, Sofia, Bulgaria, pp. 1498–1507, 2013. [Google Scholar]
35. L. Qian, G. Zhou, F. Kong, Q. Zhu and P. Qian, “Exploiting constituent dependencies for tree kernel-based semantic relation extraction,” in Proc. COLING, Manchester, UK, pp. 697–704, 2008. [Google Scholar]
36. M. Zhang, J. Zhang, J. Su and G. Zhou, “A composite kernel to extract relations between entities with both flat and structured features,” in Proc. COLING-ACL, Sydney, Australia, pp. 825–832, 2006. [Google Scholar]
37. D. Zelenko, C. Aone and A. Richardella, “Kernel methods for relation extraction,” Journal of Machine Learning Research, vol. 3, no. Feb, pp. 1083–1106, 2003. [Google Scholar]
38. T. T. Nguyen, A. Moschitti and G. Riccardi, “Convolution kernels on constituent, dependency and sequential structures for relation extraction,” in Proc. EMNLP, Singapore, pp. 1378–1387, 2009. [Google Scholar]
39. R. Grishman, D. Westbrook and A. Meyers, “NYU’s english ACE 2005 system description,” ACE 2005 Evaluation Workshop, vol. 5, pp. 1–7, 2005. [Google Scholar]
40. T. H. Nguyen and R. Grishman, “Combining neural networks and log-linear models to improve relation extraction,” 2015a. [Online]. Available: https://arxiv.org/abs/1511.05926. [Google Scholar]
41. S. Tratz and E. Hovy, “A fast, accurate, non-projective, semantically-enriched parser,” in Proc. EMNLP, Edinburgh, Scotland, UK, pp. 1257–1268, 2011. [Google Scholar]
42. C. Walker, S. Strassel, J. Medero and K. Maeda, “ACE 2005 multilingual training corpus,” Linguistic Data Consortium, Web download: https://catalog.ldc.upenn.edu/LDC2006T06, 2006. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |