Computer Systems Science & Engineering DOI:10.32604/csse.2022.028841
Article

Cold-Start Link Prediction via Weighted Symmetric Nonnegative Matrix Factorization with Graph Regularization

Minghu Tang1,2,3,*, Wei Yu4, Xiaoming Li4, Xue Chen5, Wenjun Wang3 and Zhen Liu6

1key Laboratory of Artificial Intelligence Application Technology State Ethnic Affairs Commission, Qinghai Minzu University, Xining, 810007, China
2School of Computer Science, Qinghai Minzu University, Xining, 810007, China
3College of Intelligence and Computing, Tianjin University, Tianjin, 300350, China
4School of International Business, Zhejiang Yuexiu University, Shaoxing, 312069, China
5Law School, Tianjin University, Tianjin, 300072, China
6Graduate School of Engineering, Nagasaki Institute of Applied Science, Nagasaki, 851-0193, Japan
*Corresponding Author: Minghu Tang. Email: mhtang@tju.edu.cn
Received: 19 February 2022; Accepted: 30 March 2022

Abstract: Link prediction has attracted wide attention among interdisciplinary researchers as an important issue in complex network. It aims to predict the missing links in current networks and new links that will appear in future networks. Despite the presence of missing links in the target network of link prediction studies, the network it processes remains macroscopically as a large connected graph. However, the complexity of the real world makes the complex networks abstracted from real systems often contain many isolated nodes. This phenomenon leads to existing link prediction methods not to efficiently implement the prediction of missing edges on isolated nodes. Therefore, the cold-start link prediction is favored as one of the most valuable subproblems of traditional link prediction. However, due to the loss of many links in the observation network, the topological information available for completing the link prediction task is extremely scarce. This presents a severe challenge for the study of cold-start link prediction. Therefore, how to mine and fuse more available non-topological information from observed network becomes the key point to solve the problem of cold-start link prediction. In this paper, we propose a framework for solving the cold-start link prediction problem, a joint-weighted symmetric nonnegative matrix factorization model fusing graph regularization information, based on low-rank approximation algorithms in the field of machine learning. First, the nonlinear features in high-dimensional space of node attributes are captured by the designed graph regularization term. Second, using a weighted matrix, we associate the attribute similarity and first order structure information of nodes and constrain each other. Finally, a unified framework for implementing cold-start link prediction is constructed by using a symmetric nonnegative matrix factorization model to integrate the multiple information extracted together. Extensive experimental validation on five real networks with attributes shows that the proposed model has very good predictive performance when predicting missing edges of isolated nodes.

Keywords: Link prediction; cold-start; nonnegative matrix factorization; graph regularization

1  Introduction

Link prediction, an important problem in the complex network, has achieved fruitful results [1,2]. Its aim is to use known information of the observed network to infer missing edges. Although existing link prediction methods can achieve the prediction of missing links between pairs of nodes in a network, they assume that the network is a connected graph. However, the complexity of the real world, makes the complex networks abstracted from real systems often contain many isolated nodes. This phenomenon causes that the network observed is a nonconnected graph. That is, the overall observation network is in a semi-connected state, so it is called a semi-connected network. This situation led to the traditional link prediction methods cannot use the topological information, thus affecting the prediction effect [3]. For example, in criminal networks or anti-terrorist networks, the topological structure is semi-connected, which makes it extremely difficult for link prediction methods to speculate on the social relations of criminals [4]. Thus, how to solve the prediction of missing edges of isolated nodes in the semi-connected network is a problem worth studying. In fact, as early as 2010, Leroy et al. [5] have studied the missing edge prediction problem and proposed the first concept of cold-start link prediction. They assume that the relationship of all users in the social networks are hidden, and then collect information about users' social activities, such as time of attend social events, number of communities sharing together, and length of stay in the community, through modeling to speculate the hidden links in the network. However, because the network topology information is not available and node attributes are very difficult to collect, this problem has not been well studied.

In recent years, with the increasingly severe anti-terrorism situation, the research of cold-start link prediction has gradually gained attention [6] and been widely used in fight against terrorists [4], abnormal detection [7], recommendation system [8], Community detection [9,10] and other fields [11–14]. However, many isolated nodes in the network cause the network topology becomes semi-connected states (i.e., the observed network is a non-connected graph). Existing link prediction methods based on structural similarity [1,2], network embedding [15], or neural network [16] cannot be directly used to solve this problem. Therefore, how to mine the non-topological information in the network and form a good information fusion mode becomes the key to solve the cold-start link prediction.

Currently, the studies of cold-start link prediction can be roughly divided into two categories. The first is based entirely on non-topological information methods [5]. Such methods, however, come to unsatisfactory prediction since the considerable difficulty in collecting of node attributes and the impact of noises involved. The second class of methods for cold-start link prediction is generally based on multiple auxiliary network layers to infer the missing edges of isolated nodes on the target network layers [17]. This method achieves the prediction by first exploring various auxiliary networks information of the target network, then reasoning in accordance with the relationships, and last, transferring the structure relationships at the auxiliary network level to the target network. But it is difficult to seek an auxiliary-level network and align these different networks. So, the second method has limitation with particularly strong domain. Thus, these methods which use single information cannot better solve the cold-start problem.

In this paper, considering the advantages of fusing heterogeneous information via a nonnegative matrix factorization (NMF) framework, a cold-start link prediction model, Joint weighted Symmetric NMF integrating Graph regularization information (GJSNMF), is proposed. The model first excavates non-nonlinear features in the attribute high-dimensional space and transforms it’s as weighted information. Then, using NMF framework to fuse topological information of the semi-connected network, to realize the prediction problem of the missing edges of the cold-start nodes of the network. Extensive experiments show that the model proposed achieves good effect on solving the problem of cold-start link prediction.

The rest article develops as follows. Part 2 shows the relevant works. Part 3 is about the establishment of the model and its optimization. Part 4 is experimental design. Part 5 is experiment results and related analysis. The last part contains our conclusions and prospects.

2  Related Work

Leroy et al. [5] supposed that all the nodes in a network are isolated and came up with the concept of cold-start link prediction. Ge et al. [18] proposed that some of the network structural relationships are known and the other missing, which they called pseudo cold-start link prediction. Han et al. [19] used the configuration files of online social-contact users and other non-topological information (e.g., workplace and school) to compute the attribute similarity, for counting the number of attributes the users all possess and the geographic distance between the users. Then, a prediction model was devised on the basis of support vector machines (SVM). By contrast, Wang et al. [20] extracted topological information by an implicit feature representation model. Wu et al. [21] abstracted multiple interactions as multi-relational networks, and employed robust principle component analysis to extract low-dimensional latent factors from sub-networks. Then associated auxiliary networks are exploited for cold-start link prediction. It realized the prediction by learning characteristics from the non-topological attributes they have observed. Adopting mesoscopic community membership information, Xu et al. [22,23] puts forward a community-weighted measurement learning framework for the purpose of link prediction. Yan et al. [24] paid attention to the cold-start for new users. It conducts predicting the interrelationships between new users by cross-platform transfer of the relationships via heterogenous information networks. Zhang et al. [25] tried to infer the possible link relationships between the newly registered users and old users by sampling various attribute information. Li et al. in reference [26], both the structure and attributes of a real network are considered dynamic and having an impact on the evolution of network structure with time. Alternatively, the reference [27] presents different perspectives for cold nodes.

3  Materials and Methods

3.1 Preliminaries

In this section, we first describe the problem of cold-start link prediction. In addition, we review the conventional NMF method.

3.1.1 Network Representation

Given an attribute network G(V,E,A) , where V={v1,v2,⋯vn} is the set of nodes and E={(vi,vj),1≤iandj≥n,i≠j} is the set of edges. The interaction relation between nodes is formally marked as an adjacency matrix Sn×n in network with n vertices. The element of the ith row and the jth column in the matrix correspond to the link between node i and j in the network, where Sij=1 if there is a link from i to j and Sij=0 otherwise. Generally, the adjacency matrix S represents the macro-relations of the network topology. The node attributes are represented as the matrix An×m . If the node vi has the k -th attribute, then Aik=1 , otherwise Aik=0 .

3.1.2 Cold-Start Link Prediction Problem

Assuming a real interaction system P , the network G is a model that fully characterizes the interaction relationships of various entities within the system P . But the actual observed network is G′ by the observer. It contains a lot of isolated nodes. The purpose of the cold-start link prediction is to use all these known information of the observed network G′ , to infer the missing link, so that restores the incomplete network G′ to the topological style of the real network G as much as possible. So, the problem of link prediction is inferring the probability of an existent link between nodes x and y based on known information in the network G′ , and the probability is expressed as score Pxy . The score can be viewed as the similarity of nodes x and y . The higher Pxy indicated that two nodes are more similarity. According to the score, all non-existent links in the network can be sorted in descending order. The links at the top are the most likely to exist. In this paper, we compute the score Pxy based on GJSNMF.

Fig. 1 show that the entire row(column) elements are 0 in the adjacency matrix S′ of the network G′ . It indicates that there are some isolated nodes in the network. And the network is semi-connected.

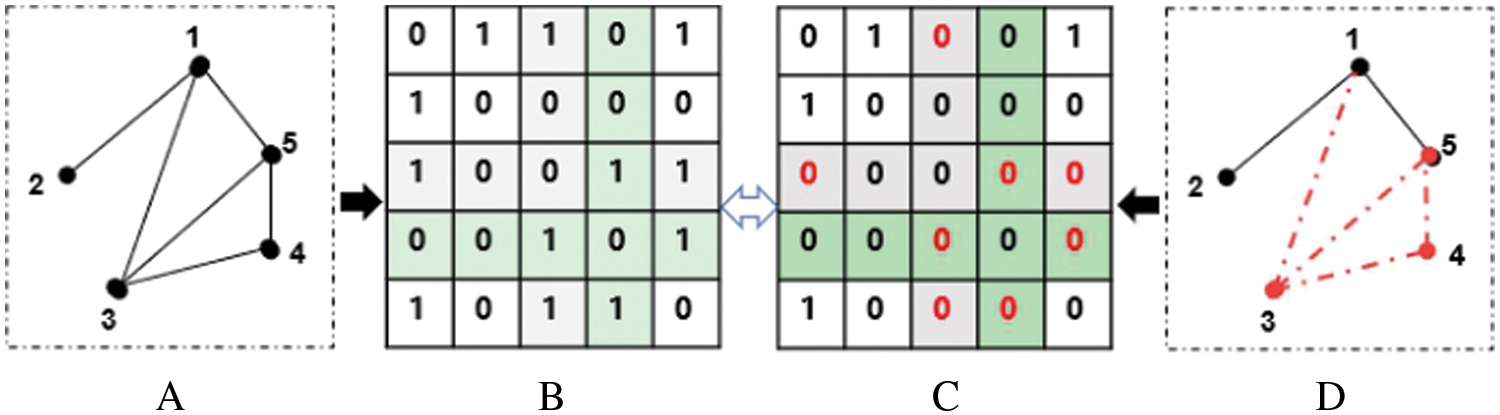
Figure 1: A toy network’s topological structure and adjacency matrix. A. Real networks G; B. Adjacency matrix S of real network G; C. Adjacency matrix S' of observed network G'; D. Actual observed networks G' with isolated nodes.

3.1.3 NMF Review

Given a matrix Y∈R+n×m , the NMF aims to find two nonnegative factor matrices B∈R+n×k and X∈R+k×m that make Y≈Y′=BX . In general, the k is the number of latent features or the inner rank of Y . It obeys the condition of the inequality, (m+n)k≪mn . The matrix B is called the basis matrix, and X is the coefficient matrix. The optimization problem of NMF is a convex optimization problem. This decompose aims to solve the following F-norm optimization problem:

minB,X⁡‖Y−BX‖F2s.t.B≥0,X≥0 (1)

where ‖⋅‖F indicates the Frobenius norm, constrain B≥0,X≥0 requires that all the elements in matrices B and X are non-negative. The Frobenius norm of the matrix X is denoted by ‖X‖F=∑ij⁡|xij|2=tr(XTX) . The T represents the transpose operation of the matrix X .

3.2 Cold-Start Link Prediction Model: GJSNMF

Information shortage shapes the major challenge for cold-start link prediction. The presence of isolated nodes leads to an incomplete network structure, so that the network structure topological information cannot be fully utilized to predict link. Therefore, it is necessary to seek more non-topological information to assist cold-start prediction, such as node attribute information.

Considering the advantages of symmetric NMF incorporating heterogeneous information [28], in this paper, using the matrix S represents the topological information and it is decomposed into S≈VVT . The node attributes information A is then mapped with the structural information to the low-rank hidden space to form a fusion pattern, i.e., A≈VUT . Although the network is a semi-connected state due to the presence of isolated nodes, part of the observed structural information can be fused with the node attribute. To integrate the topological and non-topology attributes into the same NMF framework, symmetric NMF-based objective functions are designed,

O=minV,U‖S−VVT‖F2+α‖A−VUT‖F2s.t.V≥0,U≥0 (2)

where S∈R+n×n , A ∈R+n×m , the factor matrix U∈R+m×kandV∈R+n×k represent the hidden space that integrates topological structure and node attribute information, R+ represents non-negative real number sets. The parameter α balance the availability of structure and attribute information. Because the network data matrix S is extremely sparse, during the model learning to prevent the overfitting, the constraints are introduced in the Eq. (2).

O=minV,U‖S−VVT‖F2+α‖A−VUT‖F2+β(‖V‖F2+‖U‖F2) (3)

Although the Eq. (3) achieves the predictions to some extent, but its performance will be poor due to the extremely sparsity of the semi-structured network topology. Moreover, the impact of noise in the node attribute information reduces the role of fusion to structural attributes, and for this problem, the fused node attribute information needs to be modeling to allow weighted constraints. Inspired by the jointly weighted NMF model [29], in this paper, the weight variable ΘεR+m×m is introduced to restrict each node attribute information, so that each node attribute is assigned to an appropriate weight when fused with the structure information to promote the degree of node attributes fused to the structure, i.e., AΘ≈VUT . The diagonal matrix Θ satisfies ∑i=1m⁡Θi,i=1 . To ensure that the Θ weights are assigned to a rule space, update operations need to be normalized to:

Θ=Θ∑i=1m⁡Θi,i (4)

The node attribute information of the general network has high-dimensional characteristics, and the hidden deep non-linear characteristics and the attribute-based similarity properties of nodes cannot be completely captured through the second term in Eq. (3). That is, the nonlinear manifold structure present in the high-dimensional node property space is not modeled for link prediction. This exhibits that two nodes topologically distant, actually having a very close nonlinear proximity in a high-dimensional property space.

In addition, the observed node interactions in the network semi-structured state indicate that the two nodes in the network have already structurally close distance. At this point, if the node attribute information is again fused and forced into work, it will sometimes pull away the distance between the two in the structural space. Therefore, we need to restrict the role of the attribute information and correct it to play a significant role on the unconnected nodes.

In this way, the node attribute graph regularization term is introduced based on the advantages of graph regularity in data representation [30]. Then the manifold similarity of the attributes is maintained by mining the nonlinear structure information hidden in the node attribute data. Thus, applied to the prediction missing edges of isolated nodes. Then, the existing partial topological information is used to guide the proximity of the node attribute information on the hidden space. The link between non-isolated nodes in a semi-connected network are taken as weight to restrict the similarity of attribute information for isolated nodes at the microscopic level. Thus, introducing the regularization form is expressed as:

R∗=12∑i,jn⁡W‖ui−uj‖F2 (5)

where, the W is the weight of forming edges between vi and vj vertices. And ui and uj represents the proximity degree of attributes of vertices vi and vj in the hidden space. For the Eq. (5) above, it is easily converted to a matrix format as follows:

R∗=12∑i,jn⁡W‖ui−uj‖F2=∑i=1n⁡uiTuiDii−∑i,j=1n⁡uiTujWij

=Tr(UTDU)−Tr(UTWU)=Tr(UTLU) (6)

where, the Tr(.) is the trace of the matrix, L=D−W is a Laplacian matrix based on the similarity of node properties, and the formula Dii=∑k⁡Wik is diagonal matrix. According to the above equation, the framework is proposed for missing link prediction in the semi-structured network state, that is, a cold-start link prediction model of a jointly weighted symmetric NMF with a graph regularization term.

O=minV,U,Θ‖S−VVT‖F2+α‖AΘ−VUT‖F2+β(‖V‖F2+‖U‖F2)+γTr(UTLU)

s.t.V≥0,U≥0,Θ≥0 (7)

where, V∈R+n×k,U∈R+m×k,Θ∈R+m×m , the α is balance parameters for structure and properties. The β is regular parameters to prevent overfitting, and the parameters γ control the effect of the graph regular term.

As described in the ref. [28], consider a graph with N vertices, where each vertex corresponds to a data point. For each data point au , we find its nearest neighbors and put edges between au and its neighbors. There are many choices to define the weight matrix W on the graph. Three of the most used are as follows:

1) 0–1 Weighting. Wuv=1 , if and only if nodes u and v are connected by an edge.

2) Heat Kernel Weighting. If nodes u and v are connected, put Wuv=e−‖au−av‖2σ . Heat kernel has an intrinsic connection to the Laplace-Beltrami operator on differentiable functions on a manifold.

3) Dot-Product Weighting. If nodes u and v are connected, put Wuv=auTav . Note that if a is normalized to 1, the dot product of two vectors is equivalent to the cosine similarity of the two vectors.

In this paper, the matrix W is calculated using the simplest 0–1 weighting method. It indicates that if existing a link between the two nodes, the weights are calculated as formula 1), otherwise we .

Through the weight matrix W , the links between the non-isolated nodes in the network are used to restrain and guide the similarity of the attribute vectors between two nodes, thus allowing the node attribute similarity to have the best effect in the prediction of the missing edges of the isolated nodes.

3.3 Model Solution

It is impossible that the objective function O is convex on both factor matrices U and V simultaneously. It is unrealistic to expect the algorithm to find global minima. However, alone U or V , the objective function is again convex. Its local optimal solution can be obtained by a multiplicative iterative approach. Therefore, the stochastic gradient descent method was used to seek the solutions of the model. To this end, a non-negative Lagrangian multiplier Θψ,φ,ϕ is introduced to change the Eq. (7) to the unconstrained loss function.

J=12(‖S−VVT‖F2+α‖AΘ−VUT‖F2+β(‖V‖F2+‖U‖F2)+γTr(UTLU))+Tr(ψTV)+Tr(φTU)+Tr(ϕTΘ) (8)

Then, expand the Eq. (8) and simplify it.

First of all, let Ω=Tr(ψTV)+Tr(φTU)+Tr(ϕTΘ) , then expand J to

J=12[Tr((S−VVT)T(S−VVT))+αTr((AΘ−VUT)T(AΘ−VUT))+β(Tr(VTV)+Tr(UTU))+γTr(UTLU)]+Ω

=12[Tr(STS−STVVT−VVTS+VVTVVT)+αTr(ΘTATAΘ−ΘTATVUT−UVTAΘ+UVTVUT)+β(Tr(VTV)+Tr(UTU))+γTr(UTLU)]+Ω (9)

For the Eq. (9), taking partial derivatives of J with respect to V , U and Θ , we have

∂J∂V=12[−2(ST+S)V+4VVTV+α(−2AΘU+2VUTU)+2βV]+ψ

=−(ST+S)V+2VVTV+α(−AΘU+VUTU)+βV+ψ

=−(STV+SV+αAΘU)+(2VVTV+αVUTU+βV+ψ) (10)

Similarly, the partial derivatives of J with respect to U ,

∂J∂U=12[α(−ΘTATV−(VTAΘ)T+U(VTV)T+UVTV)+2βU+γ(LU+LTU)]+φ

=−αΘTATV+αUVTV+βU+12γ(LU+LTU)+φ (11)

Because the L=D−W is symmetrical, So there are L=LT . Lead it into the Eq. (8), which can be obtained

∂J∂U=−αΘTATV+αUVTV+βU+γLU+φ (12)

Replace that L in Eq. (12), then

∂J∂U=−(αΘTATV+γWU)+(αUVTV+βU+γDU+φ) (13)

Similarly, the partial derivatives of J with respect to ,

∂J∂Θ=12[α(ATAΘ+(ATA)TΘ−ATVUT−(UVTA)T)]+ϕ

=−αATVUT+(αATAΘ+ϕ) (14)

For these equation above, in terms of the Karush-Kuhn-Tucker (KKT) complementary slackness condition ψp,rVp,r=0,φq,rUq,r=0,ϕq,qΘq,q=0 , and Let ∂J∂V=0, ∂J∂U=0 and ∂J∂Θ=0 , we can derive the following updating rules with respect to V , U and Θ :

V←V.∗STV+SV+αAΘU2VVTV+αVUTU+βV (15)

U←U.∗αΘTATV+γWUαUVTV+βU+γDU (16)

Θ←Θ.∗ATVUTATAΘ (17)

where .∗ and ./ represent the element-wise multiplication and division, respectively. According to the obtained update rules (15) to (17), a stable V is calculated, which can then be used to approximate the original network to obtain the similarity score value between nodes and realize the prediction task of the missing edges.

To sum up, the pseudo code of the proposed cold-start link prediction model of jointly weighted symmetric NMF with graph regularization (GJSNMF) is described as follows (see Tab.1):

3.4 Computational Complexity Analysis

The computational complexity of GJSNMF algorithm mainly comes from two parts. One is to compute the weight W . The second is iterative update matrices V , U and Θ at the same time. Given an attributed network with n nodes, each node contains m attributes. Suppose the algorithm iterates t times, the objective function convergence, algorithm stops updating. First, computing the W with 0–1 weights, the algorithm needs to run n2 times, then the complexity is O(n2) . So overall computational complexity is O(n2kt) for the symmetric NMF algorithm. In addition, the main complexity lies in the multipliers and division operations of the matrix when updating V,U,Θ . Each multiplication and division operation are required O(n2) times. If these operations of multiplication and division have T step in updating them. Then their complexity is O(n2Tk) times. To sum up, combined with the processing of the attribute information, the overall time cost of the algorithm is about O(n2+n2kt+n2kT) , that is nearly to O(n2) .Of course, we can also improve our algorithm according to the relevant literature to achieve parallel computing, so as to obtain performance optimization. This is what we want to do in the future.

In the experiment, the convergence of the model was verified on all the datasets, and the convergence result very well. Model convergence is shown here only on the Facebook dataset (see Fig. 2).

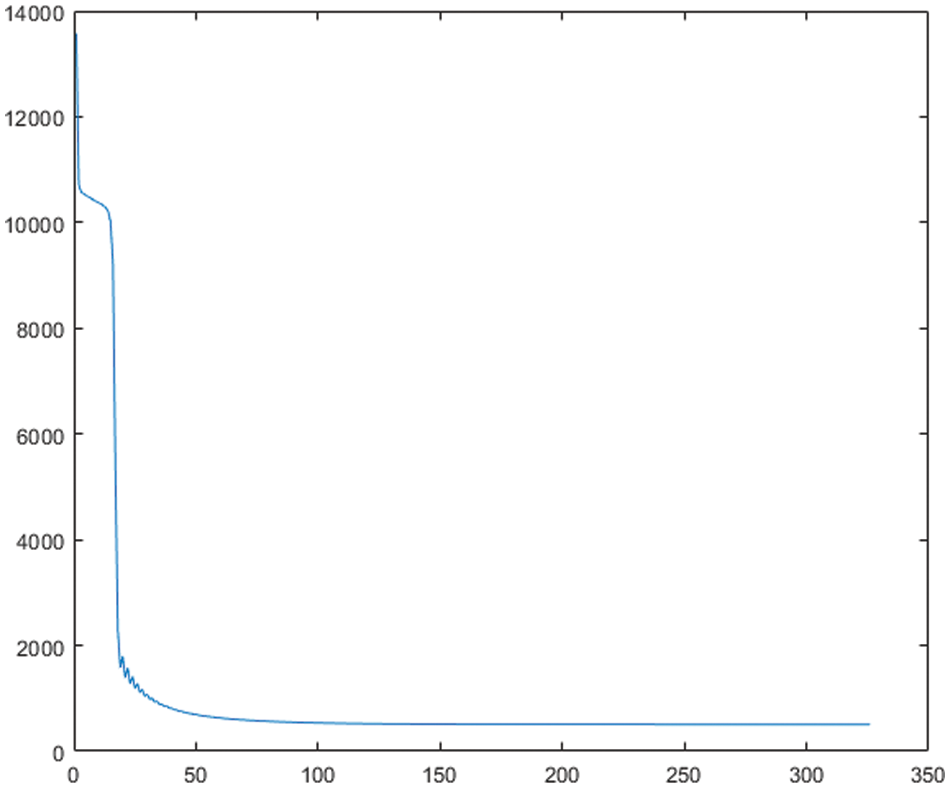
Figure 2: The convergence of the model on the Facebook dataset

4  Experimental Design

4.1 Datasets Description

We consider the following 7 real-world attribute networks datasets drawn from disparate fields.

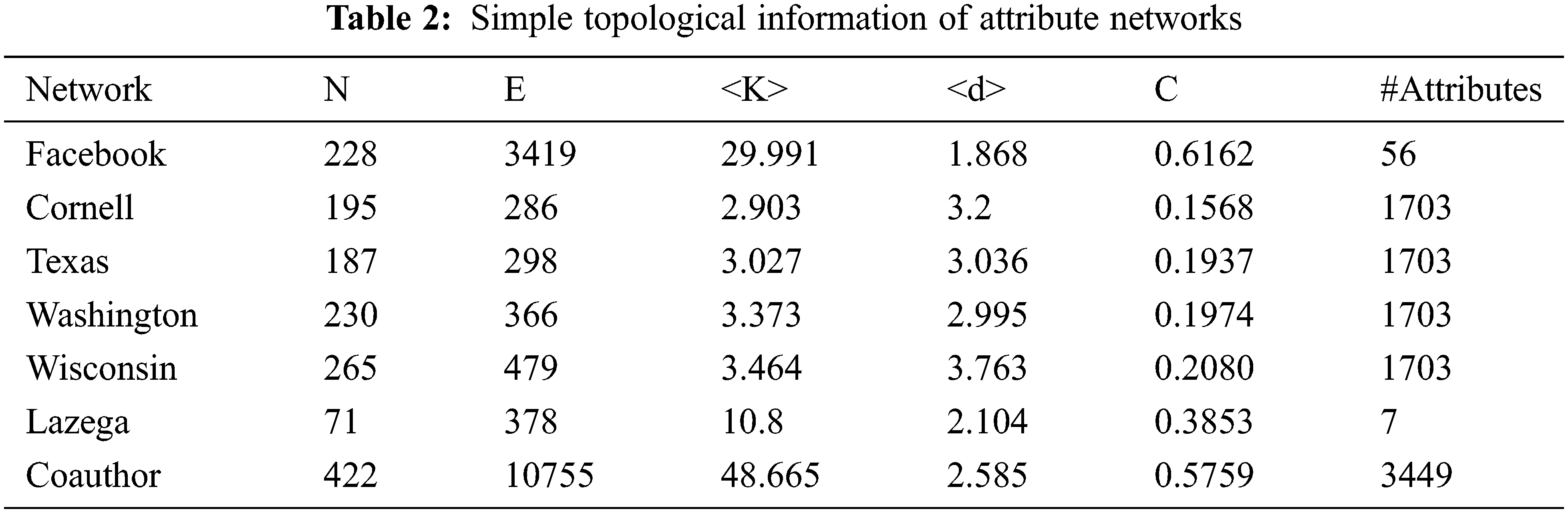
The basic topology features of these networks are summarized in Tab. 2. The symbol N and E are the total number of nodes and links, respectively. <K> is the average degree. <d> is the mean shortest distance. C is the clustering coefficient, and #Attributes is the number of node attributes. Datasets used for the experiments are available to be downloaded from these websites:

http://vladowiki.fmf.uni-lj.si/doku.php?id=pajek:data:urls:index;

http://snap.stanford.edu/data/

4.2 Evaluation Metrics

Like many existing prediction studies, in our work adopts also the most frequently-used metrics AUC (area under the ROC curve) and Precision to measure the performance of link prediction [1–3]. The metric is viewed as a robust measure in the presence of data imbalance. Furthermore, the training set partitioned from the original network dataset is treated as observed networks and thus have many isolated nodes. To evaluate the deviation between the predicted value and the true value of the network, we adopted two evaluation criteria commonly used in machine learning, MAE (Mean Absolute Error) and RMSE (Root Mean Squared Error).

4.3 Comparison Methods

The cold-start link prediction method was proposed in the reference [5] by Leroy et al., which is a combined method to count the communities that the nodes share. It is used to compare the prediction performance with our method, and it is labeled as LEROY.

SASNMF method [31]. This model is the NMF-based to implement link prediction by coupling structure attribute and node attribute information.

Matrix completion method [32] (MC). Based on the low-rank and sparse characteristics of adjacent matrices, the robust principal component analysis was used to fit the training data by minimizing the kernel norm of the matrices. In this way, a network akin to the real network was reconstructed.

NMF_LP method [33]. The method is based on the NMF framework which adopted node attributes. It directly fusion node attribute information and structure information to predict link.

SPM_NMF method [34]. The link prediction method based on matrix disturbance principle. This method formed a new network structure by randomly adding into a link as disturbances and then decomposed the new structure by NMF framework, to realize link prediction. It was labelled SPM_NMF. The best outcomes were selected under disturbance ratios of 0.06, 0.08 and 0.1, for comparison.

4.4 Division of Datasets

The network datasets need to be divided into training and test sets. A few nodes were selected randomly and made into isolated nodes by deleting all the links between them. Where, the edges were removed as the test set, while the remaining edges served as the training set. Fig. 3 is a schematic of a dataset divided into a training and test set. To further illustrate the different forms of dataset division, Fig. 3 shows the division on cold start link prediction (subgraph A), and the partition in traditional link prediction (subgraph B). This paper addresses cold-start link prediction, and therefore, the dataset partitioning is performed following the pattern of subfigure A. In addition, according to the experimental requirements, in the datasets provided in this article, the proportion of edges present in corresponding networks was about 90%–95% when the proportion of deleted nodes was within 95%–75%. The data sets were divided by K-10 folded cross validation.

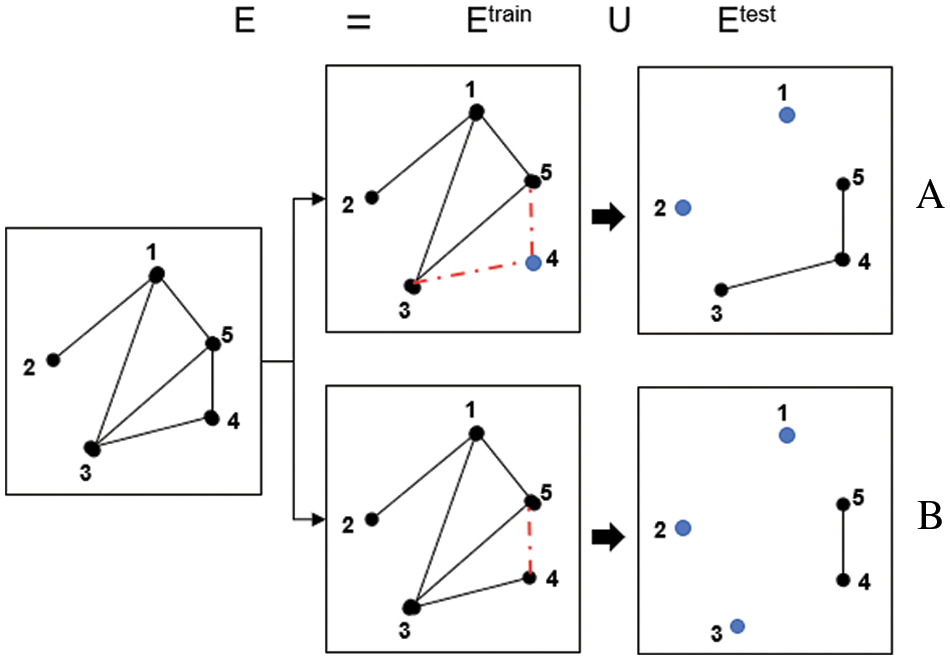
Figure 3: Schematic comparison of datasets division. A. Cold-start link prediction model, Node 4 is an isolated point; B. Structural similarity link prediction model, The link between the node pairs (4,5) is missing

4.5 Settings of Parameters α , β and γ

The sensitivity of these parameters α , β and γ in all data sets were analyzed prior to the experiment test by grid searching. To briefly illustrate the importance of the parameter setting, Fig. 4 show the predicted value when the training set and test set partition ratio on the Facebook data is 95%. In this experiment, the parameters α , β and γ were valued 13, 3 and 46, respectively.

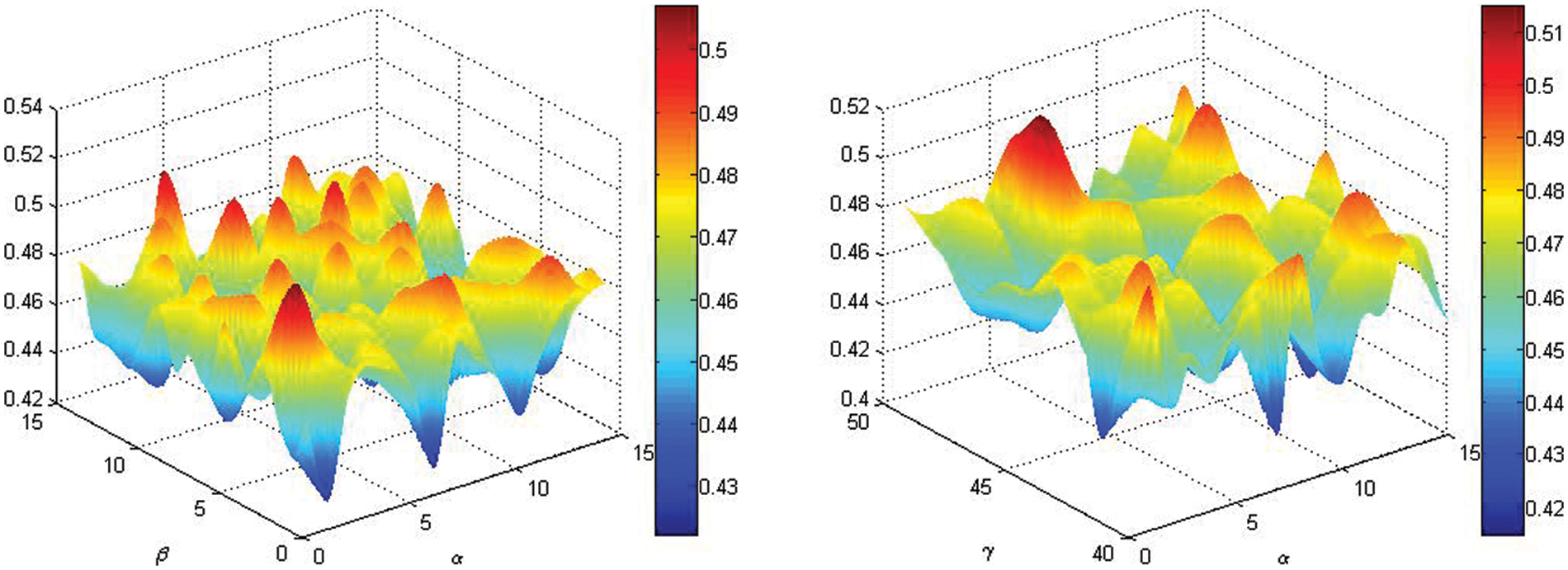
Figure 4: Parametric sensitivity analysis

5  Results and Analysis

5.1 Overall Prediction Performance of the Model

5.1.1 Prediction Effect When the Network is Fixed

In experiment, the proportion of networks divided into training and test sets ranged from 75% to 95%. The proportion of edges present under the corresponding network is approximately 50% to 90%. Tab. 3 shows the results of each comparison method on different networks.

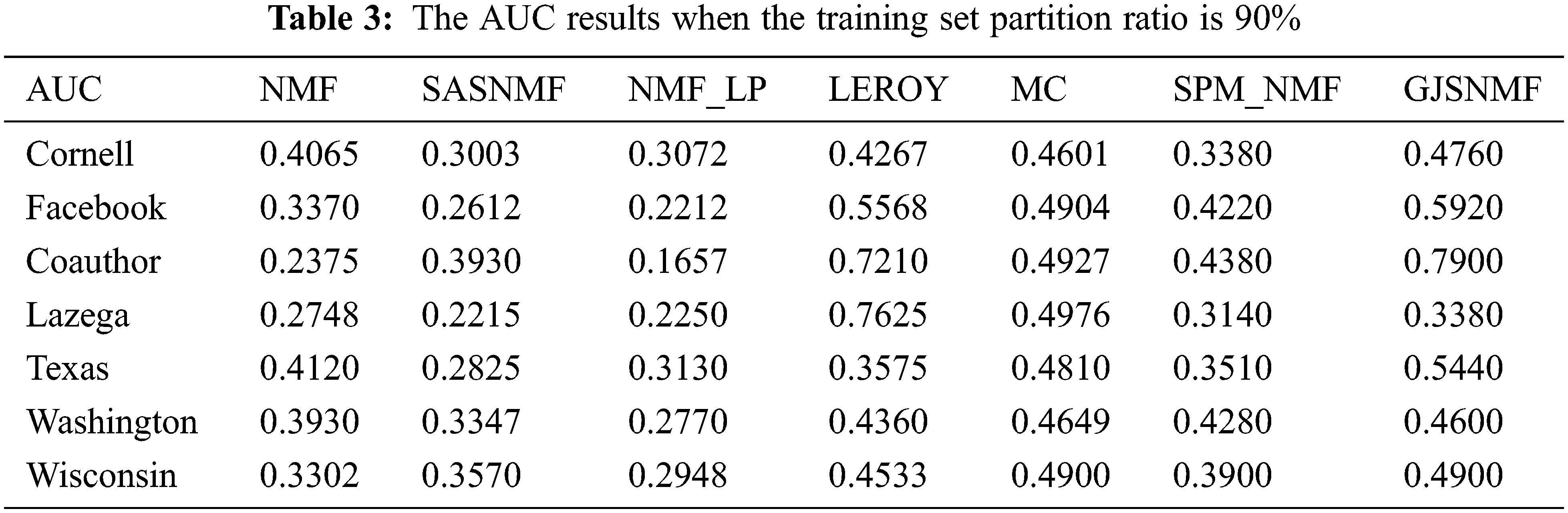
Fig. 5 show the prediction effect of the model and comparison methods on different real networks, which is obvious from Fig. 5 that the overall prediction effect of the GJSNMF method has a certain advantage, but performs poorly on the Lazega datasets.

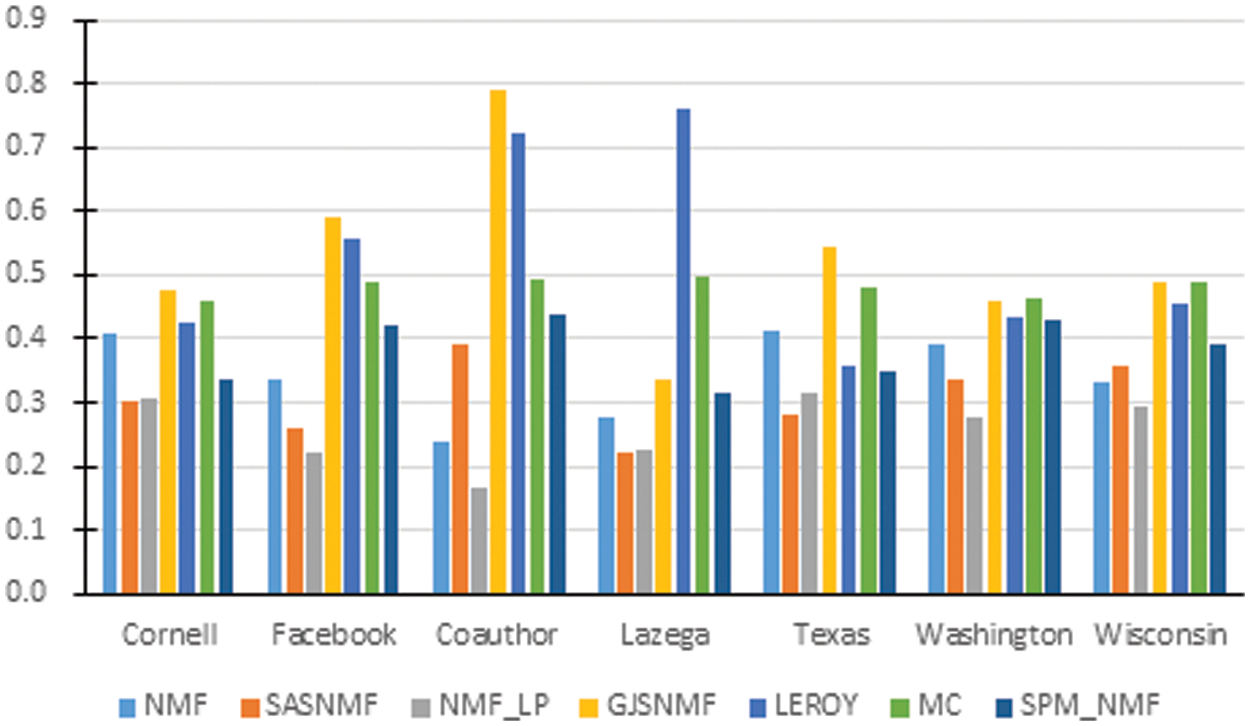
Figure 5: Comparison with contrast AUC values

5.1.2 Prediction Effects When the Network Structure is Changed

It is necessary to compare the predicted effects of models with different degrees of network structure. Therefore, after dividing existing edges from 50% to 90% in the network datasets. Various methods were subjected for comparative analysis. Fig. 6 to illustrate the prediction effect of the model in Coauthor and Washington networks.

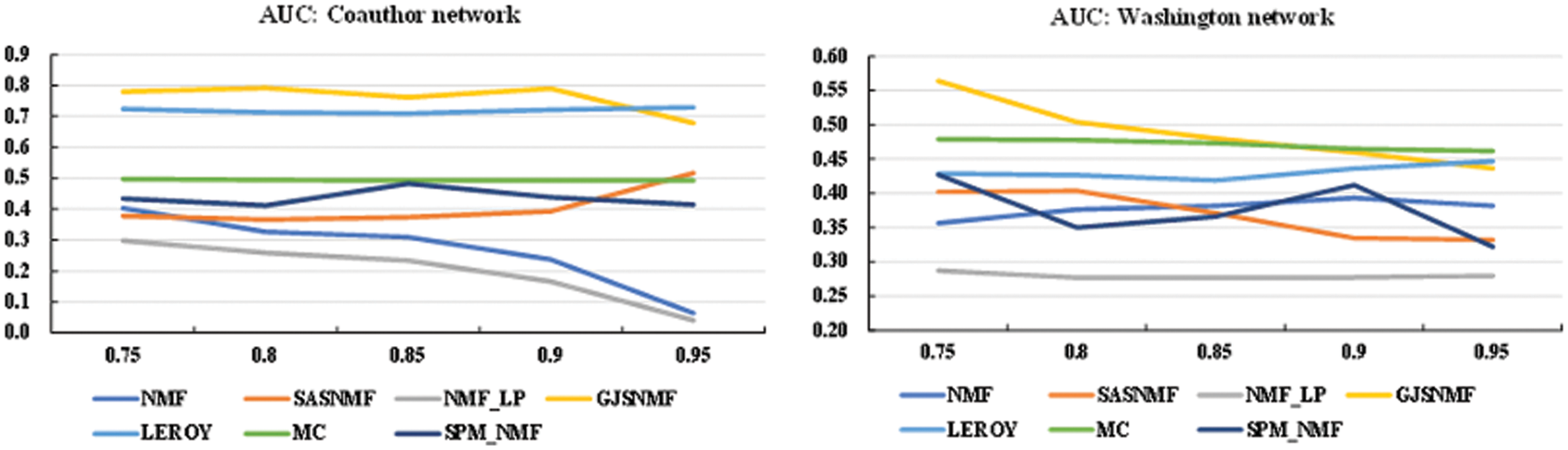
Figure 6: Predict effects under the proportion of training sets for different data

From the results, we can see that the accuracy of the GJSNMF framework decreased significantly. This shows that when the topological information of the network is seriously missing, the global structural information availability also drops sharply, resulting in the overall poor prediction performance. Therefore, it is necessary, in the network semi-structured state, to mine more available information as auxiliary properties of the prediction to enhance the overall performance of the prediction.

5.2 The Impact of Fusion Graph Regularization Information

One of the core points of building the model is to strengthen the model to learn the deep nonlinear manifold hidden attribute feature from the node attributes by adding the graph regularization terms to the model, in order to improve the model prediction performance. Therefore, to test whether the graph regularization term improves the model, this task is specially designed to test during the overall prediction effect of the model. This is to set the parameter γ to 0 to block the role of the graph regularization term in model prediction. The test results divided at the training ratio of 75% set are used below to illustrate the predictive effect tested on all networks when the graph regularization term does not function and works. The four small plots in Fig. 7 show the test results under the four criteria, AUC, Precision, MAE and RMSE. Among these, * 0 is used to represent the experimental results of the model without adding graph regularization term. * 1 Represents the test results under the corresponding evaluation criteria when the graph regularization term is added.

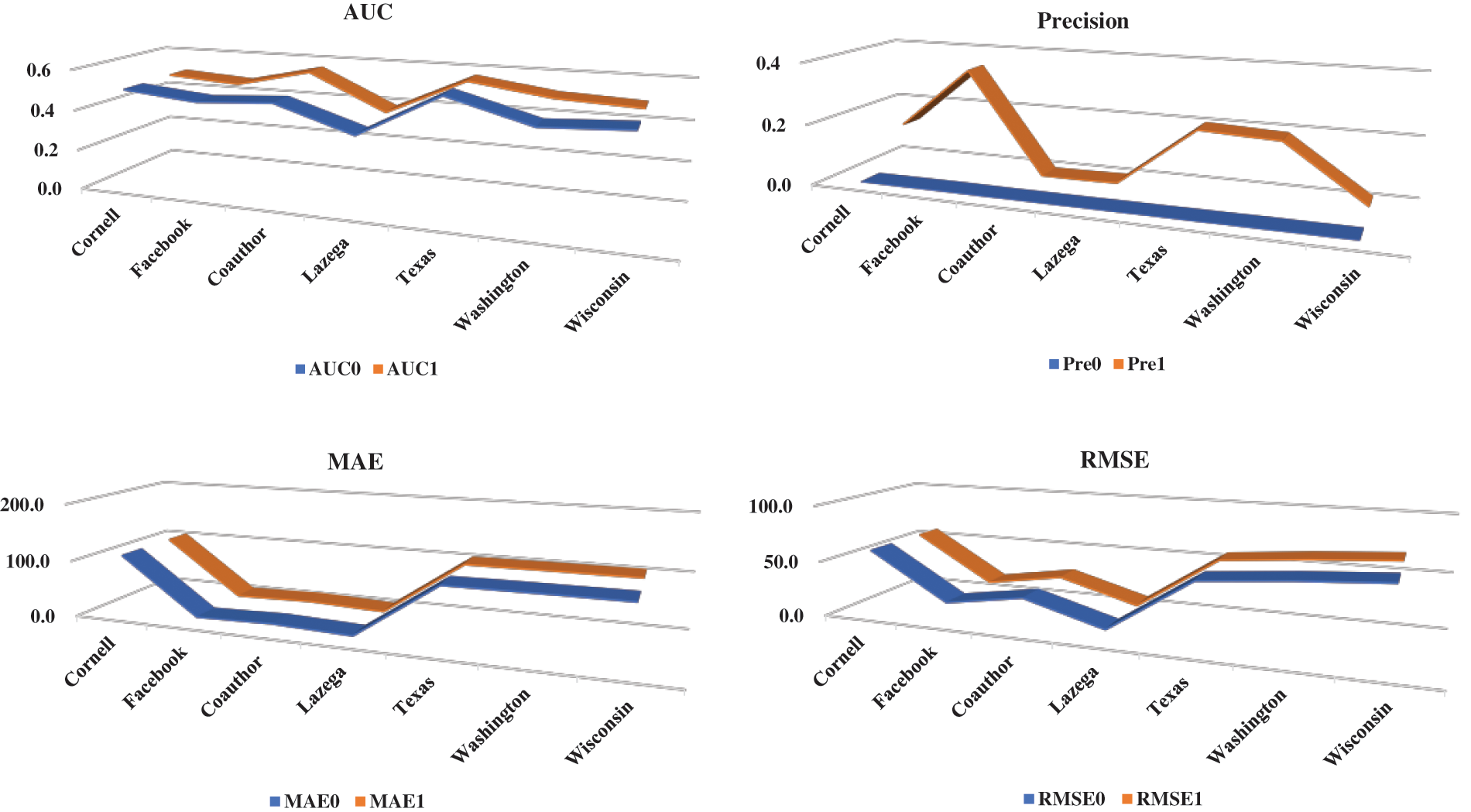
Figure 7: Prediction effect with graph regularization terms and no its

From the test results, after the model adds the graph regularization term, the utilization rate of the node attributes is higher, and the prediction effect is more obvious.

5.3 The Influence of Graph Regularization Term Weight Value

In the model construction section, there are three methods to be used to compute the corresponding weight matrix W when introducing graph regularization terms. In section, the main test is the extent to which the weights calculated under three different methods affect the overall prediction effect of the model. In Fig. 8 show the results of taking the three weight calculation methods. In the Figure, the symbol “G = 0” represents the prediction result without graph regularization term in the proposed model. The symbol “GW_*” indicates that it is a prediction result with graph regularization term. The predictive performance of the model was measured by AUC and Precision evaluation criteria. The first subfigure is the result of AUC, and the second is the result of Precision. Moreover, to further distinguish the three methods for calculating the values of the weight matrix W, they are represented by the sequence 01, 02, and 03 in Fig. 8. A detailed description of the specific calculation methods can be found in Section 3.2 of this article.

From the analysis of the experimental results, the effect of using the third weight calculation method in the model is significantly better. Of course, this is not absolute, in some datasets, the effect is bad.

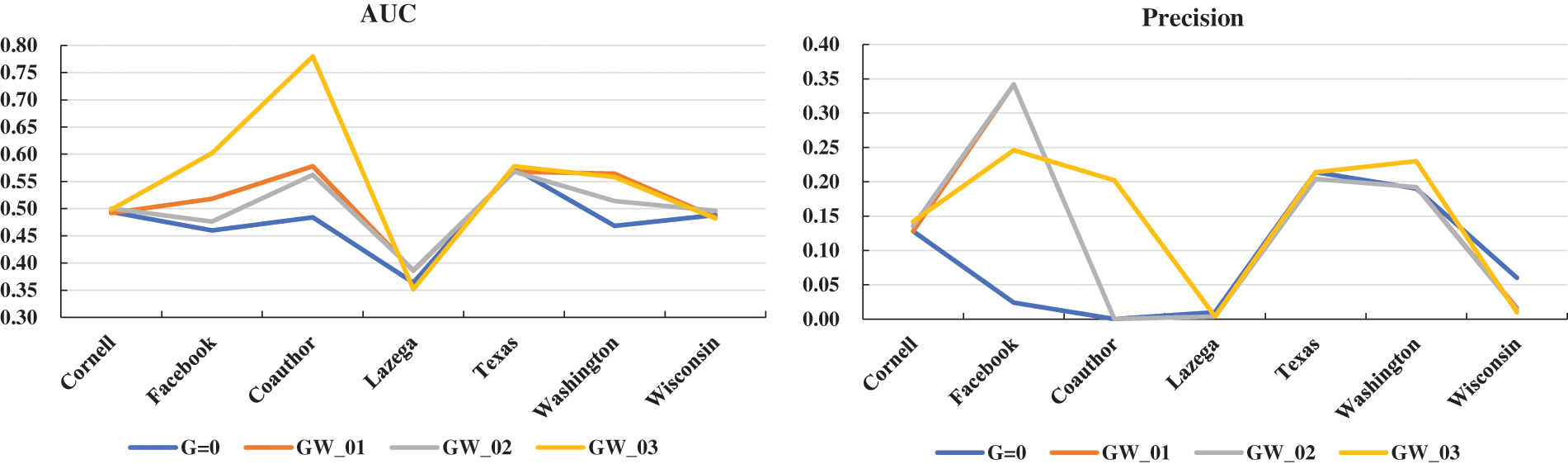
Figure 8: Effect of the different measurements of the weights (AUC and Precision)

Analyzing the test results in Fig. 8, we can see that the different weight calculation methods have some effect on the final prediction of the model. It shows from the figure that the third dot product weight effect is better overall than the other two.

6  Conclusion

The prediction of missing edges of isolated nodes in network semi-connected state has been a difficult problem. Mainly, the network topology structure is a nonconnected graph, and is extremely sparse. Traditional structural similarity methods cannot satisfy missing edge prediction of isolated nodes. In this paper, we analyze the underlying causes of the prediction difficulties and propose a joint weighted symmetric NMF model integrating graph regularization information for cold-start link prediction.

The model takes advantage of the symmetric nonnegative matrix and the graph regular non-negative matrix to integrate the nonlinear characteristics in the high-dimensional space of the node attributes, thus improving the guidance of the attribute information in the prediction process and realizing the cold-start link prediction task in the case of semi-connected network state.

Extensive experiments have validated that the proposed model globally excelled the state-of-the-art methods in the predictions of cold-start nodes. And the algorithm is highly robustness and extensibility. In the future that we would to optimize the model algorithm by parallel methods, in order to improve the prediction efficiency.

Acknowledgement: We would like to thank the anonymous reviewers for their contributions.

Data Availability: The networks used in this study are available from http://snap.stanford.edu/data/, http://vladowiki.fmf.uni-lj.si/doku.php?id=pajek:data:urls:index.

Funding Statement: This research was supported by the Teaching Reform Research Project of Qinghai Minzu University, China (2021-JYYB-009), and the “Chunhui Plan” Cooperative Scientific Research Project of the Ministry of Education of China (2018).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Martinez, F. Berzal and J. C. Cubero, “A survey of link prediction in complex networks,” ACM Computing Surveys, vol. 49, no. 4, pp. 69–102, 2017. [Google Scholar]

 2.  S. Haghani and M. R. Keyvanpour, “A systemic analysis of link prediction in social network,” Artificial Intelligence Review, vol. 52, no. 3, pp. 1961–1995, 2019. [Google Scholar]

 3.  A. Rossi, D. Barbosa, D. Firmani, A. Matinata and P. Merialdo, “Knowledge graph embedding for link prediction: A comparative analysis,” ACM Transactions on Knowledge Discovery from Data, vol. 15, no. 2, pp. 14: 1–49, 2021. [Google Scholar]

 4.  N. Assouli, K. Benahmed and B. Gasbaoui, “How to predict crime — Informatics-inspired approach from link prediction,” Physica A: Statistical Mechanics and its Applications, vol. 570, no. 8, pp. 125795, 2021. [Google Scholar]

 5.  V. Leroy, B. B. Cambazoglu and F. Bonchi, “Cold start link prediction,” in Proc. SIGKDD, Washington, DC, USA, pp. 393–402, 2010. [Google Scholar]

 6.  A. Alharbi, M. Faizan, W. Alosaimi, H. Alyami, M. Nadeem et al., “A link analysis algorithm for identification of key hidden services,” Computers, Materials & Continua, vol. 68, no. 1, pp. 877–886, 2021. [Google Scholar]

 7.  G. S. Pang, C. H. Shen, L. B. Cao and A. V. D. Hengel, “Deep learning for anomaly detection: A review,” Association for Computing Machinery, vol. 54, no. 2, pp. 1–38, 2021. [Google Scholar]

 8.  S. G. Li, X. W. Song, H. Y. Lu, L. Y. Zeng, M. J. Shi et al., “Friend recommendation for cross marketing in online brand community based on intelligent attention allocation link prediction algorithm,” Expert Systems with Applications, vol. 139, no. 3, pp. 112839, 2020. [Google Scholar]

 9.  P. Mei, G. Ding, Q. Jin, F. Zhang and Y. Chen, “Reconstruction and optimization of complex network community structure under deep learning and quantum ant colony optimization algorithm,” Intelligent Automation & Soft Computing, vol. 27, no. 1, pp. 159–171, 2021. [Google Scholar]

10. H. He, Z. Zhao, W. Luo and J. Zhang, “Community detection in aviation network based on k-means and complex network,” Computer Systems Science and Engineering, vol. 39, no. 2, pp. 251–264, 2021. [Google Scholar]

11. S. S. Singh, S. Mishra, A. Kumar and B. Biswas, “CLP-ID: Community-based link prediction using information diffusion,” Information Sciences, vol. 514, no. 3, pp. 402–433, 2020. [Google Scholar]

12. P. Chunaev, “Community detection in node-attributed social networks: A survey,” Computer Science Review, vol. 37, no. 3, pp. 100286, 2020. [Google Scholar]

13. P. Wei, M. D. Lu, X. H. Zhang and Y. L. Teng, “Analysis of flight punctuality rate based on complex network,” Journal of Quantum Computing, vol. 3, no. 1, pp. 13–23, 2021. [Google Scholar]

14. W. Y. Guo, R. X. Jia and Y. Zhang, “Semantic link network based knowledge graph representation and construction,” Journal on Artificial Intelligence, vol. 3, no. 2, pp. 73–79, 2021. [Google Scholar]

15. Q. J. Zhang, R. G. Wang, J. Yang and L. X. Xue, “Knowledge graph embedding by translating in time domain space for link prediction,” Knowledge-Based Systems, vol. 212, pp. 106564, 2021. [Google Scholar]

16. X. Z. Cao, H. K. Chen, X. J. Wang, W. N. Zhang and Y. Yu, “Neural link prediction over aligned networks,” in Proc. AAAI, New Orleans, Lousiana, USA, pp. 249–256, 2018. [Google Scholar]

17. S. Y. Wu, Q. Zhang and M. Wu, “Cold-start link prediction in multi-relational networks,” Physics Letters A, vol. 381, no. 39, pp. 3405–3408, 2017. [Google Scholar]

18. L. Ge and A. D. Zhang, “Pseudo cold start link prediction with multiple sources in social networks,” in Proc. SDM. SIAM, Anaheim, CA, USA, pp. 768–779, 2012. [Google Scholar]

19. X. Han, L. Y. Wang, S. N. Han, C. Chen, N. Crespi et al., “Link prediction for new users in social networks,” in Proc. ICC, London, UK, pp. 1250–1255, 2015. [Google Scholar]

20. Z. Q. Wang, J. Y. Liang, R. Li and Y. H. Qian, “An approach to cold-start link prediction: Establishing connections between non-topological and topological information,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, no. 11, pp. 2857–2870, 2016. [Google Scholar]

21. S. Y. Wu, Q. Zhang, C. Y. Xue and X. Y. Liao, “Cold-start link prediction in multi-relational networks based on network dependence analysis,” Physica A: Statistical Mechanics and its Applications, vol. 515, no. 3, pp. 558–565, 2019. [Google Scholar]

22. L. C. Xu, X. K. Wei, J. N. Cao and P. S. Yu, “On learning community-specific similarity metrics for cold-start link prediction,” in Proc. IJCNN, Brazil, Rio de Janeiro, pp. 1–8, 2018. [Google Scholar]

23. L. C. Xu, X. K. Wei, J. N. Cao and P. S. Yu, “On learning mixed community-specific similarity metrics for cold-start link prediction,” in Proc. WWW, Perth, Australia, pp. 861–862, 2017. [Google Scholar]

24. M. Yan, J. T. Sang, T. Mei and C. S. Xu, “Friend transfer: Cold-start friend recommendation with cross-platform transfer learning of social knowledge,” in Proc. ICME, San Jose, California, USA, pp. 1–6, 2013. [Google Scholar]

25. J. W. Zhang, X. N. Kong and P. S. Yu, “Predicting social links for new users across aligned heterogeneous social networks,” in Proc. ICDM, Dallas, TX, USA, pp. 1289–1294, 2013. [Google Scholar]

26. J. D. Li, K. W. Cheng, L. Wu and H. Liu, “Streaming link prediction on dynamic attributed networks,” in Proc. WSDM, Marina Del Rey, CA, USA, pp. 369–377, 2018. [Google Scholar]

27. Y. Hao, X. Cao, Y. X. Fang, X. K. Xie and S. B. Wang, “Inductive link prediction for nodes having only attribute information,” in Proc. IJCAI, Yokohama Yokohama, Japan, pp. 1209–1215, 2020. [Google Scholar]

28. J. Z. Gan, T. Liu, L. Li and J. L. Zhang, “Non-negative matrix factorization: A survey,” Computer Journal, vol. 64, no. 7, pp. 1080–1092, 2021. [Google Scholar]

29. Z. C. Huang, Y. M. Ye, X. T. Li, F. Liu and H. J. Chen, “Joint weighted nonnegative matrix factorization for mining attributed graphs,” in Proc. PAKDD, Jeju, South Korea, pp. 368–380, 2017. [Google Scholar]

30. D. Cai, X. F. He, J. W. Han and T. S. Huang, “Graph regularized nonnegative matrix factorization for data representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 8, pp. 1548–1560, 2011. [Google Scholar]

31. W. J. Wang, M. H. Tang and P. F. Jiao, “A unified framework for link prediction based on non-negative matrix factorization with coupling multivariate information,” PLOS ONE, vol. 13, no. 11, pp. –e0208185, 2018. [Google Scholar]

32. R. Pech, D. Hao, L. M. Pan, H. Cheng and T. Zhou, “Link prediction via matrix completion,” Europhysics Letters, vol. 117, no. 3, pp. 38002, 2017. [Google Scholar]

33. B. L. Chen, F. F. Li, S. B. Chen, R. L. Hu and L. Chen, “Link prediction based on non-negative matrix factorization,” PLOS ONE, vol. 12, no. 8, pp. e0182968, 2017. [Google Scholar]

34. W. J. Wang, F. Cai, P. F. Jiao and L. Pan, “A perturbation-based framework for link prediction via non-negative matrix factorization,” Scientific Reports, vol. 6, no. 1, pp. 38938, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.