DOI:10.32604/csse.2022.024440

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.024440 |  |
| Article |
Customized Share Level Monitoring System for Users in OSN-Third Party Applications
1Department of Information Technology, SSN College of Engineering, Kalavakkam, Chennai, 603110, India
2Department of Information Science and Technology, Anna University, Chennai, 600025, India
3Department of Information Science and Engineering, Kumaraguru College of Technology, Coimbatore, 641049, India
*Corresponding Author: T. Shanmuigapriya. Email: shanmugapriyat@ssn.edu.in
Received: 17 October 2021; Accepted: 16 December 2021
Abstract: Preserving privacy of the user is a very critical requirement to be met with all the international laws like GDPR, California privacy protection act and many other bills in place. On the other hand, Online Social Networks (OSN) has a wide spread recognition among the users, as a means of virtual communication. OSN may also acts as an identity provider for both internal and external applications. While it provides a simplified identification and authentication function to users across multiple applications, it also opens the users to a new spectrum of privacy threats. The privacy breaches costs to the users as well as to the OSN. Despite paying millions of dollars as fine every year, the OSN has not done any significant changes, as data is the fuel and what it loses as fine is far less compared to the money OSN makes out of the shared data. In this work, we have discussed a wide range of possible privacy threats and solutions prevailing in OSN-Third Party Application (TPA) data sharing scenario. Our solution models the behavior of the user, as well as TPA and pinpoints the avenues of over sharing to the users, thereby limiting the privacy loss of the user.
Keywords: Online social networks; third party applications; privacy; gaussian mixture model; fuzzy inference
Third Party Applications (TPA) are developed and maintained by vendors external to Online Social Networks (OSN). Facebook is a popular social media with a worldwide user base of 2.85 billion monthly active users. Facebook has integrated a large number of third-party applications to provide multitude of services to the users. Apart from this, the OSN also serves as an identity provider for a large number of third-party services. In both the cases, when accessing the service for the first time, users are prompted to share their attributes (optional and required attributes). On sharing the required attributes, the users will be allowed to use the service, whereas on failing to share, the users are denied to use the service. The users initially share their attributes to OSN, based on the trust they have on OSN. The same trust cannot be transferred to a TPA deployed in an unknown setup. However, the users are enticed to share their attributes for using the TPA’s services, and they end up opening channels leading to privacy infringement. The TPAs hosted in external environments, may even be a malicious application; it may even share the user’s attributes with other fourth party vendors like insurance agents, data aggregators, advertising agencies, background verifiers and so forth. The list goes on, increasing the threat spectrum (Tab. 1) to which the users are exposed. The user loses control over their information, once it is shared. Even if the user retracts from using the service, there are no guarantee that TPA will not use user’s data further. Tab. 1 lists the attributes shared, threats and the academic literature discussing the same.

Hence, the remedial action is to make the user aware of what they share and with whom they share. In our work, we model what-they-share based on the user’s previous attributes shared with TPAs. GMM allows mixed membership of observations to clusters. Each user observation can belong to each cluster with a different degree of membership. The degree is based on the probability of the observation being generated from each cluster’s multivariate normal distribution, with a mean (μ) and covariance (Σ).
The aspect of whom-they share has been modeled using a fuzzy inference system. The input to the system comprises of the following: rating given by the users, the polarity of the comments received (positive, negative or neutral), the count of users who have provided rating, and TPA’s attribute permission access pattern. The fuzzy based reliability inference system outputs the TPA’s reliability level.
When the user needs to install a new application, a fuzzy recommender prescribes whether the application is suitable for the user, based on the user and TPA models. An enhanced consent request page is displayed to the user with detailed information about the TPA, which conveys the privacy implication as compared to the regular abstract consent page, which hides the information transacted.
User sharing their attributes is not considered as a privacy breach, whereas sharing without user’s consent is a privacy breach. In one of our earlier work [1], we found that around 53% of users ended up sharing more than what they intended to share. From our findings, it is evident that the users have difficulty in comprehending the consent page displayed before TPA’s installation, and they tend to over-share their attributes without the necessary awareness. Even though sharing without consent is different from sharing without awareness, the severity of the consequences remains the same.
Moreover, the data shared in the context of TPA may in turn be shared with fourth party vendors, increasing the risk of the privacy breach [2]. A measurement platform designed by [3] revealed that 22% of Facebook applications and 69% of RenRen applications provide user’s personal information to one or more fourth-party tracking entities.
The risk faced by the user in the scenario of user-TPA sharing can be reduced by either limiting the share of sensitive attributes to TPA; or by sharing a less sensitive form of the sensitive attribute. The solutions like User to application policy Model [4], Creating awareness among the users [5–7], fine grained access control [6–8] and managing privacy setting [9] complements each other and limits the data shared to TPA.
The users will not be granted access to applications in case of limiting the data to TPA, in which case, techniques to share as well as to alleviate the risk are required. Solutions based on Data Generalization [10], Differential Privacy [11], Communication Interceptor [12–14], work for meeting the above mentioned requirement. However, the risk component is only alleviated with such solutions and not removed completely. Work done by Ding et al. [15] demonstrates that the data generalized or perturbed may still be revealing private information when correlated with information available from external sources. The data can only be generalized or perturbed to the extent it preserves utility [16], anything more than that would affect the utility.
Hosting applications in a secluded environment [17] introduces a trusted hosting platform for the TPAs. The solution solely depends on the trustworthiness of the environment. The privacy violation risk with individual TPA’s are transferred to a single hosting platform. In our solution, we make the user aware of what they share before the actual sharing. If the user data sought by a TPA deviates from the normal sharing pattern of the user, we have a two stage privacy alert. We present an enhanced consent to the user, accommodating both the sharing pattern of the user and the reliability level of the TPA. The users could thus clearly understand, the data about them being sought to be shared and could make more aware and informed decision about it.
With the current approach, the user has to share all the required data attributes with TPA to avail the service. In most cases, the users lack the competence to articulate their privacy requirement and decide whether to share or not at the time of installation. In the verge of accessing the TPA, the user agrees to share without awareness. Thus, large silos of personal information would be shared by the same person to many TPA’s at different instants. All these pieces of information could be correlated to come up with an inference which was not intended to be revealed by the user, leading to a privacy breach. In our system, we have sorted out this root-cause by alerting the user whenever the user’s actual level of privacy preference differs with that of current sharing.
Fig. 1 displays the overall block diagram. User’s sharing trait modeler is used to model user’s data sharing pattern. User’s grant of permission to applications are modeled as either privacy concerned; or pragmatic; or unconcerned. This model is used in assessing the overall sharing behavior of the user. TPA’s data access behavior is modeled for each of the application categories like games, lifestyle, music, shopping and so forth. The model is used to check the data access pattern of a TPA before installation.
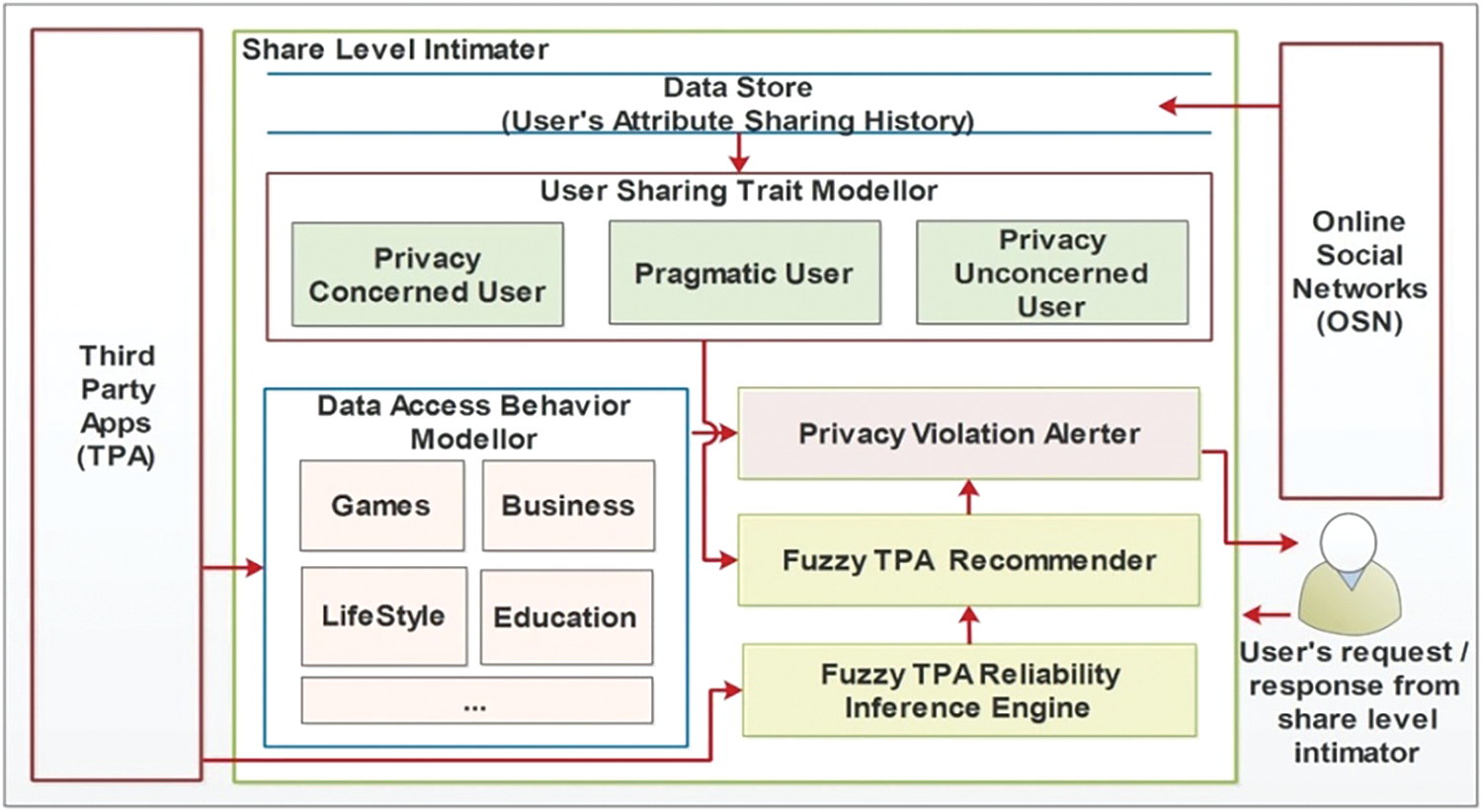
Figure 1: Block diagram of share level intimater
User’s previous sharing with the TPA is captured and is used in modeling their behavior. Each user has a set of applications they had accessed earlier and their attribute sharing decision to that application. Variable TPAi_ att j indicates attribute sharing decision of jth attribute to ith TPA. A ‘1’ indicates that the attribute is shared and ‘0’ indicates that it has not been shared.
Input: X = x1, x2, x3,..., xn be the sharing decision of N users. Where x1, x2, x3,.., xn are the data points consisting of the previous sharing decision of users 1 to N respectively.
Output: Gaussian Mixture Model representing the sharing pattern
STEP 1: Initialize GMM’s cluster centroid by clustering the data points using Kmeans.
X = x1, x2, x3,.., xn be the set of observed data points consisting of user’s previous sharing and m = m1, m2,.., mc be the set of cluster centers.
i) Choose randomly c observations as cluster centroids
ii) Compute the distance between each data point in X and assign it to the cluster with minimum distance.
Compute the new centroids as the average of the data points in the cluster
iii) Repeat steps ii and iii until the data assigned to the clusters remain in the same cluster.
STEP 2: Use the centroids calculated from step 1 as input to the Expectation-Maximization algorithm to generate the Gaussian Mixture Model representing the user’s behavior on sharing attributes.
The GMM is the weighted sum of c component Gaussian densities as in Eq. (1)
where, wiare the weights of the Gaussian densities assigned such that
Initialize mean, covariance and weights of the Gaussian densities. Mean and covariance are initialized based on the K means clustering output from step 1. Weights are initialized with equal weights such that the summation of weights assigned to Gaussian components equals 1
i) Expectation Step: Compute the posterior probability (γj(x)) of point x belonging to Gaussian Component C based on the current estimates of GMM components (mean, covariance and weights assigned to GMM components)
ii) Maximization Step: update the parameters of Gaussian components-means (Eq. (4)), covariance matrices (Eq. (5)), and mixing proportions (Eq. (6)) using the results of Expectation step (i)
Repeat (i) and (ii) until convergence.
3.1 User Sharing Trait Modeler
Input: X = x1, x2, x3,…, xn be the sharing decision of n users. Where x1, x2, x3,…, xn are the data points consisting of the previous sharing decision of users 1 to n respectively.
Output: Gaussian Mixture Model representing user clusters (The concerned user, The pragmatic user, The Unconcerned user) The input data is passed as a parameter to Sharing Trait Modeler (Section 3.1) to render the model representing user sharing pattern.
Data Access Behavior Modeler
Input: X = x1, x2, x3,…, xn be the permission acquired by TPA’s. Where x1, x2, x3,…, xn are the data points consisting of the previous permission requested by TPA to n users, for any one of the categories of application such as games, lifestyle, utility and so forth.
Output: Gaussian Mixture Model representing permissions acquired by TPA for each of the application categories (Games, Lifestyle, Business, Utility, Shopping, Education). The input data is passed as a parameter to Sharing Trait Modeler (Section 3.1) to render the model representing TPA’s data access pattern.
3.2 Fuzzy Based TPA’s Reliability Inference Engine
The Fuzzy model is used to calculate the application’s reliability value. Since this study uses data obtained in real time, Fuzzy inference is used to deal with any ambiguity in the data. The graded membership function used in Fuzzy inference expresses the distribution of truth of the variable. The features used to infer the reliability of the application has been collected from multiple sources. The preprocessing part of the input data mentioned above is available in our earlier work on computing the reliability of the TPA [18].
Let Y be universe of data, with a generic element of Y denoted by y. Thus, Y = y.
The member ship functions of rating data, number of raters, data access behavior, comments are as follows. μrlow(y), μrmed(y), μrhigh(y). μnor−low(y), μnor−med(y), μnor−high(y), μdab−opt(y), μdab−mod(y), μdab−high(y), μcom−negative(y), μcom−neutral(y), μcom−positive(y). The values of the functions are distributed between value 0 and 1 as μZ(y):Y -> [0, 1], Z is the generic membership function representation. The value refers to the membership degree of y in Z. Gaussian, Trapezoidal and Triangular membership function have been used in the application. The Gaussian membership function is defined as in Eq. (7)
where, m is the mean and, σ is the variance of the fuzzy set Zgauss. The triangular membership function is represented by Eq. (8), with points a and c representing the triangle’s base and b representing the triangle’s peak.
Eq. (9) defines the trapezoidal membership function with parameters a, b, c, and d, where a and d represent the bottom corners and b and c represent the top most edge.
The membership functions for the fuzzy sets of input parameters were chosen based on the predicted reliability score and fine-tuned to minimise the Root Mean Squared Error (RMSE).
As described in The truth value flow Inference theory [19], the truth value from the input variables are transferred to the other end to compute the reliability score of the TPA. Fuzzy rules takes the following form for inference system:
where, Ri is the i th rule,
Sample rule 1: If (Rating is low) and (Raters(N) is low) and (Data-Access is high) and (Comments is negative) then (App-Reliability-Score is low) (.75)
Sample rule 2: If (Rating is med) and (Raters(N) is med) and (Data-Access is med) and (Comments is neutral) then (App-Reliability-Score is high) (0.9)
3.2.2 Working of TPA’s Reliability Inference Model
The following steps are carried out to infer the reliability level of the TPA.
where
• In Implication, the output is obtained by mapping the input values to consequent fuzzy sets to obtain the output level. The weight (wt) assigned to a rule is used to determine the output level (zi).
• The weighted average of all the rules is calculated to arrive at the final output of the system.
The TPA recommender shown in Fig. 2 mimics the human expert thereby reducing the user’s burden on comprehending the suitability of the TPA and lowers the risk of choosing an inappropriate application. TPA’s reliability score is arrived from our previous work. TPA’s Reliability score and user sharing trait is given as the input to the fuzzy recommender. The rule base and membership functions of recommender was initially designed based on ground truth and later fine tuned.
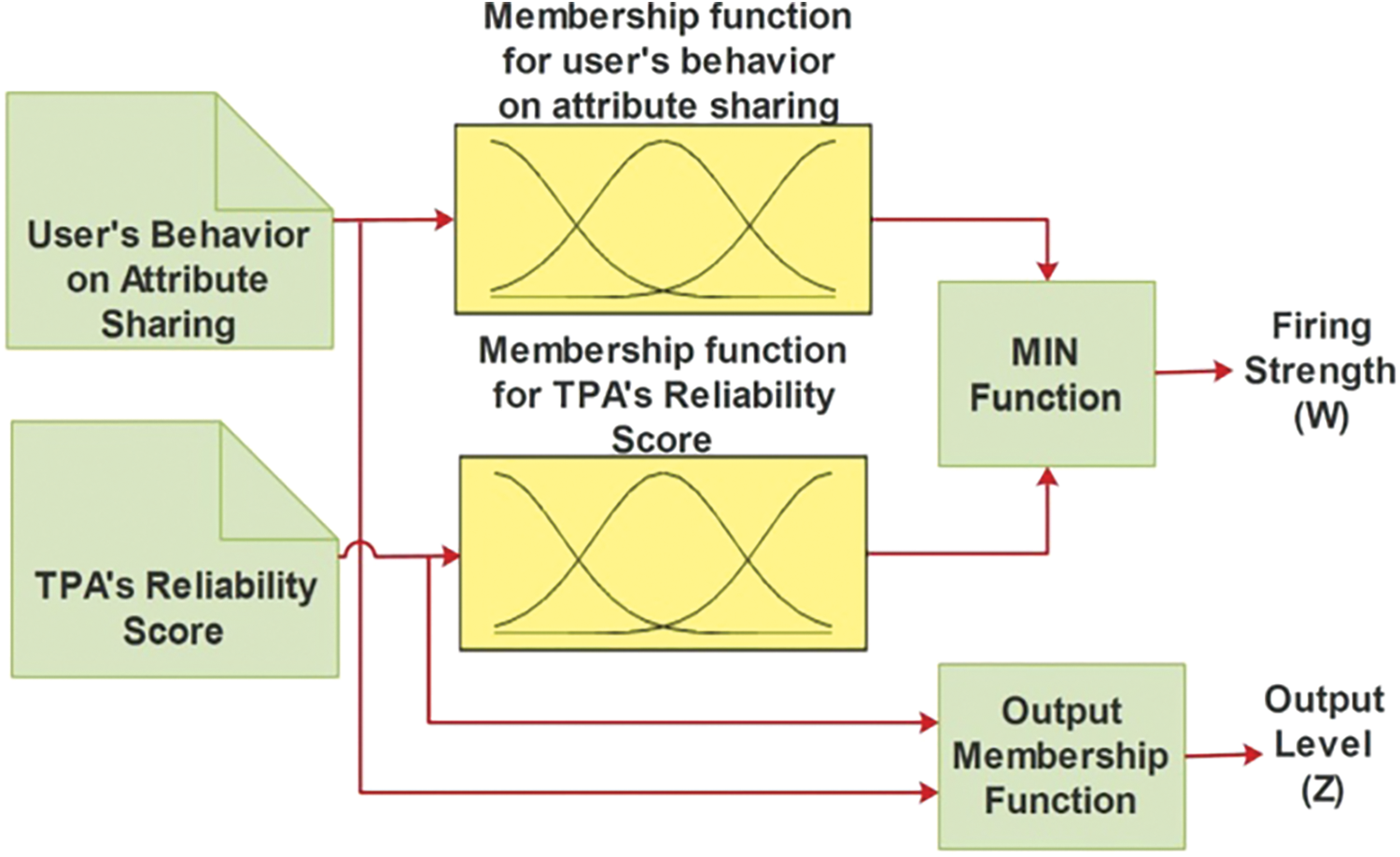
Figure 2: Fuzzy TPA recommender
Privacy Violation Alerter displays an enhanced intimation page to the user. The intimation page consists of TPA related information like comments, rating of the TPA, number of raters, Reliability Level of the TPA and how likely the TPA follows the data access pattern of applications of that category. This measure is strong indicator when the TPA has a unusual data access pattern compared to applications belonging to same domain. The user’s privacy level is also displayed. Only when the user agrees to share, the TPA installation is carried out.
Finding the likelihood: Let x be the permission requested by new application before installation. Having known the category of the application; the posterior probability
where, wi are the weights of the Gaussian densities assigned such that
When a user needs to install a new TPA, the Share Level Intimator compares the user’s previous sharing behavior to that of the new TPA’s attribute request permission. If matched, an enhanced consent page is presented to the user. Otherwise, a violation alert page followed by enhanced consent page is presented to the user. The enhanced consent page consists information about user’s sharing pattern (privacy concerned, pragmatic, unconcerned) and TPA’s information (rating, number of raters, user comments, attribute permissions requested, reliability score of the TPA and TPA’s data access pattern).
User Sharing Trait Modeler (UTM) uses GMM to capture user’s sharing pattern, Fig. 3 shows the Gaussian model generated for the collected data set. The data used for modeling user behavior consists of 850 instances of data shared by various users of age group between 18 to 40. The users are spread in all the three categories and can be seen that a large proportion of users are willing to share more attributes to get the desired service. Given the user’s previous sharing pattern, the UTM renders the likelihood of user falling in the categories, privacy concerned, pragmatic or unconcerned user. The category with highest probability is taken as the user’s sharing pattern.
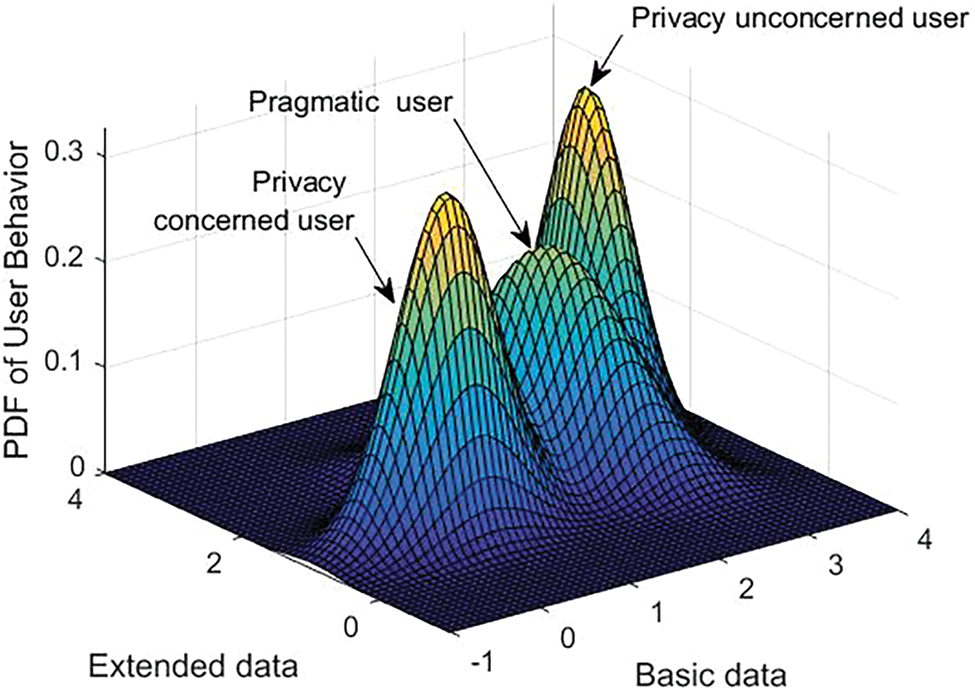
Figure 3: GMM generated user sharing pattern
TPA reliability score inference and TPA recommender has been designed using fuzzy inference system. Matlab simulation has been used to fine tune the membership function, and to decide the rules for fuzzy inference system. 81 rules have been used in total. The sample rule list can be found in Tab. 2, the rule’s weight determines its firing strength. Tab. 3 displays the reliability score.


The surface view graph for TPA recommendation based on TPA reliability score and Users Privacy Level is presented in Fig. 4 The application user choses to install is recommended to them based on the user’s privacy requirements and TPA’s reliability score.
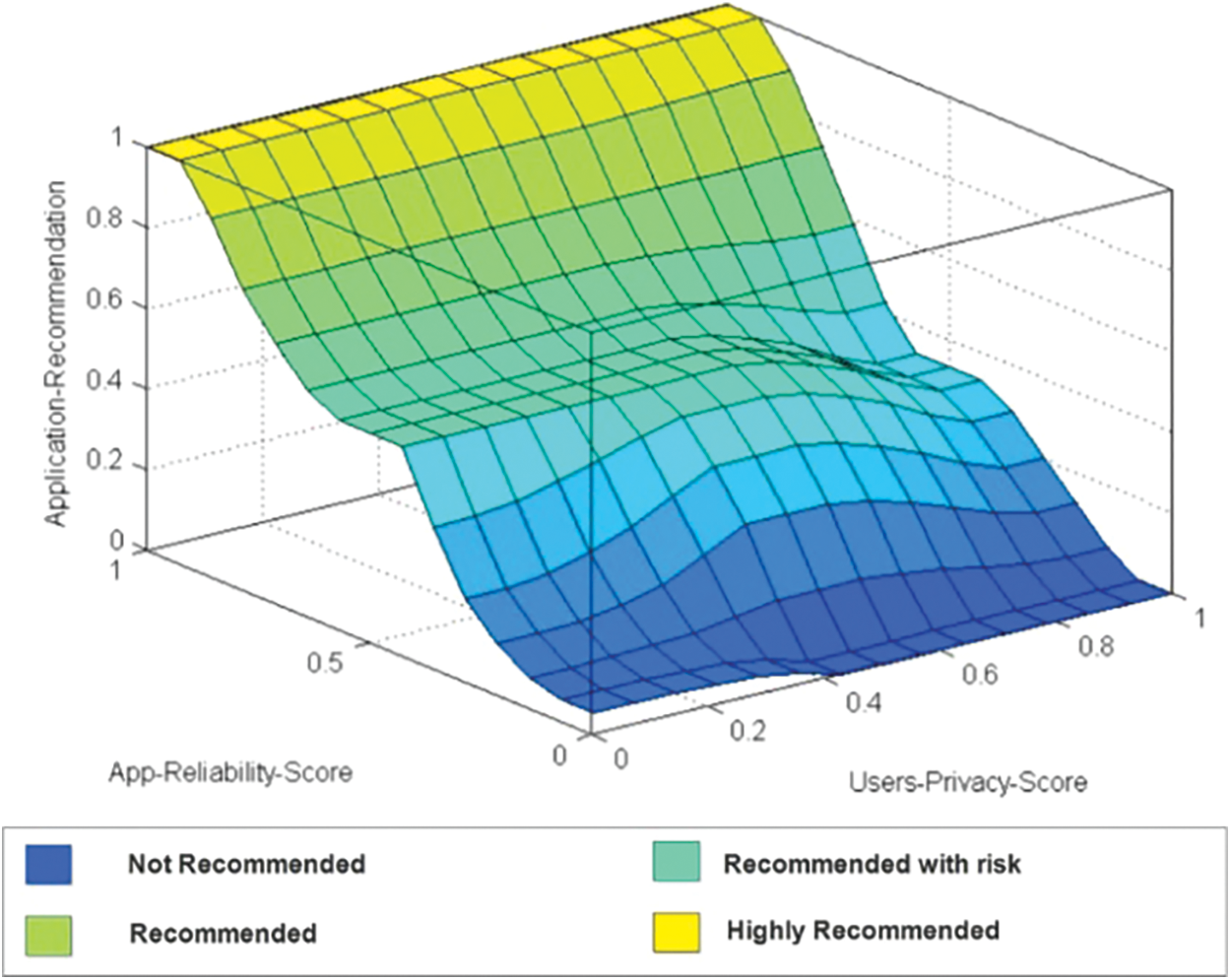
Figure 4: Surface view graph for TPA's reliability score vs. users privacy
For privacy concerned users the weight for certain rules are adjusted so that the applications with low reliability level will not be recommended to them. Blue region in Fig. 4 marks the discussed criteria. Conversely, yellow region depicts highly recommended. The recommendation for TPA, given to the user varies based on the reliability score of the TPA and the user’s privacy level. Thus the recommender is able to provide a personalized recommendation based on the user’s privacy preferences as shown in Tab. 4.

It is evident from the literature discussed earlier that the privacy infringement is more prone to happen in user-TPA data sharing context. The proposed solution attempts to solve the root cause of the problem, by explicitly alerting the user on what is being shared, and to whom it is being shared and allows the sharing only based on an explicit informed consent. The existing solutions do show a consent page containing information about the attributes requested. But, users find it difficult to comprehend the information in the consent page and compare it with their privacy preferences while making a decision to share. We have designed the solution by building a model each for both user and TPA involved in the transaction. When there is a need to install a new application, the user’s sharing pattern is compared with that of the new TPA’s posterior probability, and the users are intimated with an enhanced consent page before sharing. In the case of a violation two level alert is displayed to the user. In the first place, the privacy violation is signaled, and upon the user choosing to continue with the TPA, the enhanced consent page with additional information is rendered to the user. The user’s data is shared to the TPA, only after these two stages towards privacy preservation. In our future work, we wish to explore the use of advanced perturbing techniques assuring privacy, so as to enable the users to even utilize the services of TPA’s seeking intruding information.
Acknowledgement: We show gratitude to anonymous referees for their useful ideas.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. T. Shanmughapriya and S. Swamynathan, “An alert system based on shared score for online social networks,” in Proc. of the Second Int. Conf. on Information and Communication Technology for Competitive Strategies, New York, NY, United States, pp. 1–5, 2016. [Google Scholar]
2. J. R. Mayer and J. C. Mitchell, “Third-party web tracking: Policy and technology,” in IEEE Symp. on Security and Privacy, San Francisco, CA, USA, pp. 413–427, 2012. [Google Scholar]
3. A. Chaabane, Y. Ding, R. Dey, M. A. Kaafar and K. W. Ross, “A closer look at third-party OSN applications: Are they leaking your personal information,” in Int. Conf. on Passive and Active Network Measurement, Los Angeles, CA, USA, pp. 235–246, 2014. [Google Scholar]
4. A. Besmer, H. R. Lipford, M. Shehab and G. Cheek, “Social applications: Exploring a more secure framework,” in Proc. of the 5th Symp. on Usable Privacy and Security, New York, NY, United States, pp. 1–10, 2009. [Google Scholar]
5. V. K. Tuunainen, O. Pitkänen and M. Hovi, “Users’ awareness of privacy on online social networking sites-case facebook,” in Bled 2009 Proc., Bled, Slovenia, pp. 1–18, 2009. [Google Scholar]
6. N. Wang, H. Xu and J. Grossklags, “Third-party apps on facebook: Privacy and the illusion of control,” in Proc. of the 5th ACM Symp. on Computer Human Interaction for Management of Information Technology, United States, pp. 1–10, 2011. [Google Scholar]
7. I. Symeonidis, F. Beato, P. Tsormpatzoudi and B. Preneel, “Collateral damage of Facebook Apps: An enhanced privacy scoring model,” in IACR Cryptology ePrint Archive, Korea, pp. 456–456, 2015. [Google Scholar]
8. M. Egele, A. Moser, C. Kruegel and E. Kirda, “PoX: Protecting users from malicious Facebook applications,” Computer Communications, vol. 35, no. 12, pp. 1507–1515, 2012. [Google Scholar]
9. L. Fang and K. LeFevre, “Privacy wizards for social networking sites,” in Proc. of the 19th Int. Conf. on World Wide Web, Raleigh, NC, USA, pp. 351–360, 2010. [Google Scholar]
10. M. Shehab, A. C. Squicciarini and G. J. Ahn, “Beyond user-to-user access control for online social networks,” in Int. Conf. on Information and Communications Security, Birmingham, United Kingdom, pp. 174–189, 2008. [Google Scholar]
11. M. E. Andrés, N. E. Bordenabe, K. Chatzikokolakis and C. Palamidessi, “Geo-indistinguishability: Differential privacy for location-based systems,” in Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security, New York, NY, United States, pp. 901–914, 2013. [Google Scholar]
12. P. Anthonysamy, A. Rashid, J. Walkerdine, P. Greenwood and G. Larkou, “Collaborative privacy management for third-party applications in online social networks,” in Proc. of the 1st Workshop on Privacy and Security in Online Social Media, Lyon, France, pp. 1–4, 2012. [Google Scholar]
13. F. Adrienne and E. David, “Privacy protection for social networking APIs,” in Workshop on Web 2.0 Security and Privacy, Oakland, CA, pp. 1–9, 2008. [Google Scholar]
14. M. Shehab and S. Marouf, “Recommendation models for open authorization,” IEEE Transactions on Dependable and Secure Computing, vol. 9, no. 4, pp. 583–596, 2012. [Google Scholar]
15. X. Ding, L. Zhang, Z. Wan and M. Gu, “A brief survey on de-anonymization attacks in online social networks,” in IEEE Int. Conf. on Computational Aspects of Social Networks, Taiyuan, China, pp. 611–615, 2010. [Google Scholar]
16. T. Jahan, G. Narsimha and C. G. Rao, “Multiplicative data perturbation using fuzzy logic in preserving privacy,” in Proc. of the Second Int. Conf. on Information and Communication Technology for Competitive Strategies, Udaipur, India, pp. 1–5, 2016. [Google Scholar]
17. K. Singh, S. Bhola and W. Lee, “xBook: Redesigning privacy control in social networking platforms,” in Information Security 14th Int. Conf., ISC 2011 Xi’an, China, October 26–29, 2011, pp. 249–266, 2009. [Google Scholar]
18. T. Shanmuigapriya and S. Swamynathan, “Reliability score inference and recommendation using fuzzy-based technique for social media applications,” Soft Computing, vol. 22, no. 24, pp. 8289–8300, 2018. [Google Scholar]
19. P. Wang and S. Tan, “Soft computing and fuzzy logic,” Soft Computing, vol. 1, no. 1, pp. 35–41, 1997. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |