DOI:10.32604/csse.2022.022739

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.022739 |  |
| Article |
Grid Search for Predicting Coronary Heart Disease by Tuning Hyper-Parameters
1Department of ECE, Mahendra Institute of Technology, Namakkal, Tamilnadu, 637503, India
2Department of ECE, Sona College of Technology, Salem, Tamilnadu, 636005, India
3Department of ECE, Koneru Lakshmaiah Education Foundation, Vijayawada, Andhra Pradesh, 522502, India
4Department of Information Technology, Kongu Engineering College, Perundurai, Tamilnadu, 638060, India
5Department of Embedded Technology, Vellore Institute of Technology, Vellore, Tamilnadu, 632014, India
*Corresponding Author: S. Prabu. Email: vsprabu4u@gmail.com
Received: 17 August 2021; Accepted: 22 November 2021
Abstract: Diagnosing the cardiovascular disease is one of the biggest medical difficulties in recent years. Coronary cardiovascular (CHD) is a kind of heart and blood vascular disease. Predicting this sort of cardiac illness leads to more precise decisions for cardiac disorders. Implementing Grid Search Optimization (GSO) machine training models is therefore a useful way to forecast the sickness as soon as possible. The state-of-the-art work is the tuning of the hyperparameter together with the selection of the feature by utilizing the model search to minimize the false-negative rate. Three models with a cross-validation approach do the required task. Feature Selection based on the use of statistical and correlation matrices for multivariate analysis. For Random Search and Grid Search models, extensive comparison findings are produced utilizing retrieval, F1 score, and precision measurements. The models are evaluated using the metrics and kappa statistics that illustrate the three models’ comparability. The study effort focuses on optimizing function selection, tweaking hyperparameters to improve model accuracy and the prediction of heart disease by examining Framingham datasets using random forestry classification. Tuning the hyperparameter in the model of grid search thus decreases the erroneous rate achieves global optimization.
Keywords: Grid search; coronary heart disease (CHD); machine learning; feature selection; hyperparameter tuning
Coronary cardiovascular disease (CHD) is one kind of cardiac illness that is seen as a major health concern and one of the world’s mortality factors [1]. In recent years, this kind of cardiovascular disease has increased. The death rate of heart disease is estimated at approx. 31% globally, [2–5] according to the World Health Organization (WHO) and over 23.6 million people worldwide may die from this heart condition. Thus, doctors demand that they identify patients with heart disease not just for symptoms but also for medical testing and diagnoses [6,7]. Meanwhile, fatalities from stroke and heart attack have reached over 17.7 million in the world from coronary heart disease [8–10]. Cholesterol, obesity, smoking, hypertension, blood pressure, diabetes, fatness, tobacco use, etc. are all variables that impact cardiac disease. Cardiac illness symptoms include short breath, weakening physical, heartburn, etc. And it was exceedingly difficult in the early days to diagnose and treat this cardiac condition. Finally, if the cardiac illness is detected as soon as possible, many people’s lives can be spared to a considerable degree by medications. Machine learning has in this case become an unbelievable diagnostic answer. Machine learning is an excellent technique to handle big data sets and to turn them into knowledge-based data, forecasts, and analysis. Today, the healthcare sector generates large volumes of data that include complicated data, patient electronic data, clinical resources, and medical devices, etc.
Data mining, on the other hand, offers a set of methodologies and instruments to meet the diagnostic targets. It is mainly intended for the correct diagnosis of the disease to find the hidden pattern of patient data. Apart from features, Grid models enhance the prediction accuracy and extract and choose key features by adjusting the hyperparameters.
Machine learning nowadays makes it easier to forecast and make decisions. The study is motivated mainly by the application of grid search models to increase the performance of classificators. The hyperparameter is picked in the grid search for optimum parameters. Important characteristics are drawn from the grid search process and, during model development, appropriate features are chosen. Target classes are anticipated with these feature selections. The contribution of the proposed work is
• Pre-processing the heart disease dataset by implementing the mean imputation method.
• Feature extraction using Grid search and selection of relevant features.
• Constructing the Predictive models by tuning the hyperparameters.
• Finding the optimal parameters and optimal model.
• Assessment of the model with statistical measures.
This section summarizes the various approaches for predicting heart disease with several models. Researchers have devised many data mining models and algorithms to predict the occurrence of heart disease in a patient.
Chandrasegar et al. [11], A designed a fine-tuned model for prediction and identified the key features to build the classification methods such as Random Forest (RF), Support Vector Machine (SVM), and Decision Tree (DT) to achieve better accuracy in predicting the disease.
Melillo et al. [12] proposed an automatic classifier for predicting congestive heart failure (CHF) isolating the patients with minimum risk. The research work achieved 93.3% of sensitivity and 63.5% of specificity.
Guidi et al. [13] proposed a clinical decision support system (CDSS) for predicting heart failure The machine learning algorithms neural network (NN), SVM with fuzzy rules, and RF were deployed for predicting the disease and the best performance was achieved by the RF model.
Mantovani et al. [14] contributed a hyperparameter tuning model by implementing DT with 102 datasets. Ali [15] utilized DT, RF, Logistic Regression (LR), and SVM models to build the prediction models, and finally, RF produced the best accuracy of 90% compared to other classifiers. The paper devised a model to predict heart disease with feature selection methods by exploiting Cleveland datasets. The studyproposed a method based on characteristic data of patients by implementing an adaptive neuro-fuzzy inference system.
The classification system deploying relief and rough methods and the model achieved the classification accuracy of 92.32%. The study devised an identification method in predicting heart disease with a sequential backward selection algorithm for feature selection and K-Nearest Neighbour (K-NN) for classification and obtained high accuracy for the K-NN model.
This study is being examined in the Kaggle cardiovascular dataset (Framingham dataset). The dataset includes 16 separate characteristics with 4240 occurrences. The dataset contains both category and numerical values. It is made up of a TenYearCHD designation that implies individuals having coronary heart disease for 10 years. The 16 most significant characteristics of the Grid search are extracted. Features such as male, age, current smokers, day cigs, prevalent cigarette, prevalent hypertensive illness, BMI, are regarded as clinical factors, as well as disease characteristics such as diabetes, totChol, heart rate, BP, glucose, etc. Tab. 1 shows the functions of the data set and range description. The input data are evaluated by Random Classifier. Data imputation must be performed via the interpolation approach for filling incoherent data during the first phase [16–20]. Next, feature selection is done by setting the hyperparameter to minimize the dimensionality of the data set to get optimal search features. The function selection will eventually depend on the tuning of the hyperparameter. Random research, an embedded technique for the optimization of functional extraction is built because the observations are extracted randomly from the dataset and less likely to overfit. The characteristics are taught to reduce impurity. Thirdly, to enhance the model and to produce better accuracy of the RF model, Grid Search methods are deployed [21–25]. The proposed method is designed with three models. 1. Random Search 2. CV-Grid Search 3. Final Grid. The architecture of the proposed model is depicted in Fig. 1.


Figure 1: The architecture of the proposed model
Random cross-validated search [26–28] has evolved to pick the characteristics in this step. An accurate GBR approach is combined to provide an accurate gradient boosting method. Less than 1 is achieved in conjunction with no reduction, and subsample 0.5 is shown in Fig. 2. The learning rate is superior. The model lowers the measurement of variance to enhance the model performance. The Framingham dataset has 16 characteristics of up to 10 characteristics. A learning L technique is used to choose a random RF feature that minimizes the estimated loss (l) from normal distribution Gf across n samples. Here the learning algorithm produces Rf via optimization of training data concerning hyperparameters
In Eq. (1) Ex is an expected error on training data. And G is the distribution function.The aggregated output of all the training data can be expressed as:
where Z represents the aggregated output of train data. This function retains the subsamples from the dataset that is customized to the training samples obtaining relevant features

Figure 2: Deviance in training set with boosting iterations
In this model Radial-basis function (RBF) also known as the squared exponential kernel is implemented. Here the length scale l is taken as a parameter. This isotropic variant can be a scalar or vector holding the same dimension as the input samples Si. This kernel is produced by
where d is Euclidean distance between the input samples
where,
Thus the smoothness of the learned function is controlled by kernel function [29]. Among 16 attributes 10 features are taken as input and 3 attributes such as PrevalentStroke, PrevalentHyp, and Diabetes features are the target variable that influenced the learning function.
Grid search is an excellent technique for optimizing the dataset to find the optimum parameters. In the model given, four parameters of the Grid search algorithm, i.e., learning rate, drop rate, size of the lot, and epoch, are explored. Set and tweaked by creating a search space with an n-dimensional value, the hyper-parameters x and y are evaluated in the grid area, which enhances the score value to get the best model. The mean score and standard score are calculated by the values x and y. If the set parameter raises the score value, these parameters are set for model precision or the rest of the features will still be searched for the new parameter. In this model, the trained data is again split into K = 5 number of subsets called folds. Then the model is fit iteratively till 500 iterations for K times and evaluated every time on Kth fold to obtain the validated data. The learning rate for 10 relevant features with the increasing iterations is shown in Fig. 3.

Figure 3: Grid search optimization algorithm

The third model implements Gaussian Process Regression (GPR) and Kernel Ridge Regression (KRR) for hyperparameter tuning. The covariance of the prior model is passed through the kernel object and hyperparameters are optimized during GPR fitting. The first iteration is conducted from the initial hyperparameter set value and then the remaining iterations are chosen randomly. The noise level is specified globally as a scalar or vector product through the parameter alpha in the target variables. The linear function is influenced by the kernel corresponding to the non-linear function in the grid space whereas KRR learns a linear function to perform the grid search on the CV. GPR is exploited to learns the target function with proper intervals and KRR is deployed to provide predictions.The deviance-value during tuning concerning learn-rate, Dropout-rate is exhibited for batch size in Tab. 2.

All three models produce better accuracy in terms of dropout rate but the optimization differs concerning the batch size.
The Framingham dataset comprises 16 attributes with 4240 instances among which 644 patients with TenYearCHD and 3596 patients without CHD. Significant features are selected using Grid Search models and hyperparameters are tuned to fit the model and the best model is determined among the three models. After the feature selection process the target variables are classified with subsamples in each model and the proposed models are assessed with the recall, F1_score, and accuracy metrics. The frequency distribution of the heart disease instances concerning Age attribute is shown in Fig. 4.

Figure 4: Histogram for ten year CHD
Figs. 5a and 5b provide both the model and dataset for the second grid search model consisting of the sinusoidal target function with heavy noise. The learned model of GPR and KRR based on ExpSineSquared is shown in the Grid search graph. The kernel’s hyperparameters control both the smoothness represented by the length scale and periodicity. The KRR remains the same for second grid search and final grid search whereas the length scale and periodicity value for the GPR method differs inferring that GPR reduces the periodicity value and length scale by obtaining accuracy of the model. Though the data points are distributed similarly in both the methods, the periodicity, and the length-scale vary during hyperparameter tuning. The time taken for fitting the model with the regression techniques is portrayed in Tab. 3.

Figure 5: (a) Periodicity and length-scale in second grid search (b) Periodicity and length-scale in final grid search

With performance measurements, the correctness of Grid models is determined. In addition, it is necessary to consider the error rate during the building of the model. As the error rate is smaller, the more precisely the model is. Error statistics are measured in the proposed model using kappa values to compare the optimization of the model. Three error statistics are used for evaluation of models presented in Tab. 4, including Mean Absolute Error (MAE), Root Middle Squared Error (RMSE), and Relative Absolute Error (RAE). Final Grid Search produces a lower error rate than the two other models: 0.38 MAE, 0.43 RMSE and RAE 0.65. Similarly, the kappa statistic is also used for assessing the grid models apart from other performance metrics. The proposed model is dealt with the Random classifier with grid models. Generally, the value of kappa lies between −1 to +1. It is a suitable statistical measure to deal with multi-class target labels to solve unbalanced issues. There are four target variables in the Framingham dataset. To evaluate the three grid models randomized classification kappa is calculated for the three models in which the final grid models produce 0.62 which is considered the best version of the two models that produced 0.28 and 0.45 for a random search and second grid search models, respectively, as shown in Fig. 6.
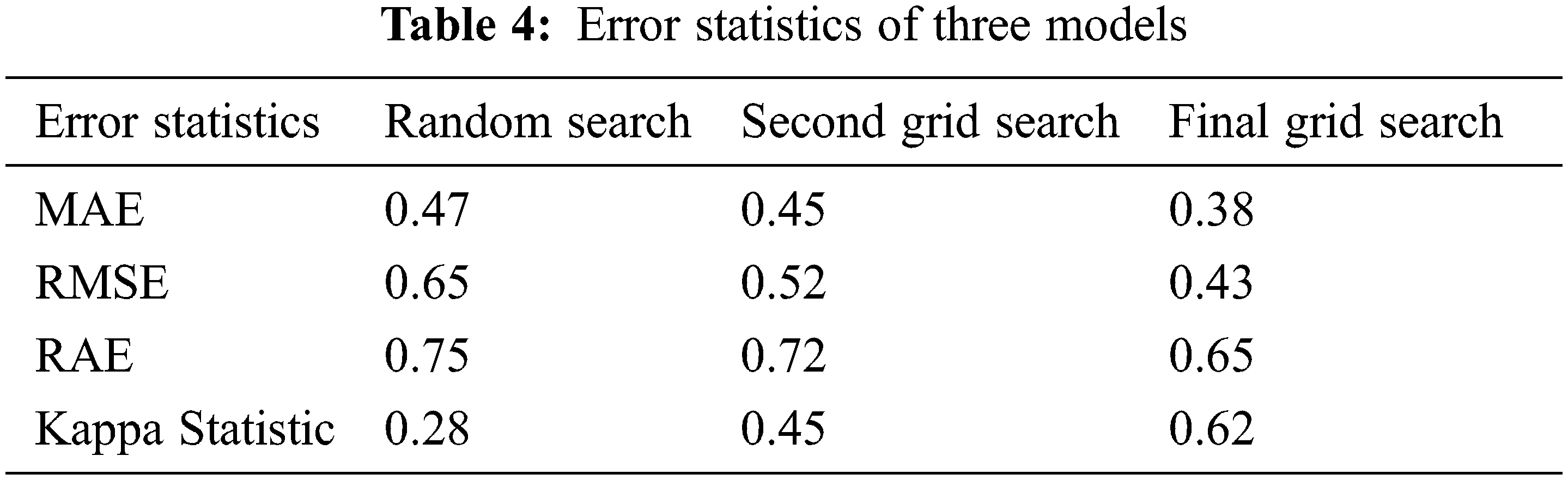

Figure 6: Statistical measures for proposed models
In the proposed model, among 4240 instances, 3700 instances are taken for training and testing the data after data imputation using the mean model. 3000 observations are taken for training data which is split into three sets utilized by the three models. 700 observations are considered for testing. For assessing the grid models 300 instances out of 700 are taken randomly. The performance of the models is evaluated for 100, 200, and 300 samples using three metrics as Recall, F1_score, and Accuracy. The main concern of the proposed work is to reduce the false rate. F1_Score is used to find the mean harmonic value of precision and Recall. Tab. 5 explicitly the performance measure of all three models. The final Grid Search model produces an average of 90.2%, 82.1%, and 86% for recall, F1_Score, and Accuracy respectively. The other two models produce an average score of 81.67%, 88.44%, 69.78%, 75.1%, 72%, and 82% of recall, F1_Score, and accuracy respectively. Figs. 7–9 portrays the performance comparison of the three models.
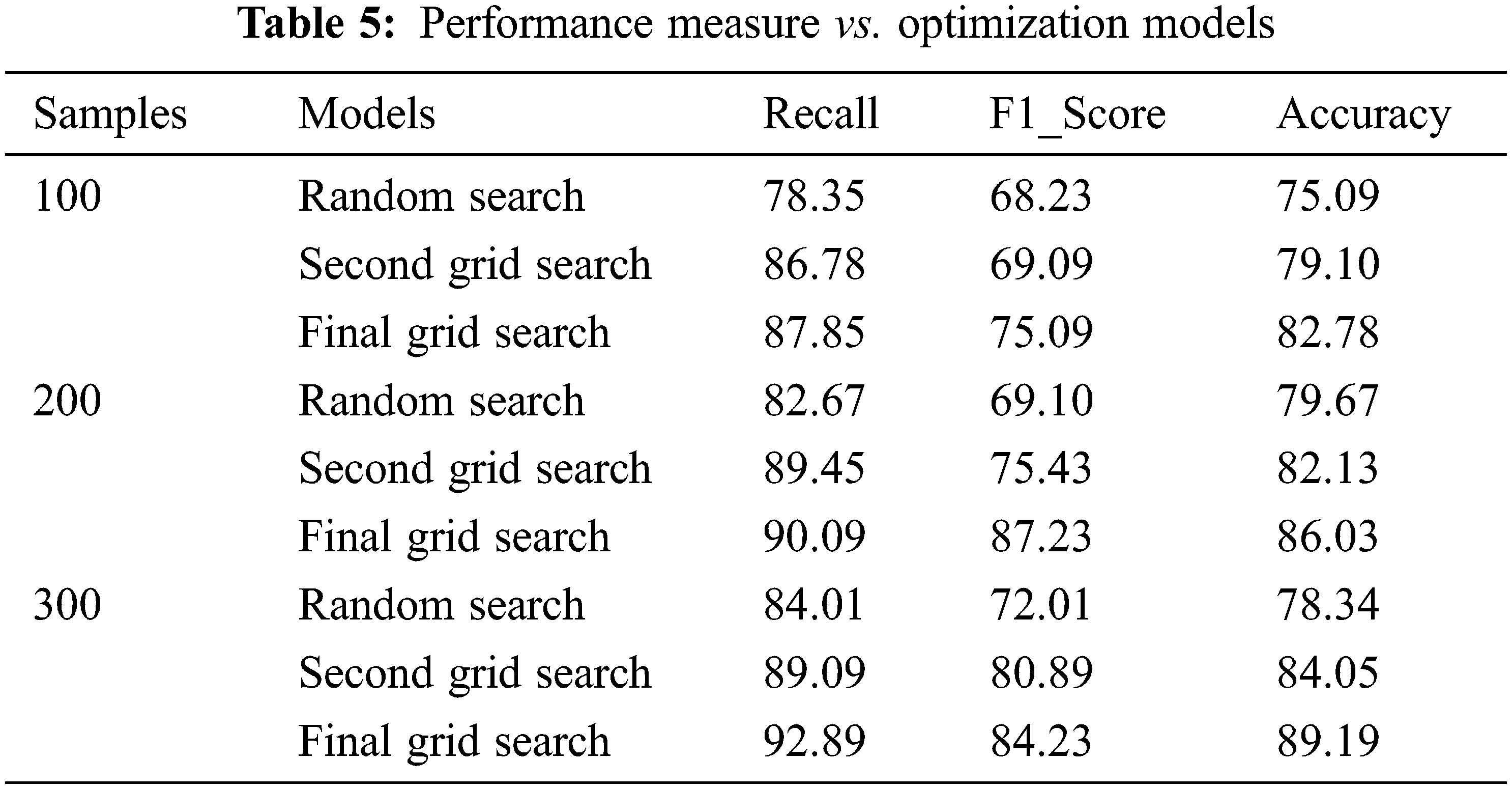

Figure 7: Recall measure for three models

Figure 8: F1-score of grid models

Figure 9: Accuracy measure for grid models
As computer-aided diagnosis is given more importance in recent years, machine learning contributes a lot to disease prediction and decision-making the diagnosis. Besides selecting the classifier, the dataset distribution plays a vital role in predicting the disease. Feature selection is a significant factor for target class prediction. In the proposed model, a grid search is implemented to select relevant features for prediction and also to improve the performance of the classifier random search and grid search models with cross-validation are taken for hyperparameter tuning. These optimization models are utilized to increase classification accuracy. The proposed model harnessed the Framingham dataset with 16 features with 1420 instances. The dataset is split into trained and test data. Important features are selected for fitting the model and hyperparameters are set manually during model construction. This is continued for several iterations until the model is fit. In the Random Search, the GBR method is implemented to reduce loss function while tuning. The second grid search introduces the RBF model to minimize the smoothness for optimal parameter selection. The Final Grid model is framed with GPR and KRR methods for learning the periodicity and length-Scale to fit the model. Finally, the performance of the models is assessed with the metrics and kappa statistics showing the comparison of the three models.
When using different classifiers in machine learning approaches, heart disease datasets used in diverse research studies may give varying findings. Aside from the dataset, the major focus is on feature selection and optimization to improve classification accuracy. The goal of this study is to combine statistical approaches with a grid search model with hyperparameter tweaking. During the grid search model, relevant characteristics are retrieved and chosen for further classification analysis. The data set is divided into training and test sets, which are then used by three models. During the Random Search, the learning rate and dropout rate are calculated. In the second grid search and the third model, the smoothness function is regularised; GPR and KRR techniques are used to improve the parameters to suit the model by comparing the periodicity and length Scale. Finally, the performance results compare three models based on an error rate, kappa statistic, recall, F1 Score, and Accuracy. Future work might include implementing numerous datasets with different classifiers.
Acknowledgement: The authors would like to thank Anna University and also we like to thank anonymous reviewers for their so-called insights.
Funding Statement:The authors received no specific funding for this study.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. P. Li, A. U. Haq, S. U. Din, J. Khan, A. Khan et al., “Heart disease identification method using machine learning classification in E-healthcare,” IEEE Access, vol. 8, pp. 107562–107582, 2020. [Google Scholar]
2. J. J. Beunza, E. Puertas, E. G. Ovejero, G. Villalba, E. Condes et al., “Comparison of machine learning algorithms for clinical event prediction (risk of coronary heart disease),” Journal of Biomedical Informatics, vol. 97, pp. 103257, 2019. [Google Scholar]
3. K. Saxena and R. Sharma, “Efficient heart disease prediction system,” Procedia Computer Science, vol. 85, no. 10, pp. 962–969, 2016. [Google Scholar]
4. H. Leopord, W. K. Cheruiyot and S. Kimani, “A survey and analysis on classification and regression data mining techniques for disease outbreak prediction in datasets,” The International Journal of Engineering and Science, vol. 5, no. 9, pp. 1–11, 2016. [Google Scholar]
5. N. S. C. Reddy, S. S. Nee, L. Z. Min and C. X. Ying, “Classification and feature selection approaches by machine learning techniques: Heart disease prediction,” International Journal of Innovative Computing, vol. 9, no. 1, pp. 39–46, 2019. [Google Scholar]
6. A. A. Ali, “Stroke prediction using distributed machine learning based on apache-spark,” Stroke, vol. 28, no. 15, pp. 89–97, 2019. [Google Scholar]
7. M. Durairaj and N. Ramasamy, “A comparison of the perceptive approaches for preprocessing the data set for predicting fertility success rate,” International Journal of Control Theory Application, vol. 9, no. 27, pp. 255–260, 2016. [Google Scholar]
8. T. Kasbe and R. S. Pippal, “Design of heart disease diagnosis system using fuzzy logic,” in Proc. Int. Conf. on Energy, Communication, Data Analytics and Soft Computing, Chennai, India, IEEE, pp. 3183–3187, 2017. [Google Scholar]
9. T. Hastie, R. Tibshirani and J. Friedman, “The elements of statistical learning,” New York Springer Series in Statistics, vol. 1, no. 10, pp. 101–138, 2001. [Google Scholar]
10. S. Ambesange, A. Vijayalaxmi, S. Sridevi and B. S. Yashoda, “Multiple heart diseases prediction using logistic regression with ensemble and hyperparameter tuning techniques,” in Proc. WorldS4, London, UK, pp. 827–832, 2020. [Google Scholar]
11. T. Chandrasegar and A. Choudhary, “Heart disease diagnosis using a machine learning algorithm,” in Proc. Innovations in Power and Advanced Computing Technologies, Vellore, India, pp. 1–4, 2019. [Google Scholar]
12. P. Melillo, N. D. Luca, M. Bracale and L. Pecchia, “Pecchia,Classification tree for risk assessment in patients suffering from congestive heart failure via long-term heart rate variability,” IEEE Journal of Biomedical and Health Informatics, vol. 17, no. 3, pp. 727–733, 2013. [Google Scholar]
13. G. Guidi, M. C. Pettenati, P. Melillo and E. Iadanza, “A machine learning system to improve heart failure patient assistance,” IEEE Journal of Biomedical and Health Informatics, vol. 18, no. 6, pp. 1750–1756, 2014. [Google Scholar]
14. R. G. Mantovani, T. Horvath, R. Cerri, J. Vanschoren and A. C. D. Carvalho, “Hyperparameter tuning of a decision tree induction algorithm,” in Proc. Brazilian Conf. on Intelligent Systems, Recife, Brazil, IEEE, pp. 37–42, 2016. [Google Scholar]
15. A. A. Ali, “Stroke prediction using distributed machine learning based on apache-spark,” Stroke, vol. 28, no. 15, pp. 89–97, 2019. [Google Scholar]
16. N. Ziasabounchi and I. Askerzade, “ANFIS based classification model for heart disease prediction,” International Journal of Electrical & Computer Science, vol. 14, no. 2, pp. 7–12, 2014. [Google Scholar]
17. X. Liu, X. Wang, Q. Su, M. Zhang, Y. Zhuet et al., “A hybrid classification system for heart disease diagnosis based on the RFRS method,” Computational and Mathematical Methods in Medicine, vol. 2017, pp. 1–11, 2017. [Google Scholar]
18. A. U. Haq, J. Li, M. H. Memon, M. H. Memon, J. Khanet et al., “Heart disease prediction system using a model of machine learning and sequential backward selection algorithm for features selection,” in Proc. Int. Conf. for Convergence in Technology, Bombay, India, pp. 1–4, 2019. [Google Scholar]
19. R. Hajar, “Framingham contribution to cardiovascular disease,” Heart Views: The Official Journal of the Gulf Heart Association, vol. 17, no. 2, pp. 78, 2016. [Google Scholar]
20. G. Castellano and A. M. Fanelli, “Variable selection using neural-network models,” Neuro Computing, vol. 31, no. 1–4, pp. 1–13, 2000. [Google Scholar]
21. T. Wang, H. Huang, S. Tian and J. Xu, “Feature selection for SVM via optimization of kernel polarization with Gaussian ARD kernels,” Expert Systems with Applications, vol. 37, no. 9, pp. 6663–6668, 2010. [Google Scholar]
22. P. Wieslaw, “Tree-based generational feature selection in medical applications,” ComputerScience, vol. 159, pp. 2172–2178, 2019. [Google Scholar]
23. J. P. Li, A. U. Haq, S. U. Din, J. Khan and A. Khanet, “Heart disease identification method using machine learning classification in E-healthcare,” IEEE Access, vol. 8, pp. 107562–107582, 2020. [Google Scholar]
24. L. Ali, A. Niamat, J. A. Khan, N. A. Golilarz, X. Xingzhonget et al., “An optimized stacked support vector machines based expert system for the effective prediction of heart failure,” IEEE Access, vol. 7, pp. 54007–54014, 2019. [Google Scholar]
25. R. F. Mansour, J. Escorcia-Gutierrez, M. Gamarra, V. G. Díaz, D. Gupta et al., “Artificial intelligence with big data analytics-based brain intracranial hemorrhage e-diagnosis using CT images,” Neural Computing and Applications, vol. 1, pp. 1–13, 2021. [Google Scholar]
26. R. F. Mansour, N. M. Alfar, S. A. Khalek, M. Abdelhaq, R. A. Saeedet et al., “Optimal deep learning-based fusion model for biomedical image classification,” Expert Systems, vol. 1, no. 10, pp. e12764, 2021. [Google Scholar]
27. R. F. Mansour, J. E. Gutierrez, M. Gamarra, J. A. Villanueva and N. Leal, “Intelligent video anomaly detection and classification using faster RCNN with deep reinforcement learning model,” Image and Vision Computing, vol. 1, pp. 104229, 2021. [Google Scholar]
28. L. Li, L. Sun, Y. Xue, S. Li, X. Huang et al., “Fuzzy multilevel image thresholding based on improved coyote optimization algorithm,” IEEE Access, vol. 9, pp. 33595–33607, 2021. [Google Scholar]
29. N. O. Aljehane and R. F. Mansour, “Big data analytics with oppositional moth flame optimization based vehicular routing protocol for future smart cities,” Expert Systems, vol. 1, pp. 12718, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |