DOI:10.32604/csse.2022.024950

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.024950 |  |
| Article |
A Real-time Cutting Model Based on Finite Element and Order Reduction
1Wuxi Research Institute, Nanjing University of Information Science & Technology, Wuxi, 214100, China
2Engineering Research Center of Digital Forensics, Ministry of Education, Jiangsu Engineering Center of Network Monitoring, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
3School of Automation, Nanjing University of Information Science & Technology, Nanjing, 210044, China
4State Key Laboratory of Bioelectronics, Jiangsu Key Lab of Remote Measurement and Control, School of Instrument Science and Engineering, Southeast University, Nanjing, 210096, China
5IT Fundamentals and Education Technologies Applications, University of Information Technology and Management in Rzeszow, Rzeszow Voivodeship, 100031, Poland
*Corresponding Author: Xiaorui Zhang. Email: zxr365@126.com
Received: 05 November 2021; Accepted: 24 December 2021
Abstract: Telemedicine plays an important role in Corona Virus Disease 2019 (COVID-19). The virtual surgery simulation system, as a key component in telemedicine, requires to compute in real-time. Therefore, this paper proposes a real-time cutting model based on finite element and order reduction method, which improves the computational speed and ensure the real-time performance. The proposed model uses the finite element model to construct a deformation model of the virtual lung. Meanwhile, a model order reduction method combining proper orthogonal decomposition and Galerkin projection is employed to reduce the amount of deformation computation. In addition, the cutting path is formed according to the collision intersection position of the surgical instrument and the lesion area of the virtual lung. Then, the Bezier curve is adopted to draw the incision outline after the virtual lung has been cut. Finally, the simulation system is set up on the PHANTOM OMNI force haptic feedback device to realize the cutting simulation of the virtual lung. Experimental results show that the proposed model can enhance the real-time performance of telemedicine, reduce the complexity of the cutting simulation and make the incision smoother and more natural.
Keywords: Virtual surgery; cutting model; finite element model; model order reduction; Bezier curve
The outbreak of COVID-19 in China at the end of 2019 has attracted extensive attention in the world. COVID-19 spreads rapidly and can spread from person to person. Once people are exposed to COVID-19, it will cause respiratory tract infection or even pneumonia. At the beginning of 2020, COVID-19 has spread quickly from Wuhan. The epidemic resulted in a serious shortage of medical resources in Wuhan and other hardest-hit areas, which makes it difficult to get a sickbed for patients. Therefore, the Chinese government allocated all kinds of resources, such as food, clothing, medicine, and assembled a large number of medical personnel in Wuhan and other hardest-hit areas. Many other cities in China have also formed a close relationship with Wuhan to provide strong support. However, due to the uneven distribution of medical resources, the aid does not work immediately, and the traditional medical model is facing challenges. So far, more than 100 million people have been diagnosed with COVID-19, which demonstrates that COVID-19 is raging and spreading all over the world. Therefore, in order to reduce the risk of cross-infection, and improve the cure rate of COVID-19, there is the increasingly urgent need for telemedicine.
Telemedicine means doctors can make a comprehensive and elaborative analysis of a patient’s condition without the presence of patients. Therefore, doctors can put forward correct diagnosis and develop scientific treatment schemes. During the treatment process of telemedicine, doctors need to perform force-tactile interactive operations on virtual diseased organs. The key technical difficulty is to reduce the calculation amount while ensuring real-time performance during surgery simulation [1,2]. For the technical difficulty above, researchers at home and abroad have made some achievements. Thieffry et al. [3] proposed a dynamic control method based on the finite element model and a model simplification strategy. Goury et al. [4] put forward an optimized finite element model to simulate the deformation of a soft robot. This model adopts the model order reduction method to reduce computational time for deformation, which improves the calculation efficiency of the model while ensuring the deformation accuracy of the soft robot. Xie et al. [5] combined the traditional nonlinear finite element method and nonlinear Kalman filter to establish an extended Kalman filter, which can be used for dynamic estimation of nonlinear mechanical deformation of biological tissues. This method improves the real-time performance of soft tissue modeling, but does not consider the cutting deformation of the biological tissues. Gao et al. [6] employed a model order reduction method to simulate the blood vessel deformation in vascular interventional surgery. This model utilized CUDA for GPU computing to speed up the simulation rate and enhance the real-time performance. Zhang et al. [7] proposed a fast and accurate vascular tissue simulation model based on point primitive method, it can enhance real-time performance of the training system under the premise of ensuring deformation accuracy, as well as simulate the elasticity of soft tissue.
In addition, when the virtual surgical instrument exerts an external force on the surface of the soft tissue, the soft tissue will be deformed, and then as the external force gradually increases, the amount of deformation of the soft tissue will gradually increase and stress concentration will appear at the deformed area. When the external force exceeds the stress threshold, the deformation reaches the limit, and the soft tissue starts to break from there, thereby forming a cut. When the soft tissue is cut, it will produce an incision on its surface. The traditional method of drawing the surface incision needs to be described by standard equations, such as the cutting model based on B-spline [8] and the cutting model based on non-uniform rational B-spline [9], thereby resulting in a more complicated calculation process. In contrast, Bezier curve, as an approximation spline curve, controls the beginning and end of the entire curve by the first and last control points of the line segment, and determines the curvature of the curve by specifying several control points in the middle of the curve. Therefore, it does not need to be described by standard algebraic equations, and only needs a given number of control points to construct itself [10]. If the Bezier curve is used to draw the incision on surface, it is expected to accurately simulate the complete incision and reduce the complexity of the cutting operation.
To address the issues mentioned above, this paper proposes a new real-time cutting model based on finite element and order reduction. The proposed model simulates the deformation of the virtual lung and the cutting operation in the lesion area. During the process of soft tissue simulation, the finite element model is used to construct model for the virtual lung deformation. Moreover, the model order reduction algorithm, which combines proper orthogonal decomposition and Galerkin projection, is added to the deformation model to reduce the calculation amount. Then, the cutting simulation is operated after the deformation simulation. According to the collision intersection position of the surgical instrument and the lesion area on the virtual lung, the cutting path is formed. Finally, the incision outline is drawn based on the Bezier curve.
The rest part of the paper is organized as follows. Section 2 elaborates on the cutting model. Then, experimental results and analysis to verify the performance of the cutting model are presented and discussed in Section 3. Finally, Section 4 concludes the paper.
The use of telemedicine to treat patients with COVID-19 first needs to model the deformation of the soft tissues of the lungs to facilitate the simulation of subsequent cutting operations [11]. This section first uses the finite element model to simulate soft tissue deformation, and uses the soft tissue deformation solution vector that is solved by the finite element model as a sample. A model reduction method that combines the eigen-orthogonal decomposition with the Galerkin projection is exploited to reduce the full-order finite element model with high dimensions to a reduced-order model with low dimensions. Then, the solution vector is projected to the reduced-order space that is determined by the reduced-order model to obtain the deformation displacement vector of the soft tissue nodes for describing the deformation process.
First, according to the finite element model, the soft tissue is divided into several non-overlapping tetrahedral elements, and the motion behavior of the tetrahedral elements is mechanically analyzed. Assuming that the displacements of the four vertices of a given tetrahedral element are u = [u1, u2, u3, u4]T, respectively, the displacement of any node in the tetrahedral element can be obtained by linear combination of the displacement of the vertices of the element and the corresponding shape function:
where U represents the displacement vector of any node in the tetrahedral element, Φ = [Φ1, Φ2, Φ3, Φ4] represents the shape function matrix, and u represents the displacement matrix of the tetrahedral vertex.
In order to describe the strain produced by the soft tissue under external forces, a linear Cauchy strain matrix is introduced:
where ɛ represents strain and L represents geometric matrix. The stress-strain relationship in the tetrahedral element based on the finite element model:
where σ represents the stress and D represents the elastic coefficient matrix. Then, substitute u, ɛ, and σ into the Eq. (5), which expresses the unit potential energy.
where P represents the internal elastic potential energy of the tetrahedral element, Ps represents the strain energy generated by the tetrahedral element,
where Ω represents the deformation solution domain, b represents the body force,
Then substituting Eqs. (2) and (4) into Eq. (7) to derive the following mechanical equilibrium equation
where
Define
Substituting Eq. (1) into
where
Substituting Eq. (1) into
where
Substituting Eqs. (10)–(12) into the mechanical equilibrium equations, yields Eq. (13).
Since δuT has arbitrary, eliminate this term and simplify Eq. (13) as
where R = Fb + Ft represents the resultant force on the node. The resultant force on the node includes the external force exerted by the virtual surgical instrument and the internal force generated by the soft tissue to resist the external force. The internal force includes elastic force and damping force, and Eq. (14) can be rewritten as a dynamic equation
Among them, M and c respectively represent the mass matrix and damping matrix of the tetrahedral element node, K represents the stiffness matrix of the tetrahedral element, and G represents the external force on the tetrahedral node.
Secondly, according to the model reduction method [4], the dynamic equation shown in Eq. (15) is rewritten into the following dynamic expression:
where M(u) represents the mass matrix, v represents the velocity vector, G(t) represents the external force on the soft tissue, t represents the iteration time, F represents the internal force on the soft tissue, such as damping force, elasticity and stiffness, λ represents the constraint parameter, and HTλ represents the added restraint when the surgical instrument is applied to the surface of the soft tissue.
Discrete the continuous iteration time into an interval
where, h represents the time interval, that is, h = tn+1 − tn, and H represents the time interval matrix. Then use the implicit Euler method [12] to perform numerical calculations on Eqs. (17) and (18) to obtain the following equations:
where
Since the internal force F(u, v) of the soft tissue is a non-linear function of position and velocity, it can be calculated iteratively using Newton-Raphson iteration [13]:
where,
Finally, the solutions of a set of finite element full-order models are obtained. The specific numerical calculation equation is:
Subsequently, a set of deformation displacement solution vectors are obtained by solving Eq. (22), which are formed into a snapshot matrix
where Φ = (ϕ1, ϕ2, …, ϕN) represents the obtained orthogonal basis function based on the eigen-orthogonal decomposition, and αi represents the corresponding coefficient of the basis function ϕi. Next, in order to obtain a low-order approximation of the original model while minimizing the dimensionality of the full-order model, the obtained orthogonal basis function is truncated, and the error function J is defined to select the orthogonal basis function that ultimately characterizes the solution vector of the full-order model.
where, J represents the error function between the solution vector sample and the basis function of the full-order model in the sense of least squares, Λ represents the parameter space,
Finally, the space formed by the orthogonal basis function of the low-order approximation of the original model obtained by Eq. (24), it is used as the function space that is produced by the reduced-order model. In this case, Galerkin projection is used to project the full-order model to the reduced order space. The Galerkin projection is used to solve the deformation displacement solution vector of the reduced-order model. The specific calculation equation is as follows:
where
The cutting path in virtual surgery can be understood as a continuous fold line drawn by the surgical instrument on the surface of the soft tissue in a discrete time. In order to solve the cutting path, this study uses a straight-line model as the basis to simulate the cutting tool, that is, the surgical instrument is simplified into a line-segment at each discrete moment, and the triangular unit is used to simulate the tissue structure. Then the collision detection between the surgical instrument and the soft tissue is transformed into the detection of the intersection of the line-segment and the surface triangle unit, as shown in Fig. 1. Calculate the intersection point of the surgical instrument and the triangle unit plane, connect the discrete points to form a cutting path.
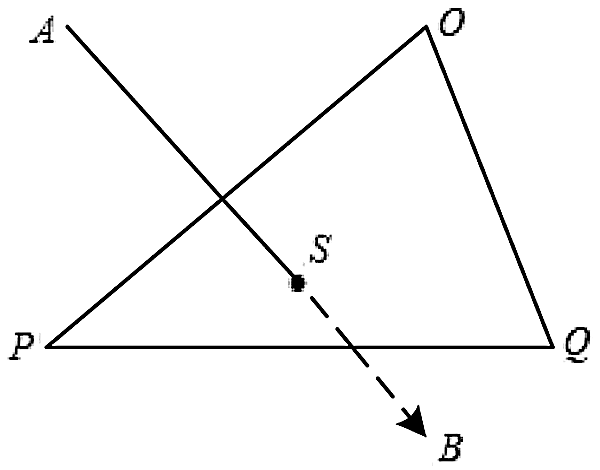
Figure 1: Intersection point of surgical instrument and triangular unit
First, determine the spacial linear equation of the surgical instrument segment at a discrete time. Assuming that the two end-points of the line-segment are A and B, and their position coordinates are uA(xA, yA, zA) and uB(xB, yB, zB), respectively, the spacial straight-line equation of the line segment AB is specifically expressed as follows:
Then the coordinates of any node on the line-segment are:
Secondly, determine the plane equation of the triangular element that intersects with the line-segment of surgical instrument. Assuming that the vertices of a triangular element on the surface of the soft tissue are O, P, and Q, their position coordinates are uO(xO, yO, zO), uP(xP, yP, zP), and uQ(xQ, yQ, zQ), respectively, and its normal vector is N(nx, ny, nz). Let the triangle element plane be:
According to the method of calculating the plane equation, the plane equation can be obtained by the coordinates of the point O and the normal vector N:
Then, combine Eqs. (27)–(29) to obtain the intersection us(xs, ys, zs) between the surgical instrument line-segment and the triangular element plane at a discrete time. The specific calculation equation is as follows:
Finally, connect the discrete intersection points, and the formed line-segment is the desired cutting path.
After the soft tissue is cut, an incision will be made on its surface. In this paper, a Bezier curve is used to draw the surface incision. Bezier curve is a kind of approximation spline curve. It does not need to be described by standard algebraic equations. It can be constructed only by a given number of control points [10]. In other words, it controls the beginning and end of the entire curve by the first and last control points of the line segment, and determines the curvature of the curve by specifying several control points in the middle of the curve. This paper selects the quadratic Bezier curve [10] to draw the surface incision. This method can accurately simulate the complete incision size from the start position to the end position of the cutting path, reduce the complexity of the cutting operation, and improve the smoothness and naturalness of the incision.
First, suppose that the positions of n + 1 control points are Pi = (xi, yi, zi), i = 0, 1, ⋅ ⋅ ⋅ , n, and the position vector P(t) is generated by mixing these control points to describe the path between P0 and Pn that approximates the Bessel polynomial function:
where n represents the degree of the polynomial, which is usually determined by the n + 1 control points of the incision curve, and Bi,n(t) is the Bessel mixing function, also called the Bernstein polynomial of degree n, which is defined as:
Secondly, the quadratic Bezier curve is generated by three control points, and n = 2 is substituted into Eq. (32) to obtain three Bezier mixed functions of the Bezier curve:
Then, the surface incision drawing equation based on the quadratic Bezier curve is obtained:
Finally, the process of drawing the incision based on the quadratic Bezier curve is shown in Fig. 2.
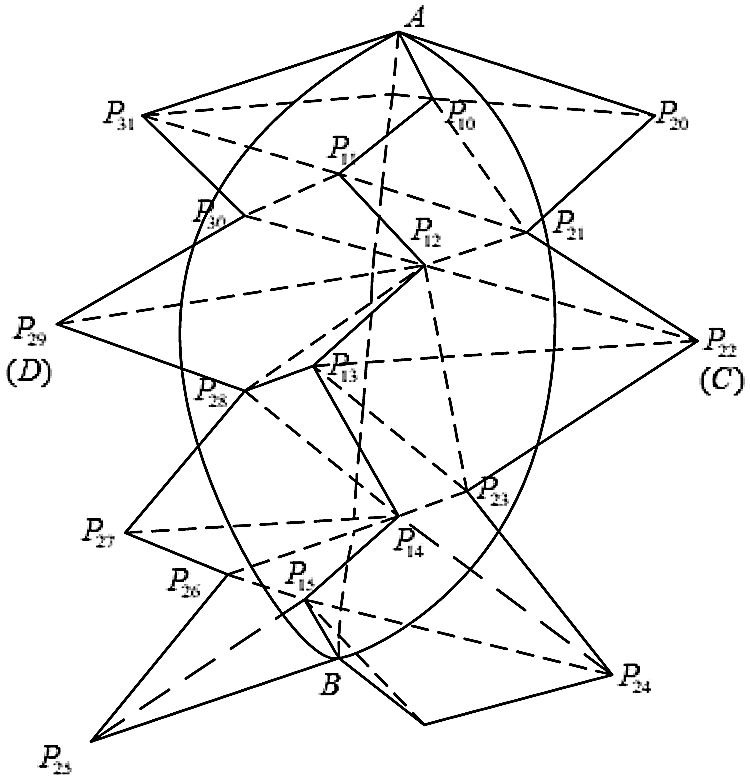
Figure 2: Quadratic Bezier curve incision drawing
Determine the start position A and the end position B of the cutting path, and obtain all the surface nodes that the cutting path passes through, record them as P1 = {P10, P11, P12, P13, P14, P15}, and the P2 = {P20, P21, P22, P23, P24, P25, P26, P27, P28, P29, P30, P31} point set is the nodes around the cutting path, which are distributed on both sides of the cutting path. Select nodes C and D as the control points that specify the curvature of the surface incision, and then draw two quadratic Bezier curves to represent the incision produced by the cutting operation according to the three control points of A, B, and C and the three control points of A, B, and D.
The computer and the force-tactile interaction device PHANTOM OMNI hand controller were used for force-tactile interaction, and the soft tissue force-tactile interaction system was built through the finite element real-time cutting model based on the model reduction method, which realized the deformation and cutting simulation of virtual lung soft tissue under interactive action, the simulation environment is shown in Fig. 3.
Figure 3: Simulation environment
In order to verify the validity and authenticity of the model proposed in this paper, the stress threshold was set to two N, the number of nodes was 1,445, and the number of tetrahedral units was 6,738 to model the virtual lung soft tissue, and the virtual finger was used to apply pressure to the lung soft tissue to simulate the simulation effect of its compression deformation, as shown in Fig. 4. During the simulated cutting experiment, as the deformation continued to increase, when the stress generated inside the soft tissue was greater than two N, the surface of the soft tissue fractured, and the virtual scalpel was used to produce a cutting action on the surface of the soft tissue. And with the change of the contact point between the scalpel and the soft tissue, the cutting marks continued to extend and finally formed the cutting path, as shown in Fig. 5.
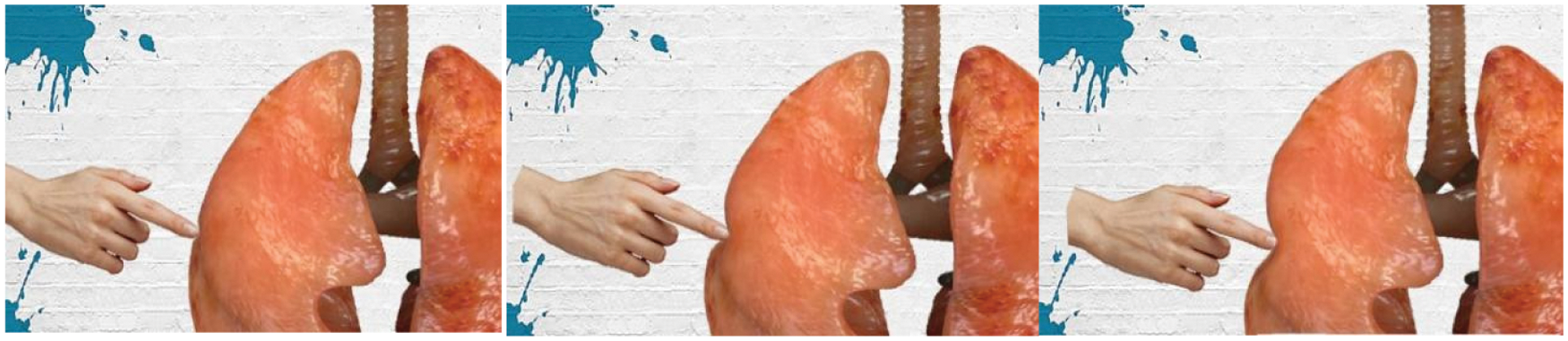
Figure 4: The effect of compression and deformation of the soft tissues of the lungs
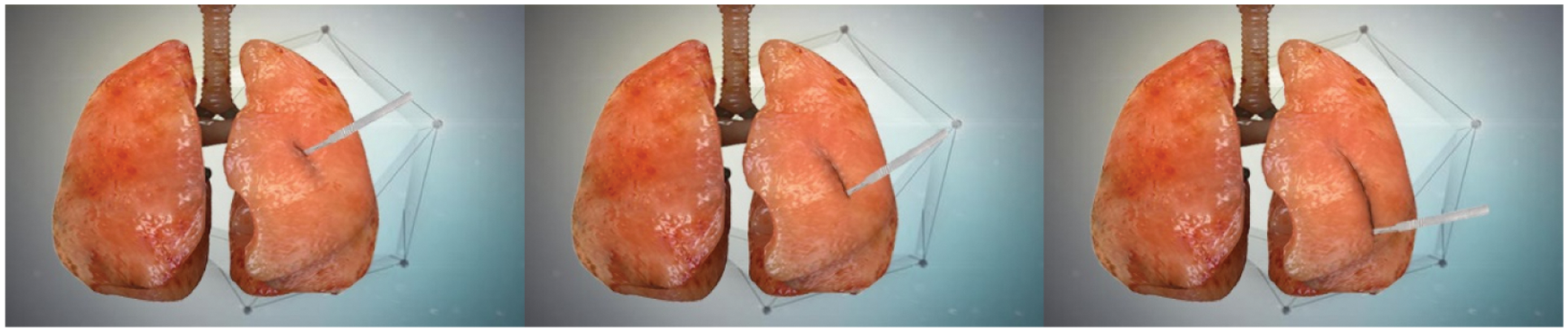
Figure 5: Simulation effect of lung soft tissue cutting
It can be seen from Figs. 4 and 5 that the operator can feel the fluency of the deformation simulation process, the fidelity of the cutting simulation process, and the smoothness and naturalness of the cutting path during the deformation and cutting operations.
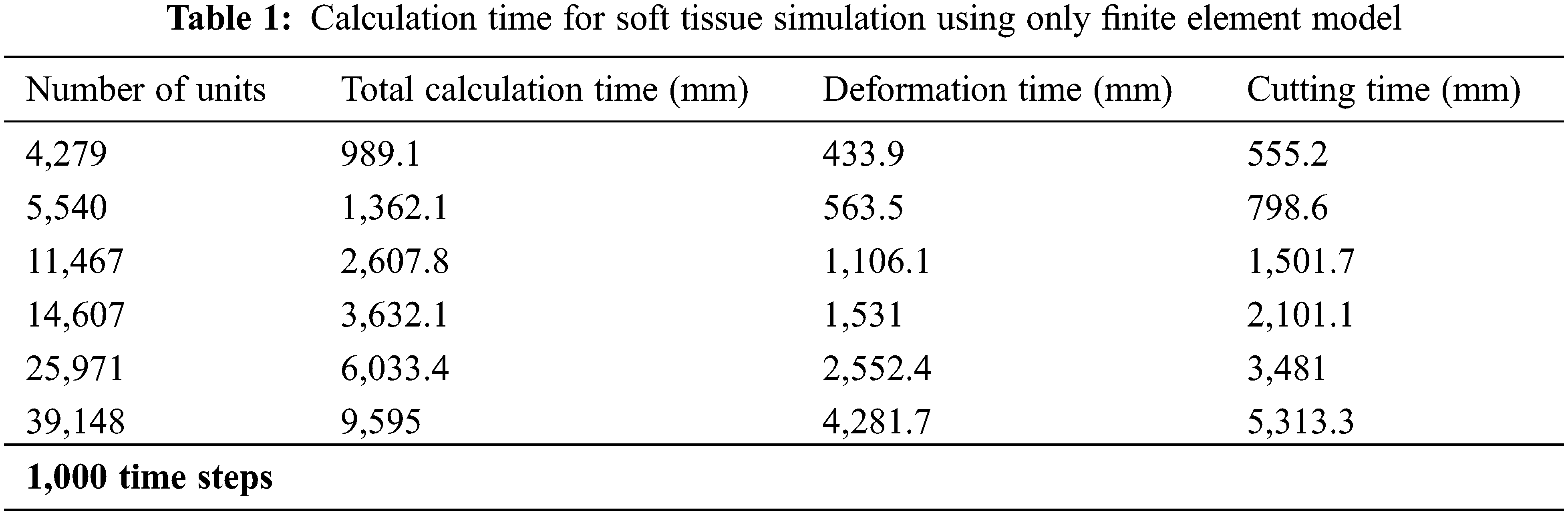
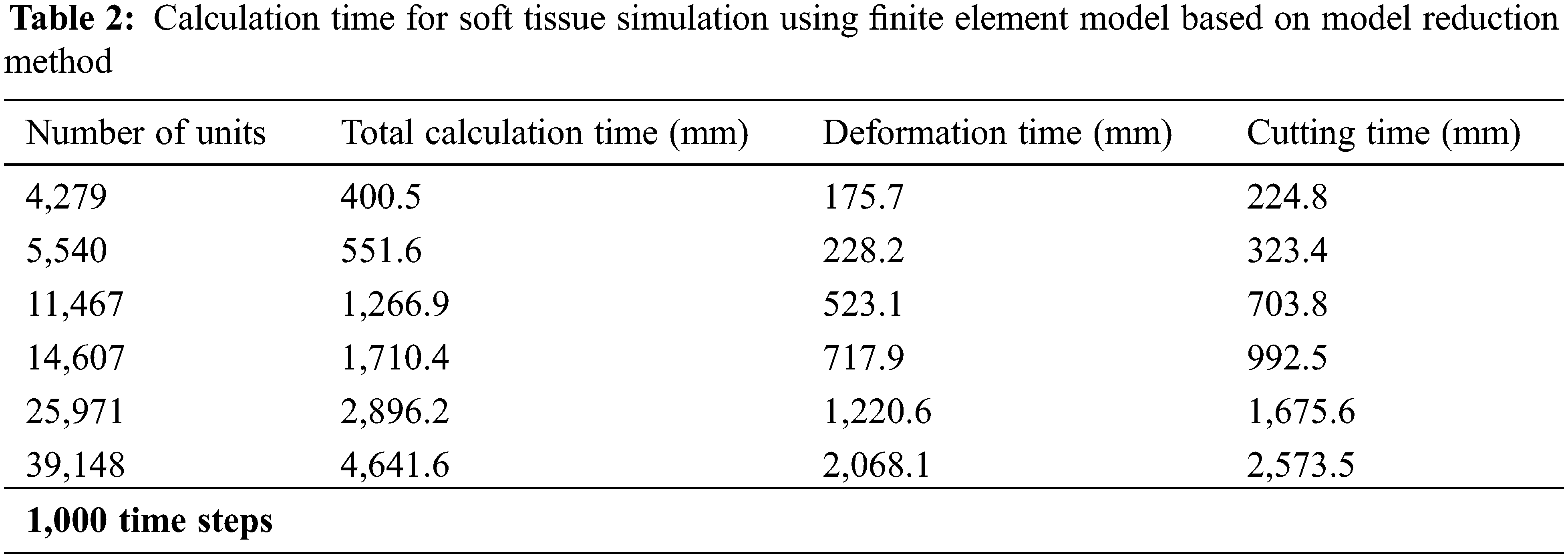
In order to verify the real-time performance of the model proposed in this article, the virtual lung soft tissue was discretized into the following six different types of units: 4,279 units, 5,540 units, 11,467 units, 14,607 units, 25,971 units, and 39,148 units. Then, only the original finite element model and the finite element model based on the model reduction method were used to simulate the deformation and cutting of the lung soft tissue, and the two models were calculated under the time step t = 0.001 s. Tabs. 1 and 2 respectively give the calculation time of soft tissue simulation based on these two different methods, including total calculation time, deformation calculation time and cutting calculation time. It can be seen that the use of the model reduction method can effectively reduce the calculation time of the finite element model during simulating soft tissue deformation and cutting, thereby improving its calculation efficiency and real-time performance of the model.
In order to verify the accuracy of the model proposed in this paper, the standard modeling software ANSYS was used to establish a reference model [16], we compared the standard mean square deviations of the nodal displacements of the three models relative to the reference model under the same force conditions. These three models are the model proposed in this paper, the co-rotating finite element model [17], and the finite element model based on neural network [18]. During the total one second of the soft tissue simulation experiment, 12 nodes were randomly marked on the surface of the virtual lung soft tissue, and the displacement of these marked nodes was measured every 0.1 s. Fig. 6 shows the positions of the 12 nodes marked.
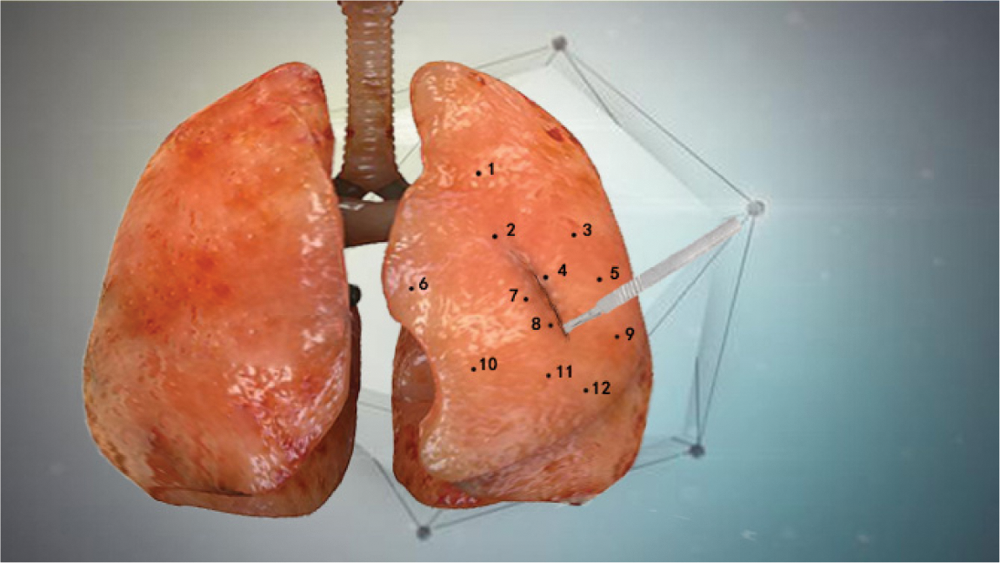
Figure 6: 12 marked node positions
Then, in order to quantitatively reflect the offset degree of the node displacement between the model proposed in this article and the reference model, the mean square error was defined:
where Nm represents the number of marked nodes,

In order to evaluate the effect of the incision after the cutting operation, three models were used to compare the cutting simulation of virtual gastric soft tissue, including the proposed model, the cutting model based on B-spline [8] and the cutting model based on non-uniform rational B-spline [9]. Figs. 7–9 show the overall effect of the soft tissue of the stomach after cutting based on different models. It can be seen that the cutting model based on the Bezier curve proposed in this paper has higher fidelity, and the incision is more real, smooth and natural.

Figure 7: Cutting simulation effect based on the model proposed in this article

Figure 8: Simulation effect based on B-spline cutting model [8]

Figure 9: Simulation effect based on non-uniform rational B-spline cutting model [9]
3.3.4 System Operation Fluency
Stability and fluency are important indicators to measure whether the virtual surgery simulation system is running well, and response time is the most intuitive manifestation of system fluency. We were fortunate to invite 20 doctors from the First Affiliated Hospital of Nanjing Medical University, including six interns, five residents, five deputy chief physicians, and four chief physicians to use the model proposed in this article to perform cutting experiments on virtual lung, stomach and spleen soft tissues. Set the internal stress threshold of the soft tissue to two N. When the stress of the soft tissue exceeds the threshold, a cutting operation is generated and the response time of the system is recorded, as shown in Tab. 4.

Generally speaking, the response time of the virtual surgery simulation system should be within 0.28 s to meet the requirements of operational fluency [19]. As seen from Tab. 4, the average response time for cutting different virtual soft tissue organs is less than 0.28 s. This shows that the system runs smoothly, so that the expert physicians can hardly feel the delay. At the same time, it is proved that the use of model reduction method to reduce the amount of calculation is effective, which improves the real-time performance and user experience of the virtual surgery simulation system. Among them, the failure rate is a manifestation of the stability of the system. Although there were several stalls in multiple interactive operations, the overall experimental process was not terminated. This shows that the virtual surgery simulation system based on the model proposed in this paper is stable.
In order to improve the real-time performance under the premise of keeping the accuracy of finite element model to the maximum extent, this paper proposes a real-time cutting model based on finite element and model reduction method. This model is used to simulate the deformation and cutting operations of the diseased lung area in the virtual surgery simulation system. The deformation solution vector obtained from the finite element solution of the soft tissue is used as a sample, and the model reduction method combining eigen-orthogonal decomposition and Galerkin projection is introduced to reduce the order of the full-order finite element model with high dimension, and then the solution vector is projected to the reduced order space, which can reduce the amount of deformation calculation. In order to reduce the computational complexity of the cutting simulation, this paper uses the line model and the straight-line between triangular units to describe the cutting path formed by the collision between the surgical instrument and the soft tissue of the diseased area, and uses the Bezier curve to draw the surface incision generated after the soft tissue is cut, which makes the incision more natural and smooth. Finally, the effectiveness of the proposed model is proved by a number of experiments in terms of the computational efficiency, accuracy, incision effect and system fluency. In the future, we will pay more attention to the study of deformation and cutting models of other human soft tissues, such as liver tissue.
Funding Statement: This work was supported, in part, by the Natural Science Foundation of Jiangsu Province under Grant Numbers BK20201136, BK20191401; in part, by the National Nature Science Foundation of China under Grant Numbers 61502240, 61502096, 61304205, 61773219; in part, by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]
2. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
3. M. Thieffry, A. Kruszewski, C. Duriez and T. Guerra, “Control design for soft robots based on reduced-order model,” IEEE Robotics and Automation Letters, vol. 4, no. 1, pp. 25–32, 2019. [Google Scholar]
4. O. Goury and C. Duriez, “Fast, generic, and reliable control and simulation of soft robots using model order reduction,” IEEE Transactions on Robotics, vol. 34, no. 6, pp. 1565–1576, 2018. [Google Scholar]
5. H. J. Xie, J. L. Song, Y. M. Zhong, J. K. Li, C. F. Gu et al., “Extended Kalman filter nonlinear finite element method for nonlinear soft tissue deformation,” Computer Methods and Programs in Biomedicine, vol. 200, pp. 105828–105828, 2021. [Google Scholar]
6. B. F. Gao and L. M. Shang, “Research on real-time simulation method of vascular interventional surgery based on model order reduction,” in 2020 IEEE Int. Conf. on Mechatronics and Automation (ICMA), Beijing, China, pp. 1026–1031, 2020. [Google Scholar]
7. X. R. Zhang, H. L. Wu, W. Sun and S. K. Jha, “A fast and accurate vascular tissue simulation model based on point primitive method,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 873–889, 2021. [Google Scholar]
8. G. D. Chen and F. F. Wang, “Medical data point clouds reconstruction algorithm based on tensor product B-spline approximation in virtual surgery,” Journal of Medical and Biological Engineering, vol. 37, no. 2, pp. 162–170, 2017. [Google Scholar]
9. S. Chavalla, T. Hoffmann and D. Juhre, “Simulation of NiTi stent deployment in a realistic patient carotid artery using isogeometric analysis,” in Int. Conf. on Stents: Materials, Mechanics and Manufacturing ICS3M 2019, London, England, pp. 8–15, 2019. [Google Scholar]
10. H. M. Li and X. Y. Lu, “Using n-order Bessel curve to draw the motion trajectory of three-dimensional objects based on unity,” Software, vol. 41, no. 9, pp. 1–4, 2020. [Google Scholar]
11. X. R. Zhang, J. L. Duan, W. Sun, T. Xu and S. K. Jha, “A three-stage cutting simulation system based on mass-spring model,” Computers, Materials & Continua, vol. 127, no. 1, pp. 117–133, 2021. [Google Scholar]
12. X. G. Xiong, W. Chen, S. H. Jin and S. Kamal, “Discrete-time implementation of continuous terminal algorithm with implicit-ruler method,” IEEE Access, vol. 7, pp. 175940–175946, 2019. [Google Scholar]
13. G. C. Wang, H. E. Huang, J. K. Yan, Y. H. Cheng and D. Y. Fu, “An integration-implemented Newton-Raphson iterated algorithm with noise suppression for finding the solution of dynamic Sylvester equation,” IEEE Access, vol. 8, pp. 34492–34499, 2020. [Google Scholar]
14. O. Goury, “Computational time savings in multiscale fracture mechanics using model order reduction,” Ph.D. Dissertation, Dept. Eng., Cardiff University, Cardiff, U.K., 2015. [Google Scholar]
15. K. Carlberg, C. Bou-Mosleh and C. Farhat, “Efficient non-linear model reduction via a least-squares Petrov–Galerkin projection and compressive tensor approximations,” International Journal for Numerical Methods in Engineering, vol. 86, pp. 155–181, 2011. [Google Scholar]
16. J. N. Zhang and S. Chauhan, “Fast computation of soft tissue thermal response under deformation based on fast explicit dynamics finite element algorithm for surgical simulation,” Computer Methods and Programs in Biomedicine, vol. 187, pp. 105244, 2020. [Google Scholar]
17. D. Marinkovic and M. Zehn, “Corotational finite element formulation for virtual-reality based surgery simulators,” Physical Mesomechanics, vol. 21, no. 1, pp. 15–23, 2018. [Google Scholar]
18. R. Q. Fuentes-Aguilar, J. C. Bello-Robles and J. Ruiz-León, “Modeling of soft object deformation using finite element differential neural networks,” IFAC PapersOnLine, vol. 51, no. 13, pp. 474–478, 2018. [Google Scholar]
19. B. J. Li, X. J. Zhang, T. Wei, J. Huang, Y. N. Wei et al., “Research on virtual simulation system of abdominal surgery,” Medical and Medical Equipment, vol. 41, no. 8, pp. 19–24, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |