DOI:10.32604/csse.2022.023991

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.023991 |  |
| Article |
PAPR Reduction of NOMA Using Vandermonde Matrix-Particle Transmission Sequence
1Department of Electronics and Communication Engineering, JECRC University, Jaipur, 303905, India
2Department of Electrical Engineering, JECRC University, Jaipur, 303905, India
3Department of Computer Science and Engineering, JECRC University, Jaipur, 303905, India
4Department of Computer Science, College of Computers and Information Technology, Taif University, 11099, Saudi Arabia
*Corresponding Author: Arun Kumar. Email: arun.kumar1986@live.com
Received: 29 September 2021; Accepted: 30 October 2021
Abstract: Non-Orthogonal Multiple Access (NOMA) is an ideal choice for 5G waveforms due to their characteristics such as high data rate, massive device connectivity, high spectral access, and effective frequency selective fading. Thus, it permits gigantic connectivity. The spectrum overlaps with NOMA, which consents several operators to segment the spectrum at the same frequency. These features make NOMA more suitable for use beyond 5G. Peak to Average Power (PAPR) is a major problem in Multi-Carrier Techniques (MCT) like NOMA and it also degrades the performance of the amplifier. The Partial Transmission Sequence (PTS) is a superior algorithm for moderating the PAPR. However, it also increases the complexity of the structure. The PAPR is reduced in NOMA by multiplying the NOMA signal with optimised phase vectors (P). The phase vectors are generated by using the Vandermonde Matrix (VM). In this work, we proposed a VM-PTS algorithm for the NOMA system, and the number of computations to search the optimal phase vectors for NOMA high PAPR signal is less as compared with existing PTS. The outcomes demonstrate that the performance of the recommended PTS in terms of PAPR, Bit Error Rate (BER), and complexity is better than the conventional PTS (C-PTS).
Keywords: VM-PTS; NOMA; PAPR; 5G
With the increase in the number of demands from users and industries, wireless communication is going through a major change. As the number of traffic and subscribers increases all over the world, there are several challenges, such as fast data transmission, high spectrum utilization, low latency, reliable connection between the devices, and good quality of service. The current technology, such as Fourth Generation (4G), is incapable of meeting the demands. However, the upcoming Fifth Generation (5G) will play a significant role in meeting subscriber and industry demands and providing the services expected. Orthogonal Frequency Division Multiplexing (OFDM) is currently utilised in 4G. However, OFDM is not seen as an ideal contender for 5G due to the several disadvantages of OFDM mentioned in [1]. Consequently, it becomes necessary to explore an alternate radio for 5G. NOMA is considered a deserving candidate for 5G and beyond. The throughput of NOMA is better than that of OFDM [2]. NOMA users access the resources at the same time, simultaneously for both users with poor and good channel conditions. Furthermore, NOMA's overlapping spectrum structure allows users to access bandwidth at the same spectrum while also allowing for device mass connectivity [3]. NOMA and OFDM both are multi-carrier techniques, where the single carrier is divided into several orthogonal sub-carriers. High PAPR is seen as one of the huge constraints for the MCT waveforms [4]. There are several PAPR algorithms [5] implemented for OFDM which efficiently lessen the PAPR of conventional method. However, the structure of NOMA and OFDM differs because conventional PAPR algorithms cannot be applied directly to NOMA. High PAPR reduces the efficiency of an amplifier, which in turn affects the performance of NOMA. C-PTS is effectively utilised in OFDM to decrease the PAPR signal. However, the number of computations required to obtain an optimal phase element is high in C-PTS, which increases the complexity of the framework. In this article, VM-PTS is seen as an attractive algorithm to lower down the PAPR of the NOMA signal. The computational search for optimal phase vectors is low due to the low complexity of VM-PTS, as compared with C-PTS. In [6], the authors introduced a combination of PTS and bacteria foraging algorithms to lower the PAPR of NOMA. The outcome of the work achieved a superior gain than the prevailing algorithms. The authors proposed a hybrid algorithm to reduce the PAPR of 5G waveforms [7]. Initially, PTS is applied to lower down the peak power and circular transformation is used to minimize the complexity of the framework. The projected PTS efficiently increases the PAPR gain of the framework. In [8], PTS is applied to the system. The optimal phase elements are obtained by using the Swarm procedure. The outcome of the work revealed that the proposed algorithm achieved a significant PAPR performance with low computational intricacy. In [9] low complexity, PTS and Selective Mapping (SLM) are applied to the OFDM structure for different transmission schemes. The projected algorithm achieved a better PAPR and BER gain for the BPSK scheme. In [10], the high PAPR of the OFDM signal is reduced by using PTS-based Minimum Trellis Code (MTC). The MTC generates the optimised phase factor multiplied by OFDM sub-blocks to lower the PAPR. The experimental outcomes confirm that the projected system outpaces the C-PTS. In [11], a PTS algorithm based on a double layer phase optimization search is proposed to lower down the PAPR of FBMC. The outcome of the experimental results shows that the proposed PTS gave much superior performance to the C-PTS. In [12], the authors introduced a PTS algorithm based on disjointed sub-blocks. It is seen that the proposed algorithm gave a superior enactment as matched with prevailing algorithms. The contribution of the proposed work is given:
• To the best of our information and literature surveyed, VM-PTS is applied on the NOMA waveform in this proposed work.
• The power saving gain, BER and PAPR performance of NOMA are efficiently enhanced. It is noted that the proposed algorithm achieved a power saving of 20%.
• We compare the performance of C-PTS and VM-PTS for different sub-blocks and phase vectors. It is concluded that the VM-PTS achieved a PAPR gain of 6.7 dB as compared with the C-PTS.
The configuration of NOMA is illustrated in Fig. 1. It represents Superposition Coding (SC) as a part of the transmitter and Successive Interference Cancellation (SIC) as a part of the receiver side [13]. In Fig. 2, it is considered that user 1 nearer to the base station will decode its own signals, considering all the other signals as noise, while user 2 will perform the SIC to eliminate the signals of user-1 and decode its own signal. Here we are considering a two-user scenario where the superposed signal is generated by the base station (BS).
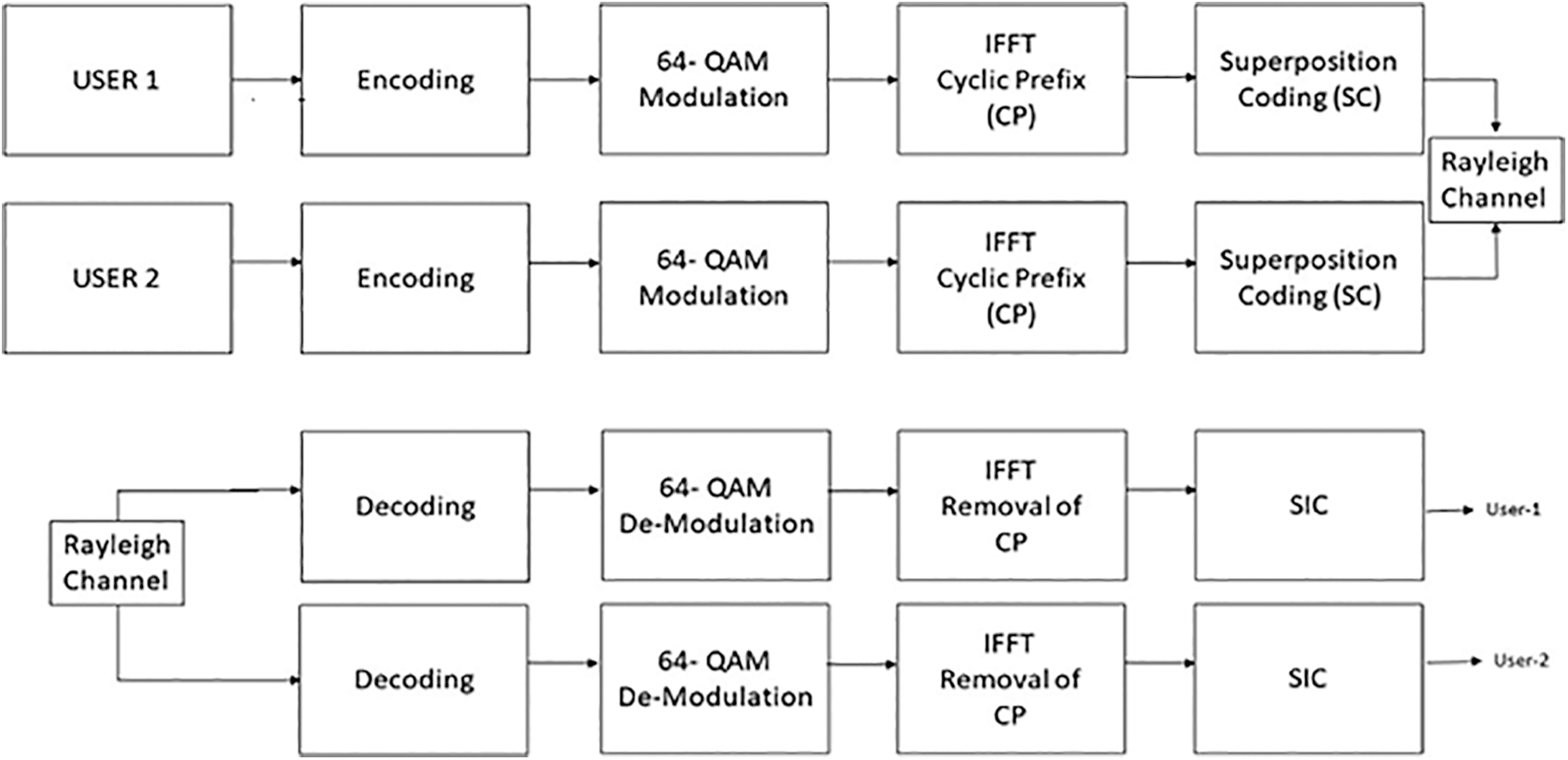
Figure 1: Block diagram of NOMA systems
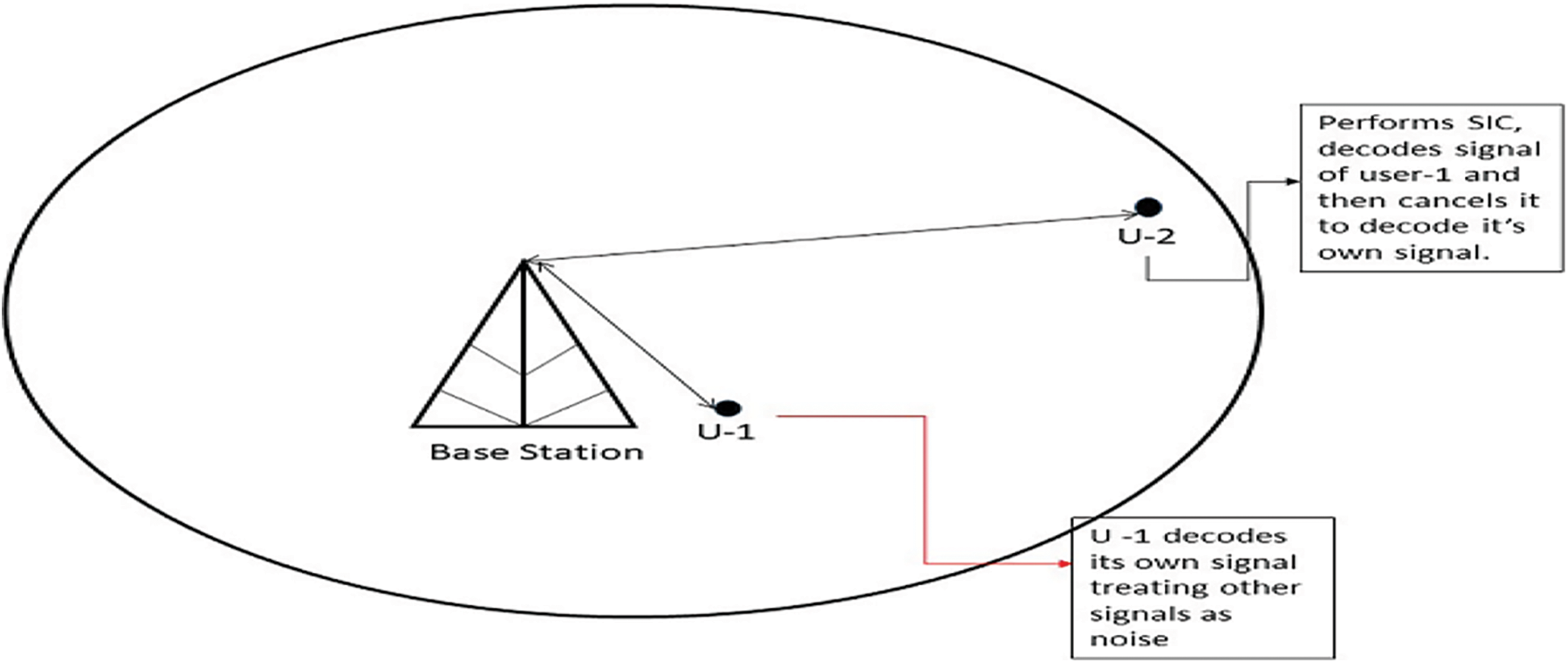
Figure 2: User scenario in NOMA system
The base station gets the complex signal comprising of symbols [14].
Base station first, decodes
Here the condition for outage for user 1 will be defined as
Condition for
The base station will decode the signal using SIC method and then remove the symbol of user 1 for interpreting the user 2.
The SINR for user 2 is given as:
Condition for outage for user 2 will be eliminated by satisfying the desired data rates as under
The system model is shown in Fig. 3. Let us consider a data sub-block of length (N) and sub-carriers (N) given as:
The NOMA symbols are modulated over N sub-carriers represented as [15]:
The estimation of PAPR is given as [16]
where T is defined as symbol duration and E is the expected operator. The length (N) of symbol is mapped into the number of sub-blocks (S) represented as
The primary aim of the VM-PTS is to obtain an optimal phase element
where
where
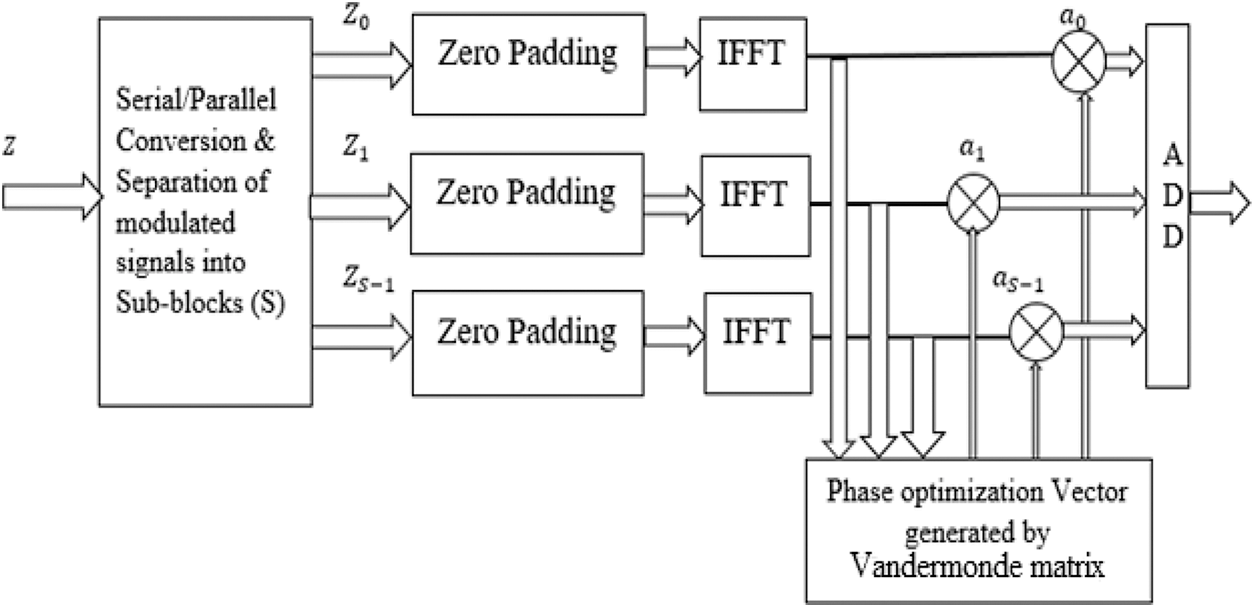
Figure 3: System model
We have analysed the efficiency of VM-PTS by using Matlab-2013. Tab. 1. Indicates the parameters used in the proposed work.

To access the effectiveness of the VM-PTS algorithm on the NOMA waveform, the PAPR curves are plotted for sub-blocks (S = 2) and phase vectors (P = 2, 4, and 8), as shown in Fig. 4. At the Complementary Cumulative Distribution Function (CCDF), the PAPR of original signal deprived of any reduction system is 12.3 dB. C-PTS reduced the PAPR to 10.6 dB and achieved a gain of 1.5 dB. Further, VM-PTS is applied to lower down the PAPR to 9.1 dB (S = 2, P = 2), 7.6 dB (S = 2, P = 4), and 4.8 dB (S = 2, P = 8). It is seen that VM = PTS (S = 2, P = 8) achieved a superior PAPR performance and obtained a gain of 5.8 dB as compared with C-PTS.
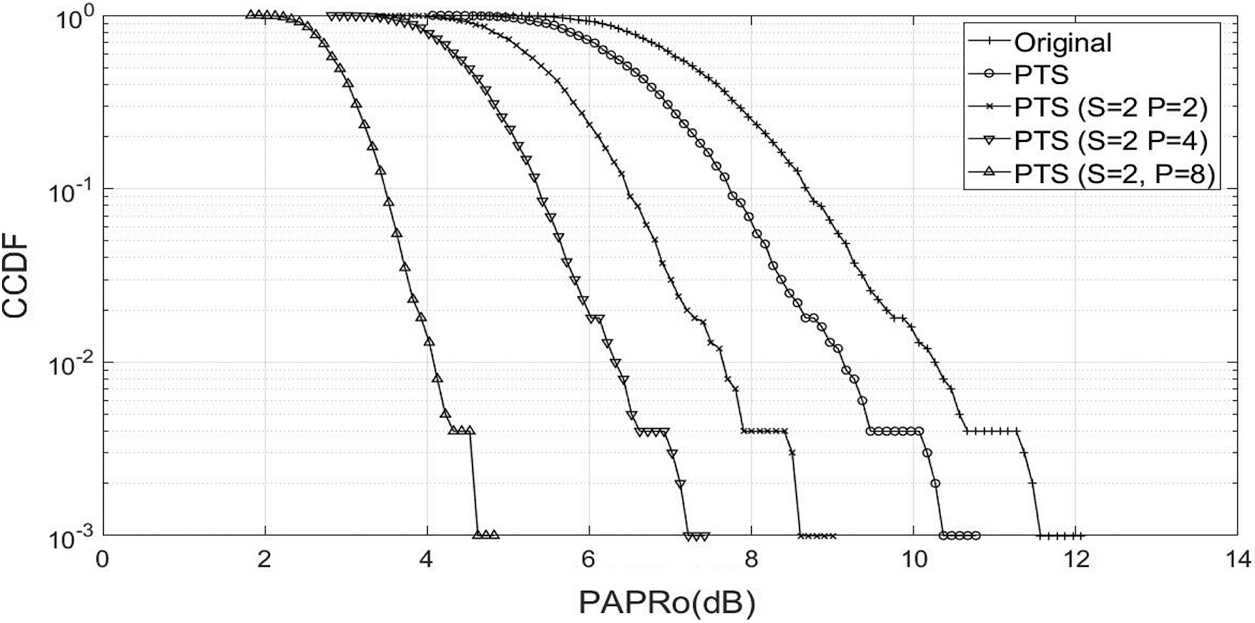
Figure 4: PAPR performance (P = 2 and S = 2, 4 and 8)
The PAPR performance of VM-PTS for NOMA waveform is estimated with sub-blocks (4) and phase vectors (P = 2, 4, and 8), given in Fig. 5. At 10−3, the PAPR of NOMA signal is lower down to 7.8 dB for VM-PTS (S = 4, P = 2), 6.1 dB for VM-PTS (S = 4, P = 4), and 3.9 dB for VM-PTS (S = 4 and P = 8). It can be seen that VM-PTS (S = 4. P = 8) gives superior performance than VM-PTS (S = 2, P = 8). Hence, it is concluded that, by changing the phase vectors and number of sub-blocks, the optimal PAPR reduction is achieved.
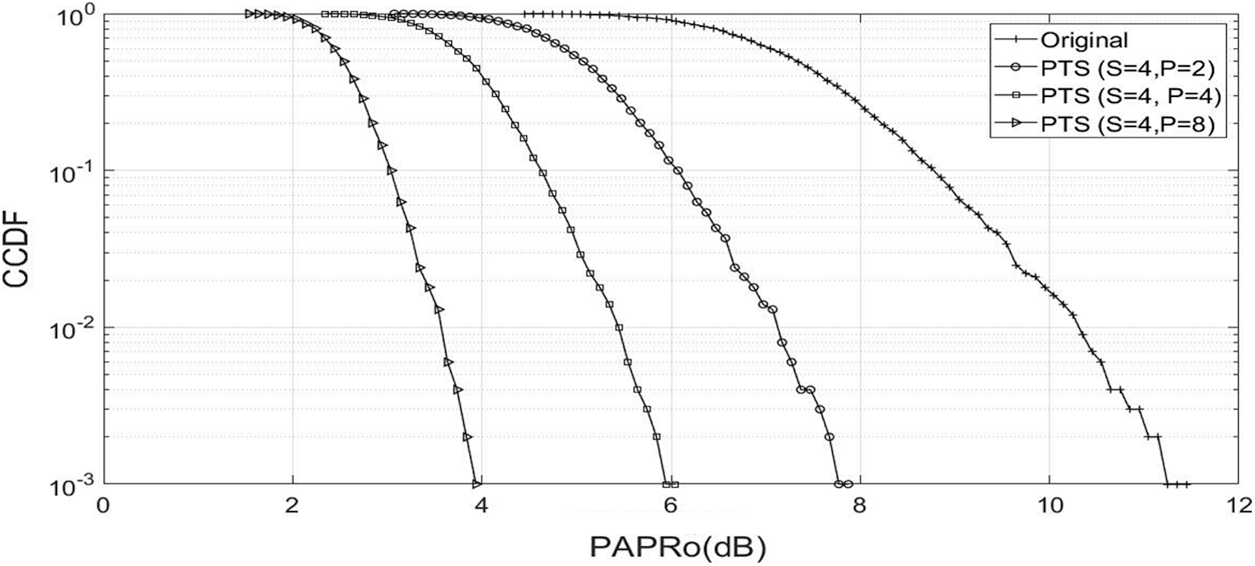
Figure 5: PAPR performance (P = 4 and S = 2, 4 and 8)
To estimate the performance of VM-PTS on the efficiency of a solid-state power amplifier (SSPA), the BER analysis is given in Fig. 6. The BER is effectively reduced for proposed algorithms. The BER of 10−5 is achieved at the SNRs of 4.9, 8.1, and 9.6 dB for VM-PTS (S = 4, P = 8), VM-PTS (S = 2, P = 8), and C-PTS. Hence, it is concluded that the VM-PTS successfully enhanced the performance of SSPA.

Figure 6: BER curves
The effect of the proposed VM-PTS algorithm on power spectral analysis for NOMA is given in Fig. 7. The spectrum leakage of NOMA signal is −250 dB, reduces to −680, −1800, and −2400 dB respectively for PTS, VM-PTS (S = 2 P = 8), and VM-PTS (4 = 2 P = 8).

Figure 7: PSD for PTS method
Tab. 2 shows the power performance of the PAPR reduction algorithm. The power efficiency of an amplifier is enhanced with the utilization of PAPR algorithms. It is seen that VM-PTS achieved 20% of power saving in the present scenario.

Presently, the rollout of an advanced radio framework is in progress. There are several advanced technologies that constitute the 5G cellular classification. In recent years, it has been noted that mobile traffic is increasing exponentially. Hence, a new radio system with an advanced waveform technique is needed. NOMA is regarded as a potential candidate to obtain the desired results as per the current need and demand. In this work, we propose a VM-PTS to down surge the PAPR of NOMA waveform. It is seen that by increasing the sub-blocks (S) and phase vectors (P), the optimal PAPR signal is achieved. We have estimated the BER, PAPR, and power gain performance of VM-PTS on the NOMA waveform. The projected VM-PTS gave a better throughput with low intricacy.
Acknowledgement: We would like to give special thanks to Taif University Research supporting project number (TURSP-2020/10), Taif University, Taif, Saudi Arabia.
Funding Statement: This work was supported by Taif University Researchers Supporting Projects (TURSP). Under number (TURSP-2020/10), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Kumar and M. Gupta, “A review on activities of fifth generation mobile communication system,” Alexandria Engineering Journal, vol. 57, no. 2, pp. 1125–1135, 2018. [Google Scholar]
2. V. Aswathi and A. V. Babu, “Non-orthogonal multiple access in full-duplex-based coordinated direct and relay transmission (CDRT) system: Performance analysis and optimization,” Eurasip Journal of Wireless Communication Network, vol. 2020, no. 1, 2020. https://doi.org/10.1186/s13638-019-1629-4. [Google Scholar]
3. O. Kucur, G. Karabulut Kurt, M. Z. Shakir and I. S. Ansari, “Non orthogonal multiple access for 5G and beyond,” Wireless Communication Mobile Computing, vol. 2018, 2018. https://doi.org/10.1155/2018/1907506. [Google Scholar]
4. A. Kumar, S. Ambigapathy, M. Masud, E. S. Jaha, S. Chakravarty et al., “An efficient hybrid PAPR reduction for 5G NOMA-FBMC waveforms,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2967–2981, 2021. [Google Scholar]
5. B. Ramakrishnan, A. Kumar, S. Chakravarty, M. Masud and M. Baz, “Analysis of FBMC waveform for 5G network based smart hospitals,” Applied Sciences, vol. 11, no. 19, pp. 1410, 2021. [Google Scholar]
6. A. Kumar, M. Gupta, D. N. Le and A. A. Aly, “PTS-PAPR reduction technique for 5G advanced waveforms using BFO algorithm,” Intelligent Automation and Soft Computing, vol. 27, no. 3, pp. 713–722, 2021. [Google Scholar]
7. A. Kumar, “A novel hybrid PAPR reduction technique for NOMA and FBMC system and its impact in power amplifiers,” IETE Journal Research, vol. 5, no. 1, pp. 1–17, 2019. [Google Scholar]
8. M. Hosseinzadeh Aghdam and A. A. Sharifi, “PAPR reduction in OFDM systems: An efficient PTS approach based on particle swarm optimization,” ICT Express, vol. 5, no. 3, pp. 178–181, 2019. [Google Scholar]
9. B. K. Babu, V. C. Kumar and P. M. K. Prasad, “Low complexity PTS and SLM techniques on PAPR reduction in SFBC MIMO-OFDM systems,” Indian Journal of Science and Technology, vol. 10, no. 11, pp. 1–7, 2017. [Google Scholar]
10. H. Chen and K. C. Chung, “A low complexity PTS technique using minimal trellis in OFDM systems,” IEEE Transaction on Vehicular Technology, vol. 67, no. 1, pp. 817–821, 2018. [Google Scholar]
11. Z. He, L. Zhou, Y. Chen and X. Ling, “Low-complexity PTS scheme for PAPR reduction in FBMC-OQAM systems,” IEEE Communication Letter, vol. 22, no. 11, pp. 2322–2325, 2018. [Google Scholar]
12. H. Chen and K. C. Chung, “A PTS Technique with non-disjoint sub-block partitions in M-QAM OFDM systems,” IEEE Transaction on Broadcasting, vol. 64, no. 1, pp. 146–152, 2018. [Google Scholar]
13. A. S. Rajasekaran, M. Vameghestahbanati, M. Farsi, H. Yanikomeroglu and H. Saeedi, “Resource allocation-based PAPR analysis in uplink SCMA-OFDM systems,” IEEE Access, vol. 7, pp. 162803–162817, 2019. [Google Scholar]
14. M. Mounir, Mb M. El, S. Berra, G. S. Gaba and M. Masud, “A novel hybrid precoding-companding technique for peak-to-average power ratio reduction in 5G and beyond,” Sensors, vol. 21, no. 4, pp. 1410, 2021. [Google Scholar]
15. A. Kumar, A. Kumar and G. S. Tomar, “Hardware chip performance of CORDIC based OFDM transceiver for wireless communication,” Computer Systems Science and Engineering, vol. 40, no. 2, pp. 645–659, 2022. [Google Scholar]
16. A. Kumar, A. kumar and A. Devrari, “Hardware chip performance analysis of different FFT architecture,” International Journal of Electronics, vol. 108, no. 7, pp. 1124–1140, 2020. [Google Scholar]
17. S. Sood, A. Singh and A. kumar, “VHDL design of OFDM transreceiver chip using variable FFT,” Singaporean Journal of Scientific Research, vol. 5, no. 2, pp. 47–58, 2013. [Google Scholar]
18. S. Chauhan, R. Miglani, L. Kansal, G. S. Gaba and M. Masud, “Performance analysis and enhancement of free space optical links for developing state-of-the-art smart city framework,” Photonics, vol. 7, no. 4, pp. 1–16, 2021. [Google Scholar]
19. A. K. Bairagi, Md S. Munir, M. Alsenwi, N. H. Tran, S. S. Alshamrani et al., “Coexistence mechanism between eMBB and uRLLC in 5G wireless networks,” IEEE Transactions on Communications, vol. 69, no. 3, pp. 1736–1749, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |