DOI:10.32604/csse.2022.023477

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.023477 |  |
| Article |
A Novel Approach Based on Hybrid Algorithm for Energy Efficient Cluster Head Identification in Wireless Sensor Networks
1Department of Electronics and Communication Engineering, Dr. N.G.P. Institute of Technology, Coimbatore, 641048, India
2Department of Electronics and Communication Engineering, Vignan’s Institute of Information Technology, Duvvada, Visakhapatnam, 530049, India
3Department of Computer Science, College of Computer Science and Information Technology, Jazan University, Jizan, 45142, Kingdom of Saudi Arabia
4Department of Electronics and Communication Engineering, K.Ramakrishnan College of Engineering, Tiruchirappalli, 621112, India
5Department of Computer Science and Engineering, JKK Munirajah College of Technology, Erode, 638506, India
6Department of Electrical and Electronics Engineering, SRM Institute of Science and Technology, Chennai, 603203, India
*Corresponding Author: C. Ram Kumar. Email: proframngp@gmail.com
Received: 09 September 2021; Accepted: 10 October 2021
Abstract: The Wireless Sensor Networks (WSN) is a self-organizing network with random deployment of wireless nodes that connects each other for effective monitoring and data transmission. The clustering technique employed to group the collection of nodes for data transmission and each node is assigned with a cluster head. The major concern with the identification of the cluster head is the consideration of energy consumption and hence this paper proposes an hybrid model which forms an energy efficient cluster head in the Wireless Sensor Network. The proposed model is a hybridization of Glowworm Swarm Optimization (GSO) and Artificial Bee Colony (ABC) algorithm for the better identification of cluster head. The performance of the proposed model is compared with the existing techniques and an energy analysis is performed and is proved to be more efficient than the existing model with normalized energy of 5.35% better value and reduction of time complexity upto 1.46%. Above all, the proposed model is 16% ahead of alive node count when compared with the existing methodologies.
Keywords: Wireless sensor network; cluster; cluster head; hybrid model; glowworm swarm optimization; artificial bee colony algorithm; energy consumption
Wireless Sensor Networks (WSN), the novel technology that stimulates innovative applications like industrial automotive monitoring, system controlling, plant or infrastructure maintenance, etc. The WSN comprises of diminutive and energized sensor nodes that are designated to monitor certain parameters with a pre-defined threshold values, exceeding which the nodes send a note to the control section [1] through other nodes. The nodes were distributed in random manner covering a geographical area to measure the certain events of parameters in the concentrated area. The variations in desired parameters like humidity, sound, pressure, fire, smoke, change in temperature, heat, motion of particles etc. The applications [2] of the WSN extends from basic industrial monitoring system to military purposed border monitoring system measuring and communication different sort of information within a certain coverage area. The sensor node, when deployed randomly occupies random position to which the relation among the sensor node position is based on Poisson distribution. The clustering is a technological manner of separating a huge network area into small cells so that to divide the workload of the network can be shared among the sensor nodes equally. Such cluster is assigned with a head known as Cluster Head (CH) [3] which is assigned with node head responsibility of routing the data efficiently employing effective routing table algorithms. The Cluster Head itself is not a special node, but one among the deployed sensor nodes which involves complex process to identify and designate a proper node with Cluster Head responsibilities. The cluster head nomination is designated based on least iterations to obtain efficient performance of data transmission and coordinating other nodes. The performance of the WSN is highly considered on the selection of Cluster Head with an optimized ability of the node to balance the entire cell with an optimized utilization of energy by the nodes. The optimization process of identifying an appropriate node as Cluster Head needs metaheuristic algorithms that depends on node variance value, Non-periodic sampled cluster formation, grid based cluster formation, Fuzzy based cluster head formation, zonal based approach, even utilization of advanced optimization algorithm like Particle Swarm Optimization (PSO), Artificial Bee Colony (ABC) algorithm, Genetic Algorithm (GA), etc. The data transfer from the cluster node to the Cluster Head via optimized shortest path with minimal energy consumption is the biggest challenge in the WSN. The supporting parameters to be considered in the WSN is not restricted to the better designation of Cluster Head, Optimized energy consumption and best shortest path to transfer the data but also extends to the delay and distance to transfer of data from the cluster node or base station to the cluster Head. These aforementioned parameters shall be effectively achieved on optimal selection of the Cluster Head in the Wireless Sensor Network.
The evolution of various optimization algorithms address certain WSN concern but however these algorithms fall short of achieving better performance in exploitation phase, convergence rate, and incapable of addressing multi task of achieving reduced delay in transmitting data in shortest path with reduced energy consumption. This paper proposes a new hybrid algorithm comprised with Glowworm Swarm Optimization (GSO) [4] and Artificial Bee Colony (ABC) [5] for optimal selection and designation of Cluster Head in the WSN.
This paper proceeds further in such a way that Section 2 narrates the related work in the domain of Cluster Head designation, while Section 3 explains the proposed hybrid model followed by the analysis of performance parameters in the Section 4. The results of the proposed model are discussed in Section 5 with a conclusion in Section 6.
Numerous novel algorithms were proposed by various researchers addressing the better optimal cluster head selection mechanism. Some of the notable research work related to the proposed model listed here for reference and for further improvements from those algorithms for better construction of novel hybrid algorithm for optimal cluster head selection process.
In 2020, Baradaran et al. [6], proposed an high quality clustering algorithm for reducing the consumption of energy by the member nodes in the WSN clusters. The notable features of this algorithm are the employment of Fuzzy logic for the Cluster Head selection in the WSN to achieve the crown of reliability, reduced error rate in the WSN. The proposed model also enhances the lifetime of the WSN nodes and its corresponding network.
In 2020, Khan et al. [7], designed an energy efficient model using adaptive and dynamic scheduling in Wireless Sensor Networks. The proposed model provides extensive sensing to maximize the sensor node life time and to optimize the consumption of energy by the member node in a cluster. The analysis of the designed model increases the lifetime of the sensor nodes by 9.65%.
In 2020, Malisetti et al. [8], proposed the analysis of Butterfly Optimization algorithm for the selection of Cluster Head in Wireless Sensor Networks. The author proposed an algorithm named Quasi Oppositional Butterfly Optimization Algorithm (QOBOA) for the optimization of energy consumption by the sensor nodes and for better designation of cluster head in the wireless sensor networks.
In 2019, Stephanakis et al. [9], designed a Subspace clustering using Expectation Maximization Gaussian Mixture Models for an efficient process of designating the cluster head in the Wireless Sensor Networks. The author designed and compared with the previous algorithms to prove that the designated model is an efficient algorithm and performs well when compared with the conventional algorithms.
In 2017, Piquer et al. [10] proposed a multi-objective clustering algorithm to improve the performance of the cluster head in effective usage of energy and for optimal routing mechanism. The proposed model ensures a better scalable parameter and optimum memory usage. In 2020, Fakhet et al. [11] proposed a K means clustering algorithm for Wireless Sensor Networks (WSN) to control the energy utilization by the member nodes in the network.
The author proposed Optimal K means clustering (OK clustering) and the output has been analyzed and it achieves a uniform distribution in the spatial domain of the Cluster Head. This OK clustering algorithm provides an optimal utilization of energy and demonstrates its entire potentials.
The Wireless Sensor Network comprises of plenty of sensor nodes and these nodes transfer the data to the sink nodes through effective shortest path routing mechanism. This data transmission consumes more energy leads to lifetime [12] reduction of the sensor nodes. The huge consumption of energy is due to long distance transmission of data by the sensor nodes which reduce the expected level of sensor’s lifetime [13]. To overcome this concern, one node among the cluster of sensor node is designated with cluster head for effective routing and energy consumption during the data communication. Consider a wireless sensor network with nc number of cluster and the cluster head of each cluster is mentioned as CHi. where the range of i tends from 1 to nc. Any node in any cluster is represented as Nij where the value of “i” tends from 1, 2,…M while j ranges from 1, 2,…N. While designating a sensor node as cluster head, the distance between other nodes to the cluster head plays a vital role along with the delay is transmission of packets and energy consumption for the data transfer. The cluster head CHi transfers the data from the cluster to the base station while other nodes cannot experience this privilege of communicating with the base station. Along with these predominant parameters, the Quality of Service (QoS) [14] is also considered during the cluster head designation so that to transfer the data effectively with reduced or no delay. The proposed model is a hybrid technology that considers the parameters aforementioned to analyze the effectiveness of the designed hybrid model.
The group of clusters with cluster head at each cluster communicating the information collected from the member node to the sink which is referred to as base station. The intention function of the proposed model is depicted in Eq. (1),
IF=αp2+(1−α);0<α<1 (1)
The “α” is a constant and the value ranges from 0 to 1. In our proposed model, the value of α is chosen at the average of 0.5. The featured parameters of remoteness between the nodes and the cluster head, energy consumption during the data transfer and the delay in delivery of packets are to be considered during the designation of cluster head in the wireless sensor network. In that case, the Eq. (2) illustrates the way in which these predominant parameters contribution in cluster head designation.
p1=β1 ∗ pdistancei+β2 ∗ penergyi+β3 ∗ pdelayi (2)
where β1, β2, and β3 are the coefficients of the parameters distance, energy consumption and delay in delivery of packets respectively. In addition to the remoteness between the sensor nodes and the cluster head, the distance between the base station and designated cluster head must be low for optimal power consumption for the data transmission. The Eq. (3) expresses the mathematical relation between the distance between the cluster head to the base station and the energy consumption for the data transmission.
p2=1ncnc∑x=1∥Dx−B∥ (3)
where, the Dx is the distance between the distance between the number of cluster head and the base station. The energy consumed by the sensor node to communication data to the cluster head and the cluster head to the base station is mathematically expressed in Eq. (4).
penergy=penergy(q)penergy(p) (4)
The penergy(q) is the optimal energy consumed by the sensor node in the cluster q. To express mathematically the energy consumption of any node, the factors of energy consumption by the sensor node to transmit data to the cluster head and the cluster head to the base station is considered as a whole and is mathematically expressed in Eq. (5).
penergy(q)=EN(x)+N∑j=1EN(j) (5)
The EN (x) is the energy consumed by the cluster head to transfer the data to the base station whereas the EN(j) is the optimal energy consumed by the sensor nodes of cluster j to transfer data to the cluster head CHj. The second predominant parameter in the cluster head designation is the distance between the member nodes and the cluster head along with the distance between the cluster head and the base station. The aforementioned distance can be mathematically expressed in the Eq. (6).
pdistance=pdistance(q)pdistance(p) (6)
The optimal distance among the common member nodes to the cluster head and the distance between the cluster head to the positioned base station is expressed in Eq. (7).
pdistance(q)=M∑i=1N∑j=1∥Di−CHj∥+∥CHj−BS∥ (7)
The third notable parameter in the cluster head designation is the time delay produced during the data transmission among the cluster node to the cluster head and between the cluster head to the base station. The delay factor directly depends on the number of member nodes in the cluster and hence the cluster with reduced number of nodes produce reduced amount of delay in the data transmission. The delay can be mathematically expressed as in Eq. (8) which depends on the cluster head and the total number of nodes in the corresponding cluster.
fDelay=∑Nj−1Max(CHj)L (8)
The quality of service is the additional parameter that to be considered during the analysis of the performance of the Wireless Sensor Network (WSN). The aforementioned factors of distance, consumption of energy and the delay must be reduced optimally to obtain an high value of QoS. The Fig. 1 narrates the steps involved in the designation of Cluster Head among the group of Sensors in the Wireless Sensor Network. From the flow chart, each node is examined for the identification of Eigen value representing the distance for data communication with other member nodes and the base station. The member node with minimal Eigen value is designated as the Cluster Head. The iteration extends from i = 1, 2…n, where the maximum value of n depends on the population of node in the cluster. On performing n counts of iterations, the iterative least Eigen Value is identified as the Cluster Head of the Corresponding Cluster and leads the communication process.

Figure 1: Flow chart for cluster head identification process
3.1 Glowworm Swarm Optimization (GSO) Algorithm for Optimal Cluster Head Selection
The Glowworm Swarm Optimization (GSO) algorithm [15] is designed by the inspiration of glowworms that were distributed in random manner based on Poisson distribution. This algorithm holds good in identifying solutions for several similar and dissimilar concerns through concurrent search method. The glowworms (lighting worms) possess certain quantity of luminescence referred to as luciferin, depends on which the intensity of the luminescence varies. The glowworm identifies its neighbor based on the luciferin value and selects one as neighbor that should possess luciferin value less than the luciferin value of its own. Similar concept is utilized in the GSO algorithm [16,17] to identify the neighbor node in the cluster with minimal distance when compared to its own distance value. The luciferin value of the cluster node is formulated and is updated as depicted in Eq. (9).
Li(t)=(1−σ)Li(t−1)+φF(pi(t)) (9)
where, Li(t) is the present luciferin value of the glowworm while Li(t − 1) is the previous luciferin value. The luciferin is a time dependent factor and its decaying factor is represented as σ, provided the value of the decaying factor must be between 0 to 1. The simplified process involved in the Glowworm Swarm Optimization (GSO) algorithm is illustrated in Fig. 2.

Figure 2: Flow chart for glowworm swarm optimization algorithm
From the Fig. 2, the GSO algorithm [18] is a four step process comprising initialization of process by predefining the parameters to consider, Updation of luciferin value of each member node of the cluster followed by the movement of cluster members within the cluster and ends up with the update of neighborhood range. In the initialization process, the sensor nodes are randomly distributed based on Poisonn distribution and the Luciferin updating is the process related to the suitability of location of the member sensors. The high value of intensity makes a best position of the cluster nodes while the contrary poor intensity value is considered as the worst or weaker position. The third phase is the movement phase to identify its neighbor and to follow it. The neighbor nodes need to satisfy certain needs like the glowworm acts as the decisive domain of the entire cluster followed by it makes a movement toward neighbor with a probability Pg(t).
Pg(t)=Uw(t)−Ug(t)∑Um(t)−Ug(t) (10)
The final phase of the GSO algorithm is the neighborhood range update process that to update the exact position of the glowworm with an updated neighborhood value.
3.2 Artificial Bee Colony (ABC) Algorithm
The Artificial Bee Colony (ABC) algorithm [19] is a meta-heuristic algorithm to solve complex problems and is used to determine the optimal distance between any two nodes which is a major function in designating a node as Cluster Head [20]. The algorithm was designed based on the inspiration of the honey bees and is composed of three components namely: employed foraging bees, unemployed foraging bees and food source bees. The generic scheme of the ABC algorithm [21] is composed of four phases inclusive of initialization phase, Employed bee phase, Onlooker bee phase and Scout bee phase.
The ABC algorithm is well suited for determining solutions for the complex problems. In the initialization phase, the vectors of the food sources are initialized by the scout bees and each food source is identified as a solution vector for the optimization problem. In the employed bee phase, each bee tries to identify new food sources and determines the nearest food source. This phase is applicable for our proposed model to determine the nearest member node in a cluster of sensors. The onlooker bees monitors the actions of the employee bees and returns the best optimal distance value to designate it as the cluster head and abandon all other food sources.
Pseudocode for ABC algorithm

The pseudocode for the Artificial Bee Colony algorithm to identify the best neighborhood which holds predominant procedure to designate a node as Cluster Head in the Wireless Sensor Network.
3.3 Proposed Hybrid Model for Cluster Head Selection
This section explains the proposed hybrid model for cluster head selection in the wireless sensor network. The proposed model is a hybridization version of GSO algorithm [22] and ABC algorithm to determine the least distance between the member node and the cluster head which will reduce the transmission delay and increase the Quality of Service. This hybridization reduces the computational speed and it overcomes the disadvantages of individual algorithms of GSO and ABC algorithm. The end result of hybridization is the generation of GSABC algorithm which yields better cluster head designation in the wireless sensor network with minimal distance between the nodes and base station, reduced transmission delay and reduced energy consumption during the data transmission. The proposed model is classified into two phases namely deployment phase, set up phase, steady state phase. In the deployment phase, the sensor nodes were deployed randomly based on Poison distribution and a group of sensor nodes were accumulated as cluster group. The set up phase involves, dividing into sub regions and the designation of cluster head using Artificial Bee Colony Algorithm [23]. The steady state phase involves shortest path using Glowworm Swarm Optimization algorithm. Certain assumption has been made before deploying and establishing a wireless sensor network. The assumptions are:
• N number of nodes were distributed uniformly in an area of 200 × 200 m2.
• Each node is assigned with an unique ID.
• Nodes located in certain geographical area are grouped as a cluster of nodes
• Nodes were location centric.
• Sensors determine the approximate distance to transmit data to the neighborhood sensor.
The proposed algorithm address multiple objectives related to distance, energy consumption, delay and improvising the QoS [24].
Pseudocode for ABC algorithm

The Artificial Bee Colony Algorithm (ABC) has finite count of optimal solutions and each solution is termed as Sij is mathematically expressed as in Eq. (11).
Sij=Sjmin+rand[0,1](Sjmax−Sjmin) (11)
The fitness of the obtained solution if found to be better than the fitness of the old solution, then the old solution is replaced with the new solution. The fitness of the solution can be computed mathematically using Eq. (12) as expressed below.
Fitness:f(x)={11+f(x);f(x)>01+|f(x)|;f(x)<0⋯ (12)
The proposed hybrid model is considered to be one of the better models for designation of Cluster head in wireless sensor network and is analyzed based on the following environmental setting.
Environmental setting:
Population of colony size (SN): 50
Population of employee bee (SN/2): 25
Maximum number of cycles: 10000
Runtime: 100
At the end of data transmission, the probability of dead nodes population is computed mathematically using Eq. (13).
PDN=({e1>eth}&{e2>eth}&…{en>eth}) (13)
The movement of the glowworm phase in the proposed hybrid model is computed as
xi(t+1)=xi(t)+S(xi−xj)/‖ (14)
The data transmission from node to cluster head and from cluster head to the base station is based on uniform distribution model, and distributes the data in uniform manner. All nodes were transmitting data and the lifetime of the sensor node depends on the fitness value of each nodes. The cluster head is responsible for the data transmission from cluster to the base station. Aiming at saving the energy during data transmission, the cluster head accumulates the data received from all the member nodes and is transmitted cumulatively to the base station such that to preserve the energy consumption. The energy of the node is measured and is compared with the threshold value of the node energy, when the node energy is less than the threshold value, the node is classified under good category of energy consumption whereas, the energy greater than the threshold value, consumed huge energy during data transmission.
This section analyzes the results yield by the proposed hybrid model and the results were compared with the conventional algorithm of GSO and ABC algorithm individually. The analysis extends from quantitative analysis [25]; cluster head distance, assessment of transmission delay, time complexity analysis, and normalized energy analysis. The simulation of developed hybrid model is executed in the MATLAB and the nodes were distributed randomly in the geographical area of 200 × 200 m2 with base station positioned at the center of the area. The parameters used for simulating the developed hybrid model is listed in the Tab. 1.
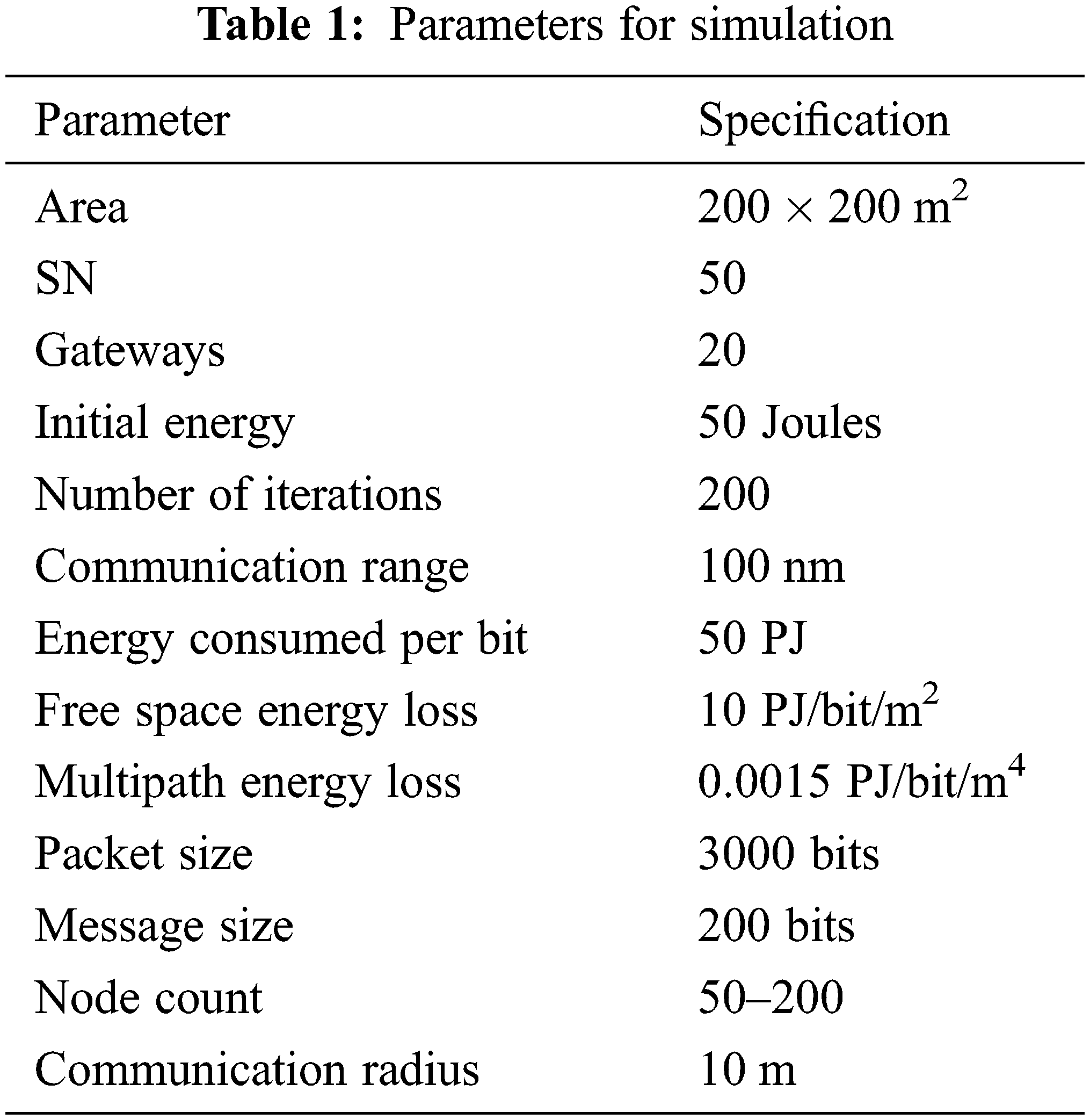
The Tab. 2 is listed with the analysis of the hybrid model and is identified that the developed hybrid model has attained high level of energy on comparing with other models. The normalized energy of the proposed hybrid model is 5.35% and is better when compared to the other models.
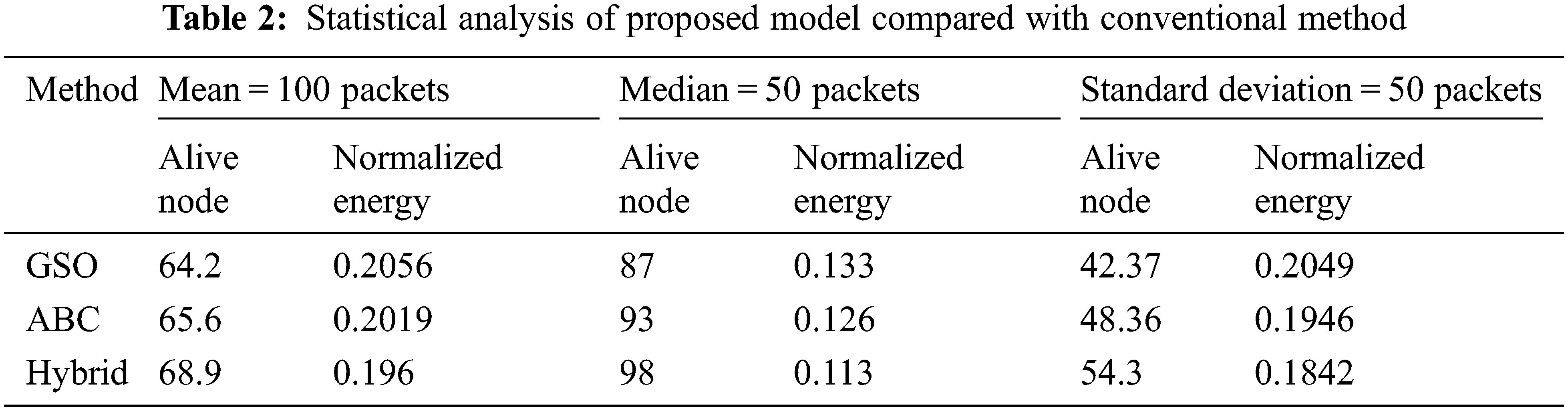
The Fig. 3 shows the graphical analysis of the conventional methods and the proposed hybrid model, in which the alive nodes in the hybrid model is comparatively more than the conventional methods whereas the hybrid model consumes reduced optimal power than the other conventional methods.

Figure 3: Statistical analysis of proposed hybrid model
The iteration process is performed to identify the distance between the cluster heads of various clusters in the Wireless Sensor Network. The measured distance between the various cluster heads in tabulated in the Tab. 3 and the analysis is performed based on the best case, worst case, mean, median and standard deviation.
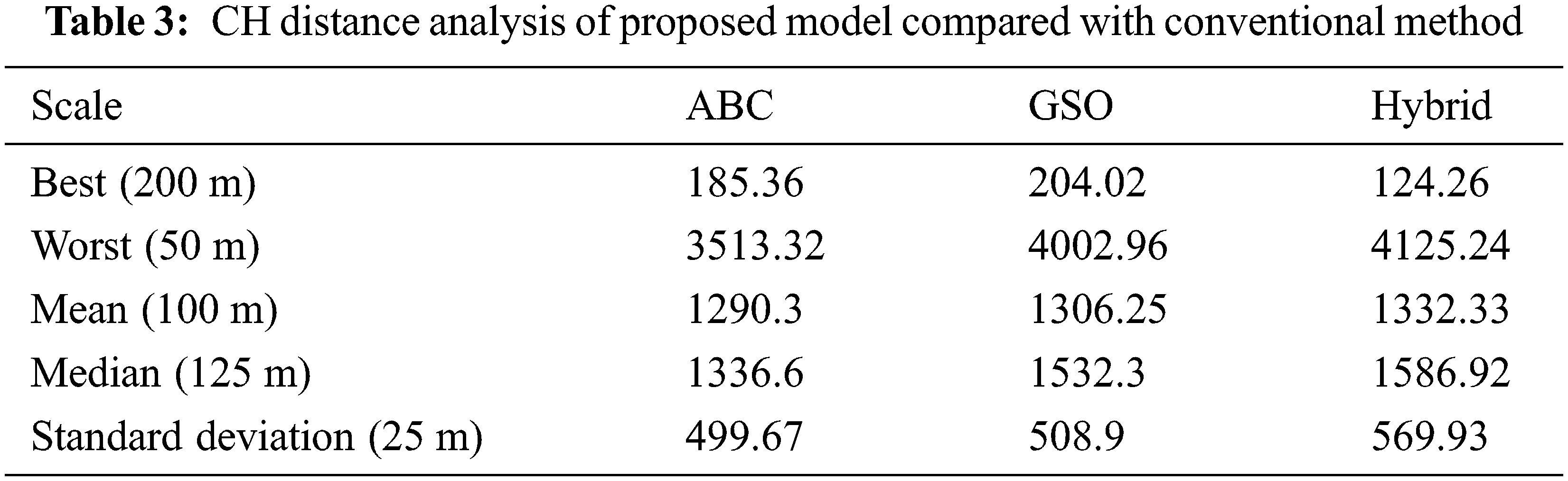
From the table, the hybrid model is efficient in the cluster head distance between all other cluster head of various clusters in the Wireless Sensor Network.
4.3 Assessment of Transmission Delay
The analysis of transmission delay for the proposed algorithm and the comparison with the conventional algorithms is performed and the observations were listed in Tab. 4. An average of 3000 rounds has been taken for the analysis of the proposed model. The analysis results in reduced transmission delay for the proposed model when compared to the conventional methods. In round 1, the transmission delay for the conventional methods are better than the proposed model whereas, on increasing the rounds from 1 to 1000, the transmission delay in the proposed model reduces further better than the conventional methods. At the end of 3000 rounds, the transmission delay of the proposed model is 0.526 whereas for the conventional methods, the delay is measured to be 0.826 and 0.863 which is proven to be better than the conventional algorithms.
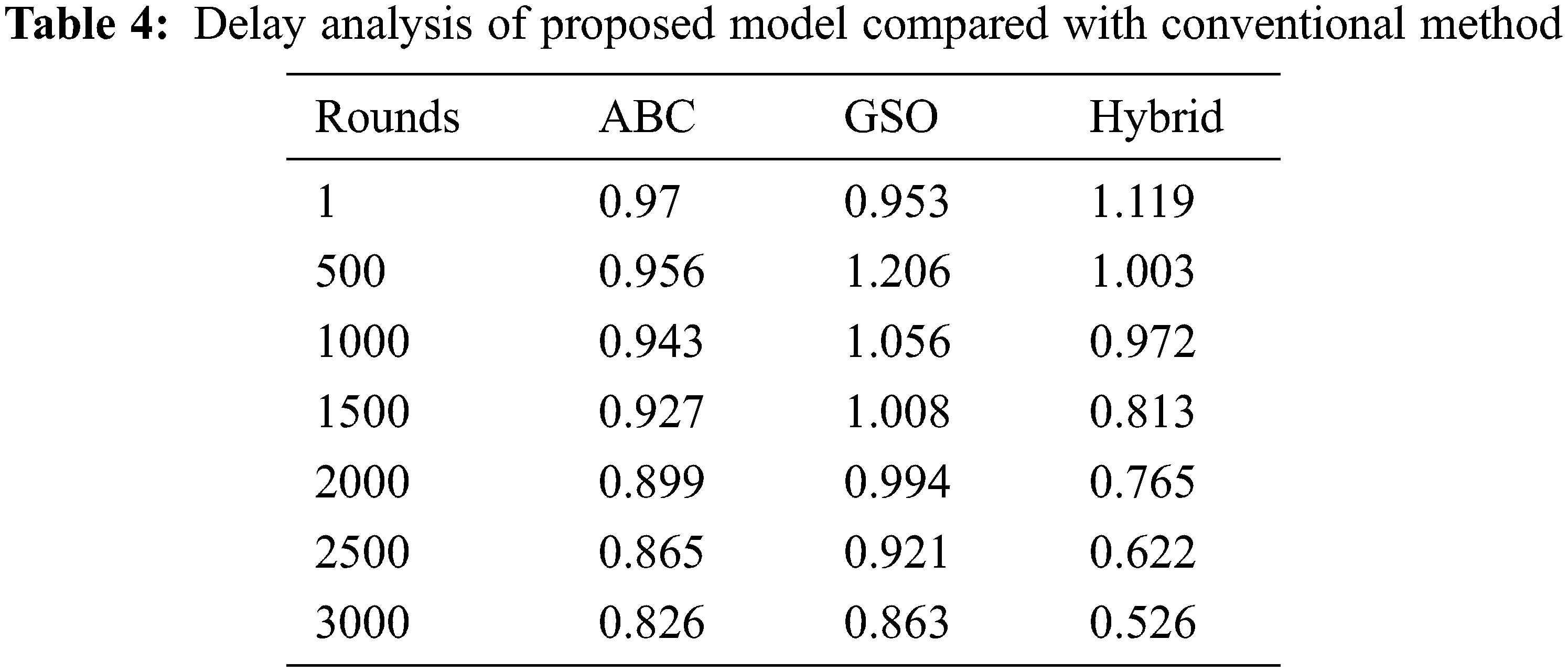
From the analysis of the transmission delay, as the number of increases the transmission delay in the proposed model decreases which is more efficient that the conventional algorithms.
4.4 Analysis of Time Complexity
The time complexity analysis for the proposed model is performed on five scales of best, worst, mean, median and standard deviation. The analysis results were tabulated in Tab. 5. The analysis results exemplify that the proposed model is 1.46% better than the existing conventional algorithms.
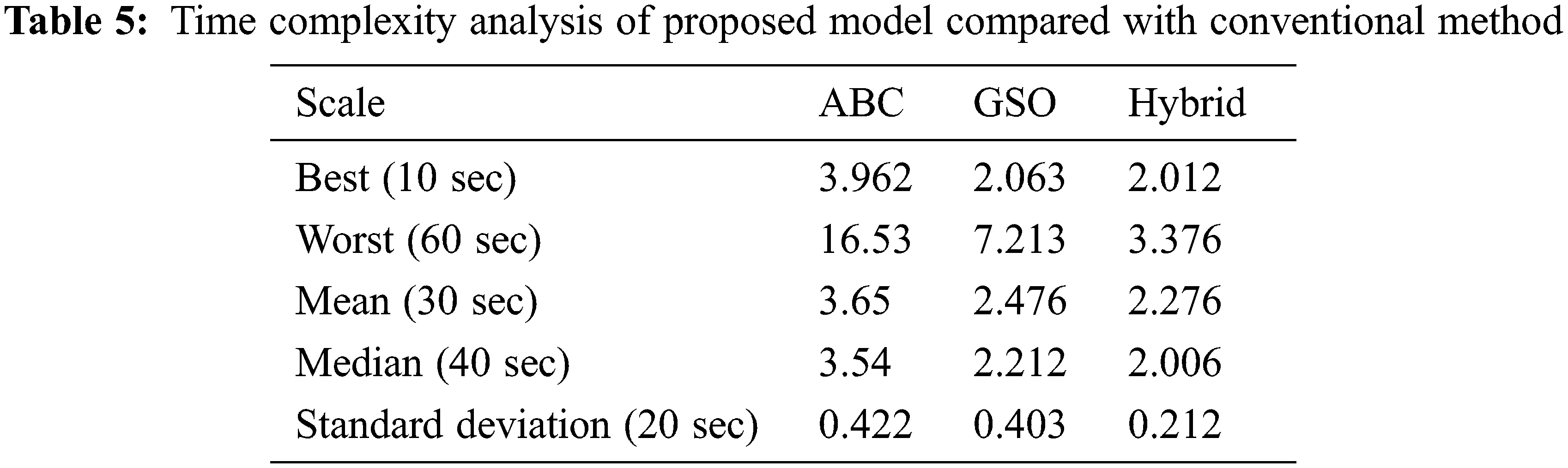
The time complexity of the proposed model is very less when compared to the conventional algorithms in all scale of measurement. The reduced time complexity is measured in terms of milli seconds and as the node count increases the time complexity also increases. The analysis performed here is based on the constant count of sensor node with 300 per cluster.
4.5 Normalized Energy Analysis
The normalized energy analysis for the proposed model is done in two aspects namely i) number of alive nodes for a scale of rounds considering maximum rounds of 3000 and a maximum of 100 nodes per cluster. and ii) Normalized network energy considering a maximum limit of 3000 rounds. The well-known factor of the Wireless Sensor Network is; the energy of the node is inversely proportional to the number of rounds. As the number of rounds increases, the nodes lose its energy and became dead nodes. The analysis is performed for a maximum of 3000 rounds and at the end of 3000 nodes, the number of alive nodes in the single cluster is measured for the proposed model and for conventional algorithms. In continuation of this analysis, the energy consumed by the single node for a packet delivery is also analyzed for the proposed model and the performance is compared with the conventional algorithms.
At the end of 3000 rounds the proposed model possesses 16% of its nodes in alive status which is better on comparing with the conventional algorithms. The analysis of normalized energy of the entire Wireless Sensor network for a maximum of 3000 rounds of data transmission is considered to analyze the proposed model and to compare with the conventional algorithms.
The Analysis depicted in Tabs. 6 and 7 clearly proves that the normalized energy of the network is better for the proposed model when compared to the conventional algorithms [26].
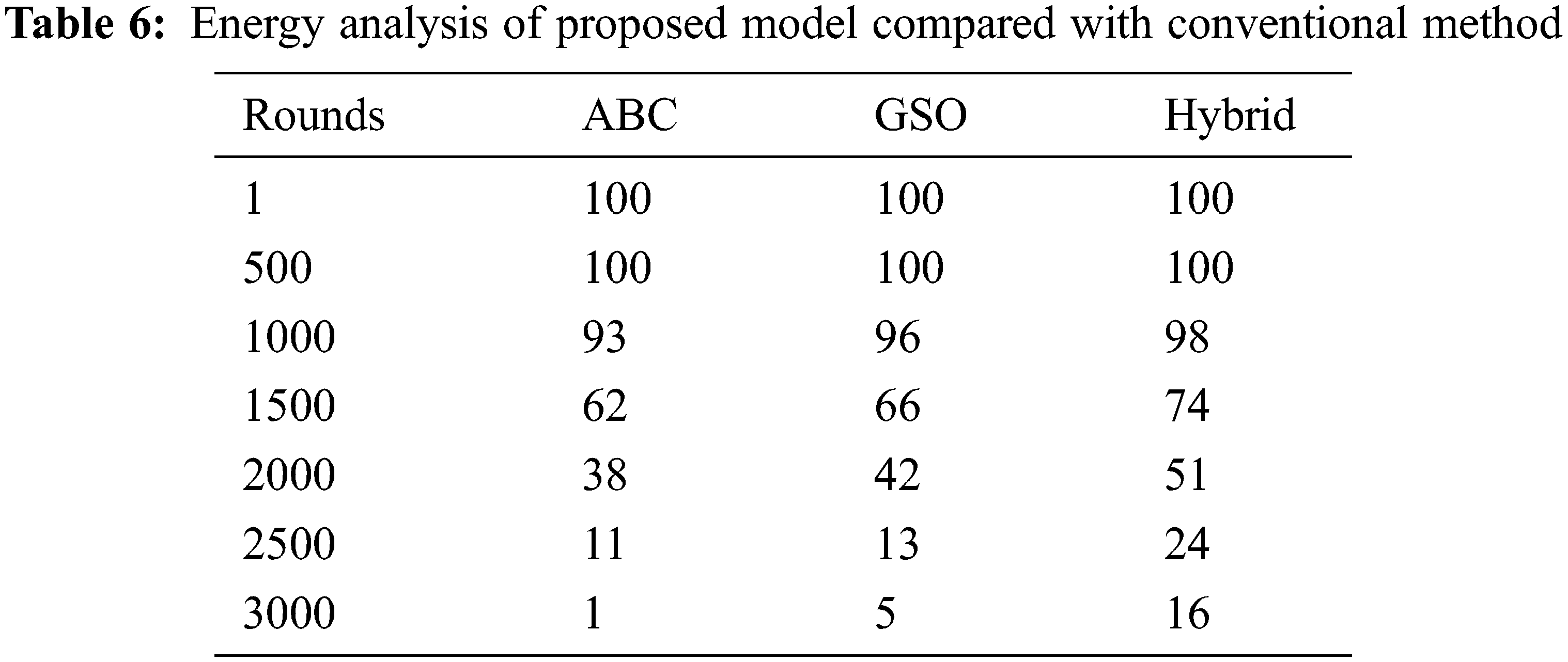
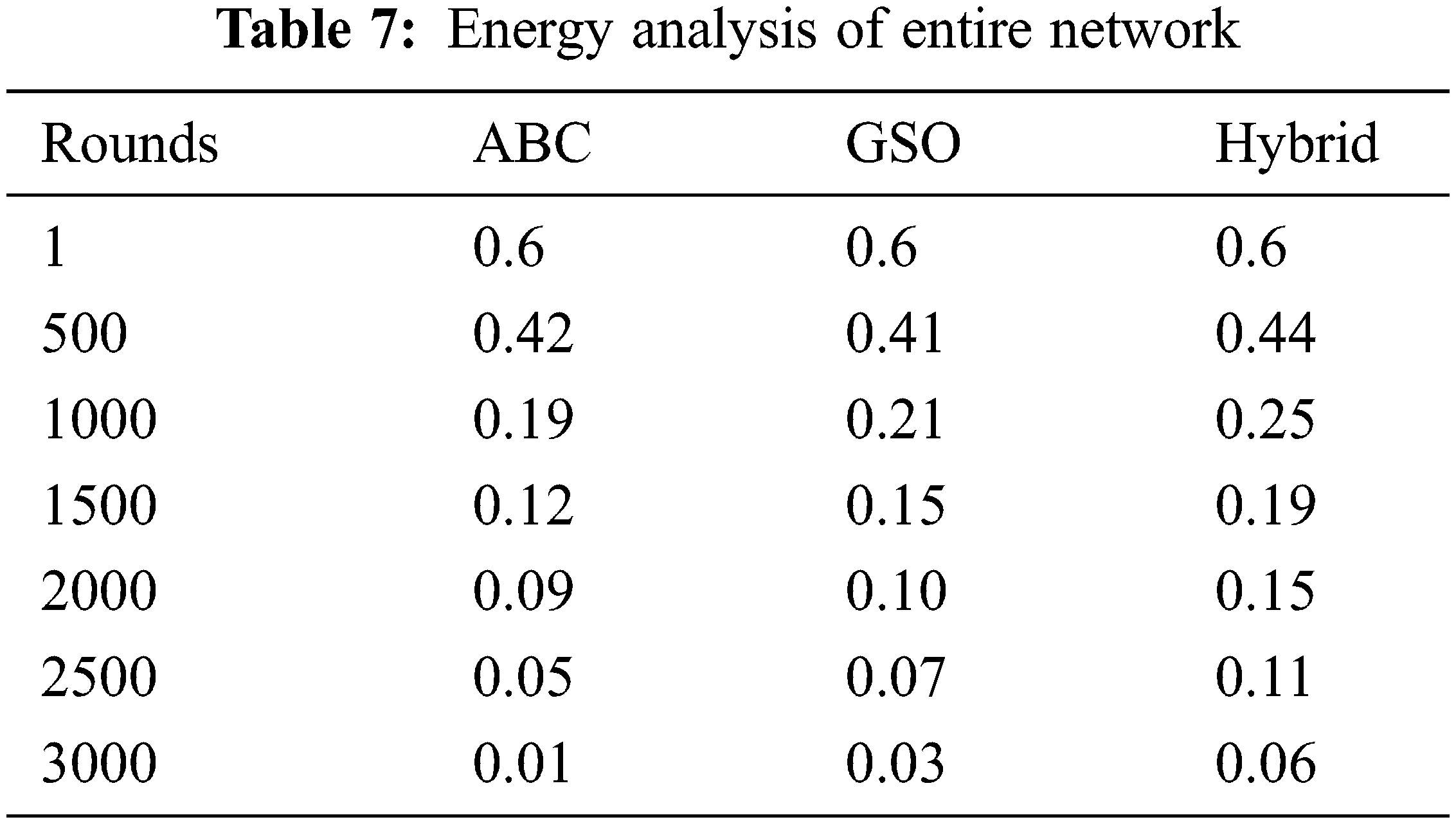
The notable concern of the Wireless Sensor Network is the better achievement of extended lifetime of nodes in the cluster, minimal consumption of energy by the nodes during the data transmission, Maximum energy possess by the network for maximum number of rounds, reduced delay and time complexity. This paper proposed a hybrid model of comprising Glowworm Swarm Optimization and Artificial Bee Colony Algorithm to attain the advantages of both the algorithms and to neutralize the pitfalls mutually to achieve a greater aforementioned expected performance. The performance of the proposed hybrid model is compared with the conventional algorithms individually in terms of quantitative analysis, cluster head distance, transmission delay analysis, time complexity analysis and finally normalized energy analysis. The analytical results prove that the proposed model exhibits better performance in all the aforementioned parameters than the conventional algorithms. All these analyses were performed with a maximum of 100 member nodes in a single cluster with a maximum of 3000 rounds taken into consideration. The end result analysis, proves that after performing 3000 rounds of data transmission, the proposed model possesses 16% of alive nodes with a normalized energy of 0.06 mJoules.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. E. Keskin, L. Kuban, N. Aras and E. Cem, “Lifetime maximization in wireless sensor networks using a mobile sink with nonzero traveling time,” The Computer Journal, vol. 54, no. 12, pp. 1987–1999, 2011. [Google Scholar]
2. R. A. Rashid, M. R. A. Rahim, M. A. Sarijari and N. Mahalin, “Design and implementation of wireless biomedical sensor networks for ECG home health monitoring,” in Int. Conf. on Electronic Design, Penang, Malaysia, vol. 1, pp. 1–4, 2008. [Google Scholar]
3. J. Sengathir, “A hybrid ant colony and artificial bee colony optimization algorithm-based cluster head selection for IoT,” Procedia Computer Science, vol. 1, no. 143, pp. 360–366, 2018. [Google Scholar]
4. P. Parameswari and R. Thamilselvan, “Multi-parameter reverse glowworm swarm optimization algorithm for energy efficient sensor movement in mobile wireless sensor network,” International Journal of Computational Research and Development, vol. 1, pp. 49–55, 2018. [Google Scholar]
5. L. Sun, W. Sun, M. He and H. Chen, “A modified surrogate-assisted multi-swarm artificial bee colony for complex numerical optimization problems,” Microprocessors and Microsystems, vol. 1, no. 76, pp. 1030–1050, 2020. [Google Scholar]
6. A. A. Baradaran and K. Navi, “HQCA-Wsn: High-quality clustering algorithm and optimal cluster head selection using fuzzy logic in wireless sensor networks,” Fuzzy Sets and Systems, vol. 15, no. 389, pp. 114–144, 2020. [Google Scholar]
7. M. N. Khan, H. U. Rahman and M. Z. Khan, “An energy efficient adaptive scheduling scheme for mesh grid wireless sensor networks,” Journal of Parallel and Distributed Computing, vol. 1, no. 146, pp. 139–157, 2020. [Google Scholar]
8. N. R. Malisetti and V. K. Pamula, “Performance of quasi oppositional butterfly optimization algorithm for cluster head selection in wsns,” Procedia Computer Science, vol. 171, pp. 1953–1960, 2020. [Google Scholar]
9. M. Stephanakis, P. Chochliouros, E. Sfakianakis S. S. Noorulhassan and H. David, “Hybrid self-organizing feature map (som) for anomaly detection in cloud infrastructures using granular clustering based upon value-difference metrics,” Information Sciences, vol. 1, no. 494, pp. 247–277, 2019. [Google Scholar]
10. A. G. Piquer, J. Bacardit, A. F. Herrera and E. Golobardes, “Scaling-up multiobjective evolutionary clustering algorithms using stratification,” Pattern Recognition Letters, vol. 1, no. 93, pp. 69–77, 2017. [Google Scholar]
11. W. Fakhet, E. L. Khediri, S. Dallali and K. Abdennaceur, “New K-means algorithm for clustering in wireless sensor networks,” in Int. Conf. on Internet of Things, Embedded Systems and Communications, Gafsa, Tunisia, pp. 67–71, 2020. [Google Scholar]
12. N. T. Tam, H. T. T. Binh, V. T. Dat and P. N. Lan, “Towards optimal wireless sensor network lifetime in three dimensional terrains using relay placement metaheuristics,” Knowledge-Based Systems, vol. 28, no. 206, pp. 106407–106418, 2020. [Google Scholar]
13. R. Yarinezhad and S. N. Hashemi, “Increasing the lifetime of sensor networks by a data dissemination model based on a new approximation algorithm,” Ad Hoc Networks, vol. 100, pp. 102084–102099, 2020. [Google Scholar]
14. S. Hashish and H. Tawalbeh, “Quality of service requirements and challenges in generic WSN infrastructures,” Procedia Computer Science, vol. 1, no. 109, pp. 1116–1121, 2017. [Google Scholar]
15. T. Kalaiselvi, P. Nagaraja and Z. A. Basith, “A review on glowworm swarm optimization,” International Journal of Information Technology, vol. 3, no. 3, pp. 49–56, 2017. [Google Scholar]
16. H. Cui, J. Feng, J. Guo and T. Wang, “A novel single multiplicative neuron model trained by an improved glowworm swarm optimization algorithm for time series prediction,” Knowledge-Based Systems, vol. 1, no. 88, pp. 195–209, 2015. [Google Scholar]
17. D. N. Jayakumar and P. Venkatesh, “Glowworm swarm optimization algorithm with topsis for solving multiple objective environmental economic dispatch problem,” Applied Soft Computing, vol. 1, no. 23, pp. 375–386, 2014. [Google Scholar]
18. B. Wu, C. Qian, W. Ni and S. Fan, “The improvement of glowworm swarm optimization for continuous optimization problems,” Expert Systems with Applications, vol. 39, no. 7, pp. 6335–6342, 2012. [Google Scholar]
19. H. Wang, W. Wang, S. Xiao, Z. Cui, M. Xu et al., “Improving artificial bee colony algorithm using a new neighborhood selection mechanism,” Information Sciences, vol. 1, no. 527, pp. 227–240, 2020. [Google Scholar]
20. T. J. Swamy, G. Ramamurthy and P. Nayak, “Optimal, secure cluster head placement through source coding techniques in wireless sensor networks,” IEEE Communications Letters, vol. 24, no. 2, pp. 443–446, 2020. [Google Scholar]
21. B. P. Kulkarni, S. S. Krishna, K. Meenakshi, P. Kora and K. Swaraja, “Performance analysis of optimization algorithms ga, pso, and abc based on dwt-svd watermarking in opencv python environment,” in Int. Conf. for Emerging Technology (INCET), Belgaum, India, vol. 5, pp. 1–5, 2020. [Google Scholar]
22. X. Xu, Q. Hou, C. Wu and Z. Fan, “Improved GSO algorithms and their applications in multi-target detection and tracking field,” IEEE Access, vol. 8, pp. 119609–119623, 2020. [Google Scholar]
23. J. Q. Li, M. X. Song, L. Wang, P. Y. Duan, Y. Y. Han et al., “Hybrid artificial bee colony algorithm for a parallel batching distributed flow-shop problem with deteriorating jobs,” IEEE Transactions on Cybernetics, vol. 50, no. 6, pp. 2425–2439, 2020. [Google Scholar]
24. S. Lenka, A. Nanda and S. K. Pradhan, “Qos provisioning based cost-effective routing in wsn based iot network using fuzzy ida* technique,” in Int. Conf. on Computing for Sustainable Global Development (INDIACom), New Delhi, India, vol. 17, pp. 591–595, 2021. [Google Scholar]
25. S. Ramachandran and V. Shanmugam, “A two-way authentication using bilinear mapping function for wireless sensor networks,” Computers & Electrical Engineering, vol. 1, no. 59, pp. 242–249, 2017. [Google Scholar]
26. Z. Wang, H. Ding, B. Li, L. Bao and Z. Yang, “An energy efficient routing protocol based on improved artificial bee colony algorithm for wireless sensor networks,” IEEE Access, vol. 8, pp. 133577–133596, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |