DOI:10.32604/csse.2022.020487

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.020487 |  |
| Article |
Feature Selection Using Grey Wolf Optimization with Random Differential Grouping
1Department of Computer Science and Engineering, Kongu Engineering College, Erode, 638060, Tamilnadu, India
2Department of Information Technology, Lebanese French University, Erbil, Iraq
3Singidunum University, Belgrade, 160622, Serbia
*Corresponding Author: R. S. Latha. Email: r.lslatha@yahoo.com
Received: 26 May 2021; Accepted: 05 August 2021
Abstract: Big data are regarded as a tremendous technology for processing a huge variety of data in a short time and with a large storage capacity. The user’s access over the internet creates massive data processing over the internet. Big data require an intelligent feature selection model by addressing huge varieties of data. Traditional feature selection techniques are only applicable to simple data mining. Intelligent techniques are needed in big data processing and machine learning for an efficient classification. Major feature selection algorithms read the input features as they are. Then, the features are preprocessed and classified. Here, an algorithm does not consider the relatedness. During feature selection, all features are misread as outputs. Accordingly, a less optimal solution is achieved. In our proposed research, we focus on the feature selection by using supervised learning techniques called grey wolf optimization (GWO) with decomposed random differential grouping (DrnDG-GWO). First, decomposition of features into subsets based on relatedness in variables is performed. Random differential grouping is performed using a fitness value of two variables. Now, every subset is regarded as a population in GWO techniques. The combination of supervised machine learning with swarm intelligence techniques produces best feature optimization results in this research. Once the features are optimized, we classify using advanced kNN process for accurate data classification. The result of DrnDG-GWO is compared with those of the standard GWO and GWO with PSO for feature selection to compare the efficiency of the proposed algorithm. The accuracy and time complexity of the proposed algorithm are 98% and 5 s, which are better than the existing techniques.
Keywords: Feature selection; data optimization; supervised learning; swarm intelligence; decomposed random differential grouping; grey wolf optimization
Big data processing in this internet world with advanced technologies, such as 4G, 5G, and 6G applications, is a challenging task. In the bulk of huge data repository, selecting the appropriate feature is still not optimal. Artificial intelligence, machine learning, and data mining algorithms have been used for optimal feature selection. A good data classifier must predict the data within a short time with high precision during feature selection. Effective preprocessing and crucial feature selection algorithms are required to achieve a fine quality of data dimensions during classification. If these two processes are highly optimal, then the classification process will be great. Thus, these aspects became the main motive for us to concentrate on effective feature selection algorithms.
Feature selection algorithms are necessary to achieve an optimal solution using many machine learning techniques. Machine learning algorithms still need some additional intelligent process for selecting highly relevant features in the database server. Demands and necessity makes us think beyond machine learning and bring a new meta-heuristic approach in feature selection. At present much optimization problems looks for swarm intelligence techniques for its optimal solution in nature. A group of animal behaviors are considered to develop a metaheuristic model, and an algorithm is developed. In this article, we use grey wolf optimization (GWO) for selecting optimal features after performing decomposition random differential grouping on the feature dataset.
The selection of appropriate feature is an interdisciplinary field of data mining. Big data cannot be easily handled with existing feature selection, classification, and optimization techniques. This aspect is necessary because big data are regarded as a collection of high dimensional data from various application sources. These new techniques help in computing the huge data with high force. Data are significant knowledge base for every business process. A core data transaction occurs every minute in the online business. This is a huge data repository were we have to implement mining techniques. In this research, we focus on selecting the appropriate features in the dataset without missing any data features and optimizing the feature for classification. The main contribution we introduce in this work is decomposition of data with random differential grouping. Decomposition divides the data and its subsets by fitness value calculation. In this work, all features are considered for decomposition. For effectiveness of feature selection, The features are divided in to subsets for an effective feature selection, and the relatedness is checked using random differential grouping. The group of population is regarded as an input for the GWO algorithm.
The rest of the papers have the following sections: Section 2 provides the literature review of this approach. Section 3 presents the proposed method description and working principal. Section 4 evaluates the results and comparison. Finally, Section 5 presents the conclusion with future scope.
Sun et al. [1] defined the high-dimensional data process by using the learning-based local search algorithm. The main issue is nonlinear complicated problems are converted into linear local groups by using a local component learning strategy. The relevant features are mined along with marginal framework. This proposed new technique uses machine learning with mathematical analysis. Fong et al. [2] implemented the accurate selection of features from the huge high-dimensional data by using an intelligent classifier. Swarm search algorithm is a novel method used for feature selection and produces optimal solutions. This mechanism is a metaheuristic approach for selecting relevant data from the dataset. The aforementioned approach is an advantageous method with flexibility using a fitness value of the data during classification. Fong et al. [3] suggested a new coefficient-based feature selection model. This method has higher accuracy compared with the other clustering techniques. Clustering with a coefficient variation has a balanced process between the generalization and the problem of over fitting to produce an optimal solution. Finally, the fastest discrimination approach is called hyper piping, which is used for checking data groups with high classification accuracy.
Peralta et al. [4] suggested the evolutionary algorithm for feature selection. Such a process uses a map reduce strategy for generating the subsets of features in a huge database. This work classifies the original dataset into various blocks for a mapping-based computation process. Classified blocks are integrated by using weights of features in reducing a phase as a finalized vector. Data assessment is performed by using SVM, logistic regression, and naïve Bayes classifier in the big data framework. The big data uses ant colony optimization (ACO) with swarm search (SS) for selecting the appropriate features with stream mining. Harde et al. [5] suggested a light weight-based novel ACO to achieve high accuracy in streaming infrastructure. This infrastructure will validate high-dimensional data during feature extraction. Selvi and Valarmathi et al. [6] suggested the firefly algorithm for feature selection for optimal local searching purposes. Firefly search is effective for local searching process. However, this work cannot provide global optimal solution in the search results. The selected features classified using various algorithms, such as kNN and multilayer perceptron utilizing a neural network classification. The outcome of this work is effective with firefly algorithm in the local optimal search process. Viegas et al. [7] demonstrated the selection of high-dimensional features by using genetic algorithm. This algorithm helps in targeting the different feature sets with unique metrics. According to Viegas, the problem of diversity in feature selection projections by hypothesis deviation are effectively handled by genetic algorithms. The classification result is more efficient than conventional classifiers.
Anusuya et al. [8] applied the map reduce-based graph mining process by using Apriori Particle Swarm Optimization (APSO). The behavior of the incoming streamed data with high dimensions is addressed in this article. The dynamic composition of the large data scale was computed using the PSO algorithm. Another category of big data classification uses different classification strategies by using machine learning, swarm intelligence, etc. Jun et al. [9] used the extreme learning method for huge data classification by fuzzy-based positive and negative categories. The central hidden layer is used to pull out the classified data from the hidden layer. The least square support vector machine and proximal-based support vector machine learning used by Huang et al. in [10,11] effectively classify the data within a short time. Here, extreme learning approaches are used to classify the disjoint vectors. Van der Char [12] proposed distributed computing-based online data classification. The learners in the distributed system used to learn the collected data sources from the distributed environment. After collecting the data which is heterogeneous as well as distributed nature is considered as distributed data context with joint classification. Grolinger et al. [13] suggested the map reduce-based data classification. The big data-based map reduce classification model is a difficult task. This process implements parallel computing and efficiently classifies the data. Rebentrost et al. [14] proposed the effective big data classification using quantum SVM. In this approach, the SVM is used in a quantum processing computer for analyzing vector logarithmic complexity with training data samples.
The various search methodology, such as greedy algorithm and evolutionary techniques [15], are used in effective feature selection. One of the effective feature selection algorithms is evolutionary algorithm [16], which is widely used in big data processing. Big data computed with cloud computing server decomposes the single complex problem into multiple subproblems. Each subproblem is individually addressed and finally combined to produce effective results [17]. The optimal decomposer and optimizer in the cloud computing infrastructure provide high performance in feature selection. Decomposition in different datasets are performed in papers [18–24] at cloud storage for an optimal solution.
3 Proposed DrnDG-GWO Methodology
Numerous optimal models are available for feature selection in the big data area. The complex nature of processing such big data is still a big challenge. Data mining techniques have proven to be the best in processing high dimensionality datasets. The preprocessing steps play a vital role in reducing the dataset for further processing the big data. Among the preprocessing phases, feature selection is an important step in selecting the optimal and relevant features for further classification or clustering. In this work, a new variant of random differential grouping with GWO is proposed as a hybrid feature selection approach to find the optimal solution. A modified kNN classifier is used for feature classification. The dataset for training and testing will be divided on the basis of the k-fold validation. An overview of the proposed architecture is shown in Fig. 1. The proposed feature selection is applied on different big datasets. The initial dataset features are decomposed into subcomponents based on the needed features for further classification. Fitness component is used for differential grouping the similar component in the dataset. Finally, the selected subcomponents are optimized by using the GWO, which is used to find the optimal solution based on the first, second, and third possible solutions.

Figure 1: Architectural overview
3.1 Decomposition Using Random Differential Grouping
Interdependence searching has been proposed for the decomposition problem to address the high computational complexity of the supervised learning algorithms [25]. Our proposed decomposition system found the inter relationship between the variables using the two subsets of the decision variables rather than two whole set of decision variables. This approach will increase the speed of the decomposition process. The differential grouping [26] identifies the interaction between the variables by using the fitness value changes of the decision variables. The fitness changes cause the change of decision variable from x to y; then, we considered that x and y are in interaction and has a relationship. The differential grouping method is proven to be the best for decomposition. The existing solutions on optimizing the big data have poor performance because the feature interactions are not properly addressed, and the dataset is statically decomposed. This process may consider only the even number of features. In this work, novel random differential grouping is proposed to dynamically decompose the big dataset and group the features that are interacting into the subset, thereby ensuring the probability of the proposed method.
The main objective of the proposed rnDG is to dynamically decompose the n feature vector into the subsets with a dimension of m = r*c. Dataset X consists of n feature vectors. The X is randomly decomposed into m subsets with s features in each subset where s < n, and it is measured as follows:
Each subset is represented as a population in GWO for optimization. “s” is the number of features in each subset (ss). The size of the subset is “sz”. Subset “ss1” consisting of individuals is represented as follows:
1 in the subset indicates that the feature is selected for feature subset, and 0 denotes that the feature is not selected for feature subset selection. Let dv be the decision variables of X, and Ux is the unit vector of the decision. X1 is the subset of the decision variables, where X1⊂X, and UX1 is the subset of UX. Unit vector U = {u1,u2 … un}, where ui = 0.
Variable d is the differential function, and u is the vector of UX. The directional derivative of d in u is expressed as follows:
The two subset interactions is declared by using the following:
All the decision variables are set as lower bounds (lb) on the search space of X(l,l).
The transition of decision variable subset X1 of the search space X(l,l) to the upper bounds (ub) is denoted as X(u,l).
The fitness difference ∂1 is calculated using X(l,l) and X(u,l) as follows:
The transition of decision variable subset X2 of the search space between X(l,l) and X(u,l) is declared as the middle between the lower and the upper bounds, which are denoted as X(l,m) and X(m,u), respectively.
The fitness difference ∂2 is calculated using X(l,m) and X(m,u) as follows:
If the difference between ∂1 and ∂2 is greater than the threshold value
Threshold
The nine features are decomposed into two subsets by using the proposed decomposition, which is represented as follows:
Such expression is decomposed using the proposed rnDG as {(f1, f7, f9, f2), (f3, f5, f8, f6, f4)}, as shown in Fig. 2.

Figure 2: Proposed random differential grouping decomposition of features


The random differential grouping algorithm dynamically decomposes the features of the dataset into subsets. One feature is assigned to subset 1 at random. Then, the interaction between the features of the subset is calculated using algorithm 2. If no interaction occurs, then the features are assigned to one subset group. If an interaction is found using algorithm 1, then it will be divided to further two groups with equal size. The interaction between the first group X1 with the two additional subgroups is identified and added to the respective decomposition group, such as X1 and X2. The next process of the proposed technique is GWO-based feature selection. The decomposed subsets are given as inputs to the GWO algorithm for feature selection.
GWO is considered the most advanced optimization algorithm due to the nature of hunters that are ready to catch their prey because of the crowd that is carefully organized. The GWO is a meta heuristic algorithm that is similar to GWO with the process of attacking and looking around their prey. The four levels of GWO leadership hierarchy are alpha (α), beta (β), delta (δ), and omega (ω). α is the male or female in charge of making decisions. β will help the α in making decisions. δ are the guides or elders or hunters. ω follows all wolves, and it will be the optimal solution, whereas the α, β, and ω are the first, second, and third best solutions.
In our proposed work, the decomposed subset from algorithm 1 is initialized as the population of n wolves in the first stage of algorithmic initialization. Every wolf is related to the desirable solutions, and n is the number of features in the original dataset. Fig. 3 shows the feature selection of the sample of nine features. According to the algorithm, the selected features that will improve the accuracy are represented as a binary value 1. Meanwhile, the features that will not improve the accuracy are represented as binary value 0.

Figure 3: Feature selection (solution) representation sample

In this proposed work, kNN is used as a classifier for the classification problem. The distance used to classify the data by using k-NN classifier is the Euclidean distance [28,29] used to find the k nearest neighbors by using:
where n is the number of features in the dataset, and Qi and Pi are the selected features in the given subset component. The dataset is divided into two parts for testing and training by using the k-fold validation. In this work, k = 5. Meanwhile, k−1 partitions are considered for training and the remaining ones for testing. The values generated from the search agent of GWO are continuous values. Hence, the resulted format is converted into the binary format by using the transform function called sigmoid function to improve the classification accuracy. The sigmoid function is as follows:
where Xsi is the search agent; i – 1, …, n denotes the number of features; max and min are the maximum and minimum values of the continuous feature vector; and Xb ∈ [0, 1] is the classification result. The overall workflow of our proposed feature selection scheme is represented in Fig. 4.
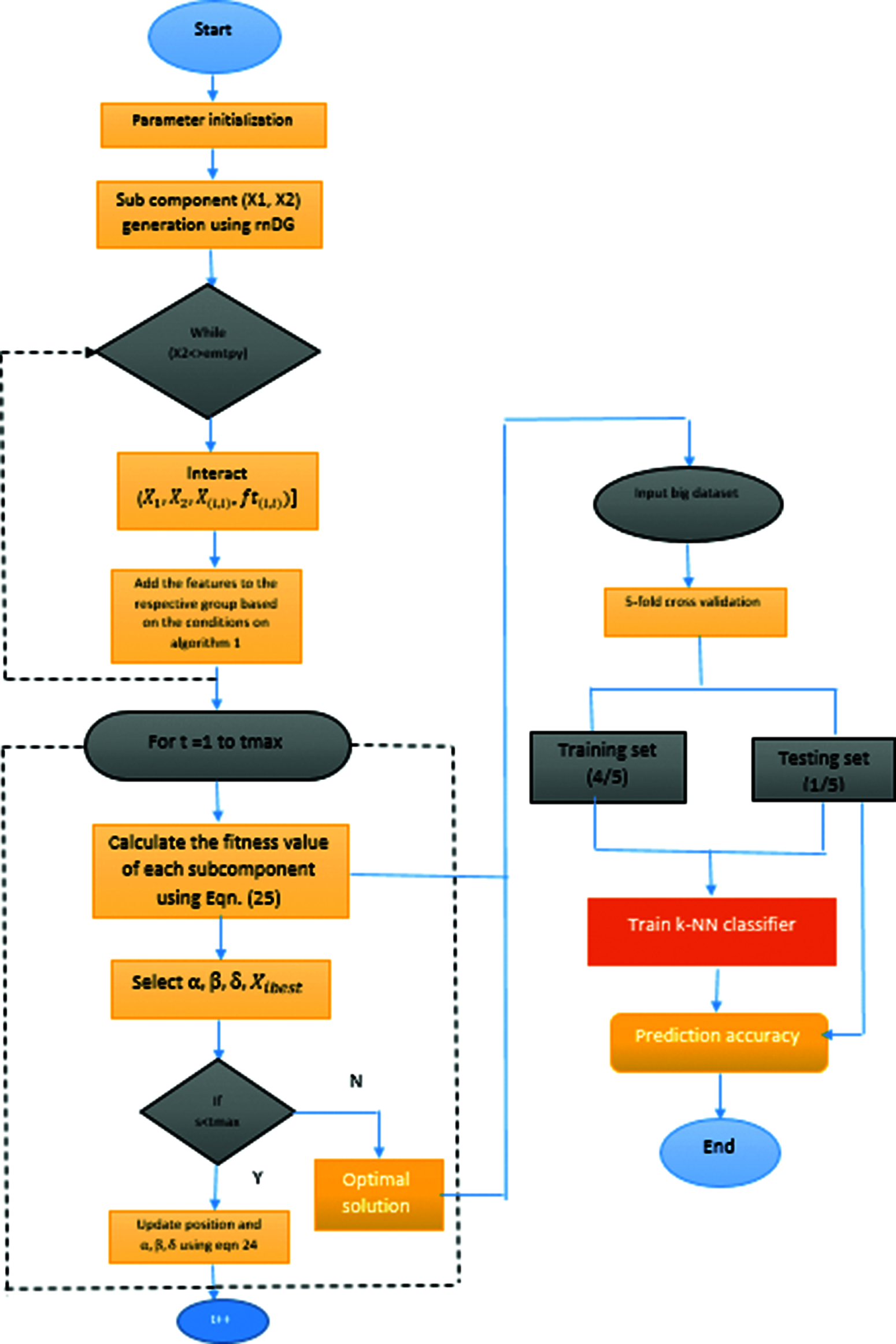
Figure 4: Work flow diagram of proposed feature selection with classification
Fig. 4 illustrates the proposed feature selection algorithm with classification. The input dataset features are first divided into subcomponents by using the random differential grouping. Then, the decomposed feature subsets are optimized using GWO to provide the optimal feature set for classification by using kNN. The prediction accuracy using the proposed feature selection is analyzed with a big dataset. Hence, our proposed feature selection algorithm using random differential grouping with GWO minimizes the dataset features by selecting the most relevant features and maximizes the classification accuracy based on the performance of the kNN classifier on various big datasets.
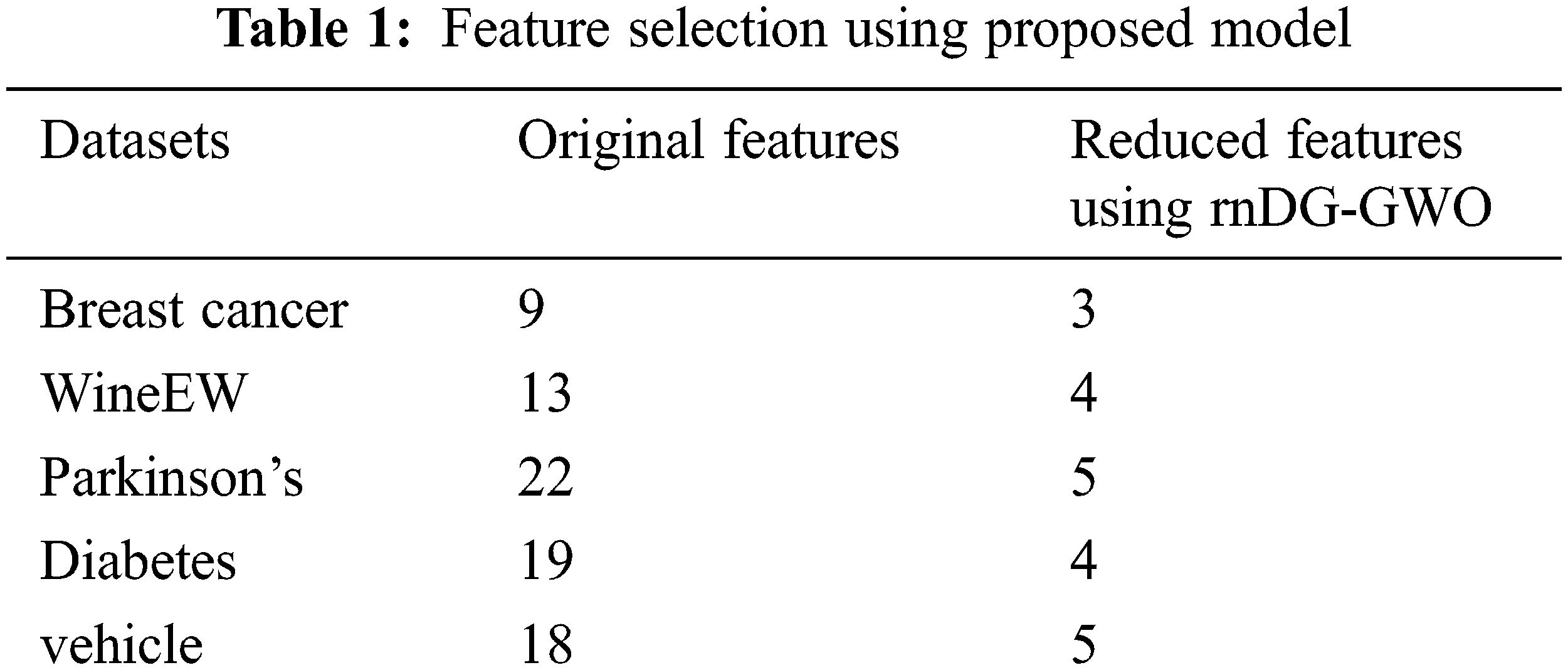
This section discusses the experimented result of the proposed feature selection algorithm using MATLAB (2018a). It is examined with the benchmark datasets from the UCI machine learning repository to check the efficiency and strength of the proposed algorithm. The datasets with original and reduced features using the proposed algorithm is shown in Tab. 1.
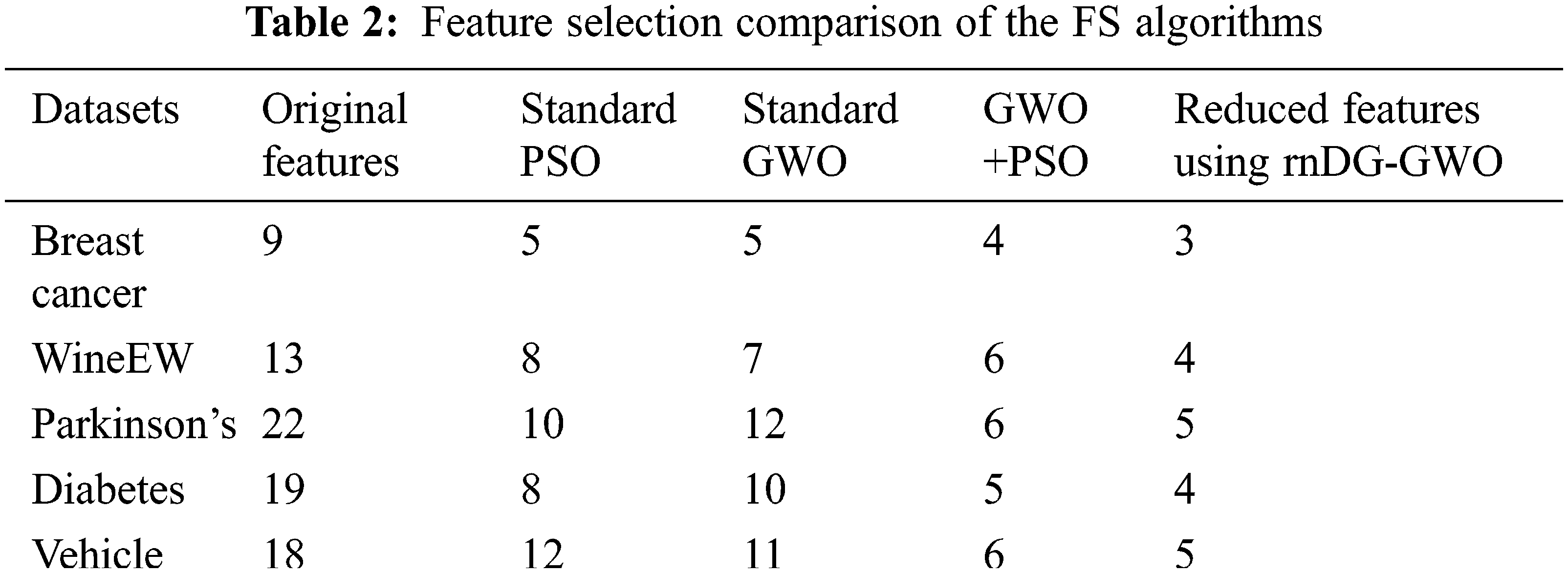
Existing standard GWO and GWO with PSO are used to compare the efficiency of the proposed algorithm. The algorithm parameters are taken from the literature and are equally compared. In this proposed work, the kNN classifier is used with the hybrid feature selection algorithm and considered the supervised learning for a fast implementation. The dataset is divided in the ratio of 4:1 as training and testing because this work uses the fivefold cross-validation technique. The comparison of selecting the number of features using the existing algorithms with proposed are shown in Tab. 2, and the comparison results are illustrated in Fig. 5.

Figure 5: Feature selection comparison of the various algorithms
The experimented results shows that our proposed algorithm efficiently reduces the irrelevant features than the original and other standard feature selection algorithms. Less number of relevant features leads to improved classification accuracy. The accuracy is calculated using the following equation:
The accuracy comparison of the original dataset and feature selection algorithm accuracy are shown in Tab. 3 and illustrated in Fig. 6. The evaluated results show that the proposed rnDG-GWO feature selection-based kNN classification obtains higher accuracy of 92%–98% on various benchmark datasets compared with the other existing feature selection-based classification accuracy.
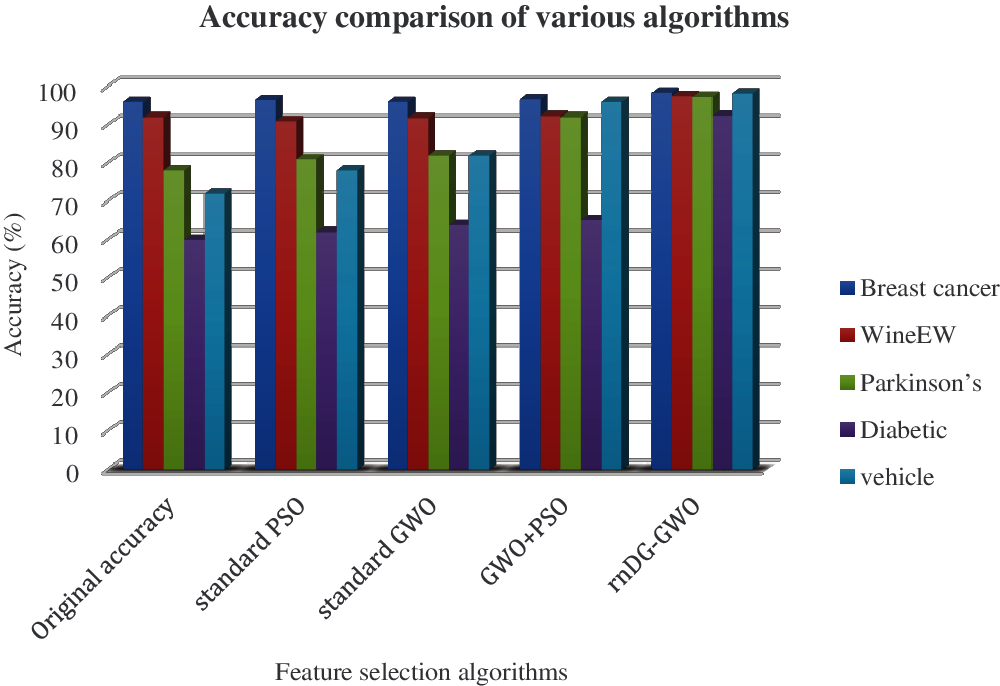
Figure 6: Accuracy of the classification with FS and without FS of various algorithms
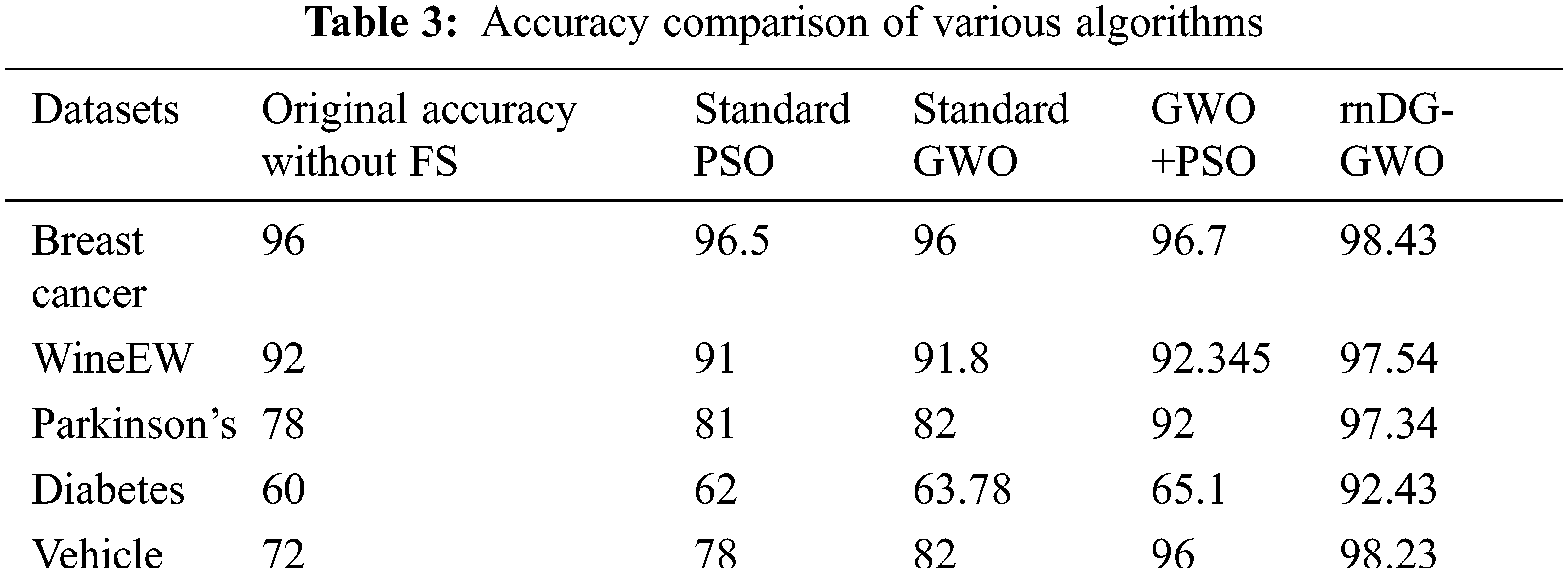
Hence, our proposed decomposed random differential grouping with GWO (DrnDG-GWO) for selecting optimal features provides high accuracy of prediction on breast cancer, wineEW, Parkinson, diabetes, and vehicle datasets. The computational time comparison of these algorithms are shown in Tab. 4 and illustrated in Fig. 7.
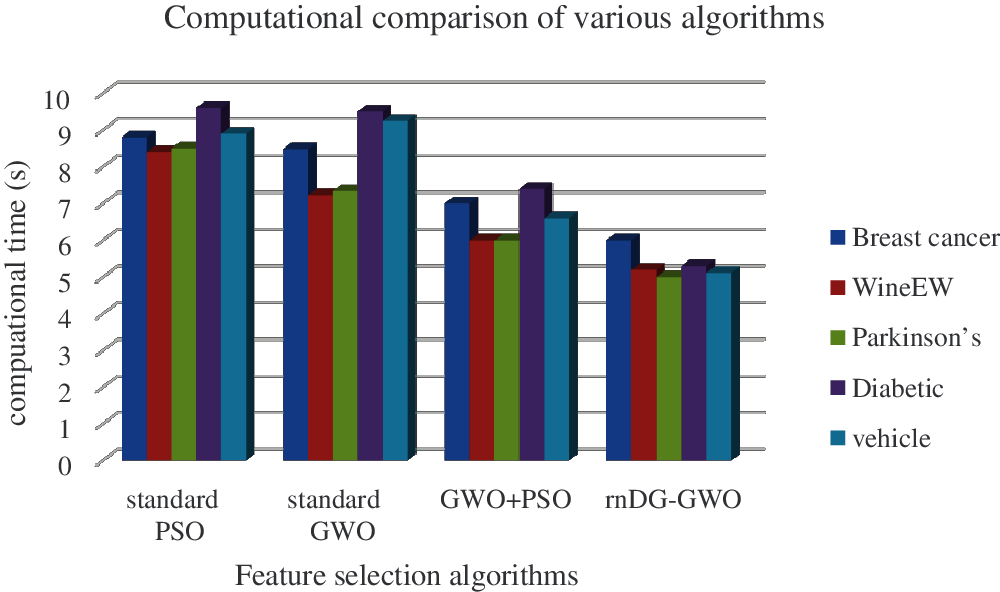
Figure 7: Computational time comparison in seconds

Tab. 4 illustrates the comparison of various feature selection methods based on classification and terms of computational time. The observed result shows that our proposed algorithm predicts in the shortest amount of time compared with the other traditional algorithms.
The observed results confirmed that the accuracy is comparatively low when no feature selection is utilized, and the classification accuracy considerably higher than the original when the proposed feature selection is used. The work aims to reduce the number of features and increase the classification accuracy with the experimentation. Hence, our proposed DrnDG-GWO feature selection-based classification is best in terms of reducing the number of features, increasing the accuracy, and reducing the computational time.
Feature selection is considered an important preprocessing step in selecting the appropriate feature from a huge dataset. Research on various selection methodology is highly improving. In our research, we focus on accurate selection of features from the dataset and increasing the accuracy of the classifier. Swarm intelligence is considered an interesting metaheuristic method for various optimization processes. Here, we use GWO, which is a swarm optimization technique for selecting the feature with global optimal solution. Decomposition of data with random differential grouping process optimally reduces the feature sets from the huge original dataset. This reduced feature set is optimized on the basis of the three optimal solutions of GWO. The accuracy, number of features retrieved, and computational cost are compared to contrast the efficiency of the proposed algorithm with existing standard GWO and GWO with PSO for feature selection. In this comparative analysis, our proposed feature optimization technique shows improved result. The numbers of features and classification are proportionate. The optimal solution would be to reduce features that are highly relevant. The classification accuracy will be relatively high when we perform classification with reduced features. In our research work, we focus on the above-mentioned two strategies for improving the feature selection and optimization. The feature reduction process with optimal feature selection is performed on the basis of decomposition and random differential grouping. Finally, reduced features are further optimized for optimal solution. The KNN classifier is used for feature classification. The result is evaluated with existing models, and our research work indicates that it outperforms them all. Decision tree-based decomposition can be suggested with swarm intelligence techniques in the future. Machine learning strategies can be used for feature selection to obtain an optimal solution.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that no conflict of interest regarding the publication of the paper.
1. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
2. Y. Sun, S. Todorovic and S. Goodison, “Local-learning-based feature selection for high-dimensional data analysis,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 32, no. 9, pp. 1610–1626, 2009. [Google Scholar]
3. S. Fong, X. S. Yang and S. Deb, “Swarm search for feature selection in classification,” in Proc. ICCSE, Sydney, Australia, pp. 902–909, 2013. [Google Scholar]
4. S. Fong, J. Liang, R. Wong and M. Ghanavati, “A novel feature selection by clustering coefficients of variations,” in Proc. ICDIM, Phitsanulok, Thailand, pp. 205–213, 2014. [Google Scholar]
5. D. Peralta, S. Del Río, S. Ramírez Gallego, I. Triguero and J. M. Benitez et al., “Evolutionary feature selection for big data classification: A mapreduce approach,” Mathematical Problems in Engineering, vol. 2015, 2015. [Google Scholar]
6. S. Harde and V. Sahare, “ACO swarm search feature selection for data stream mining in big data,” International Journal of Innovative Research in Computer and Communication Engineering, vol. 3, no.12, pp. 12087–12089, 2015. [Google Scholar]
7. R. Senthamil Selvi and M. Valarmathi, “An improved firefly heuristics for efficient feature selection and its application in big data,” Biomedical Research, vol. 28, 2017. [Google Scholar]
8. F. Viegas, L. Rocha, M. Goncalves, F. Mourao, G. Thiago et al., “A genetic programming approach for feature selection in highly dimensional skewed data,” Neurocomputing, vol. 273, pp. 554–569, 2018. [Google Scholar]
9. D. Anusuya, R. Senthilkumar and T. S. Prakash, “Evolutionary feature selection for big data processing using Map reduce and APSO,” International Journal of Computational Research and Development, vol. 1, no. 2, pp. 30–35, 2017. [Google Scholar]
10. W. Jun, W. Shitong and F. Chung, “Positive and negative fuzzy rule system, extreme learning machine and image classification,” International Journal of Machine Learning and Cybernetics, vol. 2, no. 4, pp. 261–271, 2011. [Google Scholar]
11. G. B. Huang, H. Zhou, X. Ding and R. Zhang, “Extreme learning machine for regression and multiclass classification,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 2, pp. 513–529, 2011. [Google Scholar]
12. J. Chen, G. Zheng and H. Chen, “ELM mapreduce: map reduce accelerated extreme learning machine for big spatial data analysis,” in Proc. ICCA, Hangzhou, China, pp. 400–405, 2013. [Google Scholar]
13. C. Tekin and M. Vander Schaar, “Distributed online big data classification using context information,” in Proc. Allerton, Monticello, IL, USA, pp. 1435–1442, 2013. [Google Scholar]
14. K. Grolinger, M. Hayes, W. A. Higashino, A. L’Heureux, D. S. Allison et al., “Challenges for mapreduce in big data,” in Proc. IEEE World Congress on Services, IEEE, Anchorage, AK, USA, pp. 182–189, 2014. [Google Scholar]
15. P. Rebentrost, M. Mohseni and S. Lloyd, “Quantum support vector machine for big data classification,” Physical Review Letters, vol. 113, no. 13, 2014. [Google Scholar]
16. Y. Liu, F. Tang and Z. Zeng, “Feature selection based on dependency margin,” IEEE Transactions on Cybernetics, vol. 45, no. 6, pp. 1209–1221, 2014. [Google Scholar]
17. V. Stanovov, C. Brester, M. Kolehmainen and O. Semenkina, “Why don’t you use evolutionary algorithms in Big data?,” in IOP Conf. Series: Materials Science and Engineering, vol. 173, no. 1, 2017. [Google Scholar]
18. R. Wang, F. Zhang, T. Zhang and P. J. Fleming, “Cooperative co-evolution with improved differential grouping method for large-scale global optimisation,” International Journal of Bio-Inspired Computation, vol. 12, no. 4, pp. 214–225, 2018. [Google Scholar]
19. Y. Sun, M. Kirley and S. K. Halgamuge, “On the selection of decomposition methods for large scale fully non-separable problems,” in Proc. ICGA,Yangon, Myanmar, pp. 1213–1216, 2015. [Google Scholar]
20. Y. Sun, M. Kirley and S. K. Halgamuge, “A recursive decomposition method for large scale continuous optimization,” IEEE Transactions on Evolutionary Computation, vol. 22, no. 5, pp. 647–661, 2017. [Google Scholar]
21. X. M. Hu, F. L. He, W. N. Chen and J. Zhang, “Cooperation coevolution with fast interdependency identification for large scale optimization,” Information Sciences, vol. 381, pp. 142–160, 2017. [Google Scholar]
22. A. Chen, Z. Ren, Y. Yang, Y. Liang and B. Pang, “A historical interdependency based differential grouping algorithm for large scale global optimization,” in Proc. GECCO, Kyoto, Japan, pp. 1711–1715, 2018. [Google Scholar]
23. M. Shanmugam, A. Ramasamy, S. Paramasivam and P. Prabhakaran, “Monitoring the turmeric finger disease and growth characteristics using sensor based embedded system—a novel method,” Circuits and Systems, vol. 7, no. 08, pp. 1280–1289, 2016. [Google Scholar]
24. S. Maheswaran, M. Ramya, P. Priyadharshini and P. Sivaranjani, “A real time image processing based system to scaring the birds from the agricultural field,” Indian Journal of Science and Technology, vol. 9, no. 30, pp. 1–5, 2016. [Google Scholar]
25. H. Ge, L. Sun, X. Yang, S. Yoshida and Y. Liang, “Cooperative differential evolution with fast variable interdependence learning and cross-cluster mutation,” Applied Soft Computing, vol. 36, pp. 300–314, 2015. [Google Scholar]
26. M. N. Omidvar, X. Li, Y. Mei and X. Yao, “Cooperative co-evolution with differential grouping for large scale optimization,” IEEE Transactions on Evolutionary Computation, vol. 18, no. 3, pp. 378–393, 2013. [Google Scholar]
27. Y. Mei, M. N. Omidvar, X. Li and X. Yao, “A competitive divide-and-conquer algorithm for unconstrained large-scale black-box optimization,” ACM Transactions on Mathematical Software (TOMS), vol. 42, no. 2, pp. 1–24, 2016. [Google Scholar]
28. M. El-Hasnony, S. I. Barakat, M. Elhoseny and R. R. Mostafa, “Improved feature selection model for big data analytics,” IEEE Access, vol. 8, pp. 66989–67004, 2020. [Google Scholar]
29. M. AbdelBasset, D. Shahat, I. E. Henawy, V. H. C. Albuquerque and S. Mirjalili, “A new fusion of grey wolf optimizer algorithm with a two-phase mutation for feature selection,” Expert Systems with Applications, vol. 139, pp. 122824–122837, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |