DOI:10.32604/csse.2022.021525

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021525 |  |
| Article |
Fusion Recommendation System Based on Collaborative Filtering and Knowledge Graph
1School of Artificial Intelligence, Wuxi Vocational College of Science and Technology, Wuxi, 214028, China
2School of Computer Science and Technology, Harbin Institute of Technology, Weihai, 264209, China
3School of Astronautics, Harbin Institute of Technology, Harbin, 150001, China
4Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, China
5School of Mathematical Sciences, University College Dublin, Dublin, Dublin4, Ireland
*Corresponding Author: Dongjie Zhu. Email: zhudongjie@hit.edu.cn
Received: 05 July 2021; Accepted: 14 September 2021
Abstract: The recommendation algorithm based on collaborative filtering is currently the most successful recommendation method. It recommends items to the user based on the known historical interaction data of the target user. Furthermore, the combination of the recommended algorithm based on collaborative filtration and other auxiliary knowledge base is an effective way to improve the performance of the recommended system, of which the Co-Factorization Model (CoFM) is one representative research. CoFM, a fusion recommendation model combining the collaborative filtering model FM and the graph embedding model TransE, introduces the information of many entities and their relations in the knowledge graph into the recommendation system as effective auxiliary information. It can effectively improve the accuracy of recommendations and alleviate the problem of sparse user historical interaction data. Unfortunately, the graph-embedded model TransE used in the CoFM model cannot solve the 1-N, N-1, and N-N problems well. To tackle this problem, a novel fusion recommendation model Joint Factorization Machines and TransH Model (JFMH) is proposed, which improves CoFM by replacing the TransE model with TransH model. A large number of experiments on two widely used benchmark data sets show that compared with CoFM, JFMH has improved performance in terms of item recommendation and knowledge graph completion, and is more competitive than multiple baseline methods.
Keywords: Fusion recommendation system; knowledge graph; graph embedding
In an era of rapid development of the Internet, information explosion is a problem that we must face at present. There is a huge amount of data flooding the world of the Internet, and the scale of these data will not decrease over time. On the contrary, the data that exists in the virtual Internet world will only increase to an unimaginable scale. As a result, how to extract valuable information from these massive amounts of data becomes particularly important [1]. For example, in the field of e-commerce [2], if users still have not found their favorite products after browsing a large amount of irrelevant information and products, it is easy to reduce the user's desire to buy. The personalized recommendation system can predict the user's possible purchase tendency based on the user's historical shopping preferences, and help the user make a pre-selection from a variety of product brands and thousands of product stores. In theory, e-commerce platforms can improve users’ shopping experience through the above-mentioned methods, thereby gaining more economic benefits. The formal definition of the recommendation system is as follows [3]: Given a user set U, an item set I, the user Ui's preference for the item Ij is represented by Ri,j, R ∈ ℝ|U|×|I|. Subsequently, we define the mapping function f:U × V → R. The target task of the recommendation system is to find the item Ik with the greatest preference in the item set I for any given user Ui in the user set U (The formal definition is shown in Eq. (1)).
In the actual application process, the recommendation system usually encounters a more common problem: the user historical interaction information R provided in the data source is sparse and cannot effectively model user preferences. In extreme cases, the user's historical interaction information may be empty, that is, a cold start problem. For example, in the large e-commerce platform Taobao [4], the number of the daily active user set U is relatively large, and the number of the product set I sold on the platform is even hundreds of millions. In contrast, the coverage rate of the user historical interaction information R that we can obtain is extremely low, which is a very severe challenge for the recommendation system. At present, the method based on collaborative filtering is a relatively successful practical case in the personalized recommendation algorithm [5–7]. Although this type of algorithm efficiently completes the target task of the recommendation system, due to the relatively serious cold start problem, it is helpless when the interaction relationship between the user set U and the item set I is sparse. In addition, many scholars have made many attempts, such as constructing a time-aware collaborative filtering model [8] and fusing two recommendation algorithms [9,10]. These algorithms give us a good inspiration to solve the current problem.
The knowledge graph that has emerged in recent years is essentially a special form of a knowledge base (as shown in the dashed circle in Fig. 1). The entity information and association relationships contained in the knowledge graph can be used as supplementary knowledge for the recommendation system, improving the performance and user experience of the recommendation system. For example, Wang et al. [11] introduced the knowledge graph in the news domain into the online news recommendation system, constructed a deep knowledge perception network DKN based on the knowledge graph, and proved the positive effect of introducing the knowledge graph as an external knowledge base through experiments. The CoFM model proposed by Piao et al. [12] in 2018 also applies the knowledge graph to the personalized recommendation system and creatively proposes to use user-item interaction information to complement the relationships that may be missing in the knowledge graph. However, CoFM is constructed based on the graph representation model TransE [13], which cannot well identify and utilize the 1-N, N-1, and N-N relationships in the graph structure network. This is limited to the utilization of heterogeneous relationships in the knowledge graph, which limits the overall performance of the recommendation system.
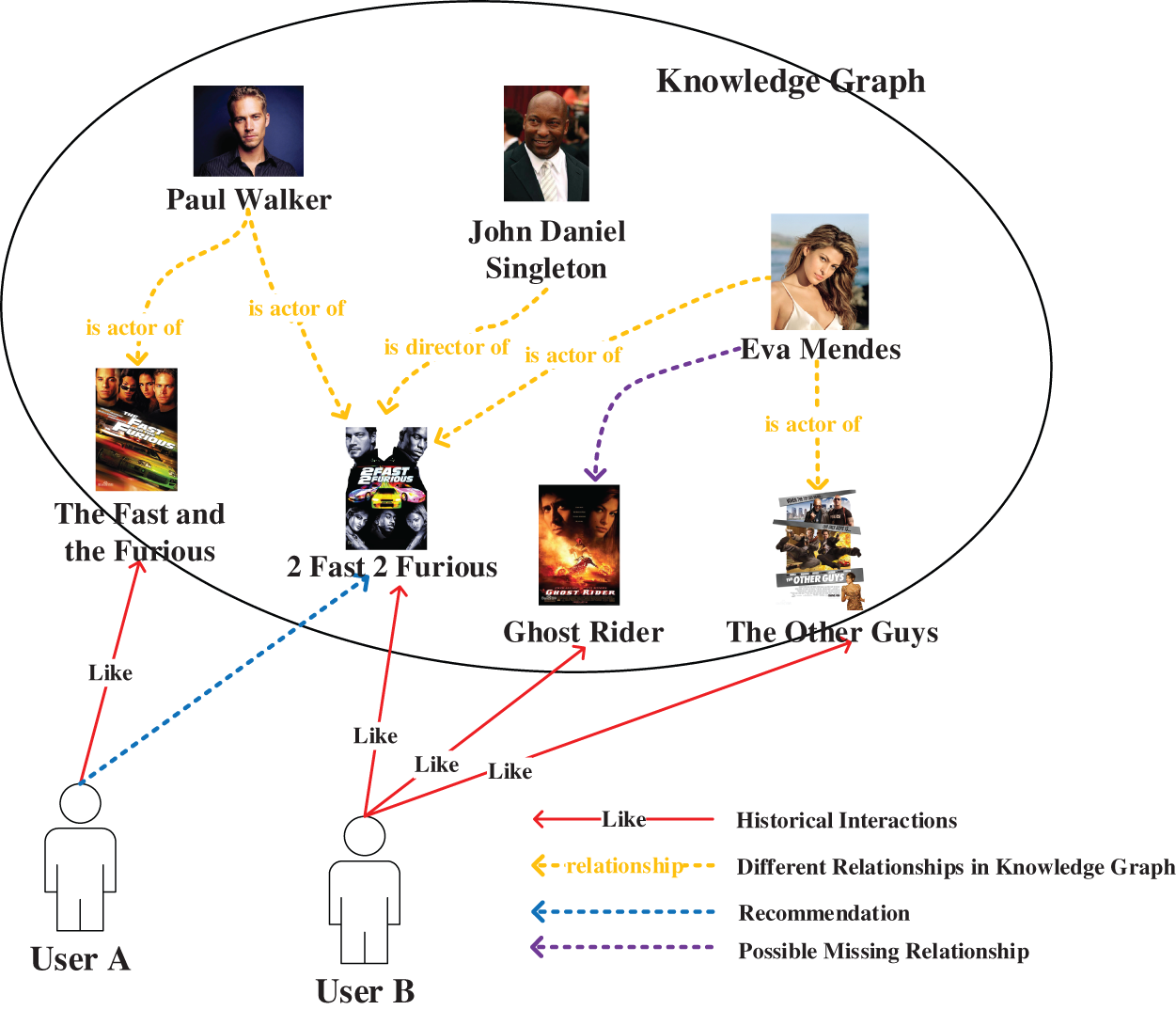
Figure 1: The knowledge graph complements the implicit association relationship, and the knowledge graph complements (the dotted circle represents the entity and association relationship stored in the knowledge graph)
Aiming at the above-mentioned problems in the recommendation system at this stage, this paper uses the knowledge graph, a special form of knowledge base, to supplement the evidence and basis for the personalized recommendation system to make recommendations. Compared with the TransE model with limited expressive power used in CoFM, we choose the TransH model [14] that can better distinguish and express the 1-N, N-1, and N-N relationships that exist objectively in the graph network. Experiments show that the graph representation learning model based on the TransH model can make better use of the heterogeneous relationship information in the graph network, which is beneficial to use the related information in the knowledge graph to help personalized recommendations. On the other hand, we aim at the problem of missing relationships that may exist in the knowledge graph [12] and consider using the user-item historical interaction data collected in the personalized recommendation system to supplement and improve the knowledge graph. And the validity of this idea is proved through experiments. The main work is summarized as follows:
1) Combine Factorization Machines (FM) [15] and TransH model to build a fusion learning model. Use FM to embed the user-item historical interaction information, and establish a graph representation model based on the TransH model to learn the knowledge graph, and use the graph embedding representation to supplement and strengthen the results of FM;
2) Use the acquired user-item historical interaction information to supplement the association relationships that may be missing in the knowledge graph;
3) Experiments on two data sets widely used in academia show the effectiveness of our method.
In this section, we will discuss two aspects related to our research: personalized recommendation based on collaborative filtering and personalized recommendation based on the knowledge graph.
2.1 Personalized Recommendation Based on Collaborative Filtering
There are two main hypotheses in the personalized recommendation algorithm based on Collaborative Filtering (CF): Similar users’ preferences for items may be similar; there may be similarities between items liked by the same user [4]. Specifically, the method based on collaborative filtering mainly mines the similarities between users and users, items, and items from user-item historical interaction data, and uses the mined associations to make personalized recommendations. Sarwar et al. [5] built a model based on the cosine similarity of item feature vectors for personalized recommendation, which achieved a great improvement compared with the traditional k-nearest neighbor algorithm. Koren improves the accuracy of recommendations by combining neighborhood models and latent factor models [6]. He et al. [7] proposed a collaborative filtering framework based on a deep neural network (NCF), which uses multi-layer perceptrons to model the user-item interaction relationship. This type of algorithm only models the user-item interaction information, and the calculation is relatively simple and the algorithm is more efficient. However, the performance is average in scenarios with high sparseness and incomplete interactive data, and it cannot deal with the cold start of new items or new users newly added to the system.
2.2 Knowledge Graph and Personalized Recommendation
The knowledge graph formally describes the knowledge information of a specific field objectively existing in the real world by constructing a heterogeneous network that uses multiple relationships to connect multiple types of entities. As shown in Fig. 1, the characters and movies contained in the dashed circles are different types of entity nodes in the knowledge graph (for example, actors, directors, and movies, or characters and movies). The yellow dashed line represents the different relationships between these entities (for example, “is director of” represents the relationship between the director and the film, “is actor of” represents the relationship between the actor and the film). For the association relationship shown in Fig. 1, we can formally define it in the form of triples: (Paul Walker, is actor of, 2 Fast 2 Furious), (John Daniel Singleton, is director of, 2 Fast 2 Furious). The large amount of entity association information contained in the knowledge graph is used as a piece of effective auxiliary information to supplement the entities in the recommendation system and the association relationships between entities. In this way, the recommendation system can dig out the hidden relationships that may exist between users and items [16,17]. Specifically, for user A in Fig. 1, we know that he likes The Fast and the Furious with Paul Walker. According to the two association relationships (Paul Walker, is actor of, 2 Fast 2 Furious) and (Paul Walker, is actor of, The Fast and the Furious) existing in the knowledge graph, we can think that user A might like the movie 2 Fast 2 Furious. Therefore, we can recommend 2 Fast 2 Furious, a movie that was not originally included in the historical interaction data, to users, making the recommendation more diverse and applicable. However, some existing recommendation system models that use knowledge graphs have some shortcomings. For example: Although the DKN model constructed by Wang et al. [11] mentioned above uses knowledge graphs to improve recommendation performance, it is only suitable for online news recommendation systems; Huang et al. [18] used the same TransE model as CoFM as the node embedding representation in the knowledge graph, and there are also 1-N, N-1, and N-N problems.
On the other hand, we also need to take an objective view of the limited knowledge of the knowledge graph as a limited knowledge base. How to use the existing interactive correlation data to complement the knowledge graph is also a work that we need to consider and complete. As shown in Fig. 1, through the collected historical interaction data, we know that user B prefers the movies The Other Guys, Ghost Rider, and 2 Fast 2 Furious. According to the existing associated information: (Eva Mendes, is actor of, 2 Fast 2 Furious), (Eva Mendes, is actor of, The Other Guys), we can infer that there may be an association relationship (Eva Mendes, is actor of, Ghost Rider). Through the above methods, we can use existing data to complement the association relationships that may be missing in the knowledge graph.
Many current pieces of research focus on using knowledge graphs as auxiliary knowledge bases to improve the performance of personalized recommendations [17,18,19]. For the first time, CoFM uses user-item interaction history information to complement the knowledge graphs to improve the performance of personalized recommendations. However, one of the core models used in CoFM, TransE, cannot well identify and distinguish the 1-N, N-1, and N-N relationships that exist in the knowledge graph. This directly limits the performance improvement threshold of the knowledge graph for a personalized recommendation.
3 JFMH: Joint Factorization Machines and TransH Model
The core work we need to do is to improve the CoFM model's ability to recognize 1-N, N-1, and N-N relationships. Specifically, we hope to improve the effectiveness of the CoFM model by solving the problem that TransE cannot well identify 1-N, N-1, and N-N relationships.
As shown in Fig. 2, we take the user-item historical interaction data collection, the specific corresponding domain knowledge graph triple set, and the entity-item mapping relationship as the input of the entire system. Among them, the data collection of the user-item historical interaction relationship is regarded as the input of the FM model (as shown in the upper right corner of Fig. 2), and the main goal is to obtain an embedded representation of the user interaction relationship. The TransH model based on graphic embedding is used to represent the structured information in the knowledge graph (as shown in the lower-left corner of Fig. 2).
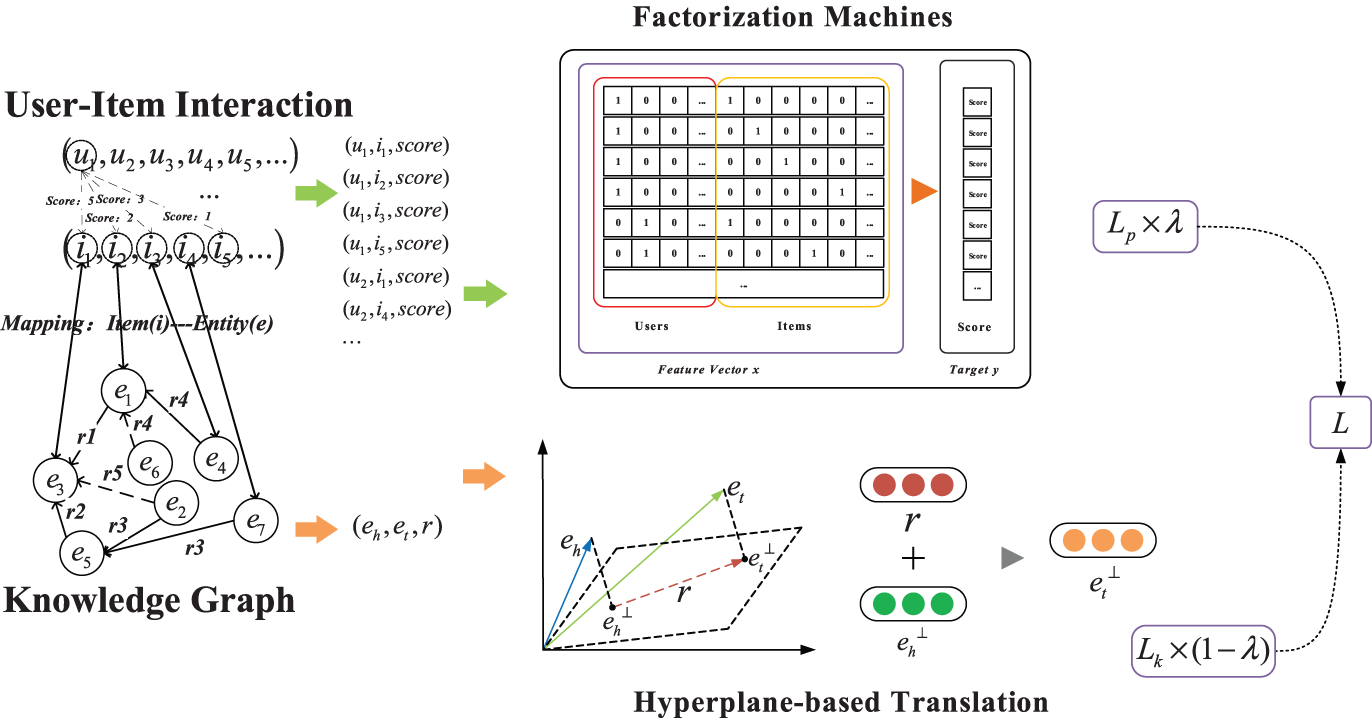
Figure 2: Framework of JFMH. Build a fusion learning model based on FM and TransH, and adjust the learning weights of the two tasks through the fusion parameter λ
3.1 Graph Representation Model
The graph representation algorithm based on representation learning is inspired by the research on word vectors in the field of NLP, such as the typical example shown in Eq. (2).
It is found that word vectors have the characteristics of spatial translation. Based on similar ideas, entities and relationships in the knowledge graph are represented by the method of graph embedding, to expand the semantic information represented by original items and users. The graph embedding algorithm mainly includes the graph embedding method based on Trans series and the graph embedding method based on heterogeneous information networks. Among them, the embedding method of the Trans series is a typical method to represent entities and relationships in the knowledge graph. The purpose of such methods is to map entities and relationships to a continuous vector space to obtain a low-dimensional dense representation, mainly including TransE, TransH. The characteristic of this method is that it can effectively reduce the dimension disaster problem. At the same time, it can capture the implicit correlation between entities and relationships, and the calculation efficiency is high [20].
TransE method as the enlightenment method of Trans series methods, its learning goals are [13]: Through continuous iterative learning of sample embedding, the model finally makes the vector embedding h of the head entity closer and closer to the vector embedding t of the tail entity after summing with the relation vector embedding r (as shown in Fig. 3a). Unfortunately, although this type of method is effective, it cannot solve the typical 1-N, N-1, and N-N problems. In the knowledge graph shown in Fig. 1, there are two triples (Eva Mendes, is actor of, The Other Guys) and (Eva Mendes, is actor of, 2 Fast 2 Furious). When learning the node embedding of Eva Mendes according to the idea of TransE based on the two samples mentioned above, we will find that since the tail entities The Other Guys and 2 Fast 2 Furious belong to two different types of movies (comedy and crime, action movies), the model cannot learn the optimal vector representation of the head entity Eva Mendes. Specifically, when the model is trained with samples (Eva Mendes, is actor of, The Other Guys), the vector representation of the node Eva Mendes is obtained. Then the model used (Eva Mendes, is actor of, 2 Fast 2 Furious) for testing, and found that the vector representation of node Eva Mendes became unsuitable, so the model optimized training in the direction of (Eva Mendes, is actor of, 2 Fast 2 Furious). As a result, the vector of the node Eva Mendes represents the problem of repeated horizontal jumps.
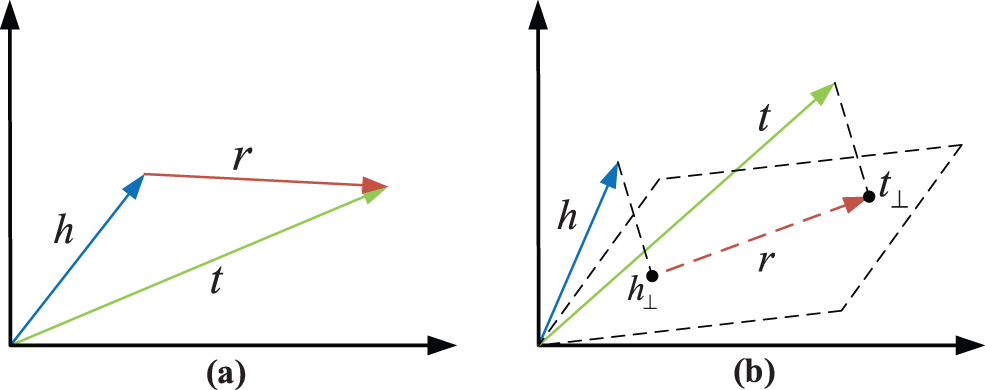
Figure 3: Representation learning method based on graph embedding: TransE (a) & TransH (b)
To solve the problems mentioned above, Wang et al. [14] proposed another representation learning model TransH (as shown in Fig. 3b). In the TransH model, we do not directly add the head and tail entities vectors and the relation vector like TransE, but do the projection operation on the head and tail entities to the hyperplane Wr to obtain the projection of the head and tail vectors to represent h⊥ and t⊥ before doing the calculation. Both of them satisfy h⊥ + r ≈ t⊥ on the hyperplane Wr, and the Eq. (3) holds.
Concerning the construction of the loss function of the graph representation task in other methods [21], we define the loss function Lk as shown in Eq. (4).
where KGneg represents our artificially constructed set of random negative samples: constructing negative samples by randomly replacing the head entity or tail entity in the original triple. γ is a constant representing the maximum distance between positive and negative samples. e or e′ represents the vector embedding representation of the node. The expression of f( ⋅ ) is
3.2 Personalized Recommendation
In the task of personalized recommendation, we use a more advanced FM model based on collaborative filtering to learn the user-item historical interactive embedding. The second-order definition of FM is shown in Eq. (5) [15].
where the function
where, vi = (vi1, vi2, …, vik) T ∈ ℝk, i = 1, 2, …, n, k ∈ ℕ+ is a hyperparameter. According to Eq. (6), we can see that the weight parameter of the second-order term in the FM model is not like the first-order term, it is a parameter constant belonging to the parameter space ℝ, but is obtained by multiplying two matrices vi and vj. In this way, FM can effectively deal with the situation where the user-item historical interaction information is highly sparse, and the parameters to be estimated for feature components that do not interact in the observed sample can still be estimated. For the loss function of the personalized item recommendation task, we refer to the work of Noia et al. [22] and define it as shown in Eq. (7).
Among them, the expression of δ is
3.3 Build a Fusion Learning Model
According to the transfer learning idea of the two tasks in the CoFM model proposed by Piao et al. [12] and the idea of balancing the two learning tasks in the KTUP model proposed by Cao et al. [21], we carry out a joint modeling representation of the two tasks of JFMH: Personalized recommendation tasks and graph representation learning and completion tasks.
Among them, Eq. (8) is the overall loss function of the JFMH model, and the weight of the loss value of the two learning tasks is adjusted through the parameter λ. Eq. (9) shows that JFMH adopts the idea of transfer fusion learning: transfer the source task S to the target task T under the guidance of the transfer weight parameter θ. Specifically, we define the Goal function as shown in the following Eq. (10).
In this section, we conduct quantitative experiments on item recommendation and knowledge graph completion. For this experiment, we used two data sets from different fields to compare our model with the baseline model as a whole.
Since we proposed the model JFMH as an improved version of CoFM, to make a more reasonable and effective comparison between the two, we refer to CoFM and selected two public data sets currently widely used in this field: MovieLens−1 m [22] and DBbook2014.
First, we need to process a given data set according to the model we proposed. Specifically, we need to process the user-item historical interaction information in the data set into a sequence of triples as shown in the upper left corner of Fig. 2, that is, user, item, and score, and construct the input feature vector of the input model based on these sequences. Secondly, it is necessary to construct the mapping relationship between the user's historical interaction information and the knowledge graph (as shown on the left side of Fig. 2), which is necessary to complete the transfer and fusion learning of the two tasks. As described in Section 3.1 and Section 3.2, constructing negative samples from the existing positive samples by randomly replacing items in the tuple is also a step of processing the original data set. Finally, we filter and clean the low-frequency items in the user-item interaction data set, and remove the rare entities in the corresponding knowledge graph.
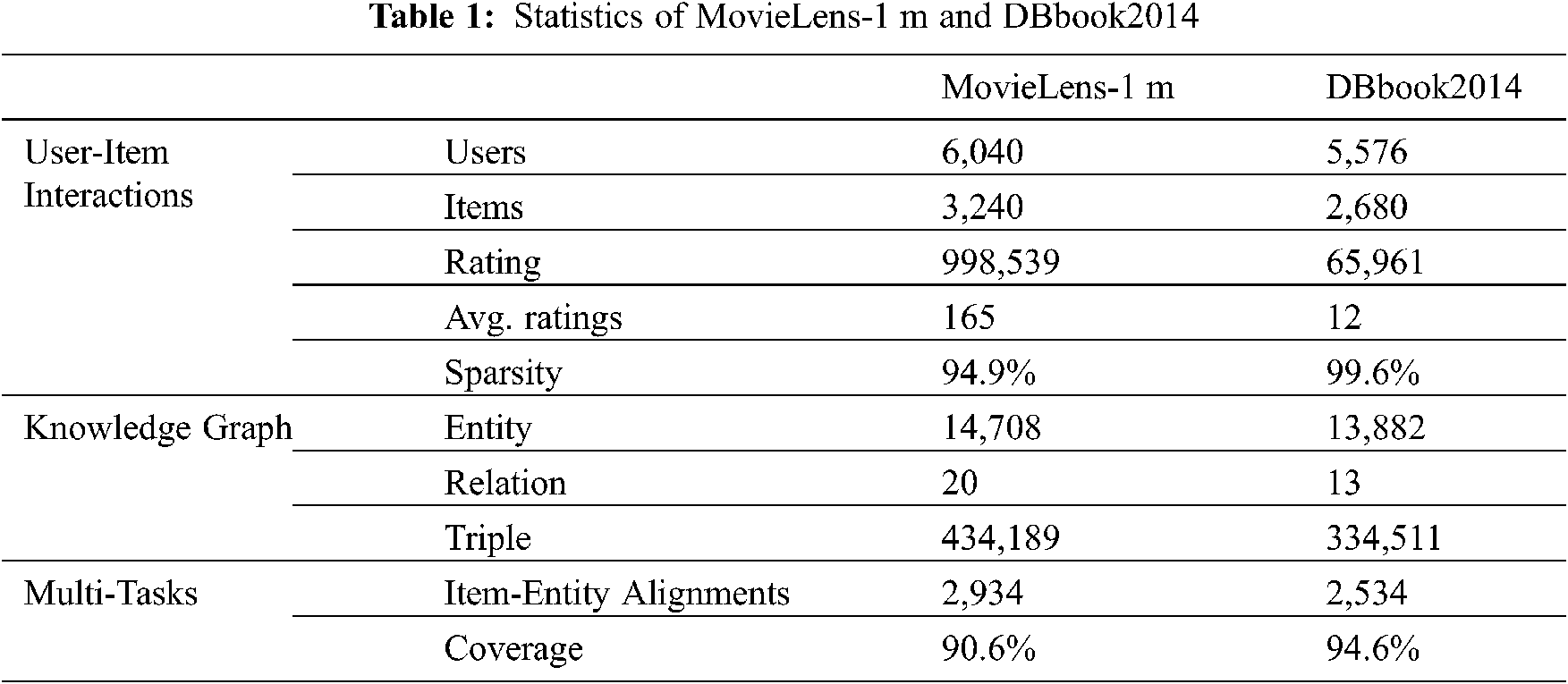
Tab. 1 shows the basic statistical information in the processed data set. The data distribution in the real data set verifies the dilemma of the data source of the recommendation system described in the previous article, that is, compared to the user set U and the item set I, we can use very little historical interactive information [4]. From Tab. 1, we can know that the sparseness of the relationship between the two data sets is 94.9% and 99.6%, respectively. On the other hand, the effective mapping between the items in the user-item interactive information and the entities in the knowledge graph reaches more than 90%, which ensures the feasibility of joint learning tasks.
For the related tasks of the recommender system, we use the following widely used model as the baseline model to compare with our proposed model.
First, as the basis of our model, it is necessary to use the FM [15] model and BPRMF [23] model based on collaborative filtering as the baseline method of our model. At the same time, this type of method has achieved relatively good results in many popular data sets, and it is reasonable to use it as a baseline method.
The second is the CFKG model [24], a typical representative of graph embedding methods based on heterogeneous information networks. This method integrates data from two different sources into a unified heterogeneous graph that includes users, items, entities, and relationships. The characteristics of the heterogeneous graph and the supplementary related information of the knowledge graph are used to improve the recommendation effect of the recommendation system. Therefore, this method also belongs to the category of hybrid recommendation algorithms. To compare with our proposed hybrid recommendation algorithm, we chose three hybrid recommendation algorithm models based on graph embedding: CKE [19], CoFM, and KTUP [21]. Among them, the CKE model uses the TransR method based on graph embedding to combine the recommendation system with the knowledge graph, and CoFM, as the improvement basis of our model method, combines the FM based on collaborative filtering and the TransE model based on graph embedding. Specifically, we label the CoFM model trained using two different training strategies as CoFM(share) and CoFM(reg). Similarly, KTUP also jointly models item recommendation and graph representation learning, so we also use it as our comparison object.
For the test and evaluation of the relevant performance of the recommendation system, we will adopt the following experimental ideas and take the relevant indicators as the main basis of the evaluation results. We use all the items in the test set as alternatives that may be recommended to a given user, and sort all items according to the likelihood score calculated by the model. Then, the recommendation system will push the top N items to the user as the final recommendation items by default (the value of N can be customized).
We have selected several evaluation indicators that are widely used in similar work.
• Precision@N: We define accuracy as the proportion of the actual number of items related to the user among the N items recommended by the system. For the experimental results of multiple given users in the test set, we calculated the average accuracy of all users as the final definition of accuracy. Precision@N is abbreviated as P@N.
• Recall@N: We define the recall rate as the proportion of items that are correctly recommended by the system about all items that are relevant to the user (i.e., the proportion of items that are successfully recommended about the user). Similarly, we calculate the average recall rate of all users as the final definition of recall rate. Recall@N is abbreviated as R@N.
• F1 score@N: The operation of calculating the harmonic average of the results of Precision@N and Recall@N, the value range is 0–1. F1 score@N is abbreviated as F1@N.
• Hit ratio@N: A measure of the quality of vector embedding. For a certain evaluation, we construct the interference item by replacing the real head entity (tail entity) with other entities. We calculate the entity distance for all interference items and the real entity-relationship triples. If the entity distance of the real entity relationship is in the top N positions, it is a hit, and the Hit ratio@N value is 1. Hit ratio@N is abbreviated as H@N.
• NDCG@N: Normalized Discounted Cumulative Gain (NDCG) is used to measure the grading correlation between positive samples and negative samples in the top N recommended items given by the system, and is an important indicator to measure the ranking quality given by the system.
In addition, in the targeted evaluation of the knowledge graph completion task, in addition to using Hit ratio@N to evaluate the embedding quality of the vector, we also used the following indicators.
• Mean Rank: This indicator is associated with Hit ratio@N, and they are both indicators for evaluating the quality of vector embedding. The difference is that Hit ratio@N focuses on whether there is a real entity relationship in the top N positions, and Mean Rank indicates how many points can be averaged in the test set to match the correct result. Mean Rank is abbreviated as MR.
According to the experimental results shown in Tab. 2, we can draw the following conclusions. Note that the values in the Tab. 2 are percentages:
1) Compared with the baseline method, the hybrid recommendation algorithm model we proposed performs well on two different data sets, and each evaluation index is better than the baseline method and has strong competitiveness.
2) In terms of performance improvement, compared with the best model results, JFMH's improvement of various indicators on the MovieLens-1 m data set is between 10% and 47.6%. In the DBbook2014 data set, except for Recall which has a decrease of about 2%, the increase of other indicators is between 0.2% and 6%. From this side, we can also see the impact of sparse interactive data on model performance.
3) Using the TransR method based on graph embedding, the CKE model combining the recommendation system and the knowledge graph takes a long time in the training process. Compared with other models, the CKE model is not suitable for the application scenarios in which the entity set is updated and iterated rapidly, and its real-time performance is poor.
4) The CoFM model with a shared parameter training strategy has better performance than the same model with another training strategy. The performance loss of mandatory alignment of entities is obvious.
5) The fusion recommendation model JFMH proposed by us is an improved model based on CoFM. Through experimental comparison, the JFMH that integrates the TransH model has obvious advantages. As predicted by our theory, the graph-embedded model TransH, which can capture the structural association of multiple entities, can better provide auxiliary help for the recommendation system.
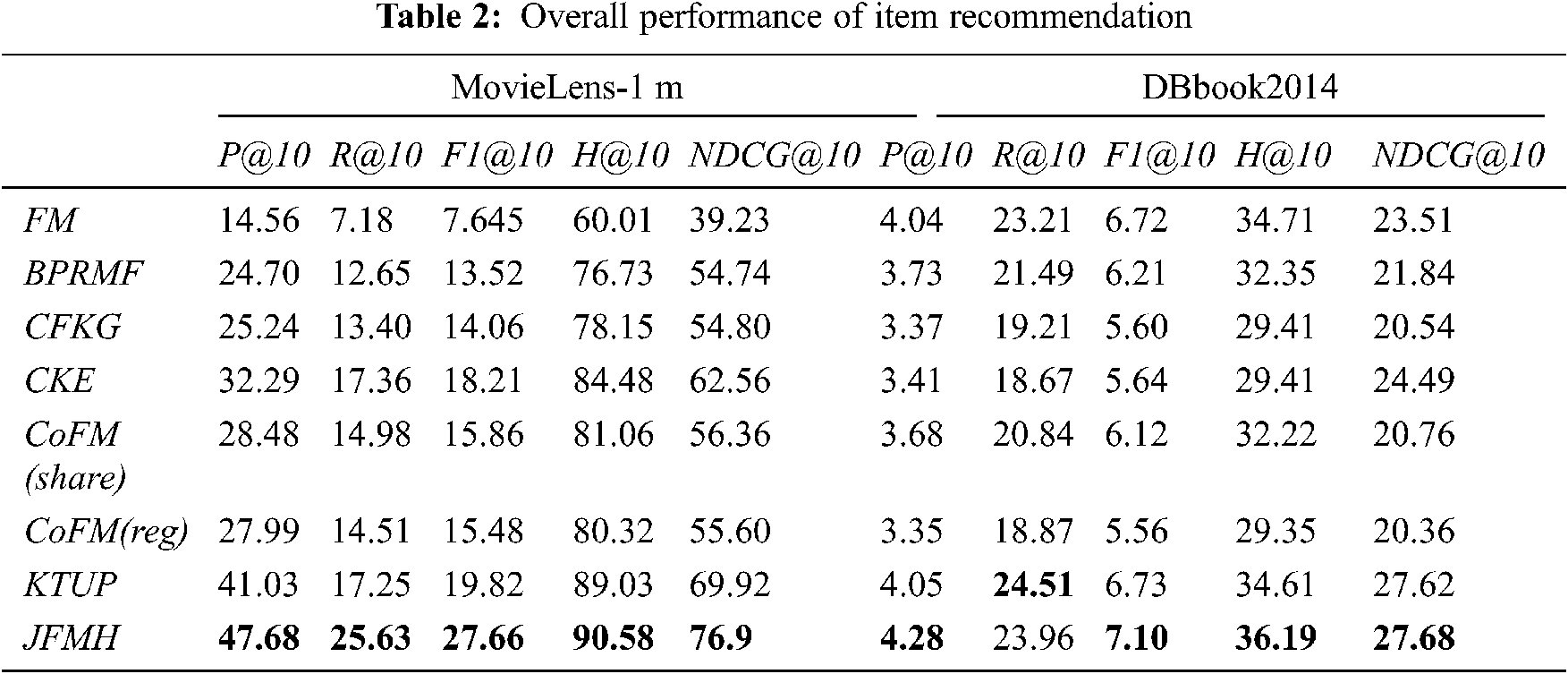
4.4.2 Knowledge Graph Completion
In this part, we conduct a targeted evaluation of the model's knowledge graph completion capability. From this evaluation dimension to evaluate the model, we can get the ability of the hybrid recommendation model to complement the triples with missing entities in the knowledge graph after combining the recommendation system and the knowledge graph. From this aspect, the hybrid recommendation model uses the knowledge graph to complete the recommendation task, and at the same time, it can feed back the knowledge graph completion task.
According to the experimental results shown in Tab. 3, we can see that JFMH performs better on the two data sets. First, a horizontal comparison of the performance of JMFH on the two data sets found that JFMH's indicators on the MovieLens-1 m data set are better than the DBbook2014 data set. Because MovieLens-1 m contains more associations between users and items, it helps to model the structural knowledge between entities. On the other hand, JFMH has a slightly lower hit rate on the DBbook2014 data set, but from the average evaluation index “MR”, our model is better in terms of average performance in most cases. We think this is better for the model. We believe that the stability of model performance is more important for the model. Note that the values in Tab. 3 are percentages.
4.4.3 Performance Improvement Test
In order to test the performance of the model more comprehensively, we designed control experiments and repeated experiments by adjusting the model parameters. Using the controlled variable method, we conducted many experiments on the model we proposed on two different data sets and obtained the index values of the model performance under different conditions and parameters. This provides data support for objectively evaluating the performance of the model.
Firstly, we balance the performance of the item recommendation task of the recommendation system and the performance of the knowledge graph completion task by adjusting the joint rate of the recommendation system and the knowledge graph. The experimental results are shown in Fig. 4.
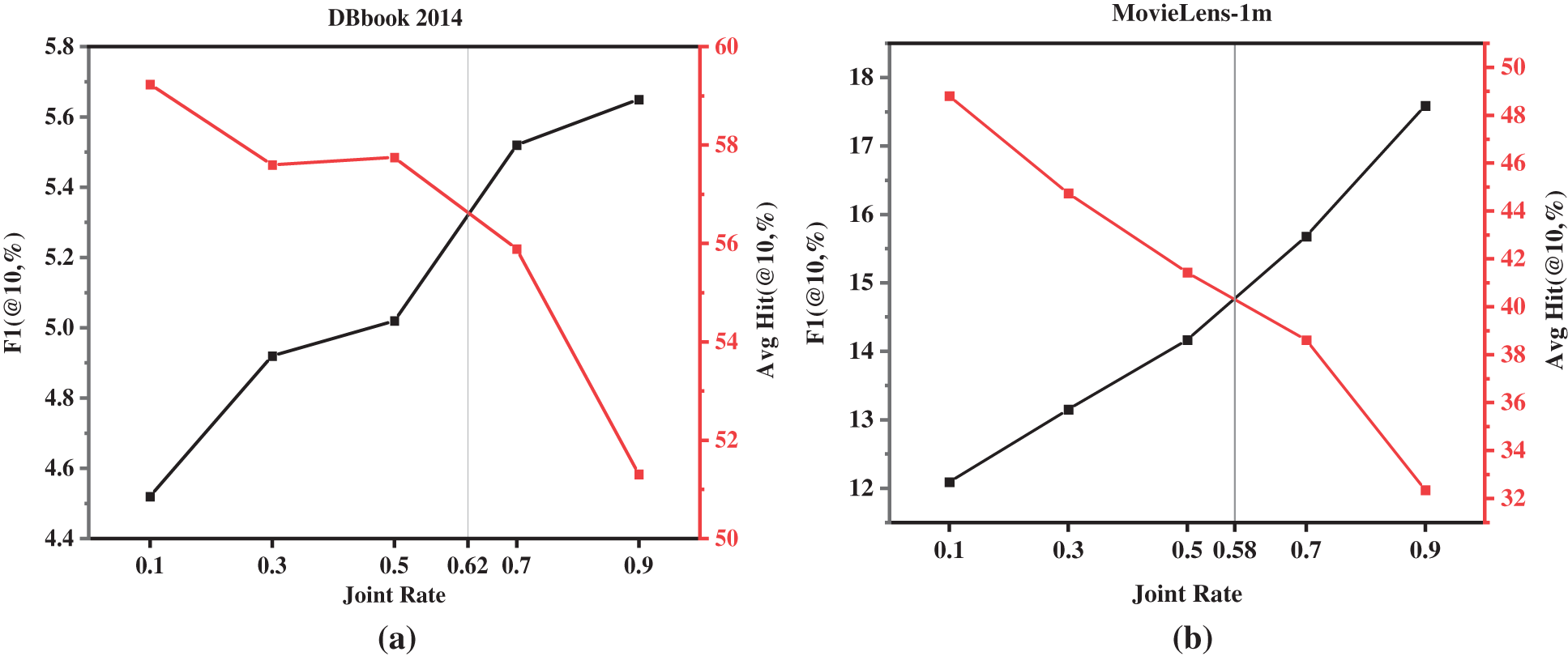
Figure 4: The effect of joint rate on model performance on different datasets
In the experiment process of two different datasets, we found that there was a negative correlation between the performance of item recommendations and knowledge graph completion. Specifically, when the item recommendation achieves better performance, the model's knowledge graph completion ability is often very poor. As can be seen from Fig. 4, when the joint rate is about 0.6, the model can balance the tasks of the two aspects and achieve relatively balanced performance.
Further, we explored the impact of different batch sizes on model performance. Based on experience, we set the batch size to 64, 128, 256, 512, and 1024. Five sets of repeated experiments were set on the two data sets, and the results of the repeated experiments were averaged to obtain the experiment shown in Fig. 5. Obviously, when the batch size is 512, the model performs well on the data set DBbook2014, but the performance on the MovieLens-1 m data set is not optimal. According to the different sparse rates of the entity-relationship of the two data sets, we can conclude that when the sparse rate is relatively low, it is a wise choice to choose a batch size of 512, otherwise, a larger batch size may be better. On the other hand, we pay more attention to the performance of the model when the data is sparse, so we fixed the batch size to 512 to continue the next experiment. Note that in order to obtain better performance of the model in item recommendation, according to the experimental results shown in Fig. 4, in this set of experiments we fixed the joint rate to 0.9.
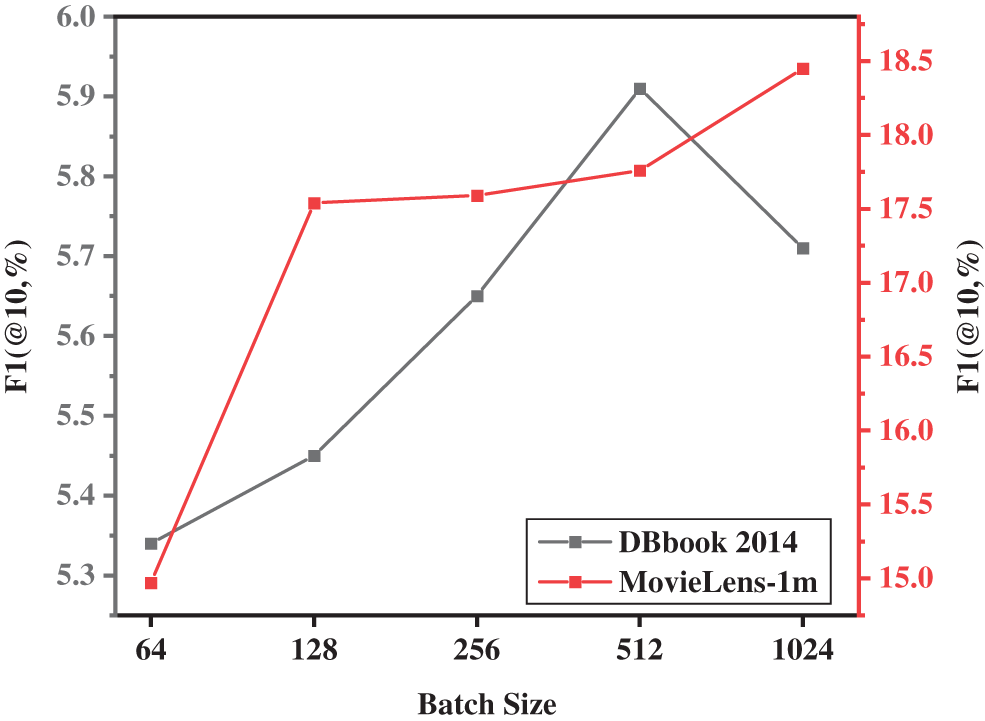
Figure 5: The impact of training batch size on model performance under different datasets
More importantly, we also conducted a grid search experiment on the hyperparameter of the dimension of the embedding vector trained in the model. We set the vector dimensions to 64, 100, 256, 512, and 1024, and set up five sets of repeated experiments on the two data sets. After averaging the results of repeated experiments, the experimental results shown in Fig. 6 are obtained. In the same way, in order to obtain better performance of the model in item recommendation, in this set of experiments, we fixed the joint rate to 0.9 and the batch size to 512. By analyzing the experimental results shown in Fig. 6, we can easily conclude that the effect of the model is very good when the vector dimension is 1024. But in this case, the training time is longer. Therefore, we can adjust the dimensionality of the embedding vector according to different application scenarios to balance the relationship between model performance and training time.
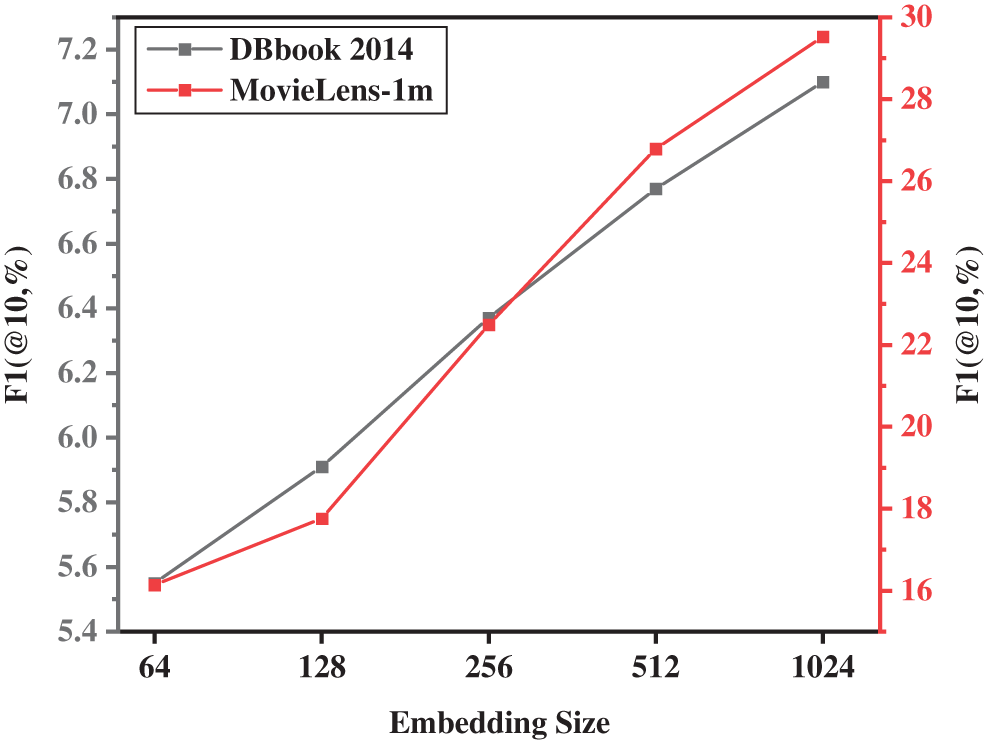
Figure 6: The impact of different embedding vector dimensions under different datasets on model perfomance
Based on the TransE-based fusion recommendation model CoFM, this paper proposes a novel TransH-based fusion recommendation model named JFMH. The model is improved based on CoFM, replacing the graph embedding-based TransE model with a TransH model that can solve 1-N, N-1, and N-N problems, thereby improving the overall recommendation performance. The TransH model is leveraged to better recognize the rich knowledge of different categories provided by the knowledge graph. It can improve the performance of the recommendation system by effectively mine the implicit association relationships in the user interaction data. Although JFMH has supplemented the implicit relationships that are not included in the historical interaction relationship between user-item interactions by introducing knowledge graphs, there are still difficulties in solving strictly cold-started items that do not include any interaction relationships. In the future, we are interested in solving the cold start problem through methods such as attribute modeling and multi-hop neighbor relationship mining.
Funding Statement: This work is funded by State Grid Shandong Electric Power Company Science and Technology Project Funding under Grant no. 520613200001, 520613180002, 62061318C002, and Weihai Scientific Research and Innovation Fund (2020).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D.Zhu,H.Du andY.Sun,“Massive files prefetching model based on LSTMneural network with cache transactionstrategy,” Computers, Materials& Continua, vol. 63, no.2, pp. 979–993,2020. [Google Scholar]
2. S.J. Ben,J.Konstan, andJ.Riedl,“Recommender systems ine-commerce,” in Proc.EC99, Denver Colorado, DC, USA, pp.158–166,1999. [Google Scholar]
3. A.Gediminas andA.Tuzhilin,“Toward the next generation of recommendersystems: A survey of the state-of-the-art and possibleextensions,” IEEE Transactions onKnowledge and Data Engineering, vol. 17, no.6, pp. 734–749,2005. [Google Scholar]
4. C.Qin,H.Zhu,F.Zhuang,Q.Guo,Q.Zhang etal., “A survey onknowledge graph-based recommender systems,”Scientia Sinica Informationis, vol.50, no. 7, pp.937–956,2020. [Google Scholar]
5. B.Sarwar,G.Karypis,J.Konstan andJ.Riedl,“Item-based collaborative filteringrecommendation algorithms,” in Proc.WWW01, Hong Kong, HK, Hong Kong, pp.285–295,2001. [Google Scholar]
6. Y.Koren,“Factorization meets the neighborhood: amultifaceted collaborative filtering model,” inProc. KDD08, Las Vegas Nevada, LVN,USA, pp. 426–434,2008. [Google Scholar]
7. X.He,L.Liao,H.Zhang,L.Nie,X.Hu etal., “Neural collaborativefiltering,” in Proc.WWW17, Perth, Australia, pp.173–182,2017. [Google Scholar]
8. W.Jiang,J.Chen andY.Jiang,“A new time-aware collaborative filteringintelligent recommendation system,”CMC-Computers Materials & Continua, vol.61, no. 2, pp.849–859,2019. [Google Scholar]
9. A.Wulam,Y.Wang andD.Zhang,“A recommendation system based on fusingboosting model and DNN model,”CMC-Computers Materials & Continua, vol.60, no. 3, pp.1003–1013,2019. [Google Scholar]
10. H.Bai,X.Li andL.He,“Recommendation algorithm based on probabilisticmatrix factorization with adaboost,”CMC-Computers Materials & Continua, vol.65, no. 2, pp.1591–1603,2020. [Google Scholar]
11. H.Wang,F.Zhang,X.Xie andM.Guo,“DKN: Deep knowledge-aware network for newsrecommendation,” in Proc. WWW18,Lyon, France, pp.1835–1844,2018. [Google Scholar]
12. G.Piao and J.G.Breslin,“Transfer learning for item recommendations andknowledge graph completion in item related domains via aco-factorization model,” in Proc.ESWC 2018, Heraklion,Crete, 2018. [Google Scholar]
13. A.Bordes,N.Usunier,A.Garcia-Duran,J.Weston andO.Yakhnenko,“Translating embeddings for modelingmulti-relational data,” Advances inNeural Information Processing Systems, vol.26, pp.2787–2795,2013. [Google Scholar]
14. Z.Wang,J.Zhang,J.Feng andZ.Chen,“Knowledge graph embedding by translating onhyperplanes,” in Proc.AAAI-14, Québec, Canada, vol.28, no. 1,2014. [Google Scholar]
15. S.Rendle,“Factorization machines,”in Proc. ICDM10, NW Washington, DC,USA, pp. 995–1000,2010. [Google Scholar]
16. X.Yu,X.Ren,Y.Sun,Q.Gu,B.Sturt etal., “Personalized entityrecommendation: A heterogeneous information networkapproach,” in Proc. WSDM2014, New York, NY, USA, pp.283–292,2014. [Google Scholar]
17. X.Wang,X.He,Y.Cao,M.Liu andT.Chua,“Kgat: knowledge graph attention network forrecommendation,” in Proc. KDD‘19, New York, NY, UnitedStates, pp. 950–958,2019. [Google Scholar]
18. J.Huang, W.X. Zhao,H.Dou, J.R. Wen andE. Y.Chang,“Improving sequential recommendation withknowledge-enhanced memory networks,” inProc. SIGIR ‘18, Ann Arbor,MI, USA, pp. 505–514,2018. [Google Scholar]
19. F.Zhang, N.J. Yuan,D.Lian,X.Xie andW.Ma,“Collaborative knowledge base embedding forrecommender systems,” in Proc. KDD‘16, San Francisco California, SFC,USA, pp. 353–362,2016. [Google Scholar]
20. D.Zhu,H.Du, andX.Li,“MINE: A method of multi-interactionheterogeneous information network embedding,”CMC-Computers Materials & Continua, vol.63, no. 3, pp.1343–1356,2020. [Google Scholar]
21. Y.Cao,X.Wang,X.He,Z.Hu andT.Chua,“Unifying knowledge graph learning andrecommendation: Towards a better understanding of userpreferences,” in Proc. the WorldWide Web Conf., San Francisco, CA, USA, pp.151–161,2019. [Google Scholar]
22. T.D. Noia,V. C.Ostuni,P.Tomeo andE. D.Sciascio,“Sprank: semantic path-based ranking for top-nrecommendations using linked open data,”ACM Transactions on Intelligent Systems and Technology(TIST), vol. 8, no.1, pp. 1–34,2016. [Google Scholar]
23. S.Rendle,C.Freudenthaler,Z.Gantner andL.Thieme,“BPR: Bayesian personalized ranking fromimplicit feedback,” arXiv preprintarXiv:1205.2618, 2012. [Google Scholar]
24. Y.Zhang,Q.Ai,X.Chen andP.Wang,“Learning over knowledge-base embeddings forrecommendation,” arXiv preprintarXiv:1803.06540, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |