DOI:10.32604/csse.2022.022107

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.022107 |  |
| Article |
Metaheuristic Based Resource Scheduling Technique for Distributed Robotic Control Systems
1Department of Computer Science and Engineering, E.G.S. Pillay Engineering College, Nagapattinam, 611002, India
2Department of Mechanical Engineering, E.G.S. Pillay Engineering College, Nagapattinam, 611002, India
*Corresponding Author: P. Anandraj. Email: anand.happy123@gmail.com
Received: 27 July 2021; Accepted: 27 September 2021
Abstract: The design of controllers for robots is a complex system that is to be dealt with several tasks in real time for enabling the robots to function independently. The distributed robotic control system can be used in real time for resolving various challenges such as localization, motion controlling, mapping, route planning, etc. The distributed robotic control system can manage different kinds of heterogenous devices. Designing a distributed robotic control system is a challenging process as it needs to operate effectually under different hardware configurations and varying computational requirements. For instance, scheduling of resources (such as communication channel, computation unit, robot chassis, or sensor input) to the various system components turns out to be an essential requirement for completing the tasks on time. Therefore, resource scheduling is necessary for ensuring effective execution. In this regard, this paper introduces a novel chaotic shell game optimization algorithm (CSGOA) for resource scheduling, known as the CSGOA-RS technique for the distributed robotic control system environment. The CSGOA technique is based on the integration of the chaotic maps concept to the SGO algorithm for enhancing the overall performance. The CSGOA-RS technique is designed for allocating the resources in such a way that the transfer time is minimized and the resource utilization is increased. The CSGOA-RS technique is applicable even for the unpredicted environment where the resources are to be allotted dynamically based on the early estimations. For validating the enhanced performance of the CSGOA-RS technique, a series of simulations have been carried out and the obtained results have been examined with respect to a selected set of measures. The resultant outcomes highlighted the promising performance of the CSGOA-RS technique over the other resource scheduling techniques.
Keywords: Distributed robotic control system; resource scheduling; load balancing; resource utilization; metaheuristics; shell game optimization
In the recent years, due to the high control performance, high reliability of the distributed control systems (DCS), low implementation costs, and reconfiguration flexibility, they have been extensively used in various areas. There are several benefits in utilizing a DCS in the robot collection procedures [1]. These systems are capable of controlling a wider range of heterogeneous devices and do so on greater physical distances. Such a scheme might be very modular and can therefore support multiple devices. The implementation and design of a DCS that works efficiently and effectively in various hardware configurations and computations may be a nontrivial task [2]. For instance, one of the most important consideration here is to ensure the accessibility of resources by the various components in the system (such as the computational units, communications channels, sensor inputs, robot chassis) for accomplishing their task efficiently [3]. Not all resources can adapt to several concurrent access requests at the same time, and several resources on the other hand can manage only a single request at a particular time instant. Another problem here is to define an appropriate procedure for the distribution of requests for the concerned resources inside the entire system. This procedure in a way ensures the balancing conditions of the computation and the resource loads and further confirms that none of the components in the system are charged beyond the defined levels. A DCS was established for handling the collection of small mobile robots possessing the required computing capabilities and restricted on-board sensing ranges [4]. Fig. 1 illustrates the overview of the robotic control model.
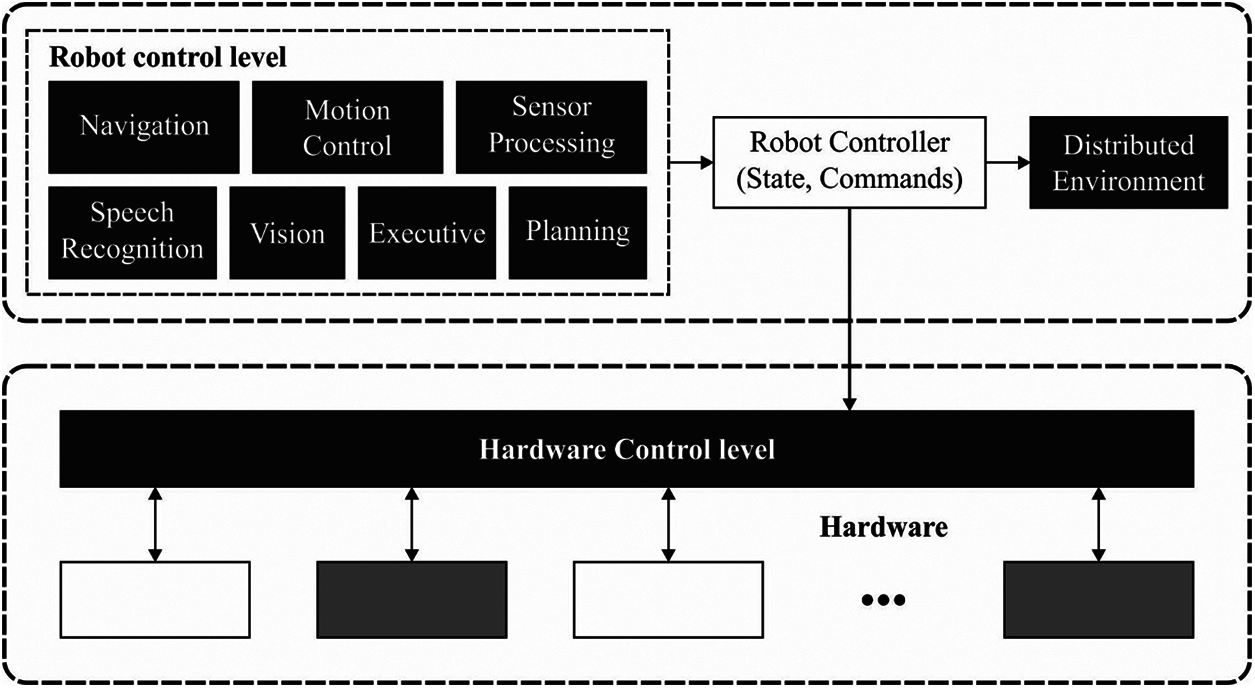
Figure 1: Overview of the robotic control system
The robots should be capable of working with teams: this ability assures that a large physical area could be surveyed by the robots and hence could provide a degree of redundancy by pointing out the robots that are either deactivated or the ones that are unable to complete their tasks on time. Moreover, the robots must function independently. Because of the weight and size constraints of the Scout's design, the computation hardware that is accessible on a Scout is constrained with a limitation of 2 8-bit microcontrollers [5]. For utilizing the processor resources, several tasks often run on a processor. The scheduling algorithms of this task not only affects the utilization of a processor but also controls the system's performance [6]. The optimum scheduling methodology opted for the multiprocessors is the NP hard, hence the heuristic algorithms are often adopted for the allocating tasks. A technique employed for scheduling the tasks in the distributed systems is the integration of the scheduling algorithms for the uniprocessor and the static task distribution algorithms [7]. Followed by which, the system would start functioning, whereas, the processor assigned tasks would be observed to remain unaltered. The algorithms are simpler and the offset of the scheduling algorithms are smaller. Another type of allocation algorithm is the dynamic allocation algorithm. The tasks in this case might migrate to the processor during the run time of the system. The algorithms are capable of achieving the required optimal objective functions such as the control performance of system, processor utilization, and so on. However, the algorithms are observed to be highly complicated with bigger offsets and the foreseeability of the algorithms appear to be weak.
This study emphases on the dynamic allocation of resources during the runtime instead of analyzing the resource requests offline, it encourages for plan changes when the requests are not fulfilled. Especially, this method is appropriate for an unpredicted environment in which the resources should be assigned in a dynamic manner that cannot be anticipated before. Load schedule is thus determined as the procedure for balancing, providing, and allocating the load in DCS effectively. The primary objective is to decrease the transmission time and the overall cost acquired for scheduling the load in the scheme. The scheduling of the load is executed by different scheduling methods. The scheduling algorithm is determined based on the dynamic and static nature of the load. Also, they are categorized into the non-heuristic and the heuristic types. The Meta heuristic algorithm plays a significant role in scheduling the load through an appropriate search procedure. At present, to conquer the disadvantages, several scientists have resolved this challenge by utilizing the optimization algorithm. However, this methodology fails to achieve the required processing cost, completion time, and load related attributes efficiently. To combat this problem, a group of metaheuristic-based load scheduling algorithms have been proposed for the DCS robotic environments.
This paper introduces a novel chaotic shell game optimization algorithm (CSGOA) for resource scheduling called as the CSGOA-RS technique for the distributed robotic control system environment. The CSGOA technique is based on the integration of the chaotic maps concept to the SGO algorithm to enhance its overall performance. The CSGOA-RS technique has derived a fitness function involving three different parameters such as the make span, the reliability cost, and the mean flow time (MFT) for the allocation of resources in such a way that the resource utilization can be considerably improved. The CSGOA-RS technique is valid even for the unforeseen environment where the resources are to be allotted dynamically using the prior estimations. The performance of the CSGOA-RS technique can be examined under different aspects and the results can be discussed extensively.
Lee et al. [8] proposed the architecture for balancing the workload and the competency adjustments in the multirobot task distributions. Competency represents the capability of a robot for executing a task based on its cost and quality, and the workload balancing mechanism represents the allocation of workloads between the robots. This method considers the cost and quality of a robot for a task and thereby adjusts them according to the changes in the environment. For balancing the workload, this method uses the idea of subsidy to inspire the participation of the lesser active member of the robot teams. Experimental result demonstrates that this model could alter the competency levels according to the changes in the environment and allocate workloads between the robots in a balanced way. Goyal et al. [9] addressed the problem of energy utilization using the cloud platforms. The techniques and algorithms should be capable of reducing the schedule resources and power consumption levels for enhancing the efficacy of the server. Also, Load balancing appears to be a significant part of cloud technique as it encourages for balanced load allocations between the servers for satisfying the user requirements. This study has made use of various optimization methodologies such as the PSO, CSO, BAT, CSA, and WOA for balancing the load, energy efficacy, and resource scheduling for creating an effective cloud platform. Blankenburg et al. [10] proposed a distributed multi-robot control framework that addresses the above mentioned problems and accomplishes the succeeding participations: i) it permits for the online and dynamic distribution of robots to the various phases of the task, ii) it makes sure that the collaborative robot scheme would follow the individual task constraints and iii) it permits for opportunistic, flexible task implementations in distinct environment conditions. This framework utilizes a distributed messaging scheme for allowing the robots to interact with each other. Every robot uses its team member and own state for monitoring the growth on a provided task and recognizes the appropriate subtask for executing an activation spreading methodology.
Zhu [11] proposed a solution to the fairness problems in multitype resource allocations for the multirobot methodologies possessing multiple resource requests. They employ DRF principles in this solution for 2 distinct schemes: STR-MRT and MTR-SRT. In STR-MRT, the robots can execute only individual tasks at a time, task is separable, and for accomplishing the entire set of tasks they would require an increased number of robots. In MTR-SRT, the robots are capable of executing multiple tasks at a time, tasks here are inseparable and the entire set of tasks can be accomplished by a single robot. Delgado et al. [12] offered a complete procedure in the event of realizing the OES on the basis of public domain real world operating systems on many low cost OES platforms. Their efficiency was compared and evaluated based on the interrupt response time, periodicity, scheduling ability, and task synchronization i.e., with respect to the critical metrics for determining the reliability and stability of the real-world regulators. Maoudj et al. [13] handled the growth of a DMAS for controlling and scheduling RFAC. In this technique, a method for solving the key challenge decision problems in RFAC was proposed and implemented. These problems are thus interrelated to the product operation scheduling features that relies on the sequencing and allocation aspects on the robots while fulfilling the robot and product based limitations under the make span minimization. The presented DMAS addresses this problem with the help of a cooperative methodology that is supported by 3 different types of independent control agents, namely, the local agent, the remote agent and the supervisory agent. Yuan et al. [14] proposed a G/G/1 queuing scheme for analyzing the efficiency of the server in DGC. Based on the single objective constraints the optimization problems are solved and formulated by a presented SBA, this is done for identifying the SBA that could minimize the energy cost of a DGC supplier by optimally assigning the tasks of heterogeneous applications amongst the various DGCs. It further specifies the running speed of the servers and the amount of power on the servers in every GC while confronting the respond time limitations of the tasks of each of the individual applications.
Gultekin et al. [15] proposed a second order cone programming formulation for detecting the Pareto efficient solutions. The conic formulation was capable of detecting the robotic schedules for the smaller cells with limited number of machines in moderate computational time durations. This approach could produce a huge set of accurate Pareto effective solutions in a shorter computation time. Wang et al. [16] addressed the multi robot task scheduling mechanism for 2 types of robots arising from the heterogeneous robotic order fulfillment system. The heterogeneous multi robot scheme consists of 2 kinds of robots with complementary and specialized abilities for achieving long cycle and multi-station order fulfilment tasks on a logistic network. Such problems are very complex due to the innate complex schedule constraint of the tasks and hence coupled based on the temporal–spatial relationships among the robots. This procedure would then be followed by the construction of a set-theoretic and mixed integer linear programming problem formulation mechanism, this essentially makes use of the coupled methodology instead of the decoupled methodologies for exploring the synergies among the heterogeneous robots, i.e., unlike the techniques proposed in the present studies.
Sun et al. [17] proposed 2 new robotic job shop scheduling methods using deadlock and robot motion considerations (RJSPDT). The presented method concurrently considers the scheduling of tack operations and motion of the robots with an aim of minimizing the make span. Two modeling methods have been employed here, namely, the conventional position and the new network based approaches i.e., stimulated by the aviation scheduling work. Fu et al. [18] focused on the online scheduling and charging approaches of the robots in warehouses using the unknown moving paths. Initially, the storage scenarios here would be abstracted to a grid methodology. Next, the shortest path algorithms would provide priority to the robotic tasks based on the coordinate differences. Later, the minimal service quantity of the MC would be defined by the arbitrary simulations.
In He et al. [19], developed the distributed cooperative controllers for a selected set of scenarios. Here, certain aspects such as the manipulability enhancement, transport of the object, and obstacle avoidance are attained online with a new optimization-based methodology. As the local controllers don't require another robot for transmitting the method or for joining the space data, the systems appear flexible with communication costs. Fang et al. [20] used an interconnected undirected graph for describing the multiple redundant manipulator systems. In the existing studies, it is observed that some constraints include the convex set built for the joint physical limit, inequality constraints are derived for avoiding the obstacles, and equality constraints are derived for tracking the required paths. New distributed neurodynamic based algorithms are evolved for solving the complicated problems in real-world, hence it is necessary to have a central coordinator in the multirobot systems.
3 Background Information: System and Task Models
The control loop must be capable of transmitting the required control signals to the concerned process, it should effectively compute the control signals and acquire the required data from a physical procedure. Such functions have been found to influence one another forming loops, these loops are named as loop tasks as they represent a task in the system. As the period of these loop tasks tend to differ to a specific extent they would not be set prior to the initialization of the process [21]. DCS operates on several processors through a transmission network. Various processors are adapted in DCS for realizing different types of control tasks, therefore DCS is heterogeneous, i.e., the implementation time is distinct on distinct processors. Depending on this, the processor and loop task models have been provided below.
Definition 1. Loop tasks set in DCS indicates S = {τ1, τ2, …, τn}(n ≥ 2). Where τi ∈ S represents the ith loop task and is quintuple.
where C,
Definition 2. DCS is defined as a processor set Ω that operates on a network: Ω = {Pr1, Pr2, …, Prm}(m ≥ 2), Pri = (ρ, u), where ρ and u represents the processing ability coefficients and the utilization of the processor Pri correspondingly.
For a loop task, the implementation time vectors are presented as follows.
Definition 3. In DCS, τi.C is determined as a vector
Definition 4. The processing ability coefficients represent the performance speed of the loop tasks on a processor. In heterogeneous DCS, processors are elected as regular processors, denoted as Prnor, and its processing ability coefficients are represented as one. The processing ability coefficients of Pri is given below
Whereas τj.C(Prnor) represents the implementation time of the loop task τj on a regular processor and τj.C(i) indicates the implementation time of the similar loop tasks on the processor Pri.
Definition 5. When each loop task in DCS completes before the assigned deadlines then the DCS can be categorized under the schedulable type.
This study is based on the following succeeding rules:
i) The required number of loop tasks and processors are to be set.
ii) The deadline of the loop task is equivalent to their period.
iii) Loop tasks are independent of one another.
In this study, an effective CSGOA-RS technique has been developed for scheduling the resources proficiently in the distributed robotic control system. The CSGOA-RS technique is intended to allot the resources in such a way that the transfer time is minimized and the resource utilization is increased. In addition, the CSGOA-RS technique has derived a fitness function involving three parameters namely the make span, the reliability cost, and the mean flow time (MFT) for the allocation of resources in such a way that the resource utilization is considerably improvised. The detailed working of the CSGOA-RS technique has been elaborated in the succeeding sections.
The shell game was inspired by inventing a novel optimization technique called as the Shell Game Optimization (SGO). Therefore, the subsequent statements are considered:
• During this game, one person would be assumed as the game operator.
• 3 shells and 1 ball would be assigned to an operator.
• All players would be provided with 2 opportunities for guessing the correct shell.
For the mathematical representation of the SGO algorithm, a set of N people would be considered as the game players. In Eq. (3), the place ‘d’ of a player ‘i’ would be demonstrated as
At this time, Xi is actually an arbitrary value to the problem variable. According to Xi, the value of the fitness function (FF) can be estimated for all the players. Fig. 2 illustrates the steps involved in the SGO techniques.

Figure 2: Steps involved in SGO algorithm
After computing the FF value for all the players, the game operator would select 3 shells in such a way that most of the shells are connected to the location of an optimum player, 2 other shells would be selected arbitrarily using Eq. (4).
where Xbest implies the place of minimal (in minimization issues) or maximal (in maximization issues) fitness,
where AIi represents the accuracy and intelligent of the players i and Xworst refers to the place of minimal (in maximization issues) or maximal (in minimization issues) fitness levels.
At this point, the player would be prepared to guess the ball. The game is to be played with 3 shells and all the players would be provided with only 2 chances, the players can make use of the available 3 states of guesses. In the beginning state, an initial guess would be correct and the place of ball could be recognized easily. In the second state, the player making a wrong guess in the primary selective state can guess the place of the ball the second time. Finally, in the third state, when both the guesses of the player go wrong, the player turns out to be unsuccessful in recognizing the place of the ball. The guess vector detailed by Gv is inspired as in Eq. (6) for all the players.
The probability of selecting most states to the shell selective is inspired by Eq. (7).
where
Eventually, the Xi vector that is considered as the place of the members of the population is upgraded with the Eqs. (8)–(11).
where ri represents the arbitrary value in the range of [0 1],

Chaotic maps are efficient enough in enhancing the solution quality of the SGO algorithm in resolving the resource scheduling problems. Generally, chaos is a deterministic arbitrary technique that is non-linear, it is dynamic model that is non-periodic, non-converging, and bounded in nature. The nature of chaos is obviously arbitrary and unpredictable, and it can retain an element of regularity. The chaos utilizes the chaotic variables instead of the arbitrary variables. Many functions (chaotic maps) and some parameters (primary condition) are vital even for the longer systems. Furthermore, a huge number of distinct sequences are created easily by altering their primary conditions. Also, this sequence is deterministic and reproducible. In addition, it is extremely sensitive depending upon their primary conditions and parameters. An extensive variation of the distinct chaotic maps is accessible in the optimization domain. In this proposed work, 10 very extensively utilized chaotic maps have been employed [23]. The mathematical modulation of these chaotic maps thus utilized have been explained in the subsequent subsections. The chebyshev map has been expressed in Eq. (12).
The circle map is a 1D map that is a member of the dynamical schemes on a circle and is initially determined by the Andrey Colmogorov. This map is determined as:
This formula is created with chaotic numbers amongst (0, 1) by utilizing Par = 0.5 and b = 0.2. Par is employed in the form of control parameters. The formulas of the Gauss map are determined as:
This map also creates a chaotic sequence in (0, 1).The iterative chaotic map formula is expressed in Eq. (16).
where Par implies the adaptable parameter. The equation for the logistic map formula is provided in Eq. (17).
where Par is the control parameter, which is set to 4 for generating numbers amongst 0 and 1. The family of the piecewise maps is expressed using Eq. (18).
where Par refers to the appropriate control parameter whose range is 0 and 0.5. The sine map is determined as:
Par implies the control parameter containing values in the ranges 0 and 4. The singer map is considered as:
where Par represents the control parameter whose values lie in the range 0.9 and 1.08. The sinusoidal map is expressed as follows:
where Par signifies the control parameter. In this case, the simplified formula of this map was utilized by employing Par = 2.3 and u0 = 0.7 that is expressed as:
The formula of the tent map is demonstrated as:
4.2 Application of CSGOA Technique for Resource Scheduling
The CSGOA-RS technique derives a fitness function and is utilized for testing the quality of the solution [24]. The FF consist of the tri-objectives such as the RC, the MS, and the MFT. It is calculated in Eq. (24), whereas the weights W1, W2, & W3 indicate the connotation of the objectives in the meta task scheduling problems.
The CSGOA-RS technique has tested the FF using the distinct weight values and hence concludes with the values of 0.4, 0.4 and 0.2 for the weights W1, W2, & W3 respectively, it further provides the optimal results in the meta task scheduling problems.
Make span (MS)
It calculates the throughput of the distributed system, assume Cij(iε{1, 2, …, n}, jε{1, 2, …, m}) represents the implementation time to perform the ith task in the jth processor and Wj jε{1, 2, …, m} indicates the prior task of Pj. Based on the above-mentioned description, it is evaluated using Eq. (25):
Mean flow time (MFT)
It measures the QoS of the distributed systems. The value of MFT is utilized for evaluating the flow time. Let k represent the overall amount of tasks allocated to the processor Pi and Fji represent the executing time of the task Tj on a processor
Reliability cost (RC)
RC is the indicator of how reliable a provided system is if a set of tasks are allocated to it. It is indirectly proportionate to reliability. It is the summation of link reliability and processor reliability. The RC can be determined using Eq. (28), whereas X(Ti) = j represents the task Ti that is assigned to Pj and λj indicates the failure rate of the processor Pj.
This section examines the resource scheduling performance of the CSGOA-RS technique in terms of different aspects. The results are inspected in terms of the following attributes, namely, the make span, the mean flow time, and the reliability cost. The experimental results have been investigated under varying number of instances and resources. A brief MS analysis of the CSGOA-RS technique takes place under distinct number of instances as represented in Tab. 1 and Fig. 3.
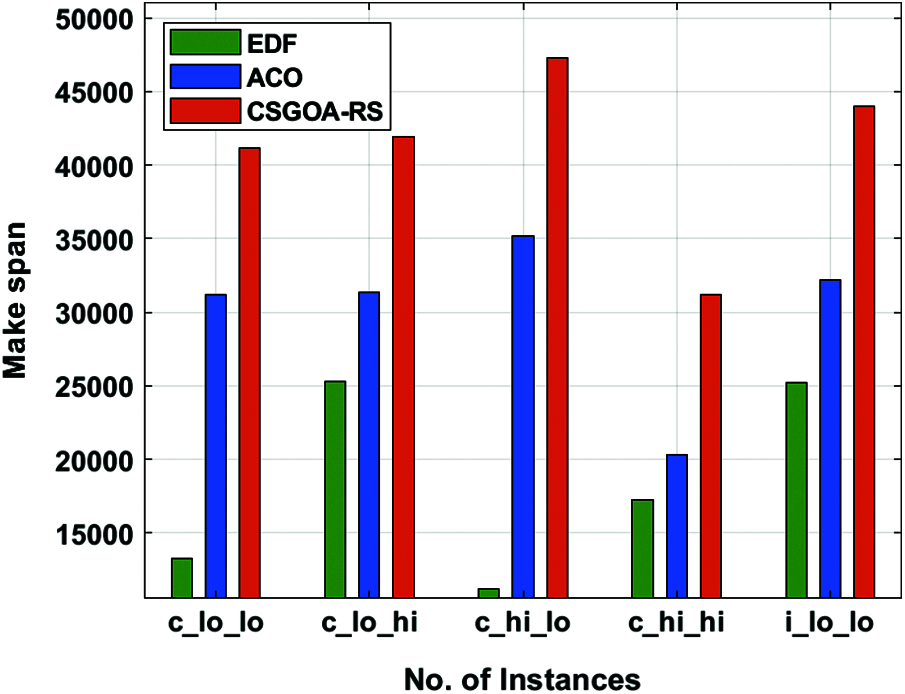
Figure 3: Make span cost analysis of the CSGOA-RS model
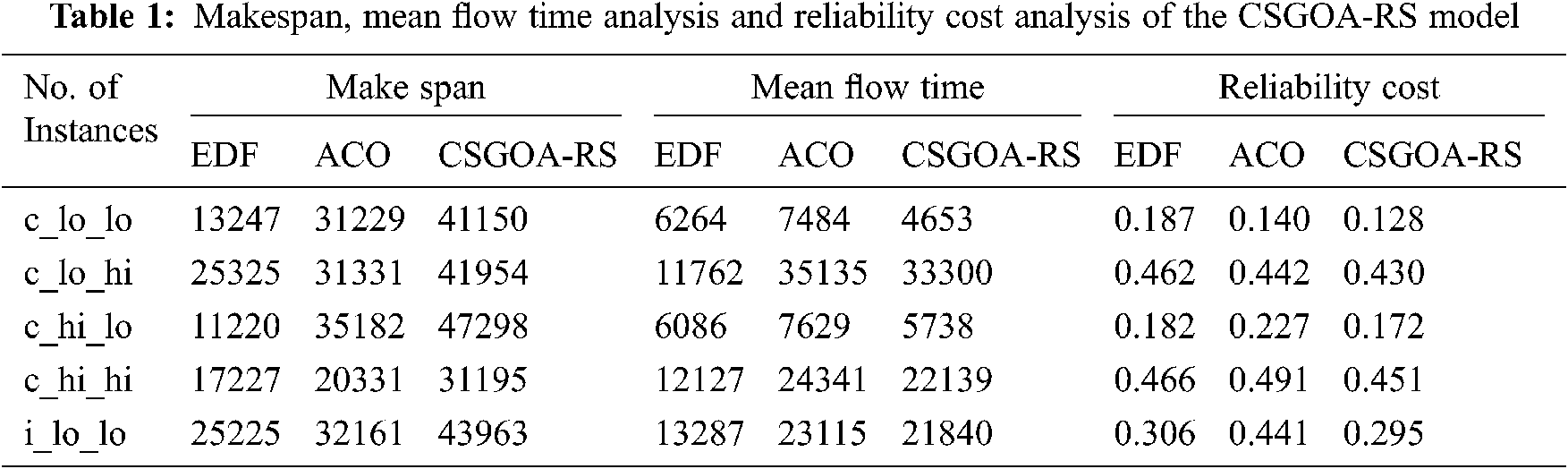
The simulation results point out the enhanced performance of the CSGOA-RS technique with that of the existing techniques with the maximum make span. For instance, with c_lo_lo instances, the CSGOA-RS technique has accomplished an increased MS of 41150 whereas the EDG and ACO algorithms have resulted in a reduced MS of 13247 and 31229. Simultaneously, with c_hi_lo instances, the CSGOA-RS technique has accomplished an increased MS of 47298 whereas the EDG and ACO algorithms have resulted in a reduced MS of 11220 and 20331. Concurrently, with i_lo_lo instances, the CSGOA-RS technique has accomplished an increased MS of 43963 whereas the EDG and ACO algorithms have resulted in a reduced MS of 25225 and 32161.
A brief MFT analysis of the CSGOA-RS technique takes place under distinct number of instances as portrayed in Tab. 1 and Fig. 4. The simulation outcomes thus point out the enhanced performance of the CSGOA-RS technique with that of the existing techniques with the maximum make span. For instance, with c_lo_lo instances, the CSGOA-RS technique has accomplished an increased MFT of 4653 whereas the EDG and ACO algorithms have resulted in a reduced MFT of 6264 and 7484.
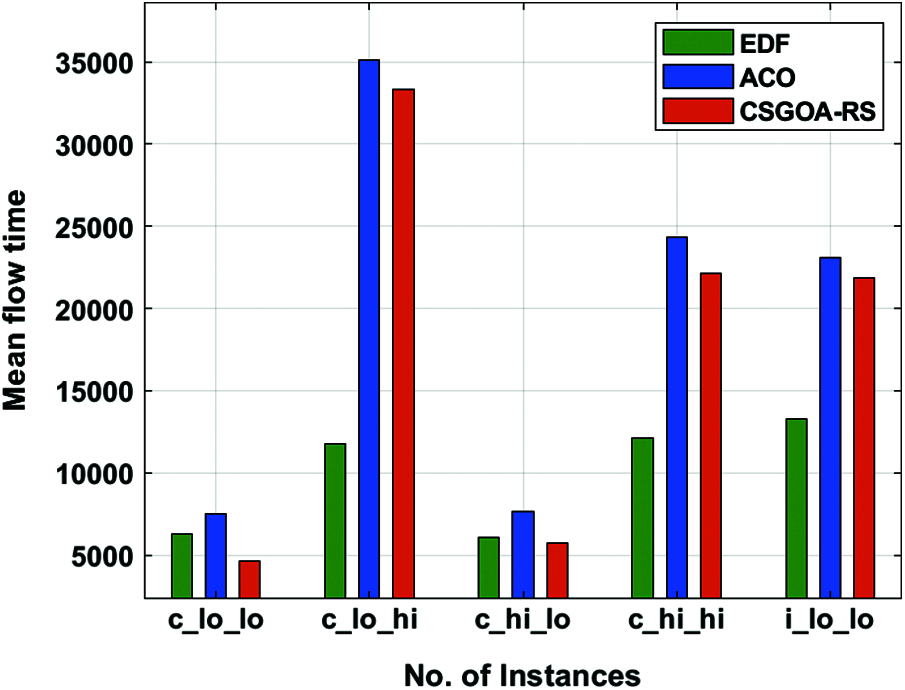
Figure 4: Mean flow time analysis of the CSGOA-RS model
Simultaneously, with c_hi_lo instances, the CSGOA-RS technique has accomplished an increased MFT of 5738 whereas the EDG and ACO algorithms have resulted in a reduced MFT of 6086 and 7629. Concurrently, with i_lo_lo instances, the CSGOA-RS technique has accomplished an increased MFT of 21840 whereas the EDG and ACO algorithms have resulted in a reduced MFT of 13287 and 23115. A reliability cost analysis of the CSGOA-RS technique with the other techniques has been represented in Tab. 1 and Fig. 5. The experimental outcomes thus demonstrate that the CSGOA-RS technique has gained effectual outcomes with the RC values. For instance, with the instance of c_lo_lo, the CSGOA-RS technique has offered a lower RC value of 0.128 whereas the EDF and ACO algorithms have obtained higher RC values of 0.187 and 0.140 respectively.
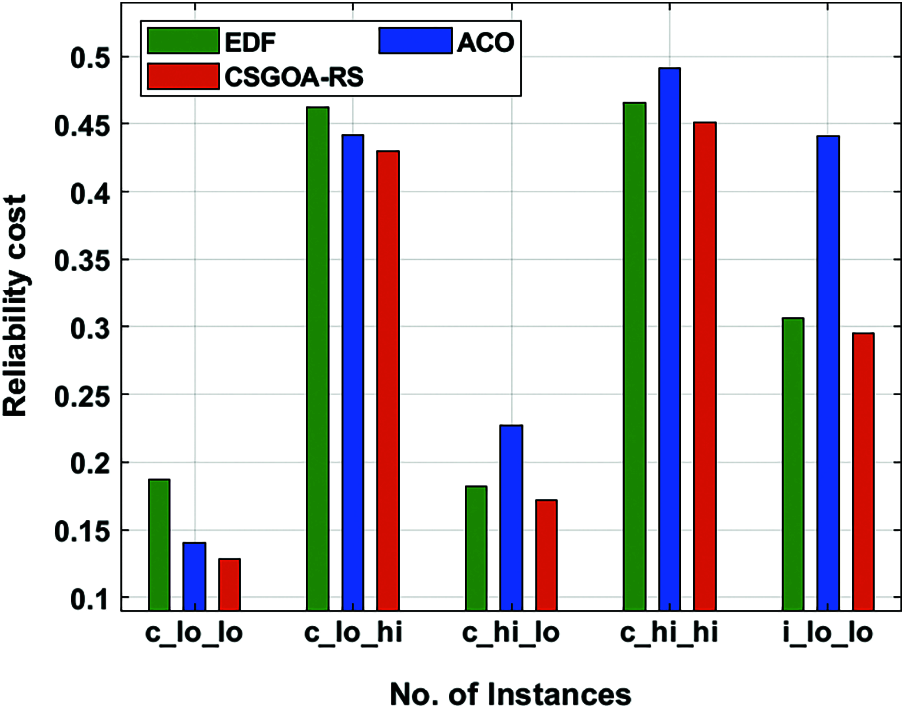
Figure 5: Reliability cost analysis of CSGOA-RS model
Eventually, with the instance of c_hi_lo, the CSGOA-RS technique has offered a lower RC value of 0.172 whereas the EDF and ACO algorithms have obtained higher RC values of 0.182 and 0.227 respectively. Meanwhile, with the instance of i_lo_lo, the CSGOA-RS technique has offered a lower RC value of 0.295 whereas the EDF and ACO algorithms have obtained a higher RC value of 0.306 and 0.441 respectively. A detailed SR analysis of the CSGOA-RS technique with the other existing techniques takes place under a distinct number of processors and resources as represented in Tab. 2 and Fig. 6. Fig. 6a investigates the SR analysis of the CSGOA-RS technique with the EDG and the ACO algorithms with two processors and varying resources. The figure thus portrays that the CSGOA-RS technique has resulted in effective performance with the maximum SR under varying resources.

Figure 6: Comparative analysis of the CSGOA-RS model in terms of SR (a) 2 processors, (b) 3 processors, and (c) 5 processors
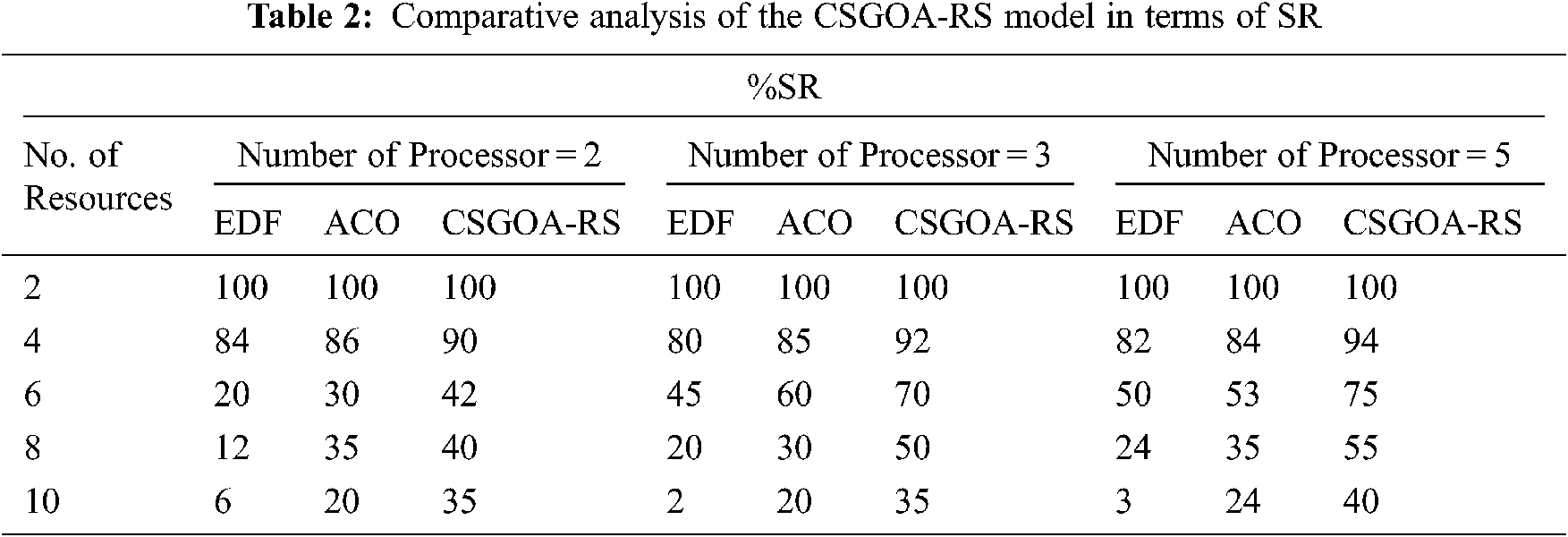
For instance, with 4 resources, the CSGOA-RS technique has gained improved outcomes with a higher SR of 90% whereas the EDF and ACO algorithms have obtained a decreased outcome of 84% and 86% respectively. Similarly, with 10 resources, the CSGOA-RS method has reached the maximum result with a higher SR of 35% whereas the EDF and the ACO algorithms have achieved a minimum result of 6% and 20% correspondingly. Fig. 6b examines the SR analysis of the CSGOA-RS approach with the EDG and the ACO algorithms with three processors and different resources. The figure depicts that the CSGOA-RS technique has resulted in effective performance with the maximum SR under varying resources. For example, with 4 resources, the CSGOA-RS approach has reached the maximum outcome with the superior SR of 92% whereas the EDF and the ACO algorithms have reached a decreased outcome of 80% and 85% correspondingly. In addition, with 10 resources, the CSGOA-RS technique has gained improved outcomes with the superior SR of 35% whereas the EDF and the ACO methodologies have obtained a lesser outcome of 2% and 20% correspondingly.
Fig. 6c demonstrates the SR analysis of the CSGOA-RS technique with the EDG and the ACO methods with five processors and varying resources. The figure thus portrays that the CSGOA-RS technique has resulted in effective performance with the maximal SR under varying resources. For instance, with 4 resources, the CSGOA-RS technique has gained enhanced outcomes with the higher SR of 94% whereas the EDF and the ACO methodologies have achieved a decreased outcome of 82% and 84% correspondingly. At the same time, with 10 resources, the CSGOA-RS approach has gained higher outcomes with a higher SR of 40% whereas the EDF and the ACO algorithms have reached a decreased outcome of 3% and 24% respectively. A comprehensive ECU analysis of the CSGOA-RS approach with the other recent methodologies takes place under different number of processors and resources as represented in Tab. 3 and Fig. 7.

Figure 7: Comparative analysis of the CSGOA-RS model in terms of ECU
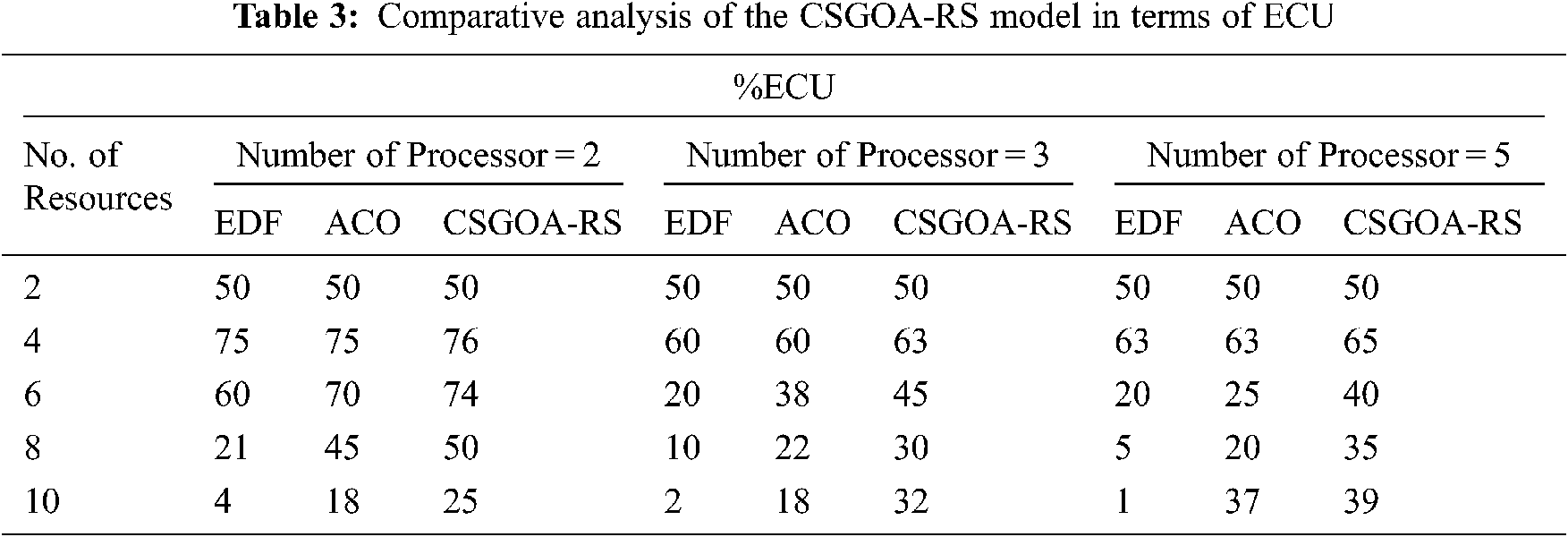
Fig. 7a examines the ECU analysis of the CSGOA-RS method with that of the EDG and the ACO algorithms with two processors and varying resources. The figure thus demonstrates that the CSGOA-RS method has resulted in effectual efficiency with the maximal ECU under varying resources. For example, with 4 resources, the CSGOA-RS technique has attained enhanced results with the superior ECU of 76% whereas the EDF and the ACO algorithms have obtained a decreased outcome of 75% and 75% correspondingly. At the same time, with 10 resources, the CSGOA-RS technique has obtained enhanced results with the maximum ECU of 25% whereas the EDF and the ACO algorithms have gained a reduced outcome of 4% and 18% correspondingly.
Fig. 7b inspects the ECU analysis of the CSGOA-RS approach with the EDG and the ACO techniques with three processors and varying resources. The figure thus demonstrates that the CSGOA-RS method has resulted in efficient performance with enhanced ECU under varying resources. For instance, with 4 resources, the CSGOA-RS technique has gained improved outcomes with a higher ECU of 63% whereas the EDF and the ACO algorithms have obtained a decreased outcome of 60% and 60% respectively. Also, with 10 resources, the CSGOA-RS method has gained enhanced outcomes with an increased ECU of 32% whereas the EDF and the ACO algorithms have obtained a minimal outcome of 2% and 18% correspondingly. Fig. 7c showcases the ECU analysis of the CSGOA-RS technique with the EDG and the ACO algorithms with five processors and different resources. The figure thus exhibits that the CSGOA-RS method has resulted in effective performance with the higher ECU under distinct resources. For example, with 4 resources, the CSGOA-RS technique has gained improved outcomes with a higher ECU of 65% whereas the EDF and the ACO algorithms have obtained a decreased outcome of 63% and 63% correspondingly.
Finally, with 10 resources, the CSGOA-RS approach has gained improved outcomes with a higher ECU of 39% whereas the EDF and ACO methodologies have gained minimal results of 1% and 37% correspondingly. By observing the details of the result analysis, it is clearly understood that the CSGOA-RS technique has gained effective performance due to the fitness function that involves the following three parameters namely the make span, the reliability cost, and the MFT for the allocation of resources.
This paper has developed an effective CSGOA-RS technique for scheduling the resources proficiently in the distributed robotic control system. The CSGOA-RS technique is primarily designed for allocating the resources in such a way that the transfer time is minimized and resource utilization is increased. The CSGOA-RS technique has derived a fitness function involving three parameters namely the make span, the reliability cost, and the mean flow time (MFT) for the allocation of resources in such a way that the resource utilization can be considerably improved. The integration of the chaotic map concepts into the SGO algorithm significantly boosts the overall performance of the CSGOA technique. The performance of the CSGOA-RS technique can be examined under different aspects and the results of the same can be discussed extensively. The experimental results showcased the significant outcomes of the proposed CSGOA-RS technique over the other existing techniques. In future, the CSGOA-RS technique can be extended to the design of load balancers and route planning techniques for the distributed robotic control system.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Zhang, L. Jin and C. Yang, “Distributed cooperative kinematic control of multiple robotic manipulators with improved communication efficiency,” IEEE/ASME Transactions on Mechatronics, vol. 1, no. 1, pp. 1–18, 2021. [Google Scholar]
2. N. Naughton, J. Sun, A. Tekinalp, T. Parthasarathy, G. Chowdhary and M. Gazzola, “Elastica: A compliant mechanics environment for soft robotic control,” IEEE Robotics and Automation Letters, vol. 6, no. 2, pp. 3389–3396, 2021. [Google Scholar]
3. F. Mondada, G. C. Pettinaro, A. Guignard, I. W. Kwee, D. Floreano et al., “SWARM-Bot: A new distributed robotic concept,” Autonomous Robots, vol. 17, no. 2, pp. 193–221, 2004. [Google Scholar]
4. F. Voigtlander, A. Ramadan, J. Eichinger, C. Lenz, D. Pensky et al., “5G for robotics: Ultra-low latency control of distributed robotic systems,” in Proc. Int. Symp. on Computer Science and Intelligent Controls (ISCSIC), Budapest, Hungary, pp. 69–72, 2017. [Google Scholar]
5. P. E. Rybski, S. A. Stoeter, M. Gini, D. F. Hougen and N. P. Papanikolopoulos, “Performance of a distributed robotic system using shared communications channels,” IEEE Transactions on Robotics and Automation, vol. 18, no. 5, pp. 713–727, 2002. [Google Scholar]
6. G. A. Barreto, A. F. R. Araujo, C. Ducker and H. Ritter, “A distributed robotic control system based on a temporal self-organizing neural network,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 32, no. 4, pp. 347–357, 2002. [Google Scholar]
7. B. Shucker and J. K. Bennett, “Scalable control of distributed robotic macrosensors,” Distributed Autonomous Robotic Systems, vol. 6, pp. 379–388, 2007. [Google Scholar]
8. D. H. Lee, S. A. Zaheer, J. H. Han, J. H. Kim and E. Matson, “Competency adjustment and workload balancing framework in multirobot task allocation,” International Journal of Advanced Robotic Systems, vol. 15, no. 6, pp. 1–15, 2018. [Google Scholar]
9. S. Goyal, S. Bhushan, Y. Kumar, M. R. Bhutta, M. F. Ijaz et al., “An optimized framework for energy-resource allocation in a cloud environment based on the whale optimization algorithm,” Sensors, vol. 21, no. 5, p.1583, 2021. [Google Scholar]
10. J. Blankenburg, S. B. Banisetty, S. P. H. Alinodehi, L. Fraser, D. Feil-Seifer et al., “A distributed control architecture for collaborative multi-robot task allocation,” in Proc. 2017 IEEE-RAS 17th Int. Conf. on Humanoid Robotics (Humanoids), Birmingham, UK, pp. 585–592, 2017. [Google Scholar]
11. Q. Zhu and J. Oh, “Deep reinforcement learning for fairness in distributed robotic multi-type resource allocation,” in Proc. 17th IEEE Int. Conf. on Machine Learning and Applications (ICMLA), Orlando, FL, USA, pp. 460–466, 2018. [Google Scholar]
12. R. Delgado, J. Park and B. W. Choi, “Open embedded real-time controllers for industrial distributed control systems,” Electronics, vol. 8, no. 2, pp. 223–236, 2019. [Google Scholar]
13. A. Maoudj, B. Bouzouia, A. Hentout, A. Kouider and R. Toumi, “Distributed multi-agent scheduling and control system for robotic flexible assembly cells,” Journal of Intelligent Manufacturing, vol. 30, no. 4, pp. 1629–1644, 2019. [Google Scholar]
14. H. Yuan, M. Zhou, Q. Liu and A. Abusorrah, “Fine-grained resource provisioning and task scheduling for heterogeneous applications in distributed green clouds,” IEEE/CAA Journal of Automatica Sinica, vol. 7, no. 5, pp. 1380–1393, 2020. [Google Scholar]
15. H. Gultekin, S. Gurel and R. Taspinar, “Bicriteria scheduling of a material handling robot in an m-machine cell to minimize the energy consumption of the robot and the cycle time,” Robotics and Computer-Integrated Manufacturing, vol. 72, no. 102207, pp. 1–15, 2021. [Google Scholar]
16. H. Wang, W. Chen and J. Wang, “Coupled task scheduling for heterogeneous multi-robot system of two robot types performing complex-schedule order fulfillment tasks,” Robotics and Autonomous Systems, vol. 131, no. 103560, pp. 1–18, 2020. [Google Scholar]
17. Y. Sun, S. H. Chung, X. Wen and H. L. Ma, “Novel robotic job-shop scheduling models with deadlock and robot movement considerations,” Transportation Research Part E: Logistics and Transportation Review, vol. 149, no. 102273, pp. 1–12, 2021. [Google Scholar]
18. X. Fu, Z. Cheng and J. Wang, “Research on online scheduling and charging strategy of robots based on shortest path algorithm,” Computers & Industrial Engineering, vol. 153, no. 107097, pp. 1–14, 2021. [Google Scholar]
19. Y. He, M. Wu and S. Liu, “An optimisation-based distributed cooperative control for multi-robot manipulation with obstacle avoidance,” IFAC-PapersOnLine, vol. 53, no. 2, pp. 9859–9864, 2020. [Google Scholar]
20. X. Fang, D. Pang, J. Xi and X. Le, “Distributed optimization for the multi-robot system using a neurodynamic approach,” Neurocomputing, vol. 367, pp. 103–113, 2019. [Google Scholar]
21. L. Huai, Z. Zheng, H. Jianxin and F. Chunmei, “Optimal scheduling algorithm for periodic tasks in distributed control systems based on PSO,” in Proc. 2011 Chinese Control and Decision Conf. (CCDC), Mianyang, China, pp. 2853–2857, 2011. [Google Scholar]
22. M. Dehghani, Z. Montazeri, O. P. Malik, H. Givi and J. M. Guerrero, “Shell game optimization: A novel game-based algorithm,” International Journal of Intelligent Systems, vol. 13, pp. 246–255, 2020. [Google Scholar]
23. S. Arora and P. Anand, “Chaotic grasshopper optimization algorithm for global optimization,” Neural Computing and Applications, vol. 31, no. 8, pp. 4385–4405, 2019. [Google Scholar]
24. T. Vairam, S. Sarathambekai and K. Umamaheswari, “Multiprocessor task scheduling problem using hybrid discrete particle swarm optimization,” Sadhana, vol. 43, no. 12, pp. 1–13, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |