DOI:10.32604/csse.2022.021729

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021729 |  |
| Article |
Solving the Task Starvation and Resources Problem Using Optimized SMPIA in Cloud
1Department of Computer, Sari Branch, Islamic Azad University, Sari, Iran
2Department of Computer, Rasht Branch, Islamic Azad University, Rasht, Iran
*Corresponding Author: Homayun Motameni. Email: h_motameni@yahoo.com
Received: 12 July 2021; Accepted: 13 August 2021
Abstract: In this study, a new feature is added to the smart message passing interface (SMPI) approach (SMPIA) based on the prioritization method, which can completely eliminate the task starvation and lack of sufficient resources problems through prioritizing the tasks. The proposed approach is based on prioritizing the tasks and the urgency of implementation. Tasks are prioritized based on execution time, workload, the task with a more sensitive priority is executed earlier by the free source. The idea of demand-bound functions (DBFs) was extended to the SMPIA setting based on partitions and caps. For each task, two DBFs are constructed, DBFLO and DBFHI, for the LO and HI criticality modes, respectively. The simulation results returned by MATLAB showed that with the optimized SMPIA (O-SMPIA), the parameters of maximum service execution time, response time, delay time, and throughput improved in this work. In addition, the results confirmed that the reduction of execution time, completion time, and resource consumption time did not affect the response time and throughput of workflow tasks and did not cause inefficient use of resources in virtual machines (VMs) and data centers (DCs). The evaluation of performance metrics showed that the delay, response time of the Greedy algorithm was less than that of Max-Min and Min-Min. At the same time, the execution time of Max-Min was less than the others and the throughput of the Greedy was longer. The effect and throughput of O-SMPIA became more obvious as change to the job count and the number of cloud workloads increased. It is also worth mentioning that one of the main advantages of the O-SMPIA to other methods is the efficient use of time to execute all the defined tasks by CPU.
Keywords: Cloud computing; O-SMPIA; task starvation; EDF-VD
Cloud computing (CC) delivers computing resources like software and hardware as a service to the users through a network. Due to the scale of the modern data centers (DCs) and their dynamic resources provisioning nature, efficient scheduling techniques are required to manage these resources [1,2]. The smart message passing interface (MPI) can be used as a new idea and scheduling technique in CC that has not been proposed in the literature yet. With the use of smart MPI in the CC structure, the task scheduling process can be performed most effectively. MPI is a main component of high performance computing (HPC) applications and it is essential to improving the HPC application performance in the cloud environment [3,4]. The communication network performance is a challenge and low latency MPI communication methods are needed for that [5–8].
The main objective of scheduling is to minimize resource starvation and to ensure fairness amongst the parties utilizing the resources. Scheduling deals with the problem of deciding which of the outstanding requests is to be allocated resources [9,10]. Starvation is a kind of problem that arises when some processes are never allocated despite the availability of resources for allocation. The priority-based scheduling algorithm is mainly focused on starvation [11]. One of the major challenges that must be taken into account in developing task scheduling is solving the starvation problem [12]. Balancing between throughput, waiting time and response time may provide how to approach scheduling optimality but on another level it is going to causes long tasks starvation [13].
In general, the optimization task starvation problems can be divided into discrete and continuous problems. The decision variables for a combinatorial problem have discrete values, while the decision variables for a continuous optimization problem can take up values within the domain of real values (Ri) [14,15]. Moreover, generating a schedule to optimize the two most important, yet conflicting, scheduling objectives (i.e., execution cost and execution make span (MS)) has become a complicated problem. For example, optimizing the execution cost increases the execution MS. This is due to the interlink that exists between these objectives. MS and cost optimization problem persist because the virtual machine (VM) selection (which is a key to managing resource utilization (RU) to improve system throughput) is usually ignored by researchers [16].
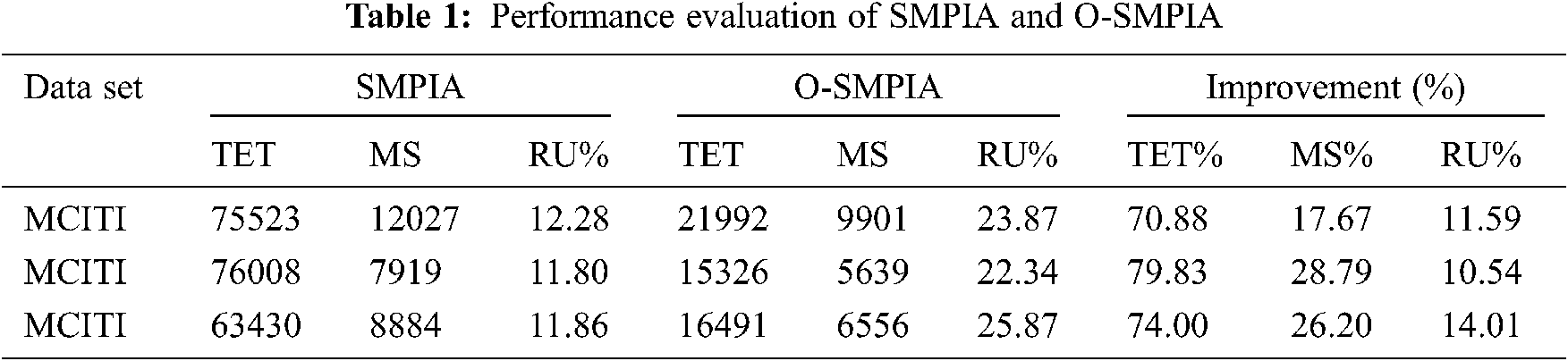
Based on the number of criteria involved in the optimization task starvation problem, this can be divided into single-criterion and multicriteria. The task of single- criterion optimization is to find the optimal solution according to only one criterion function. When the optimization starvation problem involves more than one criteria function, the task is to find one or more optimal solutions regarding each criterion. In such condition, a solution that is appropriate to one criterion can be inappropriate to another, and vice versa [17]. Therefore, the goal of multi-criteria optimization is to find a set of solutions that are optimal with respect to all other criteria. Note that, most real-world problems are of the multi-criteria type. The review of the literature shows that some research gaps such as VM selection and task mapping criteria still exist, which require further investigation [16]. The obtained results of the experiment indicate that the optimized smart MPI approach (O-SMPIA) outperform the SMPIA [18] in terms of total execution time (TET), MS and RU. Other details are listed in Tab. 1.
The aim of this work was to solve the problem of starvation of tasks and lack of sufficient resources using O-SMPIA. To this end, we combined the Greedy, Max-Min and Min-Min [18] algorithms, with the O-SMPIA. In this matter, O-SMPIA was used at the DCs level due to the increase in the use of DCs in different geographical locations and unclear the number of servers. This study attempts to run tightly coupled applications on a wide area network in DCs level in order to improve throughput, delay time, response time, and execution time. Dynamic workflow can be improved to change the workflow characteristics at runtime.
In this paper, the earliest deadline first with virtual deadlines (EDF-VD) algorithm was applied to the utilization caps. EDF-VD was combined with O-SMPIA, which resulted in the improvement of the system performance. The O-SMPIA helpeds to shorten the execution time, response time, and delay time and increased the throughput.
The main contributions of this paper are as follows:
(1) A priority-based task scheduling algorithm was developed. O-SMPIA developed in this study is based on the prioritization method that can completely solve the problem of task starvation and resource consumption. SMPIA was extended to consider tasks execution time, MS and RU as metrics for the performance evaluation and optimization goals.
(2) O-SMPIA solves the starvation problem by considering the type of urgency of the execution time. Tasks are prioritized based on the execution time; the tasks with the highest priority is executed earlier by the free source.
(3) O-SMPIA also improved the system throughput, hence significantly improving the system performance. O-SMPIA helps to efficiently use the time in a way to execute all the tasks by CPU.
(4) The idea of demand-bound functions (DBFs) was extended to the SMPIA setting based on partitions and caps. For each task, two DBFs, DBFLO and DBFHI, are constructed for the low- and high-criticality modes, respectively.
The motivation for this research is the implementation of workflow on the telecommunications transaction application in order to achieve proper processing time and manage cloud systems. It also aims to improve the performance of algorithms, increase the quality of service (QoS), solving the problem of task starvation and lack of sufficient resources considering the priority of tasks in MPI communications of the desired virtual networks. The need for this research is to delay MPI communication in the virtual MPI bus (VMPIB) [18]. Using O-SMPIA and SMPIA in a telecommunications transaction application increases the performance of the application.
The remainder of this paper is organized as follows: related work is presented in Section 2; cloud computing and task starvation model based on SMPIA in Section 3; the proposed optimized SMPIA method in Section 4; optimization criteria in Section 5; the performance evaluation in Section 6, and; ultimately, conclusions and future scope are presented in Section 7.
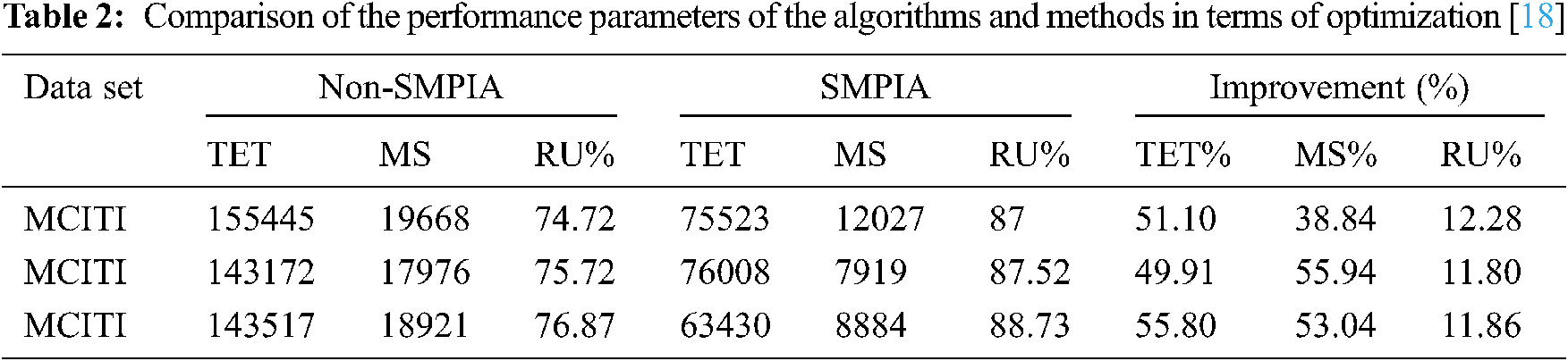
In [18], the SMPIA aimed to improve the starvation problem for workflow tasks and lack of sufficient resources at the VM level. This problem was solved with Greedy, Max-Min, and Min-Min algorithms. These algorithms, especially Max-Min and Min-Min, solves the above-mention problems based on run times of alternative virtual machines (AVMs) and priority scheduler algorithm. The TET and MS were prioritized as well.
In [16], the multi-objective workflow optimization strategy (MOWOS) employs the tasks splitting mechanism to split large tasks into sub-tasks to reduce their scheduling length. The simulation results showed that, the MOWOS algorithm had less execution cost and, better execution MS, and also it utilized the resources better than the existing HSLJF [15] and SECURE [19] algorithms.
In [13], a hybrid of shortest-job first (SJF) and round robin (RR) is one among the foremost used and powerful hybrids for solving starvation where we will enjoy SJF performance in reducing the turnaround and from RR in reducing task waiting time. But the task quantum value was always the obstacle in having the optimum hybrid.
In [12], to solve the starvation, a hybrid shortest–longest scheduling algorithm was presented. The capabilities of each VM and the length of the task to allocate the tasks to most convenient VMs were considered. Thus, their algorithm overcame the starvation problem through considering both the provider and user’s requirements. The experimental results proved that the proposed HSLJF algorithm outperformed the existing algorithms in terms of minimizing the average MS, response time, and the actual execution time of tasks, while maximizing the RU and throughput.
In [20], EDF-VD was applied to each subset or partition independently. Dividing the processor into two halves has almost no performance degradation compared to EDF-VD (with a totally dedicated processor). The use of smaller caps of a partition led to, lower performance in terms of a set of scheduled tasks. If one HI task switches to HI mode, then only those LO task within the same partition or subset will be discarded, whereas LO tasks in other partitions continue running. The main advantage over the sever-based approach is that there is no starvation period, i.e., the time interval between two runs/repetitions where no service is provided to tasks within the server. In contrast to this, tasks in a partition run as long as they have not used up their assigned utilization, i.e., as long as they are below their utilization cap.
In [11], a priority-based process scheduling (PRIPSA) algorithm was presented, which was developed with the block-based queue in CC. The proposed algorithm gives the high priority to the processes supported their lead time then burst time. Therefore, it is able to solve the starvation problem. The priority-based scheduling algorithm was focused on moderating the starvation problem. For the preventive algorithm, the starvation increased linearly, while for the priority-based scheduling algorithm, the increase rate was extremely slow.
The resources are used good in case of improved genetic algorithm, but some resources are not used efficiently in case of standard genetic algorithm, there is a large gap in the percentage usage of resources [21]. The proposed cuckoo PSO (CPSO) algorithm achieves minimal deadline violation rate when compared with algorithms such as PBACO, ACO, Min–Min, and FCFS [22]. The standard PSO easily got trapped into the local optimum solution, which results in improved being premature convergence [23]. The comparison of the improved PSO algorithm (in crossover and mutation) with PSO showed that improved PSO was not only converged faster, but also it was executed in a large scale faster than the other two algorithms [24]. According to dynamic nature of cloud and deficiencies of methods presented, proposals and solutions have been suggested to improve the accuracy and the efficiency of the prediction methods [25]. The new methods should be able to consider all dimensions of the application to making the appropriate learning model. The efficient learning model could enhance the prediction accuracy. Also, suggested new approaches to develop prediction models in a way of hybrid nature [26].
In the current paper, an important feature was added to the SMPIA based on the prioritization method, which improves the system performance to an acceptable degree and leads to higher priority tasks that need to be implemented sooner.
Tab. 2 reports the details of the comparison of performance parameters of the algorithms and methods in terms of optimization.
3 Cloud Computing and Task Starvation Model Based on SMPIA
3.1 Cloud Computing Model Based on SMPIA
The CC model is aimed at providing resources and services through a network; resource allocation and workflow scheduling are two focal points of CC [27–29]. Workflow as a service (WaaS) of deal and tenders from ministry of communication and information technology of Iran (MCITI) was defined as small and big transactions. All the flows of the selected WaaS were logged into the system after selecting the small or big WaaS of the waiting queue. Each DC had a number of servers, each of which had several VMs in VMPIB. VMs can have a two-way communication. As depicted in Fig. 1, all VMs were connected to VMPIB. The problem in the current work is task starvation and lack of sufficient resources in VMs and DCs level to optimize the performance parameters simultaneously. To this end, the O-SMPIA is presented in this study. To define the concept of the VMPIB and the VM connection approach, first, a topology was considered with the connected graph G = (D, V), where V = {VM1, VM2, VM3, …, VMm} and D = {DC1, DC2, DC3, …, DCd}. D and V represent the entire number of DCs and VMs, respectively. The function φ: V → D was considered to regulate the dependencies of flows and their tasks including the F = {F1, F2, F3, …, Ff} set. Moreover, the function θ: F→ V and T = {T1, T2, T3, …, Tt}. φ is a function, in which VM is assigned to each DC in VMPIB. θ is a function, in which the flow that could be executed by VM in VMPIB is determined. F is the total flows depending on each other. And T is defined as the total transactions [18].
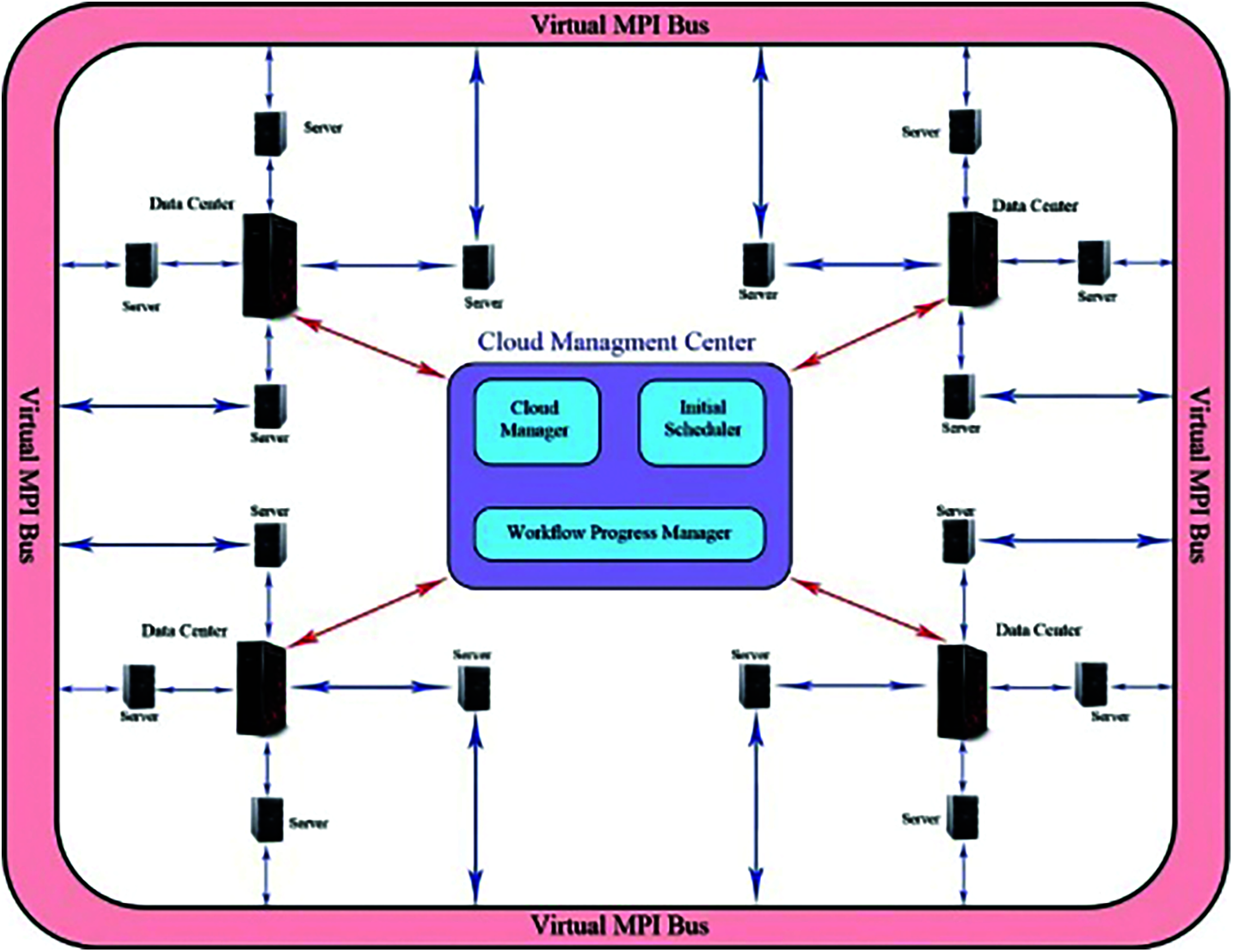
Figure 1: The cloud computing model based on SMPIA [18]
3.2 Task Starvation Model Based on Optimized SMPIA
In the present article, a new feature was added to SMPIA based on the prioritization method, which can completely eliminate the problem of task starvation and resource consumption. In this matter, the starvation of tasks and resources is addressed by prioritizing the tasks as suggested in [13,20,30]. High priority tasks are considered HI and low priority tasks are considered LO in O-SMPIA to schedule the sporadic tasks that run under preemptive uniprocessor scheduling. Each job consists of task count, job size, job priority, position, type, etc. The minimum separation between any two jobs or instances of a task is denoted by Ti, and we assume implicit deadlines, i.e.,
Finally, among the four potential criticality-to-mode combinations, note that only
Its basic idea for solving the starvation problem in this paper is to promote HI jobs in the LO mode by shortening their deadlines so as to reserve the processor capacity for the HI mode. From the above description, the LO and HI tasks need to be schedulable with their corresponding
In the following, Algorithm 1 (Tab. 3) is presented for schedule tasks.

Although using fixed UL is more straightforward, in some cases, we would like to find an optimum value of UL for a given τx ⊂ x such schedulability could be guaranteed. A DBF (τi , l) gives an upper bound on the maximum possible execution demand of task τi in any time interval of length l, where demand is calculated as the total amount of required execution time of jobs with their whole scheduling windows within the time interval. The idea of DBFs was extended in this article to the SMPIA setting based on partitions and caps. For each task, two DBFs are constructed, DBFLO and DBFHI, for the low and high-criticality modes, respectively. While the system is in low-criticality mode, each task τi behaves as a traditional sporadic task with parameters Ci(LO), Di(LO), and Ti. Note that it uses relative deadline Di(LO), where Di(LO) = Di if Li = LO and Di(LO) <= Di(HI) = Di if Li = HI. A tight DBF of such a task is known as expressed in Eq. (5) [20,31,32].
According to Fig. 2 and also as suggested in [20,33], first of all, tasks from different parts of the system will be sent to the central processor.
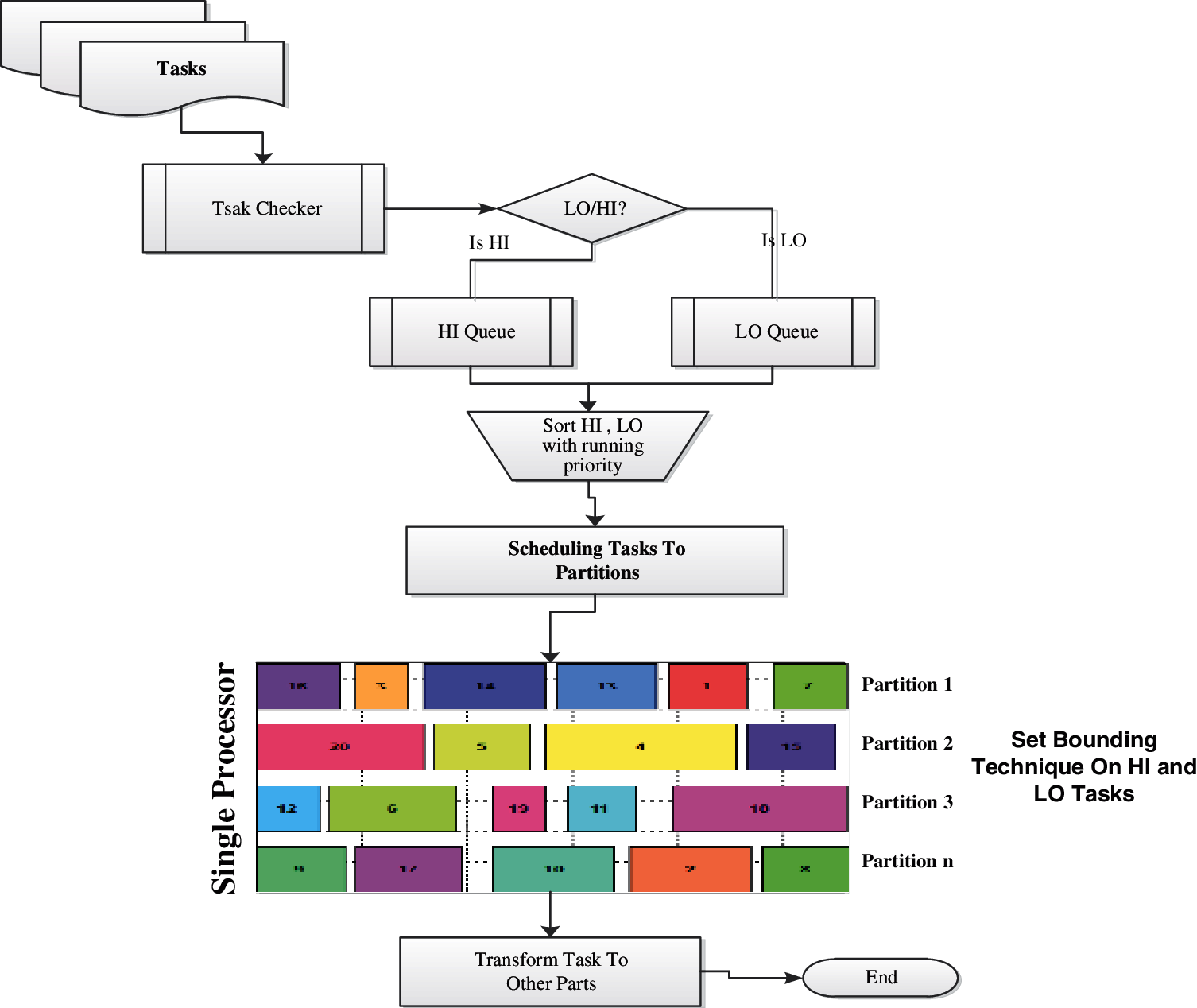
Figure 2: The flowchart of the proposed method according to [18] and also as suggested in [20,33]
The task checker interface will process all incoming tasks. Then each of the inputs LO and HI are checkeds. After diagnosis of the LO or HI tasks assigned to each tag, they are sent to the corresponding queues. Each queue, after receiving the tasks, sends them to the sorter interface. The sort by priority interface set the HI tasks on top of the table and other tasks based on priority are sorted on table. All the tasks are then entered into SMPIA, and the algorithm tasks between partitions generated by caps distribution and scheduling tasks can be done.
During the parallel execution of tasks on each partition, the bounding techniques are also applied to the HI and LO tasks. Then, the sensitivity of HI is checked. At this time, there is no need to time the processing of LO tasks. One of the main advantages of the proposed method to other methods is the efficient use of time to execute all the tasks by CPU.
4 The Proposed Optimized SMPIA Method
According to the ideas presented in this paper for solving the problem of task starvation and lack of sufficient resources, the Algorithm 2 (Tab. 4) is proposed as follows:

Therefore, one important advantages of the O-SMPIA method is that the prioritization of tasks and their scheduling using VMs in a way to solve; the starvation problem. As explained during this section, the O-SPMIA method is based on task prioritization. By prioritizing the tasks, the schedule is changed, which causes the selection of the desired VM to be done using the Greedy algorithm. The Greedy algorithm, based on calculating its variance and HI and, LO tasks, selects the acceptable VM. Therefore, the best VM is first selected according to the Max-Min or Min-Min algorithm; then, the tasks with higher priority are executed. In SMPIA and O-SMPIA, all the created processes will be submitted to one node; as a result, the first machine will have the whole load, whereas no tasks will be submitted to the other machines. The working procedures of the SMPIA and O-SMPIA are shown in Fig. 3.
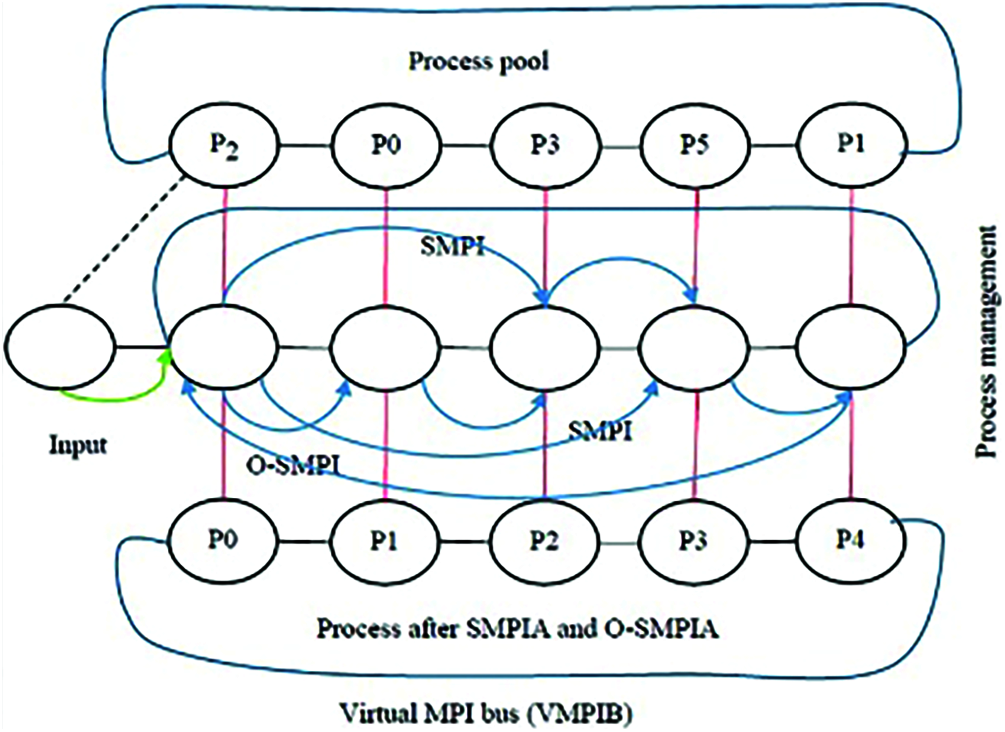
Figure 3: Process management for parallel jobs with SMPIA and O-SMPIA in VMPIB
4.1 Implementation of MPICH-3.0.4
The nfs-kernel-server and MPICH-3.0.4 packages are installed to implement MPI, thanks to a special feature in the master system. After that, the Htop software is installed to monitor the processes running in parallel in MPI. Then, in the Hosts file, the master system is defined for IP systems. The copy of the program file was compiled in the “Mirror” folder using the MPI compiler. At the end, the program file is copied to the mirror folder and compiled it using the MPI compiler. Then, the program compiled by MPICH is executed using the following command: /nfsshare$ mpirun –f hosts –n number. /MPI_sample.
It should be mentioned that instead of number, the number of processors desired to be involved with the program could be entered. Moreover, the program names are entered instead of MPI_sample. Afterwards, the program is run well on all systems and the performance of the processors is observed on each of the Slave computers with the assistance of Htop. Ultimately, the user code is copied in the AVM buffer by MPI, and then is prepared for parallel execution [18]. MPICH-3.0.4 runs using multi-purpose daemon (MPD), that is a, process manager that is able to launch the execution of a parallel program on multiple machines. Additionally, it provides communication between all launched processes to exchange data. MPD starts on all the nodes participating within the cluster. Using mpdboot, MPD launches itself on all nodes of the cluster. The MPD clusters configuration has a ring topology, where each node is connected to the next node, and therefore the last node is connected to the first one. When a parallel program calls MPI_Comm_spawn, without specifying where to run the newly spawned process through the [mpi info] parameter, the process manger MPD starts the new spawned processes on the next node in the MPD’s ring. For the newly created processes, the default is that follow the RR algorithm starting from rank (0) every time.
Therefore, the creation of processes by using MPI_Comm_spawn has two scenarios:
1. The first scenario happens when using one MPI_Comm_spawn function to create many processes by using the [Maxproc] parameter. It will follow the Greedy algorithms to distribute processes starting from rank (0), and this will distribute the load equally.
2. The second scenario suffers from a significant problem when the MPI_Comm_spawn function is called many times. For example, when calling the function iteratively inside a loop, or when making recursive calls for this function, in both cases, each call of this function will submit the new process every time to the first rank. In this case, all the created processes will be submitted to one node, the first machine. As a result, the first machine will have the whole load, whereas no tasks will be submitted to the other machines. As stated above, the decision of submitting new tasks to hosts is made in the function level. In every call to this function, the submission of tasks happens according to the Greedy algorithms starting from the clusters’ first host independent of any MPI_Comm_spawn previously named. This unbalanced load happens because of the decentralization in decision made by MPI_Comm_spawn about submitting the new spawned process to a host since MPI-2 does not introduce any way of scheduling [13,34].
This section explains the metrics used to measure the effectiveness of O-SMPIA in task scheduling. Different kinds of optimization criteria were addressed, e.g., MS, cost, budget, deadline, TET, RU, throughput, load balancing, and energy efficiency. In General, these optimization criteria are categorized into two types based on cloud service: cloud users’ type and cloud service provider’s type [1,12,18,19].
It is defined as the completion time of the last task that is required to complete and leave the cloud system [18,35,36]. It is calculated using Eq. (6).
Execution time is defined as the TET of every single task from the beginning to the end. TET of all tasks from the beginning to the end [18]. The ET is equal to execution time of task that is calculated based on Eq. (7) [12].
L indicates the length of the task which is measured with the amount of million instructions. MIPS indicates the amount of million instructions per second allocated to VMi and loadVMj indicates the previous existing tasks performed by VMj as allotted in Eq. (8), N is the number of tasks into specific VM [12,18].
It represents the termination of running tasks at a particular time [37].
5.1.4 Response Time, Delay or Latency
Indicates the total time needed to respond by a cloud computing system and this metric should be minimized. It is calculated based on the Eq. (9) [12].
The expected completion time can be determined by calculating the expected completion time of task in each VM based on Eq. (10) [12].
It refers to making the most of the available resources and keep resources as busy as possible. It is useful for service providers to get again by leasing the finite resources to the cloud user on-demand [18,38].
It measures the number of completed tasks per unit time [11,12,39,40]. The throughput is calculated through the following Eqs. (11), n is total number of tasks.
This criterion in CC refers to the distributions of loads among VMs over physical resources. Many techniques have been introduced by the authors in [41–43].
The O-SMPIA was simulated to optimize the system performance to achieve the least response time, delay time, and execution time as well as the highest throughput, and also to solve the problem of insufficient resources. In addition, the proposed O-SMPIA was compared with SMPIA. With O-SMPIA, the performance of the system was significantly improved, which is discussed in this section. The tests were conducted on the actual data in a homogenous environment including 4 DCs, 22 servers, 132 VMs, 132 flows, and 324 telecommunication equipment. To do so, 201535 records were collected on transactions (deals and tenders) of the telephone company from 2011 to 2017. We took average of 50 simulation results for each graph. The simulation and implementation were performed in MATLAB. The experiments were done on a system with the following features: Windows 10, CPU 2.5 GHz, core i7–2450 m, and 16 GB RAM. In this research, data sets of telecommunication transactions applications (deals and tenders) in MCITI and workflows were used for simulation purposes [18]. In this section, the results of O-SMPIA, including throughput, response time, delay time and execution time are presented based on three Min-Min, Max-Min, and Greedy algorithms. This section explains the metrics used to measure the effectiveness of SMPIA and O-SMPIA in task scheduling. Different kinds of optimization criteria were addressed, e.g., MS, cost, budget, deadline, TET, RU, throughput, load balancing, and energy efficiency. General, these optimization criteria are categorized into two types based on cloud service: cloud users’ type and cloud service provider’s type [1,12,18,19]. The details of simulation by data values parameters are shown in Tab. 5.
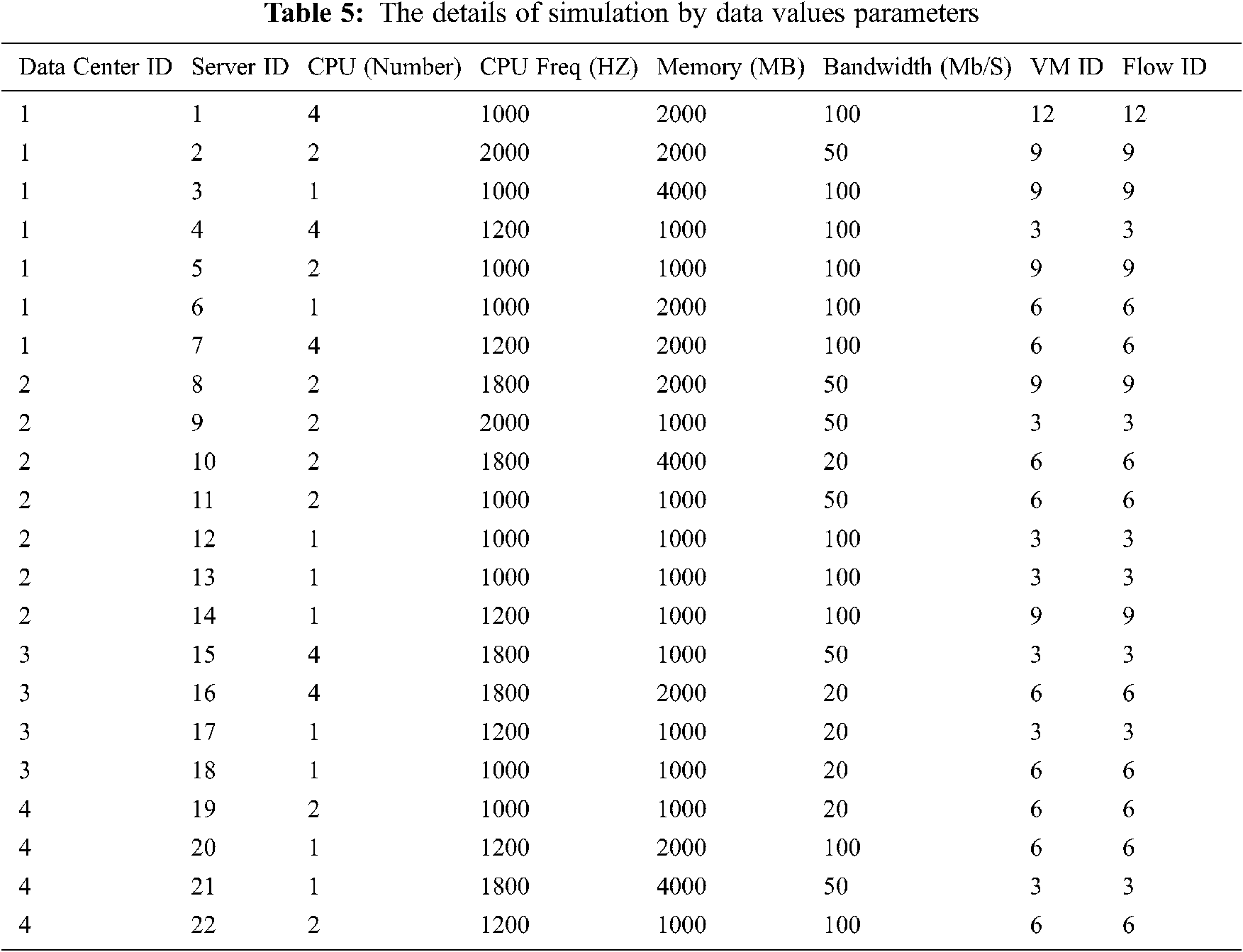
Fig. 4a, shows the delay time of SMPIA based on the number of iteration. As can be seen in this figure, the delay time in Max-Min_SMPIA based on the number of iteration is better than that of the other algorithms, and also it is faster. Therefore, the delay time for workflow in the CC systems using Max-Min_SMPIA was found more efficient than the other methods.

Figure 4: Impacts of iteration on the performance of SMPIA. (a) Delay time (b) Load balancing
Fig. 4b, shows the load balancing of SMPIA based on iteration. As this figure displays, the load balancing of Max-Min_SMPIA based on the iteration is best and more efficient than that of the other methods.
6.2 Optimized SMPIA Performance
Fig. 5a, shows the throughput of the O-SMPIA algorithms. Throughput counts the number of job count completed within the task in the per unit time. As can be seen in the figure, the throughput in O-SMPIA based on the Greedy algorithm is better than that of the other algorithms, and also has a better performance. In all three methods, throughput gradually increased. Therefore, the throughput rate for workflow in CC systems using O-SMPIA based on the Greedy algorithm was found more optimal.

Figure 5: Impacts of job counts on performance of the O-SMPIA. (a) Throughput (b) Response time (c) Execution time (d) Delay time
Fig. 5b, shows the response time of the O-SMPIA algorithms. As can be seen in this figure, the response time in O-SMPIA based on the Greedy algorithm is better than that of the other of other algorithms, and it is faster.
Fig. 5c, shows that the execution time in O-SMPIA based on the Max-Min algorithm is better than that of the other algorithms, and it is faster. Therefore, the execution time for workflow in CC systems using intelligent MPI based on the Max-Min algorithm was found more efficient than the other methods.
Fig. 5d, shows the delay time of the O-SMPIA algorithms. As demonstrated by this figure, the delay time in O-SMPIA based on the Greedy algorithm is better than that of the other algorithms, and it is faster. Therefore, the delay time for workflow in CC systems using Greedy_O-SMPIA was shown to be more efficient than the other methods.
The evaluation of performance metrics showed that the delay and response time of the Greedy algorithm were less than those of the others. At the same time, the execution time of Max-Min was less than those of the others and the throughput of the Greedy was longer.
7 Conclusions and Future Scope
In this work, O-SMPIA was presented, which was designed based on task prioritization. O-SMPIA succeeded in alleviating the problem of task starvation and lack of resource by taking into account the urgency of execution time. It also increased the throughput of the system. The HI tasks were assigned to the best available selected resource. In this paper, the EDF-VD algorithm was applied to a fixed version of utilization caps. The EDF-VD algorithm was combined with O-SMPIA, which caused the improvement of the system performance. O-SMPIA shortened the execution time, response time, and delay time and, at the same time, it increased the throughput. O-SMPIA was simulated in the MATLAB environment. The best mode was greedy, in which with O-SMPIA, delay, response time, and throughput were improved. The results with actual data of the environment showed that O-SMPIA was more efficient than SMPIA in the cloud system. Comparing the performance metrics showed that the Greedy algorithm was better than the Max-Min and, Min-Min algorithms in terms of delay, throughput and response time. On the other hand, Max-Min was found better than Greedy and Min-Min in terms of execution time. These results reflect the effectiveness of O-SMPIA on the cloud resource consumption time and resource efficiency. The simulation results show that O-SMPIA was able to increase the system throughput by quickly selecting VMs and responding to the assignment of tasks to choose VMs during a timely manner. The effect and throughput of O-SMPIA is more obvious as change within the job count and the number of cloud workloads increase. One among the most advantages of the O-SMPIA to other methods is efficient use of your time to execute all the tasks by CPU. In the future, it is recommended to analyze multiple modes (prerequisite and post-requisite) and the quality of SMPIA and O-SMPIA with scientific and artificial workflows.
Funding Statement: This Research was supported by Islamic Azad University-Sari Branch, Sari, Iran.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. A. Al-Arasi and A. Saif, “Task scheduling in cloud computing based on metaheuristic techniques: A review paper,” EAI Endorsed Transactions on Cloud Systems, vol. 6, no. 17, pp. 162829, 2020. [Google Scholar]
2. R. Jain and A. Nayyar, “A novel homomorphic RASD framework for secured data access and storage in cloud computing, “Open Computer Science, vol. 10, no. 1, pp. 431–443, 2020. [Google Scholar]
3. H. M. Wei, J. Gao, P. Qing, K. Yu, Y. F. Fang et al., “MPI-Rcdd: A framework for MPI runtime communication deadlock detection,” J. Comput. Sci. & Technol, vol. 35, no. 2, pp. 395–411, 2020. [Google Scholar]
4. L. Espnola, D. Franco and E. Luque, “Improving mpi communications in cloud,” ACM-W Europe WomENcourage Celebration of Women in Computing, 2016. [Google Scholar]
5. H. Hassanpour and M. Mokhtari, “Proposing a dynamic routing approach to improve performance of Iran data network,” World Applied Sciences Journal 7 (Special Issue of Computer & IT), vol. 7, pp. 01–07, 2009. [Google Scholar]
6. F. Gomez-Folgar, A. J. García-Loureiro, T. F. Pena, J. I. Zablah and R. V. Ferreiro, “Cloud computing for teaching and learning MPI with improved network communications,” WCLOUD, vol. 945, pp. 22–27, 2012. [Google Scholar]
7. L. Espnola, D. Franco and E. Luque, “MCM: A new MPI communication management for cloud environments,” Procedia Computer Science, vol. 108, pp. 2303–2307, 2017. [Google Scholar]
8. P. Rad, R. V. Boppana, P. Lama, G. Berman and M. Jamshidi, “Low-latency software defined network for high performance clouds,” in 2015 10th System of Systems Engineering Conf. (SoSE), San Antonio, TX, USA, IEEE, pp. 486–491, 2015. [Google Scholar]
9. A. R. Arunarani, D. Manjula and V. Sugumaran, “Task scheduling techniques in cloud computing: A literature survey,” Future Generation Computer Systems, vol. 91, pp. 407–415, 2019. [Google Scholar]
10. R. Swathy, B. Vinayagasundaram, G. Rajesh, A. Nayyar, M. Abouhawwash et al., “Game theoretical approach for load balancing using SGMLB model in cloud environment,” PLOS One, vol. 15, no. 4, pp. e0231708, 2020. [Google Scholar]
11. M. Haque, R. Islam, M. R. Kabir, F. N. Nur and N. N. Moon, “A priority-based process scheduling algorithm in cloud computing,” in Emerging Technologies in Data Mining and Information Security, Springer, Singapore, pp. 239–248, 2019. [Google Scholar]
12. M. A. Alworafi, A. Dhari, S. A. El-Booz, A. A. Nasr, A. Arpitha et al., “An enhanced task scheduling in cloud computing based on hybrid approach,” in Data Analytics and Learning, Springer, Singapore, pp. 11–25, 2019. [Google Scholar]
13. S. Elmougy, S. Sarhan and M. Joundy, “A novel hybrid of shortest job first and round robin with dynamic variable quantum time task scheduling technique,” Journal of Cloud Computing, vol. 6, no. 1, pp. 1–12, 2017. [Google Scholar]
14. A. A. Laghari, H. He, M. Shafiq and A. Khan, “Impact of storage of mobile on quality of experience (QoE) at user level accessing cloud,” in 2017 IEEE 9th Int. Conf. on Communication Software and Networks (ICCSN), Guangzhou, China, IEEE, pp. 1402–1409, 2017. [Google Scholar]
15. P. Brucker, “Scheduling algorithms 5th edition,” Berlin: Springer, 2006. https://www.taodocs.com/p-2869666.html. [Google Scholar]
16. J. K. Konjaang and L. Xu, “Multi-objective workflow optimization strategy (MOWOS) for cloud computing,” Journal of Cloud Computing, vol. 10, no. 1, pp. 1–19, 2021. [Google Scholar]
17. J. Blazewicz, K. H. Ecker, E. Pesch, G. Schmidt, M. Sterna et al., “Scheduling under resource constraints,” in Handbook on Scheduling, Springer, Berlin, Heidelberg, pp. 475–525, 2019. [Google Scholar]
18. M. Mokhtari, P. Bayat and H. Motameni, “Multi-objective task scheduling using smart MPI-based cloud resources,” Computing and Informatics, vol. 40, no. 1, pp. 104–144, 2021. [Google Scholar]
19. H. Singh, A. Bhasin and P. Kaveri, “Secure: Efficient resource scheduling by swarm in cloud computing,” J. Discret Math. Sci. Cryptogr., vol. 22, no. 2, pp. 127–137, 2019. [Google Scholar]
20. M. Mahdiani and A. Masrur, “Introducing utilization caps into mixed-criticality scheduling,” in Euromicro Conf. on Digital System Design (DSD), Lubeck, Germany, IEEE, pp. 388–395, 2016. [Google Scholar]
21. V. Singh and N. K. Verma, “An entropy-based variable feature weighted fuzzy k-means algorithm for high dimensional data,” arXiv preprint arXiv:1912.11209, Cornell University, 2019. [Google Scholar]
22. T. P. Jacob and K. Pradeep, “A multi-objective optimal task scheduling in cloud environment using cuckoo particle swarm optimization,” Wireless Personal Communications, vol. 109, no. 1, pp. 315–331, 2019. [Google Scholar]
23. F. Luo, Y. Yuan, W. Ding and H. Lu, “An improved particle swarm optimization algorithm based on adaptive weight for task scheduling in cloud computing,” in Proc. of the 2nd Int. Conf. on Computer Science and Application Engineering, Hohhot China, pp. 1–5, 2018. [Google Scholar]
24. L. Guo, S. Zhao, S. Shen and C. Jiang, “Task scheduling optimization in cloud computing based on heuristic algorithm,” Journal of Networks, vol. 7, no. 3, pp. 547, 2012. [Google Scholar]
25. M. Amiri and L. Mohammad-Khanli, “Survey on prediction models of applications for resources provisioning in cloud,” Journal of Network and Computer Applications, vol. 82, pp. 93–113, 2017. [Google Scholar]
26. K. D. Kumar and E. Umamaheswari, “Resource provisioning in cloud computing using prediction models: A survey,” International Journal of Pure and Applied Mathematics, vol. 119, no. 9, pp. 333–342, 2018. [Google Scholar]
27. T. Ma, Y. Chu, L. Zhao and O. Ankhbayar, “Resource allocation and scheduling in cloud computing: Policy and algorithm,” IETE Technical Review, vol. 31, pp. 4–16, 2014. [Google Scholar]
28. A. Nayyar, Handbook of cloud computing: Basic to advance research on the concepts and design of cloud computing, BPB Publications, Darya Ganj, 2019. [Google Scholar]
29. A. Kaur, P. Gupta, M. Singh and A. Nayyar, “Data placement in era of cloud computing: A survey, taxonomy and open research issues,” Scalable Computing: Practice and Experience, vol. 20, no. 2, pp. 377–398, 2019. [Google Scholar]
30. S. Ramanathan and A. Easwaran, “Utilization difference based partitioned scheduling of mixed-criticality systems, ” in Design, Automation & Test in Europe Conf. & Exhibition (DATE), Lausanne, Switzerland, IEEE, pp. 238–243, 2017. [Google Scholar]
31. P. Ekberg and W. Yi, “Bounding and shaping the demand of generalized mixed-criticality sporadic task systems,” Real-time Systems, vol. 50, no. 1, pp. 48–86, 2014. [Google Scholar]
32. S. Bajaj, “Current drift in energy efficiency cloud computing: New provocations, workload prediction, consolidation, and resource over commitment,” In Critical Research on Scalability and Security Issues in Virtual Cloud Environments, IGI Global, Hershey, Pennsylvania, USA, pp. 283–303, 2018. [Google Scholar]
33. M. Mahdiani and A. Masrur, “A novel view on bounding execution demand under mixed-criticality EDF,” Real-Time Systems, vol. 57, no. 1, pp. 55–94, 2021. [Google Scholar]
34. S. A. Embaby, A. S. Moussa and I. Farag, “A dynamic scheduling algorithm for spawn processes in MPI-2 to improve and maintain load balancing,” International Journal of Computer Applications, vol. 106, no. 12, 2014. [Google Scholar]
35. M. S. Abd Latiff, S. H. H. Madni and M. Abdullahi, “Fault tolerance aware scheduling technique for cloud computing environment using dynamic clustering algorithm,” Neural Computing and Applications, vol. 29, no. 1, pp. 279–293, 2018. [Google Scholar]
36. M. Kalra and S. Singh, “A review of metaheuristic scheduling techniques in cloud computing,” Egyptian Informatics Journal, vol. 16, no. 3, pp. 275–295, 2015. [Google Scholar]
37. D. Poola, S. K. Garg, R. Buyya, Y. Yang and K. Ramamohanarao, “Robust scheduling of scientific workflows with deadline and budget constraints in clouds,” in Advanced Information Networking and Applications (AINA2014 IEEE 28th Int. Conf. on, Victoria, BC, Canada, pp. 858–865, 2014. [Google Scholar]
38. J. Lin, Y. Zhong, X. Lin, H. Lin and Q. Zeng, “Hybrid ant colony algorithm clonal selection in the application of the cloud’s resource scheduling,” arXivpreprint arXiv: 1411. pp. 2528, Cornell University, 2014. [Google Scholar]
39. S. K. Panda, I. Gupta and P. K. Jana, “Task scheduling algorithms for multi-cloud systems: Allocation-aware approach,” Information Systems Frontiers, vol. 21, no. 2, pp. 241–259, 2019. [Google Scholar]
40. E. Pacini, C. Mateos and C. G. Garino, “Balancing throughput and response time in online scientific clouds via ant colony optimization (SP2013/2013/00006),” Advances in Engineering Software, vol. 84, pp. 31–47, 2015. [Google Scholar]
41. S. Dam, G. Mandal, K. Dasgupta and P. Dutta, “An ant colony based load balancing strategy in cloud computing,” in Advanced Computing, Networking and Informatics, vol. 2, Springer, International Publishing Switzerland, pp. 403–413, 2014. [Google Scholar]
42. K. Dasgupta, B. Mandal, P. Dutta, J. K. Mandal and S. Dam, “A genetic algorithm (ga) based load balancing strategy for cloud computing,” Procedia Technology, vol. 10, pp. 340–347, 2013. [Google Scholar]
43. C. Jianfang, C. Junjie and Z. Qingshan, “An optimized scheduling algorithm on a cloud workflow using a discrete particle swarm,” Cybernetics and Information Technologies, vol. 14, pp. 25–39, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |