DOI:10.32604/csse.2022.021637

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021637 |  |
| Article |
Machine Learning-Based Pruning Technique for Low Power Approximate Computing
1Department of Electronics and Communication Engineering, Madurai Institute of Engg and Technology, Sivagangai, Tamilnadu, 630611, India
2Pilecubes India Pvt Ltd., Chennai, Tamilnadu, India
3Department of Electronics and Communication Engineering, Malla Reddy Engineering College (Autonomous), Secunderabad, 500100, India
4Department of Electronics and Communication Engineering, R. M. K. Engineering College, Kavaraipettai, Chennai, Tamil Nadu, 601206, India
5Department of Electronics and Communication Engineering, K Ramakrishnan College of Engineering, Kariyamanickam Rd, Tamil Nadu, 621112, India
*Corresponding Author: B. Sakthivel. Email: 786sakthivel@gmail.com
Received: 09 July 2021; Accepted: 12 August 2021
Abstract: Approximate Computing is a low power achieving technique that offers an additional degree of freedom to design digital circuits. Pruning is one of the types of approximate circuit design technique which removes logic gates or wires in the circuit to reduce power consumption with minimal insertion of error. In this work, a novel machine learning (ML) -based pruning technique is introduced to design digital circuits. The machine-learning algorithm of the random forest decision tree is used to prune nodes selectively based on their input pattern. In addition, an error compensation value is added to the original output to reduce an error rate. Experimental results proved the efficiency of the proposed technique in terms of area, power and error rate. Compared to conventional pruning, proposed ML pruning achieves 32% and 26% of the area and delay reductions in 8*8 multiplier implementation. Low power image processing algorithms are essential in various applications like image compression and enhancement algorithms. For real-time evaluation, proposed ML optimized pruning is applied in discrete cosine transform (DCT). It is a basic element of image and video processing applications. Experimental results on benchmark images show that proposed pruning achieves a very good peak signal-to-noise ratio (PSNR) value with a considerable amount of energy savings compared to other methods.
Keywords: Machine learning; pruning; approximate computing; PSNR
Improving energy efficiency is a critical task in the modern digital world. Due to growing process-voltage–temperature (PVT) variations, enormous safety limits are needed to assure the system working among all corners [1]. This results in higher energy penalties. Due to the invention of handheld devices and IoT technologies, there is a huge need for power optimization techniques. Recently, approximate computing (AC) is one of the promising technology for achieving power optimization. Approximate computing not only reduces power consumption it also reduces critical delay in other circuits. All digital application does not require exact data processing [2]. Some application allows the user to introduce an error in computing like lossy compression. AC can be applied to all data path elements. Providing high quality and reconfigurability is mandatory for AC techniques to maintain the quality of results to a preferred level and to supply with tunable knob(s) to tradeoff quality with effectiveness.
Adder and multiplier are the key components of arithmetic processors, based on the performance of the adder and multiplier only the overall process of the system can be improved. Approximation in adder and multiplier circuits lead to a reduction in delay and power consumption [3]. many quality metrics are described for measuring the performance of Approximate computation in terms of area, delay and error rate. Recently, the quality metrics of error distance (ED), mean error distance (MED) and normalized error distance (NED) have been used for evaluating the designs of approximate circuits [4]. In early design, various transistor and logical level modifications were carried out to design an approximate circuit. Recently, accuracy configurable circuits were introduced to tradeoff the accuracy for area and energy. The major disadvantage of the previous approximation technique is that they need additional hardware for error compensation. Pruning is an approximate circuit design technique that removes gates or wires to tradeoff the circuit accuracy against power, area and critical delay. The amount of pruning can be defined by users based on application or error tolerance level [5]. The main drawback of the pruning technique is computation time. For every, the error rate and power of the circuit have to be calculated for every pruning step. The execution time of the circuit increases drastically when the bit size of the circuit increase. In order to overcome the limitations of pruning, machine learning-based pruning is presented in this paper.
This work is structured as follows. Previous works related to approximation is explained in Section 2; Section 3 describes some essential preliminaries related to pruning based approximation. Section 4 discusses the proposed ML approach for pruning. Section 5 discusses the implementation results. Finally, Section 6 concludes our work.
Several researchers in the past have analyzed the trade-off between power consumed and accuracy in approximate arithmetic circuit designs. Wang et al. [6] have proposed an accuracy configurable adder based on carrying prediction called simple accuracy reconfigurable adder (SARA). It does not require any additional hardware overhead for error compensation. The overall delay is lesser than the conventional carry look-ahead adder and combines the advantages of all other proposed adders. Sakthivel et al. [7] have proposed an accuracy configurable GDI adder for low power image processing applications. By controlling GDI gate inputs, the accuracy level of the circuits can be varied. The proposed adder has the advantage of switching between normal mode or approximated mode.
Liu et al. [8] have proposed an approximate booth multiplier for error-tolerant application. The conventional booth encoder was modified to an approximate encoder to design an approximate multiplier. The error characteristics of the proposed multiplier were analyzed for various error factors. Venkatachalam et al. [9] have designed three types of approximate booth multipliers. The partial product generation and accumulation part of the multiplier is modified to reduce an area and power. The proposed multiplier was analyzed in terms of Mean Relative Error Distance (MRED).
Xu et al. [10] have a self-tuning approximate circuit for lossy application. Self-tuning is achieved by intruding two different types of controllers. The level of accuracy varied for every interval based on a particular threshold. Jiang et al. [11]have proposed an approximate multiplier with an error correction mechanism for digital signal processing applications. The critical delay of a multiplier is solved by using newly designed approximate adders. Error compensation block is used to reduce an error rate due to approximation. Experimental results show that the proposed multiplier achieves a 42% energy reduction. Xu et al. [12] have proposed a multi-bit approximate adder by transistor-level modification. The main advantage of a proposed adder is reduced switched capacitance and critical paths. The single-bit imprecise adder is used to construct a multi-bit adder.
Gupta et al. [13] have proposed a majority logic-based design of approximate adders and multipliers. The approximate compressors are utilized to construct adder and multiplier stages. Area and power results show the superior performance of a proposed approximate design. Soares et al. [14] have proposed a hybrid adder based on minimum add and shift operations. High speed parallel prefix adder designed by approximate adders. The proposed adders are applied in Gaussian image filter Sobel operator for image processing applications to validate real-time performance. Results show that 7.7% of energy reductions were achieved for multiple levels of accuracy.
Liu et al. [15] have introduced approximate redundant binary (RB) multipliers for signal processing applications. By considering the error behaviour of the circuit, two RB 4:2 compressors were added for logic computation. Based on application and accuracy requirements, both exact and inexact output can be obtained in a single circuit. Wu et al. [16] have proposed an approximate circuit design methodology called ALFANS (approximate logic synthesis framework by approximate node simplification). The algorithms proposed to handle error rate and energy constraints. The delay and error rate for each node was computed to perform truncation. Experimental results show that proposed ALFANS produce better quality results in image processing applications than other methods.
Schlachter et al. [17] have proposed a gate-level pruning technique to tradeoff the accuracy for the area, energy and delay requirements of the circuit. The computer-aided model library was created to selectively prune the wires in a circuit. The proposed pruning is implanted in a discrete cosine transform (DCT), which is the basic component of image processing application. Results show that the pruning of wire achieves a 20% power reduction compared to the original circuit. Nepal et al. [18] have proposed an automatic inexact circuit generation methodology by the concept of abstract syntax tree (AST). It is constructed by the register-transfer level (RTL) descriptions of the circuit named ABACUS after Automated Behavioral Approximate Circuit Synthesis. Compared to other design techniques, the proposed ABACUS reduces area requirements with minimum execution time.
3 Preliminaries of Pruning Based Approximate Circuit Design
In pruning, all logic components and their connections are considered as a Direct Acyclic Graph (DAG). all nodes in the graph are gates and their input and output edges are considered as wires. Three important factors of every node or wire are defined for pruning namely the Significance (S), the Switching Activity (α) and the Fanout. The significance S is an important functional parameter used to measure the data value carried by a node through its influence on the outputs of the circuit. The fan-out of a logic gate is the number of gate inputs driven by the output of another single logic gate. The switching activity computation at a circuit node (n) occupies the signal probability estimation p1 (n), which specifies the probability of signal value at the node n is ‘1’. The node switching activity is expressed by:
The logic gate dynamic power can be expressed as:
where Vdd represents the supply voltage of gate, CL indicates the capacitance of load and f represents the signal frequency which is also the clock frequency. The load capacitance of the circuit depends upon the number of fanout of the gates. This three-factor is mostly considered for pruning due to reducing the dynamic power consumption of the circuit. By considering these factors the cost function of particular nodes is expressed as:
where, SMAX indicates the maximum importance value over the logic circuit, (Fanout.α) MAX represents the maximum value of the product between switching activity and Fanout. Then, β represents the ratio between the two sides.
4 Propose Machine Learning-Based Pruning
Machine learning is a type of artificial intelligence that automatically learn from the data with minimum human intervention. It creates model-building automation for data analysis. Random forest is a supervised machine learning algorithm that is used for data processing without any hyperparameter tuning. It processes the number of decision trees and computes the average to increase prediction accuracy. It not only depends upon a single tree, a majority based approach for taking a decision. In this work, random forest decision trees are trained to a possible combination of inputs and their corresponding pruning gates with compensation values for error reduction. The block diagram proposed work is shown in Fig. 1.
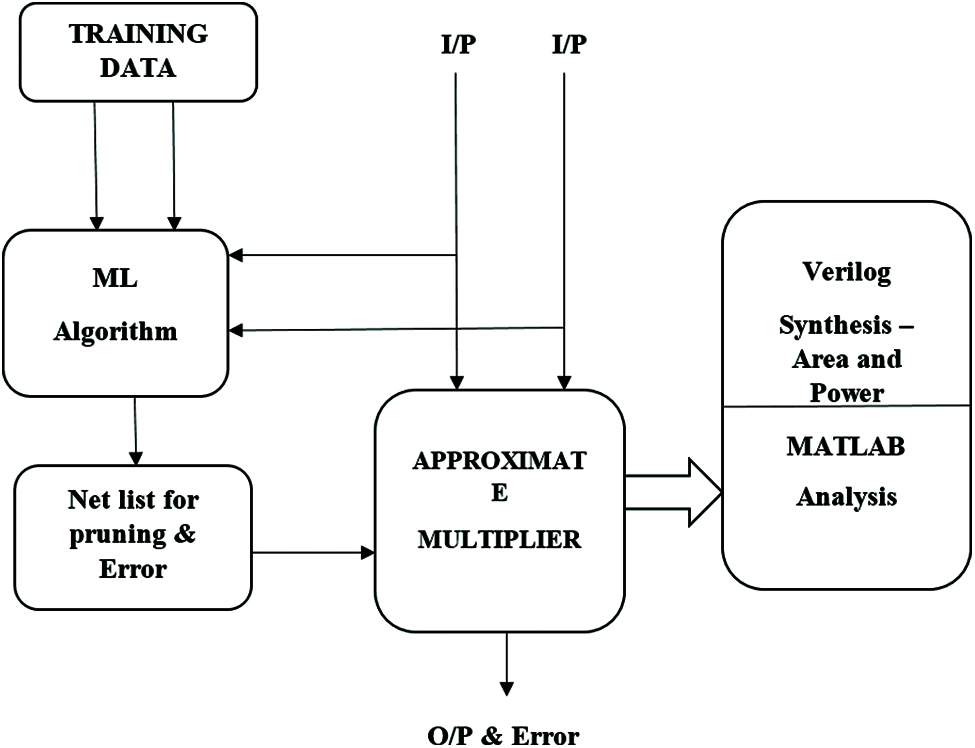
Figure 1: Proposed pruning methodology
In this work, propose a machine learning-based pruning technique for low power circuit design. The main concept is a machine learning-based gate-level netlist suggested for pruning based on trained data. In addition, the error compensation module is used to meet desired output quality. Radom forest decision tree constructed by all possible combinations of inputs, power dissipation and accuracy levels as shown in Fig. 2. The proposed approach is divided into two stages: an off-line, random forest decision tree trained by all possible combinations of inputs to produce optimum pruning cost with error compensation values. the optimum netlist gives the number of gates to be pruned based on cost with a minimum error rate. an online stage, the suitable netlist for corresponding input generated from machine learning algorithm to meet requirements.
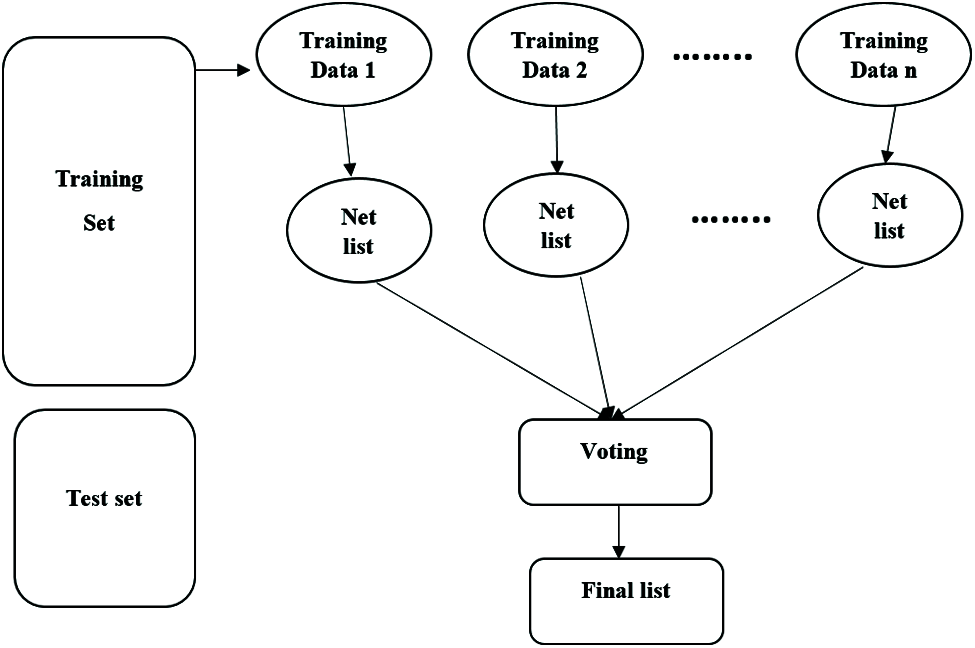
Figure 2: Random forest decision tree for pruned netlist generation
In training, we have different possible input groupings. For 9- and 16-bit designs, the size of combinations is 216 and 232, correspondingly. The random forest decision tree selects k data points from a training set. Construct a decision tree related to the selected data. Based on input values, some fixed compensation values are added to the original output in order to reduce an error. The proposed methodology is suitable for all digital designs like approximate FIR filter transforms and dividers etc. Based on architecture and input combinations different gate list output values are trained in ML. The workflow of the proposed methodology is shown in Algorithm 1.
Initially, the circuit output significance, circuit input probabilities Pi, ratio and Error threshold are defined as inputs. Then, for all nodes, find significance using depth-first search propagation going from primary outputs to primary inputs. Signal probabilities are calculated for all nodes (Pi) and switching activity (α) can be computed as Pi(1-Pi) for all nodes. Calculate the cost function using Eq. (3) for all nodes. For pruning, the pre-trained possible output values and error rates compared with current values. Finally, random forest decision tree identities suitable pruning nodes for inexact design in terms of both reduced area and error rate. The limit value for pruning is expressed as follows
After the decision, the node is either connected to supply or ground for pruning

DCT is a transformation technique used for image processing applications like image compression. It processes the image based on correlated data to reduce the memory required to represent the image. Various architectures are proposed for DCT by considering the computational complexity of DCT. It requires more adders and multipliers. To achieve a low power computation, the addition and multiplication stages are optimized. The 8-point 1-D-DCT wk of a data sequence xi is defined by
From the above equation observed that DCT needs a large number of adders and multipliers. In this work, proposed pruned addition and multiplication are applied in DCT for low power computation. Both DCT and inverse DCT were performed on dataset image computed and quality of image analyzed using MATLAB tool as shown in Fig. 3.
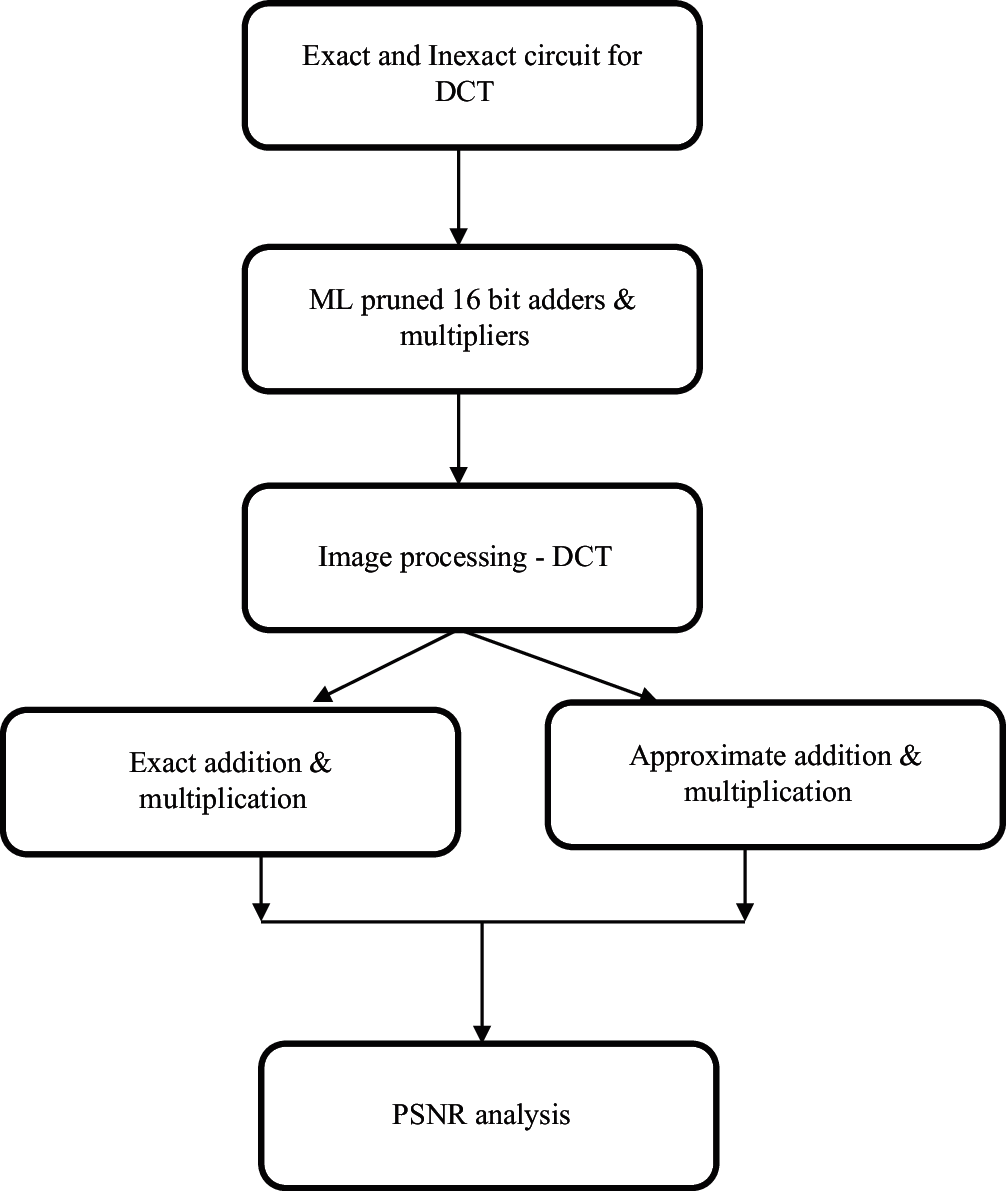
Figure 3: DCT analysis
The quality of reconstructed image calculated by the parameter called peak signal-to-noise ratio (PSNR) as follows:
→ where D denotes mean square error and D denotes the maximum pixel value of an image.
For analysis, we used the Virtex-6 family, with the device and package details of XC6VLX103T FPGA and FF484 respectively. The proposed approximate multipliers have been coded in Verilog and simulated using Xilinx 12.1. For power analysis, Xilinx XPower Analyser has been used. The performance metric used to evaluate a proposed system is slice, LU, dynamic power and error distance (ED). ED is a performance metric that is used to evaluate the reliability of a proposed pruned multiplier. In general, the Error Distance between two binary numbers, x (inexact) and y(exact), is defined as the arithmetic difference between these two numbers, i.e.,
where, i and j are the indices for the bits in x and y, respectively
Tab. 1 shows the area and power values of the 8-bit approximate multiplier for both pruning and ML-pruning algorithms. We observed better result for ML-based pruning by selecting the proper netlist for pruning. The selection higher switching activity node leads to achieving a low power consumption. From Fig. 4 observed that the power consumption and area delay product reduced considerably comapared to conventional pruning techniques.
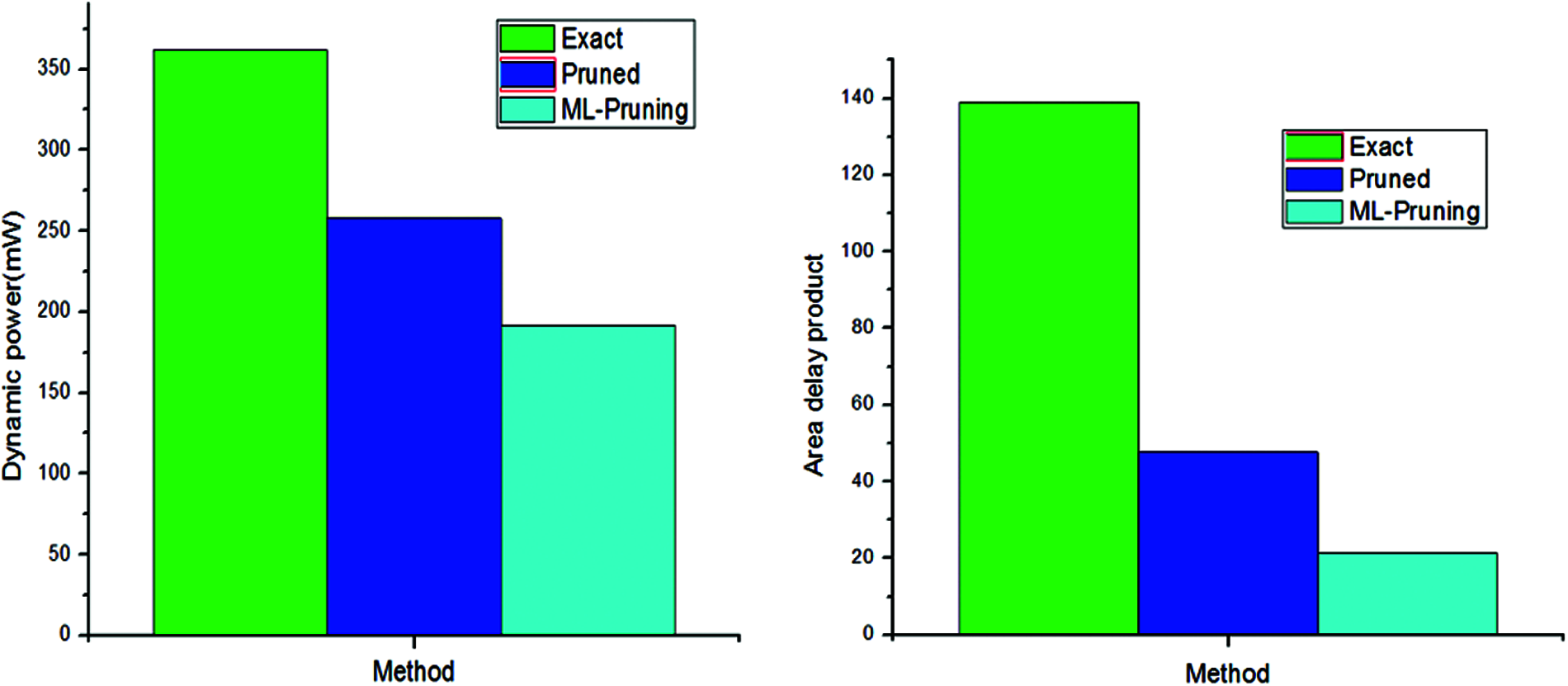
Figure 4: Power and delay analysis

Fig. 5, Shows a histogram plot of ED. From the graph observed that compared to normal pruning the proposed method shows less error rate and by compensation value, the total distance of doesn't go beyond 500. Tab. 2. Shows obtained PSNR values of the reconstructed image in standard benchmark images. By the proper selection of pruning gates, the quality of DCT computation improved by reducing the error rate.
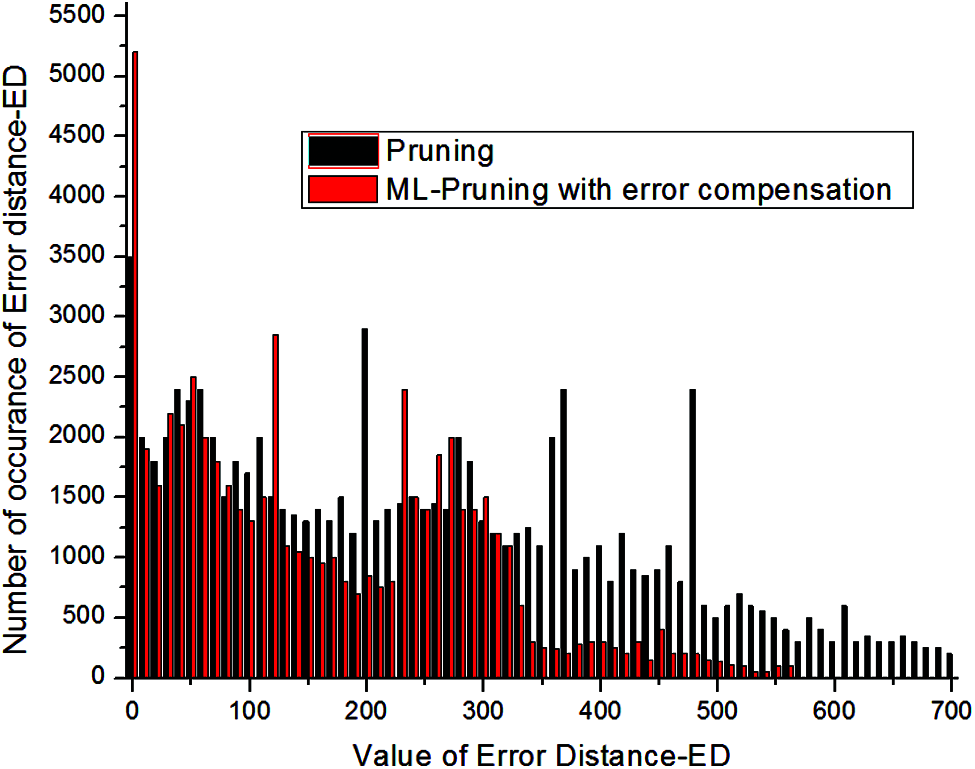
Figure 5: Histogram plot of error distance (ED) distribution in approximate multiplier
Fig. 6. Shows reconstructed DCT image by conventional and ML pruning based images. The proposed design achieves the highest PSNR rate with area reductions.

Figure 6: Results of bench mark image by conventional and ML pruning
This work proposed a methodology to design an approximate circuit using machine learning-based pruning. The proposed method is applicable to all types of digital circuits, more especially for arithmetic circuits. For different circuits, different types of training and library creation needed. The proposed methods consider the input data, construct tree-based models, and adapting the design to fulfil the area and accuracy requirement. Implementation results proved the efficiency of the proposed technique in terms of area, power and error rate. By the compensation value, the output is found to attain notable improvement in precision values without bargaining the power consumption. The results of PSNR values in DCT computation proves the real-time suitability of the proposed pruning technique.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Xu and B. C. Schafer, “Exposing approximate computing optimizations at different levels: From behavioral to gate-level,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 25, no. 11, pp. 3077–3088, 2017. [Google Scholar]
2. M. Ramasamy, G. Narmadha and S. Deivasigamani, “Carry based approximate full adder for low power approximate computing,” in Int. Conf. on Smart Computing & Communications (ICSCCSarawak, Malaysia, pp. 1–4, 2019. [Google Scholar]
3. W. Liu, L. Qian, C. Wang and H. Jiang, “Design of approximate radix-4 booth multipliers for error-tolerant computing,” IEEE Transactions on Computers, vol. 66, no. 8, pp. 1435–1441, 2017. [Google Scholar]
4. M. Masadeh, O. Hasan and S. Tahar, “Machine-learning-based self-tunable design of approximate computing,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 29, no. 4, pp. 800–813, 2021. [Google Scholar]
5. S. Shabeerkhan and A. Padma, “A novel gwo optimized pruning technique for inexact circuit design,” Microprocessors and Microsystems, vol. 1, no. 73, pp. 102961–102975, 2019. [Google Scholar]
6. Y. Wang, J. Dong and Y. Liu, “RMLIM: A runtime machine learning based identification model for approximate computing on data flow graphs,” IEEE Transactions on Sustainable Computing, vol. 1, no. 1, pp. 1–10, 2017. [Google Scholar]
7. B. Sakthivel and A. Padma, “Area and delay efficient GDI based accuracy configurable adder design,” Microprocessors and Microsystems, vol. 1, no. 73, pp. 102958–102967, 2019. [Google Scholar]
8. W. Liu, C. Tian, P. Yin and T. Wang, “Design and analysis of approximate redundant binary multipliers,” IEEE Transactions on Computers, vol. 68, no. 6, pp. 804–819, 2018. [Google Scholar]
9. S. Venkatachalam, E. Adams, H. J. Lee and S. Ko, “Design and analysis of area and power efficient approximate booth multipliers,” IEEE Transactions on Computers, vol. 68, no. 11, pp. 1697–1703, 2019. [Google Scholar]
10. W. Xu, S. S. Sapatnekar and J. Hu, “A simple yet efficient accuracy-configurable adder design,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 26, no. 6, pp. 1112–1125, 2018. [Google Scholar]
11. H. Jiang, C. Liu, F. Lombardi and J. Han, “Low-power approximate unsigned multipliers with configurable error recovery,” IEEE Transactions on Circuits and Systems, vol. 5, no. 6, pp. 1–14, 2018. [Google Scholar]
12. S. Xu and B. C. Schafer, “Toward self-tunable approximate computing,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 1, no. 1, pp. 1–12, 2018. [Google Scholar]
13. V. Gupta, D. Mohapatra and A. Raghunathan, “Low-power digital signal processing using approximate adders,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 32, no. 1, pp. 124–137, 2013. [Google Scholar]
14. L. B. Soares, M. A. Rosa, C. M. Diniz and E. A. Costa, “Design methodology to explore hybrid approximate adders for energy-efficient image and video processing accelerators,” IEEE Transactions on Circuits and Systems, vol. 66, no. 6, pp. 2137–2150, 2019. [Google Scholar]
15. W. Liu, T. Zhang and E. McLarnon, “Design and analysis of majority logic based approximate adders and multipliers,” IEEE Transactions on Emerging Topics in Computing, vol. 1, no. 1, pp. 12–18, 2019. [Google Scholar]
16. Y. Wu and W. Qian, “ALFANS: Multi-level approximate logic synthesis framework by approximate node simplification,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 39, no. 7, pp. 1470–1483, 2020. [Google Scholar]
17. J. Schlachter, V. Camus, K. V. Palem and C. Enz, “Design and applications of approximate circuits by gate-level pruning,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 25, no. 5, pp. 1694–1702, 2017. [Google Scholar]
18. K. Nepal, S. Hashemi, H. Tann and T. Bahar, “Automated high-level generation of low-power approximate computing circuits,” IEEE Transactions on Emerging Topics in Computing, vol. 7, no. 1, pp. 18–30, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |