Computer Systems Science & Engineering DOI:10.32604/csse.2022.022317
Article

Towards Public Integrity Audition for Cloud-IoT Data Based on Blockchain

Hao Yan1,2, Yanan Liu1, Shuo Qiu1, Shengzhou Hu3, Weijian Zhang4,* and Jinyue Xia5

1School of Network Security, Jinling Institute of Technology, Nanjing, 211169, China
2Fujian Provincial Key Laboratory of Network Security and Cryptology, Fujian Normal University, Fuzhou, 350007, China
3Department of Mathematics and Computer Science, Gannan Normal University, Ganzhou, 341000, China
4Network Security and Information Office, Hohai University, Nanjing, 210098, China
5International Business Machines Corporation (IBM), New York, NY, USA
*Corresponding Author: Weijian Zhang. Email: yanhaojlkj@163.com
Received: 03 August 2021; Accepted: 04 September 2021

Abstract: With the rapidly developing of Internet of Things (IoT), the volume of data generated by IoT systems is increasing quickly. To release the pressure of data management and storage, more and more enterprises and individuals prefer to integrate cloud service with IoT systems, in which the IoT data can be outsourced to cloud server. Since cloud service provider (CSP) is not fully trusted, a variety of methods have been proposed to deal with the problem of data integrity checking. In traditional data integrity audition schemes, the task of data auditing is usually performed by Third Party Auditor (TPA) which is assumed to be trustful. However, in real-life TPA is not trusted as people thought. Therefore, these schemes suffer from the underlying problem of single-point failure. Moreover, most of the traditional schemes are designed by RSA or bilinear map techniques which consume heavy computation and communication cost. To overcome these shortcomings, we propose a novel data integrity checking scheme for cloud-IoT data based on blockchain technique and homomorphic hash. In our scheme, the tags of all data blocks are computed by a homomorphic hash function and stored in blockchain. Moreover, each step within the process of data integrity checking is signed by the performer, and the signatures are stored in blockchain through smart contracts. As a result, each behavior for data integrity checking in our scheme can be traced and audited which improves the security of the scheme greatly. Furthermore, batch-audition for multiple data challenges is also supported in our scheme. We formalize the system model of our scheme and give the concrete construction. Detailed performance analyses demonstrate that our proposed scheme is efficient and practical without the trust-assumption of TPA.

Keywords: Blockchain; cloud-IoT; data integrity checking; homomorphic hash function; batch audition

1  Introduction

Internet of Things [1] connects a variety of devices such as smartphones, sensors, starwatchers etc. to the Internet. As a result, many applications based on IoT like smart home, smart city, body networks and so on become popular and available which prompt the progress of the human society [2–4]. With the fast development of IoT technique [5–7], the data generated by IoT systems increases significantly so that traditional methods of data storage cannot match the requirements of data management for IoT systems. Therefore, many enterprises have to outsource their huge IoT data to cloud server [8,9]. By renting the cloud storage service, the IoT data owner’s burden of data storage and supervision is reduced greatly. However, cloud service provider (CSP) is only semi-trusted for user, when CSP completely controls the sensitive IoT data, the security and privacy of cloud-IoT data should be solved well [10–12]. Consequently, checking the integrity of cloud-IoT data is necessary and crucial for the effective of IoT applications.

A trivial solution for cloud-IoT data integrity audition is to download and check the data in local. However, this simple solution is not practical because the volume of IoT data is normally very large. To address the problem, lots of data integrity auditing schemes for cloud-IoT data have been proposed [8–22]. However, these traditional schemes have two main problems: (1) TPA is assumed to be trustful, but in real application scenarios, TPA is not completely trusted. (2) Techniques of RSA or bilinear map which are used by most of these schemes are very expensive, so the performance bottleneck of the schemes is a big problem. Both of the two problems impede the usage of the data integrity auditing scheme in real-life.

Blockchain technique provides a new idea to check the integrity of cloud-IoT data [23]. With the advantages of decentralized, traceable and immutable characteristics, blockchain satisfies the needs of cloud-IoT data integrity checking. All the transactions recorded in the blockchain cannot be tampered and forged. Thus, storing important information of data audition into the blockchain can not only improve the audition performance, but also effectively discover the unreal audition results returned by the untrusted TPA.

Our main contributions of the manuscript are summarized as follows:

(1) We present a blockchain-based data integrity audition scheme for cloud-IoT data. We give the description of system model and security model of our scheme. All the algorithms in our scheme are also presented in detail.

(2) We prove the security of our new scheme. In our scheme, the audition results returned by TPA can be verified too so as to resist the attacks from untrusted TPA. Moreover, CSP cannot forge data integrity proof to deceive TPA.

(3) Performance comparison and analysis for multiple schemes are given, various simulation experiments are conducted, and experiment results show that our scheme reduces the computational and communication overhead significantly.

2  Related Works

Security is the basic and also the most important requirement of data stored on cloud server. By auditing data integrity, user can discover the events of data corruption and lose in time and take effective methods to deal with them. The first data integrity audition protocol was presented by Ateniese et al. [13,14] in 2007. They made use of MAC technique to design two schemes for auditing the integrity of data on remote servers. However, the overhead of communication and computational cost of these two schemes are very large. Chen et al. [15] presented a provable data possession (PDP) model to verify the integrity of the data stored in remote servers. They proposed the concept of blockless verification which was realized by homomorphic verifiable tags to drastically reduced I/O cost However, these schemes are only available for static data regardless of supporting data dynamic operations. Aim to enhance the scalability, However, this scheme is proved insecure [16]. To overcome the security problem, Yan et al. [17,18] proposed improved dynamic PDP schemes which designed a new data structure to support the dynamic operations such as data insert, delete and update. Shen et al. [19,20] concentrated on preserving the privacy of authenticators. Zhu et al. [21,22] focused on the problem of data privacy preserving, they made use of random masking technique to obscure user data when generating proofs so as to protect the data privacy. To eliminate certificate management. Yan et al. [23,24] proposed an identity-based public group data checking scheme with data owner privacy preserving. The scheme hides the identity of data owner in integrity proof so that TPA verifies the proof without knowing the owner of challenged data. Zhang et al. utilized lattices technique to propose a scheme based on identity-based encryption for secure cloud storage [25,26]. To improve the security, Li et al. [27,28] based on certificateless cryptography to present a PDP scheme for data shared within a group in which the trusted group owner is designated to be the PKG. Ming et al. [29,30] presented PDP schemes for data integrity checking which was constructed on certificateless crypto and realized user privacy protection. However, all these schemes delegate TPA to audit the data integrity on behalf of data owners. Since the TPA is not really trustworthy, there existing a security risk that the TPA may response wrong information to data owner.

To solve the problems above, many blockchain-based schemes were proposed recently. Liu et al. [31] stored the hash values of data into blockchain ledger, by which the data owner could check the audition result with smart contract. However, this scheme cannot resist replay attack. Yang et al. [32] made use of MHT to store all proofs so as to enable the behaviors of CSP and data owners’ accountable traceability. Yu et al. [33] used blockchain as a data channel to avoid the security threats of TPA, but the user cost is so high that it is not practical. Wang et al. [34] proposed a data integrity scheme for cloud-IoT data by blockchain and bilinear mapping, which introduced provable update mechanism to support dynamic IoT data. Wang et al. [35,36] proposed concrete private blockchain-based schemes which also realized client’s privacy preserving. To address the centralized problem of TPA, Dong et al. [37] presented a secure data integrity checking scheme based on consortium blockchain, which also designed a punishment mechanism to punish the TPA who failed to send the audit result in time. Chen et al. [38] described a PDP scheme based on blockchain to realize decentralized cloud storage framework, the scheme also provides dynamic operations for outsourced data. Chen et al. [39,40] considered to distribute the workload to IoT edge nodes to make the scheme more practical, they developed a stochastic blockchain in which only limit nodes can generate block tags. Huang et al. [41] presented a collaborative verification framework based on blockchain for cloud data storage. They use consensus nodes to substitute the single TPA to perform data audition to prevent entities from cheating each other.

3  Preliminaries

3.1 Blockchain Technology

Blockchain is essentially a decentralized database in which all transactions in untrusted networks are recorded. A blockchain contains a set of blocks which are linked as a growing list. Each block records many cryptographic information such as the hash value of previous block, a timestamp and transaction data. All blocks are linked by the hash value of previous one. Blocks keep one consistent ledger with the same transaction records which cannot be updated or deleted. Therefore, all the transactions occurred in the networks can be trusted without a centralized third party authority. Moreover, the records on the blockchain are transparent to all nodes, anyone can access the data in the blockchain. Fig. 1 shows the basic structure of blockchain.

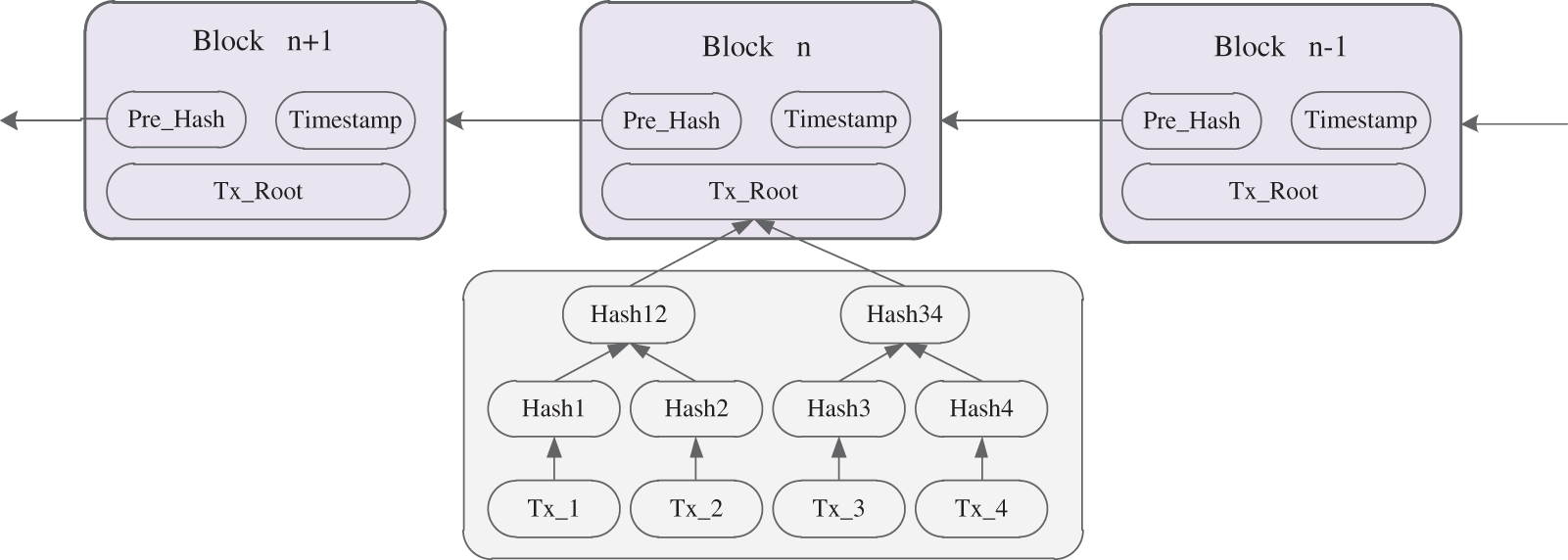
Figure 1: Basic structure of Blockchain

3.2 Homomorphic Hash Function

The homomorphic hash function [42,43] has the features of secure and efficient which are suitable for constructing data possession proofs such as in [15] and [17]. We first describe the definition of the homomorphic hash function denoted by H(⋅) in this section.

First, set two basic security parameters λp and λq , then randomly select two big primes number p and q with |p|=λp , |q|=λq , q|(p−1) . Suppose message M is consisted of n bit strings: M=(m1,m2,⋯,mn) where the size of each mi∈Zq∗ is q . Choose n random values from in Zp∗ with order q to form a vector G=[g1,g2,⋯,gn] . Thus, the homomorphic hash function is defined as:

H(M)=H(m1,m2,⋯,mn)=∏i=1ngimimod p. (1)

Obviously, the message M is compressed to one small string by the homomorphic hash function. If any part of the message M is changed, the hash value of the message will change too. Due to this property, the hash function H(⋅) can be used to audit the integrity of the message. Moreover, the homomorphic feature of H(⋅) can help to reduce the communication cost greatly. Suppose there are two messages Mi and Mj , both of which are split into n bit strings: Mi=(mi1,mi2,⋯,min) , Mj=(mj1,mj2,⋯,mjn) . Define

Mi+Mj=(mi1+mj1,mi2+mj2,⋯,min+mjn)mod q. (2)

The homomorphic property of H(⋅) can be confirmed as:

H(Mi)×H(Mj)=H(mi1,mi2,⋯,min)×H(mj1,mj2,⋯,mjn)=∏t=1ngtmit×∏t=1ngtmjt=∏t=1ngtmit+mjt=H(Mi+Mj). (3)

For the diversity of messages, the property is also hold.

H(Mi)×H(Mi+1)×⋯×H(Mj)=∏t=1ngtmit×∏t=1ngtm(i+1)t×⋯×∏t=1ngtmjt=∏t=1ngtmit+m(i+1)t+⋯+mjt=H(Mi+Mi+1+⋯+Mj) (4)

4  Problem Statement

4.1 System Model

Our proposed scheme comprises of four different entities: data collector, CSP, TPA and Blockchain. All of the data collector, CSP and TPA join the Blockchain with smart contracts designed beforehand. The system model is illustrated in Fig. 2. The interactions between entities are described as follows:

Data collectors (DC) are the entities who generate or collect huge original IoT data. DC is the owner of these data. After collecting the data, DC splits data into several data blocks and generates a tag for each block. Then DC outsources the blocks to CSP and uploads the tags to Blockchain by the corresponding smart contracts.

CSP supplies data storage and management services, DC rents CSP’s service and outsource data to CSP. CSP maintains DC’s data and responds data integrity challenges from TPA.

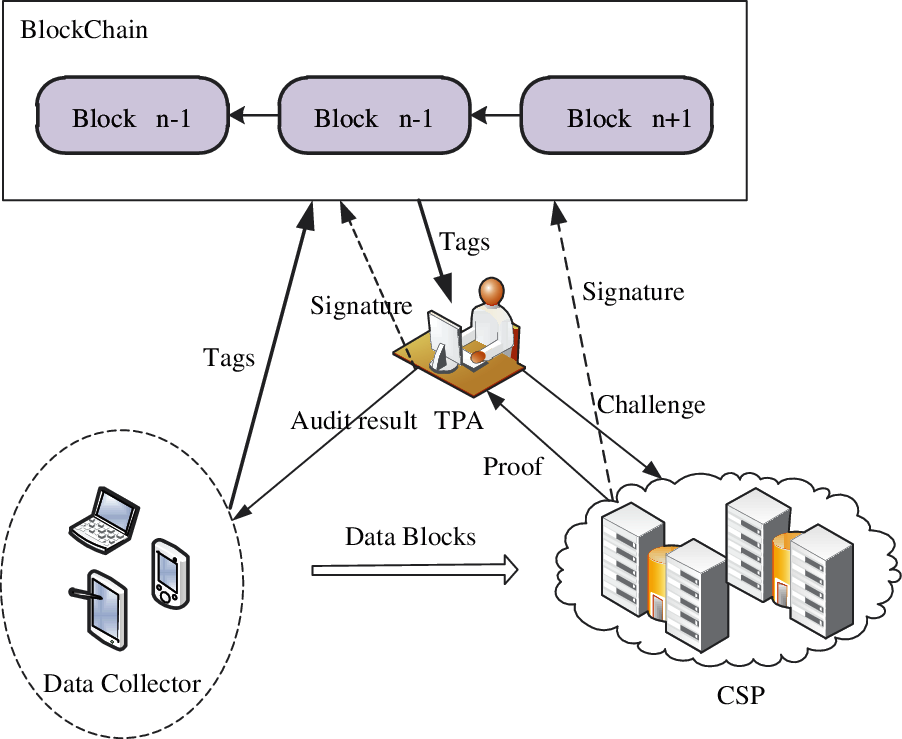
Figure 2: The system model of our scheme

TPA audits the integrity of data stored in CSP. TPA submits random data integrity challenges to CSP. By checking the rightness of the proof returned from CSP, TPA gets the audition result for the data and reports it to DC.

BlockChain is an entity that works as a trusted open database in the system. DC, CSP and TPA can access information in Blockchain and also can store information to Blockchain. All of the behaviors between DC, CSP, TPA and Blockchain are conducted by smart contracts.

4.2 Security Assumption

In our system, the Blockchain is assumed to be trustful who stores and maintains the ledger honestly. However, the CSP is assumed to be semi-trusted. Namely, CSP can execute the audition protocol honestly, but may deceive TPA with forged proofs. Likewise, TPA is also considered to be semi-trusted, because it may be tempted by illegal profit to give a fake audition result to data collector. Therefore, the security of our scheme should include two aspects, the first is to resist attacks from untrusted CSP who generates forged proofs, the second is to resist attacks from untrusted TPA who lies to data collector with fake audition results. According to Refs. [24–30], we mainly consider three security threats brought by CSP as follows:

Forgery attack: CSP forges a data integrity proof to deceive TPA.

Replacement attack: CSP replaces the corrupted challenged blocks by other uncorrupted blocks in order to pass the audition.

Replay attack: CSP sends previous valid proofs to bypass the current challenge.

However, because CSP only stores user data, the three attacks for our scheme is essentially the same one, that is CSP generates the proof with wrong data. No matter how the wrong data is produced, the results of the three attacks are the same. Based on the analysis, we define the security of our scheme to resist the attacks of CSP as:

Define 1: Our blockchain-based data integrity checking scheme is secure, if the CSP can not generate valid proof to pass the integrity audition without real data.

Strictly speaking, there is no direct method for data collector to verify the truth of audition result returned from TPA because data collector is completely out of the audition process. However, if the audition result from TPA can be audited too, untrusted TPA will be more carefully to deal with the audition result, especially when a huge compensation is along with the fake audition results. Therefore, the security for our scheme to resist the attacks from untrusted TPA can be defined as:

Define 2: Our blockchain-based data integrity auditing scheme can resist the attacks from TPA, if the data audition result reported by TPA can be verified.

4.3 Outline of Our Scheme

Our blockchain-based auditing scheme for cloud-IoT data is consisted of five algorithms which are described as follows:

Setup : This algorithm is responsible for generating system parameters λp , λq , n and G for the homomorphic hash function H(⋅) .

TagGen : This algorithm computes a tag Ti for each block mi by the homomorphic hash function H(⋅) .

Challenge : TPA uses this algorithm to output a data integrity challenge chal .

ProofGen : The algorithm outputs a data integrity proof P for the challenge chal .

Audit : TPA calls this algorithm to verify the rightness of P . If P passes the verification, the algorithm outputs ‘ 1 ’, otherwise it outputs ‘ 0 ’.

5  The Proposed Scheme

In this section, we give the detailed construction of our blockchain-based data integrity checking scheme.

Setup : the DC sets two security parameters λp and λq , then selects two big primes p and q with |p|=λp , |q|=λq , q|(p−1) . Choose n random values from Zp∗ to compose a vector G=[g1,g2,⋯,gn] where every value gi has order q . Select a secure and efficient signature scheme sig which is used to sign all behaviors in the process of data integrity checking. DC chooses a signing key pair ( dssk,dspk ). Likewise, CSP chooses a signing key pair ( cssk,cspk ) and TPA who offers the data audition service to DC also has a signing key pair ( assk,aspk ).

TagGen : suppose M identified with Fid is the data to be outsourced on CSP. DC splits M to α blocks denoted as M=(m1,m2,⋯,mα) , then further split each block to n sectors: mi=(mi1,mi2,⋯,min) . For each block mi ( 1≤i≤α ), to compute the tag Ti by the homomorphic hash function H(⋅) :

Ti=H(mi)=∏l=1nglmil mod p (5)

For the whole data M=(m1,m2,⋯,mα) , data collector can compute all the tags of T=(T1,T2,⋯,Tα) by the Eq. (1). Data collector sends the {IDDC,Fid,T,σDCT} to blockchain where IDDC is the identity of the data collector, and σDCT=sigdssk(IDDC,Fid,T) is the signature of {IDDC,Fid,T} . Further, data collector sends {IDDC,Fid,M,σDCM} to CSP where σDCM=Sigdssk(IDDC,Fid,M) is the signature of {IDDC,Fid,M} . Upon receiving {IDDC,Fid,M,σDCM} , CSP checks the validation of σDCM with DC’s public signing key dspk , if the σDCM is not correct, CSP refuses this data storage request, otherwise, CSP stores {IDDC,Fid,M,σDCM} .

Challenge : If TPA wants to audit whether the data is kept well by CSP, it randomly selects a subset chal={s1,s2,⋯,sx} form {1,2,⋯,α} and sents the chal to CSP.

ProofGen : Upon receiving the chal , CSP searches all the corresponding blocks {ms1,ms2,⋯,msx} and computes ms1+ms2+⋯+msx=∑i=s1sxmi1+∑i=s1sxmi2+⋯+∑i=s1sxmin mod q . So the proof can be computed as:

P=H(ms1+ms2+⋯+msn) mod p=∏l=1ngl∑i=s1sxmilmod p (6)

Then CSP returns {P,σCSPP} to TPA where σCSPP is the signature of σCSPP=σcssk(P) .

Audit : Upon receiving the proof P , TPA first verifies the correctness of σCSPP=Sigcssk(P) with the public signing key of cspk . If the σCSPP is valid, TPA accesses the blockchain and gets all the corresponding tags of challenged blocks from blockchain. TPA checks the following equation:

P=?∏i=s1sxTi mod p (7)

If the Eq. (3) holds, the algorithm sets Rau=1 , otherwise Rau=0 . Then, TPA returns Rau to DC and uploads {chal,Rau,P,σCSPP,σTPAP} to blockchain where σTPAP=Sigtssk(chal,Rau,P,σCSPP) is the signature of (chal,Rau,P,σCSPP) .

The correctness of Audit algorithm can be confirmed as:

P=H(ms1+ms2+⋯+msx)=H(ms1)×H(ms2)×⋯×H(msx)=∏i=s1sxTi mod p (8)

Our scheme also supports the function of batch-auditing which means multiple-data can be audited by once. Suppose t different data files M1 , M2 ,…, Mt are outsourced on CSP, TPA can audit all these files by one challenge. The updated algorithm of ProofGen and Audit are described as follows:

ProofGen : Upon receiving the chal={s1,s2,⋯,sx} , CSP gets all the corresponding blocks from all files which can be denoted as: {m1s1,m1s2,⋯,m1sx} ,…, {mts1,mts2,⋯,mtsx} , and computes m1s1+m1s2+⋯+mtsx=∑j=1t∑i=s1sxmji1+∑j=1t∑i=s1sxmji2+⋯+∑j=1t∑i=s1sxmjni . Then the proof is computed as:

P=H(m1s1+m1s2+⋯+mtsn) mod p=∏l=1ngl∑j=1t∑i=s1sxmilmod p (9)

Audit : Upon receiving the proof P , TPA gets all the corresponding tags from blockchain and checks the following equation:

P=?∏j=1t∏i=s1sxTji mod p (10)

If the Eq. (5) holds, the algorithm outputs ‘1’, otherwise outputs ‘0’.

The new Audit can be verified as:

P=H(m1s1+m1s2+⋯+mtsx)=H(m1s1)×H(m1s2)×⋯×H(mtsx)=∏j=1t∏i=s1sxTji mod p (11)

6  Security Proof and Performance Analysis

6.1 Security Proof

In this section we prove that our new blockchain-based scheme is secure against all the attacks defined in Section 3.2.

Theorem 1. If the homomorphic hash function is collision free, our blockchain-based data integrity checking scheme is secure.

With the challenge chal={s1,s2,⋯,sx} , we assume CSP successfully deceived the TPA by a forged proof P′ in which the block m is changed to m′ . According to ProofGen , P′=H(ms1)+⋯+H(m′)+⋯+H(msx) . Since P′ can pass the audition, there must be P′=∏i=s1sxTi=H(ms1)×⋯×H(m)×⋯×H(msx) . Due to the homomorphic property of H(⋅) , the equation above can be deduced to:

H(ms1+⋯+m′+⋯+msx)=H(ms1)×⋯×H(m)×⋯×H(msx) (12)

Thus, it is easy to get H(m′)=H(m) which is obviously contrast to the security property of the homomorphic hash function of H(⋅) . Therefore, the theorem 1 is proved.

Theorem 2: our scheme is secure to resist the attacks from TPA, if the signature scheme Sig selected for our scheme is secure.

Proof: From the algorithm ProofGen , we can see that each proof is signed by CSP with the signature scheme Sig . With the signature σCSPP , TPA can ensure that the proof P is generated by CSP. According to the algorithm Audit , TPA uploads all the values used among this challenge-response process to blockchain after checking the correctness of the proof P . Moreover, TPA signs all these values with the signature scheme Sig to get the signature σTPAP which is stored in blockchain too. Obviously, with these values, data collector can audit the TPA’s audition behaviors by replaying the challenge process. Specifically, data collector randomly chooses one record {chal,Rau,P,σCSPP,σTPAP} from blockchain, then checks the validity of σTPAP with the public singing key tspk of TPA. If the σTPAP passes the verification, it is no doubt all these values are generated by TPA. Data collector gets the chal from the record and sends the chal to CSP to get the integrity proof P . Finally, data collector calls the Audit algorithm to verify the correctness of P . If the verification result is not equal to Rau , data collector believes that TPA has lied before. With these audition proofs, data collect can get huge compensation from TPA and terminates the cooperation with TPA. Therefore, if the signature scheme Sig is secure, our scheme can resist the attacks from TPA.

6.2 Performance Evaluation

We present the performance analysis of our scheme in this section. Let E , P , CAdd , Cmul denote the costs of exponentiation, pairing, addition and multiplication respectively which have different values in different experimental environments. The summaries of the computational cost for the four algorithms are listed below:

DC runs the Setup algorithm to generate parameters for homomorphic hash. Because the values of p , q and G are selected randomly, the computational cost of Setup cannot ensured strictly. However, according to [12], the average time of Setup is very low. Moreover, Setup runs only once in the system, it brings little impact on the performance of the whole system.

Suppose a block is cut into |n| sectors, the computation cost of TagGen is |n|⋅(E+Cmul) . The ProofGen costs |n|⋅(E+Cmul+Cadd) and the Audit costs |c|⋅Cmul where |c| denotes total number of challenged blocks for one integrity audition.

To exhibit the validity of our scheme, we make comparative analyses of our scheme with other two existing blockchain-based schemes in Tab. 1, in which |b| denotes the number of data blocks, |n| denotes the number of sectors in one data block and |c| denotes the number of challenged blocks for one integrity audition.

In [35] and [37], the data block won’t be divided further into several sectors, which means each data block has only one sector. Therefore, the computational costs of these two schemes only depend on |b| and |c| . However, in our scheme each block is split into |n| sectors, the value |n| impacts the performance deeply especially in the phases of tag generation and proof generation. Outwardly, our scheme consumes more costs than that in other two schemes because of the value |n| . In fact, our scheme can deal with |n| times longer data block than in the schemes of [35] and [37]. If we compare the three schemes at the same level with |n|=1 , it is easy to get that our scheme has the best performance.

The communication cost of DC is |b|⋅|n|⋅|q|+|b|⋅|p|+2(|Sig|+|Fid|+|IDDC|) which mainly contains the data M and all tags. To verify data integrity, TPA sends a challenge with the size of 4|c| to CSP and CSP returns the proof {P,σCSPP} whose length is |p|+|Sig| . Easy to see that the communication cost of our scheme is very low especially in the process of data integrity checking.

Based on our prototype system, we set up multi experiments to validate the performance of our scheme. The experiment environment includes: a PC laptop with CentOS 7, 64 bit, i5-6200U, 2.4 GHz, 8GB Ram; a blockchain based on Hyperledger Fabric 1.4 platform; three peers of DC, CSP and TPA; pairing based cryptography library and miracle library. The experiments set the work of [35] on 1024-bit RSA, the work of [37] on an elliptic curve with 160-bit group order and our work on |p| = 1024, |q| = 512, |n|=16 . Thus, for the data of 1M (1024*1024 bit), there should be 1024∗10241024=1024 blocks in the scheme of [35], 1024∗1024160=6554 blocks in the scheme of [37] and 1024∗1024512∗16=128 blocks in our scheme. The computation costs of generating tags for 1M data are shown in Tab. 2.

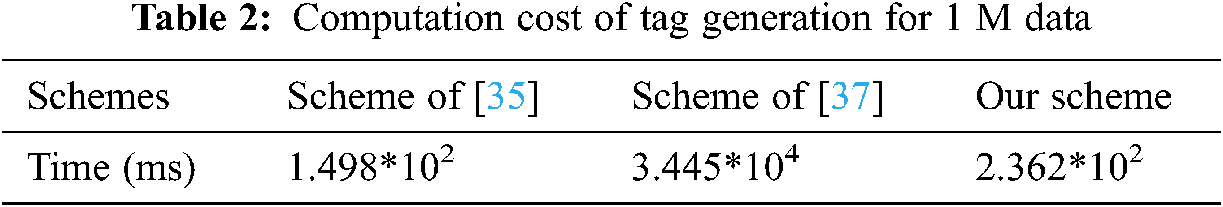
Tab. 2 shows that the scheme of [35] is the most efficient one of the three schemes in tag-generation step, and our scheme is a little more expensive than that of [35] but more efficient than the scheme in [37]. Further, 0.236 seconds for dealing with 1M data is practical for real application.

Next, we make experiments to evaluate the ‘proof generation’ performance of the three schemes. We set up total 2000 blocks in each scheme and keep other parameters the same as in the first experiment. The experimental results are shown in Fig. 3.

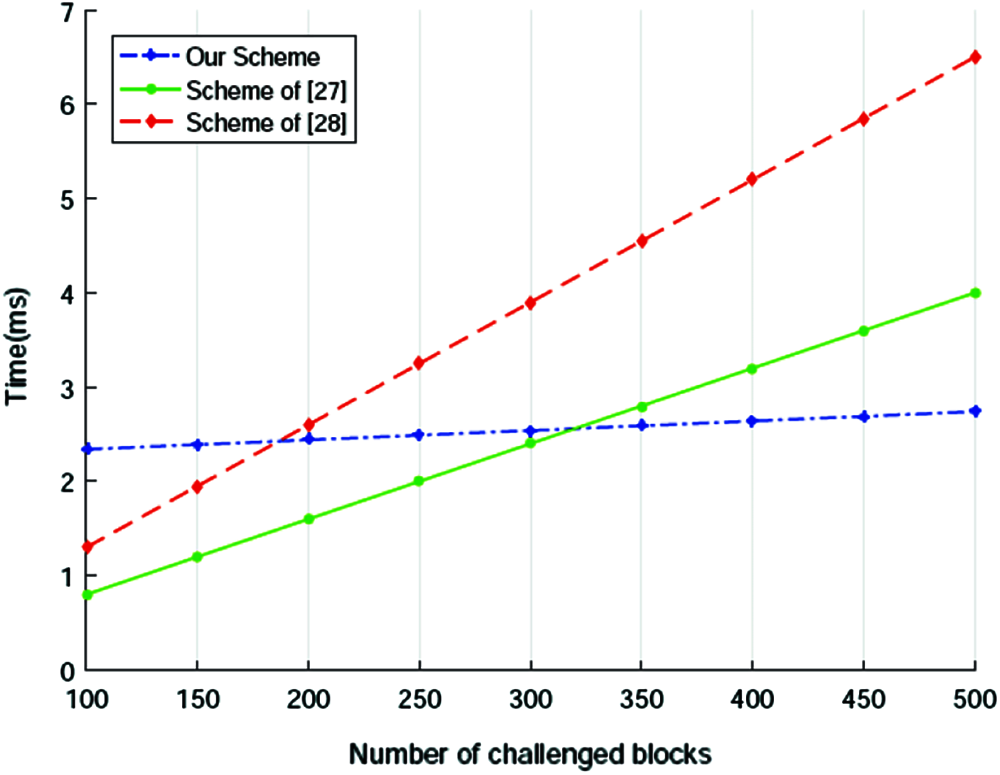
Figure 3: Computation cost of proof generation

From Fig. 3 we can see that the increasing ratio of the time cost for schemes in [35] and [37] are very high, but in our scheme, the time cost of this phase almost keeps constant. When the number of challenged blocks is less than about 170, our scheme costs longer time than that in other two schemes. However, as Fig. 3 shown, with the number of challenged blocks increasing, the time costs of schemes in [35] and [37] surpass that of our scheme rapidly. Generally speaking, to get more accurate integrity audition result, the number of challenged blocks in one audition behavior should be more than 460 [13]. Therefore, our scheme is very efficient in real applications.

Fig. 4 demonstrates the time costs of the ‘audition’ phase in the three schemes. Obviously, due to the expensive pairing operations, scheme of [37] consumes heavy cost in this phase which is much larger than that of scheme in [35] and ours. We further compare the performance of scheme in [35] and our scheme, the result of which is shown in Fig. 5. It is easy to see that the performance difference between the scheme of [35] and our scheme is still big, and it grows fast with the number of challenged blocks increasing.

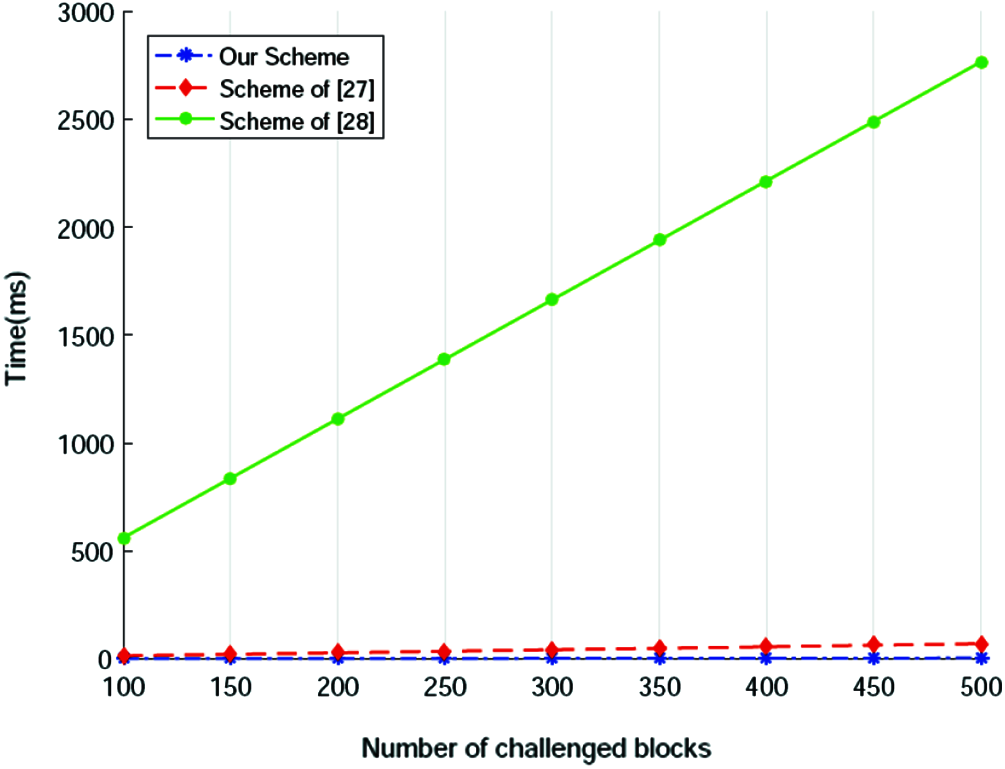
Figure 4: Computation cost of audition (a)

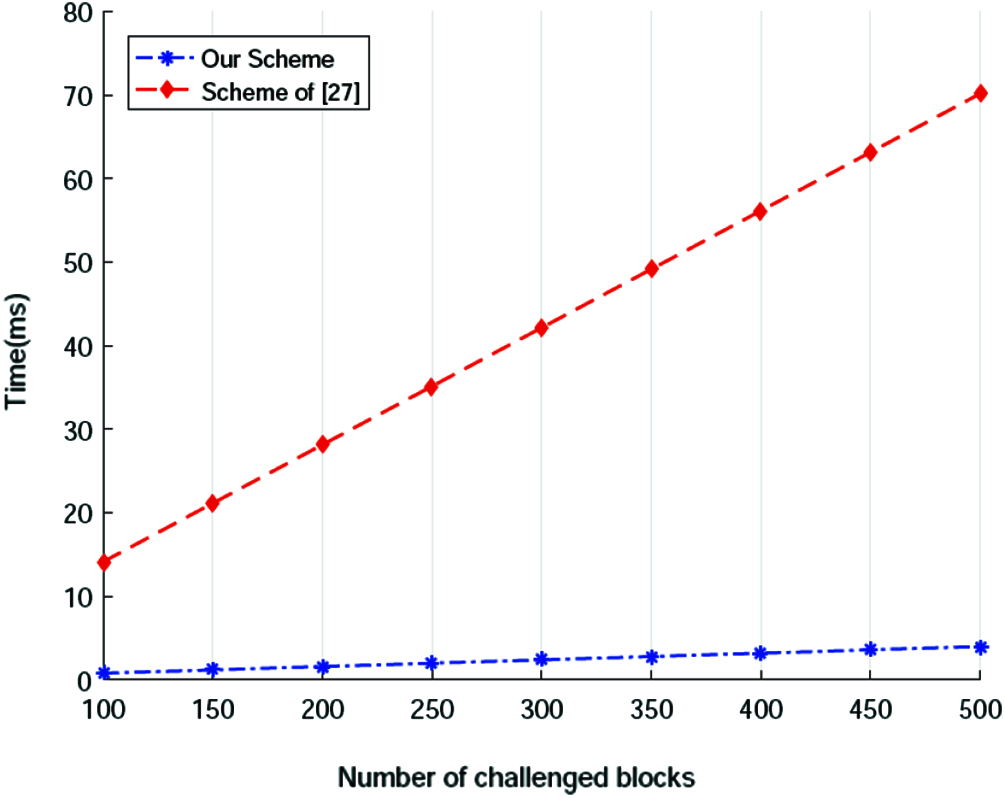
Figure 5: Computation cost of audition (b)

7  Conclusion

In this paper, a blockchain-based cloud-IoT data integrity auditing scheme is proposed. The scheme makes use of a homomorphic hash function to generate tags for data blocks and stores all the tags in blockchain. The homomorphic feature of the tags improves the efficiency of the proof generation and integrity audition. The blockchain ensures the security and immutability of all tags, which avoids most of threats in previous schemes. We prove the security of our scheme and the performance evaluation results show that our scheme is efficient and practical. Next, we will focus on upgrading the scheme to support data dynamic which is another attractive feature for secure cloud storage.

Funding Statement: This work is supported by Program for Scientific Research Foundation for Talented Scholars of Jinling Institute of Technology (No. JIT-B-202031), H. Yan received it and the URLs is www.jit.edu.cn. H. Yan also received the Opening Foundation of Fujian Provincial Key Laboratory of Network Security and Cryptology Research Fund of Fujian Normal University (NSCL-KF2021-02) and the URLs is www.fjnu.edu.cn. Y. Liu received the funding of the National Natural Science Foundation of China (No. 61902163,) and the URLs is www.nsfc.gov.cn. S. Hu received the funding of the Science and Technology Project of Education Department in Jiangxi Province (No. GJJ201402) and the URLs is www.gnnu.cn.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  I. Lee and K. Lee, “The Internet of Things (IoTApplications, investments, and challenges for enterprises,” Business Horizons, vol. 58, no. 4, pp. 431–440, 2105, 2015. [Google Scholar]

 2.  J. Xiong, R. Bi, M. Zhao, J. Guo and Q. Yang, “Edge-assisted privacy-preserving raw data sharing framework for connected autonomous vehicles,” IEEE Wireless Communications, vol. 27, no. 3, pp. 24–30, 2020. [Google Scholar]

 3.  Y. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 3, pp. 304–313, 2021. [Google Scholar]

 4.  C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Xia et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 3, pp. 1–12, 2021. [Google Scholar]

 5.  Z. Li, B. Chang, S. Wang, A. Liu, F. Zeng et al., “Dynamic compressive wide-band spectrum sensing based on channel energy reconstruction in cognitive Internet of things,” IEEE Transactions on Industrial Informatics, vol. 14, no. 6, pp. 2598–2607, 2018. [Google Scholar]

 6.  G. Xu, X. Li, L. Jiao, W. Wang, A. Liu et al., “BAGKD: A batch authentication and group key distribution protocol for VANETs,” IEEE Communications Magazine, vol. 58, no. 7, pp. 35–41, 2020. [Google Scholar]

 7.  L. Fang, Y. Li, X. Yun, Z. Wen, S. Ji et al., “THP: A novel authentication scheme to prevent multiple attacks in SDN-based IoT network,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 5745–5759, 2020. [Google Scholar]

 8.  A. Botta, W. D. Donato and V. Persico, “Integration of cloud computing and Internet of things: A survey,” Future Generation Computer Systems, vol. 56, no. 7, pp. 684–700, 2016. [Google Scholar]

 9.  J. Hu, G. Hu, J. Cai, L. Xu and Q. Wang, “Hospital bed allocation strategy based on queuing theory during the COVID-19 epidemic,” Computers Materials & Continua, vol. 66, no. 1, pp. 793–803, 2021. [Google Scholar]

10. J. Wang, W. Chen, L. Wang, Y. Ren and R. S. Sherratt, “Blockchain-based data storage mechanism for industrial Internet of Things,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1157–1172, 2020. [Google Scholar]

11. Y. Yu, Y. Li, J. Tian and J. Liu, “Blockchain-based solutions to security and privacy issues in the Internet of things,” IEEE Wireless Communications, vol. 25, no. 6, pp. 12–18, 2018. [Google Scholar]

12. Z. Li, J. Kang, R. Yu, D. Ye, Q. Deng et al., “Consortium blockchain for secure energy trading in industrial Internet of things,” IEEE Transactions on Industrial Informatics, vol. 8, no. 14, pp. 3690–3700, 2018. [Google Scholar]

13. G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. CCS, VA, USA, pp. 598–609, 2007. [Google Scholar]

14. T. Li, Y. Ren and J. Xia, “Blockchain queuing model with non-preemptive limited-priority,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1111–1122, 2020. [Google Scholar]

15. L. Chen, S. Zhou, X. Huang and L. Xu, “Data dynamics for remote data possession checking in cloud storage,” Computers & Electrical Engineering, vol. 39, no. 7, pp. 2413–2424, 2013. [Google Scholar]

16. Y. Yu, J. Ni, M. H. Au, H. Liu, H. Wang et al., “Improved security of a dynamic remote data possession checking protocol for cloud storage,” Expert Systems with Applications, vol. 41, no. 7, pp. 7789–7796, 2014. [Google Scholar]

17. H. Yan, J. Li, J. Han and Y. Zhang, “A novel efficient remote data possession checking protocol in cloud storage,” IEEE Transactions on Information Forensics and Security, vol. 12, no. 1, pp. 78–88, 2017. [Google Scholar]

18. C. Ge, Z. Liu, J. Xia and L. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]

19. W. Shen, G. Yang, J. Yu, H. Zhang, F. Kong et al., “Remote data possession checking with privacy preserving authenticators for cloud storage,” Future Generation Computer Systems, vol. 76, no. 4, pp. 136–145, 2017. [Google Scholar]

20. Y. Ren, F. Zhu, K. S. Pradip, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]

21. H. Zhu, Y. Yuan, Y. Chen, Y. Zha, W. Xi et al., “A secure and efficient data integrity verification scheme for cloud-IoT based on short signature,” IEEE Access, vol. 7, pp. 90036–90044, 2019. [Google Scholar]

22. C. Ge, W. Susilo, Z. Liu, J. Xia, P. Szalachowski et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 20, no. 8, pp. 1–12, 2020. [Google Scholar]

23. H. Yan and W. Gui, “Efficient identity-based public integrity auditing of shared data in cloud storage with user privacy preserving,” IEEE Access, vol. 9, no. 3, pp. 45822–45831, 2021. [Google Scholar]

24. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 21, no. 8, pp. 1–10, 2021. [Google Scholar]

25. X. Zhang, Y. Tang, H. Wang, C. Xu, Y. Miao et al., “Lattice-based proxy-oriented identity-based encryption with keyword search for cloud storage,” Information Sciences, vol. 494, no. 3, pp. 193–207, 2019. [Google Scholar]

26. Y. Tian, Z. Wang, J. Xiong and J. Ma, “A blockchain-based secure key management scheme with trustworthiness in DWSNs,” IEEE Transactions on Industrial Informatics, vol. 16, no. 9, pp. 6193–6202, 2020. [Google Scholar]

27. J. Li, H. Yan and Y. Zhang, “Certificateless public integrity checking of group shared data on cloud storage,” IEEE Transactions on Services Computing, vol. 14, no. 1, pp. 71–81, 2021. [Google Scholar]

28. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]

29. Y. Ming and W. Shi, “Efficient privacy-preserving certificateless provable data possession scheme for cloud storage,” IEEE Access, vol. 7, pp. 122091–122105, 2019. [Google Scholar]

30. Y. J. Ren, Y. Leng, Y. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]

31. B. Liu, X. L. Yu, S. Chen, X. Xu and L. Zhu, “Blockchain based data integrity service framework for IoT data,” in Proc. ICWS, Honolulu, HI, USA, pp. 468–475, 2017. [Google Scholar]

32. C. Yang, X. Chen and Y. Xiang, “Blockchain-based publicly verifiable data deletion scheme for cloud storage,” Journal of Network and Computer Applications, vol. 103, no. 6, pp. 185–193, 2018. [Google Scholar]

33. H. Yu, Z. Yang and R. O. Sinnott, “Decentralized big data auditing for smart city environments leveraging blockchain technology,” IEEE Access, vol. 7, pp. 6288–6296, 2019. [Google Scholar]

34. H. Wang and J. Zhang, “Blockchain based data integrity verification for large-scale IoT data,” IEEE Access, vol. 7, pp. 164996–165006, 2019. [Google Scholar]

35. H. Wang, Q. Wang and D. He, “Blockchain-based private provable data possession,” IEEE Transactions on Dependable and Secure Computing, pp. 1, 2019. [Google Scholar]

36. Y. Ren, J. Qi, Y. Cheng, J. Wang and A. Osama, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]

37. G. Dong and X. Wang, “A secure IoT data integrity auditing scheme based on consortium blockchain,” in Proc. ICBDA, Xiamen, China, pp. 246–250, 2020. [Google Scholar]

38. R. Chen, Y. Li, Y. Yu, H. Li, X. Chen et al., “Blockchain-based dynamic provable data possession for smart cities,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4143–4154, 2020. [Google Scholar]

39. Y. Chen, L. Wang and S. Wang, “Stochastic blockchain for IoT data integrity,” IEEE Transactions on Network Science and Engineering, vol. 7, no. 1, pp. 373–384, 2020. [Google Scholar]

40. Y. Ren, J. Qi, Y. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–19, 2021. [Google Scholar]

41. P. Huang, K. Fan, H. Yang, K. Zhang, H. Li et al., “A collaborative auditing blockchain for trustworthy data integrity in cloud storage system,” IEEE Access, vol. 8, pp. 94780–94794, 2020. [Google Scholar]

42. M. N. Krohn, M. J. Freedman and D. Mazieres, “On-the-fly verification of rateless erasure codes for efficient content distribution,” in Proc. S&P, New York, NY, USA, pp. 226–240, 2004. [Google Scholar]

43. L. Fang, M. Li, Z. Liu, C. Lin, S. Ji et al., “A secure and authenticated mobile payment protocol against off-site attack strategy,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 8, pp. 77–90, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.