Computer Systems Science & Engineering DOI:10.32604/csse.2022.022100
Article

A Novel Post-Quantum Blind Signature for Log System in Blockchain

Gang Xu1,2, Yibo Cao1, Shiyuan Xu1, Ke Xiao1, Xin Liu3, Xiubo Chen4,* and Mianxiong Dong5

1School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
2Beijing Key Laboratory of Security and Privacy in Intelligent Transportation, Beijing Jiaotong University, Beijing, 100044, China
3School of Information Engineering, Inner Mongolia University of Science & Technology, Baotou, 014010, China
4Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
5Muroran Institute of Technology, Muroran, 050-8585, Japan
*Corresponding Author: Xiubo Chen. Email: flyover100@163.com
Received: 27 July 2021; Accepted: 02 September 2021

Abstract: In recent decades, log system management has been widely studied for data security management. System abnormalities or illegal operations can be found in time by analyzing the log and provide evidence for intrusions. In order to ensure the integrity of the log in the current system, many researchers have designed it based on blockchain. However, the emerging blockchain is facing significant security challenges with the increment of quantum computers. An attacker equipped with a quantum computer can extract the user's private key from the public key to generate a forged signature, destroy the structure of the blockchain, and threaten the security of the log system. Thus, blind signature on the lattice in post-quantum blockchain brings new security features for log systems. In our paper, to address these, firstly, we propose a novel log system based on post-quantum blockchain that can resist quantum computing attacks. Secondly, we utilize a post-quantum blind signature on the lattice to ensure both security and blindness of log system, which makes the privacy of log information to a large extent. Lastly, we enhance the security level of lattice-based blind signature under the random oracle model, and the signature size grows slowly compared with others. We also implement our protocol and conduct an extensive analysis to prove the ideas. The results show that our scheme signature size edges up subtly compared with others with the improvement of security level.

Keywords: Log system; post-quantum blockchain; lattice; blind signature; privacy protection

1  Introduction

Log system is a significant implement for a complete information system, which provides log collection, log storage, log query, etc. However, confronting illegal online access and malicious tampering, the log system lacks in log validation and user consensus. As a result, data privacy and integrity have been facing a tremendous threat [1–3].

In recent years, blockchain technology has set off a subversive revolution and significantly changed current transaction networks [4], especially for log system aspects. Many people favor it because of less expense and easier maintenance compared with traditional systems [5]. More importantly, decentralized structure is an innovative feature of blockchain and point-to-point direct interaction can be achieved, which helps people reach a consensus without the control of the administrators in the current log system to ensure the irreversibility of data [6]. This feature attracts many researchers to study how to design decentralized applications based on blockchain [7–10].

As the modern network information society tending to globalization, log systems based on the blockchain can withstand the attack of adversaries equipping traditional computers, but the emergence of quantum computing has threatened the security of log systems again. The importance of security is profound in terms of a more robust demand for privacy protection and identity authentication. In this way, research on blockchain security should consider traditional cryptography and other potential threats, such as quantum attacks [11]. Therefore, blockchain-based systems against quantum computing play an irrevocable role in the next few decades. In a conventional log system, blockchain is based on the Elliptic Curve Digital Signature Algorithm (ECDSA) [12] and RSA algorithm [13], which cannot deal with quantum attacks. However, suppose some individuals utilize the Shor algorithm [14] and Grover algorithm [15] to extract users’ secret keys from their public keys to produce numerous unauthorized transactions or forged signatures. In that case, the valid customers will lose their privacy.

Many researchers have focused on anti-quantum methodologies [16]. Specifically, the research of lattice cryptography has been widely used against quantum computing. Some researchers proposed lattice-based construction of preimage sampleable trapdoor function in 2008 [17], and a signature scenario which is dependable security under the random oracle model based on Small Integer Solution (SIS) problem. In 2010, Cash et al. [18] proved to design other beneficial characteristics of lattice trapdoors, defined as bonsai tree technology.

Further, an effective signature protocol utilizes to identify the facticity of node content [19]. Many security protection scenarios have been proposed for the aspect of blockchain, which is roughly classified into pseudonym-based authentication, group signature [20], and blind signature. According to protecting blockchain privacy, pseudonym-based schemes are prevalent and have been researched a lot. However, it requires constant modification as to protect privacy, which creating a bottleneck for the log system. Thus, this scheme may not be the most appropriate one for our scheme. We then consider a group signature, which utilized features traits of anonymity and traceability to construct anonymous certificates. For instance, Lin et al. [21] utilized group signature to security-preserving systems. Nevertheless, as one log system needs to store revocation lists which might cause some troubles as for group signature mainly because they have to face up to a significant problem that how to choose administrators in a group which holds the most extraordinary power in the scheme, but we cannot assure whether they are honest and reliable.

Blind signature based on lattice designed by Rückert [22]. It has been getting more attention since the emergence of digital cash schemes on the blockchain, which Chaum initially introduced to make signers sign the information without seeing the plaintext. Nevertheless, the signer notices nothing about and the security signature proved by Juels et al. [23] Furthermore, Pointcheval et al. [24] studied two essential points, which are blindness and one-more unforgeability. Blindness means a signer could sign one passage without being noticed by other people. The one-more unforgeability, which could allow the signer to master the number of exceptions of valid signatures, is also essential in lattice-based blind signature. In 2019, Li et al. [25] proposed an anti-quantum proxy blind signature scheme based on lattice cryptography, ensuring user anonymity and untraceability in the Internet of Things (IoT).

In summary, our proposed scheme also has the features above. The significant contributions of this article are as follows:

(1)   In the current blockchain-based log system, the signer can view the log information he signed during the signing process, which poses a great threat to the security and privacy of log information. Fortunately, blind signature can effectively solve this problem. Moreover, with the development of quantum computers, malicious attackers can launch quantum computing attacks on log system, which makes the traditional cryptographic-based signature lose its protection for log information. Based on the above reasons, we have proposed a novel post-quantum blind signature scheme for log system in blockchain.

(2)   Firstly, in response to the problem of excessive power in the central organization of the log system, we have used blockchain technology, which can eliminate the centralized system to ensure the immutability of log information. Secondly, since the log system faces quantum computing attacks, we use lattice-based cryptography to resist quantum computing attacks from malicious attackers. Further, for the issue that signers can threaten the privacy of log information, we proposed a novel lattice-based blind signature scheme enhanced the security level to complete the signature operation in this system, which blindness protects the privacy of log information, and one-more unforgeability keeps the validity of the blind signature.

(3)   We analyze the security in theory and implement a complete security proof, which reduces the difficulty of malicious attackers to forge signatures to the SIS problem. Moreover, we evaluate the comprehensive performance and prove that our scheme has a smaller signature length compared with similar schemes.

2  Log System Vulnerability and Post-Quantum Blockchain

2.1 Log System Vulnerability

People could collect various information by utilizing log systems, attracting more and more individuals to adopt log systems in various circumstances. In order to figure out the shortage which traditional log systems cannot avert the log from being tampered with, many researchers have applied blockchain to log systems. In 2019, Huang not only proposed a blockchain-based framework for log storage, but also utilized Inter Planetary File System (IPFS) to store log files which decreased the expenditure of storing enormous files in the blockchain [26]. However, many log systems, which storage privacy information in the blockchain, show apparent vulnerability to attackers equipped with quantum computers. The proposal of the quantum algorithm takes severe challenges to existing conventional cryptographies and results in the current blockchain system break down [27] since the Shor algorithm can solve the prime factorization problem during the polynomial-time using quantum computers.

Moreover, Proof of Work (PoW) in blockchain depends on a search problem. Unfortunately, the Grover algorithm is a robust quantum search algorithm that provides square root acceleration for many search problems. By this, the privacy of individuals’ information in the log system will be seriously exposed, and the security of the log system will no longer exist.

Thus, log security in blockchain cannot be guaranteed. In our paper, a post-quantum blockchain is applied to the log system so as to solve this urgent problem.

2.2 Post-Quantum Blockchain

As interpreted in Section 2.1, our paper emphasizes the vulnerability of log to quantum attacks in systems equipping with blockchain. Therefore, we adopt post-quantum cryptography so as to make sure the security of blockchain in quantum circumstances [28]. Post-quantum cryptography includes hash function, code, lattice, and multivariate [29]. Some researchers have explored these ways deeply, like using Quantum Key Distribution (QKD) in traditional blockchain to avoid quantum attacking, but this cost too much time during new blocks generating step in most log systems.

Post-Quantum Blockchain (PQB) includes conventional blockchain and quantum cryptography, which combines the features of blockchain and resisting quantum adversary. In this paper, we apply PQB in order to not only maintain decentralization but also withstand quantum computing attacks.

3  Preliminaries

In this paper, we use ℝ for real numbers, and ℤ for integers. For any positive integer k, it is represented by [k] together with {1, 2, …, k}. If s is a string, the length of s is denoted by |s|. The string a||b represents a new string which is concatenated by a as well as b. For a matric A = [a1, …, am] ∈ ℤn×m. Use A~ to represent the result of matrix A after Gram-Schmidt orthogonalization. And let ||s|| = maxi∈[m]||ai||, where || ⋅ || represents the Euclidean norm. The expression b ← B means that b is randomly and uniformly derive from the set B.

3.1 Blind Signature

Blind Signature (BS) protocol includes four concrete algorithms (Setup, Key-Gen, Sign-Gen, Sign-Veri). In the Key-Gen step, signer has to keep his/her secret key sk and the user has his/her public key pk.

Sign-Gen is an interactive scheme between signer S and user U, which shows in Fig. 1. Initially, the user computes a blinded message mb and the signer receives it. Then, signer generates a corresponding signature σ′. Lastly, user utilizes σ′ to obtain a new valid signature σ.

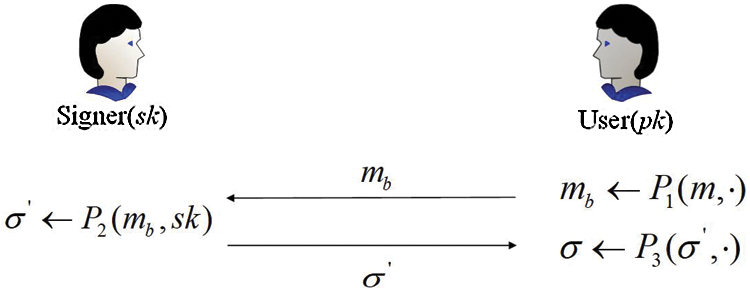
Figure 1: A blind signature general scheme

For the Sign-Veri part, we have to input(pk, mb, σ), and it will output for accepting as well as 0 to reject through this protocol. Therefore, we could consider blind signature is correct iff ∀m,m∈M and (pk, sk) ← Key − Gen( ⋅ ) and the Sign − Veri(pk, m, σ) = 1.

Concerning security, blind signature consists of two main proportions, which is blindness and one-more unforgeability [23]. First of all, blindness means that there is an adversarial signer S∗ who only knows independent views. We take SU(pk,mb,m1−b)∗ to represent two messages mb and m1−b with a reliable user U. We then let σb as the output U(pk, mb), and σ1−b as the corresponding U(pk, m1−b). According to these, even if one of them is wrong, the scheme will be halted. Then, the advantage of SU(pk,mb,m1−b)∗ can be defined as:

AdvBSblindnessSU(pk,mb,m1−b)∗=|PrExpSU(pk,mb,m1−b)∗,BSblindness(n)=1−12|=|Pr[b=b′:(pk,sk)←Key−Gen(⋅)(m0,m1)←S∗(pk,sk)b←{0,1}b′←S∗(guess,σ0,σ1,SU(pk,mb,m1−b)∗(⋅))]−12| (1)

For the other part, one-more unforgeability characteristic guarantees an adversary user U∗ only generates l successful interactions for maximum. We take UU(pk,mb,m1−b)∗ to denote two messages mb and m1−b with U∗ . Having noticed the unblinded signatures initially, the signer has to guess the bit b as for respect to m0, m1. Therefore, the advantage of UU(pk,mb,m1−b)∗ is defined as:

AdvBSomufUU(pk,mb,m1−b)∗=|Pr[b=1:(pk,sk)←Key−Gen(⋅)((m1,σ1),(m2,σ2),…,(ml+1,σl+1))←UU(pk,mb,m1−b)∗S(sk)∞(pk)b←Sign−Veri(mi,σi,pk),i=1,2,…,l]| (2)

Our blind signature protocol is accurately blind if AdvBSblindnessSU(pk,mb,m1−b)∗ of all attackers are negligible, and it also achieves one-more unforgeability if the corresponding AdvBSomufUU(pk,mb,m1−b)∗ is negligible.

3.2 Gaussian Distribution

Gaussian distribution with lattices has been a standard model in mathematics, which use it to randomly select sections in Zqn so as to be associated with complex problems on any lattice.

Definition 6 (Gaussian function): Λ ∈ ℝm is an m-dimensional lattice. Take each vector c ∈ ℝm and a positive number σ > 0. Then the Gaussian function is defined as: ρσ,c(x)=exp⁡(−π‖x−c‖22σ2) . Among them, c represents the center of Λ, and σ represents the standard deviation. If c = 0, we simplify ρσ,c(x) to ρσ(x) .

Definition 7 (Discrete Gaussian distribution): Let ρσ,c(ℤm) as a means of the discrete integral of ρσ,c over ℤm, then the discrete Gaussian distribution in ℤm can be defined as: DΛ,σ,c(x)=ρσ,c(x)ρσ,c(Zm) .

Lemma 1 [30]: For j ≥ 1, z←Dσm , it follows that Pr[‖z‖>jσm]<jmem(1−k2)2 . Moreover, for any vector v ∈ ℝm, z←Dσm , and r > 0, σ > 0, we have Pr[|⟨z,v⟩|>r]≤2e−r22||v||2σ2 .

Lemma 2 [30]: For any v ∈ ℤm, z←Dσm , if δ > 0 and σ= δ||v|| , then:

3.3 Rejection Sampling

There is an aborting methodology used in lattice-based cryptography for rejection samples. In this protocol, one could prevent the interactive protocol if his/her secret key leaked. As for almost all x, after taken a probability distribution f(x), we have to seek other probability distributions g(x) to certify f(x)g(x)≤M , which M is excepted number of times for output the sample. Then, x ← g will be rejected if f(x)Mg(x)≠f . Furthermore, we have Lemma 3 in the following paragraph.

Lemma 3 [31]: Let V be a set of ℤm, σ ∈ ℝ and h: V → ℝ be a probability distribution. If σ=ω(Tlog⁡m) , then it will exist a constant M as the following algorithm: For each v ← h, z←Dσm , we can get (z, v) under the probability of 1M , which is with the statistical distance of 2−ω(log⁡m)M towards the distribution: for every v ← h, z←Dσvm , the output of (z, v) is min(Dσm(z)MDσvm(z),1) with some probability.

4  Our Scheme

4.1 Architecture

In this paper, we propose a log storage system on the post-quantum blockchain, including a lattice-based blind signature scheme to resist quantum computing attacks and ensure signers’ log information privacy. The architecture of our system shows in Fig. 2, and the log uploading process describes as follows.

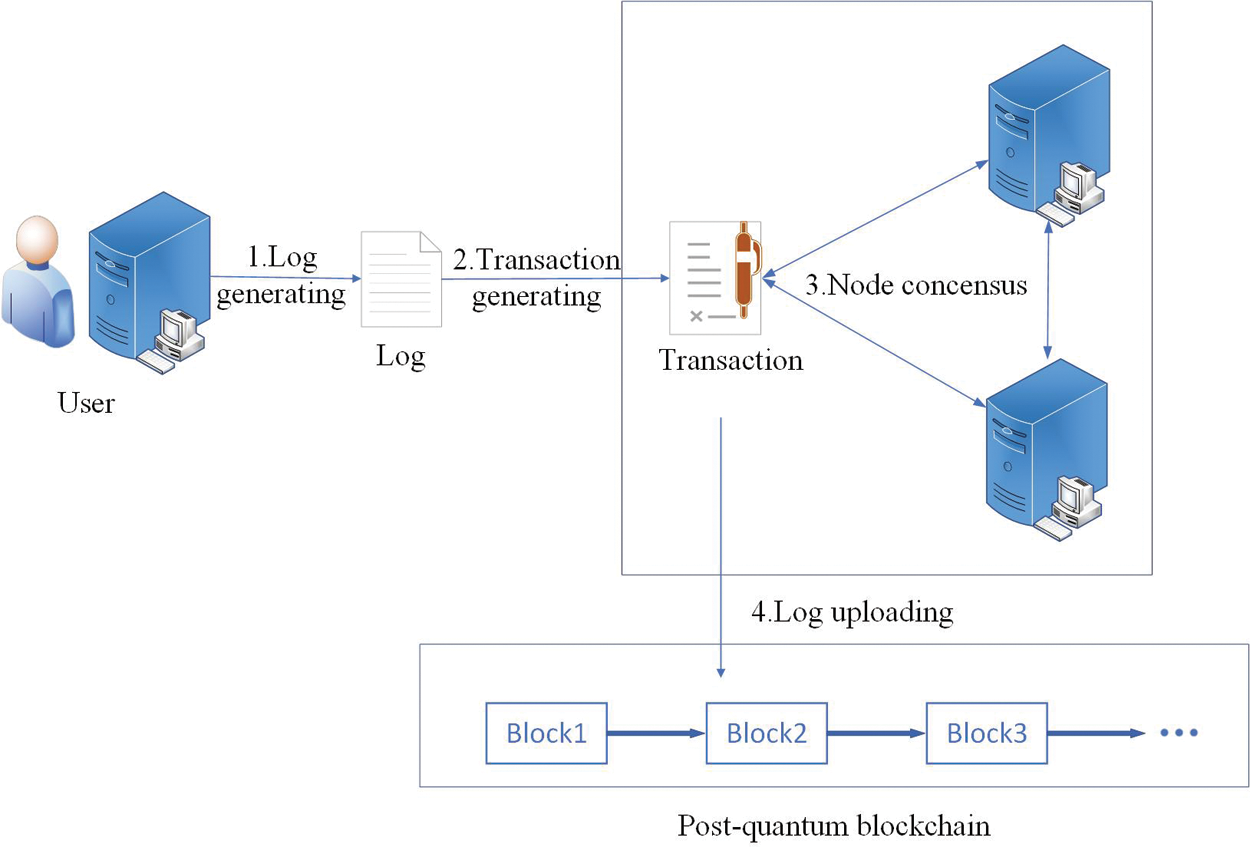
Figure 2: Our scheme architecture

To begin with, a log owner packages her log information which she will upload. The log information is integrated into blocks in a period and stored in our post-quantum blockchain. The current owner uses her secret key to sign a signature to the transaction and to the next owner, which appends to the end of the currency. In order to ensure that the content of the transaction is kept secret from the current owner, we use a blind signature in our system.

Then, the current owner broadcasts his/her transaction to the entire network, where every network node collects several unverified transactions into blocks and completes the qualification of creating a new block for these transactions through PoW. When a node accomplished PoW, it will generate a new block as well as data fingerprint including log information, public key, signature, and data fingerprint of the previous transaction so as to verify the validity of its information and link to the next block.

After that, this node broadcasts the block to the whole network, and the rest of the network checks whether the transactions contained in the block are valid. As the block containing log information passes all authentication, it is formally added to the post-quantum blockchain automatically. Consequently, log system utilized lattice-based blind signature has more robust security resisting quantum attackers and privacy protection capability for log information.

4.2 Blind Signature Algorithm

In this sector, we introduce our blind signature based on lattice protocol, which is under the average case SIS problem including four Probabilistic Polynominal−Time(PPT) algorithms which contain Setup(U, S, pk, sk, M), Key − Gen(pk, sk), Sign − Gen(sk, S, U), Sign−Veri(A,B,M,z,ϵ) .

1.    Setup(U, S, pk, sk, M): Initially, we denote user as U, signer as S as well as the public key and secret key denoted as pk and sk. Moreover, we let message as M.

2.    Key − Gen(pk, sk): The algorithm generates A←Zqn×m and Sk ← { − a, …, 0, …, a}m×kfor the secret key. Considering the security as well as efficiency, we choose a as small as possible. The calculation method of the public key is (A, B), which is named pk. And B ← ASk. Therefore, the reliability of sk is depends on the SIS problem.

3.    Sign − Gen(sk, S, U): The signature algorithm involves for a signer S and a user U. Having used Sign − Gen(sk, S, U) algorithm, the user outputs a signature <ϵ∗,ϵ> . For each vector r←Dσ2m , signer sends a commitment x ← Ar. Then the user gets blind factors a←Dσ3m , b←Dσ1m , and they compute x + Aa + Bb. Moreover, the user sets a hash function H:{0,1}∗→{v∈{−1,0,1}k,||v||1≤κ} to hash x + Aa + Bb with C = com(M, t), and the resulting value ε is a part of the signature. After that, the signer sends ϵ∗= ϵ+b to user for cover ε. Having received ϵ∗ , the user figures out r+Sϵ∗ , then sends it to the signer. In order to make sure that S is classified, the process may restart with some probability. After that, the user computes z=r+Sϵ∗+a , and combines (z, ε) as last signatures. In this section, R′ denotes a rejection in the rejection sampling lemma. If the resulting signature z is included R′, it will be useless. Moreover, user can contact signer to reopen this process and the signer could know user whether gained one valid signature because user has to send (a, b, ε, C) to the signer as a result. Consequently, the signer will verify its credibility of user who desires to reopen it, although she owns a valid signature.

4.    Sign − Veri(A, B, M, z, ε) = True only if ||z||≤ησ3m , and ε = H(Az − Tε, C), where η exceeding 1. Furthermore, detailed steps elaborate in the following Algorithm 1.

5  Security Analysis

5.1 Correctness

In this sector, we prove our protocol for correctness, blindness, one-more unforgeability under random oracle. For each, we propose some theorems which prove theoretically. It is unquestionable that the correctness in our proposed protocol. First, when received a blind signature <ϵ∗,ϵ> , the verifier utilizes Algorithm 1 to verify whether it is legal. If ‖ϵ∗‖>β2 or ‖ϵ∗‖∞>94 , the signature will reject.

Theorem 2: After at most e2 repetitions, the blind signature process is effective.

Proof of Theorem 2: To begin with, we prove the current correctness of ε = H(Az − Tε, C). Given a message M, public key A and B, and signature (z, ε), We get:

Az−Bϵ=A(r+Sϵ∗+a)−Bϵ=A(r+Sϵ∗)+Aa−B(ϵ∗−b)=Ar+Aa+ASϵ∗−Bϵ∗+Bb=x+Aa+Bϵ∗−Bϵ∗+Bb=x+Aa+Bb (3)

Therefore, H(Az − Tε, C) = H(x + Aa + Bb, C) = ε. In Lemma 1, we know that the probability of ‖z‖≤ησm is preponderant for η > 1. Thus, we get Sign − Veri(A, B, M, z, ε) = True. Moreover, we prove that the probability probm,v,σ∗=Dσm(z)MDv,σm(z) is not bigger than 1. We let the probability probm,v,σ∗ = Dσm(z)MDv,σm(z)=e−2⟨z,v⟩+‖v‖22σ2≤M . According to Lemma 1, we have|〈z, v〉| ≤ 12‖v‖σ. Thus, we have probm,v,σ∗= Dσm(z)MDv,σm(z)≤e−2⟨z,v⟩+‖v‖22σ2M≤1 . Consequently, we set M=e24‖v‖σ+‖v‖22σ2 in order to let M as small as possible. Therefore, we know that e has not do anything with correctness mainly because users can only use it.

5.2 Blindness

Blindness is one of the most significant characters that the signer only knows independent of signed message views. Thus, attackers cannot discern the views produced by different kinds of information.

Theorem 3: Our BS scheme is statistically blind since the signer only understands values that are independent of the signed message.

Proof of Theorem 3: Adversaries with advantage AdvBSblind(S∗) , S∗ interact with two different users U(pk, μb),U(pk, μ1−b) to attack our scheme. In order to prove blindness to malicious S∗ , we merely illustrates that the output of users are self-governed of their corresponding message m∗ , which involving signature (z, ε) with a challenge ϵ∗ .

To begin with, as a challenge ϵ∗ , we take ϵb∗,ϵ1−b∗ generated by the user U(pk, μb) and U(pk, μ1−b). As we calculate ϵ∗=ϵ+b which be outputted with the probability of min(Dσ1k(ϵ)M1Dσ1,ϵk(ϵ),1) , we have tailored εb and ε1−b depending on the same distribution Dσ1k . Therefore, Dσ1k is distributed with the signed message.

Furthermore, according to the signature z, which resembles to ϵ∗ , take zb and z1−b is the signature of U(pk, μb) responding U(pk, μ1−b) as z = y + a and output it with probability min(Dσ3k(z)M3Dσ3,yk(z),1) .

5.3 One-more Unforgeability

One-more unforgeability represents adversary U∗ will get l valid signatures at most which l is the amount of successful processes. We prove forging our blind signature by an adversary is equal to find an answer to the SISq,n,m,β problem for β = 2β2.

Theorem 4: With probabilityδ, an attacker can fight one-more unforgeability to our blind signature. Ands, h is the account of queries towards H. Then, there is an answer to the SISq,n,m,β problem for β = 2β2 where β2=m(ησ3+dκ) , with probability = δ22(s+h) in a polynomial-time algorithm.

Proof of Theorem 4: It is abided by the fact that our signature output is self-governed of the signing key. Further, the simulator will generate a solution to the SIS problem when a malicious forger fights with one-more unforgeability.

Lemma 4: Assume that D is a user that will test Algorithm 2, s is the amount of testing D to the blind signing oracle, and h is the number of a random oracle H. Then user has the ability to differentiate the correct blind signature process from that in Algorithm 2 with the maximum probability probl,hmax=2−n+1⋅s(h+s)+1M2−100⋅s .

Proof of Lemma 4: In the first part, we design Algorithm 3 as follows, which is as same as a real blind signature algorithm except for output ε.

We note w = a + r + Sb. Since ε ← Bk, and Bk = {v ∈ { − 1, 0, 1}k:‖v‖1 ≤ k}, it is the answer of H(Az − Bε, M) = H(Aw, M). As s is the amount of D and h is the number of random oracle H, it is unessential for use to check values (Aw, M) which will ever be h + s values. Moreover, we show that every time the Algorithm is called, with at most 2−n+1of probability, D will create a value y which Ay is the previous queried one. Therefore, A is regarded as A=A¯‖I , and notice that w follows Dσ′m . Consequently, for each w←Dσ′m , we have Pr[Aw=t]=Pr[w1=(t−A¯w0)]≤maxt′∈Zqn⁡Pr[w1=t′:w1←Dσ′m]≤2−n+1 .

Therefore, if Algorithm 3 is accessed s times, with probability at most 2−n+1s + 2−n+1h, the probability that occurs after a query is at most M3Dy,σ3m(z)≥Dσ3m(z) .

After that, we calculate that the outputs of Algorithm 2 and Algorithm 3 is similar at most 2−100M . Thus, it is obvious for all z that the statistical distance has been vanished since we have M3Dy,σ3m(z)≥Dσ3m(z) according to Lemma 3.

Lemma 5: There is an opponent S∗ which breaks one more unforgeability successfully with probability δ, s is the amount of testing D to the blind signature protocol and h is the number of random oracle H. Consequently, with probability =δ22(s+h) , we compute a non-zero vector v ∈ ℤm such that ||v|| < 2β2 and Av = 0.

Proof of Lemma 5: We set randomly b ← {0, 1}, b′ ← {0, 1} to forger and signer, respectively. Then, let l = s + h , and the responses of H is ε1, ε2, …, εl ← Bk and select the appropriate value. It starts a functional element program A taking as input (A, B, b, b′, ε1, ε2, …, εl). After that, A has a table consisting of all queries to H in order to make sure that an element does not appear twice.

The functional element program A sends the (A, B) and b to S∗ randomly. When S∗ supposed to sign it, A will utilize a stochastic number b′ to produce the signature through Algorithm 2. During signing steps for H, the answer should be the first ci in a set (ε1, ε2, …, εl) that has not been used. S∗ will get s + 1 valid signature (z1, ε1), (z2, ε2), …, (zs+1, εs+1) for different messages with probability δ when S∗ accomplishes running after s queries.

All the output of A maintains ||z||≤ησ3m . On condition that c does not respond to H, S∗ can generate a c = H(w, μ) with probability =1|Bk| . In other words, c comes from (ε1, ε2, …, εl) with probability =1−1|Bk| . Therefore, for some indexes i, S∗ success and generate ε = εi with probability =δ−1|Bk| . To a signing query, if εi was an action by S∗ on (Az′ − Bεi, μ′), then c = c′.

There is an overwhelming probability Az = Az′, and we note that it as a means of S∗ can seek a preimage of εi since if it not the case. Consequently, we have A(z − z′) = 0. We may figure out z ≠ z′ because the signature is different. Therefore, if ‖z‖,‖z′‖≤ησ3m , we can gain ‖z−z′‖≤2ησ3m .

Furthermore, we assume that εj is an action computing by an adversary to a random oracle H. To begin with, the blind signature is recorded as (z, εj), and then produce disparate (ϵj′,…,ϵs′)←Bk randomly. Then, we run the subroutine again (A,B,b,b′,ϵ1,ϵ2…,ϵj−1,ϵj′,ϵj+1′…,ϵs′) . According to the lemma [28], with the probability of at least δ′=(δ−1|Bk|s−1|Bk|)(δ−1|Bk|) , ϵj≠ϵj′ and attacker utilizes the action ϵj′ .

Thus, we get the subroutine's blind signature (z′,ϵj′) so that A(z−z′+Sϵj′−Sϵj)=0 . We also get ‖Sϵj′−Sϵj+z−z′‖≤2m(ησ+dκ) due to the fact that ‖Sϵj‖,‖Sϵj′‖≤dκm .

Lemma 6 [31]: For matrix A←Zqn×m , m > nlog (q), and secret key S, there is another secret key S′ such that AS = AS′ with probability at least 1 − 2−100.

For any adversary, secret S or S′ has equal probability to be used, so the probability is at least 12 . Consequently, we obtain a non-zero vector v with at least probability of (12−1|Bk|)(δ−1|Bk|s−1|Bk|)(δ−1|Bk|)=δ22(l+h) such that ‖v‖ ≤ 2(ησ3 + dκ) and Av = 0. Due to Lemma 6, we know that A(Sϵj′−Sϵj+z−z′)=0 when z−z′+Sϵj′−Sϵj=0 and z−z′+S′ϵj′−S′ϵj≠0 .

In a nutshell, there is a non-zero solution to figure the SISq,n,m,β problem with probability =δ22(l+h) .

6  Performance Evaluation

6.1 Parameters Setting

The methodology of selecting parameters is the same as in [31] shown in Tab. 1. We choose the k = 128 bits in terms of security level; for instance, we take the Hermite factor δ= 1.007 [32] as the notion, which considers having around 80 bits of security. Meanwhile, the complexity of the SIS problem has around 80 bits of security and considers choosing parameters n, m, q to maintain the SIS problem.

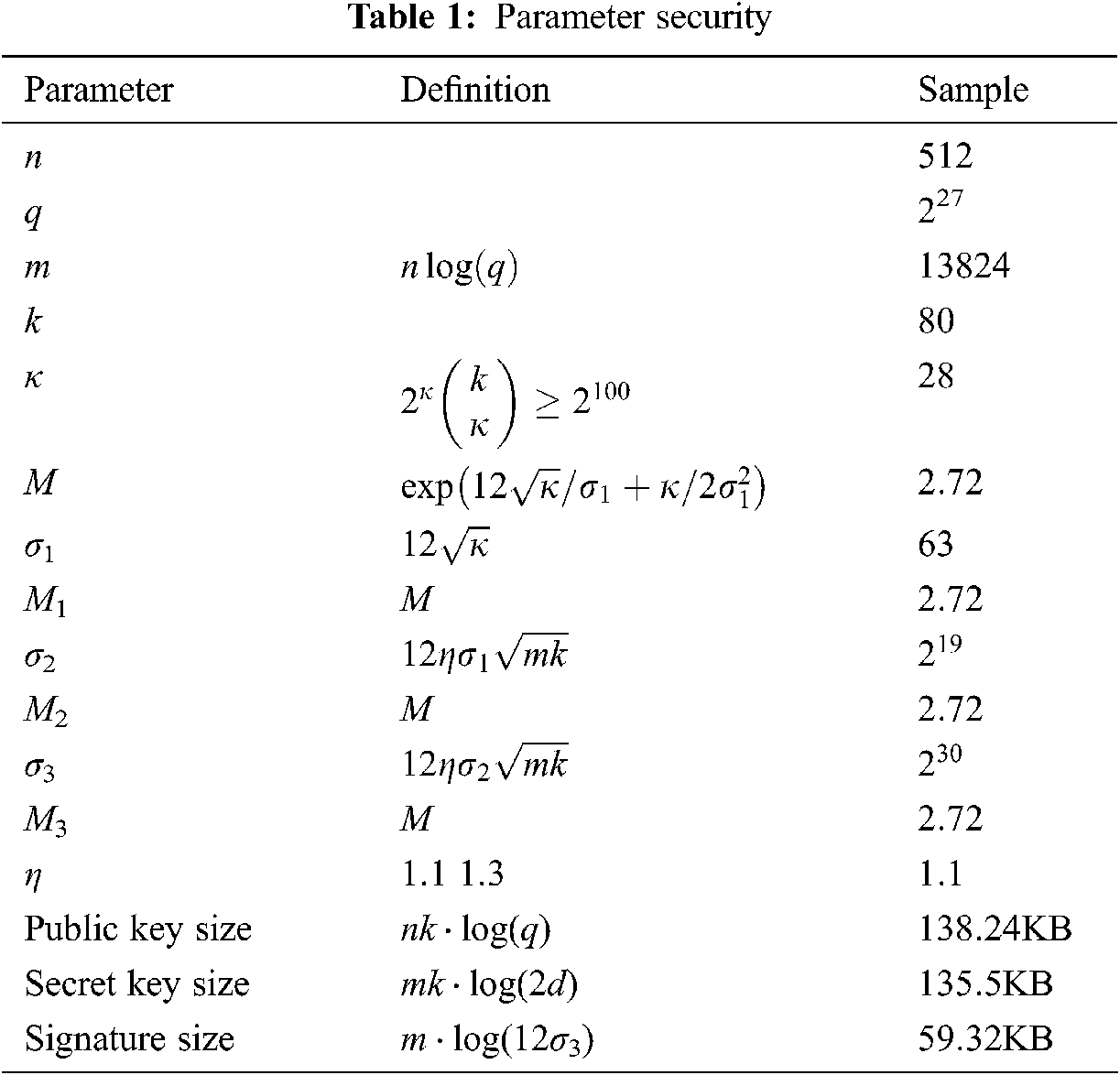
We use m = n ⋅ log (q) in order to prove the security and also let parameters k to define the size of challenges, which k should satisfy 2k(kk)≥100 . σ = 12‖v‖ from Lemma 2, we derive this equation as below: M=e24‖v‖σ+‖v‖22σ2=e1+1288≈2.72 . Thus, we obtain M1, M2, M3 for σ1, σ2, σ3 in the protocol, which does not depend on ‖v‖ and σ. Concretely, we set σ1=12‖ϵ‖=12k . Thus, we have M1=e(12kσ1+k2σ12) . M2 together with M2 will be derived in same way. Moreover, the signature size is roughly affected by vector z as ε is merely a little bit. As for the signature z←Dσ3m , therefore, the approximate size is mlog (12σ3) bits.

6.2 Comparison

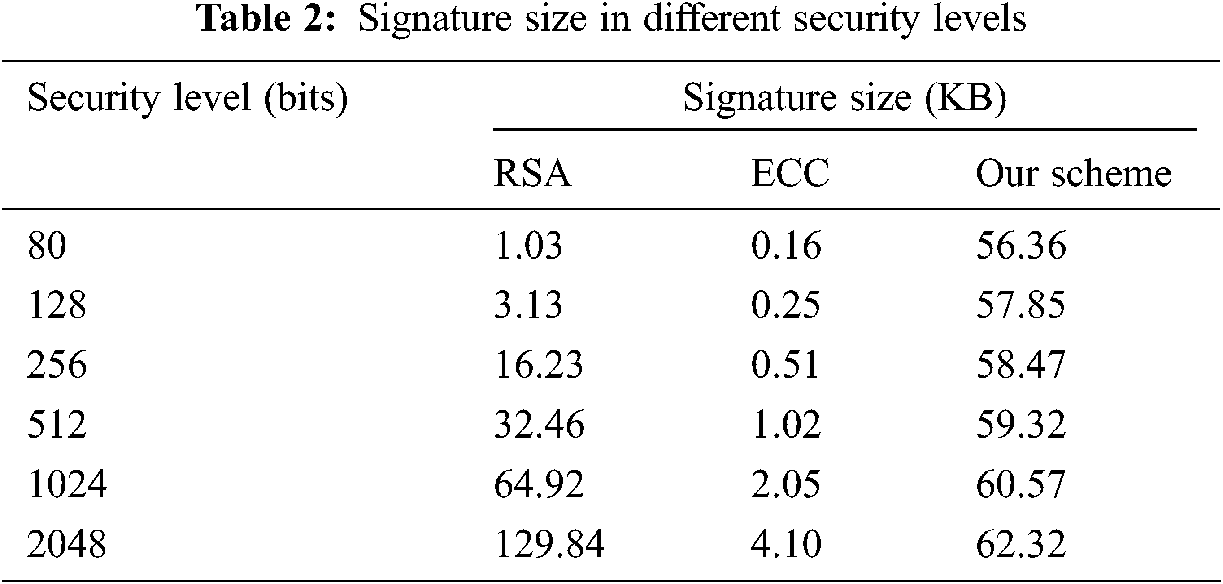
We conduct on Windows 10, AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz processor, 16.0GB running in RAM, and produce the simulation through MATLAB 2020. In Fig. 3, we compare the security among three blind signature schemes, including RSA blind signature, lattice-based blind signature [22], and our protocol. Although RSA blind signature size is the smallest, it could not resist quantum attacks, and also the security level of our scheme is 80 bits, but the signature size is 56.36 KB, which is smaller than [22]. This result demonstrates that our scheme can not only resist quantum computing attacks, but also has higher efficiency in same security level. Furthermore, we calculate the signature size in terms of separate security levels, including 80, 128, 256, 512, 1024, and 2048 bits, respectively, which shows in Tab. 2. The signature size of RSA and ECC according to different levels illustrate. As we present in Tab. 2, with the rising security level, its signature size of RSA skyrockets and the signature size of our protocol increases slightly. It permanently stabilizes regardless of the increment of security level shown in Fig. 4 with more concrete. This phenomenon reveals that our scheme has superior signature generation efficiency and stable storage consumption under the condition of significantly improved security level, which reflects the practicality of the scheme.

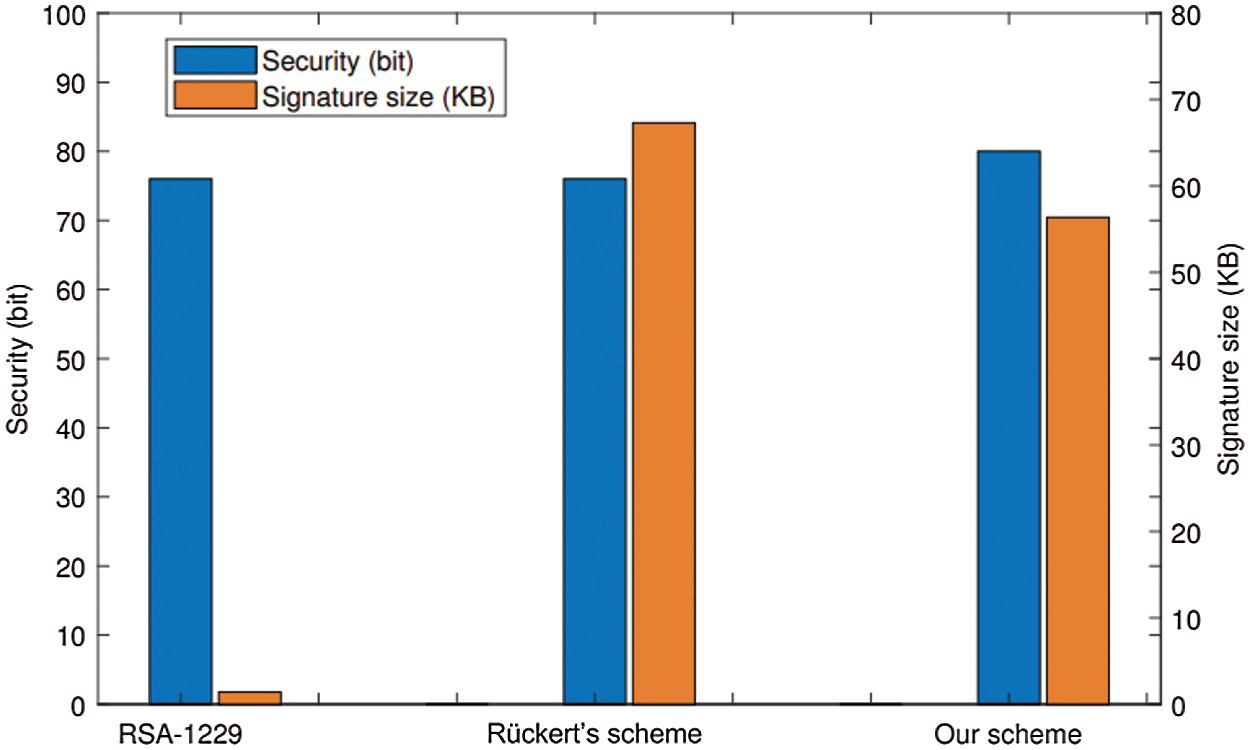
Figure 3: The comparison with the security of other schemes

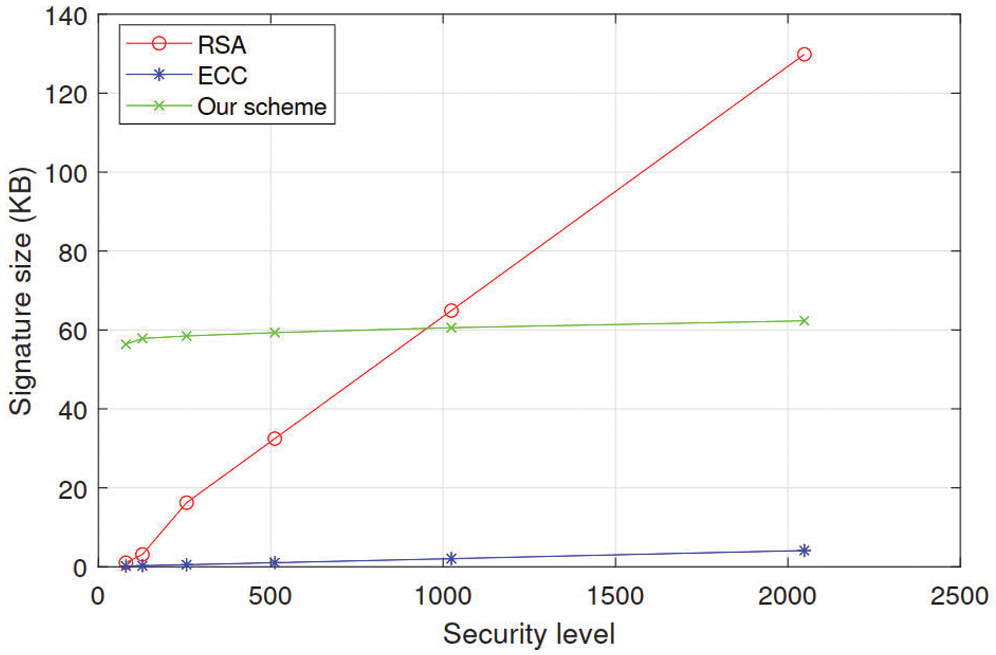
Figure 4: The comparison with the signature size

Though the signature size of ECC edges up, it is frequently 2 times of its security level. Last but not least, those two algorithms cannot resist quantum computing attacks. Therefore, our scheme is more useful in terms of security, blindness, and unforgeability than other methods utilized in the log system.

7  Conclusion

We present a novel post-quantum blind signature scheme for log system, which integrates a post-quantum blockchain to achieve decentralization and undeniability. Moreover, we designed a lattice-based blind signature not only maintains our protocol to resist quantum computing, but satisfies the blindness and one-more unforgeability, ensuring the privacy of log information and the validity of the blind signature. In addition, through the theoretical security analysis and the comprehensive performance evaluation to prove that our scheme has superior efficiency. As this is the first paper regarding to the post-quantum blind signature to secure log system, there are still some open questions for researchers to solve and enhance like how to minimize the signature size and how to improve the security without any increase in the communication overhead.

Funding Statement: This work is supported by the NSFC (Grant Nos. 92046001, 61962009), JSPS KAKENHI Grant Number JP20F20080, the Natural Science Foundation of Inner Mongolia (2021MS06006), Baotou Kundulun District Science and technology plan project (YF2020013), Inner Mongolia discipline inspection and supervision big data laboratory open project fund (IMDBD2020020), and the Scientific Research Foundation of North China University of Technology.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. H. Huh, K. Seo, “Blockchain-based mobile fingerprint verification and automatic log-in platform for future computing,” Journal of Supercomputing, vol. 75, pp. 3123–3139, 2019. [Google Scholar]

 2.  C. T. Poomagal, G. A. Sathish Kumar and D. Mehta, “Multi level key exchange and encryption protocol for internet of things (iot),” Computer Systems Science and Engineering, vol. 35, no. 1, pp. 51–63, 2020. [Google Scholar]

 3.  S. Long, W. Long, Z. Li, K. Li, Y. Xia et al., “A game-based approach for cost-aware task assignment with QoS constraint in collaborative edge and cloud environments,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 7, pp. 1629–1640, 2021. [Google Scholar]

 4.  J. Soria-Comas, J. Domingo-Ferrer, D. Sánchez and D. Megías, “Individual differential privacy: A utility-preserving formulation of differential privacy guarantees,” IEEE Transactions on Information Forensics and Security, vol. 12, no. 6, pp. 1418–1429, 2017. [Google Scholar]

 5.  G. Hong, J. Kim and H. Chang, “Blockchain technology based information classification management service,” Computers, Materials & Continua, vol. 67, no. 6, pp. 1489–1501, 2021. [Google Scholar]

 6.  M. Bhavin, S. Tanwar, N. Sharma, S. Tyagi and N. Kumar, “Blockchain and quantum blind signature-based hybrid scheme for healthcare 5.0 applications,” Journal of Information Security and Applications, vol. 56, pp. 102673, 2021. [Google Scholar]

 7.  H. Chen, G. Xu, Y. Chen, X. Chen, Y. Yang et al., “Cipherchain: A secure and efficient ciphertext blockchain via mPECK,” Journal of Quantum Computing, vol. 2, no. 1, pp. 57–83, 2020. [Google Scholar]

 8.  S. Xu, X. Chen and Y. He, “EVchain: An anonymous blockchain-based system for charging-connected electric vehicles,” Tsinghua Science and Technology, vol. 26, no. 6, pp. 845–856, 2021. [Google Scholar]

 9.  Y. Gao, X. Chen, G. Xu, W. Liu, M. Dong et al., “A new blockchain based personal privacy protection scheme,” Multimedia Tools and Applications, vol. 4, pp. 1–14, 2020. [Google Scholar]

10. C. Li, Y. Xu, J. Tang and W. Liu, “Quantum blockchain: A decentralized, encrypted and distributed database based on quantum mechanics,” Journal of Quantum Computing, vol. 1, no. 2, pp. 49–63, 2019. [Google Scholar]

11. M. Mosca, “Cybersecurity in an era with quantum computers: Will we be ready?,” IEEE Security & Privacy, vol. 16, no. 5, pp. 38–41, 2018. [Google Scholar]

12. D. Johnson, A. Menezes and S. A. Vanstone, “The elliptic curve digital signature algorithm (ECDSA),” International Journal of Information Security, vol. 1, no. 1, pp. 36–63, 2001. [Google Scholar]

13. R. L. Rivest, A. Shamir and L. Adleman, “A method for obtaining digital signatures and public-key cryptosystems,” Communications of the ACM, vol. 21, no. 2, pp. 120–126, 1978. [Google Scholar]

14. P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” Siam Review, vol. 26, no. 5, pp. 1484–1509, 1997. [Google Scholar]

15. L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proc. of the 28th Annual ACM Symposium on the Theory of Computing (STOCPhiladelphia, PA, USA, pp. 212–219, 1996. [Google Scholar]

16. V. Lyubashevsky, “Fiat-shamir with aborts: applications to lattice and factoring-based signatures,” in Advances in Cryptology, ASIACRYPT 2009. Proc.: Lecture Notes in Computer Science (LNCS 5912Tokyo, Japan, pp. 598–616, 2009. [Google Scholar]

17. C. Gentry, C. Peikert and V. Vaikuntanathan, “Trapdoors for hard lattices and new cryptographic constructions,” in Proc. of the 40th Annual ACM Symposium on Theory of Computing (STOCVictoria, British Columbia, Canada, pp. 197–206, 2008. [Google Scholar]

18. D. Cash, D. Hofheinz, E. Kiltz and C. Peikert, “Bonsai trees, or how to delegate a lattice basis,” Journal of Cryptography, vol. 25, pp. 601–639, 2012. [Google Scholar]

19. B. Sengupta, Y. Li, Y. Tian and R. H. Deng, “Editing-enabled signatures: A new tool for editing authenticated data,” IEEE Internet of Things Journal, vol. 7, no. 6, pp. 4997–5007, 2020. [Google Scholar]

20. D. Chaum and E. V. Heyst, “Group signatures,” in Advances in Cryptology, EUROCRYPT 1991, Proc.: Lecture Notes in Computer Science (LNCS 547Brighton, UK, pp. 257–265, 1991. [Google Scholar]

21. X. Lin, X. Sun, P. Ho and X. Shen, “GSIS: A secure and privacy-preserving protocol for vehicular communications,” IEEE Transactions on Vehicular Technology, vol. 56, no. 6, pp. 3442–3456, 2007. [Google Scholar]

22. M. Rückert, “Lattice-based blind signatures,” in Advances in Cryptology, ASIACRYPT 2010. Proc.: Lecture Notes in Computer Science (LNCS 6477Singapore, pp. 413–430, 2010. [Google Scholar]

23. A. Juels, M. Luby and R. Ostrovsky, “Security of blind digital signatures,” in Advances in Cryptology, CRYPTO 1997, Proc.: Lecture Notes in Computer Science (LNCS 1294Santa Barbara, California, USA, pp. 150–164, 1997. [Google Scholar]

24. D. Pointcheval and J. Stern, “Security arguments for digital signatures and blind signatures,” Journal of Cryptology, vol. 13, no. 3, pp. 361–396, 2000. [Google Scholar]

25. C. Li, G. Xu, Y. Chen, H. Ahmad and J. Li, “A new anti-quantum proxy blind signature for blockchain-enabled internet of things,” Computers, Materials & Continua, vol. 58, no. 2, pp. 711–726, 2019. [Google Scholar]

26. W. Huang, “A blockchain-based framework for secure log storage,” in 2019 IEEE 2nd Int. Conf. on Computer and Communication Engineering Technology (CCETBeijing, China, pp. 96–100, 2019. [Google Scholar]

27. C. Li, X. Chen, Y. Chen, Y. Hou and J. Li, “A new lattice-based signature scheme in post-quantum blockchain network,” IEEE Access, vol. 7, pp. 2026–2033, 2019. [Google Scholar]

28. X. Zhang, F. Wu, W. Yao, W. Wang and Z. Zheng, “Post-quantum blockchain over lattice,” Computers, Materials & Continua, vol. 63, no. 2, pp. 845–859, 2020. [Google Scholar]

29. Y. Gao, X. Chen, Y. Chen, Y. Sun, X. Niu et al., “A secure cryptocurrency scheme based on post-quantum blockchain,” IEEE Access, vol. 6, pp. 27205–27213, 2018. [Google Scholar]

30. M. Bellare and G. Neven, “Multi-signatures in the plain public-key model and a general forking lemma,” in Proc. of the 13th ACM Conf. on Computer and Communications Security (CCSAlexandria, VA, USA, pp. 390–399, 2006. [Google Scholar]

31. V. Lyubashevsky, “Lattice signatures without trapdoors,” in Advances in Cryptology, EUROCRYPT 2012, Proc.: Lecture Notes in Computer Science (LNCS 7237Cambridge, UK, pp. 738–755, 2012. [Google Scholar]

32. N. Gamsa and P. Q. Nguyen, “Predicting lattice reduction,” in Advances in Cryptology, EUROCRYPT 2008, Proc.: Lecture Notes in Computer Science (LNCS 4965Istanbul, Turkey, pp. 31–51, 2008. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.