Computer Systems Science & Engineering DOI:10.32604/csse.2022.020312
Article

Energy Efficient QoS Aware Cluster Based Multihop Routing Protocol for WSN

M.S. Maharajan1,* and T. Abirami2

1Department of Computer Science and Engineering, GRT Institute of Engineering and Technology, Tiruttani, 631209, India
2Department of Information Technology, Kongu Engineering College, Erode, 638060, India
*Corresponding Author: M. S. Maharajan. Email: msmaharajan12017@gmail.com
Received: 19 May 2021; Accepted: 20 June 2021

Abstract: Wireless sensor networks (WSN) have become a hot research area owing to the unique characteristics and applicability in diverse application areas. Clustering and routing techniques can be considered as an NP hard optimization problem, which can be addressed by metaheuristic optimization algorithms. With this motivation, this study presents a chaotic sandpiper optimization algorithm based clustering with groundwater flow optimization based routing technique (CSPOC-GFLR). The goal of the CSOC-GFLR technique is to cluster the sensor nodes in WSN and elect an optimal set of routes with an intention of achieving energy efficiency and maximizing network lifetime. The CSPOC algorithm is derived by incorporating the concepts of chaos theory to boost the global optimization capability of the SPOC algorithm. The CSPOC technique elects an optimum set of cluster heads (CH) whereas the other sensors are allocated to the nearer CH. Extensive experimentation portrayed the promising performance of the CSPOC-GFLR technique by achieving reduced energy utilization, improved lifetime, and prolonged stability over the existing techniques.

Keywords: Clustering; routing; wireless sensor networks; energy efficiency; network lifetime; metaheuristics

1  Introduction

The current development in the area of wireless communications, MEMS (microelectromechanical system), and digital electronics have led to the growth of microsensors. This small sensor comprises multifunction, transfer easily on shorter distance, requires lower power, and inexpensive [1]. The sensor nodes are accountable for sensing, processing, and delivering data to the base station (BS). They must operate together to create a wireless sensor network (WSN). A WSN comprises a huge amount of sensor nodes that are manually/arbitrarily placed in a provided coverage area. The nodes collect the local physical data, aggregate, and transmit them to BS named sink. For public notable events, the BS is linked to the internet. Rather than transmitting raw data to the node accountable for data fusion, the sensor node could utilize their functioning capabilities to execute evaluation, and fusion operation is to transfer the required data [2]. This feature of wireless sensor allows utilizing in several fields particularly for monitoring and surveillance.

Related to conventional methods of environmental observing, WSN method is a significant green technique for the upcoming detection effectively in the environment variations. The WSN for monitoring environments comprises of huge amount of lower cost battery powered sensor nodes, closely placed through a remote/inaccessible physical space [3,4]. But the major problem is the restricted power assets of sensor nodes. It isn’t real-world for recharging the nodes battery/interchange them once whole depletion of their energies are placed in hostile environment. Thus, when conventional network aims to attain higher level QoS, the sensor network protocol should emphasize mainly energy conservation for maximizing network lifespan. Implementation of energy efficient clustering and routing methods is one of the significant challenges between them. Clustering in WSN comprises combination of effective sensor nodes to different clusters; every cluster has single leader named cluster head (CH). The CH collects the information from every equivalent member, processes it, and sends them to BS. Every sensor node belongs to single cluster and communicates with CH. Then, CH selection requires to be accurately tackled to balance the energy consumption of CH; or else, they will pass away fast because of additional workload to information forwarding and aggregations. Each cluster based routing technique selects primarily the CH arbitrarily or likelihoods and later creates the cluster. But every CH could be placed in a smaller network area and few regular nodes would be separated that might affect network dysfunctions.

Hierarchical routing is an effective manner to reduce energy consumption with the cluster and execute data aggregation. It enables combining tasks for reducing transmit packet amount to the sink [5,6]. An accurate protocol should contain mechanism to save energy in the node as recharging their battery is typically hard, impossible, or risky. Each aspect of the node from the hardware to their executed operation would assist in distributing energy load. Due to hierarchical routing have various parts to assist distinguished possible phases in protocol operation, the presence of 2 operations modes in the sensor could predict high energy costs. But, various communication modes like CH and standard sensors could be useful when executed in all layers. Alternatively, metaheuristic approaches are the optimization systems that can resolve the difficult system. These methods are stimulated by this precise knowledge of biological/social processes that form an abstraction level that could be assumed as search approaches. Few instances of common metaheuristic approach include Genetic Algorithms, Particle Swarm Optimization (PSO), Differential Evolution (DE), Artificial Bee Colony (ABC), Flower Pollination Algorithm (FPA), and Gravitational Search Algorithm (GSA). The Metaheuristic system doesn’t continuity differentiability, require convexity, or particular early condition that corresponds to significant benefits related to other methods. In spite of stimulating outcomes, these search approaches preserve various problems while they are employed to higher multi modal optimization problems [7–9].

This study presents a chaotic sandpiper optimization algorithm based clustering with groundwater flow optimization based routing technique (CSPOC-GFLR). The CSOC-GFLR technique aims to construct clusters and choose optimal set of routes with an intention of achieving energy efficiency and maximizing network lifetime. The CSPOC algorithm is derived by incorporating the concepts of chaos theory to boost the global optimization capability of the SPOC algorithm. The CSPOC technique elects an optimum set of cluster heads (CH) whereas the other sensors are allocated to the nearer CH. A comprehensive set of simulations take place to exhibit the significant performance of the CSPOC-GFLR technique interms of different measures.

2  Literature Review

Gupta et al. [10] proposed genetic algorithm (GA) based method to cluster and routing in WSN. The clustering is depending upon residual energy of gateway and distance from sensor node to their matching CH. The routing system is depending upon residual energy of gateway together with trade off among communication distance and number of forwards. They execute broad simulation of presented method and relate the simulations outcome with the present technique. Shankar et al. [11] utilize distinct PSO-LEACH and Harmony Search Algorithm (HSA) methods. This technique contains exploitation and exploration trade off with local search HSA limitation. To attain a global search with quicker convergence, hybrid of PSO and HSA methods are presented for selecting energy efficiency CH. The introduced technique demonstrates higher search effectiveness of HSA and dynamic capability of PSO enhances the lifespan of sensor nodes. The efficiency of hybrid method is calculated by the number of alive nodes, residual energy, amount of dead nodes, and throughput.

Oladimeji et al. [12] proposed a new Heuristic Algorithm for Clustering Hierarchy (HACH) that are consecutively executes selection of inactive and CH nodes at all rounds. The inactive node selection utilizes a random sleep scheduling method for determining the node selection which could be placed to sleep mode without harmfully influencing the network coverage. Similarly, the clustering method utilizes a new heuristic crossover function for combining 2 distinct solutions to attain an enhanced solution which improves the distribution of CH nodes and manages energy consumption in WSN. Mann et al. [13] proposed an improved Artificial bee colony (iABC) metaheuristic, with an enhanced search formula that is capable of searching for an optimum solution to develop its exploitation capacity and population sample by utilizing initial type of compact Student’s t-distribution for enhancing global convergences of the presented metaheuristic. Additionally, to exploit the capacity of the presented metaheuristic, an energy efficient bee clustering protocol (EEBC) dependent iABC metaheuristic was established that select optimum CH with energy efficiency method in WSN.

Zachariah et al. [14] presented HECK and HOCK a new energy efficient clustering method for increasing the network lifespan for heterogeneous and homogeneous platforms, correspondingly. This method is created by Cuckoo search and Krill herd. When the optimum cluster centroid locations are calculated by the Krill herd method, and the Cuckoo search is employed for selecting the optimum CH. The efficiency of HOCK method is calculated by the variation of BS position and node density. For evaluating HECK method, 2 and 3 levels of heterogeneity are deliberated. In Idrees et al. [15], a protocol named distributed GA for lifetime coverage optimisation (DiGALCO) is recommended for preserving the coverage and improve the lifespan of WSN. The DiGALCO integrates 3 energy efficiency systems: virtual network section to sub domains, distributed CH selection in every subfield, following sensor activity scheduling based genetic algorithm (GA) optimisation executed by every CH. The DiGALCO is working to round. Every round comprises 3 stages: sensing, CH selection, discovery, and GA decision.

In Bhushan et al. [16], a method called fuzzy attribute based joint integrated scheduling and tree formation (FAJIT) approach for tree formation and parent node selection by utilizing FL in heterogeneous networks was projected. The FAJIT is mostly concentrating on tackling the parent node selection problem in heterogeneous networks to aggregate various kinds of data packets for improving energy efficient. The parent node selection is executed depending upon candidate node with least amount of dynamic neighbors. The FL is employed in the event of an equivalent amount of dynamic neighbors. In the presented method, FL is initially employed to WSN, and later min and max normalization are utilized for retrieving the normalization weight (i.e., membership value) for the provided graph edge. This membership value is exploited for representing the degree of a component belonging to a group. Thus, the node with least number of weights is assumed by the parent node. Though several models are existed in the literature, there is still needed to design a new technique to accomplish improved energy efficiency and network lifetime. Therefore, this paper designs the CSOC-GFLR technique aims to construct clusters and choose optimal set of routes with an intention of achieving energy efficiency and maximizing network lifetime.

3  System Model

In this study, the sensor nodes are arbitrarily distributed in a 2D region; The BS is available in the center of the monitoring region and has limitless power; each sensor node and BS are fixed; all nodes could alter their transmission range and calculate distance [17]; all sensor nodes have single ID and recognize its individual position; every sensor nodes have restricted power; all clusters have 2 CHs , named vice and main heads; the main CH of all clusters involves in multi hop routing; the vice CH gathers information from CM and conveys the processed information to the main CH. A huge amount of energy is consumed by the transmission, hence the processing and sensing are ignored in this study. The procedure of receiving, and transmitting communication consumes high energy compared to sleeping and monitoring. Thus, it assumes receiving and transmitting as communication. The radio module in this study is similar as defined in Soro et al. [18] The energy consumed via the transmission of one-bit data is estimated by Eq. (1)

ETX(l,d)={lEelec+lϵfsd2,d≤d0lEelec+lϵmpd4,d≥d0 (1)

where Eelec represents energy consumption to send/receive one-bit data, it denotes data transmission length, ϵfs indicates coefficient of energy consumption to amplify radio at free space mode, ϵmp represents coefficient of energy consumption to amplify radio at multi fading mode, d indicates transmission distance, and d0 denotes threshold value, d0=ϵfs/ϵmp.

Consumed energy of getting m bit data is estimated in Eq. (2)

ERX(m)=mEelec (2)

where Eelec represents energy consumption for receiving/sending one bit data, and m indicates data length. In this study, they consider every node send similar data of the length to its CH , and its process data to a fixed length packet.

4  The Proposed CSPOC-GFLR Technique

The workflow involved in the CSPOC-GFLR technique is demonstrated in Fig. 1. Usually, the sensor nodes in WSN are randomly positioned in the target area and the nodes get initialized to aware of the neighboring nodes [19–22]. Followed by, the CPSOC based clustering technique is applied to cluster the nodes and elect an optimal set of CHs. Then, the GFLR based routing technique is involved to choose optimal route for inter cluster transmission. When the routes are elected, the CMs send the sensed data to CHs and the CHs forwards it to BS via the intercluster communication.

Figure 1: The working process of CSPOC-GFLR model

4.1 CPSOC Based Clustering Technique

At this stage, the CPSOC algorithm is executed to determine an optimal set of CHs and organize clusters. Sandpipers are seabirds that could be made around the world. There are extensive sandpiper species with distinct lengths and masses. They consist of fish, earthworms, amphibians, reptiles, omnivorous, and eat insects, etc. They are highly sharper birds. They used bread crumbs for hunting fishes and experts in making rain like sounds by their feet to hunt for underground earthworms. Furthermore, it contains an uncommon pair of glands right above their eyes that assist to flush the extra salt from their system. Commonly, they live in groups. They utilized their knowledge for finding and attacking the prey [23]. An essential thing regarding sandpipers is their attacking and migrating behaviors. The Migration is determined by cyclic motion of sandpipers from one place to other for locating rich food and source that would give enough energy. It is given by:

•   In migration, they travel in a group. The early location of sandpipers is distinct to prevent the collision among them.

•   In a group, sandpipers could be traveling to the path of an optimum survival fittest sandpiper that is a sandpiper fitness value1 is lower than other.

•   According to fittest sandpiper, another sandpiper could upgrade their early location.

It often attacks the migrating birds on sea while they migrate from one side to the other. They could create spiral natural shape motion in attacking. Such behavior is equated in this manner related to decision criterion should be improved. This creates it probable to equate a novel technique. Fig. 2 illustrates the flowchart of SOA. The scientific module of attack and migrating behaviors are deliberated below.

Figure 2: Flowchart of SOA

4.1.1 Migration Behavior (Exploration)

This method examines the set of sandpipers that moves from one place to other in migration. In this phase, a sandpiper must fulfill the succeeding 3 scenarios:

Collision avoidance: Further parameter CA is utilized for computing novel search agent places to prevent collision avoidance among their adjacent sandpipers.

Csp→=CA×Psp→(z) (3)

where Csp→ indicates location of search agent that doesn’t collide with another search agent, Psp→ determines present location of search agent, z denotes present iteration, and CA determines motion of search agent in a search space.

where,

z=0,1,2,…,Maxiterations (4)

where Cf denotes control frequency to alter parameter CA that is linearly reduced from Cf to zero. For example, when variable Cf is fixed to two, the parameter CA is always reduced from two to zero. The value of Cf is fixed to two in this study. The word fitness value is determined as an aggregate that calculates the population and provides a fitness/score. While the aggregate is a process that evaluates the quality of denoted solution.

Converge in the direction of an optimum neighbor: In collision avoidance, the search agent converges (move) to the direction of optimum neighbor.

Msp→=CB×(Pbst→(z)−Psp→(z)) (5)

where Msp→ denotes positions of search agent Psp→ to an optimum fittest search agent Pbst→ (fitness value is lesser). CB indicates arbitrary parameter that is accountable for an optimum exploration. The CB calculated by:

CB=0.5×Rand (6)

where Rand denotes arbitrary amount in the range of zero and one .

Upgrade regarding optimism search agent: Lastly, the search agent/sandpiper could upgrade its location equivalent to optimum search agent.

Dsp→=Csp→+Msp→ (7)

where Dsp→ determines the gap among search agents and optimum fittest search agents.

4.1.2 Attacking Behavior (Exploitation)

In migration, sandpipers could always alter their angle and speed of attack. They utilize their wings for increasing altitude. It creates the spiral behavior, when attacking prey, in the air. This behavior in three-dimension plane is given by.

x′=Radius×sin(i) (8)

y′=Radius×cos(i) (9)

z′=Radius×i (10)

r=u×ekv (11)

where Radius represents radius of every turn of spiral, i indicates parameter in the range of [0≤k≤2π]. u and v indicate constant to determine spiral shape, and e represents base of natural logarithm. Consider the constant values of u and v as one. If the constant values are greater compared to one, the shape of spiral is highly complicated. Thus, the upgraded location of search agent is calculated by Eqs. (8)–(11).

Psp→(z)=(Dsp→×(x′+y′+z′))×Pbst→(z) (12)

where Psp→(z) upgrades position of another search agent and saves an optimum solution.

4.1.3 Design of CSPO Algorithm

In order to improve the performance of the SPO algorithm, chaos concept is integrated into it. Chaos is an unstable condition/dynamic behavior that is highly sensitive in early conditions. It has been employed in several optimization techniques for avoiding traps in local optimal and enhance the quality of solution. The metaheuristic technique is depending upon 2 methods: exploration and exploitation. By exploitation, the search is created for an optimum solution, where the exploration enables search for an effective solution [24]. The chaos is introduced to metaheuristic technique for striking a balance among exploitation and exploration, hence it efficiently attains an optimum solution. The chaos is included in GFLR method for obtaining enhanced features for exploitation and exploration in every search space and improves the efficiency of the recommended method in detecting an optimum global solution. The Chaotic map is utilized in determining the location of xik , while the variable θ is replaced with an obtained value via chaotic map is given by

xik+1=xik+Cnap×(xBH−xik),i=1,2,…,N∇ (13)

where xik and xikþ1 represents position of ith star at iterations k and k+1 , correspondingly. xBH indicates location of BH in the space, Cmap denotes chaotic map, and Ns indicates number of stars. The 10 chaotic maps have been utilized for manipulating the value of arbitrary variables in SPO, and the early value of every map was fixed to 0.7.

4.1.4 Process Involved in CSPO Based Clustering Technique

Let N nodes in WSN are used as K clusters with M(K<<M) candidate CH. Following, the method with Cnk feasible clustering techniques and elect better clustering model is a challenging optimization problem. Utilizing the fitness function (FF) of CSPOC solves the problem from clustering model, and framework of FF is considered as distance to neighboring nodes (DNN), distance to BS (DTBS), and residual energy (RE). Initially, BS estimates the high power of nodes based on the energy accessible in network. The node with superior RE is considered that the candidate CH. Then, BS executes CSPOC to carry out clustering by FF as demonstrated in Eq. (14).

f(x)=ϵ1 f1(pj)+ϵ2 f2(pj)+ϵ3 f3(pj)+ϵ4 f4(pj) (14)

The local density ρi of CH is utilized in kernel function as expressed in Eq. (15)

ρi=∑j∈IS⁡e−(dijdc)2 (15)

where S={ai}i−1k implies a CH set in WSN, dc refers a truncation distance, and d(ai,aj) denotes the distance among CH ai and aj.f1 refers the DNN value. When the neighboring distance is maximal, next CH with and with no local densities are distributed to particular extent. Also, dispersal of CH is obtained by diminishing the adjacent distance of CH. The term f1 is determined as Eq. (16).

f1={minj∈ISi⁡{dij},ISi≠∅maxj∈ISi⁡{dij},ISi=∅ (16)

where f2 shows a CCEF and low average distance among the node as well as CH is defined as Eq. (17).

f2=1maxK=1,2⋯K{∑∀ni∈CPj,Kd(ni,CHPj,K)|CPj,K|}, (17)

where d(ni,CHPj,K) stands for distance in node ni and CH, and |CPj,K| indicates the number of nodes from cluster CK. Lastly, f3 signifies the CH, RE factor, NC refers the network center, and CH place is established utilizing Eq. (18).

f3=K×d(BS,NC)∑i=1K⁡d(BS,CHpj,k) (18)

The weight coefficient of evaluated factor fulfills ϵ1+ϵ2+ϵ3=1 . Based on the FF, maximal FF score is appropriate to meet the provided condition like considerable CH dispersion, maximum CH power, and CH is nearer to sink node. In addition, the cluster utilized by FF implements minimum energy and holds many CHs; so, small clusters are recognized from vicinity of sink and overcome the power dispersion in all clusters.

4.2 GFLR Based Routing Technique

The GFL algorithm is based on the movement of groundwater from recharging regions to discharging regions stimulating the concept of Darcy’s law. A major idea of GFL algorithm is the flow of ground water is mainly directed by Darcy’s law [25]. Earlier works explored that the velocity of the groundwater flows highly based on height difference and gap in position. Once the function undergo initiation, the candidate solution can be defined by

Gmn=LBn(i)+Rn(1)∗(UBn(i)−LBn(i)) (19)

m=1,2,…i (20)

n=1,2,…Dim (21)

where Gmn denotes the value of m the candidate solution in n dimension, UBn(i) and LBn(i) are the maximum and minimum bounds of function i correspondingly and Rn is an arbitrary number lies in the range of 0–1. All the candidate solutions are supported by a velocity element, and it can be defined by

veln→(0)=0 (22)

where (0) defines the initial velocity of the candidate solution. Next to the initialization process, the position update takes place using the groundwater flow rules and Darcy’s law. Groundwater is majorly supported by height difference (∆h) and gap length (L). Then, the present candidate solution can be mathematically represented using the present functional values, as defined in Eq. (23):

DisAn→(i)=R(DisA1→(i),DisA1→(t)…DisAn→(t) (23)

where D is denotes the chosen Discharged region. R and t signify the discharge area water flow and ground water flow correspondingly. The discharge velocity is directly proportional to the Hydraulic gradient (hg), as defined in the following

The production of hg with a discharge velocity (vel) based on the discharge region and ground water for all individuals are determined. In addition, the P is called as the coefficient of permeability. Vel is the discharge velocity. So, the total time complexity (TC) is defined by

Fitnesscomputation=Tc(GW×Itern×dim) (24)

where GW is the number of ground water, Itern represents the number of rounds, dim indicates the dimensionality count in the objective function. Fig. 3 demonstrates the flowchart of GFL.

Figure 3: Flowchart of GFL

The main principle of GFLR is for finding new route from CHS to BS. The new path is recognized by utilizing GFLR as FF metric that is included of RE, distance to BS (DTBS), and NDE.

At the initialization stage, all FFs determine fittest solution to implemented problem. In routing, all FFs imply the data forwarding route in CH to sink node. The importance of FF is related to CH accessible from the network, and additional location is added to sink. The supremacy of FF is similar to m+1 , where m signifies the number of CH contained from the system. Let, Fi=(Fi,1(t),Fi,2(t)…Fi,m+1(t)) be ith FF, and the positions Fi,d,∀i1≤i≤m+1,∀d1≤d≤m+1, determines next-hop to send data to BS . It can be extremely focused on deciding optimum route from CH to sink. It can be obtained by utilizing FF in several sub objectives namely RE, Euclidean distance, as well as NDE. In order to deliver data, consecutive hop obtains the data and transmitting to BS. So, maximal RE of next-hop is prioritized prominently. Moreover, primary sub objective by means of RE f1 is improved by,

f1=∑i=1m⁡ECHi (25)

Euclidean Distance can be represented as distance among CH to next hop and sink. If the distance is minimal after the power utilization rate is also decreased. The second objective is for minimizing the distance amongst CHs to sink measured by,

f2=1∑i=1m⁡dis(CHi,NH)+dis(NH,BS) (26)

ND It implies the count of nodes in next-hop. When next-hop is contained of restricted CH members, after it utilizes minimum energy in gained data in neighboring members and stays alive to longer duration. Then, the next-hop with restricted node degree is elected prominently. Lastly, NDE is determined interms of node degree of f3 and written as,

f3=1Σi=1mIi (27)

Afterward, the weighted sum model is implemented to each sub objective and converted as single objective as represented in Eq. (28). Now α1,α2 and α3 signifies the weights assigned to all sub objectives, and αiϵ(0,1) and α1+α2+α3=1.

Fitness=α1(f1)+α2(f2)+α3(f3) (28)

5  Performance Validation

This section examines the performance of the proposed CSPOC-GFLR technique with other existing techniques. The proposed model is simulated using MATLAB R2014. The results are examined under varying number of nodes. In addition, the performance of the CSPOC-GFLR technique is investigated interms of network lifetime (NLT), total energy consumption (TEC), throughput, normalized overhead (NOH), and end to end (ETE) delay. A brief comparative study of the CSPOC-GFLR technique with state of art methods [26,27] takes place interms of NLT, TEC, and throughput as shown in Tab. 1.

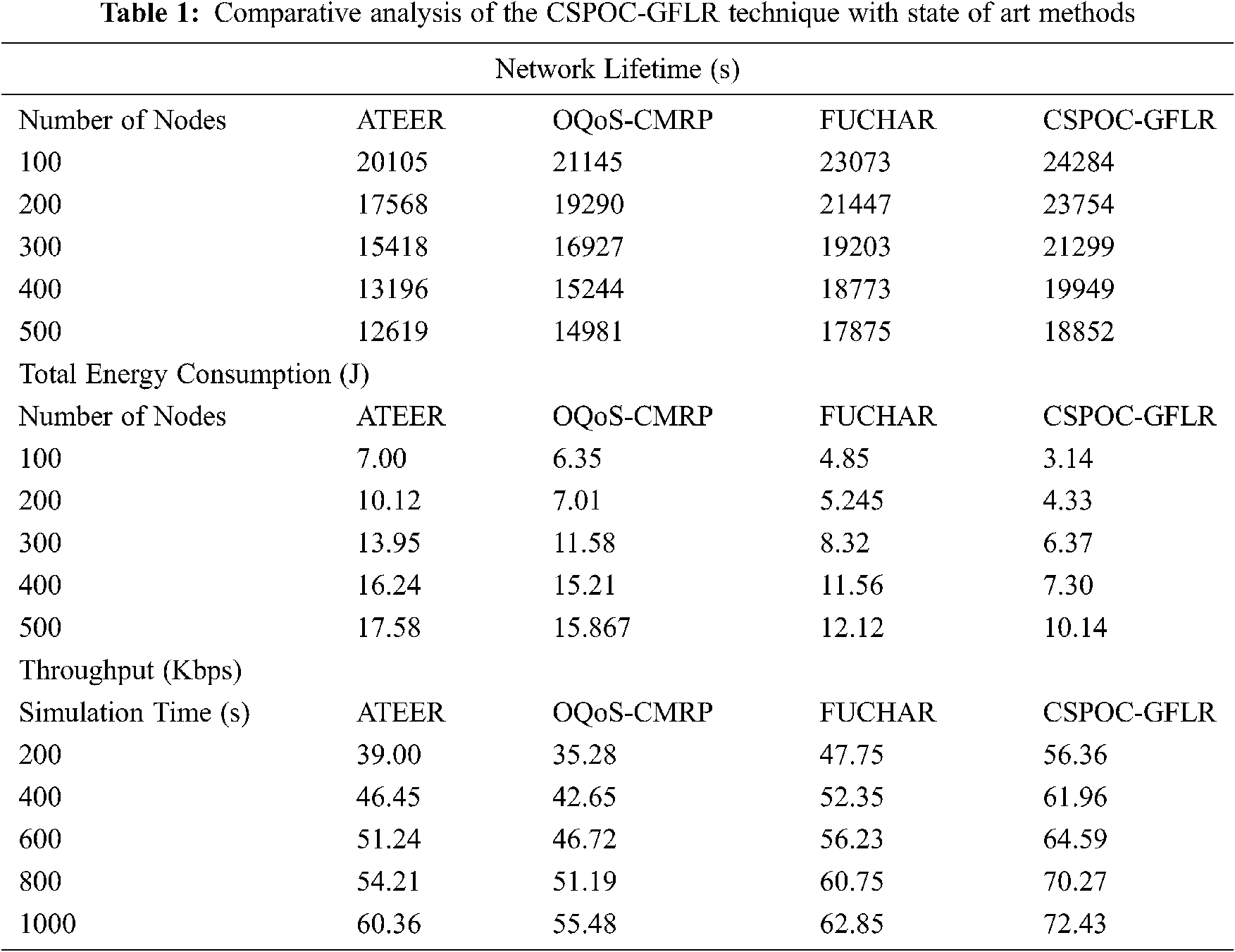
Figure 4: Network lifetime analysis of CSPOC-GFLR model

Figure 5: Total energy consumption analysis of CSPOC-GFLR model

Fig. 4 investigates the NLT analysis of the CSPOC-GFLR technique with existing ones under varying node count. The figure demonstrated that the ATEER technique has offered an insignificant outcome with the minimum NLT over the other methods. Similarly, the OQoS-CMRP technique has showcased certainly increased NLT over the ATEER technique. Likewise, the FUCHAR technique has portrayed somewhat improved NLT over the previous methods. But the proposed CSPOC-GFLR technique has gained maximum NLT over the existing methods under different node count. Particularly, the CSPOC-GFLR technique has resulted in a higher NLT of 24284 s, 23754 s, 21299 s, 19949 s, and 18852 s under the varying node count of 100–500.

An extensive TEC analysis of the CSPOC-GFLR technique with compared methods is provided in Fig. 5. From the figure, it is apparently clear that the ATEER technique has appeared as a worse performance which has obtained maximum TEC. At the same time, the OQoS-CMRP technique has accomplished slightly decreased TEC over the ATEER technique. Simultaneously, the FUCHAR technique has demonstrated competitive outcome with the moderately lower TEC. However, the CSPOC-GFLR technique has resulted in a minimum TEC over the existing methods. Specially, the CSPOC-GFLR technique requires the least TEC of 3.14 J, 4.33 J, 6.37 J, 7.30 J, and 10.14 J under varying number of 100–500 nodes.

A detailed throughput analysis of CSPOC-GFLR technique with existing techniques takes place in Fig. 6. The figure reported that the existing ATEER technique has attained lowest throughput under varying simulation time. Moreover, the OQoS-CMRP technique has obtained slightly increased throughput over the ATEER technique, but not than FUCHAR and CSPOC-GFLR techniques. Though the FUCHAR technique has accomplished reasonable throughput, the CSPOC-GFLR technique shows promising results by demonstrating maximum throughput. For instance, the CSPOC-GFLR technique has achieved a higher throughput of 56.36 kbps,61.96 kbps, 64.59 kbps, 70.27 kbps, and 72.43 kbps under varying simulation time of 200–1000 s.

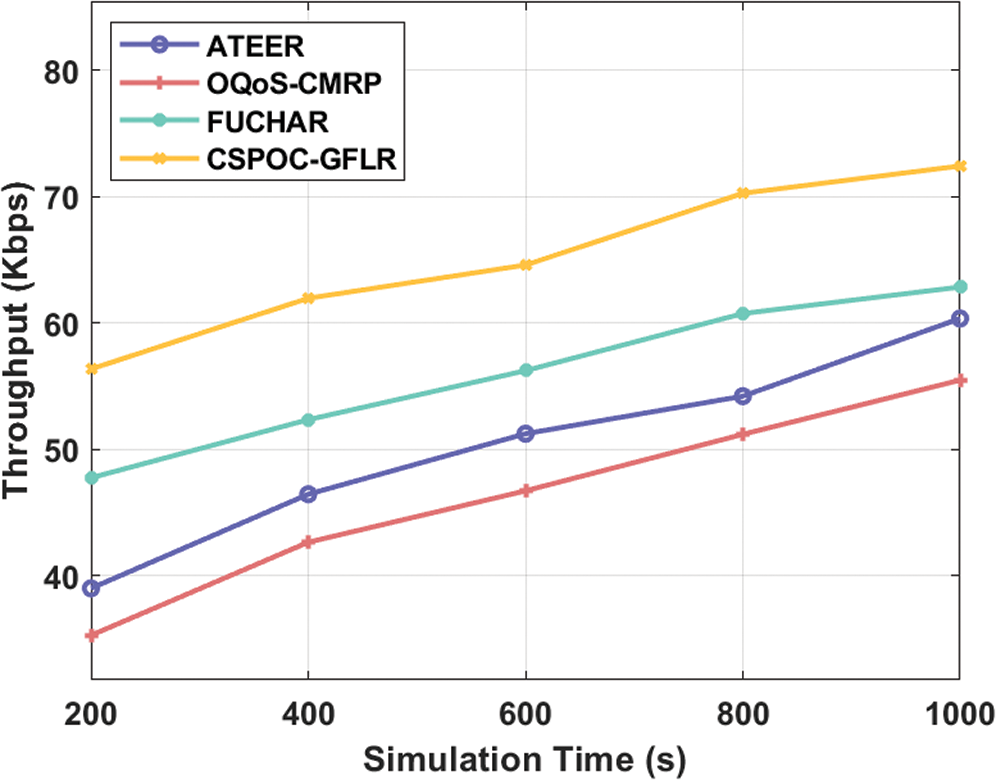
Figure 6: Throughput analysis of CSPOC-GFLR model

Tab. 2 examines the NOH and ETE delay analysis of the CSPOC-GFLR technique under varying nodes and simulation time. A comprehensive NOH analysis of the CSPOC-GFLR technique with existing techniques takes place in Fig. 7. The figure portrayed that the ATEER technique has exhibited least outcome and offered highest NOH compared to other methods. Eventually, the OQoS-CMRP technique has depicted somewhat reduced NOH over the ATEER technique. Concurrently, the FUCHAR technique has displayed reasonable performance with the considerably minimal NOH. But, the CSPOC-GFLR technique has outperformed the other methods by offering the least NOH over the existing methods. For instance, the CSPOC-GFLR technique requires the least NOH of 1.97, 2.56, 3.14, 4.79, and 3.51 under varying number of 100–500 nodes.

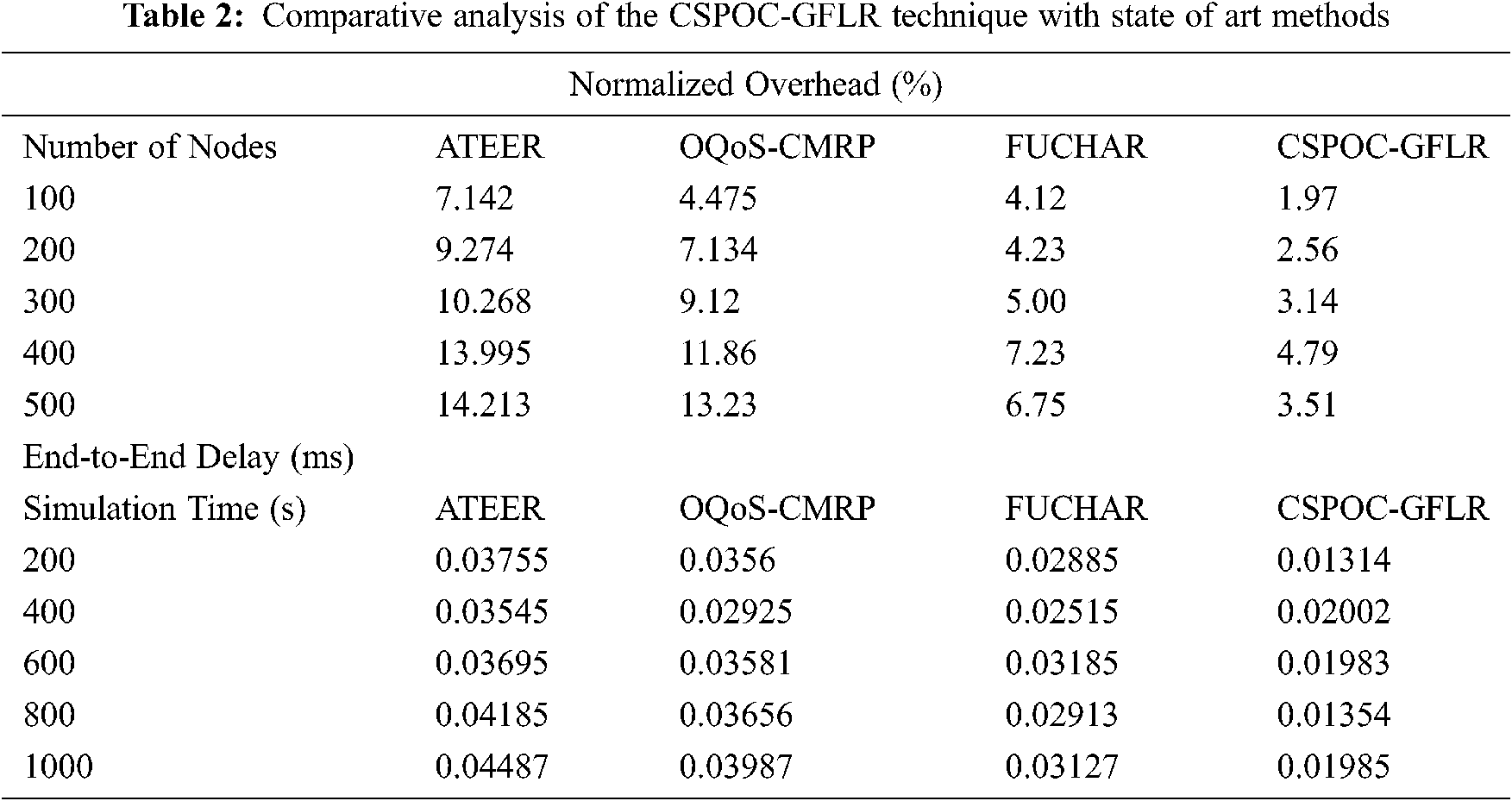
Figure 7: Normalized overhead analysis of CSPOC-GFLR model

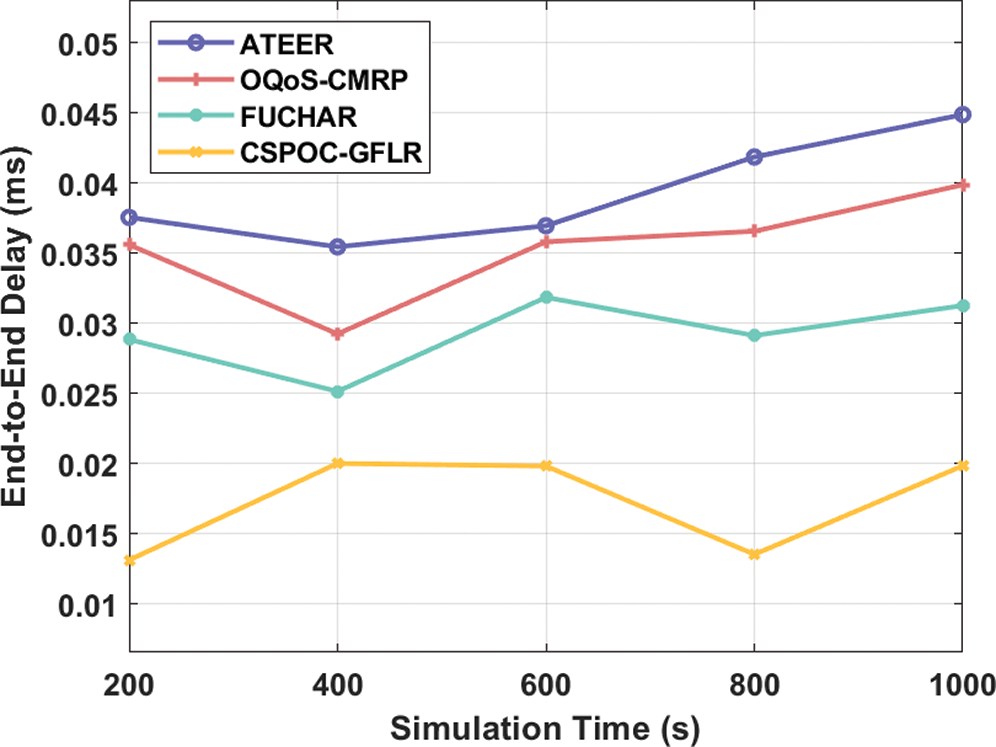
Figure 8: ETE delay analysis of CSPOC-GFLR model

Finally, a complete ETE delay analysis of CSPOC-GFLR technique is investigated in Fig. 8. From the figure, it is noticed that the ATEER technique has resulted in a maximum ETE delay under different simulation times. Meanwhile, the OQoS-CMRP technique has gained somewhat decreased ETE delay over the ATEER technique except for FUCHAR and CSPOC-GFLR techniques. Though the FUCHAR technique has resulted to considerably lower throughput, the CSPOC-GFLR technique achieves significant performance with the least ETE delay under varying simulation times. For instance, the CSPOC-GFLR technique has achieved the lowest ETE delay of 0.01314 ms, 0.02002 ms, 0.01983 ms, 0.01354 ms, and 0.01985 ms under varying simulation time of 200–1000 s. The experimental results stated that the proposed model outperformed the existing techniques due to the following reasons: CSPOC based clustering and GFLR based routing process. Besides, the CSPOC algorithm is derived by incorporating the concepts of chaos theory to boost the global optimization capability of the SPOC algorithm.

6  Conclusion

This study has developed a novel CSPOC-GFLR technique to construct clusters and choose optimal set of routes with an intention of achieving energy efficiency and maximizing network lifetime. The CSPOC-GFLR technique involves two major phases namely CSPOC based clustering and GFLR based routing process. The CSPOC algorithm is derived by incorporating the concepts of chaos theory to boost the global optimization capability of the SPOC algorithm. A comprehensive set of simulations take place to exhibit the significant performance of the CSPOC-GFLR technique interms of different measures. The experimental outcomes portrayed the promising performance of the CSPOC-GFLR technique by achieving reduced energy utilization, improved lifetime, and prolonged stability over the existing techniques. As a part of future work, the CPSOC-GFLR technique can be deployed in a real time physical environment. Besides, data aggregation and scheduling techniques can be introduced to boost the overall network performance.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Jorio, S. El Fkihi, B. Elbhiri and D. Aboutajdine, “An energy-efficient clustering routing algorithm based on geographic position and residual energy for wireless sensor network,” Journal of Computer Networks and Communications, vol. 2015, no. 8, pp. 1–11, 2015. [Google Scholar]

 2.  I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “A survey on sensor networks,” IEEE Communications Magazine, vol. 40, no. 8, pp. 102–114, 2002. [Google Scholar]

 3.  J. Uthayakumar, T. Vengattaraman and P. Dhavachelvan, “A new lossless neighborhood indexing sequence (NIS) algorithm for data compression in wireless sensor networks,” Ad Hoc Networks, vol. 83, no. 2009, pp. 149–157, 2019. [Google Scholar]

 4.  J. Uthayakumar, T. Vengattaraman and J. Amudhavel, “Data compression algorithm to maximize network lifetime in wireless sensor networks,” Journal of Advanced Research in Dynamical and Control Systems, vol. 12, pp. 2156–2167, 2017. [Google Scholar]

 5.  A. Rodríguez, C. Del-Valle-Soto and R. Velázquez, “Energy-efficient clustering routing protocol for wireless sensor networks based on yellow saddle goatfish algorithm,” Mathematics, vol. 8, no. 9, pp. 1515, 2020. [Google Scholar]

 6.  M. Elhoseny, R. S. Rajan, M. Hammoudeh, K. Shankar and O. Aldabbas, “Swarm intelligence-based energy efficient clustering with multihop routing protocol for sustainable wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 16, no. 9, pp. 1–12, 2020. [Google Scholar]

 7.  G. Kadiravan, A. Sariga and P. Sujatha, “A novel energy efficient clustering technique for mobile wireless sensor networks,” in 2019 IEEE Int. Conf. on System, Computation, Automation and Networking (ICSCANPondicherry, India, pp. 1–6, 2019. [Google Scholar]

 8.  S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

 9.  Y. Liang and Y. Li, “An efficient and robust data compression algorithm in wireless sensor networks,” IEEE Communication Letters, vol. 18, no. 3, pp. 439–442, 2014. [Google Scholar]

10. S. K. Gupta and P. K. Jana, “Energy efficient clustering and routing algorithms for wireless sensor networks: GA based approach,” Wireless Personal Communications, vol. 83, no. 3, pp. 2403–2423, 2015. [Google Scholar]

11. T. Shankar, S. Shanmugavel and A. Rajesh, “Hybrid HSA and PSO algorithm for energy efficient cluster head selection in wireless sensor networks,” Swarm and Evolutionary Computation, vol. 30, no. 4, pp. 1–10, 2016. [Google Scholar]

12. M. O. Oladimeji, M. Turkey and S. Dudley, “HACH: Heuristic algorithm for clustering hierarchy protocol in wireless sensor networks,” Applied Soft Computing, vol. 55, no. 6, pp. 452–461, 2017. [Google Scholar]

13. P. S. Mann and S. Singh, “Improved artificial bee colony metaheuristic for energy-efficient clustering in wireless sensor networks,” Artificial Intelligence Review, vol. 51, no. 3, pp. 329–354, 2019. [Google Scholar]

14. U. E. Zachariah and L. Kuppusamy, “A hybrid approach to energy efficient clustering and routing in wireless sensor networks,” Evolutionary Intelligence, pp. 1–13, 2021. https://doi.org/10.1007/s12065-020-00535-0. [Google Scholar]

15. A. K. Idrees and W. L. A. Yaseen, “Distributed genetic algorithm for lifetime coverage optimisation in wireless sensor networks,” International Journal of Advanced Intelligence Paradigms, vol. 18, no. 1, pp. 3, 2021. [Google Scholar]

16. S. Bhushan, M. Kumar, P. Kumar, T. Stephan, A. Shankar et al., “FAJIT: A fuzzy-based data aggregation technique for energy efficiency in wireless sensor network,” Complex & Intelligent Systems, vol. 7, no. 2, pp. 997–1007, 2021. [Google Scholar]

17. F. Zhu and J. Wei, “An energy-efficient unequal clustering routing protocol for wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 15, no. 9, pp. 1–15, 2019. [Google Scholar]

18. S. Soro and W. B. Heinzelman, “Prolonging the lifetime of wireless sensor networks via prolonging the lifetime of wireless sensor networks via,” in 19th IEEE Int. Parallel and Distributed Processing Sym., Denver, CO, USA, pp. 236b, 2005. [Google Scholar]

19. M. S. Maharajan, T. Abirami, I. V. Pustokhina, D. A. Pustokhin and K. Shankar, “Hybrid swarm intelligence based QoS aware clustering with routing protocol for WSN,” Computers Materials & Continua, vol. 68, no. 3, pp. 2995–3013, 2021. [Google Scholar]

20. G. Kadiravan, P. Sujatha, T. Asvany, R. Punithavathi, M. Elhoseny et al., “Metaheuristic clustering protocol for healthcare data collection in mobile wireless multimedia sensor networks,” Computers Materials & Continua, vol. 66, no. 3, pp. 3215–3231, 2021. [Google Scholar]

21. T. Vaiyapuri, V. S. Parvathy, V. Manikandan, N. Krishnaraj, D. Gupta et al., “A novel hybrid optimization for cluster-based routing protocol in information-centric wireless sensor networks for IOT based mobile edge computing,” Wireless Personal Communications, vol. 49, pp. 145, 2021. [Google Scholar]

22. G. N. Nguyen, N. H. Le Viet, A. F. S. Devaraj, R. Gobi and K. Shankar, “Blockchain enabled energy efficient red deer algorithm based clustering protocol for pervasive wireless sensor networks,” Sustainable Computing: Informatics and Systems, vol. 28, pp. 100464, 2020. [Google Scholar]

23. A. Kaur, S. Jain and S. Goel, “Sandpiper optimization algorithm: A novel approach for solving real-life engineering problems,” Applied Intelligence, vol. 50, no. 2, pp. 582–619, 2020. [Google Scholar]

24. O. S. Qasim, N. A. Al-Thanoon and Z. Y. Algamal, “Feature selection based on chaotic binary black hole algorithm for data classification,” Chemometrics and Intelligent Laboratory Systems, vol. 204, pp. 104104, 2020. [Google Scholar]

25. D. C. Secui, C. Hora, G. Bendea and C. Bendea, “Parameter estimation using a modified whale optimization algorithm for input-output curves of thermal and hydro power plants,” International Transactions on Electrical Energy Systems, vol. 30, no. 2, pp. 191, 2020. [Google Scholar]

26. O. Deepa and J. Suguna, “An optimized QoS-based clustering with multipath routing protocol for Wireless Sensor Networks,” Journal of King Saud University—Computer and Information Sciences, vol. 32, no. 7, pp. 763–774, 2020. [Google Scholar]

27. S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.